Implementation of Pruned Backpropagation Neural Network Based on Photonic Integrated Circuits
Abstract
:1. Introduction
2. Materials and Methods
2.1. Backpropagation Neural Network
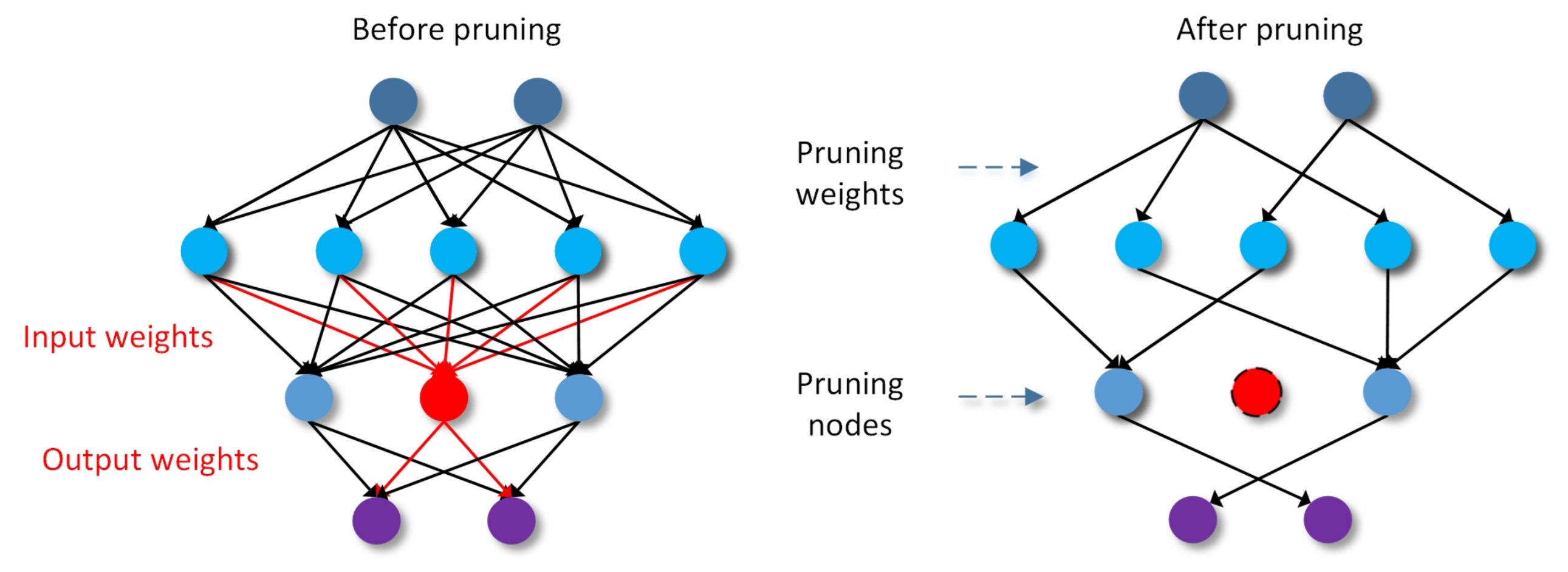
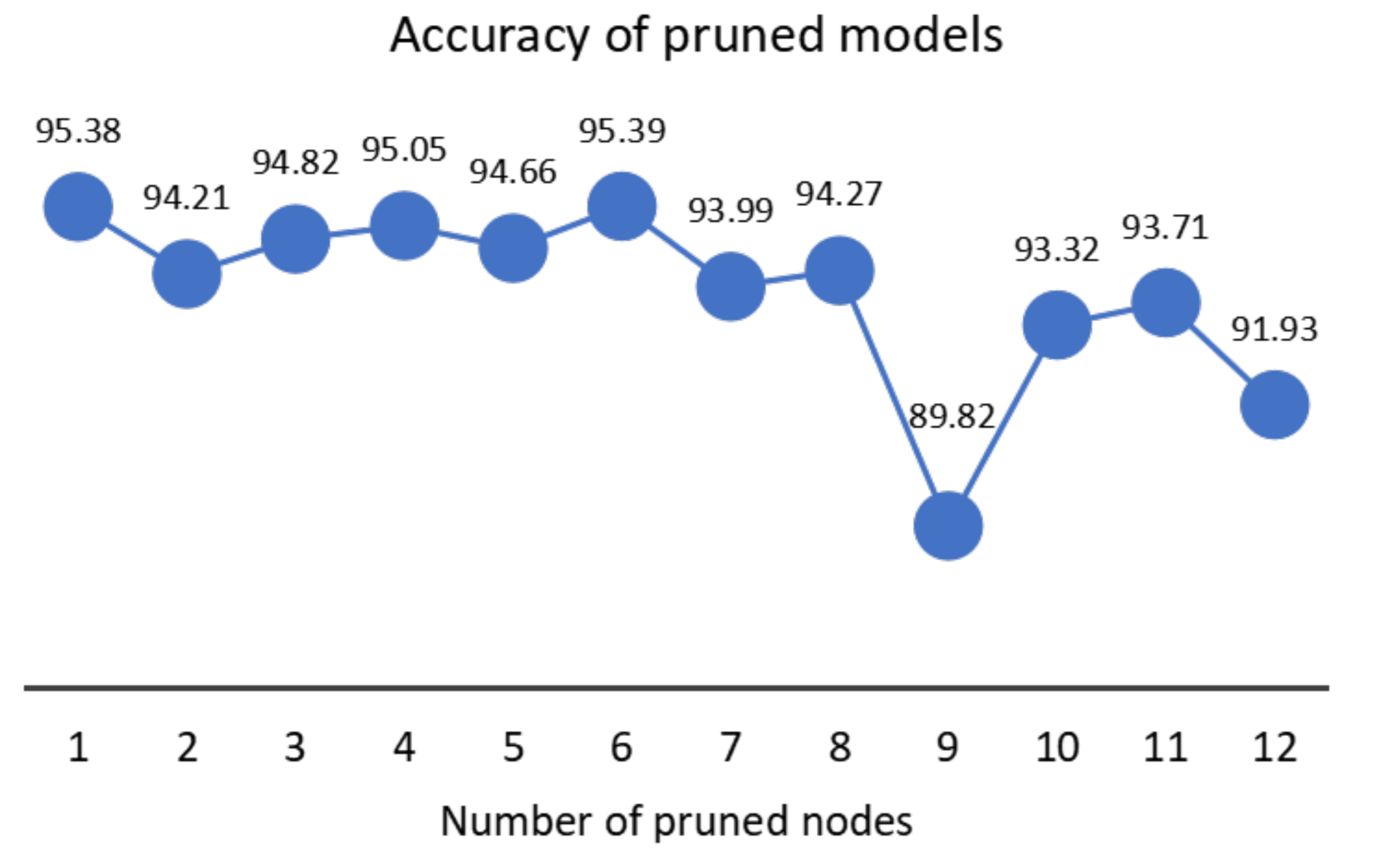
2.2. Network Pruning
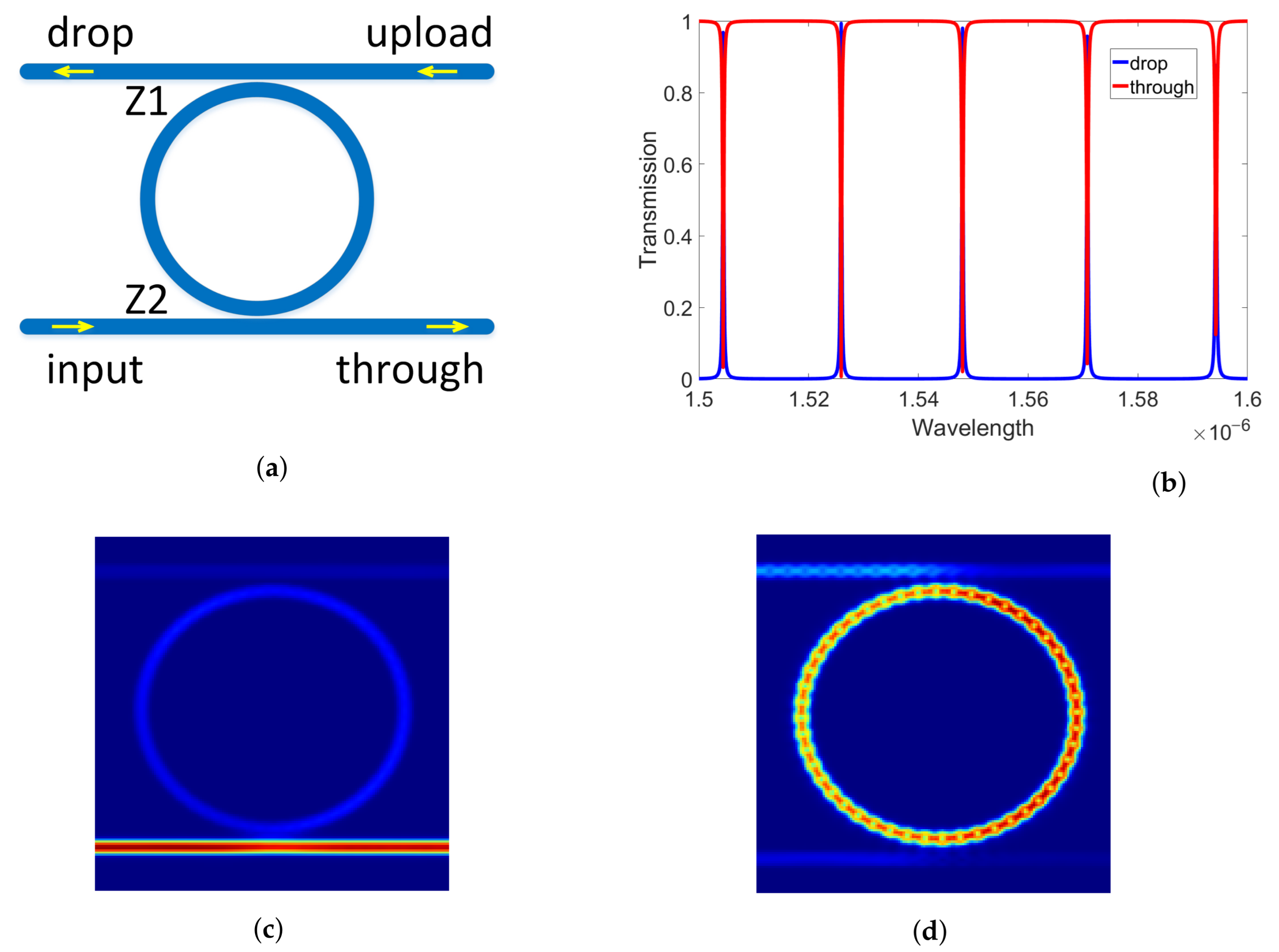
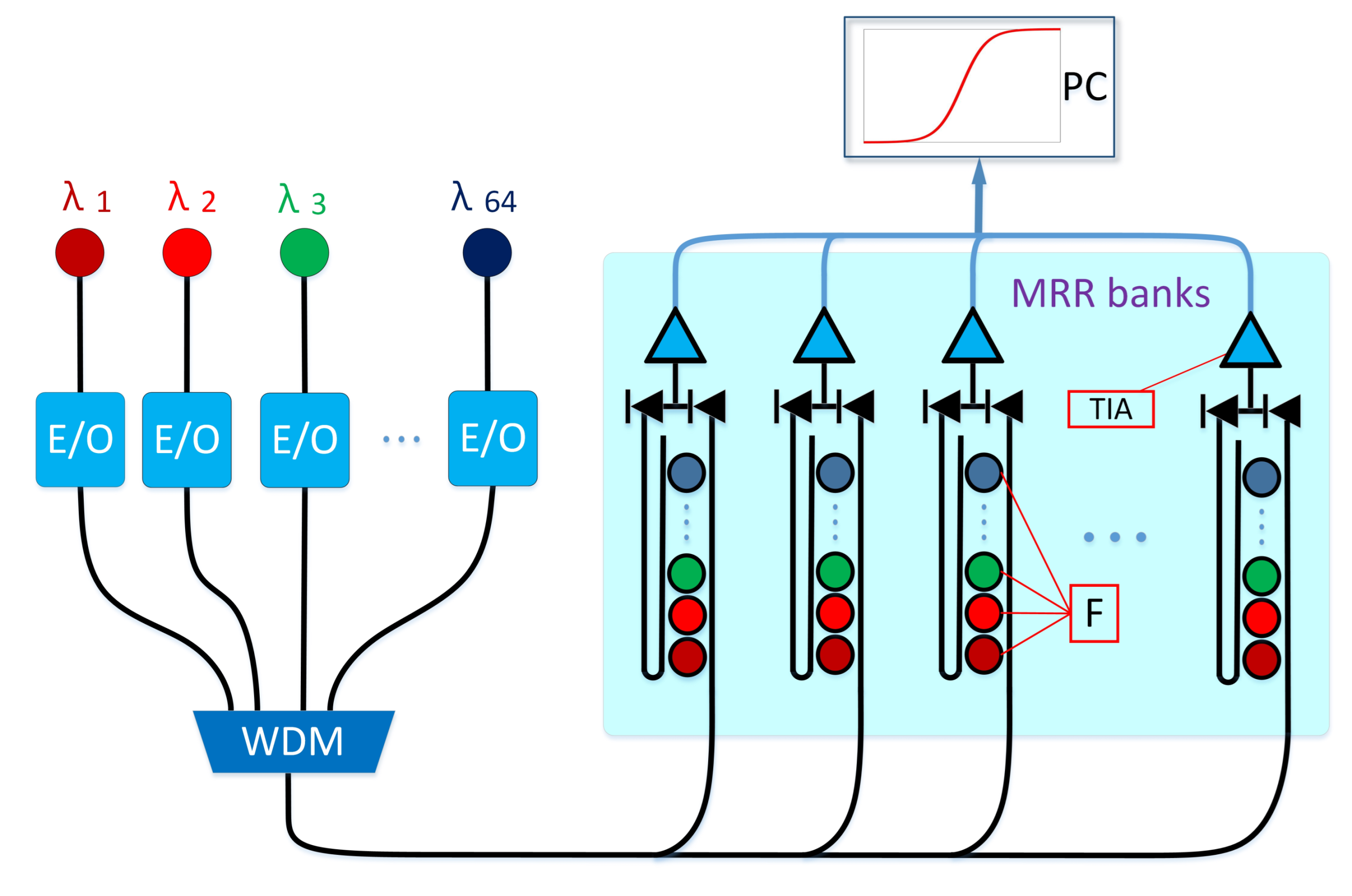
2.3. Optical Components and Silicon Photonic Architecture
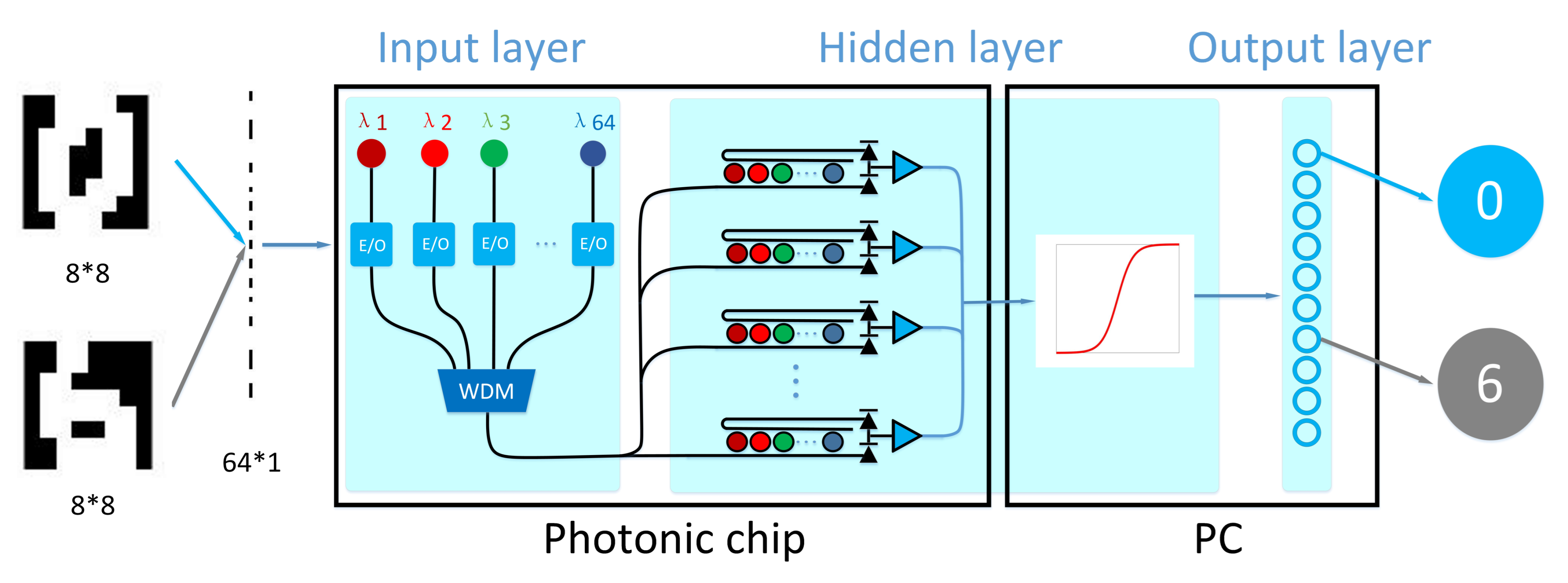
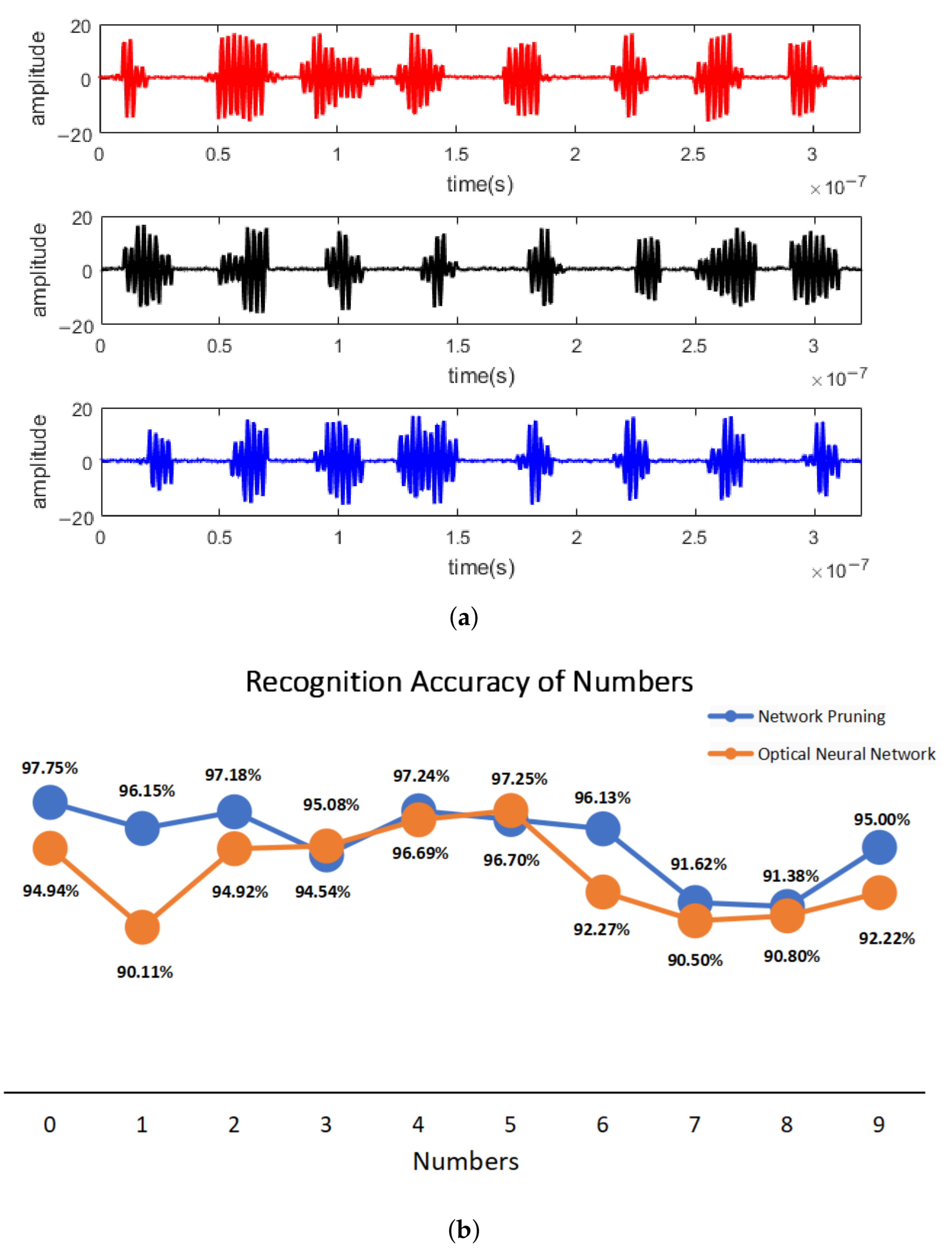
2.4. Photonic Pruning Neural Network
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sallab, A.E.; Abdou, M.; Perot, E.; Yogamani, S. Deep reinforcement learning framework for autonomous driving. Electron. Imaging 2017, 2017, 70–76. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; Srivastava, S. Stock prediction using deep learning. Multimed. Tools Appl. 2017, 76, 18569–18584. [Google Scholar] [CrossRef]
- Zhang, J.; Zong, C. Deep Neural Networks in Machine Translation: An Overview. IEEE Intell. Syst. 2015, 30, 16–25. [Google Scholar] [CrossRef]
- Lu, C.; Tang, X. Surpassing human-level face verification performance on LFW with GaussianFace. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Rahim, A.; Spuesens, T.; Baets, R.; Bogaerts, W. Open-Access Silicon Photonics: Current Status and Emerging Initiatives. Proc. IEEE 2018, 106, 2313–2330. [Google Scholar] [CrossRef] [Green Version]
- Soref, R.A.; Bennett, B.R. Electrooptical effects in silicon. IEEE J. Quantum Electron. 1987, 23, 123–129. [Google Scholar] [CrossRef] [Green Version]
- Cardenas, J.; Poitras, C.B.; Robinson, J.T.; Preston, K.; Chen, L.; Lipson, M. Low loss etchless silicon photonic waveguides. Opt. Express 2009, 17, 4752–47577. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, R.; Li, X.; Li, T. Development trends in silicon photonics for data centers. Opt. Fiber Technol. 2018, 44, 13–23. [Google Scholar] [CrossRef]
- Tamura, P.N.; Wyant, J.C. Two-Dimensional Matrix Multiplication using Coherent Optical Techniques. Opt. Eng. 1979, 18, 182198. [Google Scholar] [CrossRef]
- Xiang, S.; Han, Y.; Song, Z.; Guo, X.; Zhang, Y.; Ren, Z.; Wang, S.; Ma, Y.; Zou, W.; Ma, B.; et al. A review: Photonics devices, architectures, and algorithms for optical neural computing. J. Semicond. 2021, 42, 023105. [Google Scholar] [CrossRef]
- Shen, Y.; Harris, N.C.; Skirlo, S.; Englund, D.; Soljacic, M. Deep learning with coherent nanophotonic circuits. Nat. Photon 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Tait, A.N.; Lima, T.; Zhou, E.; Wu, A.X.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 2017, 7, 7430. [Google Scholar] [CrossRef]
- Feldmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef]
- Xiang, S.; Ren, Z.; Song, Z.; Zhang, Y.; Hao, Y. Computing Primitive of Fully VCSEL-Based All-Optical Spiking Neural Network for Supervised Learning and Pattern Classification. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2494–2505. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.W.; Momchil, M.; Yu, S.; Fan, S. Training of photonic neural networks through in situ backpropagation. Optica 2018, 5, 864–871. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, L.; Ji, R. On-chip optical matrix-vector multiplier. Proc. SPIE Int. Soc. Opt. Eng. 2013, 8855, 88550F. [Google Scholar] [CrossRef]
- Tait, A.N.; Wu, A.X.; Lima, T.; Zhou, E.; Prucnal, P.R. Microring Weight Banks. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 1–14. [Google Scholar] [CrossRef]
- Bangari, V.; Marquez, B.A.; Miller, H.; Tait, A.N.; Nahmias, M.A. Digital Electronics and Analog Photonics for Convolutional Neural Networks (DEAP-CNNs). IEEE J. Sel. Top. Quantum Electron. 2020, 26, 7701213. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, J.; Sitzmann, V.; Dun, X.; Heidrich, W.; Wetzstein, G. Hybrid optical-electronic convolutional neural networks with optimized diffractive optics for image classification. Nature 2018, 8, 12324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qian, C.; Lin, X.; Lin, X.; Xu, J.; Chen, H. Performing optical logic operations by a diffractive neural network. Light. Sci. Appl. 2020, 9, 59. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Y.; Li, B.; Zhao, Y.; Jiang, Y.; Chen, Y.C.; Chen, P.; Jo, G.B.; Liu, J.; Du, S. All Optical Neural Network with Nonlinear Activation Functions. Optica 2019, 6, 1132–1137. [Google Scholar] [CrossRef]
- Hamerly, R.; Bernstein, L.; Sludds, A.; Soljai, M.; Englund, D. Large-Scale Optical Neural Networks Based on Photoelectric Multiplication. Phys. Rev. X 2019, 9, 021032. [Google Scholar] [CrossRef] [Green Version]
- Shi, B.; Calabretta, N.; Stabile, R. Deep Neural Network Through an InP SOA-Based Photonic Integrated Cross-Connect. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–11. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Wang, R.; Chen, J.; Zou, W. High-accuracy optical convolution unit architecture for convolutional neural networks by cascaded acousto-optical modulator arrays. Opt. Express 2019, 27, 19778–19787. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Zou, W. Optical Convolutional Neural Network with WDM-Based Optical Patching and Microring Weighting Banks. IEEE Photonics Technol. Lett. 2021, 33, 89–92. [Google Scholar] [CrossRef]
- Wetzstein, G.; Ozcan, A.; Gigan, S.; Fan, S.; Englund, D.; Soljacic, M.; Denz, C.; Miller, D.A.B.; Psaltis, D. Inference in artificial intelligence with deep optics and photonics. Nature 2020, 558, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Bilodeau, S.; Lima, T.; Tait, A.N.; Prucnal, P.R. Demonstration of scalable microring weight bank control for large-scale photonic integrated circuits. APL Photonics 2020, 5, 040803. [Google Scholar] [CrossRef]
- LeCun, Y.; Denker, J.; Solla, S. Optimal brain damage. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 1990; pp. 598–605. [Google Scholar] [CrossRef]
- Hecht-Nielsen. Theory of the backpropagation neural network. Neural Netw. 1988, 1, 445. [Google Scholar] [CrossRef]
- Zhu, M.; Gupta, S. To prune, or not to prune: Exploring the efficacy of pruning for model compression. arXiv 2017, arXiv:1710.01878. [Google Scholar]
- Weigend, A.S.; Rumelhart, D.E. Weight elimination and effective network size. Proceedings of a Workshop on Computational Learning Theory and Natural Learning Systems; ACM: New York, NY, USA, 1994; Volume 1, pp. 457–476. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Jayatilleka, H.; Murray, K.; Caverley, M.; Jaeger, N.; Chrostowski, L.; Shekhar, S. Crosstalk in SOI Microring Resonator-Based Filters. J. Light. Technol. 2016, 34, 2886–2896. [Google Scholar] [CrossRef]
- Zhu, S.; Liow, T.Y.; Lo, G.Q.; Kwong, D.L. Fully complementary metal-oxide-semiconductor compatible nanoplasmonic slot waveguides for silicon electronic photonic integrated circuits. Appl. Phys. Lett. 2011, 98, 83. [Google Scholar] [CrossRef]
- Baehr-Jones, T.; Ding, R.; Ayazi, A.; Pinguet, T.; Streshinsky, M.; Harris, N.; Li, J.; He, L.; Gould, M.; Zhang, Y.; et al. A 25 Gb/s Silicon Photonics Platform. arXiv 2012, arXiv:1203.0767v1. [Google Scholar]
- Jayatilleka, H.; Murray, K.; Guillén-Torres, M.; Caverley, M.; Hu, R.; Jaeger, N.; Chrostowski, L.; Shekhar, S. Wavelength tuning and stabilization of microring-based filters using silicon in-resonator photoconductive heaters. Opt. Express 2015, 23, 25084–25097. [Google Scholar] [CrossRef]
- Ohno, S.; Toprasertpong, K.; Takagi, S.; Takenaka, M. Si microring resonator crossbar array for on-chip inference and training of optical neural network. arXiv 2021, arXiv:2106.04351v2. [Google Scholar]
- Williamson, I.A.D.; Hughes, T.W.; Minkov, M.; Bartlett, B.; Pai, S.; Fan, S. Reprogrammable Electro-Optic Nonlinear Activation Functions for Optical Neural Networks. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 7700412. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Barrett, T.D.; Wang, Z.M.; Lvovsky, A.I. Backpropagation through nonlinear units for the all-optical training of neural networks. Photonics Res. 2021, 9, 71–80. [Google Scholar] [CrossRef]
- Steinbrecher, G.R.; Olson, J.P.; Englund, D.; Carolan, J. Quantum optical neural networks. NPJ Quantum Inf. 2019, 5, 60. [Google Scholar] [CrossRef] [Green Version]
- Qiang, X.; Wang, Y.; Xue, S.; Ge, R.; Wu, J. Implementing graph-theoretic quantum algorithms on a silicon photonic quantum walk processor. Sci. Adv. 2021, 7, eabb8375. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Xing, Z.; Huang, D. Implementation of Pruned Backpropagation Neural Network Based on Photonic Integrated Circuits. Photonics 2021, 8, 363. https://doi.org/10.3390/photonics8090363
Zhang Q, Xing Z, Huang D. Implementation of Pruned Backpropagation Neural Network Based on Photonic Integrated Circuits. Photonics. 2021; 8(9):363. https://doi.org/10.3390/photonics8090363
Chicago/Turabian StyleZhang, Qi, Zhuangzhuang Xing, and Duan Huang. 2021. "Implementation of Pruned Backpropagation Neural Network Based on Photonic Integrated Circuits" Photonics 8, no. 9: 363. https://doi.org/10.3390/photonics8090363
APA StyleZhang, Q., Xing, Z., & Huang, D. (2021). Implementation of Pruned Backpropagation Neural Network Based on Photonic Integrated Circuits. Photonics, 8(9), 363. https://doi.org/10.3390/photonics8090363




