Optical See-through 2D/3D Compatible Display Using Variable-Focus Lens and Multiplexed Holographic Optical Elements
Abstract
:1. Introduction
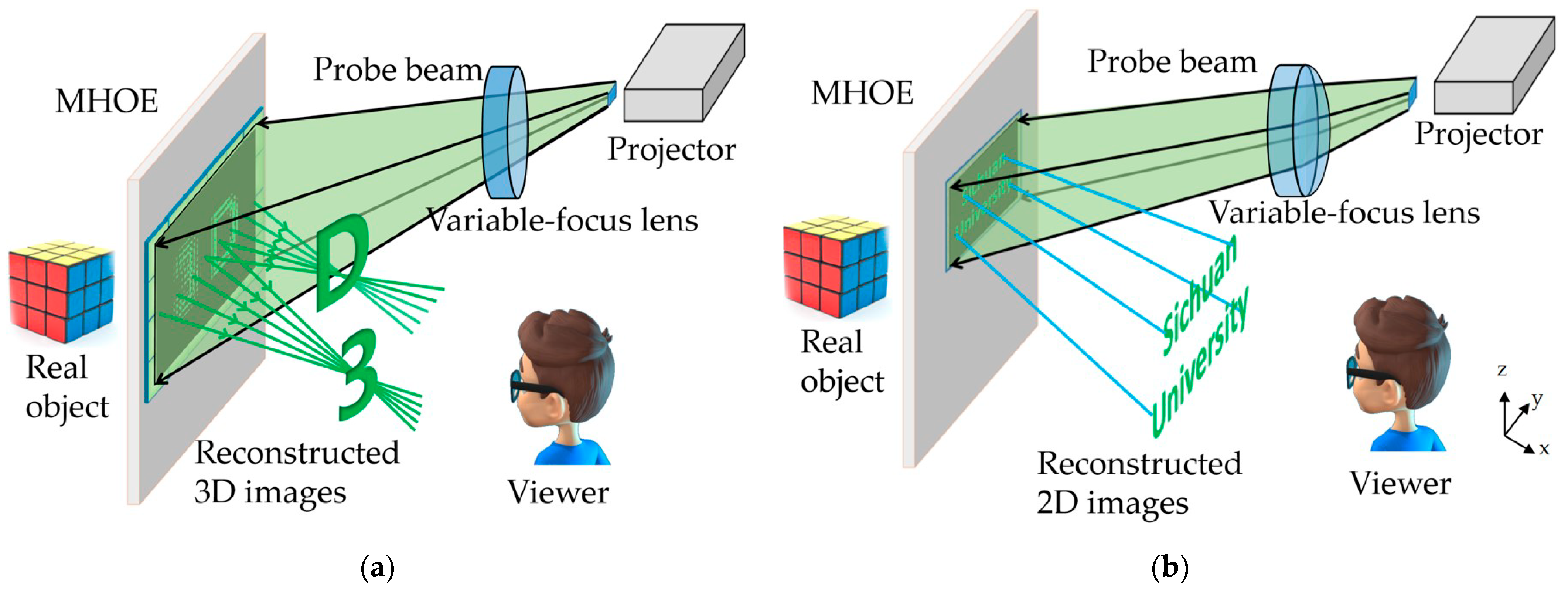
2. Structure and Principle
3. Experiments and Results
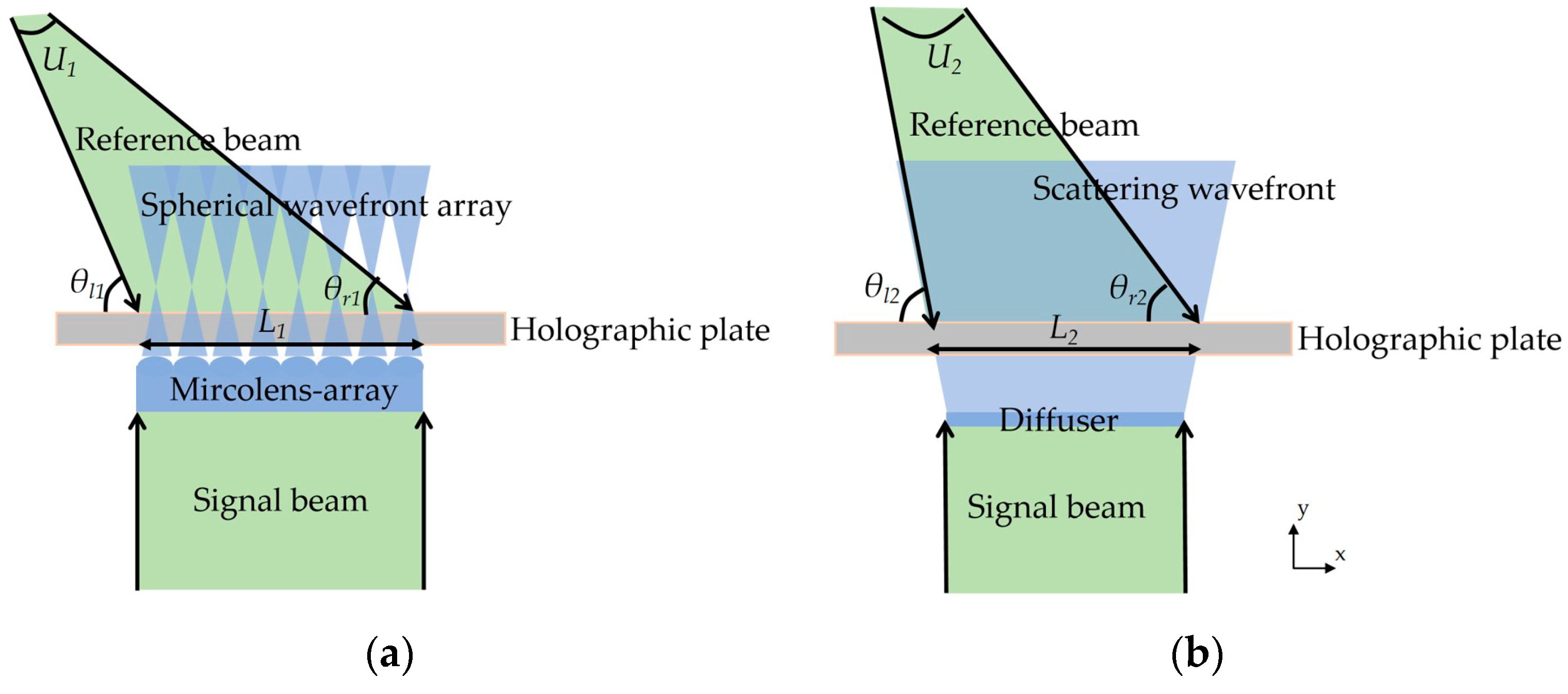
3.1. Fabrication of Variable-Focus Liquid Lens and MHOE
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, F.; Duh, H.B.L.; Billinghurst, M. Trends in augmented reality tracking, interaction and display: A review of ten years of ISMAR. In Proceedings of the 7th IEEE/ACM International Symposium on Mixed and Augmented Reality, Washington, DC, USA, 15–18 September 2018; pp. 193–202. [Google Scholar]
- Lee, Y.H.; Zhan, T.; Wu, S.T. Prospects and challenges in augmented reality displays. Virtual Real. Intell. Hardw. 2019, 1, 10–20. [Google Scholar] [CrossRef]
- Murdoch, M.J. Brightness matching in optical see-through augmented reality. J. Opt. Soc. Am. A 2020, 37, 1927–1936. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.L.; Wang, P.; Sang, X.Z.; Li, C.Y. Augmented reality three-dimensional display with light field fusion. Opt. Express 2016, 24, 11483–11494. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Li, Q.; He, W.; Li, X.W.; Ren, H.; Chen, C. 2D/3D mixed frontal projection system based on integral imaging. Opt. Express 2020, 28, 26385–26394. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; He, W.; Deng, H.; Zhong, F.Y.; Chen, Y. High-performance reflection-type augmented reality 3D display using a reflective polarizer. Opt. Express. 2021, 29, 9446–9453. [Google Scholar] [CrossRef]
- Martínez-Corral, M.; Javidi, B. Fundamentals of 3D imaging and displays: A tutorial on integral imaging, light-field, and plenoptic systems. Adv. Opt. Photonics 2018, 10, 512–566. [Google Scholar] [CrossRef] [Green Version]
- Javidi, B.; Moon, I.; Yeom, S. Three-dimensional identification of biological microorganism using integral imaging. Opt. Express 2006, 14, 12096–12108. [Google Scholar] [CrossRef]
- Hong, J.; Min, S.W.; Lee, B. Integral floating display systems for augmented reality. Appl. Opt. 2012, 51, 4201–4209. [Google Scholar] [CrossRef]
- Shen, X.; Javidi, B. Large depth of focus dynamic micro integral imaging for optical see-through augmented reality display using a focus-tunable lens. Appl. Opt. 2018, 57, B184–B189. [Google Scholar] [CrossRef]
- Deng, H.; Xiong, Z.L.; Xing, Y.; Zhang, H.L.; Wang, Q.H. A high optical efficiency 3D/2D convertible integral imaging display. J. Soc. Inf. Disp. 2016, 24, 85–89. [Google Scholar] [CrossRef]
- Choi, H.; Cho, S.W.; Kim, J.; Lee, B. A thin 3D-2D convertible integral imaging system using a pinhole array on a polarizer. Opt. Express 2006, 14, 5183–5190. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Xing, Y.; Zhang, H.L.; Li, Q.; Wang, L.; Deng, H.; Wang, Q.H. 2D/3D mixed display based on integral imaging and a switchable diffuser element. Appl. Opt. 2019, 58, G276–G281. [Google Scholar] [CrossRef]
- Zhang, Y.A.; Jin, T.; He, L.C.; Chu, Z.H.; Guo, T.L.; Zhou, X.T.; Lin, Z.X. Controllable liquid crystal gratings for an adaptive 2D/3D auto-stereoscopic display. Opt. Commun. 2017, 384, 16–24. [Google Scholar] [CrossRef]
- Hua, H.; Javidi, B. A 3D integral imaging optical see-through head-mounted display. Opt. Express 2014, 22, 13484–13491. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Hua, H. High-performance integral-imaging-based light field augmented reality display using freeform optics. Opt. Express 2018, 26, 17578–17590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, H.; Chen, C.; He, M.Y.; Li, J.J.; Zhang, H.L.; Wang, Q.H. High-resolution augmented reality 3D display with use of a lenticular lens array holographic optical element. J. Opt. Soc. Am. A 2019, 36, 588–593. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.B.; Park, J.H. Optical see-through Maxwellian near-to-eye display with an enlarged eyebox. Opt. Lett. 2018, 43, 767–770. [Google Scholar] [CrossRef] [PubMed]
- Jang, C.; Lee, C.K.; Jeong, J.; Li, G.; Lee, S.; Yeom, J.; Hong, K.; Lee, B. Recent progress in see-through three-dimensional displays using holographic optical elements. Appl. Opt. 2016, 55, A71–A85. [Google Scholar] [CrossRef] [PubMed]
- Yeom, J.; Jeong, J.; Jang, C.; Li, G.; Hong, K.; Lee, B. Three-dimensional/two-dimensional convertible projection screen using see-through integral imaging based on holographic optical element. Appl. Opt. 2015, 54, 8856–8862. [Google Scholar] [CrossRef]
- Chou, P.Y.; Wu, J.Y.; Huang, S.H.; Wang, C.P.; Qin, Z.; Huang, C.T.; Hsieh, P.Y.; Lee, H.H.; Lin, T.H.; Huang, Y.P. Hybrid light field head-mounted display using time-multiplexed liquid crystal lens array for resolution enhancement. Opt. Express 2019, 27, 1164–1177. [Google Scholar] [CrossRef]
- Zhang, H.L.; Deng, H.; Li, J.J.; He, M.Y.; Li, D.H.; Wang, Q.H. Integral imaging-based 2D/3D convertible display system by using holographic optical element and polymer dispersed liquid crystal. Opt. Lett. 2019, 44, 387–390. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Fox, D.; Andrew Anderson, P.; Wu, B.; Wu, S.T. Tunable-focus liquid lens controlled using a servo motor. Opt. Express 2006, 14, 8031–8136. [Google Scholar] [CrossRef] [PubMed]






| Components | Parameters | Values | |
|---|---|---|---|
| Bragg diffraction conditions | Bragg matching angles 1 | θl1 | 57.2° |
| θr1 | 32.8° | ||
| Bragg matching angles 2 | θl2 | 45° | |
| θr2 | 45° | ||
| Recording region | Width L1 | 23 mm | |
| Width L2 | 18 mm | ||
| MLA | Pitch | 1 mm | |
| Focal length | 3.3 mm | ||
| Diffuser | Scattering angle | 20° | |
| Photopolymer plate | Thickness | 15 ± 1 µm | |
| Sensitive wavelength | 532 nm | ||
| Sensitivity | 10 mJ/cm² | ||
| Averaged refractive index | 1.47 | ||
| Refractive index modulation | >0.02 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Q.; Deng, H.; Zhang, H.; Jiang, W.; Zhong, F.; Rao, F. Optical See-through 2D/3D Compatible Display Using Variable-Focus Lens and Multiplexed Holographic Optical Elements. Photonics 2021, 8, 297. https://doi.org/10.3390/photonics8080297
Ji Q, Deng H, Zhang H, Jiang W, Zhong F, Rao F. Optical See-through 2D/3D Compatible Display Using Variable-Focus Lens and Multiplexed Holographic Optical Elements. Photonics. 2021; 8(8):297. https://doi.org/10.3390/photonics8080297
Chicago/Turabian StyleJi, Qinglin, Huan Deng, Hanle Zhang, Wenhao Jiang, Feiyan Zhong, and Fengbin Rao. 2021. "Optical See-through 2D/3D Compatible Display Using Variable-Focus Lens and Multiplexed Holographic Optical Elements" Photonics 8, no. 8: 297. https://doi.org/10.3390/photonics8080297
APA StyleJi, Q., Deng, H., Zhang, H., Jiang, W., Zhong, F., & Rao, F. (2021). Optical See-through 2D/3D Compatible Display Using Variable-Focus Lens and Multiplexed Holographic Optical Elements. Photonics, 8(8), 297. https://doi.org/10.3390/photonics8080297





