Absolute Absorption Cross-Section of the Ã←
Abstract
:1. Introduction
2. Materials and Methods
3. Results
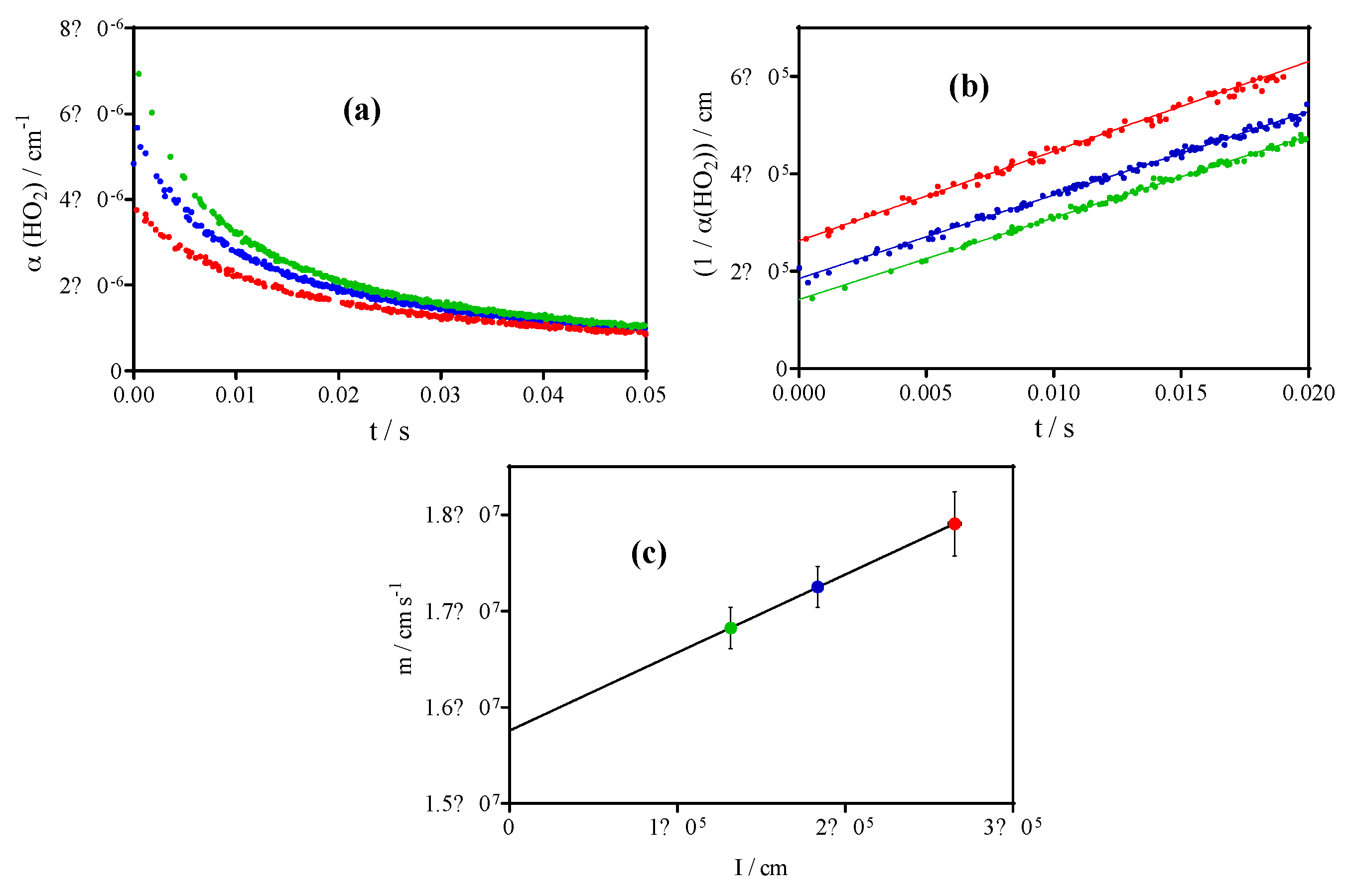
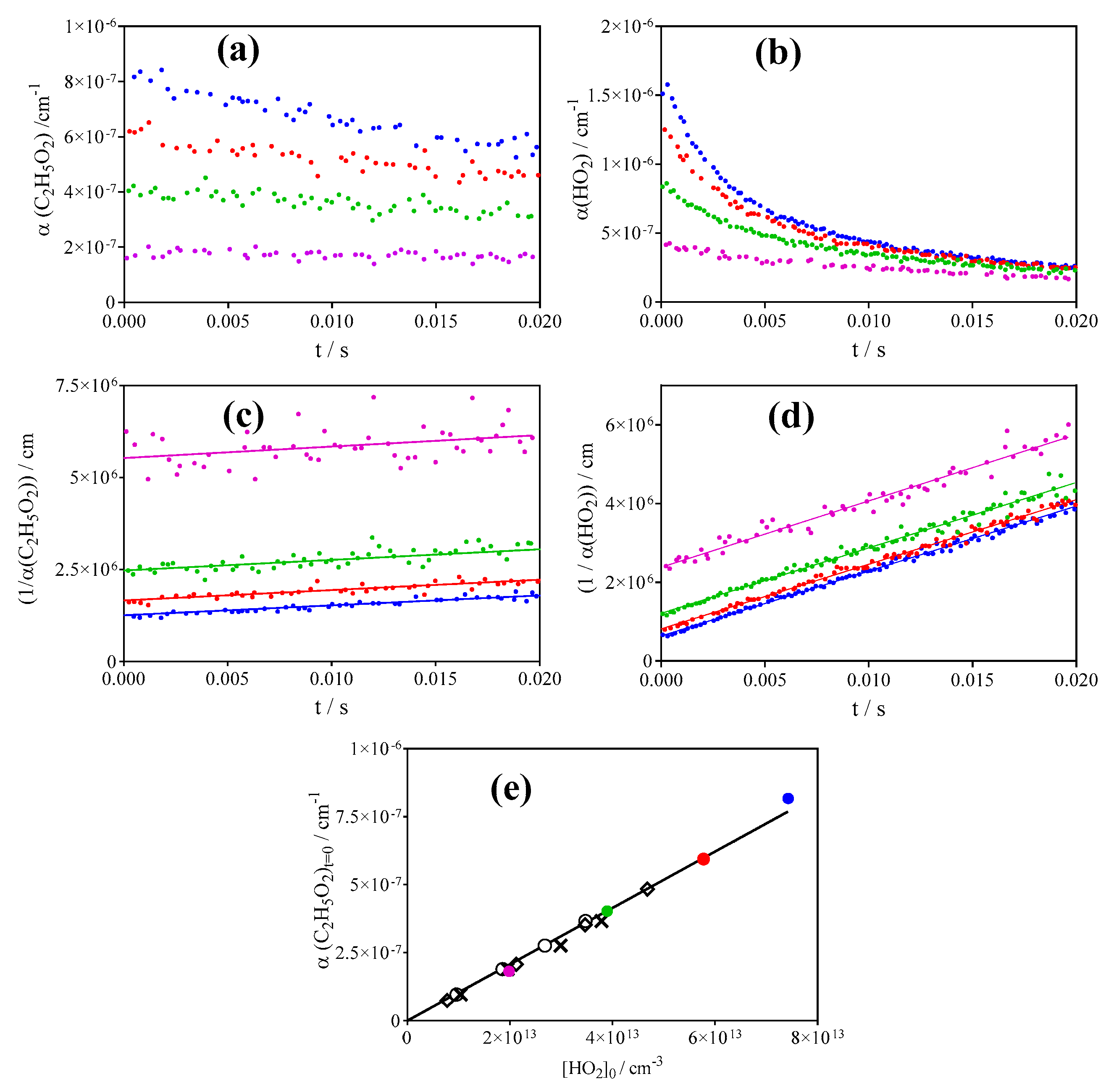
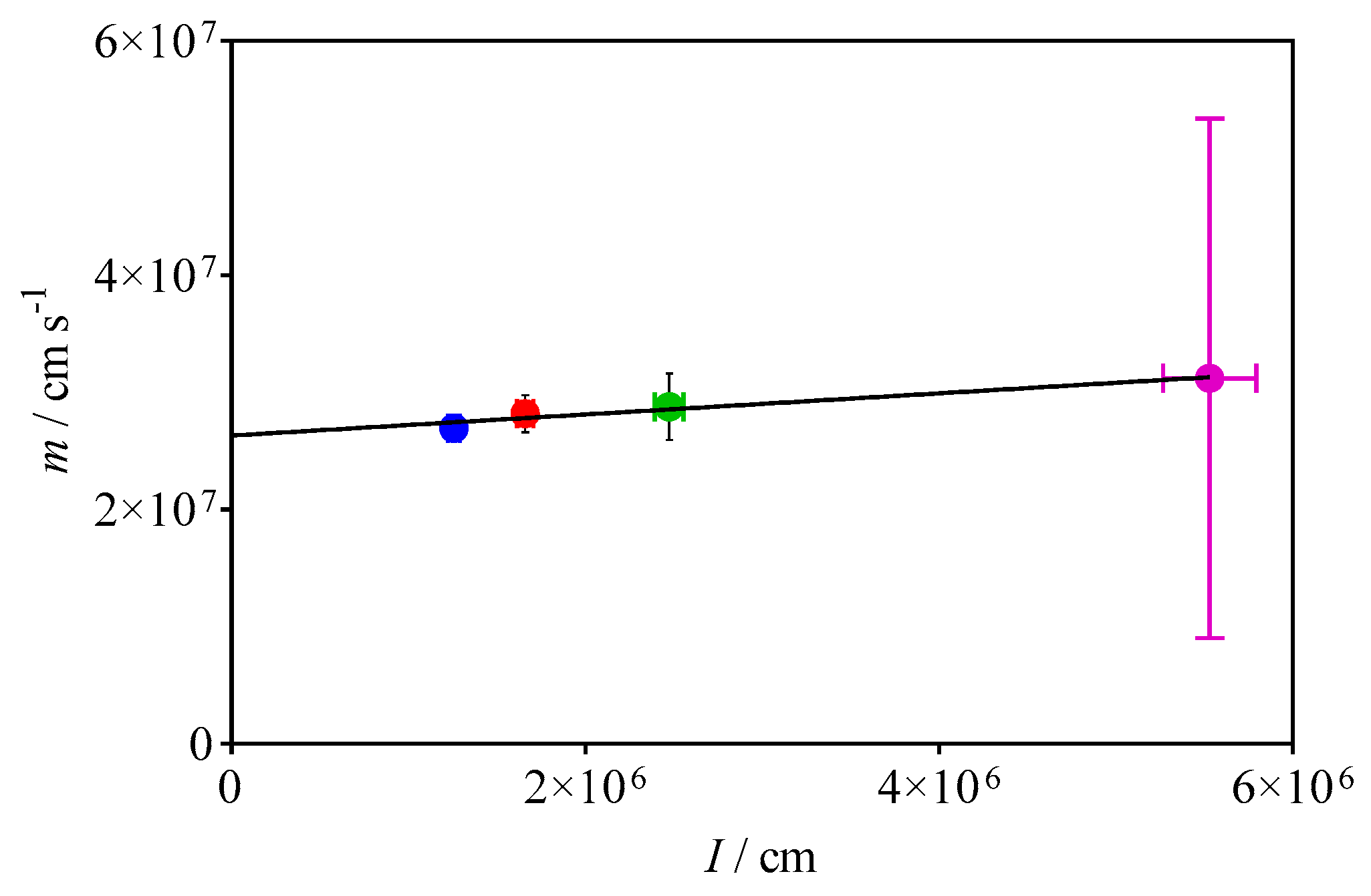
3.1. Quantification of C2H5O2 in Back-to-Back Experiments
3.2. Quantification of C2H5O2 by Measuring the Rate Constant of C2H5O2 + HO2
| Reaction | k/cm3molecule−1s−1 | Reference | |
|---|---|---|---|
| 1a | 2 C2H5O2 → 2 C2H5O + O2 | 2.6 × 10−14 | Ref [32] * |
| 1b | 2 C2H5O2 → C2H5OH + CH3CHO + O2 | 6.7 × 10−14 | Ref [32] * |
| 2 | C2H5O + O2 → CH3CHO + HO2 | 8 × 10−15 | Ref [39] |
| 3 | C2H5O2 + HO2 → C2H5OOH + O2 | 6.2 × 10−12 | This work |
| 5 | Cl + C2H6 → C2H5 + HCl | 5.9 × 10−11 | Ref [31] |
| 6a | C2H5 + O2 + M → C2H5O2 + M | 4.8 × 10−12 | Ref [40] |
| 6b | C2H5 + O2 → C2H4 + HO2 | 3-4× 10−14 | This work ** |
| 7 | Cl + CH3OH → CH2OH + HCl | 5.5 × 10−11 | Ref [31] |
| 8 | CH2OH + O2 → CH2O + HO2 | 9.6 × 10−12 | Ref [31] |
| 9 | 2 HO2 → H2O2 + O2 | 1.7 × 10−12 | Ref [30] |
| 10 | C2H5O2 + Cl → products | 1.5 × 10−10 | Ref [41] |
| 11 | C2H5O2 → diffusion | 2 s−1 | This work |
| 12 | HO2 → diffusion | 3 s−1 | This work |
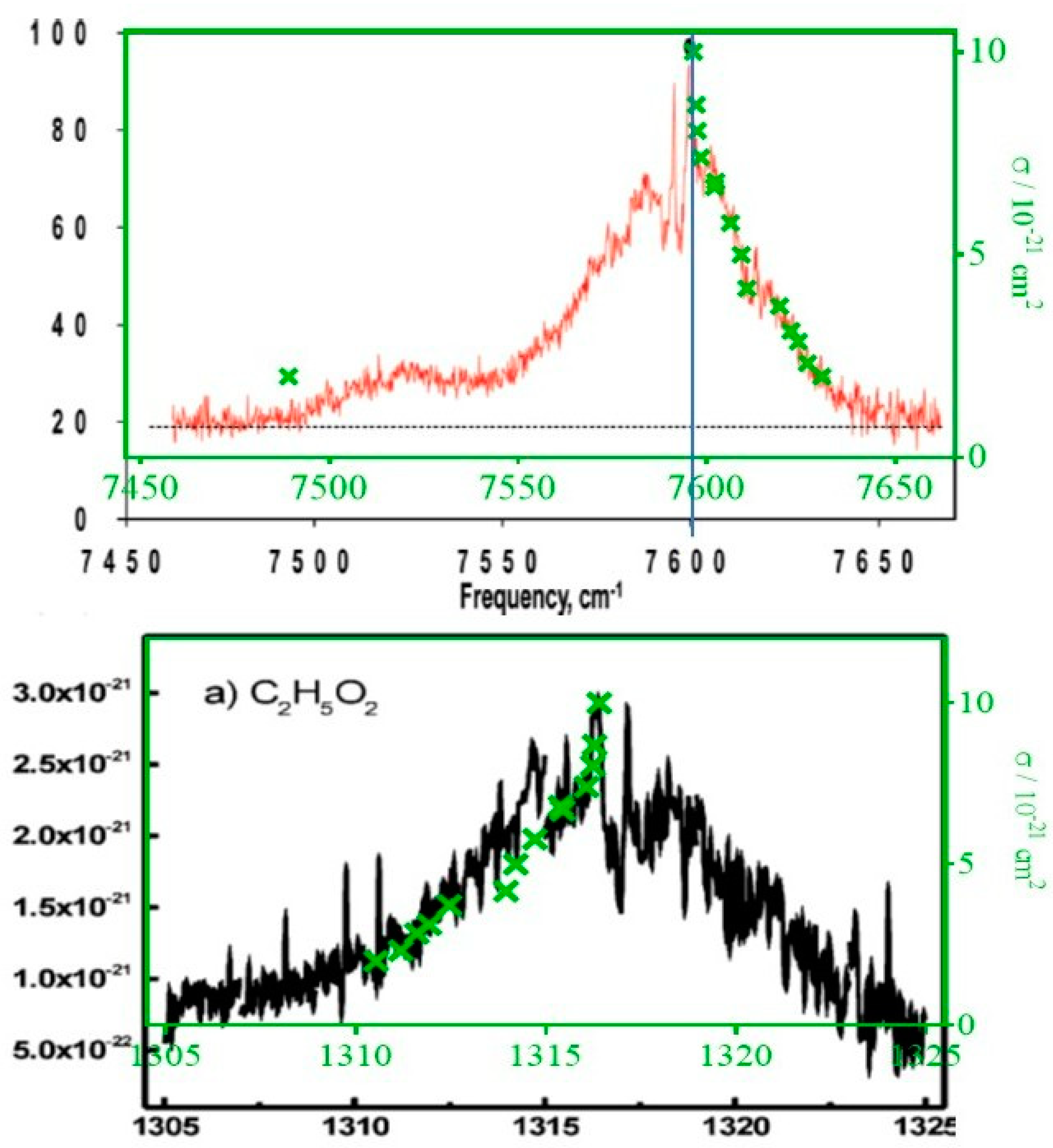
3.3. Measuring the Relative Absorption Spectrum
4. Discussion
Comparison of the Absorption Cross-Section with Literature Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Orlando, J.J.; Tyndall, G.S. Laboratory studies of organic peroxy radical chemistry: An overview with emphasis on recent issues of atmospheric significance. Chem. Soc. Rev. 2012, 41, 6294–6317. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fittschen, C. The reaction of peroxy radicals with OH radicals. Chem. Phys. Lett. 2019, 725, 102–108. [Google Scholar] [CrossRef]
- Assaf, E.; Song, B.; Tomas, A.; Schoemaecker, C.; Fittschen, C. Rate Constant of the Reaction between CH3O2 Radicals and OH Radicals revisited. J. Phys. Chem. A 2016, 120, 8923–8932. [Google Scholar] [CrossRef]
- Hasson, A.S.; Tyndall, G.S.; Orlando, J.J. A Product Yield Study of the Reaction of HO2 Radicals with Ethyl Peroxy (C2H5O2), Acetyl Peroxy (CH3C(O)O2), and Acetonyl Peroxy (CH3C(O)CH2O2) Radicals. J. Phys. Chem. A 2004, 108, 5979–5989. [Google Scholar] [CrossRef]
- Tyndall, G.S.; Cox, R.A.; Granier, C.; Lesclaux, R.; Moortgat, G.K.; Pilling, M.J.; Ravishankara, A.R.; Wallington, T.J. Atmospheric Chemistry of Small Organic Peroxy Radicals. J. Geophys. Res. 2001, 106, 12157–12182. [Google Scholar] [CrossRef]
- Hunziker, H.E.; Wendt, H.R. Electronic Absorption Spectra of Organic Peroxyl Radicals in the Near Infrared. J. Chem. Phys. 1976, 64, 3488–3490. [Google Scholar] [CrossRef]
- Hunziker, H.E.; Wendt, H.R. Near infrared absorption spectrum of HO2. J. Chem. Phys. 1974, 60, 4622–4623. [Google Scholar] [CrossRef]
- O’Keefe, A.; Deacon, D.A.G. Cavity ring-down optical spectrometer for absorption measurements using pulsed laser sources. Rev. Sci. Instrum. 1988, 59, 2544–2551. [Google Scholar] [CrossRef] [Green Version]
- Romanini, D.; Kachanov, A.A.; Sadeghi, N.; Stoeckel, F. CW cavity ring down spectroscopy. Chem. Phys. Lett. 1997, 264, 316–322. [Google Scholar] [CrossRef]
- Pushkarsky, M.B.; Zalyubovsky, S.J.; Miller, T.A. Detection and Characterization of Alkyl Peroxy Radicals using Cavity Ringdown Spectroscopy. J. Chem. Phys. 2000, 112., 10695–10698. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, D.B.; Spillman, J.L. Alkyl Peroxy Radical Kinetics Measured Using Near-infrared CW-Cavity Ring-down Spectroscopy. J. Phys. Chem. A 2002, 106, 8891–8902. [Google Scholar] [CrossRef]
- Faragó, E.P.; Viskolcz, B.; Schoemaecker, C.; Fittschen, C. Absorption Spectrum and Absolute Absorption Cross Sections of CH3O2 Radicals and CH3I Molecules in the Wavelength Range 7473–7497 cm–1. J. Phys. Chem. A 2013, 117, 12802–12811. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Tang, X.; Fittschen, C.; Zhang, C.; Wang, T.; Wang, C.; Gu, X.; Zhang, W. Online analysis of gas-phase radical reactions using vacuum ultraviolet lamp photoionization and time-of-flight mass spectrometry. Rev. Sci. Instrum. 2020, 91. [Google Scholar] [CrossRef] [Green Version]
- Wen, Z.; Tang, X.; Wang, C.; Fittschen, C.; Wang, T.; Zhang, C.; Yang, J.; Pan, Y.; Liu, F.; Zhang, W. A vacuum ultraviolet photoionization time-of-flight mass spectrometer with high sensitivity for study of gas-phase radical reaction in a flow tube. Int. J. Chem. Kinet. 2019, 51, 178–188. [Google Scholar] [CrossRef]
- Thiebaud, J.; Crunaire, S.; Fittschen, C. Measurement of Line Strengths in the 2ν1 Band of the HO2 Radical using Laser Photolysis / Continous wave Cavity Ring Down Spectroscopy (cw-CRDS). J. Phys. Chem. A 2007, 111, 6959–6966. [Google Scholar] [CrossRef]
- Rupper, P.; Sharp, E.N.; Tarczay, G.; Miller, T.A. Investigation of Ethyl Peroxy Radical Conformers via Cavity Ringdown Spectroscopy of the Ã- X Electronic Transition. J. Phys. Chem. A 2007, 111, 832–840. [Google Scholar] [CrossRef] [PubMed]
- Melnik, D.; Chhantyal-Pun, R.; Miller, T.A. Measurements of the Absolute Absorption Cross Sections of the A-X Transition in Organic Peroxy Radicals by Dual-Wavelength Cavity Ring-Down Spectroscopy. J. Phys. Chem. A 2010, 114, 11583–11594. [Google Scholar] [CrossRef] [PubMed]
- Melnik, D.; Miller, T.A. Kinetic measurements of the C2H5O2 radical using time-resolved cavity ring-down spectroscopy with a continuous source. J. Chem. Phys. 2013, 139, 094201. [Google Scholar] [CrossRef]
- Thiebaud, J.; Fittschen, C. Near Infrared cw-CRDS Coupled to Laser Photolysis: Spectroscopy and Kinetics of the HO2 Radical. Appl. Phys. B 2006, 85, 383–389. [Google Scholar] [CrossRef]
- Parker, A.E.; Jain, C.; Schoemaecker, C.; Szriftgiser, P.; Votava, O.; Fittschen, C. Simultaneous, time-resolved measurements of OH and HO2 radicals by coupling of high repetition rate LIF and cw-CRDS techniques to a laser photolysis reactor and its application to the photolysis of H2O2. Appl. Phys. B. 2011, 103, 725–733. [Google Scholar] [CrossRef]
- Votava, O.; Mašát, M.; Parker, A.E.; Jain, C.; Fittschen, C. Microcontroller based resonance tracking unit for time resolved continuous wave cavity-ringdown spectroscopy measurements. Rev. Sci. Instrum. 2012, 83, 043110. [Google Scholar] [CrossRef]
- Assaf, E.; Asvany, O.; Votava, O.; Batut, S.; Schoemaecker, C.; Fittschen, C. Measurement of line strengths in the à 2A’ ← X 2A” transition of HO2 and DO2. J. Quant. Spectrosc. Radiat. Transfer 2017, 201, 161–170. [Google Scholar] [CrossRef]
- Thiebaud, J.; Aluculesei, A.; Fittschen, C. Formation of HO2 Radicals from the Photodissociation of H2O2 at 248 nm. J. Chem. Phys. 2007, 126, 186101. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Tyndall, G.S.; Orlando, J.J. Spectroscopic and Kinetic Properties of HO2 Radicals and the Enhancement of the HO2 Self Reaction by CH3OH and H2O. J. Phys. Chem. A 2010, 114, 369–378. [Google Scholar] [CrossRef]
- DeSain, J.D.; Ho, A.D.; Taatjes, C.A. High-resolution diode laser absorption spectroscopy of the O–H stretch overtone band (2,0,0)(0,0,0) of the HO2 radical. J. Mol. Spectrosc. 2003, 219, 163–169. [Google Scholar] [CrossRef]
- Ibrahim, N.; Thiebaud, J.; Orphal, J.; Fittschen, C. Air-Broadening Coefficients of the HO2 Radical in the 2v1 Band Measured Using cw-CRDS. J. Mol. Spectrosc. 2007, 242, 64–69. [Google Scholar] [CrossRef]
- Onel, L.; Brennan, A.; Gianella, M.; Ronnie, G.; Lawry Aguila, A.; Hancock, G.; Whalley, L.; Seakins, P.W.; Ritchie, G.A.D.; Heard, D.E. An intercomparison of HO2 measurements by Fluorescence Assay by Gas Expansion and Cavity Ring–Down Spectroscopy within HIRAC (Highly Instrumented Reactor for Atmospheric Chemistry). Atmos. Meas. Tech. Discuss. 2017, 10, 4877–4894. [Google Scholar] [CrossRef] [Green Version]
- Assaf, E.; Liu, L.; Schoemaecker, C.; Fittschen, C. Absorption spectrum and absorption cross sections of the 2v1 band of HO2 between 20 and 760 Torr air in the range 6636 and 6639 cm-1. J. Quantitat. Spectrosc. Radiat. Transf. 2018, 211, 107–114. [Google Scholar] [CrossRef]
- Assali, M.; Rakovsky, J.; Votava, O.; Fittschen, C. Experimental Determination of the Rate Constants of the Reactions of HO2 + DO2 and DO2 + DO2. Int. J. Chem. Kinet. 2019, Submitted. [Google Scholar]
- Atkinson, R.; Baulch, D.L.; Cox, R.A.; Crowley, J.N.; Hampson, R.F.; Hynes, R.G.; Jenkin, M.E.; Rossi, M.J.; Troe, J. Evaluated Kinetic and Photochemical Data for Atmospheric Chemistry: Volume 1 – Gas Phase Reactions of Ox, HOx, NOx, and SOx, Species. Atmos. Chem. Phys. 2004, 4, 1461–1738. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, R.; Baulch, D.L.; Cox, R.A.; Crowley, J.N.; Hampson, R.F.; Hynes, R.G.; Jenkin, M.E.; Rossi, M.J.; Troe, J. Evaluated Kinetic and Photochemical Data for Atmospheric Chemistry: Volume II - Gas Phase Reactions of Organic Species. Atmos. Chem. Phys. 2006, 6, 3625–4055. [Google Scholar] [CrossRef] [Green Version]
- Noell, A.C.; Alconcel, L.S.; Robichaud, D.J.; Okumura, M.; Sander, S.P. Near-Infrared Kinetic Spectroscopy of the HO2 and C2H5O2 Self-Reactions and Cross Reactions. J. Phys. Chem. A 2010, 114, 6983–6995. [Google Scholar] [CrossRef]
- Boyd, A.A.; Flaud, P.-M.; Daugey, N.; Lesclaux, R. Rate Constants for RO2 + HO2 Reactions Measured under a Large Excess of HO2. J. Phys. Chem. A 2003, 107, 818–821. [Google Scholar] [CrossRef]
- Raventós-Duran, M.T.; Percival, C.J.; McGillen, M.R.; Hamer, P.D.; Shallcross, D.E. Kinetics and branching ratio studies of the reaction of C2H5O2 + HO2 using chemical ionisation mass spectrometry. Phys. Chem. Chem. Phys. 2007, 9, 4338–4348. [Google Scholar] [CrossRef]
- Maricq, M.M.; Szente, J.J. A Kinetic Study of the Reaction between Ethylperoxy Radicals and HO2. J. Phys. Chem. 1994, 98, 2078–2082. [Google Scholar] [CrossRef]
- Fenter, F.F.; Catoire, V.; Lesclaux, R.; Lightfoot, P.D. The ethylperoxy radical: Its ultraviolet spectrum, self-reaction, and reaction with hydroperoxy, each studied as a function of temperature. J. Phys. Chem. 1993, 97, 3530–3538. [Google Scholar] [CrossRef]
- Dagaut, P.; Wallington, T.J.; Kurylo, M.J. Flash photolysis kinetic absorption spectroscopy study of the gasphase reaction HO2 + C2H5O2 over the temperature range 228 - 380K. J. Phys. Chem. 1988, 92, 3836–3839. [Google Scholar] [CrossRef]
- Cattell, F.C.; Cavanagh, J.; Cox, R.A.; Jenkin, M.E. A kinetic study of reactions of HO2 and C2H5O2 using diode-laser absorption spectroscopy. J. Chem. Soc.-Faraday Trans. Ii 1986, 82, 1999–2018. [Google Scholar] [CrossRef]
- Fittschen, C.; Frenzel, A.; Imrik, K.; Devolder, P. Rate Constants for the Reactions of C2H5O, i-C3H7O, and n-C3H7O with NO and O2 as a Function of Temperature. Int. J. Chem. Kinet. 1999, 31, 860–866. [Google Scholar] [CrossRef]
- Fernandes, R.X.; Luther, K.; Marowsky, G.; Rissanen, M.P.; Timonen, R.; Troe, J. Experimental and Modeling Study of the Temperature and Pressure Dependence of the Reaction C2H5 + O2 (+ M) → C2H5O2 (+ M). J. Phys. Chem. A 2015, 119, 7263–7269. [Google Scholar] [CrossRef] [PubMed]
- Maricq, M.M.; Szente, J.J.; Kaiser, E.W.; Shi, J. Reaction of Chlorine Atoms with Methylperoxy and Ethylperoxy Radicals. J. Phys. Chem. 1994, 98, 2083–2089. [Google Scholar] [CrossRef]
- Seakins, P.W.; Woodbridge, E.L.; Leone, S.R. A laser flash photolysis, time-resolved Fourrier Transform Infrared Emission study of the reaction Cl + C2H5 --> HCl + C2H4. J. Phys. Chem. 1993, 97, 5633–5642. [Google Scholar] [CrossRef]



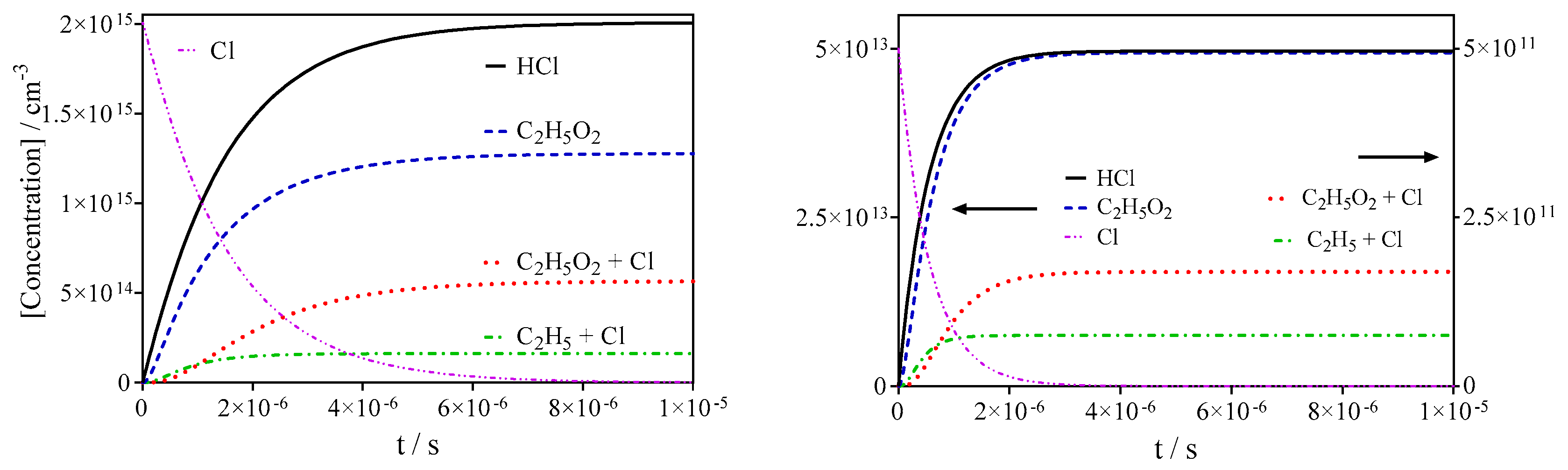
| σ/10−21 cm2 | Method | Reference |
|---|---|---|
| 3.0 ± 1.5 | Kinetic method, no other radical losses considered | Atkinson and Spillman [11] |
| 4.4 | Depletion of photolysis energy through precursor with [Cl] = [C2H5O2], i.e., no secondary reactions considered | Rupper et al. [16] |
| 5.29 ± 0.20 | Measurement of HCl in dual path CRDS with [Cl] = [C2H5O2], i.e., no secondary reactions considered | Melnik et al. [17] |
| 5.29 | Kinetic method used for validation of Ref. [17] | Melnik et al. [18] |
| 10 ± 2 | Measurement of HO2/C2H5O2 in dual path CRDS with [Cl] = [HO2] = [C2H5O2] | This work |
| 10 ± 2 | Kinetic method from C2H5O2 + HO2 | This work |
| [C2H6]/1015 cm−3 | [CH3OH]/1015 cm−3 | [C2H5O2]max/1013 cm−3 | [HO2]max/1013 cm−3 |
|---|---|---|---|
| 1.94 | 5.0 | 3.4 | 8.3 |
| 2.74 | 5.0 | 4.3 | 7.4 |
| 3.45 | 5.0 | 5.0 | 6.7 |
| 4.30 | 5.0 | 5.6 | 6.1 |
| 5.91 | 2.8 | 8.1 | 3.6 |
| 7.50 | 2.8 | 8.6 | 3.0 |
| Wavenumber/cm−1 | σ/10−20 cm2 |
|---|---|
| 7596.47 | 10.0 |
| 7597.20 | 8.7 |
| 7597.44 | 8.1 |
| 7598.40 | 7.4 |
| 7602.02 | 6.7 |
| 7602.38 | 6.8 |
| 7606.25 | 5.8 |
| 7609.16 | 5.0 |
| 7610.66 | 4.2 |
| 7619.28 | 3.7 |
| 7622.36 | 3.1 |
| 7624.28 | 2.9 |
| 7626.72 | 2.3 |
| 7630.50 | 2.0 |
| 7489.16 | 2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Shamas, M.; Assali, M.; Tang, X.; Zhang, W.; Pillier, L.; Schoemaecker, C.; Fittschen, C.
Absolute Absorption Cross-Section of the Ã←
Zhang C, Shamas M, Assali M, Tang X, Zhang W, Pillier L, Schoemaecker C, Fittschen C.
Absolute Absorption Cross-Section of the Ã←
Zhang, Cuihong, Mirna Shamas, Mohamed Assali, Xiaofeng Tang, Weijun Zhang, Laure Pillier, Coralie Schoemaecker, and Christa Fittschen.
2021. "Absolute Absorption Cross-Section of the Ã←
Zhang, C., Shamas, M., Assali, M., Tang, X., Zhang, W., Pillier, L., Schoemaecker, C., & Fittschen, C.
(2021). Absolute Absorption Cross-Section of the Ã←






