Next Article in Journal
Comparison of Refractive and Visual Outcomes after Transepithelial Photorefractive Keratectomy (TransPRK) in Low versus Moderate Myopia
Previous Article in Journal
Machine Learning Assisted Inverse Design for Ultrafine, Dynamic and Arbitrary Gain Spectrum Shaping of Raman Amplification
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 8
Issue 7
10.3390/photonics8070261
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Thermal Noise in Cubic Optical Cavities

by
Guanjun Xu
1,2,†,
Dongdong Jiao
2,†,
Long Chen
2,
Linbo Zhang
2,
Ruifang Dong
2,*,
Tao Liu
2 and
Junbiao Wang
1
1
School of Mechanical Engineering, Northwestern Polytechnical University, 127 West Youyi Road, Xi’an 710072, China
2
National Time Service Center, Chinese Academy of Sciences, 3 East Shuyuan Road, Xi’an 710600, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Photonics 2021, 8(7), 261; https://doi.org/10.3390/photonics8070261
Submission received: 11 June 2021 / Revised: 5 July 2021 / Accepted: 5 July 2021 / Published: 6 July 2021
(This article belongs to the Section Lasers, Light Sources and Sensors)
Browse Figures
Versions Notes

Abstract

Thermal noise in optical cavities sets a fundamental limit to the frequency instability of ultra-stable lasers. Numata et al. derived three equations based on strain energy and the fluctuation–dissipation theorem to estimate the thermal noise contributions of the spacer, substrates, and coating. These equations work well for cylindrical cavities. Extending from that, an expression for the thermal noise for a cubic spacer based on the fluctuation–dissipation theorem is derived, and the thermal noise in cubic optical cavities is investigated in detail by theoretical analysis and finite element simulation. The result shows that the thermal noise of the analytic estimate fits well with that of finite element analysis. Meanwhile, the influence of the compressive force Fp on the thermal noise in cubic optical cavities is analyzed for the first time. For a 50 mm long ultra-low expansion cubic cavity with fused silica substrates and GaAs/AlGaAs crystalline coating, the displacement noise contributed from every Fp of 100 N is about three times more than that of the substrate and coating.

1. Introduction

Ultra-stable lasers have many applications, such as frequency metrology [1,2,3,4,5], gravitational wave detection [6], fundamental physics tests [7,8], and coherent optical links [9,10]. A state-of-the-art ultra-stable laser shows that the linewidth is less than 10 mHz. The fractional frequency instability reaches a 10−17 order of magnitude at 1 s [11,12]. Ultra-stable lasers can be achieved by locking the lasers onto optical cavities with the Pound–Drever–Hall (PDH) technique, and the frequency instability of the ultra-stable laser is then defined by the stability of the optical length of the optical cavity [13,14]. The fractional length stability of optical cavities is inevitably limited by thermal noise in the cavity. Several thermal noise sources have been identified, such as Brownian thermal noise and thermo-elastic noise. Among them, the influence of Brownian thermal noise is quite remarkable, and considerable effort has been invested in reducing it [15,16,17,18,19,20,21,22,23,24]. Y. Levin proposed an efficient way to calculate thermal noise based on the fluctuation–dissipation theorem (FDT) and some significant efforts have been expended to reduce it [15,16,17,18,19,20,21,22,23,24]. A set of equations was given by Numata et al. [16] for estimating the noise contribution of a spacer, substrates, and coating of cylindrical cavities using this approach. High mechanical quality substrates and coating materials are being used in state-of-the-art optical cavities to reduce the thermal noise of the optical cavity [11,12,13,14].
The cubic optical cavity is based on a cubic geometry with four supports placed symmetrically about the optical axis in a tetrahedral configuration [25]. It plays an essential role for transportable ultra-stable lasers, which are used outside the laboratory for applications such as space optical clocks, geodesy, tests of fundamental physics in space, and the generation of ultra-stable microwaves for radar [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. A compressive force Fp must be applied to fix the cavity to resist the extreme vibrations and impact of rocket launching. Previous studies have shown that the cubic optical cavity can still maintain a low vibration sensitivity in a wide compressive range [25,40]. However, a large Fp will increase the elastic energy of the optical cavity, inducing thermal noise and adversely affecting applications of ultra-stable lasers in some high-precision fields [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]. Therefore, to evaluate the performance of transportable ultra-stable lasers using a cubic cavity, it is necessary to propose a reasonable method to analyze the thermal noise in a cubic cavity.
Detailed theoretical analysis and finite element simulation (FEA) of the Brownian thermal noise in cubic optical cavities are presented herein. First, based on FDT and strain energy, the theoretical estimation formula of the Brownian thermal noise in a cubic spacer is derived. We compare the new analysis method and FEA for the same conditions. The two results are in good agreement. The new analysis formula in this work fits well with any edge dimension of the cubic spacer. A complete explanation of the divergence between the simulation and analytical estimation is presented in detail. Second, the influence of Fp on the thermal noise in cubic optical cavities is investigated for the first time. For a 50 mm long ultra-low expansion (ULE) optical cavity, the displacement noise contributed from each 100 N Fp is about three times that of FS substrates and GaAs/AlGaAs crystalline coating when the Fp is larger than 100 N.
The paper is organized as follows: In Section 2, the theoretical framework of the thermal noise in the cubic optical cavities is discussed. The FEA simulation is applied to a typical cubic optical cavity design in Section 3.1. The deviations from the analytical estimate for the cubic spacer are discussed. To better understand the divergence between the simulation and analytical estimation, the thermal noise of cubic spacers under various conditions is investigated in Section 3.2, which focuses on the influence of Fp, the materials, and the edge length of the cubic optical cavity. In Section 4, the thermal noise of cubic optical cavities of mixed materials is investigated. The conclusions are summarized in Section 5.

2. Theoretical Framework

The effect of Brownian motion thermal noise on the length stability of optical cavities has been discussed by Numata et al. [16], following Y. Levin’s direct approach [15]. For clarity, this concept is illustrated by the following example.
Assuming that x is the distance between two mirrors of the optical cavity, and based on FDT, the power spectral density Sx(f) of the optical length fluctuations along the x-axis can be expressed as [16].
S x ( f ) = 4 k B T U ϕ π f F 2
where kB is the Boltzmann constant, T is the temperature, F and f are the amplitude and frequency of an oscillatory force [16], respectively. U is the maximum elastic strain energy, and ϕ is the loss angle of the materials.
For an optical cavity, Sx(f) is mainly caused by the spacer, substrate, and coating. The analytic estimates of Sx(f) for substrates and coatings in this work are cited in Ref. [16]. Based on Y. Levin’s direct approach [15], the analytic estimate of Sx(f) for a cubic spacer shown in Figure 1 can be expressed as
U s p a c u b = L c u b F 2 2 ( L c u b 2 − 2 l c u b 2 − π r s p a 2 ) E s p a S x ( f ) = 4 k B T π f L c u b 2 ( L c u b 2 − 2 l c u b 2 − π r s p a 2 ) E s p a ϕ s p a }
where S x ( f ) s p a c u b is the power spectral density of length fluctuations. Espa is the elastic modulus of the spacer. This estimate focuses on the cubic spacer. As an estimate for the spacer contribution to the optical cavity noise, the thermal fluctuations of the length of a cube, averaged over the spacer whole front face area, are calculated. Y. Levin’s direct approach demands a that is pressure uniformly distributed across its front faces with the area. Equation (2) takes into account that the areas of the central bore and the cut vertices reduce the front face area of the spacer. To derive these equations, the formula for the position fluctuations of one end of a free elastic bar is used. According to Y. Levin’s direct approach, calculating the length fluctuation requires applying opposite forces simultaneously to both ends.
According to Ref. [16], the power spectral density of the length fluctuations may be converted to power spectral density of the frequency noise, which can be conventionally characterized by the Allan deviation σy of the fractional frequency fluctuations y and expressed as
σ y = 2 ( ln 2 ) f S υ ( f ) υ = 2 ( ln 2 ) f S x ( f ) L
From Equations (2) and (3), a strain energy of 0.1 nJ corresponds to a length fluctuation Sx(f) = 0.858 × 10−35 m2/Hz at 1 Hz and a corresponding Allan deviation of σy = 6.88 × 10−17 at 1s for a 50 mm long ULE cavity [17].

3. Estimation Calculation and Simulation

The FEA software is used to calculate the strain energy and thermal noise in the cubic optical spacer. As the thermal noise of the cavity is proportional to strain energy, the results are given in terms of elastic strain energy for convenience. The most important parameters used in the calculation, including dimensions and materials, are given in Table 1 and Table 2.
To increase the simulation accuracy, approximately 200,000 tetrahedral elements were used. We assumed that the pressure distribution on the mirror was in accordance with the laser beam profile, and a Gaussian laser beam with a 1/e2 beam radius ω of 250 μm was used. Thus, the pressure distribution was [17]:
p ( r ) = ± 2 F π ω 2 e − 2 r 2 ω 2
According to FDT, F is the force applied at the location where the laser beam hits the mirrors. The absolute value of the force is not critical, provided the stress–strain relationship of the elastic–mechanical system remains linear. For simplicity, in the calculation, we have used a force F of 1 N.

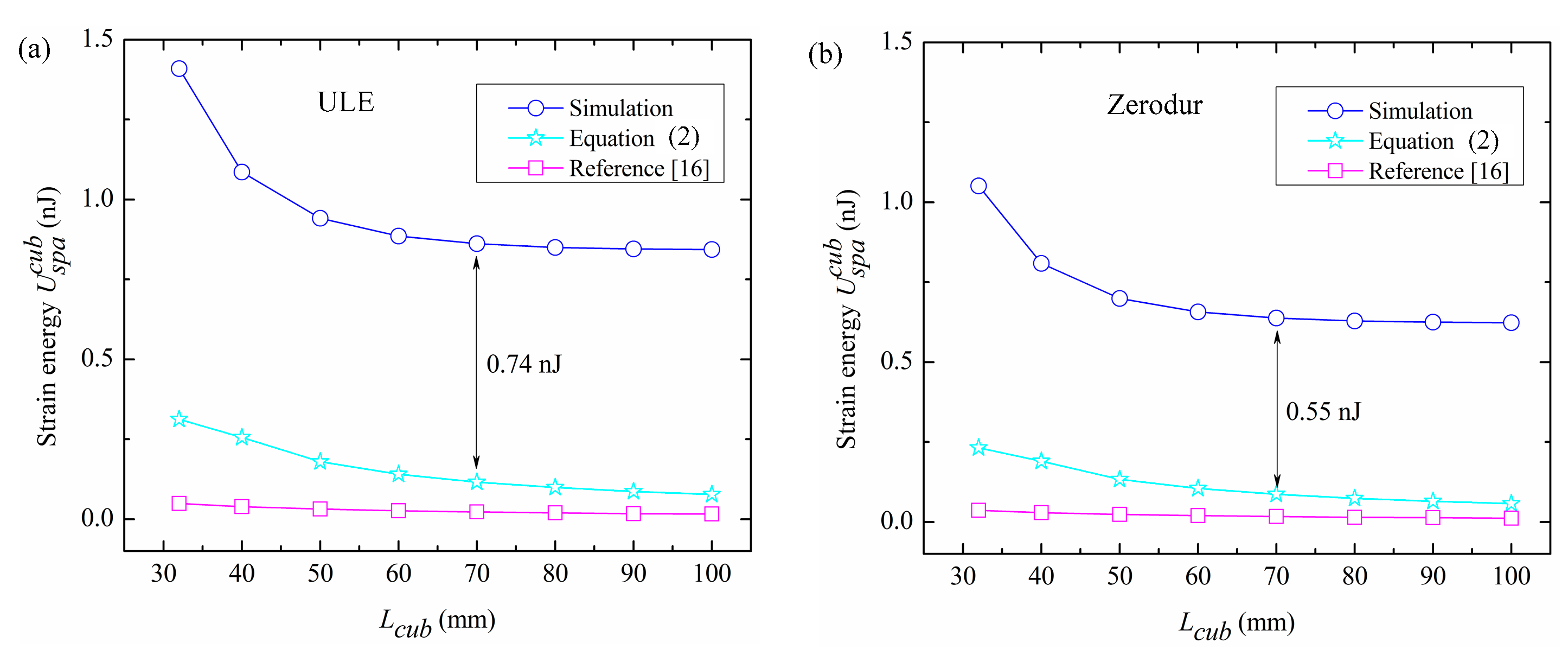
3.1. Comparison of Estimation and Simulation

As shown in Figure 2, most of the elastic strain energy for the cubic optical cavity is concentrated in the mirror substrate, similar to the cylindrical and spindle cavity case [16,17,23]. The deformation shape of the substrate reflects the Gaussian beam profile. For illustration purposes, a beam waist of 2 mm has been chosen. For the cubic spacer, the maximum elastic strain energy occurs around the central bore near the contact area with the mirrors. Strong local deformations occur at the boundary between substrate and spacer extending into the spacer. At a distance exceeding this critical depth, a homogeneous energy density distribution is obtained. According to Equation (2) in Ref. [16], the analytic estimate of the spacer contribution does not hold for the full spacer length as it neglects local deformations arising from the non-uniform pressure distribution on its front face.
The strain energy for six kinds of cubic optical cavities was estimated and simulated to verify the accuracy of Equation (2). The results are shown in Table 3. For convenience, the length of the cubic optical cavity was chosen according to Ref. [25], which is the cubic optical cavity designed by S. Webster et al. [25]. Furthermore, the other cavity parameters are obtained by calculating the zero vibration sensitivity of the cavity.
As shown in Table 3, the strain energy of FEA is closer to the result calculated by Equation (2) in this paper, differing by a factor of approximately 5. In comparison, Equation (2) in Ref. [16] differs by a factor of approximately 16. For a pure ULE cubic cavity, compared to the result simulated by FEA, the strain energy of approximately 0.88 nJ stored in the spacer is underestimated by Equation (2) in Ref. [16]. This underestimation is attributed to the complex local deformations produced by the non-uniform pressure and strain caused in different materials. Kessler et al. [17] and G. Xu et al. [23] have noticed a similar divergence in the case of a cylindrical cavity and spindle cavities. There are two possible reasons for this. One reason is that the transition produces the stress concentration from the mirror to the spacer. The other one is that bending strain energy was not considered. Note that Teflon or Viton pads have not been included in our numerical simulations. T. Kessler et al. [17] studied the contribution of Viton to the thermal noise, and the results showed that the contribution of Viton can be ignored for the widely used optical cavity at present. However, once low-loss coatings with sufficient reflectivities are available, this might need attention.

3.2. The Effect of Cavity Dimensions on Elastic Energy

To better understand the divergence between the simulation and analytical estimation, we investigated the thermal noise of cubic spacers under varying conditions, including the spacer’s edge length, materials, and Fp.

3.2.1. Room Temperature Materials

As shown in Figure 3, for a cubic optical cavity made of ULE or Zerodur, the strain energy calculated by FEA, the two equations expressed by Equation (2) in this paper, and Equation (2) in Ref. [16] decrease with the increase in cavity length. As Figure 3a,b shows, for the two spacers, the results of FEA are approximately a factor of 5 larger than that of Equation (2) in this paper and a factor of 14 larger than that of Equation (2) in Ref. [16], respectively. For the two spacers, the gaps of strain energy between FEA and Equation (2) in this paper are near-constant offsets of approximately 0.74 nJ and 0.55 nJ, respectively, and those between the simulation and Equation (2) in Ref. [16] are approximately 0.82 nJ and 0.6 nJ, respectively. The above results indicate that Equation (2) from this paper is more consistent with the results of FEA than that of Equation (2) in Ref. [16].

3.2.2. Low-Temperature Materials

For low-temperature material cubic optical cavities, such as silica and sapphire, Figure 4 shows that the strain energy calculated by Equation (2) in this paper is more consistent with the results of FEA than that of Equation (2) from Ref. [16], which is similar to the case of room temperature materials. For the two spacers, the results of FEA are approximately a factor of 5 greater than that of Equation (2) in this paper and a factor of 18 greater than that of Equation (2) in Ref. [16]. As the spacer edge length increases, for the all-silica and all-sapphire cubic optical cavities, the gap of the strain energy in the spacers between FEA and Equation (2) tends to near-constant offsets of approximately 0.27 nJ and 0.12 nJ, respectively. We believe that this divergence is similar to the case of room temperature material cubic optical cavities.

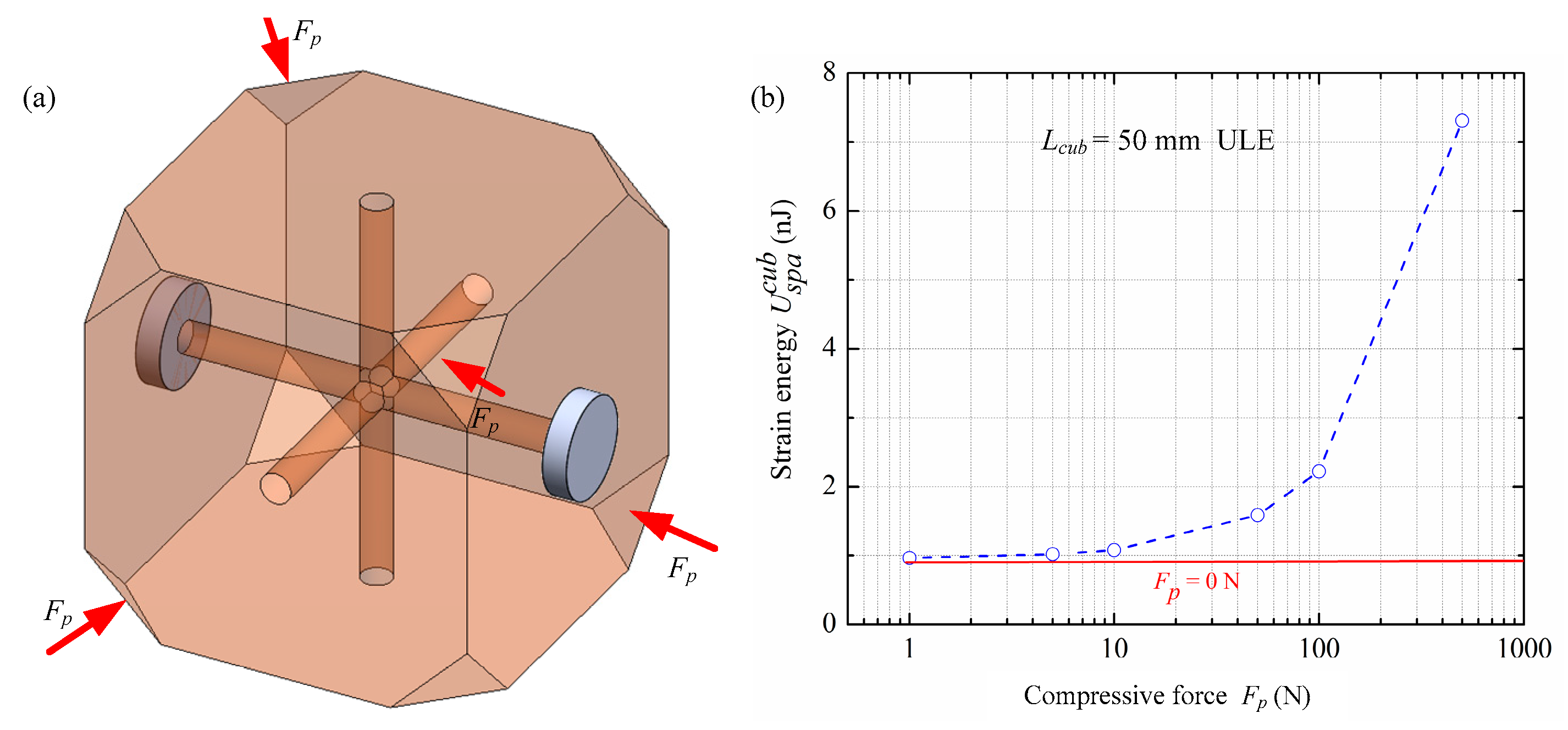
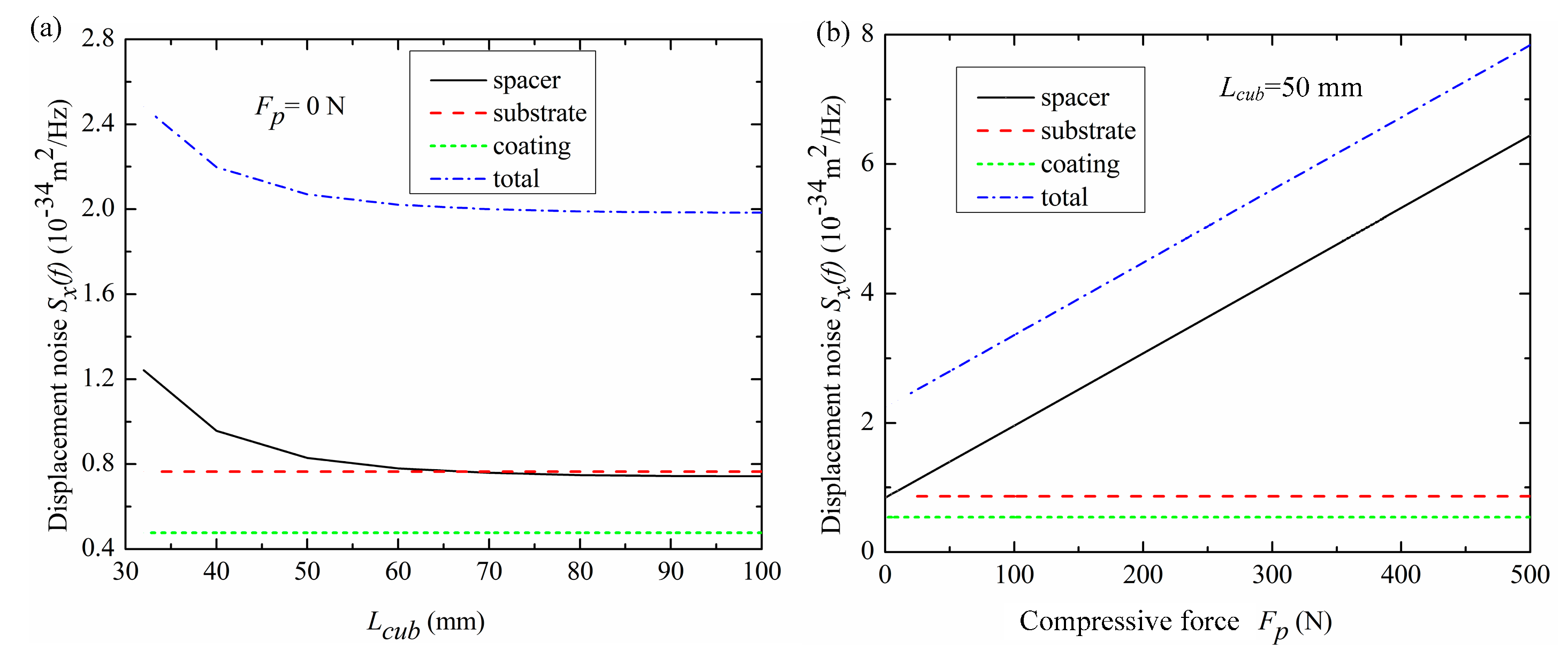
3.3. The Effect of Compressive Force on Elastic Energy

To rigidly mount the cubic optical cavity, four Fps were used to load the cut faces of the cubic cavity. Fp will change the stress field inside the cubic optical cavity, affecting the strain energy contributed from the force F in Equation (1). Assuming that the strain energy produced by four Fps where F = 0 N is defined as Up, and the strain energy produced by four Fps and F = 1 N is Up+F, then the strain energy contributed from the force F = 1 N can be expressed as
U F = U p + F − U p
As shown in Figure 5b, the strain energy UF in the spacer of a 50 mm long ULE cavity as a function of Fp is obtained by FEA. The divergence between UF and U0 becomes more pronounced as Fp increases. Generally, the results show that there is an approximately linear relationship between the strain energy UF and Fp. When Fp is about 80 N, strain energy UF is 1 nJ larger than U0. The strain energy divergences are about 1.2 nJ and 6.5 nJ, where Fp is 100 N and 500 N. A strain energy of 1.2 nJ corresponds to an Allan deviation of σy = 2.4 × 10−16 at 1s for a 50 mm long ULE cavity. Therefore, an appropriate Fp should be chosen for a lower thermal noise of the cubic optical cavity.

4. Mixed Material Cavities

In cavities with ULE, the major contribution to thermal noise arises from the mirror substrates and coating. Substrate materials with a higher mechanical Q-factor, such as fused silica (FS), have been used to reduce the thermal noise of mirror substrates [17,19]. However, fused silica shows a relatively large room temperature coefficient of thermal expansion (CTE). The large CTE difference in such a mixed material cavity leads to an unwanted lowering of the zero-crossing temperature of the cavity’s CTE. Either special mirror configurations have been applied, or additional ULE rings have been optically contacted with the back surfaces of the FS mirrors to compensate for this effect [18].
T. Kessler et al. [17] investigated the thermal noise of a mixed material cavity with a SiO2/Ta2O5 coating. The results show that the contribution from the coating to the total thermal noise of the cylindrical cavity is considerable. A GaAs/AlGaAs crystalline coating with a low loss angle was applied to reduce the thermal noise of the coating [21]. This research used the FEA model discussed above to investigate the percent contribution of Sx(f) in the mixed material cavity, including the ULE cubic spacer and the FS substrates with a GaAs/AlGaAs crystalline coating and a SiO2/Ta2O5 coating. A 50 mm edge cubic optical cavity was simulated. Additional 6 mm thick ULE rings with a diameter of 25.4 mm and a central bore of 14 mm were added, where Fp of 100 N was applied.
Figure 6 shows the FEA results of the Sx(f) contributions caused by the different cavity components. We find that the additional Sx(f) of the ULE ring is approximately equal to that of the spacer. Neither can be neglected. Using a GaAs/AlGaAs crystalline coating, the Sx(f) contribution in a spacer for an optical cavity with and without ULE rings is about 59% and 32%, respectively, corresponding to the contribution of thermal noise in a spacer to the total thermal noise. The ULE ring noise contributions are much higher than that of the coating thermal noise. However, when using a SiO2/Ta2O5 coating, the main contribution of Sx(f) in the optical cavity comes from the spacer and coating, and Sx(f) in the spacer accounts for 38% of the total Sx(f) for the optical cavity without a ULE ring, corresponding to the proportion of spacer thermal noise in total thermal noise. We have the paradoxical situation that a mixed material cavity with additional rings shows more thermal noise than one without these rings, which is different from a cylindrical optical cavity. The main reason may be attributed to Fp resulting in a change in the internal stress in the optical cavity.
In mixed material cavities with FS substrates and an AlGaAs crystalline coating, the ULE spacer limits performance of the cubic optical cavity. Contributions to the thermal noise from the optical length Sx(f) as functions of the spacer length Lcub and Fp are shown in Figure 7. Under the condition of Fp = 0 N, when the spacer length Lcub is greater than 60 mm, the contribution of Sx(f) from the spacer equals that of the substrates. The total Sx(f) in the cubic optical cavity tends to a constant. As shown in Figure 7b, Sx(f) in the cubic cavity is proportional to Fp. For a 50 mm long ULE cubic optical cavity, when Fp is greater than 100 N, the displacement noise contributed from every 100 N Fp is about three times that of FS substrates and the GaAs/AlGaAs crystalline coating, corresponding to the contribution to the thermal noise by Fp.

5. Discussions and Conclusions

This research investigates the thermal noise in cubic optical cavities in detail through theoretical analysis and FEA. We derive an analytic formula for the thermal noise in the cubic spacer based on the FDT theory and strain theory. The calculation results based on this formula demonstrate qualitative agreement with that of the simulation. Compared with the previous estimation formula, this formula is more suitable for the estimation of the thermal noise of the cubic optical cavity. The reasons for the divergence of the results between the theoretical analysis and FEA are also provided.
For the cubic optical cavity, a compressive force Fp must be applied. We investigate the influence of the compressive force Fp on the thermal noise in cubic optical cavities in detail. This contribution to thermal noise has not been previously considered. To our knowledge, this is the first study of the compressive force influence Fp by numerical simulations.
For a 50 mm long mixed material cubic cavity with a ULE spacer and FS substrates, the displacement noise contributed from every 100 N of Fp is about three times that of the FS substrates and the GaAs/AlGaAs crystalline coating when Fp is larger than 100 N. The results show that Fp is the dominant noise source for some material choices and cavity geometries. Future studies about the thermal noise contributions in other shapes of optical cavities with different geometries should focus on the compressive force Fp, such as the spherical optical cavities. The results of this research offer guidance for cubic optical cavity design and minimizing the thermal noise.

Author Contributions

Conceptualization, G.X. and D.J.; methodology, G.X.; software, D.J.; validation, G.X. and D.J.; investigation, G.X.; data curation, L.Z.; writing—original draft preparation, G.X.; writing—review and editing, G.X.; visualization, L.C. and L.Z.; supervision, R.D.; project administration, T.L. and J.W. All authors have read and agreed to the published version of the manuscript.

Funding

The project is partially supported by the Youth Innovation Promotion Association of the Chinese Academy of Sciences (Grant No. 1188000XGJ), the Chinese National Natural Science Foundation (Grant No. 11903041), and the Young Innovative Talents of the National Time Service Center of the Chinese Academy of Sciences (Grant No. Y917SC1).

Acknowledgments

We would like to acknowledge contributions of the strain energy theory of the optical cavity to this paper from X. Zhang of Northwestern Polytechnical University, and F. Sun of National Time Service Center.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Katori, H. Optical lattice clocks and quantum metrology. Nat. Photonics 2011, 5, 203–210. [Google Scholar] [CrossRef]
  2. Swallows, M.D.; Bishof, M.; Lin, Y.; Blatt, S.; Martin, M.J.; Rey, A.M.; Ye, J. Suppression of collisional shifts in a strongly interacting lattice clock. Science 2011, 331, 1043–1046. [Google Scholar] [CrossRef] [PubMed]
  3. Huntemann, N.; Okhapkin, M.; Lipphardt, B.; Weyers, S.; Tamm, C.; Peik, E. High-accuracy optical clock based on the octupole transition in 171Yb+. Phys. Rev. Lett. 2012, 108, 090801. [Google Scholar] [CrossRef]
  4. Sherman, J.; Lemke, N.; Hinkley, N.; Pizzocaro, M.; Fox, R.; Ludlow, A.; Oates, C. High-accuracy measurement of atomic polarizability in an optical lattice clock. Phys. Rev. Lett. 2012, 108, 153002. [Google Scholar] [CrossRef]
  5. McFerran, J.J.; Yi, L.; Mejri, S.; Di Manno, S.; Zhang, W.; Guéna, J.; Le Coq, Y.; Bize, S. Neutral atom frequency reference in the deep ultraviolet with fractional uncertainty = 5.7 × 10−15. Phys. Rev. Lett. 2012, 108, 183004. [Google Scholar] [CrossRef]
  6. Herrmann, S.; Senger, A.; Mohle, K.; Nagel, M.; Kovalchuk, E.; Peters, A. Rotating optical cavity experiment testing Lorentz invariance at the 10−17 level. Phys. Rev. D 2009, 80, 105011. [Google Scholar] [CrossRef]
  7. Kennedy, C.; Oelker, E.; Robinson, J.M.; Bothwell, T.; Kedar, D.; Milner, W.; Marti, E.; Derevianko, A.; Ye, J. Precision metrology meets cosmology: Improved constraints on ultralight dark matter from atom-cavity frequency comparisons. Phys. Rev. Lett. 2020, 125, 201302. [Google Scholar] [CrossRef] [PubMed]
  8. Chou, C.W.; Hume, D.B.; Rosenband, T.; Wineland, D.J. Optical clocks and relativity. Science 2010, 329, 1630–1633. [Google Scholar] [CrossRef] [PubMed]
  9. Jiang, H.; Kéfélian, F.; Crane, S.; Lopez, O.; Lours, M.; Millo, J.; Holleville, D.; Lemonde, P.; Chardonnet, C.; AmyKlein, A.; et al. Long-distance frequency transfer over an urban fiber link using optical phase stabilization. J. Opt. Soc. Am. B 2008, 25, 2029–2035. [Google Scholar] [CrossRef]
  10. Predehl, K.; Grosche, G.; Raupach, S.M.F.; Droste, S.; Terra, O.; Alnis, J.; Legero, T.; Hnsch, T.W.; Udem, T.; Holzwarth, R.; et al. A 920-kilometer optical fiber link for frequency metrology at the 19th decimal place. Science 2012, 336, 441–444. [Google Scholar] [CrossRef] [PubMed]
  11. Matei, D.G.; Legero, T.; Häfner, S.; Grebing, C.; Weyrich, R.; Zhang, W.; Sonderhouse, L.; Robinson, J.M.; Ye, J.; Riehle, F.; et al. 1.5 μm Lasers with Sub-10 mHz Linewidth. Phys. Rev. Lett. 2017, 118, 263202. [Google Scholar] [CrossRef] [PubMed]
  12. Robinson, J.M.; Oelker, E.; Milner, W.R.; Zhang, W.; Legero, T.; Matei, D.G.; Riehle, F.; Sterr, U.; Ye, J. Crystalline optical cavity at 4 K with thermal-noise limited instability and ultralow drift. Optica 2019, 6, 240–243. [Google Scholar] [CrossRef]
  13. Barger, R.L.; Sorem, M.S.; Hall, L.J. Frequency stabilization of a cw dye laser. Appl. Phys. Lett. 1973, 22, 573–575. [Google Scholar] [CrossRef]
  14. Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 22, 97–105. [Google Scholar] [CrossRef]
  15. Levin, Y. Internal thermal noise in the LIGO test masses: A direct approach. Phys. Rev. D 1998, 57, 110403. [Google Scholar] [CrossRef]
  16. Numata, K.; Kemery, A.; Camp, J. Thermal-noise limit in the frequency stabilization of lasers with rigid cavities. Phys. Rev. Lett. 2004, 93, 250602. [Google Scholar] [CrossRef] [PubMed]
  17. Kessler, T.; Legero, T.; Sterr, U. Thermal noise in optical cavities revisited. J. Opt. Soc. Am. B 2012, 29, 178. [Google Scholar] [CrossRef]
  18. Legero, T.; Kessler, T.; Sterr, U. Tuning the thermal expansion properties of optical reference cavities with fused silica mirrors. J. Opt. Soc. Am. B 2010, 27, 914. [Google Scholar] [CrossRef]
  19. Webster, S.A.; Gill, P. Low-thermal-noise optical cavity. In Proceedings of the 2010 IEEE International Frequency Control Symposium, Newport Beach, CA, USA, 1–4 June 2010; Volume 470. [Google Scholar]
  20. Zhang, J.; Luo, Y.; Ouyang, B.; Deng, K.; Lu, Z.; Luo, J. Design of an optical reference cavity with low thermal noise limit and flexible thermal expansion properties. Eur. Phys. J. D 2013, 67, 46. [Google Scholar] [CrossRef][Green Version]
  21. Cole, G.D.; Zhang, W.; Martin, M.J.; Ye, J.; Aspelmeyer, M. Tenfold reduction of Brownian noise in high-reflectivity optical coatings. Nat. Photonics 2013, 67, 46. [Google Scholar] [CrossRef]
  22. Bruckner, F.; Friedrich, D.; Clausnitzer, T.; Britzger, M.; Burmeister, O.; Danzmann, K.; Kley, E.B.; Tunnermann, A.; Schnabel, R. Realization of amonolithic high-reflectivity cavity mirror from a single silicon crystal. Phys. Rev. Lett. 2010, 104, 163903. [Google Scholar] [CrossRef]
  23. Xu, G.; Zhang, L.; Liu, J.; Gao, J.; Chen, L.; Dong, R.; Liu, T.; Zhang, S. Estimation of thermal noise for spindle optical reference cavities. Opt. Commun. 2016, 360, 61–67. [Google Scholar] [CrossRef]
  24. Robinson, J.M.; Oelker, E.; Milner, W.R.; Kedar, D.; Zhang, W.; Legero, T.; Matei, D.G.; Hafner, S.; Riehle, F.; Sterr, U.; et al. Thermal noise and mechanical loss of SiO2/Ta2O5 optical coatings at cryogenic temperatures. Opt. Lett. 2021, 46, 592–595. [Google Scholar] [CrossRef] [PubMed]
  25. Webster, S.; Gill, P. Force-insensitive optical cavity. Opt. Lett. 2011, 36, 3572. [Google Scholar] [CrossRef]
  26. Leibrandt, D.R.; Thorpe, M.J.; Notcutt, M.; Drullinger, R.E.; Rosenband, T.; Bergquist, J.C. Spherical reference cavities for frequency stabilization of lasers in non-laboratory environments. Opt. Express 2011, 19, 3471–3482. [Google Scholar] [CrossRef] [PubMed]
  27. Leibrandt, D.R.; Thorpe, M.J.; Bergquist, J.C.; Rosenband, T. Field-test of a robust, portable, frequency-stable laser. Opt. Express 2011, 19, 10278–10286. [Google Scholar] [CrossRef]
  28. Vogt, S.; Lisdat, C.; Legero, T.; Sterr, U.; Ernsting, I.; Nevsky, A.; Schiller, S. Demonstration of a transportable 1 Hz-linewidth laser. Appl. Phys. B 2011, 104, 741. [Google Scholar] [CrossRef]
  29. Argence, B.; Argence, B.; Prevost, E.; Lévèque, T.; Le Goff, R.; Bize, S.; Lemonde, P.; Santarelli, G. Prototype of an ultra-stable optical cavity for space applications. Opt. Express 2012, 20, 25409–25420. [Google Scholar] [CrossRef]
  30. Leibrandt, D.R.; Bergquist, J.C.; Rosenband, T. Cavity-stabilized laser with acceleration sensitivity below 10−12 g−1. Phys. Rev. A 2013, 87, 023829. [Google Scholar] [CrossRef]
  31. Chen, Q.; Nevsky, A.; Cardace, M.; Schiller, S.; Legero, T.; Häfner, S.; Uhde, A.; Sterr, U. A compact, robust, and transportable ultra-stable laser with a fractional frequency instability of 1 × 10−15. Rev. Sci. Instrum. 2014, 85, 113107. [Google Scholar] [CrossRef] [PubMed]
  32. Świerad, D.; Häfner, S.; Vogt, S.; Venon, B.; Holleville, D.; Bize, S.; Kulosa, A.; Bode, S.; Singh, Y.; Bongs, K.; et al. Ultra-stable clock laser system development towards space applications. Sci. Rep. 2016, 6, 33973. [Google Scholar] [CrossRef] [PubMed]
  33. Koller, S.B.; Grotti, J.; Vogt, S.; Al-Masoudi, A.; Dörscher, S.; Häfner, S.; Sterr, U.; Lisdat, C. Transportable Optical Lattice Clock with 7 × 10−17 Uncertainty. Phys. Rev. Lett. 2017, 187, 073601. [Google Scholar] [CrossRef]
  34. Cao, J.; Zhang, P.; Shang, J.; Cui, K.; Yuan, J.; Chao, S.; Wang, S.; Shu, H.; Huang, X. A compact, transportable single-ion optical clock with 7.8 × 10−17 systematic uncertainty. Appl. Phys. B 2017, 123, 112. [Google Scholar] [CrossRef]
  35. SOC2-Towards Neutral-Atom Space Optical Clocks. Available online: http://www.exphy.uni-duesseldorf.de/optical_clock/soc2/index.php (accessed on 5 July 2021).
  36. LISA-Laser Interferometer Space Antenna-NASA Home Page. Available online: https://lisa.nasa.gov/index.html (accessed on 5 July 2021).
  37. Luo, J.; Sheng, L.; Duan, H.; Gong, Y.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quantum Grav. 2016, 33, 035010. [Google Scholar] [CrossRef]
  38. Tao, B.; Chen, Q. A vibration-sensitive-cavity design holds impact of higher than 100g. Appl. Phys. B 2018, 124, 228. [Google Scholar] [CrossRef]
  39. Hafiz, M.A.; Ablewski, P.; Masoudi, A.A.; Martínez, H.Á.; Balling, P.; Barwood, G.; Benkler, E.; Bober, M.; Borkowski, M.; Bowden, W.; et al. Guidelines for developing optical clocks with 10–18 fractional frequency uncertainty. arXiv 2019, arXiv:1906.11495. [Google Scholar]
  40. Chen, X.; Jiang, Y.; Li, B.; Yu, H.; Jiang, H.; Wang, T.; Yao, Y.; Ma, L. Laser frequency instability of 6 × 10−16 using 10-cm-long cavities on a cubic spacer. Chin. Opt. Lett. 2020, 18, 030201. [Google Scholar] [CrossRef]
  41. Wang, S.; Cao, J.; Yuan, J.; Liu, D.; Shu, H.; Huang, X. Integrated multiple wavelength stabilization on a multi-channel cavity for a transportable optical clock. Opt. Express 2020, 28, 11852–11860. [Google Scholar] [CrossRef] [PubMed]
  42. Cerdonio, M.; Conti, L.; Heidmann, A.; Pinard, M. Thermoelastic effects at low temperatures and quantum limits in displacement measurements. Phys. Rev. D 2001, 63, 082003. [Google Scholar] [CrossRef]
  43. Jiang, H. Development of Ultra-Stable Laser Sources and Long-Distance Optical Link via Telecommunication Networks. Ph.D. Thesis, University Pairs, Pairs, France, 2010. [Google Scholar]
Photonics 08 00261 g001
Figure 1. Sketch of the cubic optical cavity model with dimensions used for the analysis and FEA simulations in this publication. (a) Side view of the cubic optical cavity. (b) Front view of the cubic optical cavity.
Figure 1. Sketch of the cubic optical cavity model with dimensions used for the analysis and FEA simulations in this publication. (a) Side view of the cubic optical cavity. (b) Front view of the cubic optical cavity.
Photonics 08 00261 g001
Photonics 08 00261 g002
Figure 2. Deformation and contour plot of elastic strain energy density of element (ESEDEN) in the cavity for a Gaussian pressure profile with a 2 mm waist on the mirror surface. The color coding corresponds to the log(ESEDEN). The edge Lcub of the cubic optical cavity is 32 mm. Note that the deformation has been amplified by a factor of 9 × 105 for demonstration.
Figure 2. Deformation and contour plot of elastic strain energy density of element (ESEDEN) in the cavity for a Gaussian pressure profile with a 2 mm waist on the mirror surface. The color coding corresponds to the log(ESEDEN). The edge Lcub of the cubic optical cavity is 32 mm. Note that the deformation has been amplified by a factor of 9 × 105 for demonstration.
Photonics 08 00261 g002
Photonics 08 00261 g003
Figure 3. Strain energy as a function of edge Lcub of the cubic spacer. The solid blue line with circles represents the simulation results. Magenta solid line with squares presents the analytic estimate according to Equation (2) in Ref. [16]. Cyan solid line with stars presents the analytic estimate according to Equation (2). (a) ULE cubic spacer with ULE substrates. (b) Zerodur cubic spacer with Zerodur substrates.
Figure 3. Strain energy as a function of edge Lcub of the cubic spacer. The solid blue line with circles represents the simulation results. Magenta solid line with squares presents the analytic estimate according to Equation (2) in Ref. [16]. Cyan solid line with stars presents the analytic estimate according to Equation (2). (a) ULE cubic spacer with ULE substrates. (b) Zerodur cubic spacer with Zerodur substrates.
Photonics 08 00261 g003
Photonics 08 00261 g004
Figure 4. Strain energy as a function of edge Lcub of the cubic spacer. The solid blue line with circles presents the simulation results. Magenta solid line with squares presents the analytic estimate according to Equation (2) in Ref. [16]. Cyan solid line with stars presents the analytic estimate according to Equation (2). (a) Silica cubic spacer with silica substrates. (b) Sapphire cubic spacer with sapphire substrates.
Figure 4. Strain energy as a function of edge Lcub of the cubic spacer. The solid blue line with circles presents the simulation results. Magenta solid line with squares presents the analytic estimate according to Equation (2) in Ref. [16]. Cyan solid line with stars presents the analytic estimate according to Equation (2). (a) Silica cubic spacer with silica substrates. (b) Sapphire cubic spacer with sapphire substrates.
Photonics 08 00261 g004
Photonics 08 00261 g005
Figure 5. Compressive force model of a cubic optical cavity and strain energy as a function of the compressive force. Fp is the compressive force. The red arrows indicate the directions of Fp. Blue dashed line with circles represents the simulation results of strain energy of cubic optical cavities. When Fp is 0 N, the strain energy U0 is indicated by a red solid line. Note that Lcub and material of the cubic cavity are 50 mm and ULE, respectively. (a) Compressive force model of a cubic optical cavity. (b) Strain energy as a function of Fp.
Figure 5. Compressive force model of a cubic optical cavity and strain energy as a function of the compressive force. Fp is the compressive force. The red arrows indicate the directions of Fp. Blue dashed line with circles represents the simulation results of strain energy of cubic optical cavities. When Fp is 0 N, the strain energy U0 is indicated by a red solid line. Note that Lcub and material of the cubic cavity are 50 mm and ULE, respectively. (a) Compressive force model of a cubic optical cavity. (b) Strain energy as a function of Fp.
Photonics 08 00261 g005
Photonics 08 00261 g006
Figure 6. Contributions to the thermal noise of the optical length Sx(f) of a cubic optical cavity with and without thermal expansion compensation rings. (a) ULE spacer, FS substrates, SiO2/Ta2O5 coating, and ULE rings, the thickness dcoa = 2 μm cited from Refs. [17,43]. (b) ULE spacer, FS substrates, GaAs/AlGaAs crystalline coating, and ULE rings, the thickness dcoa = 6.83 μm cited from Ref. [21].
Figure 6. Contributions to the thermal noise of the optical length Sx(f) of a cubic optical cavity with and without thermal expansion compensation rings. (a) ULE spacer, FS substrates, SiO2/Ta2O5 coating, and ULE rings, the thickness dcoa = 2 μm cited from Refs. [17,43]. (b) ULE spacer, FS substrates, GaAs/AlGaAs crystalline coating, and ULE rings, the thickness dcoa = 6.83 μm cited from Ref. [21].
Photonics 08 00261 g006
Photonics 08 00261 g007
Figure 7. Contributions to the thermal noise of the optical length Sx(f) as functions of the spacer length Lcub and Fp. The spacer is made of ULE. The substrates and coating of the two mirrors are FS and GaAs/AlGaAs crystalline, respectively. (a) The spacer length Lcub. (b) Compressive force Fp.
Figure 7. Contributions to the thermal noise of the optical length Sx(f) as functions of the spacer length Lcub and Fp. The spacer is made of ULE. The substrates and coating of the two mirrors are FS and GaAs/AlGaAs crystalline, respectively. (a) The spacer length Lcub. (b) Compressive force Fp.
Photonics 08 00261 g007
Table 1. Parameters used for estimation and simulation.
Table 1. Parameters used for estimation and simulation.
Parametersdsub (mm)rmirror (mm)rvent (mm)rspa (mm)lcub (mm)kB
Value6.312.73716.41.381 × 10−23 J/K
Table 2. Material properties.
Table 2. Material properties.
Material PropertiesULE [18]FS [1,2,3,4,5,6,7,8]Silica
<111> [14]		Zerodur [21]Sapphire [42]SiO2/Ta2O5 [21]GaAs/Al GaAs [21]
Elastic modulus (GPa)67.673187.59140091100
Poisson ratio0.170.160.230.240.290.190.32
Loss angle1.67 × 10−510−610−73 × 10−43 × 10−94 × 10−42.5 × 10−5
Table 3. The elastic strain energy of the spacer calculated by FEA and two equations.
Table 3. The elastic strain energy of the spacer calculated by FEA and two equations.
MaterialElastic Strain Energy of Spacer (nJ)
SpacerSubstrateEstimationFEA
Equation (2)Reference [16]
ULEULE0.180.060.94
ULEULE0.180.060.93
ZerodurZerodur0.140.040.69
ZerodurZerodur0.140.040.74
SilicaSilica0.070.020.34
SapphireSapphire0.030.010.16
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Xu, G.; Jiao, D.; Chen, L.; Zhang, L.; Dong, R.; Liu, T.; Wang, J. Thermal Noise in Cubic Optical Cavities. Photonics 2021, 8, 261. https://doi.org/10.3390/photonics8070261

AMA Style

Xu G, Jiao D, Chen L, Zhang L, Dong R, Liu T, Wang J. Thermal Noise in Cubic Optical Cavities. Photonics. 2021; 8(7):261. https://doi.org/10.3390/photonics8070261

Chicago/Turabian Style

Xu, Guanjun, Dongdong Jiao, Long Chen, Linbo Zhang, Ruifang Dong, Tao Liu, and Junbiao Wang. 2021. "Thermal Noise in Cubic Optical Cavities" Photonics 8, no. 7: 261. https://doi.org/10.3390/photonics8070261

APA Style

Xu, G., Jiao, D., Chen, L., Zhang, L., Dong, R., Liu, T., & Wang, J. (2021). Thermal Noise in Cubic Optical Cavities. Photonics, 8(7), 261. https://doi.org/10.3390/photonics8070261

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop