A Broadband High-Diffraction-Efficiency Electro-Optic Bragg Deflector Based on Monolithic Dual-Grating Periodically-Poled Lithium Niobate

Chiang, An-Chung; Lin, Yuan-Yao; Lin, Shou-Tai; Lin, Yen-Yin

doi:10.3390/photonics8070242

Open AccessArticle

A Broadband High-Diffraction-Efficiency Electro-Optic Bragg Deflector Based on Monolithic Dual-Grating Periodically-Poled Lithium Niobate

¹

Nuclear Science and Technology Development Center, National Tsing-Hua University, Hsinchu 300044, Taiwan

²

Department of Photonics, National Sun Yat-Sen University, Kaohsiung 804201, Taiwan

³

Department of Photonics, Feng Chia University, Taichung 407802, Taiwan

⁴

JelloX Biotech Inc., Hsinchu 300044, Taiwan

^*

Author to whom correspondence should be addressed.

^†

These authors contributed equally to this work.

Photonics 2021, 8(7), 242; https://doi.org/10.3390/photonics8070242

Submission received: 31 May 2021 / Revised: 22 June 2021 / Accepted: 26 June 2021 / Published: 28 June 2021

(This article belongs to the Special Issue Electro-Optic Modulator)

Download

Browse Figures

Versions Notes

Abstract

:

Electro-optic (EO) Bragg deflectors have been extensively used in a variety of applications. Recent developments show that bandwidths and deflection efficiencies, as well as angular bandwidths, would significantly limit the utilization of EO Bragg deflectors, especially for applications which need strong focusing, such as intra-cavity applications. In this paper, we introduce a broadband EO Bragg deflector based on periodically-poled lithium niobate with a monolithic dual-grating design. We analyzed the deflection properties of this device by using a modified coupled wave theory and showed that this device can be still efficient for a small beam radius under strong focusing, whereas a single-grating one becomes very inefficient. Using a 1064-nm laser beam with a 100-μm beam radius, we obtained a 74% deflection efficiency with a 190-V bias voltage with a 0.5-mm-thick and 7.5-mm-long dual-grating sample. The acceptance angle for the Bragg condition of this device is as large as a few tens of mrad. The potential bandwidth of this device exceeds 500 nm if the proper operation region is chosen.

Keywords:

lithium niobite; PPLN; Bragg deflectors

1. Introduction

The electro-optics modulator (EOM) and acoustic-optics modulator (AOM) are two major photonic devices used to manipulate laser power. The modulation bandwidth of an AOM is limited by the propagation speed of the transmitted acoustic waves that act as a dynamic Bragg grating. An EOM, on the other hand, can provide much better modulation speed due to the fast electric response, but usually requires extra polarization components for intensity modulation, and thus the supported wavelength is strongly limited.

In 1996, domain-inverted lithium niobate devices were investigated to equip an efficient Bragg deflector with improved modulation bandwidth by the electro-optic (EO) effect [1]. The domain-inverted lithium niobate, also known as periodically-poled lithium niobate (PPLN), has become an important optical material in nonlinear frequency mixing processes due to its high nonlinearity, artificial phase-matching condition, and repeatable fabrication. The fabricating techniques are now well developed and device-quality PPLN crystals can be routinely manufactured [2]. Measurements on diffraction efficiencies for performance enhanced PPLN Bragg switches for statically and dynamically applied electric fields were also demonstrated [3]. M. Yamada published a review article, summarized the main concept of PPLN Bragg devices and demonstrated several useful applications [4]. Recently, such an electro-optic PPLN Bragg deflector (EOPBD) was adopted to be a laser Q-switch in laser cavities as well as a parametric down conversion device due to its insensitivity to temperature variation [5,6,7]. Moreover, the intrinsic wavelength sensitivity of EOPBD made it applicable for selecting oscillation wavelengths in a continuous-wave laser cavity [8]. The cascaded design of ref [8] is adopted to construct a wavelength selectable actively Q-switched Tm:YAP laser [9].

However, the decrease in deflection efficiency of EOPBD for smaller laser beam radii is experimentally observed [6,10]. The reduced deflection efficiency is caused by the angular distribution of the incident laser beam which does not completely match the Bragg condition given by the grating period of the EOPBD. Conventional coupled wave theory uses a plane wave assumption, ignoring the angular distribution of the incident laser beam, would not expect the reduced deflection efficiency which significantly limits the performance of EOPBD [11], in particular, in a laser cavity, as well as an optical parametric oscillator or similar nonlinear optical processes that require high intensities as a result of strong beam focusing.

To extend the function of EOPBD, we introduce a broadband EO Bragg deflector based on PPLN with a monolithic dual-grating design. The deflection properties of this device were analyzed theoretically and experimentally. Experimental results showed good deflection efficiency and broad angular bandwidth that justified the theoretical prediction.

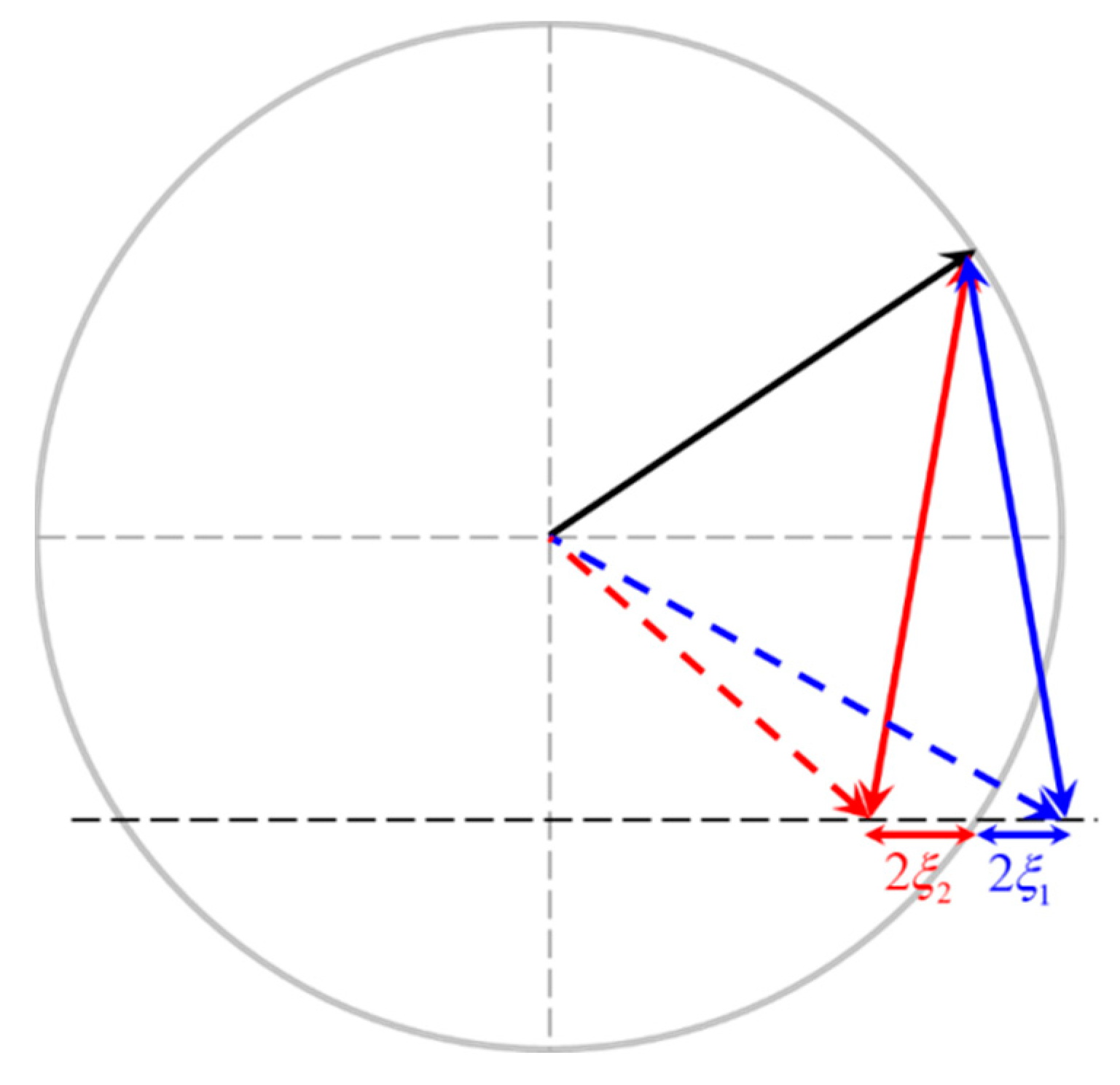
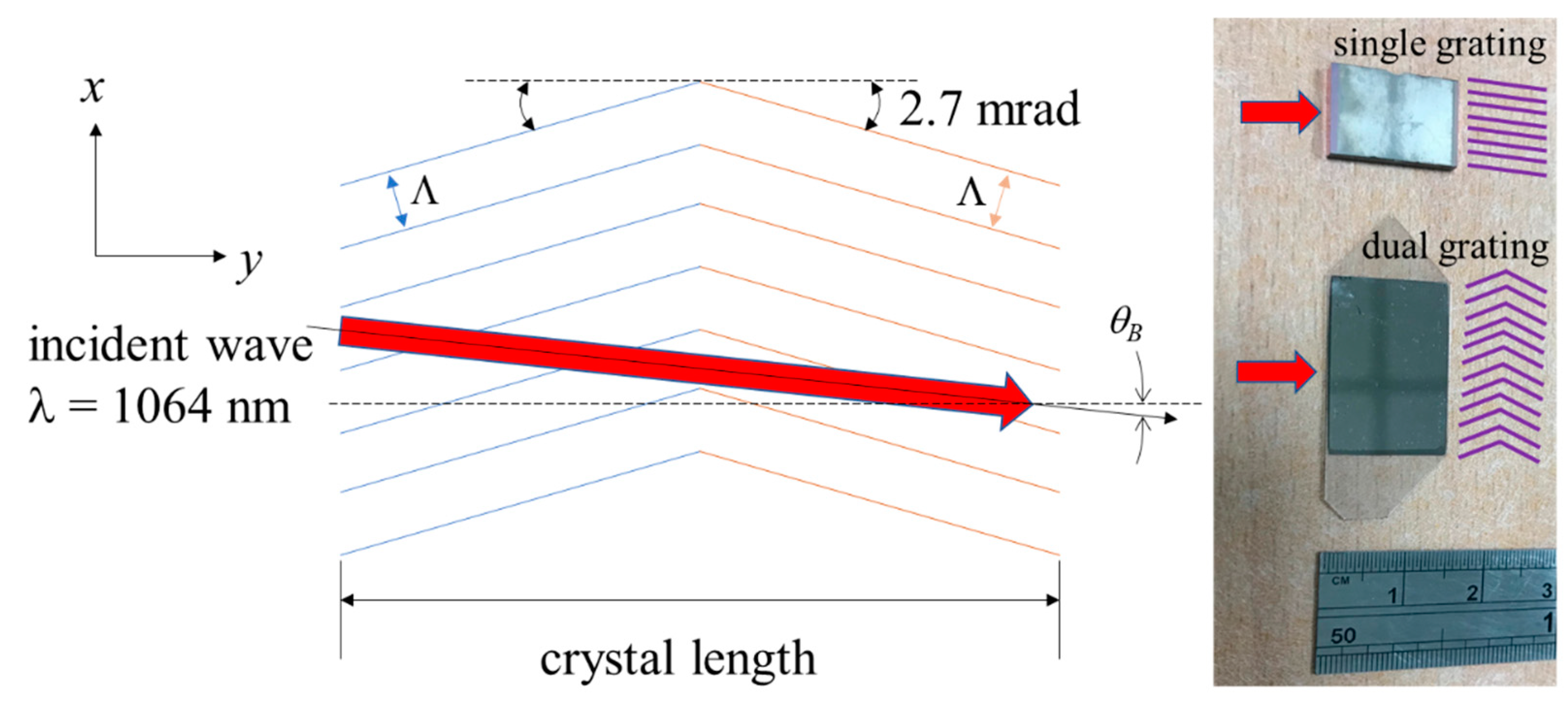
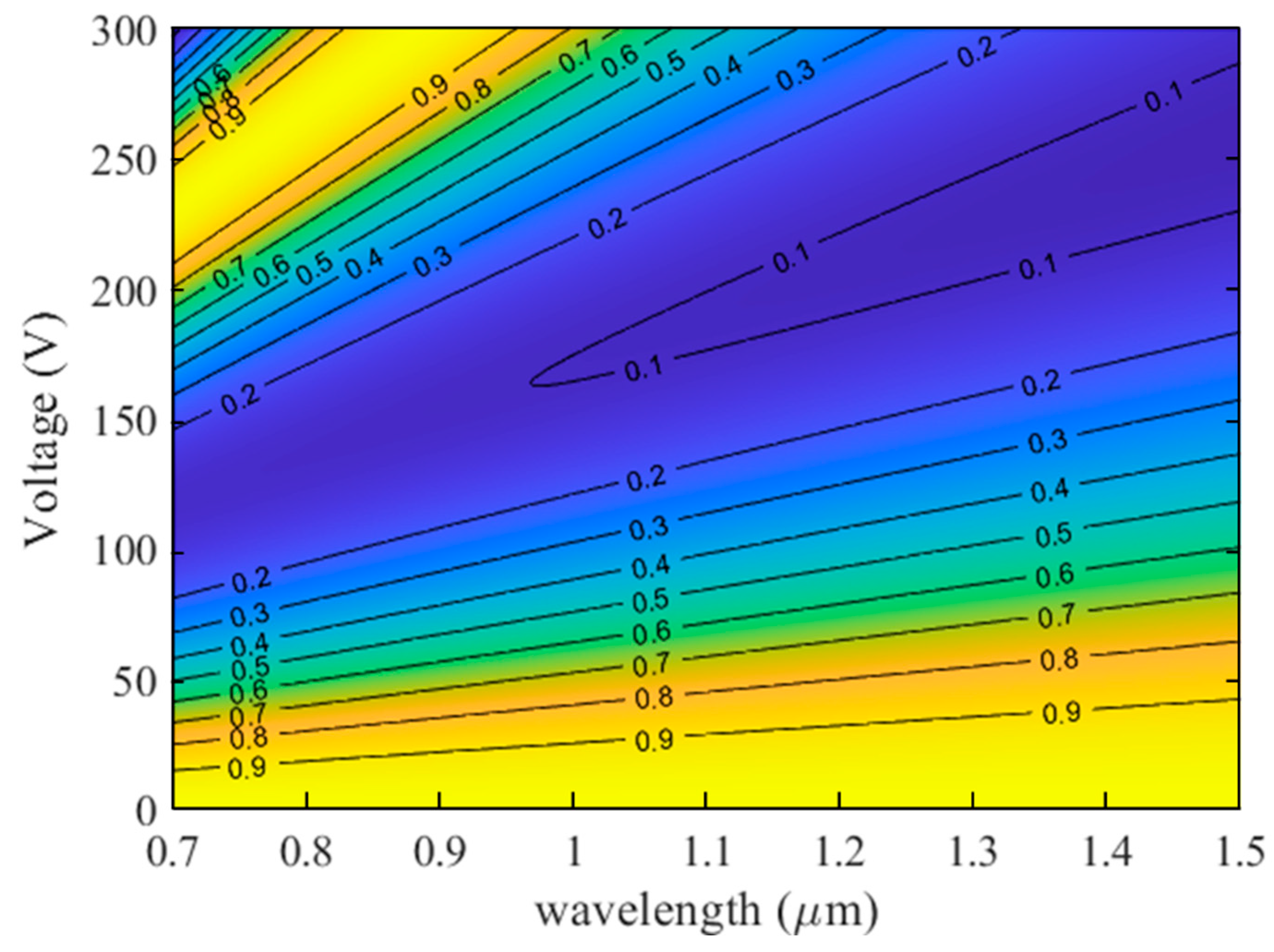
2. Device Design and Theoretical Modeling

Considering the angular distribution of an incident laser beam, we have developed a coupled wave theory for EOPBD with an incident laser beam containing multiple wave vectors. In this model, we assume each spatial component is linearly coupled to the associated diffracted components subject to the Bragg condition. The interactions among spatial components in the incident beam are excluded because the coupling between each component is insignificant and the phase matching condition is not fulfilled. The procedure of the numerical simulation mainly consists of the following steps: (1) Express the PPLN refractive index as a periodic function subject to its position; (2) Express the electric field in the EOPBD as the superposition of the incident wave and the reflected wave; (3) Apply the refractive index function and the electric field into the Helmholtz equation and find the solution subject to the boundary condition; (4) Conduct linear superposition of plane waves spanning a finite angular spectrum approximately within the diffraction angle for a finite beam size and a very large grating dimension. Appendix A shows the detailed steps of the extended model for single-grating-based EOPBD. This model has been applied to the experimental measurement of the deflection efficiency of a single-grating EOPBD incident by a Gaussian beam with a waist radius of 210 μm, showing great consistency with experimental observation both qualitatively and quantitatively [6].

Supported by the same extended model, a monolithic dual-grating structure, as schematically shown in Figure 1, was designed and characterized. Appendix B conceptually shows the extended model for dual grating based EOPBD. The incident wave containing multiple spatial components has a wavelength of 1064 nm and propagates toward the y-direction. The two PPLN grating vectors form ±2.7-mrad angles with respect to the y-axis, as shown in Figure 1. The PPLN grating period is 20.25 μm. Figure 1 also shows a picture of the single-grating and the dual-grating PPLN samples used in the experimental section of this paper. The grating vectors are illustrated schematically in the picture. In Figure 2, the simulated transmission curves of the single-grating and the dual-grating EOPBDs for different beam sizes are plotted as a function of θL given in Equation (A5), where θ denotes a parameter related to the phase-mismatching and the coupling coefficients, and L is the length of the crystal (See Appendix A for more information). Due to the Pockels effect, the coupling strength of EOPBD is linearly proportional to the biased voltage applied to the crystalline c-axis (z-axis) if the thickness and the length of the crystals are identified. Figure 2 shows that for both the single-grating and the dual-grating configurations, the deflection efficiency is degraded by the decreasing waist size. When the waist size is small, the incident wave contains multiple spatial components with more different wave vectors, which result in more phase mismatch with respect to the EOPBD grating vector(s). As the waist size of the incident beam increases, the behavior of the incident wave acts more like a plane wave, thus yields to a more ideal deflection efficiency.

Figure 3 shows the first minimum transmission of the transmission curves versus incident beam radius for the single-grating and the dual-grating configurations for θL < 1. Notice that the first minimum transmission occurs at different θL as shown in Figure 2. When the beam radius is 100 μm, the transmission of the single- and the dual-grating configurations are 16.46% and 18.30%, respectively, when proper coupling strength is applied. Under this focusing condition, the beam radius does not cause significant reduction in deflection efficiencies for the two configurations. However, as the beam radius decreases, the first minimum transmission gradually increases. The first minimum transmission of the single-grating configuration increases to 37.54% if the beam radius is 50 μm, while that of the dual-grating one is 16.77%. This demonstrates that the dual-grating configuration can sustain better deflection efficiency than the single-grating one when the beam size is smaller. Moreover, when the beam radius is reduced to 10 μm, the transmission of the single- and the dual-grating configurations are 82.30% and 42.92%, respectively. The single-grating configuration no longer provides significant deflection efficiency under such a strong focusing condition.

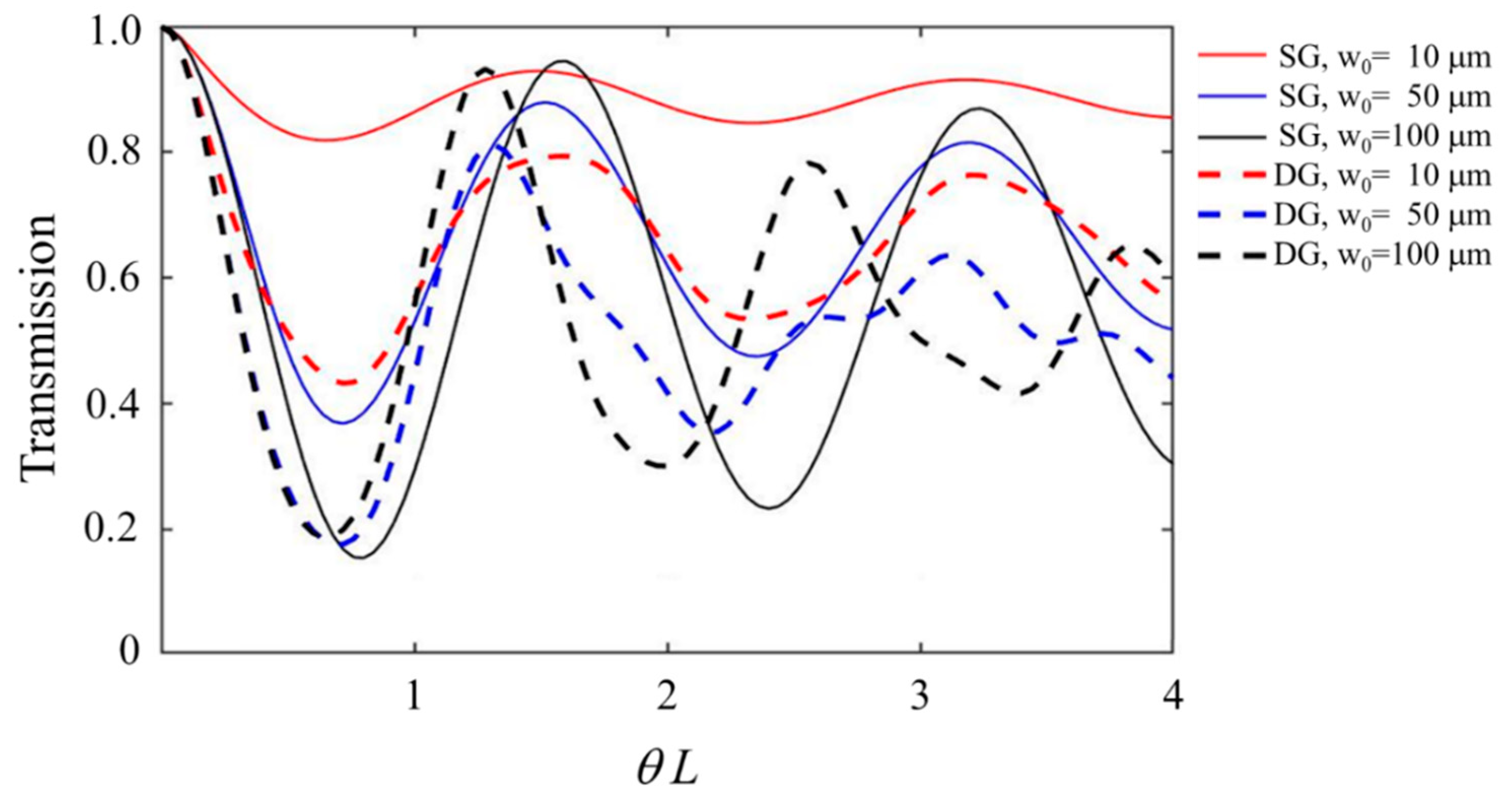
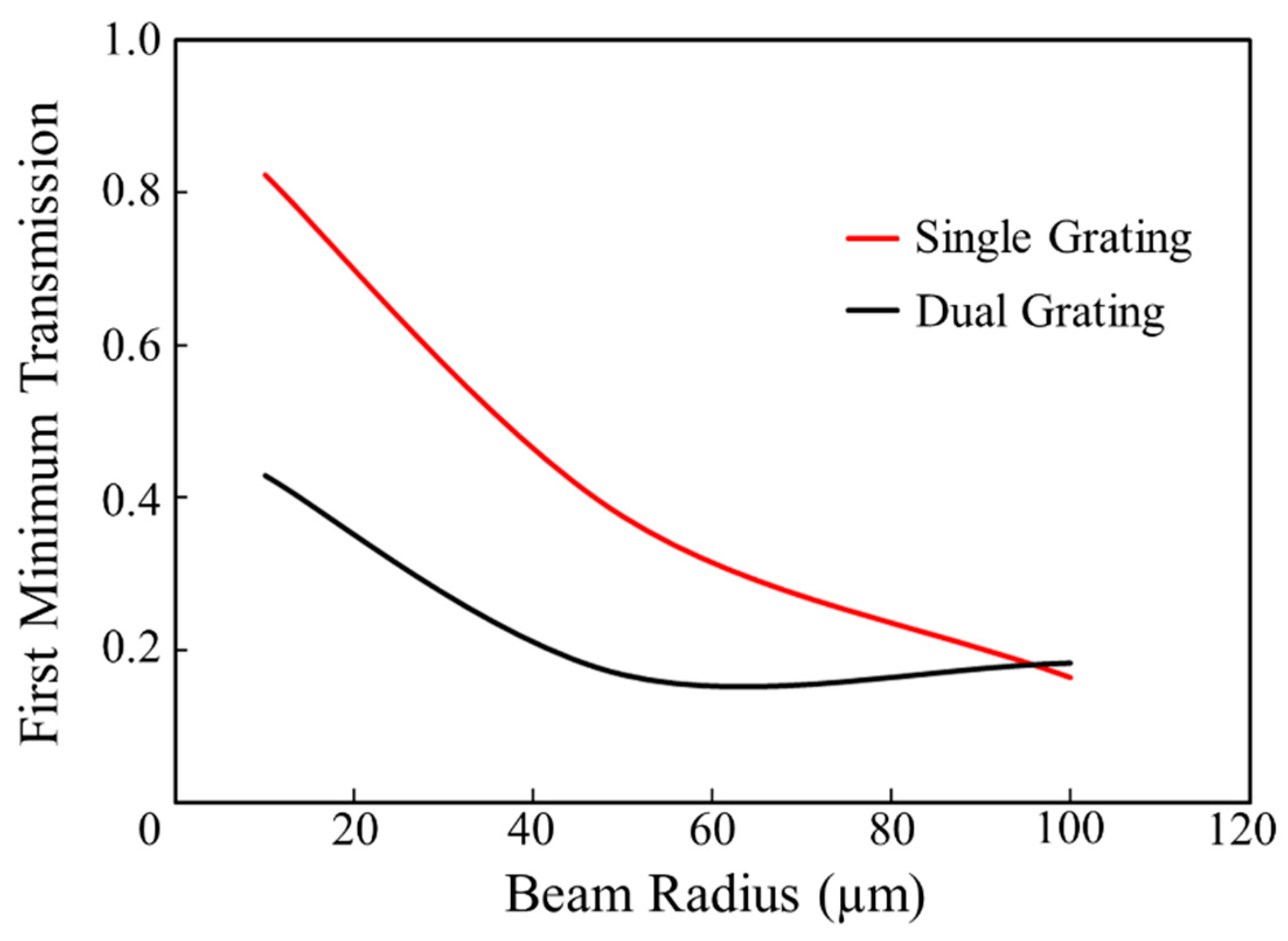
3. Experimental Results

We prepared a 0.5-mm-thick, 15-mm-long, dual-grating EOPBD sample with its two grating vectors form ±2.7-mrad angles with respect to the y axis as shown in Figure 1. The grating period of the dual-grating EOPBD sample was 20.25 μm. The top and the bottom surfaces were coated with 50-nm NiCr electrodes on which a high voltage from a high-voltage amplifier was applied to form a Bragg grating. We also prepared a 2-mm-thick, 13.5-mm-long, single-grating EOPBD sample with a 20.30-μm grating period for a comparison experiment. While using a 1064-nm laser beam as the incident wave, the half-wave voltage

V_{π}

can be determined by [12]:

V_{π} = \frac{4}{π} \frac{λ}{r_{33} n_{e}^{3}} \frac{d}{L},

(1)

where

r_{33}

(29.4 pm/V) is the Pockels coefficient of LiNbO₃,

n_{e}

(2.156) is the extraordinary refractive index, λ (1064 nm) is the wavelength of the incident wave, d is the thickness, and L is the effective length of the crystal. As the dual-grating sample can be regarded as a PPLN crystal in which two single-grating sections cascade in series, the effective length of the dual-grating one is 15 mm/2 = 7.5 mm. This can be confirmed in the numerical results from the extended wave theory shown in this paper. As a result, the half-wave voltages of the dual-grating and the single-grating samples are calculated to be 190 V and 420 V, respectively.

With the 1064 nm incident wave, the Bragg condition for the 20.25- and 20.30-μm grating periods required a ~0.69° incident angle as the Bragg angle. We optimized the incident angle of the incident laser beam so that the Bragg condition is satisfied. If the incident angle differed too much from the Bragg angle, the deflection efficiency would dramatically drop. As the applied voltage ranged from −500 V to + 500 V, we measured the 1064-nm zero-th order transmission of the two EOPBD samples. Figure 4 shows the theoretical and experimental results for the two samples. The beam size in the samples was controlled to be about 100 μm. The theoretical prediction is calculated using Equations (A5) and (A7), respectively for the single-grating and the dual-grating configurations. It is found that the experimental results showed great agreement with the theoretical predictions.

For the dual-grating sample, the first two transmission dips occurred when the bias voltage was −165.5 V and +263.5 V and the corresponding half-wave voltage was about 210 V. The transmission at these two locations are 26.62% and 25.15%, respectively, showing a ~74% deflection efficiency for the dual-grating EOPBD. For the single-grating sample, the first two transmission dips occurred when the bias voltage was −432.5 V and +543 V and the corresponding half-wave voltage was about 480 V. The transmission at these two locations are 52.85% and 53.15%, respectively, showing a ~47% deflection efficiency for the single-grating EOPBD. Due to the stress-induced refractive-index change between adjacent ferroelectric domains [13], the peak transmittance of the curve is slightly shifted away from the zero-voltage point. The inset of Figure 4 shows the typical diffraction patterns of the single-grating and the dual-grating samples viewing from an infrared sensor card. The single-grating diffraction pattern shows a typical zero-th order beam and a first-order diffraction beam. The dual-grating diffraction pattern shows a zero-th order beam and several diffraction beams which can be realized from the schematic sketch in Figure 4.

While optimizing the incident angle to fulfill the Bragg condition, we also recorded the transmission curves for different incident angles. Figure 5 shows the transmission curves for the dual-grating EOPBD, demonstrating that the deflection efficiency became poorer when the incident angle started to deviate from the Bragg angle. Notice that the 0° curve represents that incident angle is right at the Bragg angle, giving the best transmission contrast. When the deviation angle was 1.6° (28 mrad), the minimum transmission was 45.65%. When the deviation angle was further increased to 4° (70 mrad), it became difficult to find out a minimum transmission near the ±200 V region. This means that the dual-grating EOPBD was efficient within a few-tens-of-mrad acceptance angle, which is good for beam alignment and helpful for system stability.

The same experiment was performed for the single-grating EOPBD. It was found that even the incident angle was right at the Bragg angle, the minimum transmission was already higher than 52% and increased to 60% when the deviation angle was 0.8° (14 mrad). If the deviation angle was larger than 0.8° (14 mrad), we could not find a transmission minimum within ±600 V for the single-grating EOPBD. The acceptance angle of the single-grating EOPBD was very small compared to the dual-grating one.

In addition to the deflection efficiency measurement, we also did a theoretical simulation about the bandwidth of the dual-grating EOPBD with an incident laser beam of 100 μm. Figure 6 shows the theoretical contour plot of the transmission as a function of wavelengths and applied voltages. It is found that there is a simultaneous broadband and high-deflection efficiency operation region during the 150~200-V region. During this region, the deflection bandwidth exceeds 500 nm. Dispersion of refractive indices is included in the simulation.

4. Conclusions

In conclusion, we introduced a monolithic dual-grating configuration of EOPBD for broadband operation with high deflection efficiency according to a modified coupled wave theory. Experimental results showed a greatly improved deflection efficiency and justified the theoretical prediction. This device not only remains efficient for strong focusing operation but also provides a good angular bandwidth for easy alignment and good system ruggedness. The potential bandwidth of this device exceeds 500 nm if the proper operation region is chosen. As reported in [6], the low bias voltage, which would result in small refractive-index change, does not cause significant scattering loss due to the high-order Fourier components of the square-wave PPLN grating. This gives a promising future for developing a novel active mode-locking laser using an EOPBD as an intra-cavity EO modulator.

Author Contributions

Conceptualization, A.-C.C., Y.-Y.L. (Yen-Yin Lin) and S.-T.L.; methodology, S.-T.L.; software, Y.-Y.L. (Yuan-Yao Lin); validation, Y.-Y.L. (Yuan-Yao Lin); formal analysis, Y.-Y.L. (Yuan-Yao Lin); investigation, S.-T.L.; resources, A.-C.C.; data curation, A.-C.C. and S.-T.L.; writing—original draft preparation, A.-C.C. and Y.-Y.L. (Yuan-Yao Lin); writing—review and editing, A.-C.C.; visualization, A.-C.C.; supervision, A.-C.C., S.-T.L. and Y.-Y.L. (Yen-Yin Lin); project administration, A.-C.C.; funding acquisition, A.-C.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science and Technology (MOST) of Taiwan, Grant number MOST 108-2221-E-007-049; National Tsing-Hua University (NTHU) of Taiwan, Grant number 110H0000L1.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

The authors thank P.C. Liu for assisting experimental measurement and data acquisition.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Extended Model for Single Grating Based EOPBD

Applying an electric field upon a PPLN crystal, the periodic domain inversion causes the refractive index in the PPLN periodic. When an external electric field is applied along z-direction, the reflective indices in the positive (un-poled) and negative (poled) domains are

Δ n_{e}^{+} = - \frac{1}{2} n_{e}^{3} r_{33} E_{3}

and

Δ n_{e}^{-} = + \frac{1}{2} n_{e}^{3} r_{33} E_{3}

, respectively.

n_{e}^{}

is the extraordinary refractive index,

r_{33}

is the Pockels coefficient of LiNbO₃, and

E_{3}

is the static electrical field applied across the PPLN crystal in z-direction. The period of square-wave typed modulated refractive index is

Λ_{G}

, which corresponds to the domain inversion period of the PPLN crystal. Assuming the periodic modulation is along x-direction, the refractive index can then be written as:

n_{e} (x) = n_{e} + Δ n_{e} \sum_{m = - \infty}^{\infty} G_{m} \exp (- j m k_{G} x)

(A1)

where

Δ n_{e}^{} = - \frac{1}{2} n_{e}^{3} r_{33} E_{3}

,

k_{G} = \frac{2 π}{Λ_{G}}

, and

G_{m} = \frac{2}{π m} \sin (π m D)

in which the PPLN duty cycle D is defined to be the positive-domain percentage in one PPLN period and m is an integer. In this paper, D = 50% is used. Although electromagnetic wave propagation in periodic media can be expanded by the spatial harmonics according to the Flochet theory, the dispersion relation and momentum conservation of electromagnetic waves set a possible selection rule for efficient couplings between the harmonics. In particular when the propagation distance is large and the grating strength is low, only a few harmonics are significant. We consider electromagnetic waves polarized along the z-direction and propagating paraxially along y-direction in EOPBD with transverse modulation along x-direction, its electrical field E is conventionally expressed by the superposition of incident and reflected waves:

E = E_{I} (y) \exp [i k_{I} x] \exp [i β_{I} y] + E_{R} (y) \exp [i k_{R} x] \exp [i β_{R} y]

(A2)

where

E_{I}

and

E_{R}

are complex amplitude of incident and reflected waves which are slowly varying function of position y.

k_{I}

(

β_{I}

) and

k_{R}

(

β_{R}

) are the projection of wave vector onto x- and y-direction of incident wave along x-y plane. Without loss of generality, the momentum conservation imposes that

k_{R} = k_{I} - k_{G}

and

β_{R} = β_{I}

. The dispersion relation further introduces the relation

k_{R}^{2} + β_{R}^{2} = k_{I}^{2} + β_{I}^{2}

. In this case, one readily obtains

k_{R} = - k_{I} = - \frac{k_{G}}{2} \equiv k_{B}

, known as the Bragg condition as illustrated in Figure A1 and

β_{R} = β_{I} = \sqrt{n_{e}^{2} k_{0}^{2} - k_{B}^{2}} \equiv β

in which k₀ is the wave vector of electromagnetic wave propagating in vacuum. Moreover, in case the incident wave propagating along the direction

k_{I} = k_{B} + δ

deviates from the Bragg condition as shown in Figure A1, the mismatch in wave vector along the y-direction can be calculated using the dispersion relation and expressed as

β_{I} = β - ξ

,

β_{R} = β + ξ

, and

ξ \approx \frac{k_{B} δ}{β_{y} (δ)}

. Taking the expression in Equation (A2) and the refractive index in Equation (A1) into the Helmholtz equation, the coupled wave equation is as follows:

\begin{array}{l} \frac{\partial E_{I}}{\partial y} = - i κ_{I} E_{R} \exp [- i ξ y] \\ \frac{\partial E_{R}}{\partial y} = - i κ_{R} E_{I} \exp [+ i ξ y] \end{array}

(A3)

in which the coupling coefficient is given by:

κ_{I} = κ_{R} = \frac{n_{e}^{4} k_{0}^{2} r_{33}}{π β} E_{3} \equiv κ

(A4)

In practice, only the incident wave presents at the beginning of the EOPBD crystal. One imposes the conditions

E_{R} (0) = 0

and sets the initial field amplitudes

E_{I} (0)

and EOPBD crystal length L. This suffices to obtain the solution to Equation (A3):

\begin{array}{l} E_{I} (L) = \frac{E_{I} (0)}{θ} \exp [- i \frac{ξ}{2} L] [i \frac{ξ}{2} \sin (θ L) + θ \cos (θ L)] \\ E_{R} (L) = \frac{κ E_{I} (0)}{θ} \exp [i \frac{ξ}{2} L] \sin (θ L) \end{array}

(A5)

where

θ = \sqrt{{(\frac{ξ}{2})}^{2} + κ_{I} κ_{R}}

. The above derivation is based on an infinite beam size and infinite grating dimension. In practical, it is only valid when the laser waist of the radius is much larger than the grating period. Moreover, the grating dimension is required to overwhelm the laser beam radius. When a finite beam size and very large grating dimension are concerned, the incident laser can be formed by the linear superposition of plane waves spanning a finite angular spectrum approximately within the diffraction angle about the incident direction with the transverse wave vector equal to

k_{B}

. For any angular spatial component with the transverse wave vector

k_{I} = k_{B} + δ

, the transmitted and reflected angular waves density have the amplitudes following the result in Equation (A5). The transmitted and reflected waves are expressed by:

\begin{array}{l} E_{I} (L) = \int_{- \infty}^{\infty} d x \int_{- \infty}^{\infty} \frac{d δ κ A (k_{B} + δ)}{θ} \exp [- i \frac{ξ}{2} y] [i \frac{ξ}{2} \sin (θ L) + θ \cos (θ L)] \exp [i (β - ξ) L + i (k_{B} + δ) x] \\ E_{R} (L) = \int_{- \infty}^{\infty} d x \int_{- \infty}^{\infty} \frac{d δ κ A (k_{B} + δ)}{θ} \exp [i \frac{ξ}{2} y] \sin (θ L) \exp [i β L] \exp [i (β + ξ) L + i (- k_{B} + δ) x] \end{array},

(A6)

where

A (k_{B} + δ) d δ

is the angular field amplitude.

Figure A1. Wavevector representation illustrating phase mismatching of the incident and reflected waves in the single-grating EOPBD with a grating period of Λ_G. The annotation in black shows the perfect phase matching under the Bragg condition. The annotation in red reveals the quantity of phase mismatch when the incident wave is slightly deviated from the Bragg condition.

Appendix B. Extended Model for Dual Grating Based EOPBD

In general, the refractive index distribution formed by electric voltage biased EOPBD can exhibit multiple periods in x- and in y-directions when 2D poling techniques are utilized. We may write the refractive index distribution as a sum of cosine series:

n_{e} + Δ n_{e} (x, y) = n_{e} + \sum_{l} Δ n_{l} \cos (g_{x}^{l} x + g_{y}^{l} y + ϕ_{l}) .

(A7)

For each l in Equation (A7),

Δ n_{l}

is the change of refractive index due to external electric fields,

g_{x, y}^{l}

are spatial frequencies along the x- and y-directions, and

ϕ_{l}

is the phase offset associated with the grating component.

Incidencing a z-polarized electromagnetic field,

E (x, y) = E_{i} (y) \exp [- j k_{x}^{i} x - j k_{y}^{i} y]

, into the multiple-period EOPBD leads the reflected beam to many different directions when the phase mismatch is small. One sees an example in Figure A2, in which dual-grating vectors can reflect the incident wave (in black) propagating close to the Bragg condition to two different directions, along the direction illustrated by the dashed line in red and blue of Figure A2. The phase mismatch between the incident wave and two reflected waves are given by 2ξ₁ and 2ξ₂, respectively. Assuming direct coupling between the reflected fields are insignificant due to large phase mismatch, the set of coupled wave equations can be obtained by substituting the electromagnetic fields:

E (x, y) = E_{i} (y) \exp [- j k_{x}^{i} x - j k_{y}^{i} y] + \sum_{1 \leq l \leq N} E_{r}^{(l)} \exp [- i k_{x}^{(l)} x - i k_{y}^{(l)} y]

(A8)

into the Helmholtz equation with a multiple-period refractive index given by Equation (A7):

\begin{array}{l} \frac{\partial E_{i}}{\partial y} + j \sum_{1 \leq l \leq N} κ_{i}^{(l)} E_{r}^{(l)} \exp [i ξ_{l} y] = 0 \\ \frac{\partial E_{r}^{(l)}}{\partial y} + j κ_{r}^{(l)} E_{i} \exp [- i ξ_{l} y] = 0 \end{array},

(A9)

where

E_{r}^{(l)}

are the electric field reflected from the l-th grating component propagating along the direction characterized by wave vector components

k_{x}^{(l)}

and

k_{y}^{(l)}

.

In particular we consider a dual-grating structure as illustrated in Figure A2. The coupled wave equation writes:

\begin{array}{l} \frac{d E_{i}}{d y} = - j κ_{i}^{(1)} E_{r}^{(1)} \exp [i ξ_{1} y] - j κ_{i}^{(2)} E_{r}^{(2)} \exp [i ξ_{2} y] \\ \frac{d E_{r}^{(1)}}{d y} = - j κ_{r}^{(1)} E_{i} \exp [- i ξ_{1} y] \\ \frac{d E_{r}^{(2)}}{d y} = - j κ_{r}^{(2)} E_{i} \exp [- i ξ_{2} y] \end{array},

(A10)

where

κ_{i}^{(l)} = \frac{n_{e} k_{0}^{2} Δ n_{l}}{k_{y}^{i}}

,

κ_{r}^{(l)} = \frac{n_{e} k_{0}^{2} Δ n_{l}}{k_{y}^{(l)}}

,

ξ_{l} = \frac{\vec{ξ_{l}} \cdot \vec{ξ_{l}}}{\vec{ξ_{l}} \cdot \hat{y}} = \frac{| \vec{ξ_{l}} |}{\cos (θ)}

,

\vec{ξ_{l}} = {\vec{k}}_{r}^{(l)} - ({\vec{k}}_{i} + {\vec{G}}_{l})

and l = 1, 2. The symbol

{\vec{G}}_{l}

denotes the grating vectors in the EOPBD crystal. From Equation (A11) a linear ordinary differential equation can be expressed in the following form:

\frac{d^{3} E_{i}}{d y^{3}} - i (ξ_{1} + ξ_{2}) \frac{d^{2} E_{i}}{d y^{2}} - (ξ_{1} ξ_{2} - κ_{i}^{(1)} κ_{r}^{(1)} - κ_{i}^{(2)} κ_{r}^{(2)}) \frac{d E_{i}}{d y} - i (κ_{i}^{(1)} κ_{r}^{(1)} ξ_{2} + κ_{i}^{(2)} κ_{r}^{(2)} ξ_{1}) E_{i} = 0 .

(A11)

This homogeneous ordinary differential equation can be solved by the ansatz:

E_{i} = \sum_{l = 1, 2, 3} c_{l} \exp [i α_{l} y],

(A12)

under the boundary conditions that,

E_{r}^{(l)} (y = 0) = 0

, l = 1, 2.

Figure A2. Wavevector representation illustrating the phase mismatching of an incident wave (in black) propagating close to the Bragg condition reflected to two different directions along the directions illustrated by the dashed lines in red and blue.

References

Yamada, M.; Saitoh, M.; Ooki, H. Electric-field induced cylindrical lens, switching and deflection devices composed of the inverted domains in LiNbO₃ crystals. Appl. Phys. Lett. 1996, 69, 3659–3661. [Google Scholar] [CrossRef]
Myers, L.; Eckardt, R.; Fejer, M.; Byer, R.; Bosenberg, W.; Pierce, J. Quasi-phase-matched optical parametric oscillators in bulk periodically poled LiNbO₃. J. Opt. Soc. Am. B 1995, 12, 2102–2116. [Google Scholar] [CrossRef]
Gnewuch, H.; Pannell, C.N.; Ross, G.W.; Smith, P.G.R.; Geiger, H. Nanosecond Response of Bragg Deflectors in Periodically Poled LiNbO₃. IEEE Photonics Technol. Lett. 1998, 10, 1730–1732. [Google Scholar] [CrossRef]
Yamada, M. Electrically induced Bragg-diffraction grating composed of periodically inverted domains in lithium niobate crystals and its application devices. Rev. Sci. Instrum. 2000, 71, 4010–4016. [Google Scholar] [CrossRef]
Lin, Y.Y.; Lin, S.T.; Chang, G.W.; Chiang, A.C.; Huang, Y.C.; Chen, Y.H. Electro-optic periodically poled lithium niobate Bragg modulator as a laser Q-switch. Opt. Lett. 2007, 32, 545–547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Lin, S.T.; Chang, G.W.; Lin, Y.Y.; Huang, Y.C.; Chiang, A.C.; Chen, Y.H. Monolithically integrated laser Bragg Q-switch and wavelength converter in a PPLN crystal. Opt. Express 2007, 15, 17093–17098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Chen, Y.H.; Chang, W.K.; Hsu, N.; Chen, C.Y.; Chang, J.W. Internal Q-switching and self-optical parametric oscillation in a two-dimensional periodically poled Nd:MgO:LiNbO₃ laser. Opt. Lett. 2012, 37, 2814–2816. [Google Scholar] [CrossRef] [PubMed]
Lin, S.T.; Hsieh, C.S. Triple-wavelength Nd-laser system by cascaded electro-optic periodically poled lithium niobate Bragg modulator. Opt. Express 2012, 20, 29659–29664. [Google Scholar] [CrossRef] [PubMed]
Lin, S.T.; Qiu, Z.R.; Chen, C.P. Actively Q-Switched Tm:YAP laser constructed using an electro-optic periodically poled lithium niobate Bragg modulator. IEEE Photonics J. 2020, 12, 1503509. [Google Scholar] [CrossRef]
Okazaki, M.; Chichibu, T.; Yoshimoto, S.; Inoue, T.; Suhara, T. Electro-optic Bragg deflection modulator for UV laser light using periodically poled MgO:s-LiTaO₃. IEEE Photonics Technol. Lett. 2011, 23, 1709–1711. [Google Scholar] [CrossRef]
Zheng, G.; Wang, H.; She, W. Wave coupling theory of quasi-phase-matched linear electro-optic effect. Opt. Express 2006, 14, 5535–5540. [Google Scholar] [CrossRef] [PubMed]
Saleh, B.E.A.; Teich, M.C. Electro Optics. In Fundamentals of Photonics; Wiley: New York, NY, USA, 1991; pp. 712–720. [Google Scholar]
De Angelis, M.; De Nicola, S.; Finizio, A.; Pierattini, G.; Ferraro, P.; Grilli, S.; Paturzo, M. Evaluation of the internal field in lithium niobate ferroelectric domains by an interferometric method. Appl. Phys. Lett. 2004, 85, 2785–2787. [Google Scholar] [CrossRef]

Figure 1. Schematic design of the dual-grating structure. The incident wave containing multiple spatial components has a wavelength of 1064 nm and propagates toward the y-direction. The two PPLN grating vectors form ±2.7-mrad angles with respect to the y-axis. The PPLN grating period Λ is 20.25 μm. The Bragg angle θ_B is 0.69° (12 mrad). Notice that the angle of the grating vector is exaggeratedly shown in this figure. The right picture shows the single-grating and the dual-grating samples used in the experiment.

Figure 2. The simulated transmission curves of the single-grating (SG) and the dual-grating (DG) EOPBD for different beam sizes are plotted as a function of θL in solid lines and dashed lines, respectively. Different beam radii are presented in red: 10 μm, blue: 50 μm and black: 100 μm.

Figure 3. The first minimum transmission versus incident beam radius for the single-grating and the dual-grating EOPBD for θL < 1. The first minimum transmission is higher for a smaller beam radius, showing a poorer deflection efficiency. The dual-grating configuration gives a better deflection efficiency for a smaller beam radius, compared to the single-grating one.

Figure 4. Transmission curves of the dual-grating (in black) and the single-grating (in red) configurations. The solid lines show the theoretical predictions calculated using Equations (A5) and (A11), respectively for the single-grating and the dual-grating configurations. The circle and square markers show the experimental results. The inset pictures show the typical diffraction patterns of the single-grating and the dual-grating samples viewing by an infrared sensor card.

Figure 5. Transmission curves for different incident angles. The 0° curve shows that the incident angle is right at the Bragg angle (0.69°). As the incident angle deviated from the Bragg angle, the dual-grating EOPBD became inefficient.

Figure 6. Theoretical contour plot of the transmission as a function of wavelengths and applied voltages. It is found that there is a simultaneous broadband and high-deflection efficiency operation region during the 150~200-V region. Dispersion of refractive indices is included in the simulation.

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Chiang, A.-C.; Lin, Y.-Y.; Lin, S.-T.; Lin, Y.-Y. A Broadband High-Diffraction-Efficiency Electro-Optic Bragg Deflector Based on Monolithic Dual-Grating Periodically-Poled Lithium Niobate. Photonics 2021, 8, 242. https://doi.org/10.3390/photonics8070242

AMA Style

Chiang A-C, Lin Y-Y, Lin S-T, Lin Y-Y. A Broadband High-Diffraction-Efficiency Electro-Optic Bragg Deflector Based on Monolithic Dual-Grating Periodically-Poled Lithium Niobate. Photonics. 2021; 8(7):242. https://doi.org/10.3390/photonics8070242

Chicago/Turabian Style

Chiang, An-Chung, Yuan-Yao Lin, Shou-Tai Lin, and Yen-Yin Lin. 2021. "A Broadband High-Diffraction-Efficiency Electro-Optic Bragg Deflector Based on Monolithic Dual-Grating Periodically-Poled Lithium Niobate" Photonics 8, no. 7: 242. https://doi.org/10.3390/photonics8070242

APA Style

Chiang, A. -C., Lin, Y. -Y., Lin, S. -T., & Lin, Y. -Y. (2021). A Broadband High-Diffraction-Efficiency Electro-Optic Bragg Deflector Based on Monolithic Dual-Grating Periodically-Poled Lithium Niobate. Photonics, 8(7), 242. https://doi.org/10.3390/photonics8070242

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu

A Broadband High-Diffraction-Efficiency Electro-Optic Bragg Deflector Based on Monolithic Dual-Grating Periodically-Poled Lithium Niobate

Abstract

1. Introduction

2. Device Design and Theoretical Modeling

3. Experimental Results

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Acknowledgments

Conflicts of Interest

Appendix A. Extended Model for Single Grating Based EOPBD

Appendix B. Extended Model for Dual Grating Based EOPBD

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI