Image Transmission Based on Spiking Dynamics of Electrically Controlled VCSEL-SA Neuron
Abstract
:1. Introduction
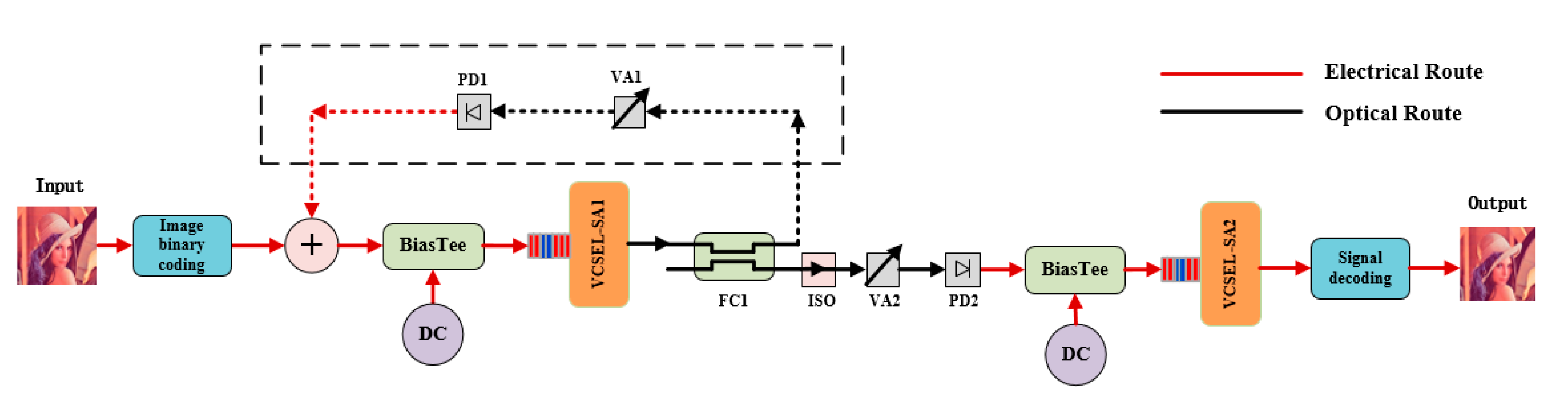
2. Theoretical Model
3. Results and Discussions
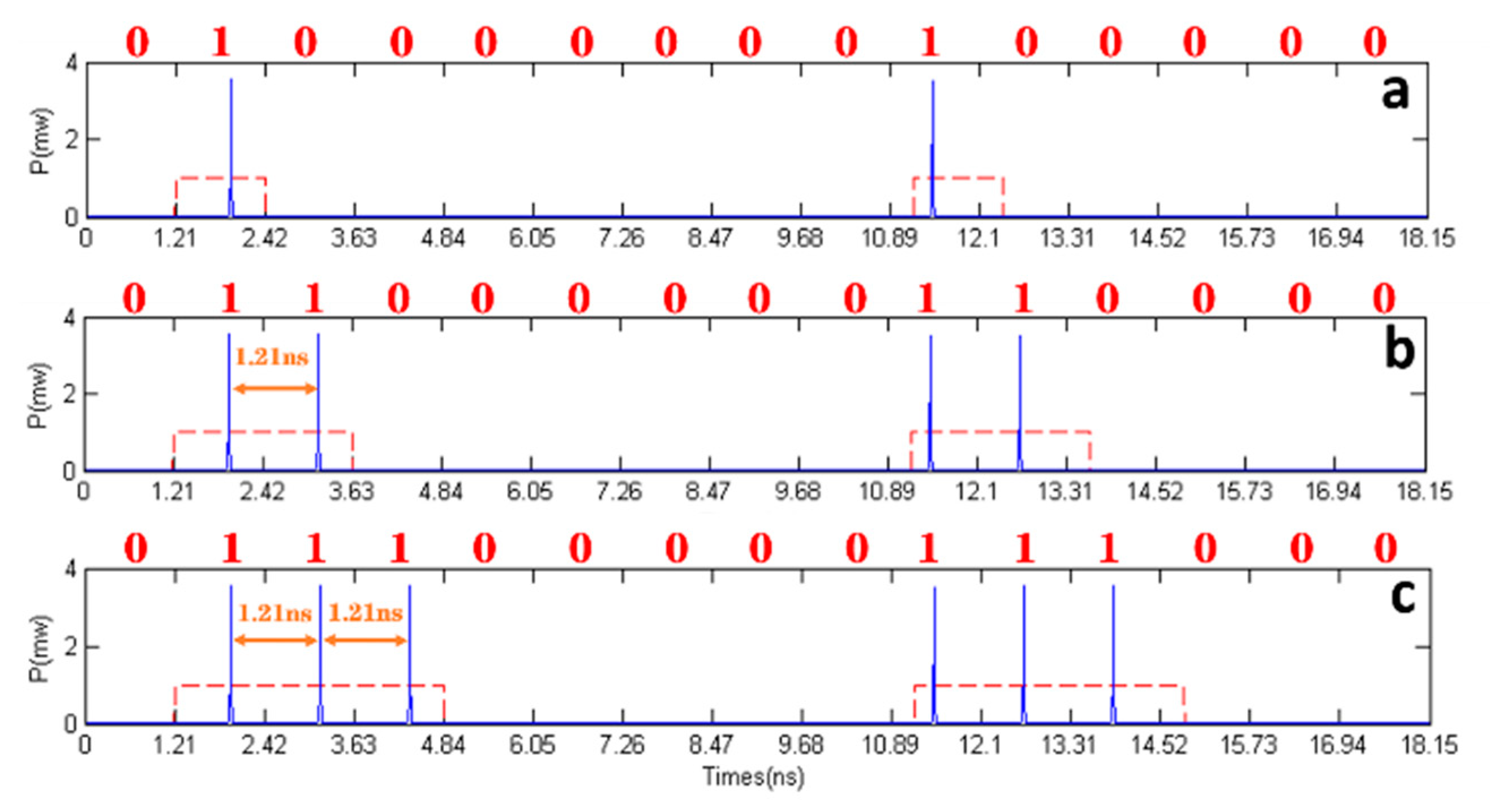
3.1. Spiking Coding
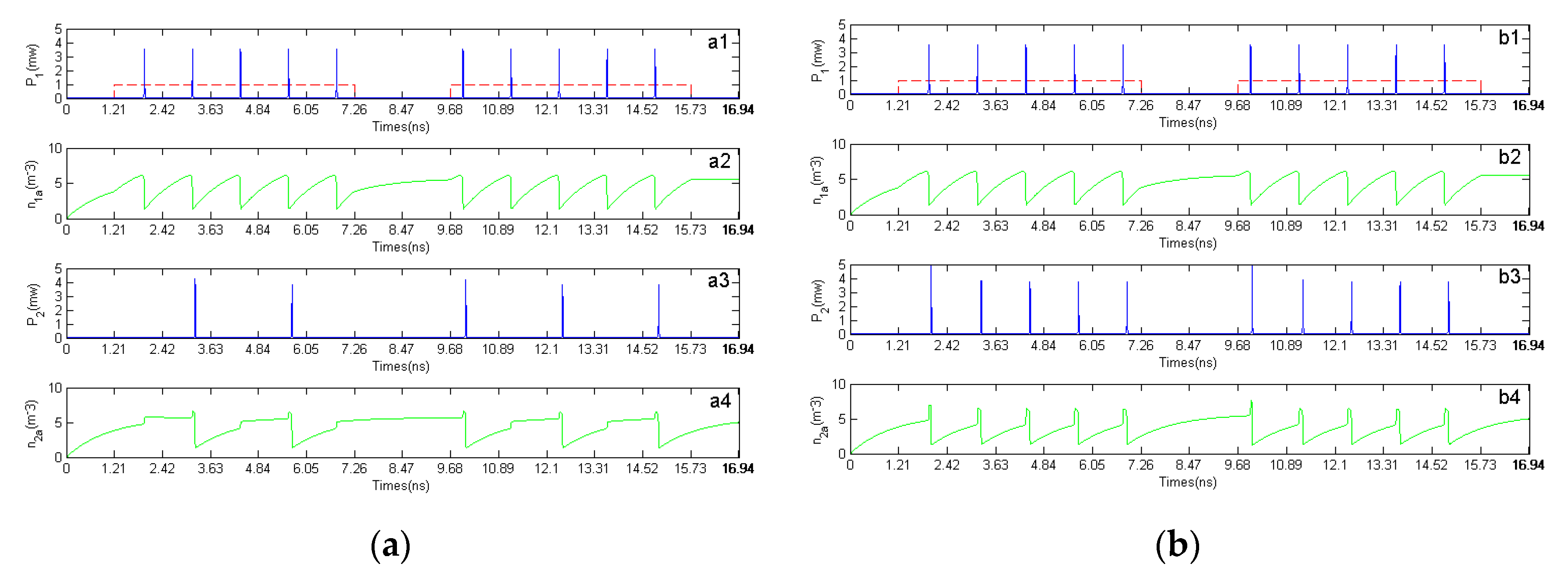
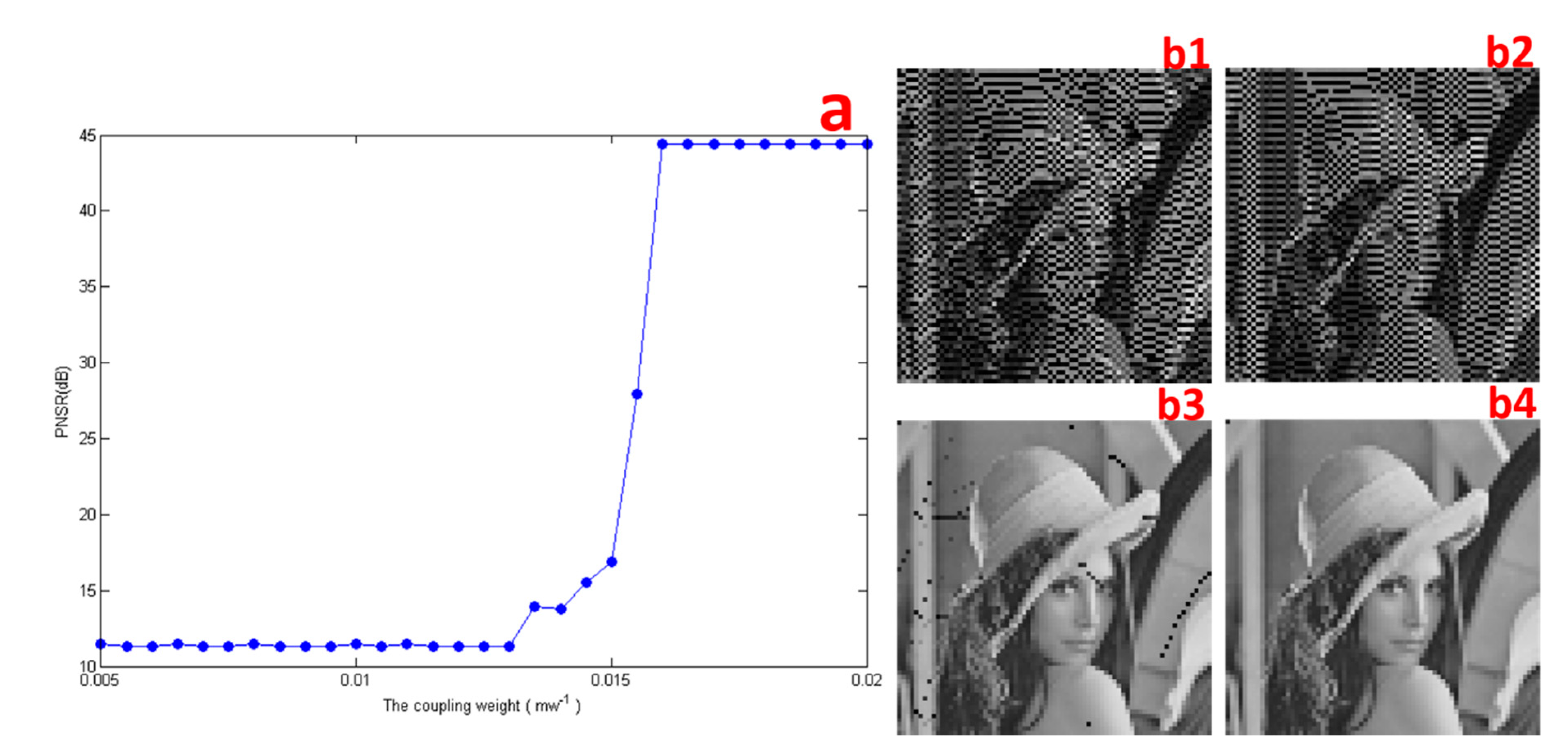
3.2. Image Transmission
3.3. Storage of Spiking Patterns
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, J.Q.; Wang, R.; Ren, Y.; Mao, J.Y.; Wang, Z.P.; Zhou, Y.; Han, S.T. Neuromorphic engineering: From biological to spike-based hardware nervous systems. Adv. Mater. 2020, 32, 2003610. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Gu, Z.; Pan, G. A survey of neuromorphic computing based on spiking neural networks. Chin. J. Electron. 2018, 27, 667–674. [Google Scholar] [CrossRef]
- Huang, H.; Ge, C.; Liu, Z.; Zhong, H.; Guo, E.; He, M.; Wang, C.; Yang, G.; Jin, K. Electrolyte-gated transistors for neuromorphic applications. J. Semicond. 2021, 42, 81–93. [Google Scholar] [CrossRef]
- Hasler, J.; Marr, B. Finding a roadmap to achieve large neuromorphic hardware systems. Front. Neurosci. 2013, 7, 118. [Google Scholar] [CrossRef] [Green Version]
- Roy, K.; Jaiswal, A.; Panda, P. Towards spike-based machine intelligence with neuromorphic computing. Nature 2019, 575, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Watson, A. Neuromorphic engineering—Why can’t a computer be more like a brain. Science 1997, 277, 1934–1936. [Google Scholar] [CrossRef]
- Woods, D.; Naughton, T.J. Optical computing photonic neural networks. Nat. Phys. 2012, 8, 257–259. [Google Scholar] [CrossRef]
- James, C.D.; Aimone, J.B.; Miner, N.E.; Vineyard, C.M.; Rothganger, F.H.; Carlson, K.D.; Mulder, S.A.; Draelos, T.J.; Faust, A.; Marinella, M.J.; et al. A historical survey of algorithms and hardware architectures for neural-inspired and neuromorphic computing applications. Inspir. Cogn. Arc. 2017, 19, 49–64. [Google Scholar] [CrossRef] [Green Version]
- De Lima, T.F.; Peng, H.T.; Tait, A.N.; Nahmias, M.A.; Miller, H.B.; Shastri, B.J.; Prucnal, P.R. Machine learning with neuromorphic photonics. J. Lightwave Technol. 2019, 37, 1515–1534. [Google Scholar] [CrossRef]
- Xiang, S.Y.; Han, Y.N.; Song, Z.W.; Guo, X.X.; Zhang, Y.H.; Ren, Z.X.; Wang, S.H.; Ma, Y.T.; Zou, W.W.; Ma, B.W.; et al. A review: Photonics devices, architectures, and algorithms for optical neural computing. J. Semicond. 2021, 42, 023105. [Google Scholar] [CrossRef]
- Garbin, B.; Javaloyes, J.; Tissoni, G.; Barland, S. Topological solitons as addressable phase bits in a driven laser. Nat. Commun. 2015, 6, 5915. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Fan, L.; Liu, N.; Wu, Z.; Xia, G. Generation of broadband optical frequency comb based on a gain-switching 1550 nm vertical-cavity surface-emitting laser under optical injection. Photonics 2020, 7, 95. [Google Scholar] [CrossRef]
- Zhong, D.Z.; Zeng, N.; Yang, H.; Xu, Z.; Hu, Y.; Zhao, K.K. Precise ranging for the multi-region by using multi-beam chaotic polarization components in the multiple parallel optically pumped spin-VCSELs with optical injection. Opt. Express 2021, 29, 7809–7824. [Google Scholar] [CrossRef]
- Iga, K. Surface-emitting laser—its birth and generation of new optoelectronics field. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1201–1215. [Google Scholar] [CrossRef]
- Koyama, F. Recent advances of VCSEL photonics. J. Lightwave Technol. 2006, 24, 4502–4513. [Google Scholar] [CrossRef]
- Liu, A.J.; Wolf, P.; Lott, J.A.; Bimberg, D. Vertical-cavity surface-emitting lasers for data communication and sensing. Photon. Res. 2019, 7, 121–136. [Google Scholar] [CrossRef]
- Hurtado, A.; Javaloyes, J. Controllable spiking patterns in long-wavelength vertical cavity surface emitting lasers for neuromorphic photonics systems. Appl. Phys. Lett. 2015, 107, 241103. [Google Scholar] [CrossRef] [Green Version]
- Robertson, J.; Deng, T.; Javaloyes, J. and Hurtado, A. Controlled inhibition of spiking dynamics in VCSELs for neuromorphic photonics: Theory and experiments. Opt. Lett. 2017, 42, 1560–1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, T.; Robertson, J.; Hurtado, A. Controlled propagation of spiking dynamics in vertical-cavity surface-emitting lasers: Towards neuromorphic photonic network. IEEEJ. Sel. Top. Quantum Electron. 2017, 23, 1800408. [Google Scholar] [CrossRef] [Green Version]
- Nahmias, M.A.; Shastri, B.J.; Tait, A.N.; Prucnal, P.R. A leaky integrate-and-fire laser neuron for ultrafast cognitive computing. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1800212. [Google Scholar] [CrossRef]
- Barbay, S.; Kuszelewicz, R.; Yacomotti, A.M. Excitability in a semiconductor laser with saturable absorber. Opt. Lett. 2011, 36, 4476–4478. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.X.; Wu, Z.M.; Lu, D.; Xia, G.Q.; Deng, T. Controllable spiking dynamics in cascaded VCSEL-SA photonic neurons. Nonlinear Dyn. 2020, 99, 1103–1114. [Google Scholar] [CrossRef]
- Shchukin, V.A.; Ledentsov, N.N.; Qureshi, Z.; Ingham, J.D.; Penty, R.V.; White, I.H.; Nadtochy, A.M.; Maximov, M.V.; Blokhin, S.A.; Karachinsky, L.Y.; et al. Digital data transmission using electro-optically modulated vertical-cavity surface-emitting laser with saturable absorber. Appl. Phys. Lett. 2014, 104, 051125. [Google Scholar] [CrossRef]
- Nugent, D.G.H.; Plumb, R.G.S.; Fisher, M.A.; Davies, D.A.O. Self-pulsations in vertical-cavity surface-emitting lasers. Electron. Lett. 1995, 31, 43–44. [Google Scholar] [CrossRef]
- Burr, G.W. A role for optics in AI hardware. Nature 2019, 569, 199–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, Y.C.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.J.; Larochelle, H.; Englund, D. Deep learning with coherent nanophotonic circuits. Nat. Photon. 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Ren, Q.; Zhang, Y.L.; Wang, R.; Zhao, J.Y. Optical spike-timing-dependent plasticity with weight-dependent learning window and reward modulation. Opt. Express 2015, 23, 25247–25258. [Google Scholar] [CrossRef]
- Tan, H.L.; Li, Z.G.; Tan, Y.H.; Rahardja, S.; Yeo, C. A perceptually relevant mse-based image quality metric. IEEE Trans. Image Process. 2013, 22, 4447–4459. [Google Scholar]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal. Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Giudice, G.E.; Kuksenkov, D.V.; Temkin, H.; Lear, K.L. Differential carrier lifetime in oxide-confined vertical cavity lasers obtained from electrical impedance measurements. Appl. Phys. Lett. 1999, 74, 899–901. [Google Scholar] [CrossRef] [Green Version]
- Shastri, B.J.; Chen, C.; Choquette, K.D.; Plant, D.V. Circuit modeling of carrier-photon dynamics in composite-resonator vertical-cavity lasers. IEEE J. Quantum Elect. 2011, 47, 1537–1546. [Google Scholar] [CrossRef]
- Fledmann, J.; Youngblood, N.; Wright, C.D.; Bhaskaran, H.; Pernice, W.H.P. All-optical spiking neurosynaptic networks with self-learning capabilities. Nature 2019, 569, 208–214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prucnal, P.R.; Shastri, B.J. Neuromorphic Photonics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Song, Z.W.; Xiang, S.Y.; Ren, Z.X.; Wang, S.H.; Wen, A.J.; Hao, Y. Photonic spiking neural network based on excitable VCSELs-SA for sound azimuth detection. Opt. Express 2020, 28, 1561–1573. [Google Scholar] [CrossRef]
- Ma, P.Y.; Shastri, B.J.; De Lima, T.F.; Tait, A.N.; Nahmias, M.A.; Prucnal, P.R. All-optical digital-to-spike conversion using a graphene excitable laser. Opt. Express 2017, 25, 33504–33513. [Google Scholar] [CrossRef]
- Kistler, W.M.; Gerstner, W. Stable propagation of activity pulses in populations of spiking neurons. Neural Comput. 2002, 14, 987–997. [Google Scholar] [CrossRef] [PubMed]
- Brakensiek, J.; Guruswami, V.; Zbarsky, S. Efficient low-redundancy codes for correcting multiple deletions. IEEE Trans. Inf. Theory 2016, 64, 3403–3410. [Google Scholar] [CrossRef] [Green Version]
- Sima, J.; Bruck, J. Optimal k-deletion correcting codes. IEEE Int. Symp. Inform. Theory France 2019, 67, 3360–3375. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, M.; Lin, X.; Tang, X.; Gao, Z.; Xiao, L.; Wang, J.; Ma, F.; Zheng, Q.; Deng, T. Image Transmission Based on Spiking Dynamics of Electrically Controlled VCSEL-SA Neuron. Photonics 2021, 8, 238. https://doi.org/10.3390/photonics8070238
Ni M, Lin X, Tang X, Gao Z, Xiao L, Wang J, Ma F, Zheng Q, Deng T. Image Transmission Based on Spiking Dynamics of Electrically Controlled VCSEL-SA Neuron. Photonics. 2021; 8(7):238. https://doi.org/10.3390/photonics8070238
Chicago/Turabian StyleNi, Min, Xiaodong Lin, Xi Tang, Ziye Gao, Luyao Xiao, Jun Wang, Fan Ma, Qiulan Zheng, and Tao Deng. 2021. "Image Transmission Based on Spiking Dynamics of Electrically Controlled VCSEL-SA Neuron" Photonics 8, no. 7: 238. https://doi.org/10.3390/photonics8070238
APA StyleNi, M., Lin, X., Tang, X., Gao, Z., Xiao, L., Wang, J., Ma, F., Zheng, Q., & Deng, T. (2021). Image Transmission Based on Spiking Dynamics of Electrically Controlled VCSEL-SA Neuron. Photonics, 8(7), 238. https://doi.org/10.3390/photonics8070238




