Quantum-Optical Spectrometry in Relativistic Laser–Plasma Interactions Using the High-Harmonic Generation Process: A Proposal
Abstract
1. Introduction
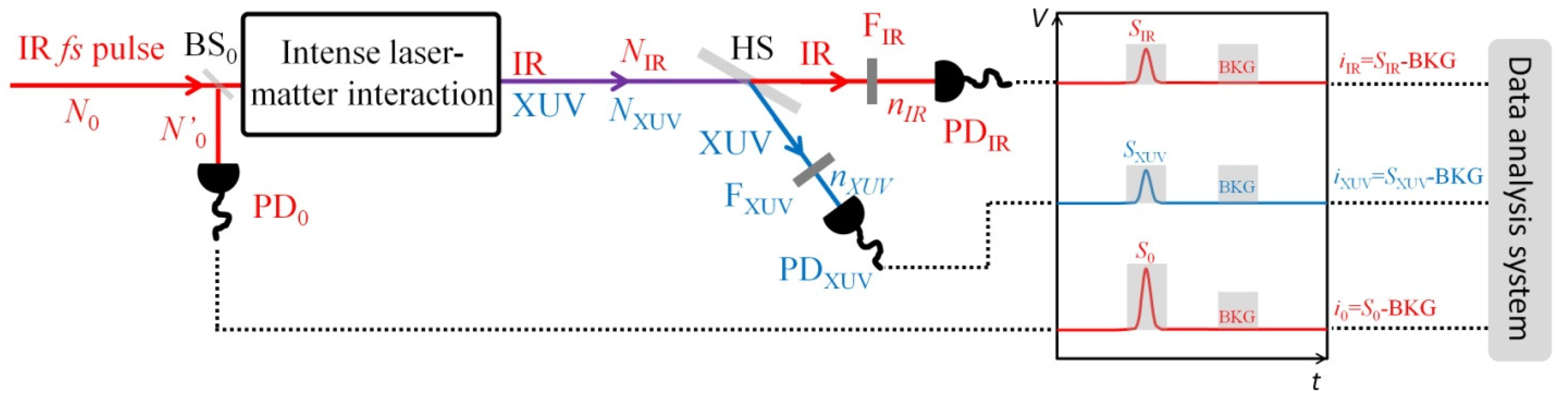
2. Operation Principle of the Quantum Spectrometer
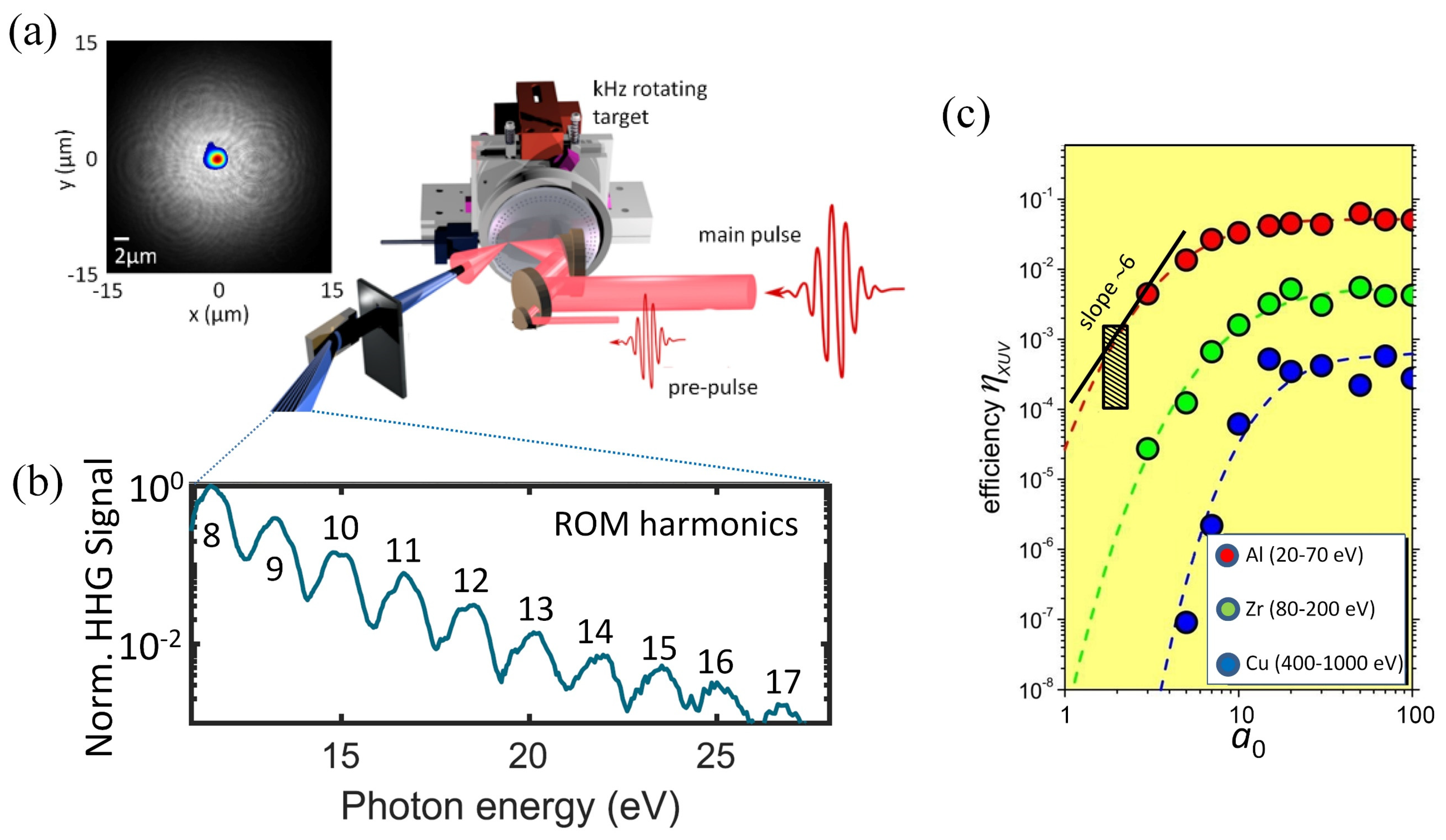
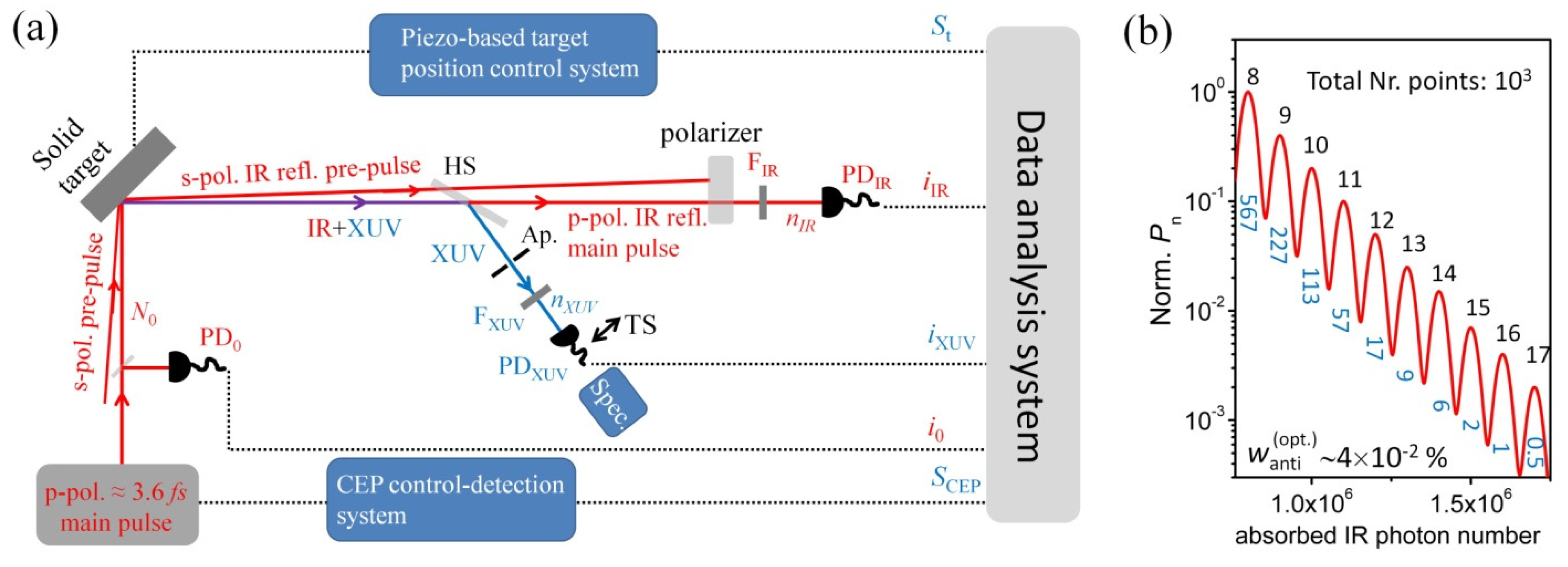
3. Quantum Spectrometry in Laser–Plasma Interactions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maiman, T. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Glauber, R.J. Nobel Lecture: One hundred years of light quanta. Rev. Mod. Phys. 2006, 78, 1267–1278. [Google Scholar] [CrossRef]
- Mourou, G. Nobel Lecture: Extreme light physics and application. Rev. Mod. Phys. 2019, 91, 030501. [Google Scholar] [CrossRef]
- Strickland, D. Nobel Lecture: Generating high-intensity ultrashort optical pulses. Rev. Mod. Phys. 2019, 91, 030502. [Google Scholar] [CrossRef]
- Protopapas, M.; Keitel, C.H.; Knight, P.L. Atomic physics with super-high intense lasers. Rep. Prog. Phys. 1997, 60, 389–486. [Google Scholar] [CrossRef]
- Brabec, T.; Krausz, F. Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 2000, 72, 545–591. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Kruchinin, S.Y.; Krausz, F.; Yakovlev, V.S. Colloquium: Strong-field phenomena in periodic systems. Rev. Mod. Phys. 2018, 90, 021002. [Google Scholar] [CrossRef]
- Nayak, A.; Dumergue, M.; Kühn, S.; Mondal, S.; Csizmadia, T.; Harshitha, N.G.; Füle, M.; Kahaly, M.U.; Farkas, B.; Major, B.; et al. Saddle point approaches in strong field physics and generation of attosecond pulses. Phys. Rep. 2019, 833, 1–52. [Google Scholar] [CrossRef]
- Given the existence of a vast number of relevant literature in the field, we apologize for any unintentional omission of original research papers having significant contribution on the development of the research field.
- Acin, A.; Bloch, I.; Buhrman, H.; Calarco, T.; Eichler, C.; Eisert, J.; Esteve, D.; Gisin, N.; Glaser, S.J.; Jelezko, F.; et al. The quantum technologies roadmap: A Eurpean community view. New J. Phys. 2018, 20, 080201. [Google Scholar] [CrossRef]
- Walmsley, I.A. Quantum optics: Science and technology in a new light. Science 2015, 348, 525–530. [Google Scholar] [CrossRef]
- Deutsch, I.H. Harnessing the Power of the Second Quantum Revolution. Phys. Rev. X Quantum 2020, 1, 020101. [Google Scholar] [CrossRef]
- Leonhardt, U. Measuring the Quantum State of Light, 1st ed.; Cambridge Studies in Modern Optics; Knight, P.L., Miller, A., Eds.; Cambridge University Press: Cambridge, UK, 1997; ISBN 0-521-49730-2. [Google Scholar]
- Strekalov, D.V.; Leuchs, G. Nonlinear Interactions and Non-classical Light. In Quantum Photonics: Pioneering Advances and Emerging Applications; Springer Series in Optical Sciences; Boyd, R.W., Lukishova, S.G., Zadkov, V.N., Eds.; Springer Nature: Cham, Switzerland, 2019; Volume 217, pp. 51–101. ISBN 978-3-319-98400-1. [Google Scholar]
- Andersen, U.L.; Gehring, T.; Marquardt, C.; Leuchs, G. 30 years of squeezed light generation. Phys. Scr. 2016, 91, 053001. [Google Scholar] [CrossRef]
- Spasibko, K.Y.; Kopylov, D.A.; Krutyanskiy, V.L.; Murzina, T.V.; Leuchs, G.; Chekhova, M.V. Multiphoton Effects Enhanced due to Ultrafast Photon-Number Fluctuations. Phys. Rev. Lett. 2017, 119, 223603. [Google Scholar] [CrossRef] [PubMed]
- Lamprou, T.; Liontos, I.; Papadakis, N.C.; Tzallas, P. A perspective on high photon flux nonclassical light and applications in nonlinear optics. High Power Laser Sci. Eng. 2020, 8, e42. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef]
- Kulander, K.C.; Schafer, K.J.; Krause, J.L. Dynamics of short-pulse excitation, ionization and harmonic conversion. In Super-Intense Laser Atom Physics; NATO Advanced Studies Institute Series B; L’Huillier, A., Piraux, B., Rzazewski, K., Eds.; Springer: Boston, MA, USA, 1993; Volume 316, pp. 95–110. ISBN 978-1-4615-7965-6. [Google Scholar]
- Tajima, T.; Malka, V. Laser Plasma Accelerators. Plasma Phys. Control. Fusion 2020, 62, 034004. [Google Scholar] [CrossRef]
- Malka, V. Laser Plasma Accelerators. Phys. Plasmas 2012, 19, 055501. [Google Scholar] [CrossRef]
- Amini, K.; Biegert, J.; Calegari, F.; Chacón, A.; Ciappina, M.F.; Dauphin, A.; Efimov, D.K.; de Morisson Faria, C.F.; Giergiel, K.; Gniewek, P.; et al. Symphony on strong field approximation. Rep. Prog. Phys. 2019, 82, 116001. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Ciappina, M.F.; Pisanty, E.; Rivera-Dean, J.; Lamprou, T.; Tzallas, P. The quantum nature of light in high harmonic generation. arXiv 2020, arXiv:2008.10221. [Google Scholar]
- Tsatrafyllis, N.; Kominis, I.K.; Gonoskov, I.A.; Tzallas, P. High-order harmonics measured by the photon statistics of the infrared driving-field exiting the atomic medium. Nat. Commun. 2017, 8, 15170. [Google Scholar] [CrossRef]
- Tsatrafyllis, N.; Kühn, S.; Dumergue, M.; Foldi, P.; Kahaly, S.; Cormier, E.; Gonoskov, I.A.; Kiss, B.; Varju, K.; Varro, S.; et al. Quantum Optical Signatures in a Strong Laser Pulse after Interaction with Semiconductors. Phys. Rev. Lett. 2019, 122, 193602. [Google Scholar] [CrossRef] [PubMed]
- Böhle, F.; Thévenet, M.; Bocoum, M.; Vernier, A.; Haessler, S.; Lopez-Martens, R. Generation of XUV spectral continua from relativistic plasma mirrors driven in the near-single-cycle limit. J. Phys. Photonics 2020, 2, 034010. [Google Scholar] [CrossRef]
- Gonoskov, I.A.; Tsatrafyllis, N.; Kominis, I.K.; Tzallas, P. Quantum optical signatures in strong-field laser physics: Infrared photon counting in high-order harmonic generation. Sci. Rep. 2016, 6, 32821. [Google Scholar] [CrossRef] [PubMed]
- Chatziathanasiou, S.; Kahaly, S.; Skantzakis, E.; Sansone, G.; Lopez-Martens, R.; Haessler, S.; Varju, K.; Tsakiris, G.; Charalambidis, D.; Tzallas, P. Generation of Attosecond Light Pulses from Gas and Solid State Media. Photonics 2017, 4, 26. [Google Scholar] [CrossRef]
- Baeva, T.; Gordienko, S.; Pukhov, A. Theory of high-order harmonic generation in relativistic laser interaction with overdense plasma. Phys. Rev. E 2006, 74, 046404. [Google Scholar] [CrossRef]
- Gibbon, P. Harmonic Generation by Femtosecond Laser-Solid Interaction: A Coherent “Water-Window” Light Source? Phys. Rev. Lett. 1996, 76, 50–53. [Google Scholar] [CrossRef] [PubMed]
- Lichters, E.; Meyer-Teh-Vehn, J.; Pukhov, A. Short-pulse laser harmonics from oscillating plasma surfaces driven at relativistic intensity. Phys. Plasmas 1996, 3, 3425–3437. [Google Scholar] [CrossRef]
- Gonoskov, A.A.; Korzhimanov, A.V.; Kim, A.V.; Marklund, M.; Sergeev, A.M. Ultrarelativistic nanoplasmonics as a route towards extreme-intensity attosecond pulses. Phys. Rev. E 2011, 84, 046403. [Google Scholar] [CrossRef]
- Edwards, M.R.; Mikhailova, J.M. The X-Ray Emission Effectiveness of Plasma Mirrors: Reexamining Power-Law Scaling for Relativistic High-Order Harmonic Generation. Sci. Rep. 2020, 10, 5154. [Google Scholar] [CrossRef]
- Dromey, B.; Adams, D.; Hörlein, R.; Nomura, Y.; Rykovanov, S.G.; Carroll, D.C.; Foster, P.S.; Kar, S.; Markey, K.; McKenna, P.; et al. Diffraction-limited performance and focusing of high harmonics from relativistic plasmas. Nat. Phys. 2009, 5, 146–152. [Google Scholar] [CrossRef]
- Heissler, P.; Hörlein, R.; Mikhailova, J.M.; Waldecker, L.; Tzallas, P.; Buck, A.; Schmid, K.; Sears, C.M.S.; Krausz, F.; Veisz, L.; et al. Few-Cycle Driven Relativistically Oscillating Plasma Mirrors: A Source of Intense Isolated Attosecond Pulses. Phys. Rev. Lett. 2020, 108, 235003. [Google Scholar] [CrossRef] [PubMed]
- Teubner, U.; Gibbon, P. High-order harmonics from laser irradiated plasma surfaces. Rev. Mod. Phys. 2009, 81, 445–479. [Google Scholar] [CrossRef]
- Tsakiris, G.D.; Eidmann, K.; Meyer-ter-Vehn, J.; Krausz, F. Route to intense single attosecond pulses. New J. Phys. 2006, 8, 19. [Google Scholar] [CrossRef]
- Chopineau, L.; Leblanc, A.; Blaclard, G.; Denoeud, A.; Thévenet, M.; Vay, J.-L.; Bonnaud, G.; Martin, P.; Vincenti, H.; Quéré, F. Identification of Coupling Mechanisms between Ultraintense Laser Light and Dense Plasmas. Phys. Rev. X 2019, 9, 011050. [Google Scholar] [CrossRef]
- Rödel, C.; an der Brügge, D.; Bierbach, J.; Yeung, M.; Hahn, T.; Dromey, B.; Herzer, S.; Fuchs, S.; Galestian Pour, A.; Eckner, E.; et al. Harmonic Generation from Relativistic Plasma Surfaces in Ultrasteep Plasma Density Gradients. Phys. Rev. Lett. 2012, 109, 125002. [Google Scholar] [CrossRef] [PubMed]
- Heissler, P.; Barna, A.; Mikhailova, J.M.; Ma, G.; Khrennikov, K.; Karsch, S.; Veisz, L.; Földes, I.B.; Tsakiris, G.D. Multi-μJ harmonic emission energy from laser-driven plasma. Appl. Phys. B 2015, 118, 195–201. [Google Scholar] [CrossRef]
- Jahn, O.; Leshchenko, V.E.; Tzallas, P.; Kessel, A.; Krüger, M.; Münzer, A.; Trushin, S.A.; Tsakiris, G.D.; Kahaly, S.; Kormin, D.; et al. Towards intense isolated attosecond pulses from relativistic surface high harmonics. Optica 2019, 6, 280–287. [Google Scholar] [CrossRef]
- Kahaly, S.; Monchocé, S.; Vincenti, H.; Dzelzainis, T.; Dromey, B.; Zepf, M.; Martin, P.; Quéré, F. Direct Observation of Density-Gradient Effects in Harmonic Generation from Plasma Mirrors. Phys. Rev. Lett. 2013, 110, 175001. [Google Scholar] [CrossRef] [PubMed]
- Haessler, S.; Böhle, F.; Bocoum, M.; Ouillé, M.; Kaur, J.; Levy, D.; Daniault, L.; Vernier, A.; Faure, J.; Lopez-Martens, R. Relativistic high-harmonic generation and correlated electron acceleration from plasma mirrors at 1 kHz repetition rate. arXiv 2020, arXiv:2005.01343. [Google Scholar]
- Vincenti, H.; Monchoce, S.; Kahaly, S.; Bonnaud, G.; Martin, P.; Quéré, F. Optical properties of relativistic plasma mirrors. Nat. Commun. 2014, 5, 3403. [Google Scholar] [CrossRef]
- Thévenet, M.; Leblanc, A.; Kahaly, S.; Vincenti, H.; Vernier, A.; Quéré, F.; Faure, J. Vacuum laser acceleration of relativistic electrons using plasma mirror injectors. Nat. Phys. 2016, 12, 355–360. [Google Scholar] [CrossRef]
- Kormin, D.; Borot, A.; Ma, G.; Dallari, W.; Bergues, B.; Aladi, M.; Földes, I.B.; Veisz, L. Spectral interferometry with waveform-dependent relativistic high-order harmonics from plasma surfaces. Nat. Commun. 2018, 9, 4992. [Google Scholar] [CrossRef]
- Borot, A.; Douillet, D.; Iaquaniello, G.; Lefrou, T.; Audebert, P.; Geindre, J.-P.; Lopez-Martens, R. High Repetition Rate Plasma Mirror Device for Attosecond Science. Rev. Sci. Instr. 2014, 85, 013104. [Google Scholar] [CrossRef]
- Bocoum, M.; Böhle, F.; Vernier, A.; Jullien, A.; Faure, J.; Lopez-Martens, R. Spatial-domain interferometer for measuring plasma mirror expansion. Opt. Lett. 2015, 40, 3009. [Google Scholar] [CrossRef] [PubMed]
- Mondal, S.; Shirozhan, M.; Ahmed, N.; Bocoum, M.; Boehle, F.; Vernier, A.; Haessler, S.; Lopez-Martens, R.; Sylla, F.; Sire, C.; et al. Surface plasma attosource beamlines at ELI-ALPS. JOSA B 2018, 35, A93–A102. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamprou, T.; Lopez-Martens, R.; Haessler, S.; Liontos, I.; Kahaly, S.; Rivera-Dean, J.; Stammer, P.; Pisanty, E.; Ciappina, M.F.; Lewenstein, M.; et al. Quantum-Optical Spectrometry in Relativistic Laser–Plasma Interactions Using the High-Harmonic Generation Process: A Proposal. Photonics 2021, 8, 192. https://doi.org/10.3390/photonics8060192
Lamprou T, Lopez-Martens R, Haessler S, Liontos I, Kahaly S, Rivera-Dean J, Stammer P, Pisanty E, Ciappina MF, Lewenstein M, et al. Quantum-Optical Spectrometry in Relativistic Laser–Plasma Interactions Using the High-Harmonic Generation Process: A Proposal. Photonics. 2021; 8(6):192. https://doi.org/10.3390/photonics8060192
Chicago/Turabian StyleLamprou, Theocharis, Rodrigo Lopez-Martens, Stefan Haessler, Ioannis Liontos, Subhendu Kahaly, Javier Rivera-Dean, Philipp Stammer, Emilio Pisanty, Marcelo F. Ciappina, Maciej Lewenstein, and et al. 2021. "Quantum-Optical Spectrometry in Relativistic Laser–Plasma Interactions Using the High-Harmonic Generation Process: A Proposal" Photonics 8, no. 6: 192. https://doi.org/10.3390/photonics8060192
APA StyleLamprou, T., Lopez-Martens, R., Haessler, S., Liontos, I., Kahaly, S., Rivera-Dean, J., Stammer, P., Pisanty, E., Ciappina, M. F., Lewenstein, M., & Tzallas, P. (2021). Quantum-Optical Spectrometry in Relativistic Laser–Plasma Interactions Using the High-Harmonic Generation Process: A Proposal. Photonics, 8(6), 192. https://doi.org/10.3390/photonics8060192





