Electromagnetic Hanbury Brown and Twiss Effect in Atmospheric Turbulence
Abstract
1. Introduction
2. Method
2.1. The Average Stokes Parameters in Turbulence
2.2. The Correlations in Stokes Parameters in Turbulence
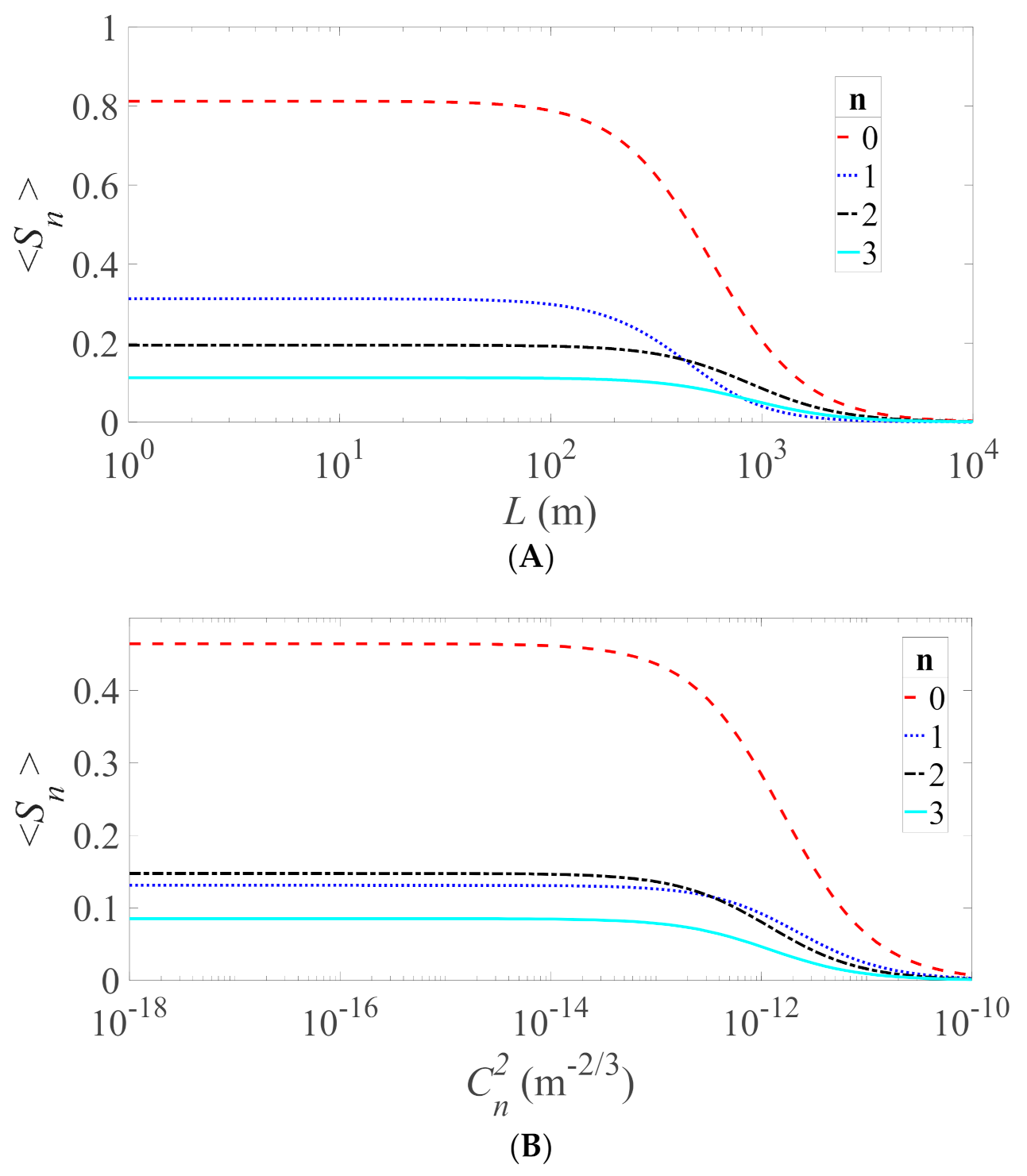
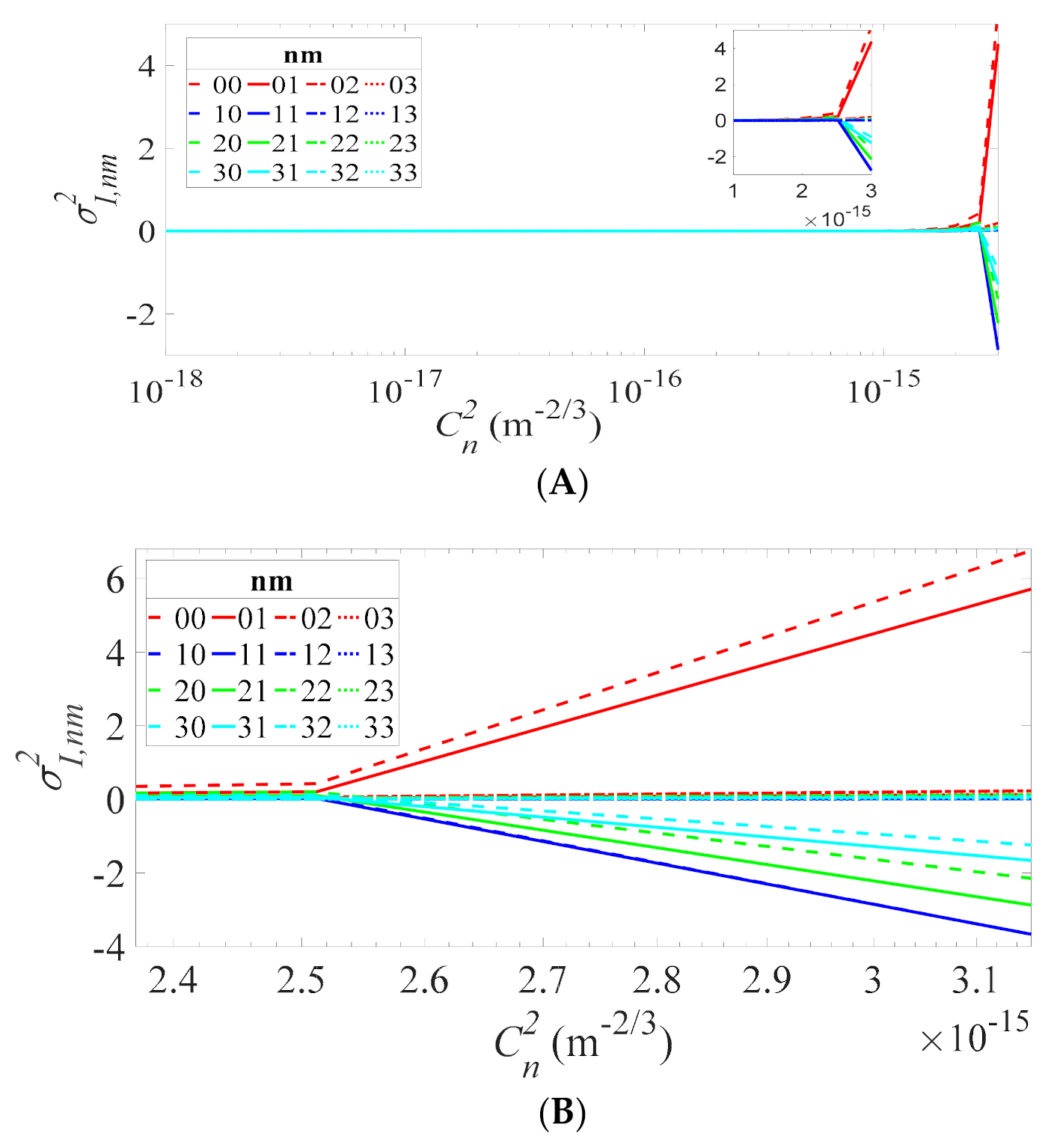
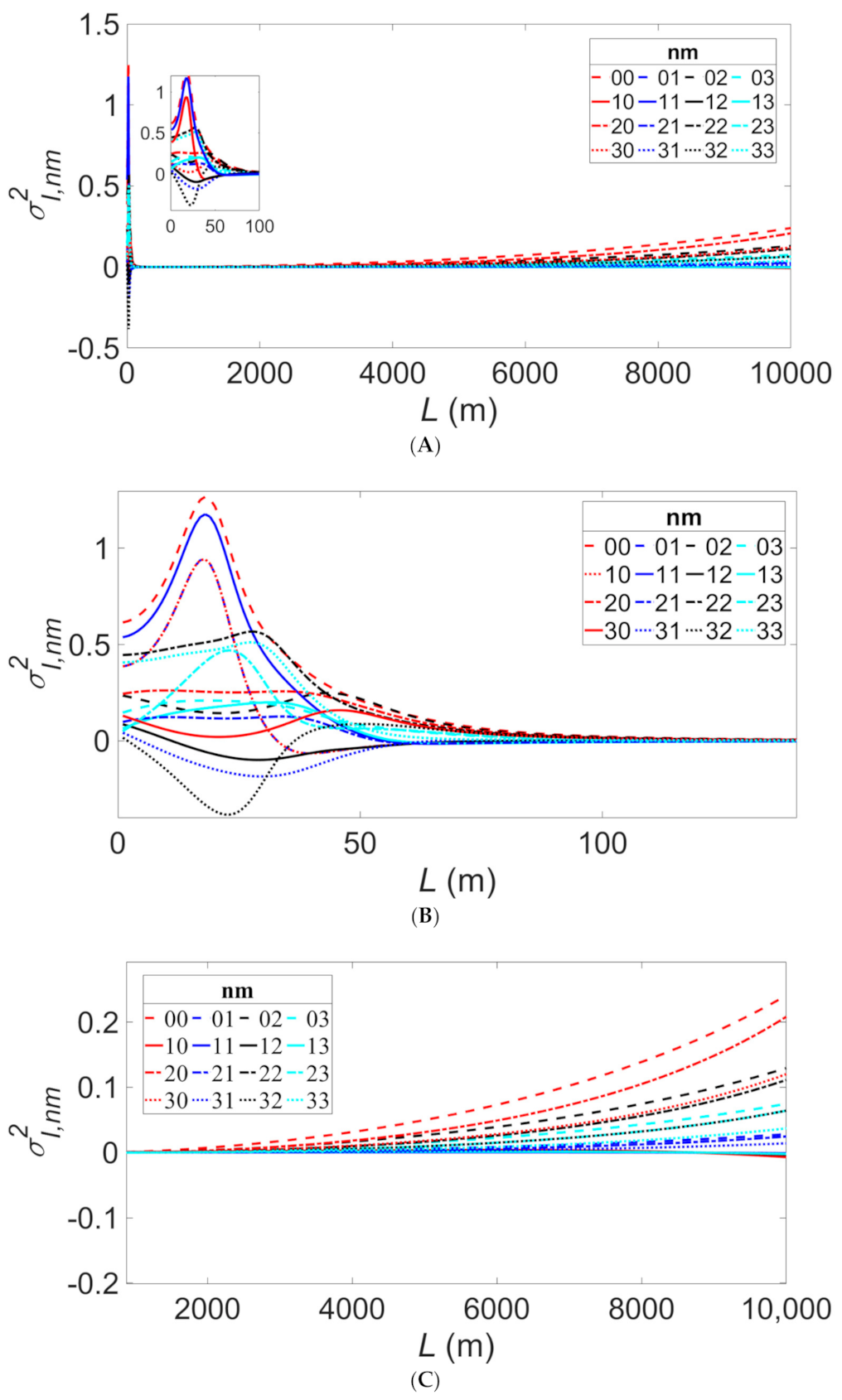
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Brown, R.H.; Twiss, R.Q. A new type of interferometer for use in radio astronomy. Philos. Mag. 1954, 45, 663–682. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R.Q. Correlation between photons in two coherent beams of light. Nature 1956, 177, 27–29. [Google Scholar] [CrossRef]
- Brown, R.H.; Davis, J.; Allen, L.R. The stellar interferometer at Narrabri Observatory. Mon. Not. R. Astron. Soc. 1967, 137, 375–392. [Google Scholar] [CrossRef]
- Moreau, P.A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Ghost imaging using optical correlations. Laser Photon. Rev. 2018, 12, 1700143. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics, 1st ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE Press: Bellington, WA, USA, 2005. [Google Scholar]
- Leader, J.C. Intensity fluctuations resulting from a spatially partially coherent light propagating through atmospheric turbulence. J. Opt. Soc. Am. A 1979, 69, 73–84. [Google Scholar] [CrossRef]
- Fante, L. Intensity fluctuations of an optical wave in a turbulent medium, effect of source coherence. Opt. Acta 1981, 28, 1203–1207. [Google Scholar] [CrossRef]
- Banakh, V.A.; Buldakov, V.M.; Mironov, V.L. Intensity fluctuations of a partially coherent light beam in a turbulent atmosphere. Opt. Spectrosk. 1983, 54, 1054–1059. [Google Scholar]
- Baykal, Y.; Plonus, M.A.; Wang, S.J. The scintillations for weak atmospheric turbulence using a partially coherent source. Radio Sci. 1983, 18, 551–556. [Google Scholar] [CrossRef]
- Baykal, Y.; Plonus, M.A. Intensity fluctuations due to a spatially partially coherent source in atmospheric turbulence as predicted by Rytov’s method. J. Opt. Soc. Am. A 1985, 2, 2124–2132. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian Beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Atmospheric optical communication with a Gaussian Schell beam. J. Opt. Soc. Am. A 2003, 20, 856–866. [Google Scholar] [CrossRef]
- Korotkova, O.; Andrews, L.C.; Phillips, R.L. A Model for a Partially Coherent Gaussian Beam in Atmospheric Turbulence with Application in LaserCom. Opt. Eng. 2004, 43, 330–341. [Google Scholar] [CrossRef]
- Li, J.; Chen, X.; McDuffie, S.; Najjar, M.; Rafsanjani, S.M.H.; Korotkova, O. Mitigation of atmospheric turbulence with random beams carrying OAM. Opt. Commun. 2019, 446, 178–185. [Google Scholar] [CrossRef]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Korotkova, O. Random Beams: Theory and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Barakat, R. Statistics of the Stokes parameters. J. Opt. Soc. Am. A 1987, 4, 1256–1263. [Google Scholar] [CrossRef]
- Brosseau, C.; Barakat, R.; Rockower, E. Statistics of the Stokes parameters for Gaussian distributed fields. Opt. Commun. 1991, 82, 204–208. [Google Scholar] [CrossRef]
- Eliyahu, D. Vector statistics of correlated Gaussian fields. Phys. Rev. E 1993, 47, 2881. [Google Scholar] [CrossRef]
- Korotkova, O. Changes in the intensity fluctuations of a class of random electromagnetic beams on propagation. J. Opt. A Pure Appl. Opt. 2006, 8, 30–37. [Google Scholar] [CrossRef]
- Korotkova, O. Changes in statistics of the instantaneous Stokes parameters of a quasi-monochromatic electromagnetic beam on propagation. Opt. Commun. 2006, 261, 218–224. [Google Scholar] [CrossRef]
- Korotkova, O. Scintillation index of a stochastic electromagnetic beam propagating in random media. Opt. Commun. 2008, 281, 2342–2348. [Google Scholar] [CrossRef]
- Şahin, S.; Korotkova, O. Fluctuations in the instantaneous Stokes parameters of stochastic electromagnetic beams propagating in the turbulent atmosphere. Proc. SPIE 2009, 7200, 720005. [Google Scholar]
- Avramov-Zamurovic, S.; Nelson, C.; Malek-Madani, R.; Korotkova, O. Polarization-induced reduction in scintillation of optical beams propagating in simulated turbulent atmospheric channels. Waves Random Complex Media 2014, 24, 452–462. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, S.; Dang, A. Polarization property changes of optical beam transmission in atmospheric turbulent channels. Appl. Opt. 2017, 56, 5145–5155. [Google Scholar] [CrossRef]
- Kuebel, D.; Visser, T.D. Generalized Hanbury Brown–Twiss effect for Stokes parameters. J. Opt. Soc. Am. A 2019, 36, 362. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yan, S.; Kuebel, D.; Visser, T.D. Generalized Hanbury Brown–Twiss effect and Stokes scintillations in the focal plane of a lens. Phys. Rev. A 2019, 100, 023821. [Google Scholar] [CrossRef]
- Pu, J.; Korotkova, O. Propagation of the degree of cross-polarization of a stochastic electromagnetic beam through the turbulent atmosphere. Opt. Commun. 2009, 282, 1691–1698. [Google Scholar] [CrossRef]
- Shirai, T.; Wolf, E. Correlations between intensity fluctuations in stochastic electromagnetic beams of any state of coherence and polarization. Opt. Commun. 2007, 272, 289–292. [Google Scholar] [CrossRef]
- Charnotskii, M. Extended Huygens–Fresnel principle and optical waves propagation in turbulence: Discussion. J. Opt. Soc. Am. A 2015, 32, 1357–1365. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O.; Wolf, E. Generalized Stokes parameters of random electromagnetic beams. Opt. Lett. 2005, 30, 198–200. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Tatarskii, V.I. The Effects of the Turbulent Atmosphere on Wave Propagation; Israel Program for Scientific Translations: Jerusalem, Israel, 1971. [Google Scholar]
- Wang, S.J.; Baykal, Y.; Plonus, M.A. Receiver-aperture averaging effects for the intensity fluctuaion of beam wave in the turbulent atmosphere. J. Opt. Soc. Am. 1983, 73, 831–837. [Google Scholar] [CrossRef]
- Piquero, G.; Gori, F.; Romanini, P.; Santarsiero, M.; Borghi, R.; Mondello, A. Synthesis of partially polarized Gaussian Schell-model sources. Opt. Commun. 2002, 208, 9–16. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series and Products, 7th ed.; Academic Press Inc.: San Diego, CA, USA, 2007. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korotkova, O.; Ata, Y. Electromagnetic Hanbury Brown and Twiss Effect in Atmospheric Turbulence. Photonics 2021, 8, 186. https://doi.org/10.3390/photonics8060186
Korotkova O, Ata Y. Electromagnetic Hanbury Brown and Twiss Effect in Atmospheric Turbulence. Photonics. 2021; 8(6):186. https://doi.org/10.3390/photonics8060186
Chicago/Turabian StyleKorotkova, Olga, and Yalçın Ata. 2021. "Electromagnetic Hanbury Brown and Twiss Effect in Atmospheric Turbulence" Photonics 8, no. 6: 186. https://doi.org/10.3390/photonics8060186
APA StyleKorotkova, O., & Ata, Y. (2021). Electromagnetic Hanbury Brown and Twiss Effect in Atmospheric Turbulence. Photonics, 8(6), 186. https://doi.org/10.3390/photonics8060186



