Experimental Measurement of Absorption Coefficients for Effective Erbium-Doping Concentration to Optimize Few-Mode Erbium-Doped Fiber Amplifiers with Low Differential Mode Gain
Abstract
1. Introduction
2. Analytical Expression for FM-EDFA’s Gain
3. Experimental Measurement of Modal Absorption Coefficient
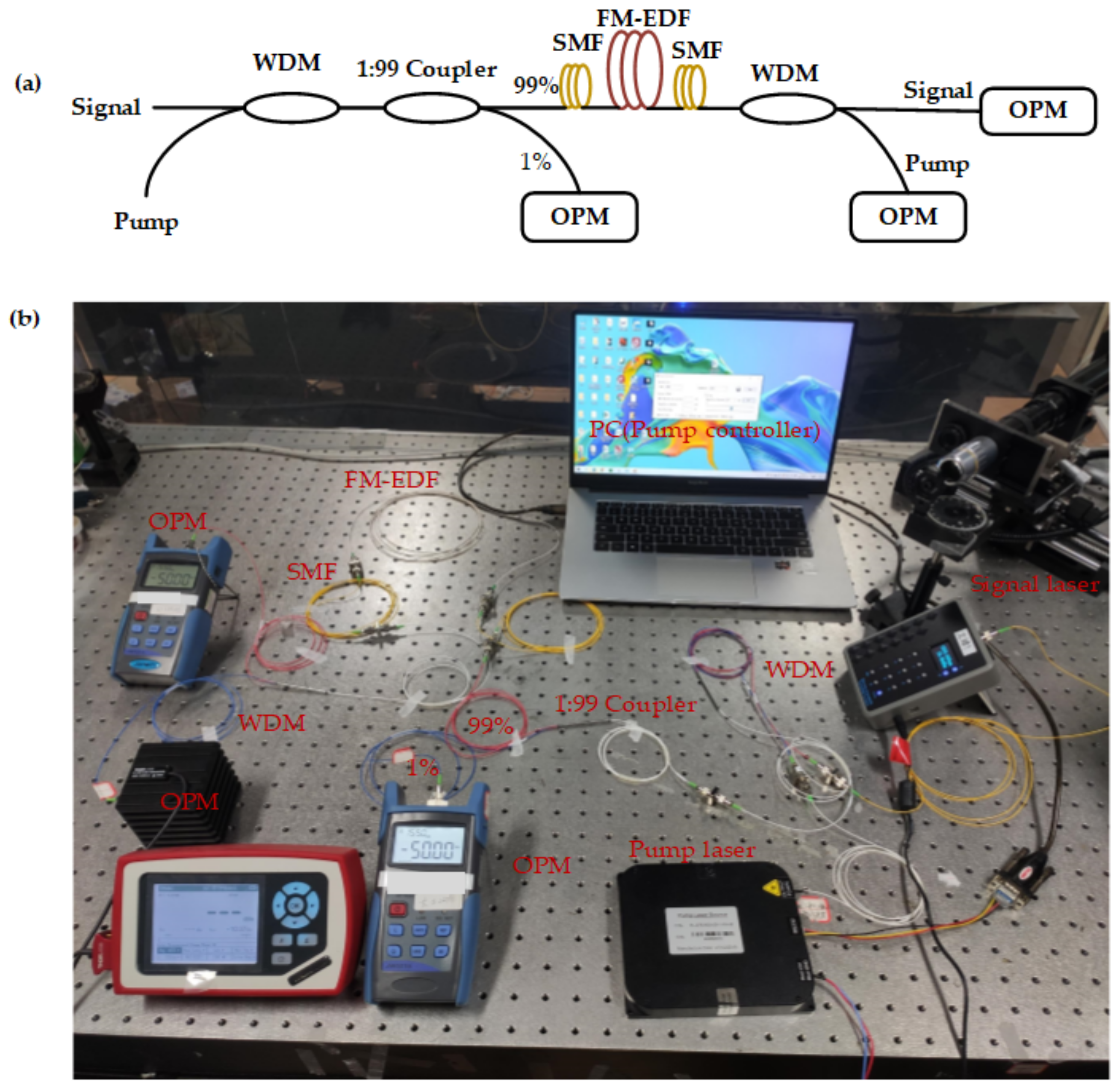
3.1. Description of the Experimental Platform
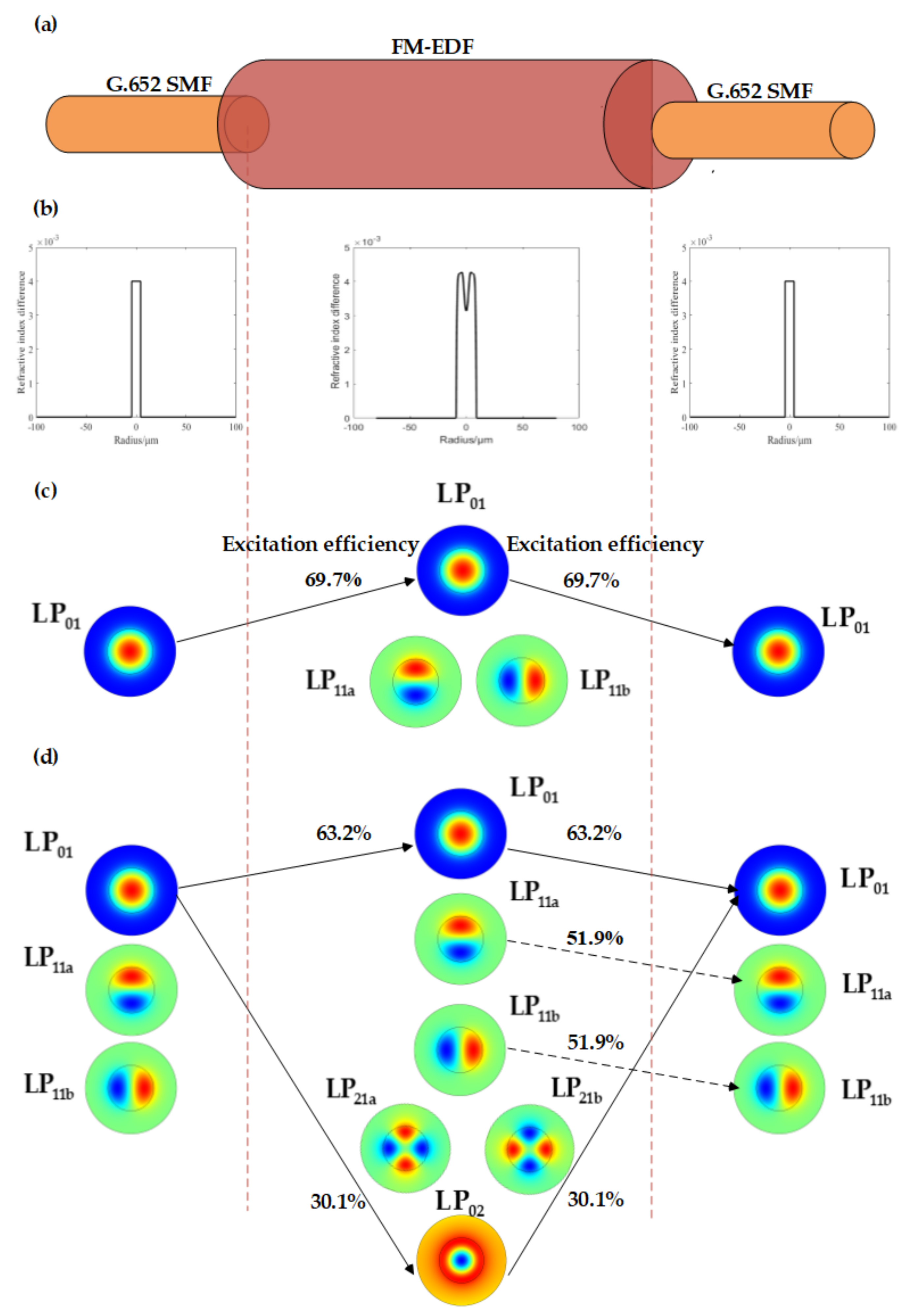
3.2. Mode Coupling and Excitation
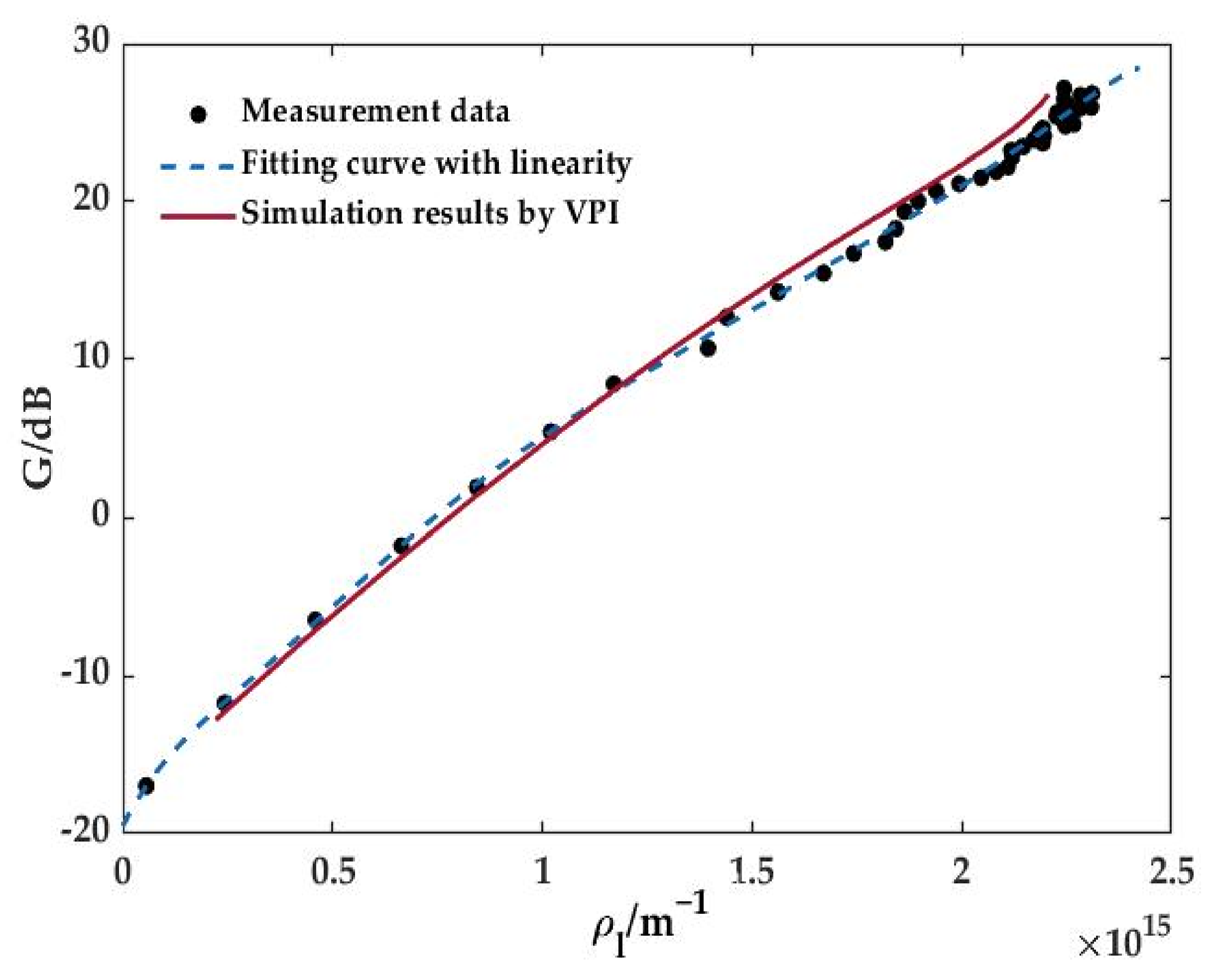
3.3. Extrapolation Method for Measurement of the Absorption Coefficient
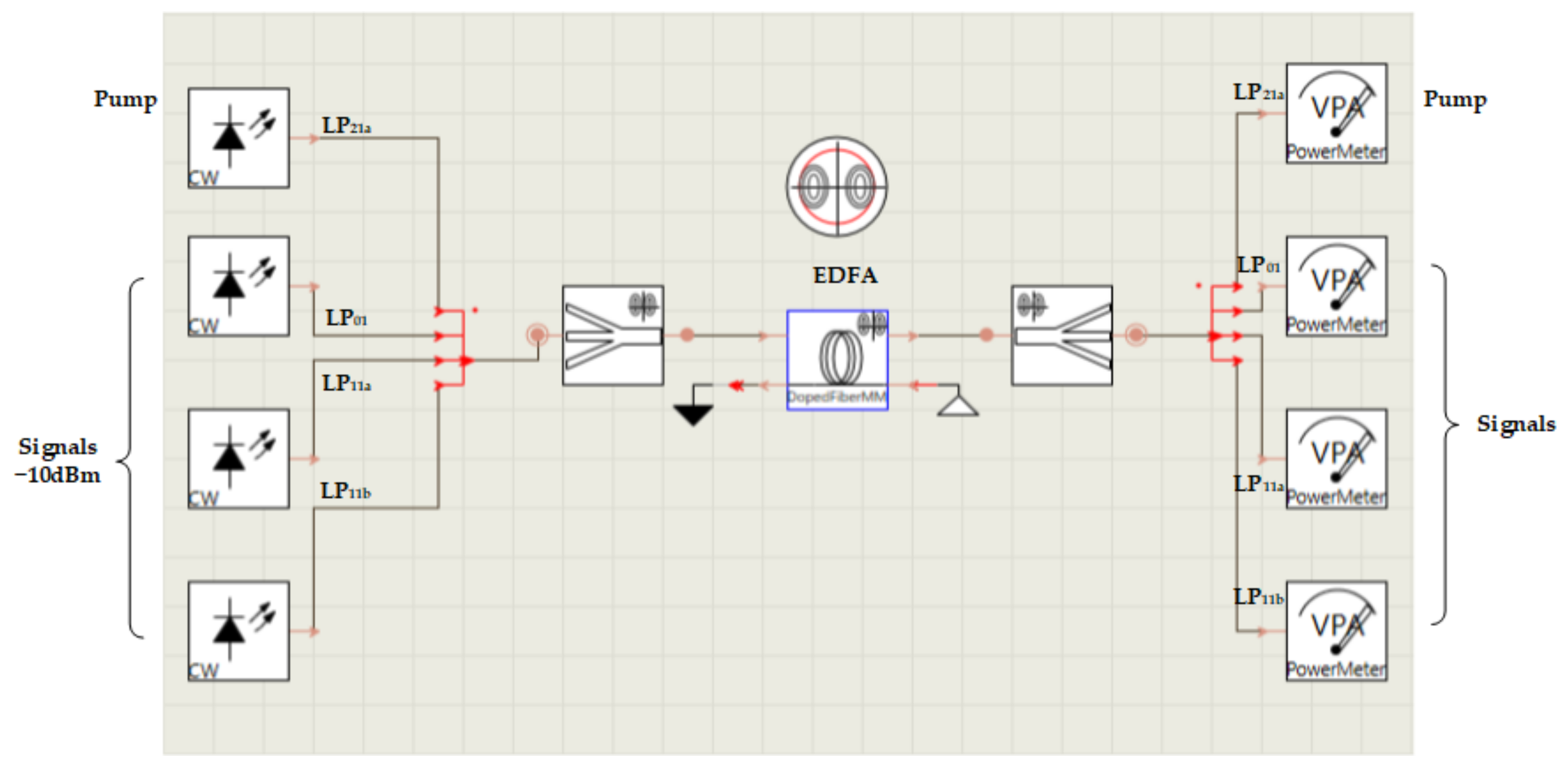
4. Comparison of Experimental and Simulated Results
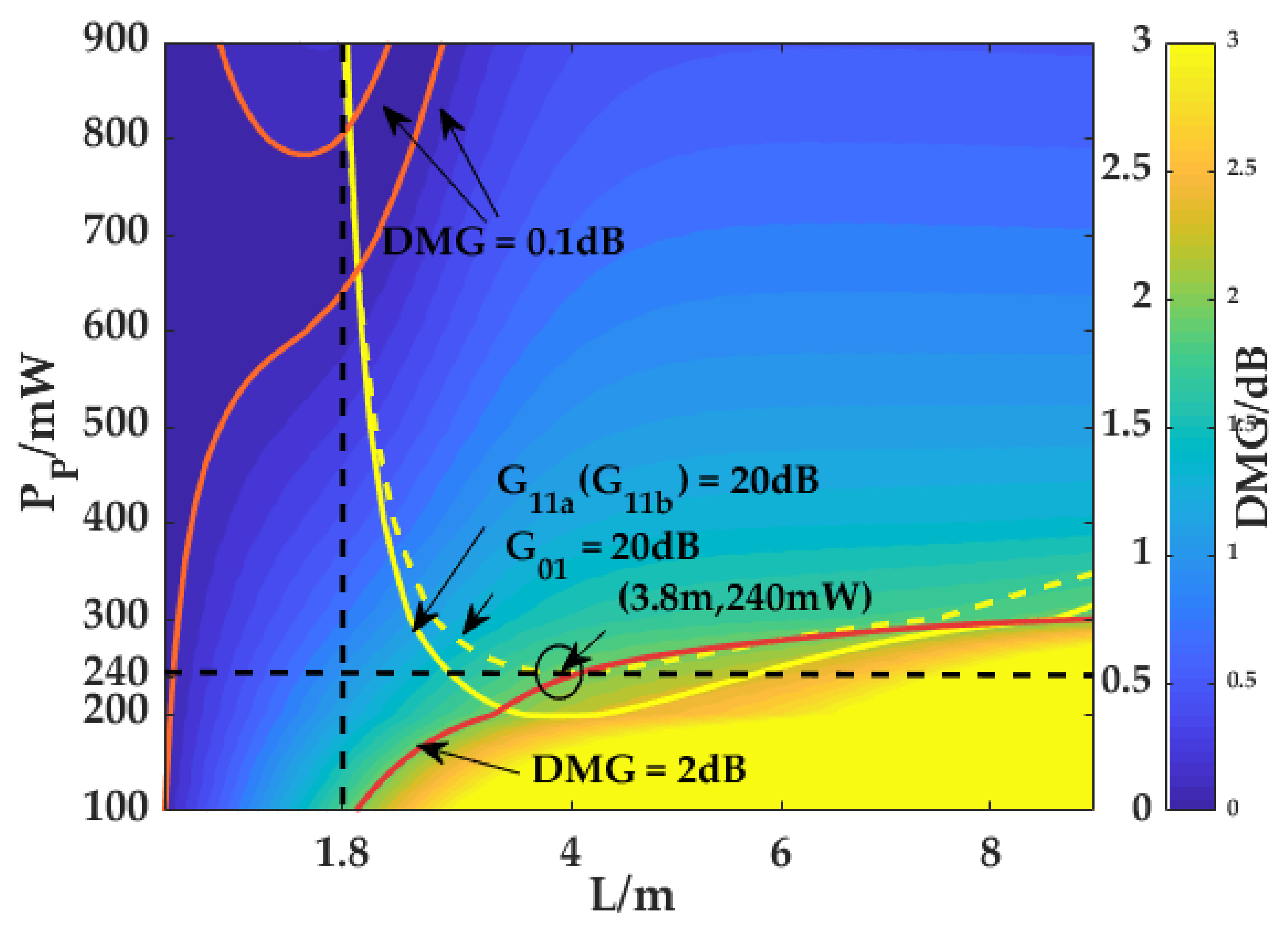
5. Optimal Design of the 3M-EDFAs with forward Pumping LP21-Mode
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Essiambre, R.-J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. Lightwave Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Guan, P.; Tang, M.; Cao, M.; Mi, Y.; Liu, M.; Ren, W.; Ren, G. Transverse Asymmetry of the Index Modulation Profile in Few-Mode Fiber Bragg Grating. Photonics 2021, 8, 87. [Google Scholar] [CrossRef]
- Sillard, P.; Bigot-Astruc, M.; Molin, D. Few-Mode Fibers for Mode-Division-Multiplexed Systems. J. Lightwave Technol. A Jt. IEEE/OSA Publ. 2014, 32, 2824–2829. [Google Scholar] [CrossRef]
- Ono, H.; Hosokawa, T.; Ichii, K.; Matsuo, S.; Yamada, M. Improvement of differential modal gain in few-mode fiber amplifier by employing ring-core erbium-doped fiber. Electron. Lett. 2015, 51, 172–173. [Google Scholar] [CrossRef]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Essiambre, R.J.; Winzer, P.J.; Peckham, D.W.; McCurdy, A.; Lingle, R. Space-division multiplexing over 10 km of three-mode fiber using coherent 6 × 6 MIMO processing. In National Fiber Optic Engineers Conference; Optical Society of America: Los Angeles, CA, USA, 2011; p. PDPB10. [Google Scholar]
- Jung, Y.; Alam, S.; Li, Z.; Dhar, A.; Giles, D.; Giles, I.P.; Sahu, J.K.; Poletti, F.; Grüner-Nielsen, L.; Richardson, D.J. First demonstration and detailed characterization of a multimode amplifier for Space Division Multiplexed transmission systems. Opt. Express 2011, 19, B952–B957. [Google Scholar] [CrossRef] [PubMed]
- Bai, N.; Ip, E.; Wang, T.; Li, G. Multimode fiber amplifier with tunable modal gain using a reconfigurable multimode pump. Opt. Express 2011, 19, 16601–16611. [Google Scholar] [CrossRef] [PubMed]
- Kang, Q.; Lim, E.L.; Jung, Y.; Sahu, J.K.; Poletti, F.; Baskiotis, C.; Alam, S.; Richardson, D.J. Accurate modal gain control in a multimode erbium doped fiber amplifier incorporating ring doping and a simple LP01 pump configuration. Opt. Express 2012, 20, 20835–20843. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.; Kang, Q.; Sleiffer, V.A.J.M.; Inan, B.; Kuschnerov, M.; Veljanovski, V.; Corbett, B.; Winfield, R.; Li, Z.; Teh, P.S.; et al. Three mode Er3+ ring-doped fiber amplifier for mode-division multiplexed transmission. Opt. Express 2013, 21, 10383–10392. [Google Scholar] [CrossRef] [PubMed]
- Vigneswaran, D.; Ayyanar, N.; Sumathi, M.; Rajan, M.M. Tunable differential modal gain in FMEDFA system using dual pumping scheme at 100 Gbps system capacity. Photonic Netw. Commun. 2017, 34, 3. [Google Scholar] [CrossRef]
- Qayoom, T.; Qazi, G. A comparative perspective on Differential Modal Gain reduction techniques for optimized few mode EDFA systems. Optik 2021, 230, 166285. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, B.; Xie, Y.; Wen, F.; Qiu, K. A semi-analytic method for FM-EDFA intensity model. Opt. Fiber Technol. 2021, 64, 102546. [Google Scholar] [CrossRef]
- Lim, E.L.; Kang, Q.; Gecevicius, M.; Poletti, F.; Alam, S.U.; Richardson, D.J. Vector Mode Effects in Few Moded Erbium Doped Fiber Amplifiers. In Proceedings of the 2013 Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013; pp. 1–3. [Google Scholar]
- Chen, X.; Wu, B.; Xie, Y.; Wen, F.; Qiu, K. Analytical method for few-mode erbium doped fiber amplifiers. Laser Phys. Lett. 2020, 17, 035102. [Google Scholar] [CrossRef]
- Noordegraaf, D.; Skovgaard, P.M.; Nielsen, M.D.; Bland-Hawthorn, J. Efficient multi-mode to single-mode coupling in a photonic lantern. Opt. Express 2009, 17, 1988–1994. [Google Scholar] [CrossRef] [PubMed]
- Ho, K.P.; Kahn, J.M. Mode Coupling and Its Impact on Spatially Multiplexed Systems. In Optical Fiber Telecommunications VI; Kaminow, I.P., Li, T., Willner, A.E., Eds.; Academic Press: Los Angeles, CA, USA, 2013; pp. 491–568. [Google Scholar]
- Giles, C.R.; Desurvire, E. Modeling Erbium-Doped Fiber Amplifiers. J. Lightwave Technol. 1991, 9, 271–283. [Google Scholar] [CrossRef]
- Barnes, W.L.; Laming, R.I.; Morkel, P.R.; Tarbox, E.J. Absorption and Emission Cross Section of Er3+ Doped Silica Fibers. Quantum Electron. 1991, 27, 1004–1010. [Google Scholar] [CrossRef]
- Jopson, R.M.; Saleh, A.A. Modeling of gain and noise in erbium-doped fiber amplifiers. IEEE Photonics Technol. Lett. 1990, 2, 714–717. [Google Scholar]
- Lavrinovica, I.; Supe, A.; Porins, J. Experimental Measurement of Erbium-Doped Optical Fibre Charecteristics for Edfa Performance Optimization. Latv. J. Phys. Tech. Sci. 2019, 56, 33–41. [Google Scholar] [CrossRef]
- Le Cocq, G.; Bigot, L.; Le Rouge, A.; Bigot-Astruc, M.; Sillard, P.; Koebele, C.; Salsi, M.; Quiquempois, Y. Modeling and Characterization of a Few-Mode EDFA Supporting Four Mode Groups for Mode Division Multiplexing. Opt. Express 2012, 20, 27051–27061. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Wu, B.; Jiang, X.; Guo, H.; Wen, F. Experimental Measurement of Absorption Coefficients for Effective Erbium-Doping Concentration to Optimize Few-Mode Erbium-Doped Fiber Amplifiers with Low Differential Mode Gain. Photonics 2021, 8, 185. https://doi.org/10.3390/photonics8060185
Xu Y, Wu B, Jiang X, Guo H, Wen F. Experimental Measurement of Absorption Coefficients for Effective Erbium-Doping Concentration to Optimize Few-Mode Erbium-Doped Fiber Amplifiers with Low Differential Mode Gain. Photonics. 2021; 8(6):185. https://doi.org/10.3390/photonics8060185
Chicago/Turabian StyleXu, Yan, Baojian Wu, Xinrui Jiang, Haomiao Guo, and Feng Wen. 2021. "Experimental Measurement of Absorption Coefficients for Effective Erbium-Doping Concentration to Optimize Few-Mode Erbium-Doped Fiber Amplifiers with Low Differential Mode Gain" Photonics 8, no. 6: 185. https://doi.org/10.3390/photonics8060185
APA StyleXu, Y., Wu, B., Jiang, X., Guo, H., & Wen, F. (2021). Experimental Measurement of Absorption Coefficients for Effective Erbium-Doping Concentration to Optimize Few-Mode Erbium-Doped Fiber Amplifiers with Low Differential Mode Gain. Photonics, 8(6), 185. https://doi.org/10.3390/photonics8060185





