Adaptive Gradient Estimation Stochastic Parallel Gradient Descent Algorithm for Laser Beam Cleanup

Abstract

For a high-power slab solid-state laser, obtaining high output power and high output beam quality are the most important indicators. Adaptive optics systems can significantly improve beam qualities by compensating for the phase distortions of the laser beams. In this paper, we developed an improved algorithm called Adaptive Gradient Estimation Stochastic Parallel Gradient Descent (AGESPGD) algorithm for beam cleanup of a solid-state laser. A second-order gradient of the search point was introduced to modify the gradient estimation, and it was introduced with the adaptive gain coefficient method into the classical Stochastic Parallel Gradient Descent (SPGD) algorithm. The improved algorithm accelerates the search for convergence and prevents it from falling into a local extremum. Simulation and experimental results show that this method reduces the number of iterations by 40%, and the algorithm stability is also improved compared with the original SPGD method.

1. Introduction

High-power solid-state lasers have been widely used in many fields such as machinery, medical, and defense [1,2,3,4,5,6]. With the development of lasers, applications such asspace-based laser space debris cleanup have put forward new requirements for laser systems. These scenarios require the laser system to have a high average output power and high output beam quality and require the system to be simple, compact, and miniaturized. However, the thermal effect of the laser introduces wavefront distortion, which leads to degradation of beam quality [7,8,9]. With the rapid development of gain materials, pump sources, laser extraction structures, and adaptive optics (AO) technology, the output power and beam quality of solid-state lasers have been significantly improved [10,11,12,13,14,15,16]. The adaptive optics technology measures the wavefront distortion through the wavefront sensor and uses the control system to control the deformable mirror to correct the wavefront distortion, which can effectively improve the laser beam quality [15,17]. Compared with classical AO, the wavefront sensor-less AO (WFSless AO) system does not need a wavefront sensor to measure the wavefront distortion; the control signal of the correction element is obtained by optimization algorithm, so it has a simpler structure and it is easier for the system to achieve lightweight requirements [18,19,20,21].

Commonly used optimization algorithms include the hill climbing algorithm [20], genetic algorithm [22], simulated annealing algorithm [23,24], stochastic parallel gradient descent (SPGD) algorithm [25,26,27,28,29,30,31,32], etc. Among these, the SPGD algorithm is more efficient and more applicable than other algorithms in AO systems and has been widely used for laser beam cleanup [27,33]. However, the convergence speed of the classical SPGD algorithm is slower, and it would have a probability of converging to a local extremum [34]. In recent years, a variety of improved algorithms aimed at increasing the speed of the algorithm were proposed and widely used to optimize the connection weights of deep neural networks, such as the AdaGrad algorithm [28], RMSProp algorithm [30], and Adam algorithm [31]. In 2020, Hu et al. proposed an adaptive stochastic parallel gradient descent method based on the Adam algorithm to achieve efficient fiber coupling [32]. Although these methods have achieved excellent results, most of them were aimed at specific problems in application and cannot be directly used to achieve beam cleanup. In addition, these algorithms introduce momentum and multiple hyperparameters, which increase the difficulty of calculation and parameter selection.

In our work, we developed an adaptive gradient estimation stochastic parallel gradient descent (AGESPGD) algorithm in the WFSless AO system for beam cleanup of solid-state lasers. In the iterative process of the algorithm, both the gradient and the second-order gradient are considered. The gradient value controls the direction of the iteration, and the second-order gradient is introduced to adaptively modify the gradient estimate factor to increase the convergence and prevent falling into local extremes. This article is organized as follows: Firstly, we analyze and derive the principle and iterative formula of the AGESPGD method. Second, this method is verified by a large number of simulations. Finally, the performance of the algorithm is tested in a real experimental system. Both simulation and experimental results prove that our proposed method has a significant improvement in convergence speed and robustness to search step-size.

2. Principle of the AGESPGD Algorithm

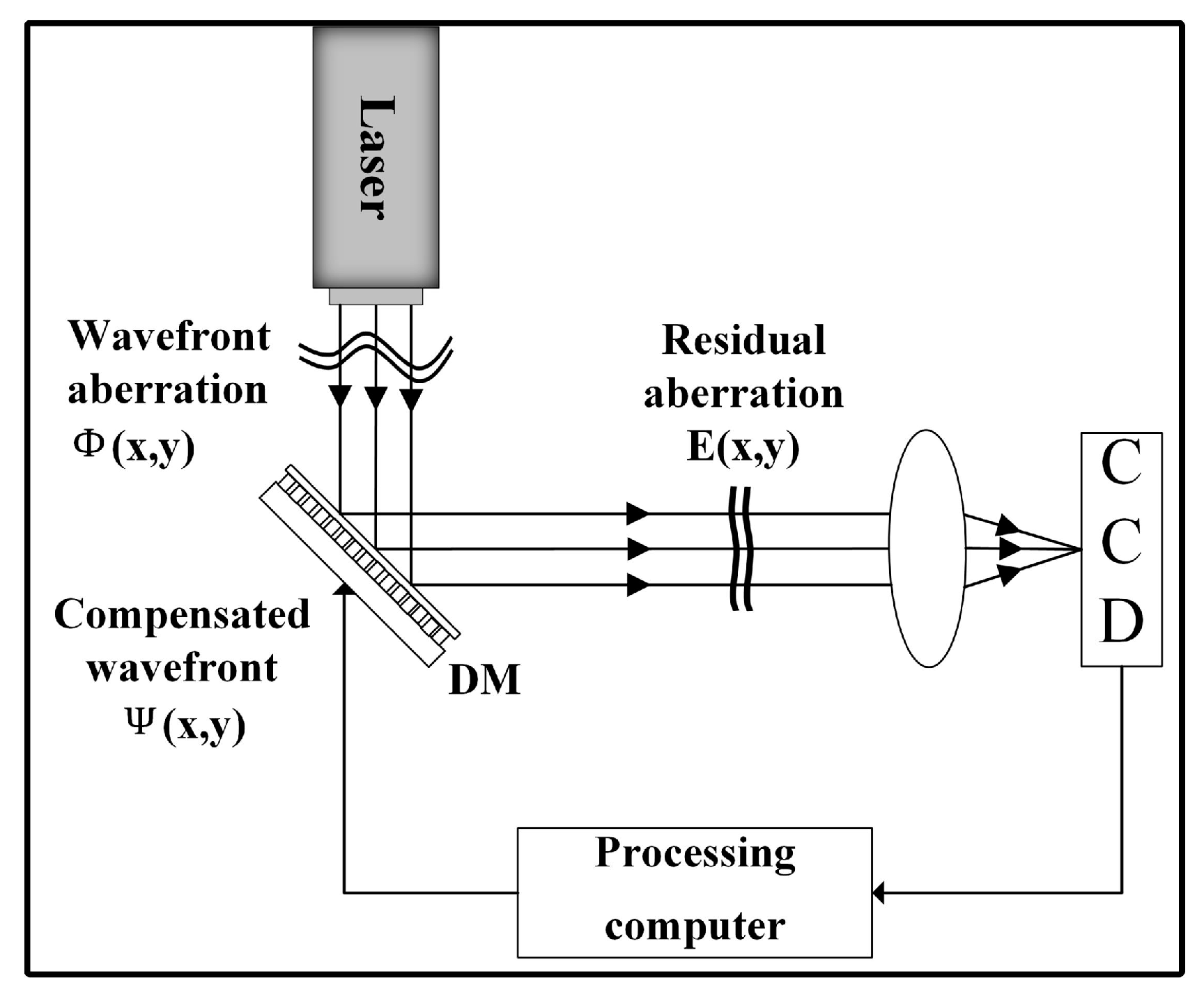
2.1. Model of Laser Beam Cleanup System

Wavefront sensor-less adaptive optics technology is a simple but effective method for beam cleanup in solid-state laser systems. The schematic of the WFSless AO system is shown in Figure 1. It consists of a deformable mirror (DM), a set of solid-state laser systems, a CCD camera, and a set of optical focusing lenses. The distorted beam is converged on the CCD camera through the focusing lens, and the camera can collect the degraded far-field spot.

The basic principle of WFSless AO is using an optimization algorithm to search for the best voltage matrix $U=\left(u_1,u_2,u_3,\cdots ,u_n\right)$ (n is the number of DM actuator) to minimize the residual wavefront surface $E\left(x,y\right)=\Phi \left(x,y\right)-\Psi \left(x,y\right)$. Φ (x,y) represents the wavefront aberration of the beam. Ψ (x,y) represents the surface shape of the DM driven by voltage matrix U. The expression of $\Psi \left(x,y\right)$ is

$$\Psi \left(x,y\right)={\displaystyle \sum _{i=1}^n{u}_i{f}_i\left(x,y\right)}.$$

(1)

where i is the number of actuators, and f_i (x,y) is the surface function generated by applying a unit voltage to the i-th actuator. The beam quality of the degraded far-field image can be used as a merit function $J\left(U\right)$ to evaluate the magnitude of the wavefront residual $E\left(x,y\right)$. The merit function usually selects a certain evaluation index of beam quality, such as sharpness function, Strehl ratio (SR), power in the bucket (PIB), etc. This method does not require a complex wavefront sensor system to measure wavefront distortion. Therefore, the laser beam cleanup could be achieved by searching for the best voltage matrix of DM to optimize the merit function, as shown in Equation (2).

$$\underset{U}{\max }J\left(U\right)$$

(2)

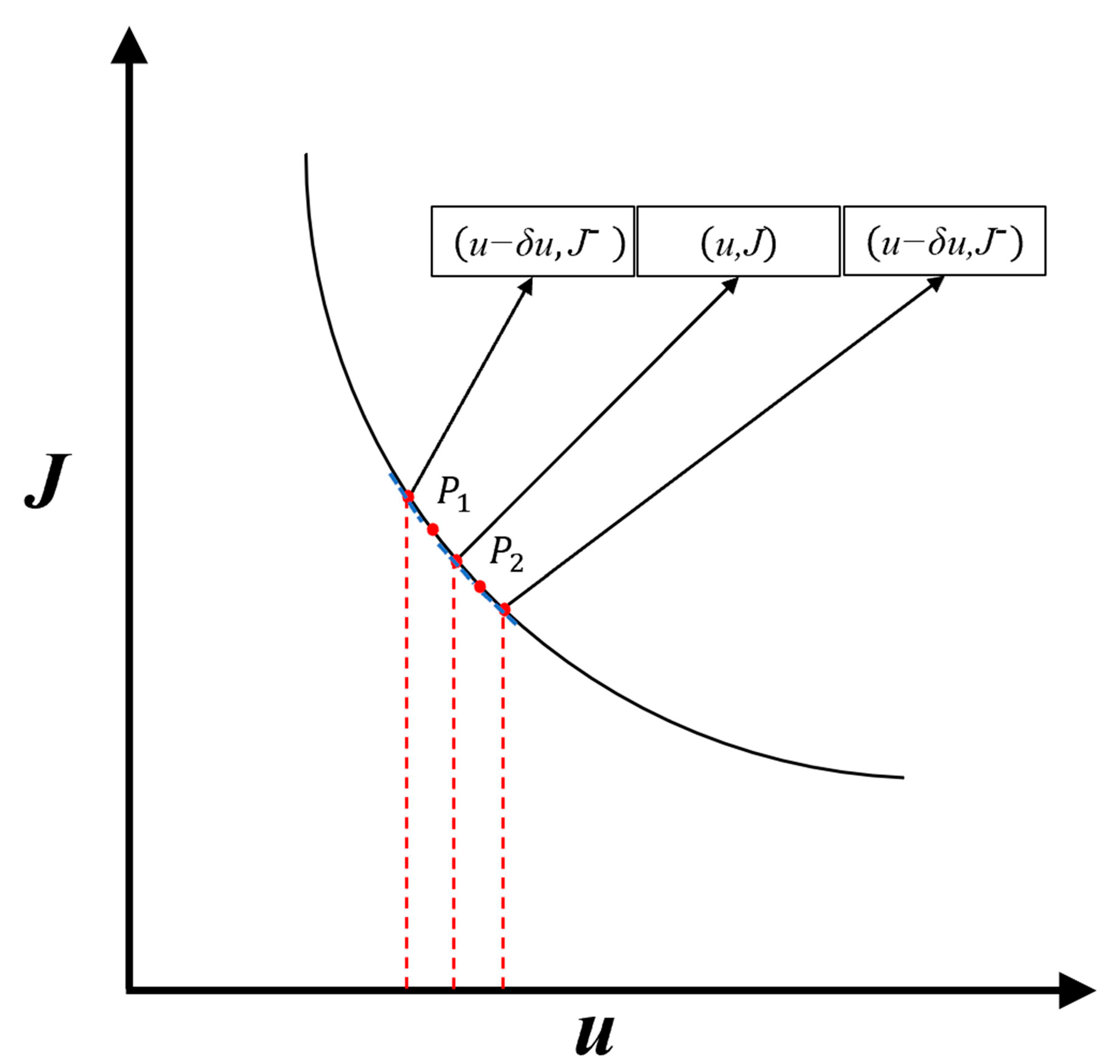
2.2. AGESPGD

For the classic SPGD method, the convergence speed and direction are only determined by the gradient value of the search point. When the gradient of the merit function is variable, the algorithm performance is seriously degraded by this method. Specifically, the algorithm would repeatedly oscillate near the optimal point or even fall into the local optimal because the search speed accelerates as the gradient gradually increases. When the gradient gradually decreases, the algorithm convergence speed becomes extremely slow because the search speed also decreases. Therefore, we introduce a value of second-order gradient of current point to predict the change of the gradient, which makes the convergence process more effective.

The classical SPGD algorithm originated from the gradient descent method in artificial neural networks [25,35,36]. The principle is to apply a combination of interference voltages $\Delta U=\left(\delta u_1,\delta u_2,\delta u_3,\cdots ,\delta u_n\right)$ to multiple actuators to obtain changes in the value of the merit function [33]:

$$\begin{array}{cc}\delta J& =J^{+}-J\hfill \\ & =J\left(u_1+\delta u_1,u_2+\delta u_2,\cdots ,u_n+\delta u_n\right)-J\left(u_1,u_2,\cdots ,u_n\right),\end{array}$$

(3)

where $J^{+}$ and $J^{-}$ represent the value of the merit function after and without disturbance, respectively. Taylor expansion of Equation (3) can be obtained:

$$\delta J={\displaystyle \sum _{i=1}^n\frac{\partial J}{\partial u_i}\delta }{u}_i+O\left(\left[\delta u_i\right]\right).$$

(4)

By simply transforming and ignoring higher-order terms, we can obtain

$$\delta J\delta u_i=\frac{\partial J}{\partial u_i}{\left(\delta u_i\right)}^2+{\displaystyle \sum _{j\ne i}^n\frac{\partial J}{\partial u_j}\delta }{u}_j\delta u_i+\cdots .$$

(5)

The disturbance voltage applied to each actuator is independently and randomly distributed, so we can get ${\displaystyle \sum _{i\ne j}^n\frac{\partial J}{\partial u_i}}\delta u_i\delta u_j=0$ and an estimate of the gradient can be approximately written as

$${\overline{J^{\prime }}}_i\approx \delta J\delta u_i\approx \Delta J_i\delta u_i/{\left(\delta u_i\right)}^2.$$

(6)

According to mathematical proof, when the random characteristics of random disturbances are equal in amplitude $\left|\delta u_i\right|=du$, the random characteristics of each disturbance degenerate to Bernoulli distribution and would not affect the convergence. According to the previous derivation, the iterative formula can be rewritten as

$$u_i^{t+1}=u_i^t-\gamma {\overline{J^{\prime }}}_i=u_i^t-\gamma \left(J^{+}-J\right)\delta u_i.$$

(7)

In practical applications, the bilateral disturbance strategy is usually used to improve the accuracy of gradient estimation [30], that is, to apply positive disturbance and negative disturbance to the actuator and measure the corresponding index function value. ${\overline{J^{\prime }}}_i$ in Equation (7) can be written as

$${\overline{J^{\prime }}}_i=\left(J^{+}-J^{-}\right)\delta u_i.$$

(8)

where $J^{+}$ and $J^{-}$ represent the value of the merit function after applying positive and negative disturbances, respectively. The relationship between $J^{+}$, $J^{-}$, and $J$ is described in Figure 2. Two virtual points (P₁ and $P_2$) are added between them, which represent the half-step length of the positive and negative disturbances, respectively, and their corresponding mathematical expressions for gradient estimation are

$$\begin{array}{l}{\overline{J}}_i{{}_1}^{\prime }=\left(J-J^{-}\right)\delta u_i/2,\\ {\overline{J^{\prime }}}_{i2}=\left(J^{+}-J\right)\delta u_i/2.\end{array}$$

(9)

From these two virtual points, we can calculate the second-order gradient at the point $\left\{u_i\right\}$ as

$$\begin{array}{cc}{\overline{J^{″}}}_i& \approx \left({\overline{J^{\prime }}}_{i1}-{\overline{J^{\prime }}}_{i2}\right)\delta u_i\hfill \\ & =\left[\left(J^{+}-J\right)\delta u_i/2-\left(J-J^{-}\right)\delta u_i/2\right]/\delta u_i\\ & =C\left(J^{+}+J^{-}-2J\right).\hfill \end{array}$$

(10)

According to the previous analysis, the second-order gradient is introduced to control gradient estimation (${\overline{J^{\prime }}}_i$). Therefore, by introducing a parameter $\eta =\frac{C}{J^{″}}$ (C is constant) that is negatively related to the second-order gradient $J^{″}$ into Equation (7), we get the iterative formula of the AGESPGD as follows:

$$u_i^{t+1}=u_i^t-\gamma {\overline{J^{\prime }}}_i/{\overline{J^{″}}}_i.$$

(11)

Algorithm 1 shows the process of the AGESPGD algorithm. The termination condition is generally selected to reach a certain value or reach a certain number of iterations.

Algorithm 1. The procedure of the Adaptive Gradient Estimation Stochastic Parallel Gradient Descent (AGESPGD) method

Require: the stochastic merit function J (u1, u2, u3, …, un), the amplitude of disturbance $\delta u$, the gain rate $\mathsf{\gamma }$, the certain value of $J_0$, and the maximal number of iterations T.

Ensure: The optimal parameters γ and du

Initialize the indexes $J=0$, J′ = 0, J″ = 0.

Initialize the voltages u1, u2, u3, …, un.

while $t\le T$ or J ≥ Jc  do

Randomly generate the values of $\Delta U_t=\left(\delta u^t{}_1,\delta u^t{}_2,\delta u^t{}_3,\cdots ,\delta u^t{}_n\right)$.

Calculate the value of index $J^{+}$ $J^{-}$ $J$.

${\overline{J^{\prime }}}_i=\left(J^{+}-J^{-}\right)\delta u_i.$.

${\overline{J^{″}}}_i=J^{+}+J^{-}-2J.$.

$u_i^{t+1}=u_i^t-\gamma {\overline{J^{\prime }}}_i/{\overline{J^{″}}}_i.$

$t=t+1$.

end while

In order to verify our proposed AGESPGD method, we constructed a unary function $f\left(x\right)$. This function has multiple local minima; its curve is shown in Figure 3, and its expression is given by Equation (12). From the simulation results, the classical SPGD only converge to the local minimum, while the AGESPGD method can converge to the optimal solution and only requires 88 iterations. From this simple simulation, we can see that our proposed AGESPGD algorithm converges faster and avoids the local extremum problem.

$$f\left(x\right)={\left(x-3\right)}^2+3\sin \left(2\pi x\right)+5.$$

(12)

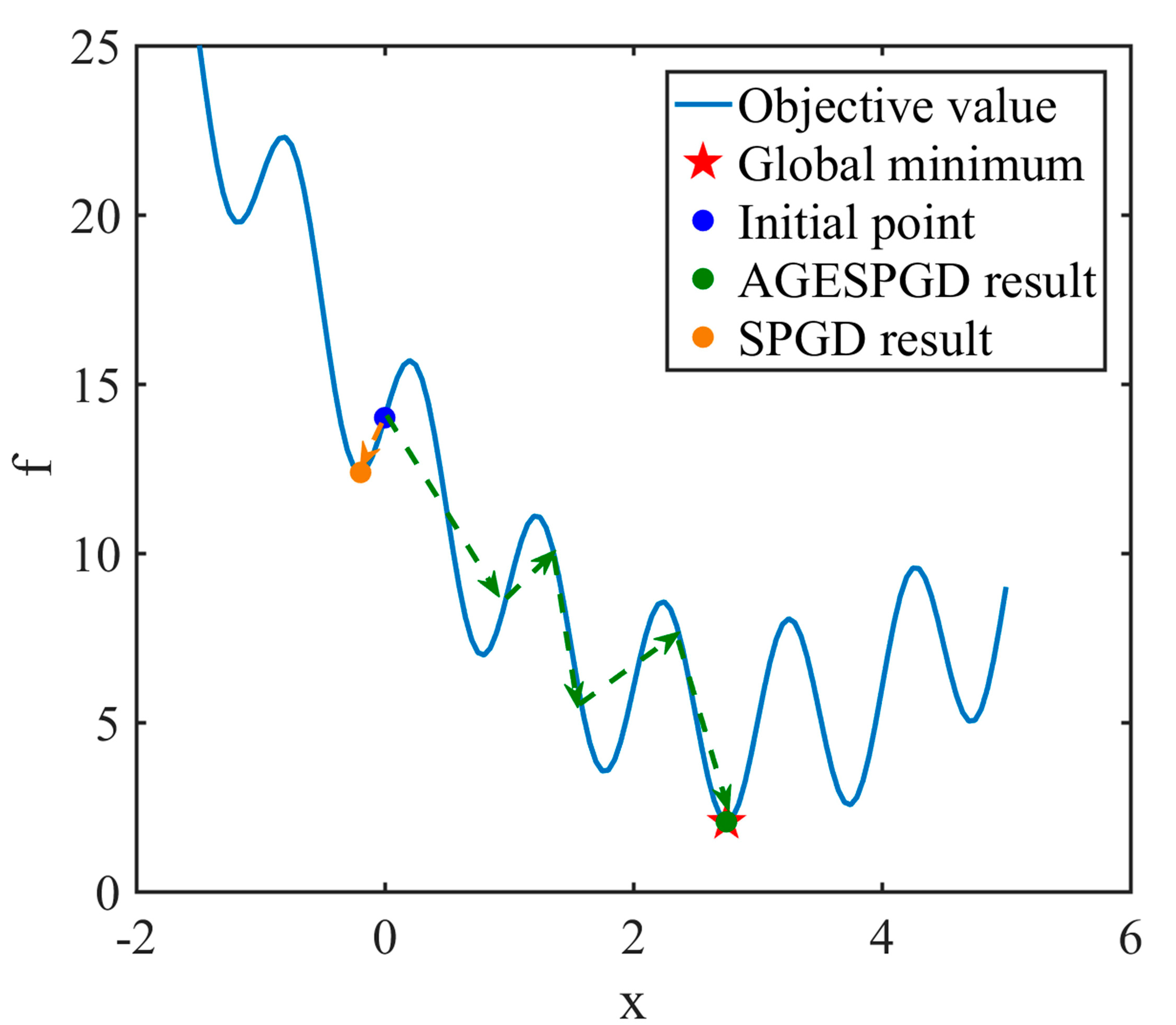
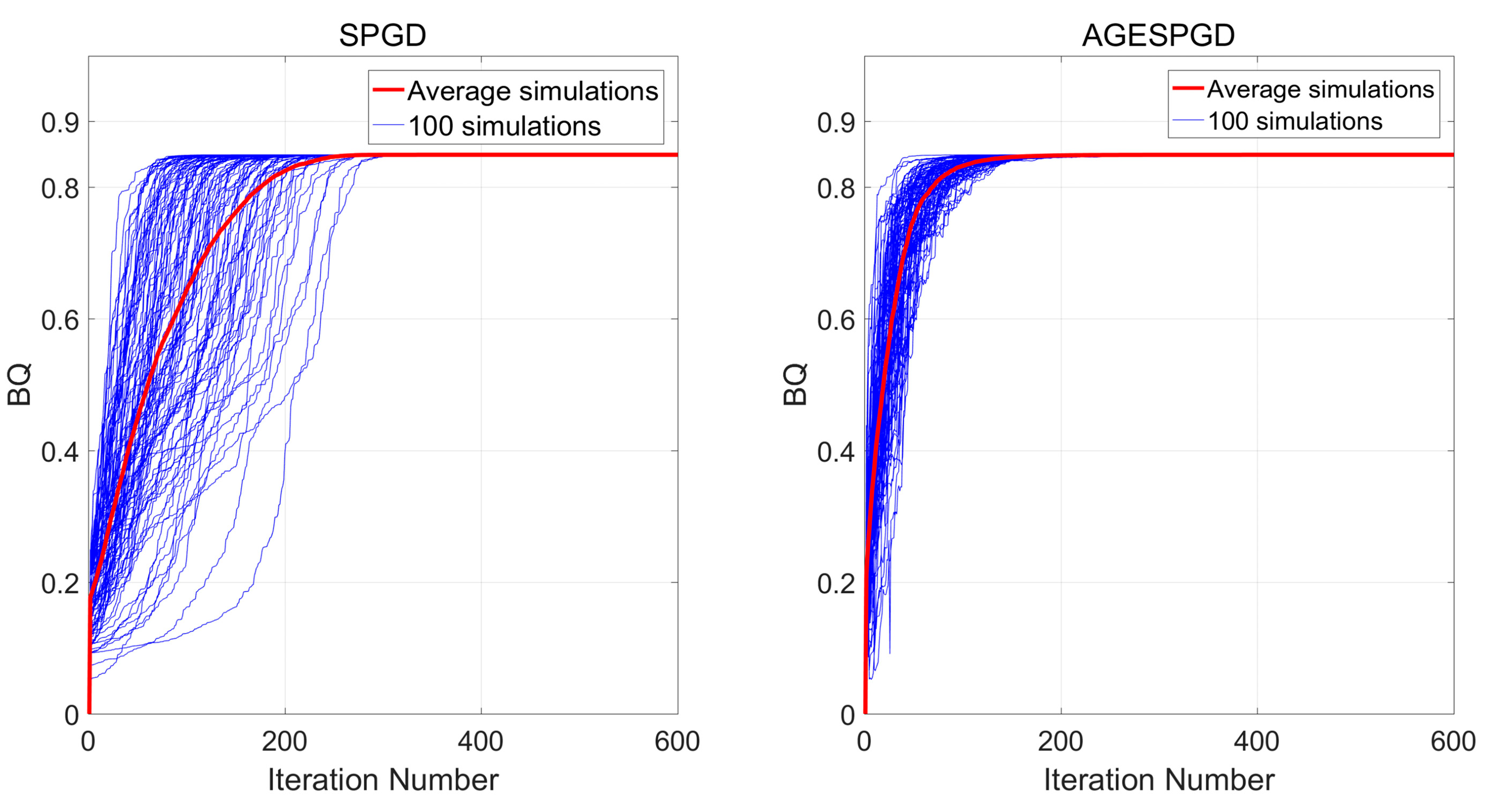
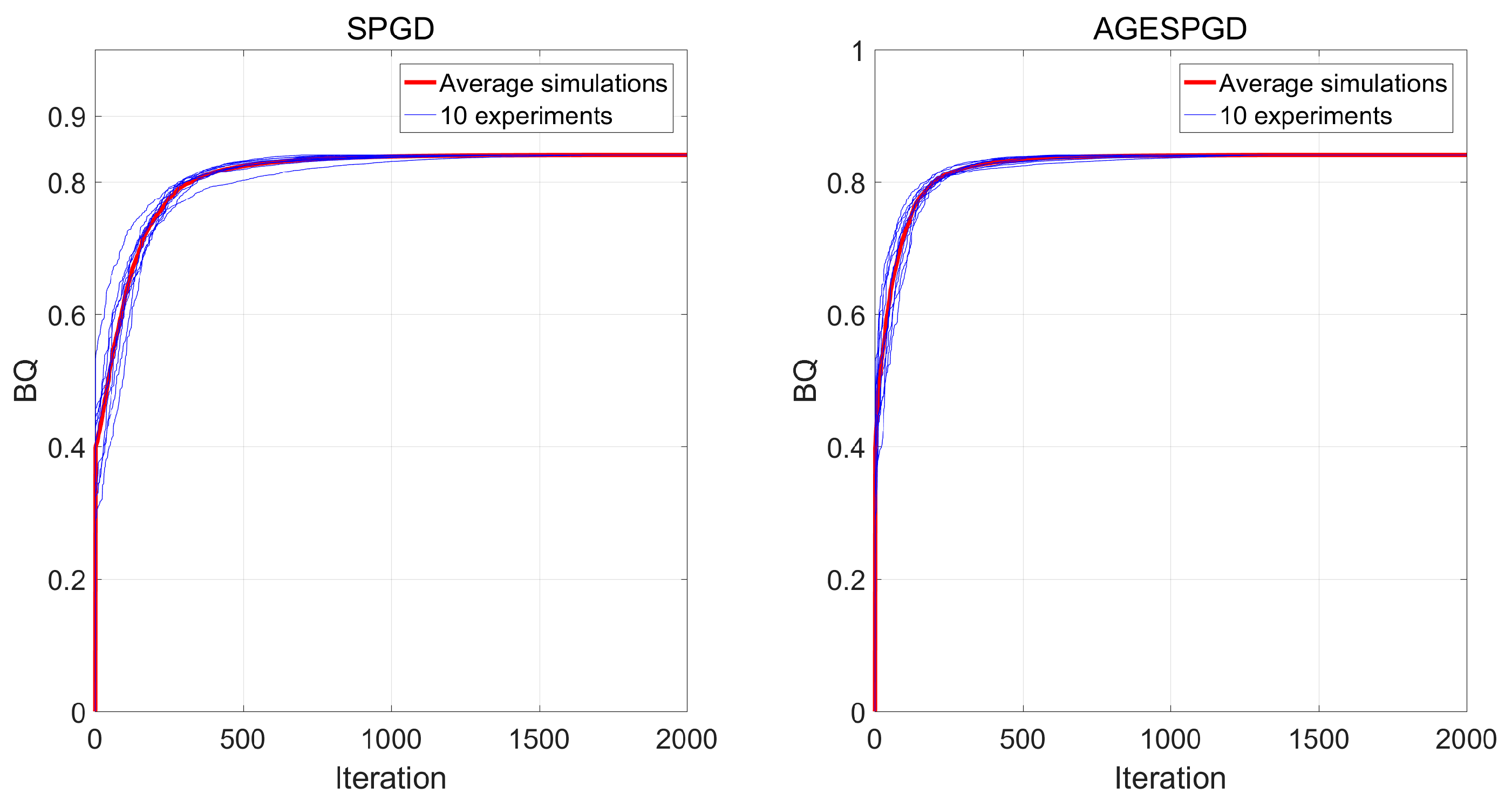
3. Simulation

We performed numerical simulations to verify the application of our proposed AGESPGD method in a laser beam cleanup system. The scheme of the beam cleanup system is shown in Figure 1. The wavefront aberration $\Phi \left(x,y\right)$ of the input beam is generated by the Zernike polynomial [37]. $\Phi \left(x,y\right)$ can be described as a linear combination of various orders of the Zernike polynomial:

$$\Phi \left(x,y\right)={\displaystyle \sum _{i=1}^j{a}_i{Z}_i\left(x,y\right)}.$$

(13)

$Z_i\left(x,y\right)$ is the i order Zernike polynomial expression, and $a_i$ is the corresponding coefficient of polynomials. The aberration represented by $Z_0$ is the overall phase shift, which will not cause degradation of the beam quality. The aberration Z₁ and Z₂ respectively represent the tilt in two directions, which can be corrected by beam pointing control. Therefore, in the simulation, wavefront aberration was simulated using 3~5 order Zernike polynomial. All coefficients were randomly generated. The relationship between the far-field intensity distribution of the beam and the wavefront aberration can be expressed as [25]

$$I\left(x^{\prime },y^{\prime }\right)={\left|{\displaystyle \iint A_0\left(x,y\right)\exp \left\{j\left[\Phi \left(x,y\right)-\Psi \left(x,y\right)\right]\right\}•{\exp }^{\frac{jk\left[{\left(x^{\prime }-x\right)}^2+{\left(y^{\prime }-y\right)}^2\right]}{2f}}dxdy}\right|}^2.$$

(14)

where (x′,y′) is the rectangular coordinate in the input plane of the camera, (x,y) is the pupil plane coordinate, k=2π/λ is wave number, λ is the wavelength of the input wavefront, f is the focal length of the optical focusing lens, and j is the imaginary unit. A₀ (x,y) is the amplitude of the input wavefront, which is generally set to be unity. In the simulation, power in the bucket (PIB) was used as the optimization merit function [38,39], and its expression is represented by Equation (15), where S₀ is the area of the bucket.

$$J=\frac{{\displaystyle {\iint }_{S_0}I\left(x^{\prime },y^{\prime }\right)}dxdy}{{\displaystyle {\iint }_{S}I\left(x^{\prime },y^{\prime }\right)}dxdy}.$$

(15)

The parameters of the simulation system were set as follows: beam aperture D = 80 mm, wavelength λ = 1064 nm, optical lens f = 5 m, camera pixel size pix = 7.4 μm. A total of 150 sets of random aberrations were generated; one part was used to obtain the best parameters of the algorithm, and the other part was used to compare the performance of the two methods. The iteration curve is shown in Figure 4, and the parameters of the two methods were set as (SPGD: δ_u = 0.01 y = 10 and AGESPGD: δ_u = 0.1 $\mathsf{\gamma }=0.05$). The classical SPGD requires an average of 215 iterations to complete convergence. Our developed AGESPGD method only needed an average of 124 iterations to complete the convergence in 100 simulation experiments, and its average convergence was about 40% faster than the classical SPGD.

Subsequently, we also analyzed the peak–valley (PV) value and root-mean-square (RMS) value of the residual wavefront after correction, and the beam quality (times-diffraction-limit factor, $\beta$) of the far-field spot. Figure 5 shows the comparison result of a certain random aberration. For the classical SPGD method, the average result of 100 random aberrations was that the PV and RMS were improved from 2.3 and 0.127 to 0.27 and 0.0025, respectively (unit is wavelength λ = 1064 nm), and the beam quality improved from 3.84 times the diffraction limit to 1.37 times the diffraction limit. For the AESPGD method, the PV and RMS were improved from 2.3 and 0.122 to 0.27 and 0.0028, respectively (unit is wavelength λ = 1064 nm), and the beam quality was improved from 3.84 times the diffraction limit to 1.35 times the diffraction limit.

To further analyze the performance of the two methods, we used different values of $\delta u$ to evaluate the two methods. The iteration curve is shown in Figure 6. The values of δ_u were set to 0.025, 0.01, and 0.005. The AGESGD method can converge stably for different values of δ_u. However, the classical SPGD method would show the phenomenon of slow convergence or oscillating back and forth. Overall, the AGESPGD method exhibited better performance in terms of convergence and robustness to $\delta u$ than the classic SPGD in these simulations.

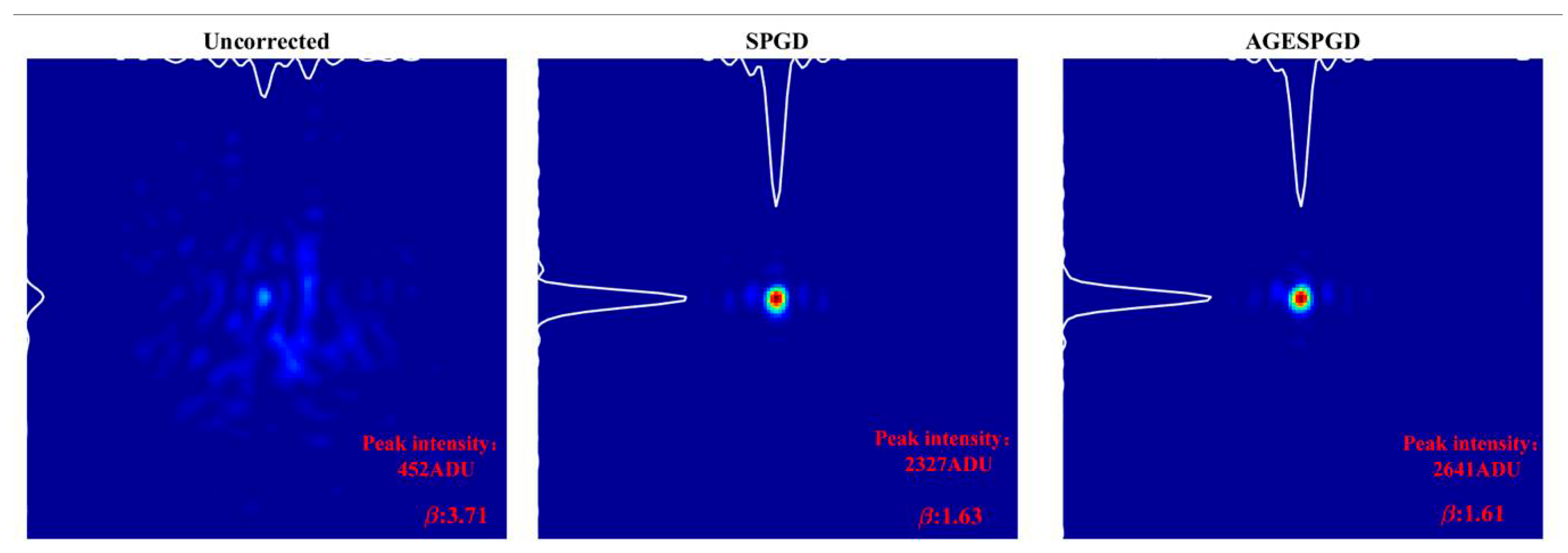
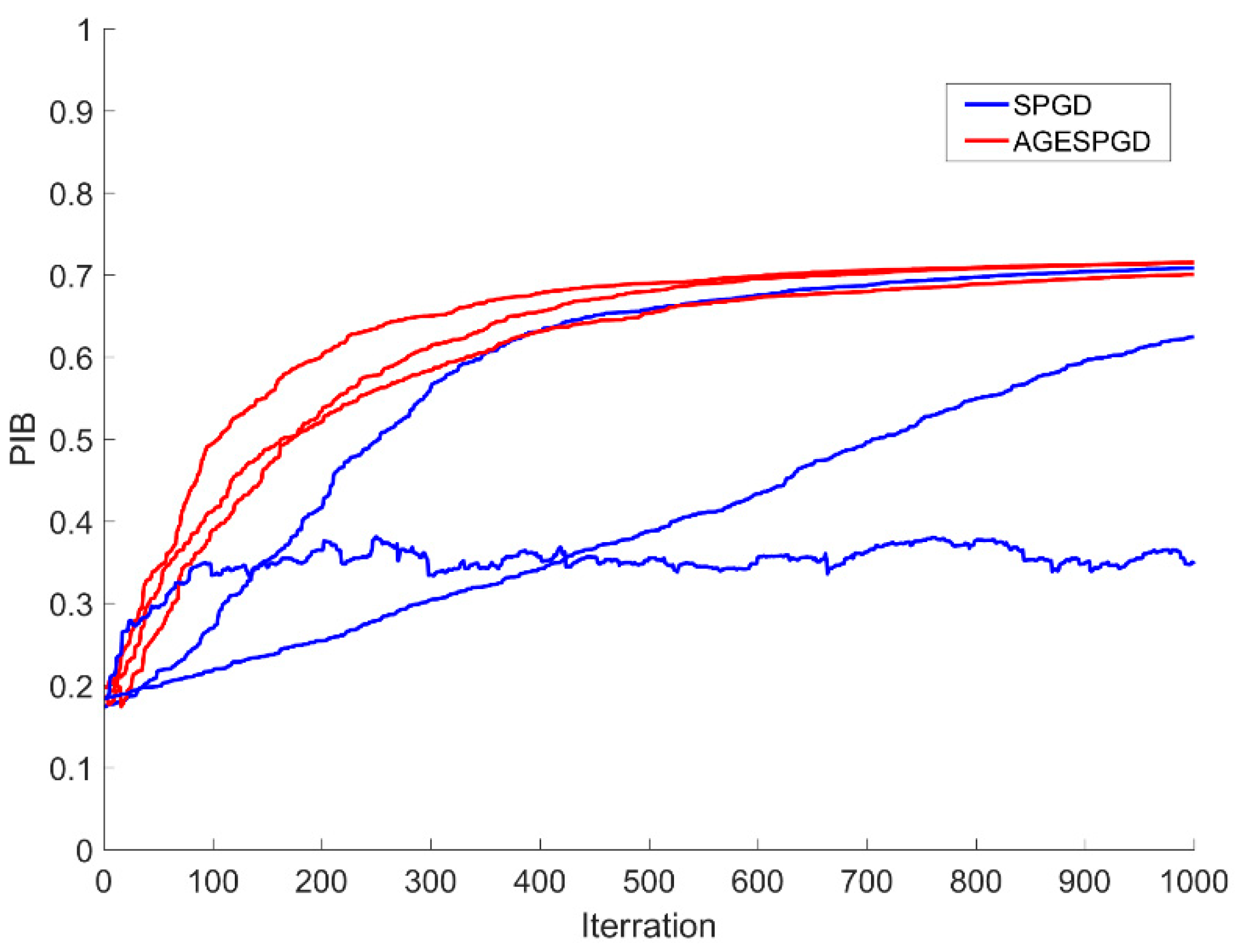
4. Experiment

In this section, the AGESPGD method was additionally studied in a real beam cleanup system. The experimental configuration is shown in Figure 7. The number of actuators of the deformable mirror (DM) was 59, and the laser used was an all-solid-state single-longitudinal-mode infrared laser with a wavelength of 1064 nm and an aperture of 80 mm. The beam passed through DM1, TM, and DM2 in sequence. DM1 was used to generate analog aberrations, and TM was used to control light stability to prevent speckle jitter. DM2 was used for aberration correction. Then, the beam entered a far-field imaging system that included a set of focusing lenses with an equivalent focal length of 5 m and a CCD camera (camera parameters: BAUMER, TXG03, CCD, 656 × 494 pixels, 7.4 μm pixel pitch).

We set the same initial point for the two methods and set the best parameter combination, respectively. DM1 generated a series of aberrations that were calculated from the wavefront aberrations collected by a real slab solid-state laser. Figure 8 shows 10 sets of iteration curves with different aberrations. It can be seen from the experimental results that the classical SPGD method required about 200 iterations to achieve a stable value. The AGESPGD algorithm only needed about 120 times, and the convergence was increased by nearly 40%. Figure 9 shows the far-field spots corrected by the two respective methods. After correction, the beam quality was improved from 3.71 times diffraction limit to 1.63 times by the classical SPGD method and from 3.71 times to 1.61 times by the AGESPGD method. Experiments showed that the convergence of the AGESPGD method was greatly improved compared with the classical SPGD method.

Figure 10 shows the iterative curves of the two methods under different search steps δ_u. When δ_u was within the interval of [0.001, 0.05], the AGESPGD method could converge stably, while the classical SPGD method could not. Experimental results showed that the AGESPGD method not only had a much faster convergence rate than classical SPGD, but also had a better robustness to δ_u.

5. Conclusions

In this article, an adaptive gradient estimation stochastic parallel gradient descent (AGESPGD) method is developed for solid-state laser beam cleanup. The gradient estimate is modified by the second-order gradient of the search point. This modification is combined with adaptive gain estimation to improve the classical SPGD. The improved algorithm is able to accelerate the convergence speed and prevent it from falling to local extremum. The simulation and experiment results show that our developed method converges much faster than the classical SPGD method, and the robustness of the algorithm in searching step-size is also improved. Compared with the classical SPGD, the iteration number of the AGESPGD is reduced by 40%, and this method can converge stably when the search step is in the range of [0.001, 0.05]. At the same time, this method can improve the beam quality from 3.71 to 1.61 times the diffraction limits.