Linear Combinations of the Complex Degrees of Coherence
Abstract
1. Introduction
2. Proposition
3. Examples
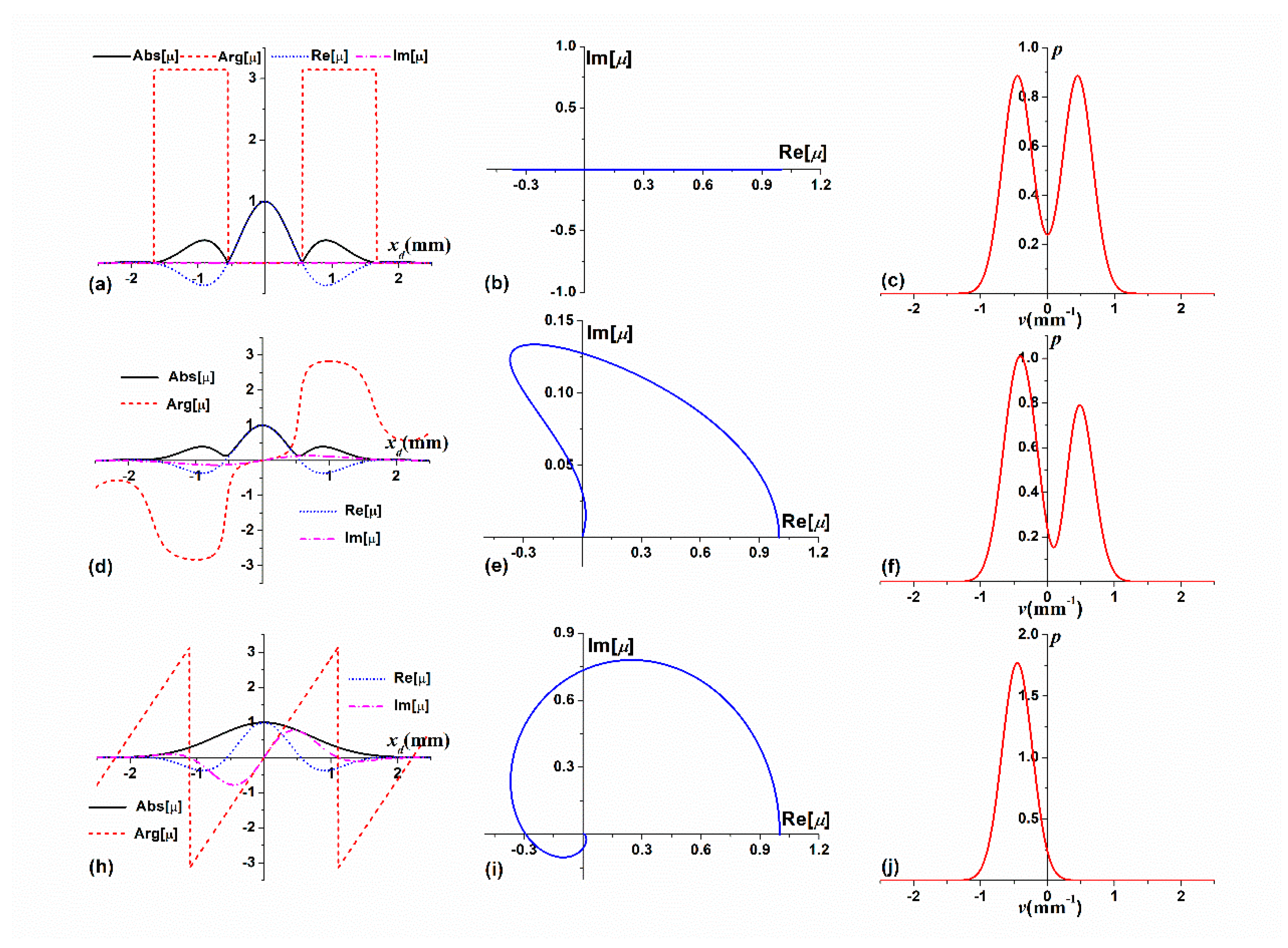
3.1. Difference between Two CDCs
3.2. Combination of Four CDCs
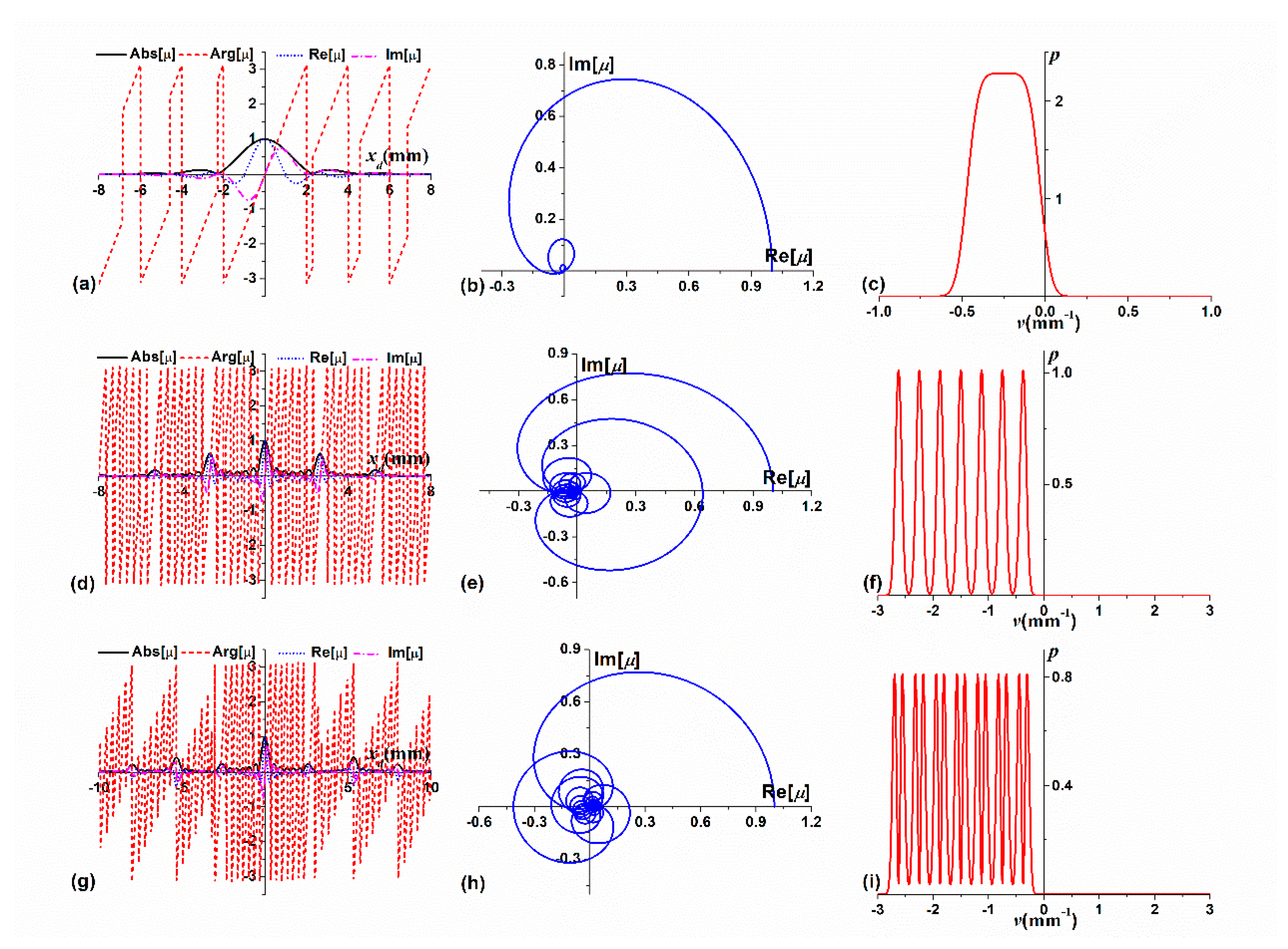
3.3. Series Combination of CDCs
4. Discussion: Correlation Linear Phase Plates
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University: Cambridge, UK, 1995. [Google Scholar]
- Korotkova, O. Random Beams: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Sahin, S.; Korotkova, O. Light sources generating far fields with tunable flat profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef] [PubMed]
- Santarsiero, M.; Piquero, G.; de Sande, J.C.G.; Gori, F. Difference of cross-spectral densities. Opt. Lett. 2014, 39, 1713–1716. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Difference of two Gaussian Schell-model cross-spectral densities. Opt. Lett. 2014, 39, 2731–2734. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.; Korotkova, O. Alternating series of cross-spectral densities. Opt. Lett. 2015, 40, 2473–2476. [Google Scholar] [CrossRef] [PubMed]
- Wolf, E. Significance and measurability of the phase of a spatially coherent optical field. Opt. Lett. 2003, 28, 5–6. [Google Scholar] [CrossRef] [PubMed]
- Gbur, G.; Visser, T.D. Coherence vortices in partially coherent beams. Opt. Commun. 2003, 222, 117–125. [Google Scholar] [CrossRef]
- Wolf, E. Solution of the phase problem in the theory of structure determination of crystals from x-ray diffraction experiments. Phys. Rev. Lett. 2009, 103, 075501. [Google Scholar] [CrossRef] [PubMed]
- Popescu, G. Quantitaive Phase Imaging of Cells and Tissues; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Ng, J.; Lin, Z.; Chan, C.T. Theory of optical trapping by an optical vortex beam. Phys. Rev. Lett. 2010, 104, 103601. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Advances in communications using optical vortices. Photon. Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Nagali, E.; Sciarrino, F.; De Martini, F.; Marrucci, L.; Piccirillo, B.; Karimi, E.; Santamato, E. Quantum information transfer from spin to orbital angular momentum of photons. Phys. Rev. Lett. 2009, 103, 013601. [Google Scholar] [CrossRef] [PubMed]
- Divitt, S.; Novotny, L. Spatial coherence of sunlight and its implications for light management in photovoltaics. Optica 2015, 2, 95–103. [Google Scholar] [CrossRef]
- Korotkova, O.; Chen, X. Phase structuring of the complex degree of coherence. Opt. Lett. 2018, 43, 4727–4730. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Korotkova, O. Complex degree of coherence modeling with famous planar curves. Opt. Lett. 2018, 43, 6049–6052. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Korotkova, O. Phase structuring of the 2D complex coherence states. Opt. Lett. 2019, 44, 2470–2473. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O. Multi-Gaussian Schell-model source with a complex coherence state. J. Opt. 2019, 21, 045607. [Google Scholar] [CrossRef]
- Korotkova, O.; Chen, X.; Setälä, T. Electromagnetic Schell-model beams with arbitrary complex correlation states. Opt. Lett. 2019, 44, 4945–4949. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.; Korotkova, O. Asymmetric coherence gratings. Opt. Lett. 2020, 45, 1366–1369. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.; Korotkova, O. Cosine-Gaussian Schell-model sources. Opt. Lett. 2013, 38, 2578–2580. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Statistical Optics; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hyde, I.V.M.W.; Basu, S.; Xiao, X.; Voelz, D.G. Producing any desired far-field mean irradiance pattern using a partially-coherent Schell-model source. J. Opt. 2015, 17, 055607. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Z.; Korotkova, O. Linear Combinations of the Complex Degrees of Coherence. Photonics 2021, 8, 146. https://doi.org/10.3390/photonics8050146
Mei Z, Korotkova O. Linear Combinations of the Complex Degrees of Coherence. Photonics. 2021; 8(5):146. https://doi.org/10.3390/photonics8050146
Chicago/Turabian StyleMei, Zhangrong, and Olga Korotkova. 2021. "Linear Combinations of the Complex Degrees of Coherence" Photonics 8, no. 5: 146. https://doi.org/10.3390/photonics8050146
APA StyleMei, Z., & Korotkova, O. (2021). Linear Combinations of the Complex Degrees of Coherence. Photonics, 8(5), 146. https://doi.org/10.3390/photonics8050146




