Peak-to-Average Power Ratio Reduction of Carrier-Suppressed Optical SSB Modulation: Performance Comparison of Three Methods

Abstract

We compare the performances of three previously proposed methods to reduce the peak-to-average power ratio (PAPR) of the carrier-suppressed optical single-sideband (OSSB-SC) signal. PAPR of OSSB-SC signal becomes high due to the peaky Hilbert-transformed signal which is used for spectral suppression. Nonlinear phase shifts induced by high PAPR degrade OSSB-SC signal during fiber transmission. Previously, we proposed peak folding, peak clipping, and high-pass Hilbert transform methods to reduce the PAPR of OSSB-SC modulation. In this study, we numerically compare the effectiveness of proposed methods in a 10 Gbit/s non-return-to-zero (NRZ)-coded 100-km single-channel transmission link. Due to the reduced PAPR, peak folding and peak clipping can increase the self-phase modulation (SPM) threshold of the studied system by 2.40 dB and 2.63 dB respectively. The high-pass Hilbert transform method improves the SPM threshold by more than 9 dB.

1. Introduction

Tremendous amounts of data traffic being added to short-reach networks are expediting data rate scaling of 100 to 400 G and beyond [1,2,3]. Intensity modulation-direct detection (IM-DD) transmission is preferred for short-reach links because of its simplicity and cost-effectiveness [4,5,6]. However, to meet the capacity requirements, it is becoming obvious that more degree of freedom is required in short-reach links. Driven by emerging capacity hungry applications, digital coherent transmission with the high-order degree of freedom using polarization and wavelength-multiplexing is gaining attention in short-reach links, regardless of the cost [7,8,9].

Recently, optical single-sideband (OSSB) modulation with direct-detection took the attention of researchers as a cost-effective solution for increasing the capacity of short-reach links [10,11,12]. In C-band transmission, OSSB modulation can tolerate signal distortions induced by chromatic dispersion because of the single-sided spectrum [13,14]. Moreover, the phase information of the transmitted optical signal is preserved even after direct detection. Therefore, electrical dispersion compensation can be done in the receiver [15,16]. However, signal-signal beat interference (SSBI) caused by square-law detection of the OSSB signal degrades the received signal. Several methods have been studied to reduce or eliminate the SSBI of the direct-detected OSSB signal [17,18,19,20]. Kramers-Kroning (KK) relation-based receiver outperforms all the SSBI-cancellation schemes proposed so far [20]. Nevertheless, the KK receiver requires faster digital signal processing (DSP) and a high carrier-to-signal power ratio (CSPR) [21,22].

Even though KK reception is applicable for both double sideband (optical double-sideband signal+ optical tone at the edge of the spectrum) and SSB (OSSB + optical tone) transmission [23], SSB transmission is preferred to save the DSP bandwidth at the receiver [24,25]. Equivalently, the addition of optical tone at the receiver is preferred because it allows polarization division multiplexing (PDM) while increasing the transmission power efficiency [26]. In this manner, adding an optical tone to transmitted carrier-suppressed OSSB signal (OSSB-SC) at the receiver can overcome two major technical challenges of the KK receiver.

Despite OSSB-SC transmission’s capability of overcoming the above-mentioned challenges, inherited high peak-to-average power ratio (PAPR) of OSSB-SC signal introduces two new challenges; fiber nonlinearity-based signal distortions and requirement of high tone power at the receiver to meet the minimum phase condition. OSSB-SC signal consists of high peaks in the optical waveform. This is because of the Hilbert-transform pair relation of in-phase and quadrature-phase components of the OSSB signal [27].

Paying attention to the fiber nonlinearity-based signal distortions, the authors previously proposed three methods for alleviating PAPR of OSSB-SC signal, namely, peak folding using optical modulator nonlinearity [28], peak clipping [29], and high-pass Hilbert transforming [30]. The proposed methods use transmitter side digital processing or nonlinear modulation characteristics of the LN (Lithium niobate: LiNbO₃) IQ modulator. Extending our previous work, after brief introductions of operation principles, we compare the effectiveness of the above three methods in a 100-km transmission system in this paper. To clarify the transmission performance improvements by PAPR reduction, we restrict ourselves to single-channel single-polarization binary phase-shift keying (BPSK) transmission. To avoid the effect of the receiver DSP parameters on the proposed methods, we use ideal coherent detection to recover the transmitted signal. Because PAPR is closely related to self-phase modulation (SPM)-based signal distortions, the SPM threshold is used as a figure of merit. PAPR reductions by proposed methods are compared and changes of modulated signal spectra during the PAPR reduction process are discussed.

The rest of this paper is organized as follows; in Section 2, the principal of the phase-shift method OSSB-SC signal generation and characteristics of OSSB-SC signal are discussed. Section 3 describes the PAPR reduction of the OSSB-SC signal by folding the peaks of the Hilbert-transformed signal. PAPR reduction by peak clipping is discussed in Section 4. High-pass Hilbert transform-based PAPR reduction is discussed in Section 5. The effectiveness of three PAPR reduction techniques in fiber transmission is compared in Section 6. In Section 7, we discussed the reported results in detail before conclusions are drawn.

2. Phase-Shift Method OSSB-SC Signal and Its PAPR

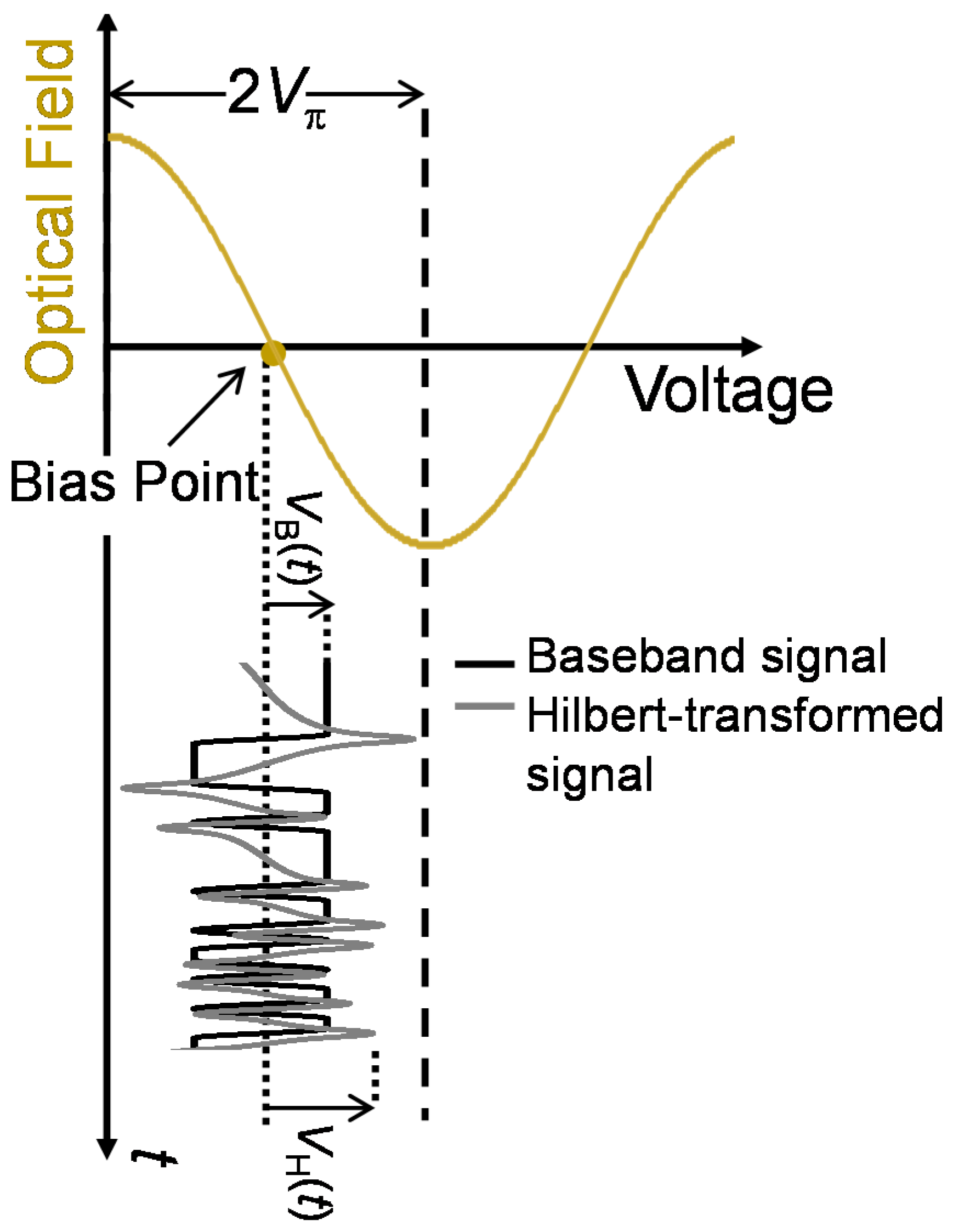
Figure 1a shows the schematic of the optical IQ modulator-based optical SSB transmitter. IQ modulator is composed of two sub-Mach-Zehnder interferometers (sub-MZIs) in a dual parallel structure. To generate OSSB-SC signal, baseband signal V_B(t) and its Hilbert transform V_H(t) are used to drive the two sub-MZIs which are biased at their transmission null points. Hilbert transform is defined as in Equation (1).

$$H\left(\omega \right)=\{\begin{array}{cc}-j\mathrm{sgn}\left(\omega \right)& \left(\omega \ne 0\right)\\ 0& \left(\omega =0\right)\end{array}$$

(1)

Here, sgn(⋅) denotes the signum function. ω is the angular frequency. Hilbert transform creates a π-phase difference between the upper and lower frequency components of the baseband spectrum separated by the center frequency. By orthogonally combining the output light of two sub-MZIs, a side-band suppressed signal is generated. Sideband suppression is achieved due to the π-phase difference between the spectral sidebands. Therefore, this modulation is named the phase-shift method [31].

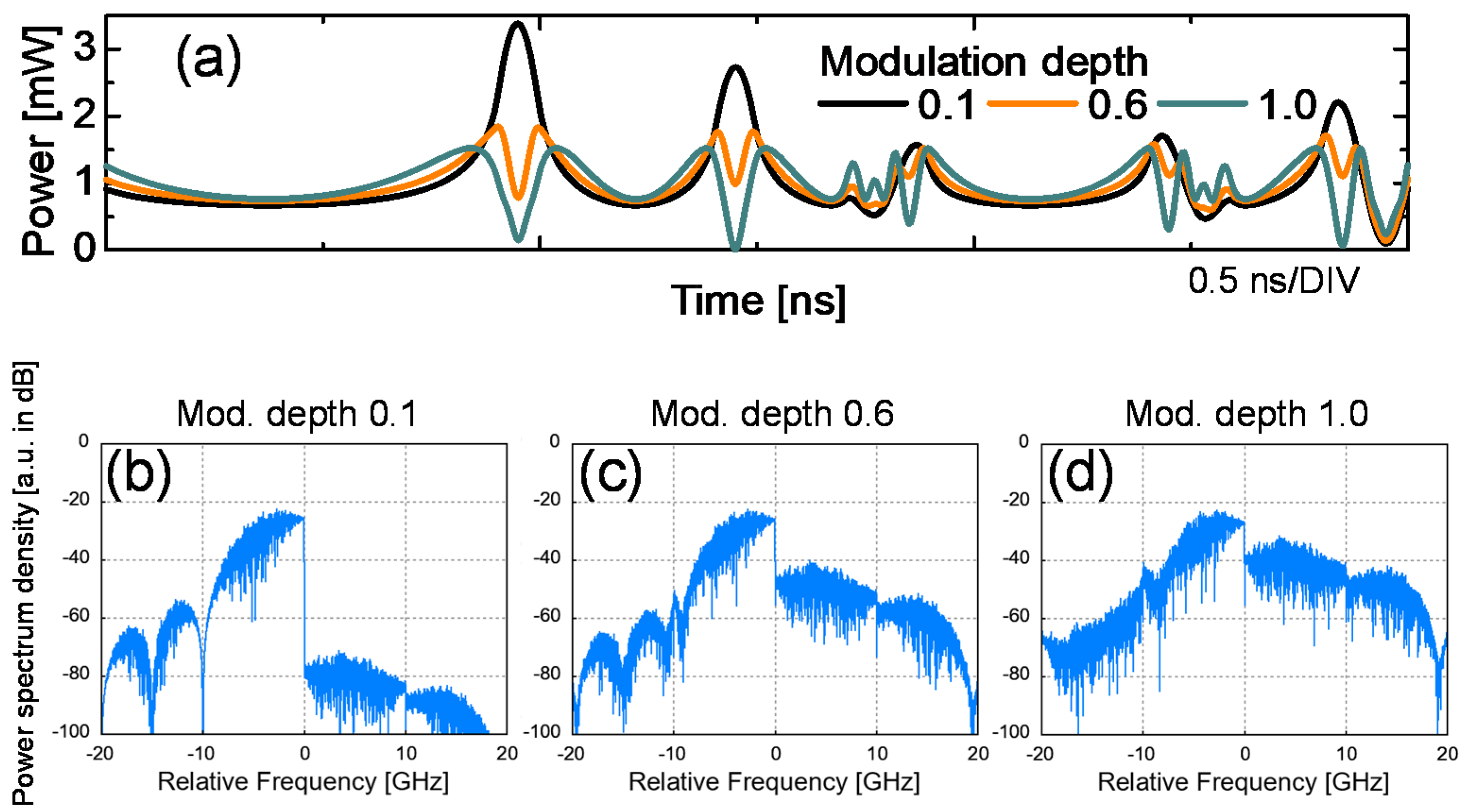
We define modulation depth as the ratio of the peak voltage of the baseband signal (V_B-Peak) to the half-wave voltage (V_π) of the IQ modulator. Figure 1b compares the optical power spectra of OSSB-SC modulated and optical on-off keying (OOK) modulated 10 Gbit/s non-return-to-zero (NRZ)-coded sequence when modulation depth is 0.1. Over 40-dB spectral sideband suppression can be observed in the OSSB-SC spectrum compared to that of the intensity-modulation. The output optical waveform and the two driving signal waveforms of the IQ modulator are depicted in Figure 1c,d, respectively. Here, the baseband signal is an NRZ-coded binary sequence. Peaks appear in the Hilbert-transformed waveform following the transmission points of the baseband signal between marks and spaces. The height of the peaks in the Hilbert-transformed waveform depends on the transfer function of the Hilbert transform [27] and the bit pattern of the baseband signal. As can be noticed by comparing the driving signals and the modulator output optical waveforms, peaks of the Hilbert-transformed component cause peaks in the modulator output waveform. Subsequently, the PAPR of the modulator output increases. High PAPR of the optical output leads to signal distortions at the receiver due to nonlinear phase-shifts caused by SPM during the transmission.

3. Peak Folding Using LN Modulator Non-Linearity

3.1. Principle

The operation condition of the IQ modulator for OSSB-SC signal generation is illustrated in Figure 2. To modulate the amplitude of the optical carrier, two sub MZIs of the IQ modulator are biased into their transmission null points. In conventional OSSB-SC modulation schemes, electrical input signals are driven within the range of 2V_π. However, peaks of Hilbert-transformed signal which causes high PAPR can be suppressed using the sinusoidal shape of the MZI modulation curve [28]. Portions of the Hilbert transformed signal which surpass the range of 2V_π are folded back. One can use this peak folding property of the IQ modulator to suppress the peaks of the Hilbert-transformed signal and to reduce the PAPR of the OSSB-SC signal.

Because the peak-to-peak voltage of the Hilbert transformed signal (V_pp-H) is about 2.5 times that of the baseband signal, V_pp-H exceeds 2V_π range for modulation depths larger than 0.4. Peak folding was implemented by increasing the voltage of the Hilbert-transformed signal component. Accordingly, the modulation depth was increased.

3.2. Characteristics of Peak-Folded OSSB-SC Signal

We numerically investigated the OSSB-SC signal generated using a peak-folded Hilbert-transformed component. The OSSB-SC transmitter model is depicted in Figure 1a. A continuous-wave (CW) light of 1552.5 nm from a laser diode (LD) was sent to the IQ modulator. Optical BPSK-SSB signal was generated by driving two MZIs of IQ modulator by 10 Gbit/s NRZ coded (pseudo-noise (PN)-stage 10) baseband signal generated at a random bit sequence generator and its Hilbert transform. Peak folding was achieved for the values of V_H(t) greater than V_π. Modulator output power also increases with modulation depth. However, for a better comparison of waveform changes, the average modulator output power was kept constant by adjusting the LD power when the modulation depth was changed. We assumed identical half-wave voltages for the two-sub MZIs.

Figure 3a presents modulator output waveforms when the modulation depth was 0.1, 0.6, and 1. When the modulation depth is 0.1, sharp peaks can be noticed in the modulator output waveform. This is because of the peaks of the Hilbert-transformed waveform which have transferred linearly from the electrical domain to the optical domain at the linear region of the modulation curve when the modulation depth was small. The peaks of the modulator output start to shrink when the modulation depth is increased. For the modulation depths greater than 0.4, V_H(t) becomes larger than V_π. Hence the peaks of the Hilbert transformed waveform are folded back by the modulation curve. This peak folding back of the Hilbert-transformed waveform appears as peak shrinking in the modulator output waveform. The minimum PAPR of 1.52 was achieved by peak folding at a modulation depth of 1.0.

Spectra of the modulator output signal are depicted for comparison in Figure 3b–d when the modulation depth was 0.1, 0.6, and 1.0, respectively. The power spectrum density of the suppressed sideband has increased with the modulation depth. In this study, we define the sideband suppression ratio (SSR) as the difference of peak power spectral densities of the suppressed sideband and the unsuppressed sideband as shown in the inset of Figure 4. SSR of 48.7 dB at the modulation depth of 0.1 increased to 17.6 dB when the modulation depth was changed to 0.6.

PAPR and SSR variations of the modulator output signal with the modulation depth are depicted in Figure 4. By increasing the modulation depth from 0.1 to the maximum modulation depth of 1, PAPR is reduced from 4.26 to 1.52. During the increase of modulation depth, the Hilbert-transformed waveform was degraded by peak folding. Peak-folded Hilbert-transformed component leads to harmonics in the optical spectrum because of the nonlinear modulation characteristics of the IQ modulator. Subsequently, an increase in suppressed sideband power is observed causing degradation of SSR. However, it is noticeable that SSR greater than 20 dB is achievable for the modulation depth of 0.5 where PAPR becomes 2.13.

4. Peak Clipping

4.1. Principle

Another approach for PAPR reduction of the OSSB-SC signal is clipping the peaks of the Hilbert-transformed signal in the electrical domain [29]. Peak clipping was proposed and extensively studied as a PAPR reduction method for wireless orthogonal frequency-division multiplexing (OFDM) transmission [32,33]. Peak clipping of OFDM results in direct signal-amplitude distortions since peaks of the OFDM signal are superpositions of OFDM subcarriers where the data is encoded [32]. However, since the peaks of modulator output optical signal are resulted by peaky Hilbert-transformed component in OSSB-SC modulation, the peak clipping of Hilbert-transformed signal does not cause direct harm to baseband signal amplitude.

Peak clipping of Hilbert transformed signal can be implemented using a clipper circuit which was introduced to the transmitter after Hilbert transformer (Figure 1a). Peak clipped Hilbert-transformed waveform is illustrated in Figure 5 with a pink line. The maximum value of clipping voltage V_CL is restricted to V_π by the sinusoidal shape modulation curve of MZI. Here V_pp-B denotes peak-to-peak voltages of the baseband signal. V_B-Peak is the peak voltage of the baseband signal.

4.2. Characteristics of Peak-Clipped OSSB-SC Signal

Properties of the peak clipped OSSB-SC signal were analyzed using the transmitter model in Figure 1a. The effect of peak clipping was studied for a fixed clipping voltage [29] and variable clipping voltages [34]. The same driving signals described in 3.2 were used to drive the modulator. The Hilbert-transformed signal component which produces peaks in the modulator output waveform was clipped using the clipper circuit before connecting to the modulator.

4.2.1. Fixed Clipping Voltage

When the clipping voltage is fixed, the clipping amount of Hilbert-transformed waveform depends on the values of modulation depth and the clipping voltage V_CL. Here we discuss the peak clipped OSSB-SC signal when V_CL equals V_π. The clipping amount was adjusted by changing the modulation depth by varying V_B-Peak. An increase of V_B-Peak increases V_pp-H accordingly. When the modulation depth is greater than 0.4, V_pp-H exceeds ±V_π range. Because V_CL equals V_π, Hilbert transformed waveform is clipped when the amplitude surpasses the range of ±V_π. For modulation depths greater than 0.4, Hilbert transformed waveform exceeds ±V_π range. Consequently, the upper MZI of the IQ modulator was driven by the peak-clipped Hilbert-transformed waveform.

In both fixed and variable clipping voltage studies, the modulator output power was unchanged. We adjusted the LD output power in the case of modulation depth or clipping voltage was changed.

Modulator output waveforms of peak-clipped OSSB-SC signal are compared in Figure 6a. The waveforms of Figure 6a are calculated for modulation depths of 0.1, 0.4, 0.6, and 1.0 when the average modulator output power was 0 dBm. Because V_CL was set to V_π, there were no peak clippings when the modulation depth was 0.1 where V_pp-H nearly equals 0.5V_π. As a consequence, high peaks appear in modulator output intensity waveform as mentioned in Section 3.2. Peak reduction can be seen at the modulation depth of 0.4 where the peak clipping has just started. The cause of peak reduction up to modulation depth of 0.4 was the nonlinearity of the modulator transfer function. When the amplitude of the modulator input signal becomes sufficiently large with increasing modulation depth, the effect from the sinusoidal shape of the transfer function of MZI appears as peak folding of modulated signals. Since the Hilbert-transformed signal has a larger amplitude it is affected by the nonlinearity of the modulator first and reduces the peaks of the modulator output signal [28]. For modulation depths greater than 0.4, V_pp-H exceeded the ±V_π range and peak clipping was implemented. Consequently, peak suppression of modulated output waveform can be seen which results in a reduction of PAPR.

Figure 6b–e show the power spectra of the modulator output signal when the modulation depths were 0.1, 0.4, 0.6, and 1.0, respectively. Compared with Figure 6b where peak clipping was not implemented, a rise in suppressed sideband power can be noticed in peak-clipped signal spectra. Both peak clipping and the nonlinearity of the IQ modulator contribute to this spectral degradation [29].

PAPR and SSR variations of the peak-clipped OSSB-SC signal are depicted in Figure 7. With increasing modulation depth, the clipping amount of the Hilbert-transformed signal increases consequently reducing the PAPR. Due to peak clipping, the value of SSR decreases. SSR becomes 13.57 dB at the modulation depth of 1.0 where the minimum PAPR of 1.41 was achieved. PAPR and SSR characteristics of peak-folded OSSB-SC signal are also shown for comparison. PAPR, SSR values of both peak-folded and peak-clipped signals resemble lower modulation depths. Compared with peak folding, peak clipping reduces waveform degradations of Hilbert-transformed signal at high modulation depths and thereby reducing harmonics generated during the modulation. Subsequently, peak- clipped OSSB-SC signal shows lower PAPR and higher sideband suppression relative to the peak-folded signal. Peak clipping improves PAPR by 6.9% and SSR by 4.7 dB at the modulation depth of 1.0.

4.2.2. Variable Clipping Voltage

Then the effect of the clipping voltage was studied while varying the clipping voltage when the modulation depth was fixed. We compared the characteristics of peak-clipped OSSB-SC signal when the modulation depth was 0.1 and 0.4. Modulator output waveforms and their spectra at modulation depths of 0.1 and 0.4 are depicted in Figure 8 for varied clipping voltages. To check the effect of variable clipping voltage, clipping ratio r is defined as

$$r=\frac{V_{CL}}{V_{B-Peak}}$$

(2)

The voltages of modulator input electrical signals vary with the modulation depth. However, the waveforms and spectra of Figure 8 are compared when the amount of clipping of the Hilbert-transformed waveform relative to the baseband signal is equal. The average modulator output power was 0 dBm in each case.

For larger r, modulator output waveforms show peaks in both 0.1 and 0.4 modulation depths. Because the clipping amount increases with decreasing r, peaks start to shrink. Waveforms of both modulation depths start to resemble when r becomes smaller. Suppression of peaks in modulator output waveform can be observed for the modulation depth of 0.4 even for smaller values of r. This difference of peak powers of two modulation depths at higher values of r is due to the nonlinearity of the IQ modulator.

The effect of the modulator nonlinearity can be also seen in the power spectra of peak clipped OSSB-SC signal. For greater modulation depths, the power spectrum density of the suppressed sideband becomes high. Harmonics generated due to the nonlinearity of the modulation curve of the IQ modulator increases the power of the suppressed sideband. Spectra and modulator output intensity waveforms of the modulation depth of 0.1 mimic those of the modulation depth of 0.4 since the baseband signal component of the OSSB-SC signal becomes dominant with decreasing r.

PAPR and SSR variations of the peak-clipped OSSB-SC signal are illustrated in Figure 9. PAPR of 4.14 was noticed for the modulation depth of 0.1 when r is 2.5. As a result of peak folding, PAPR was reduced to 2.51 at the modulation depth of 0.4. Because of suppressed peaks by peak clipping, PAPR reduces gradually with r. Minimum PAPR of 1.30 was achieved for r < 0.5. SSR becomes small with decreasing r for both modulation depths. For large r, the SSR becomes smaller for the modulator output signal at a modulation depth of 0.4, because of harmonics generated due to the nonlinearity of the modulator. Because peak clipping of the Hilbert-transformed component also contributes to spectral degradation by adding harmonics, the SSR becomes small for smaller r. It is noteworthy that the SSR for both modulation depths coincides when r is decreased.

5. High-Pass Hilbert Transform

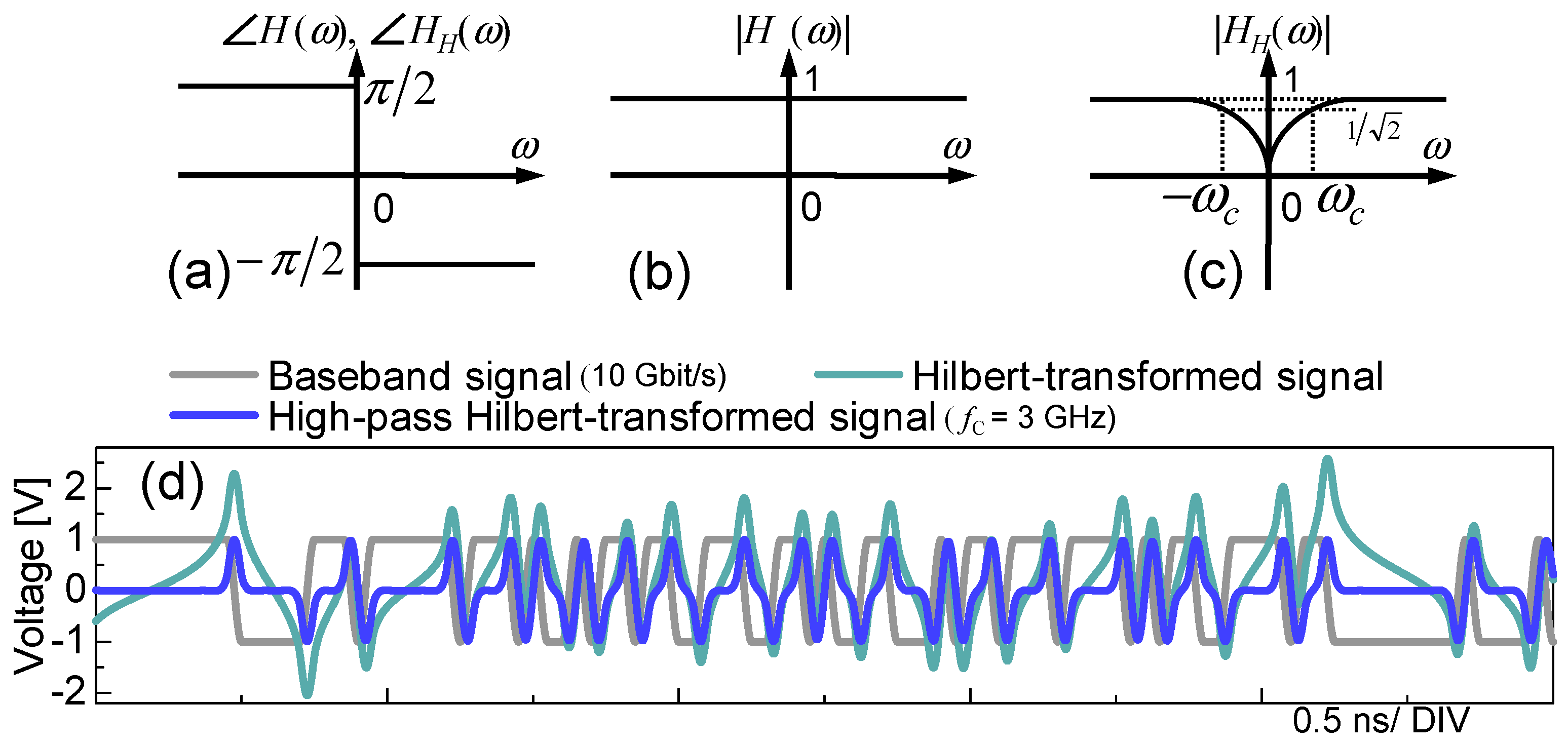
PAPR of OSSB-SC signal also can be reduced by manipulating the spectrum of peaky Hilbert-transformed components [30]. Because the shape of the waveform is largely determined by low-frequency components, peaks of the Hilbert-transformed waveform can be suppressed by reducing their power. To suppress the low-frequency components power of Hilbert-transformed signal, we modify the flat amplitude response of Hilbert transform to a high-pass response. The modified transfer function of the Hilbert transform is as follows

$$H_H\left(\omega \right)=\{\begin{array}{cc}-j \mathrm{sgn}\left(\omega \right)& \left(\left|\omega \right|>2{\omega }_c\right)\\ -j \mathrm{sgn}\left(\omega \right)\sin \left\{\pi \left(\left|\omega \right|/4{\omega }_c\right)\right\}& \left(\left|\omega \right|\le 2{\omega }_c\right)\end{array}$$

(3)

Here, ω_c is the cut-off frequency. Amplitude and phase responses of modified Hilbert transform are compared with those of ideal Hilbert transform in Figure 10a–c. Because of the high-pass amplitude response, we name H_H as high-pass Hilbert transform. The high-pass Hilbert-transformed waveform at a cut-off frequency of 3 GHz is portrayed in Figure 10d and compared with 10 Gbit/s NRZ-coded baseband signal and its ideal Hilbert-transformed waveforms. The high-pass Hilbert transform reduces the peaks of the Hilbert-transformed waveform. The peak-to-peak voltage of the high-pass Hilbert-transformed waveform reached that of the baseband signal at the cut-off frequency of 3 GHz.

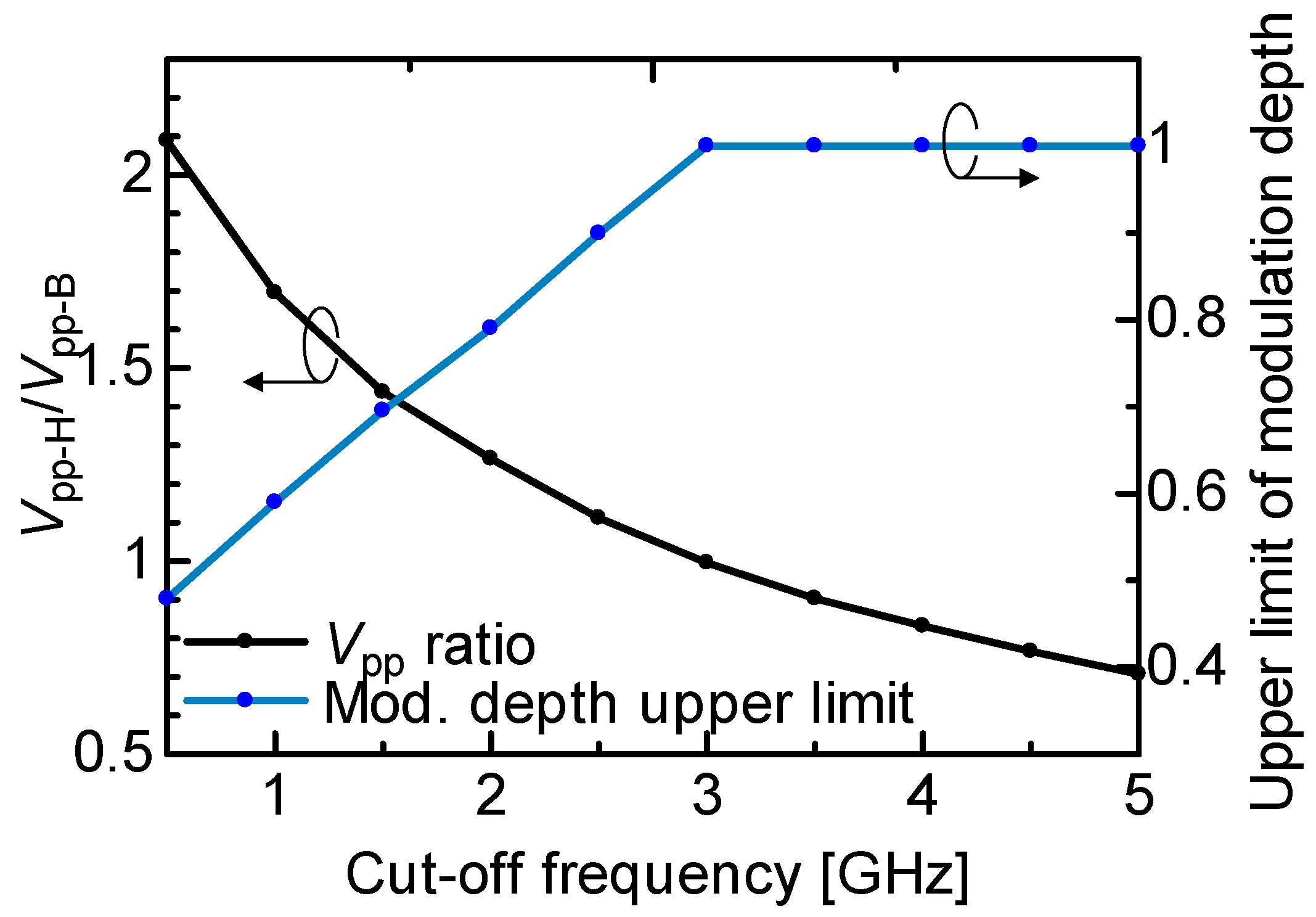
Figure 11 shows the relation of driving signals voltage ratio and the upper limit of the modulation depth of high-pass Hilbert transformer-based OSSB-SC signal. The baseband signal is a 10 Gbit/s NRZ-coded sequence. With increasing cut-off frequency, peaks of Hilbert-transformed signal component reduce. This reduction of Hilbert-transformed signal amplitude can be observed as a reduction of the driving signal peak-to-peak voltage (V_pp) ratio which is defined as the ratio of V_pp-H to V_pp-B. The V_pp ratio reaches unity at the cut-off frequency of 3 GHz. Further increase of the cut-off frequency results in V_pp ratios smaller than 1 because the peak-to-peak voltage of the Hilbert-transformed signal becomes smaller than that of the baseband signal. Because the V_pp ratio becomes unity for cut-off frequencies greater than 3 GHz, maximum modulation depth can be achieved for cut-off frequencies greater than 3 GHz. Different from peak folding and peak clipping, the high-pass Hilbert transform allows modulation at higher modulation depths with lower spectral degradations due to the decrease of V_pp-H.

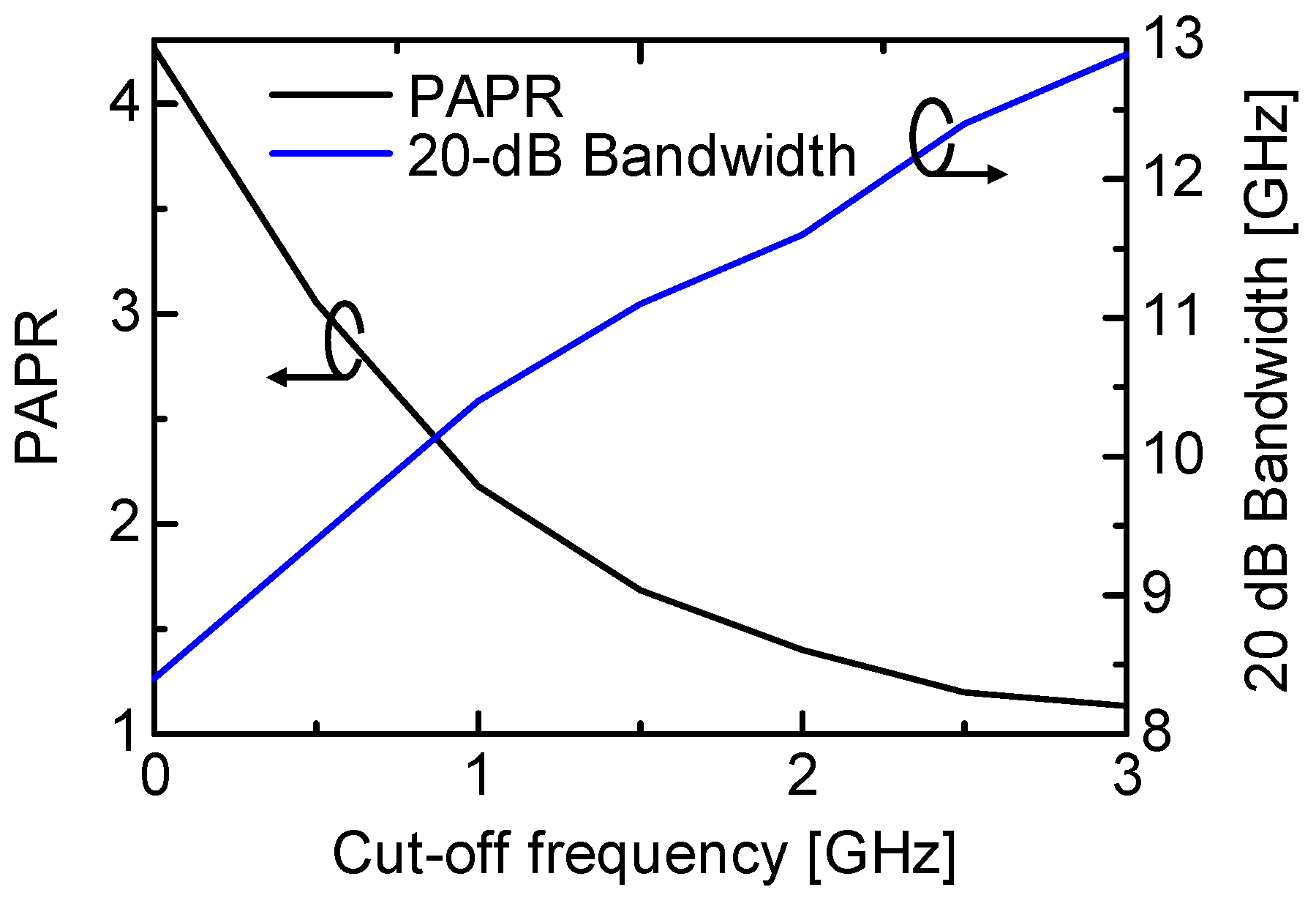
PAPR and optical bandwidth of the modulator output signal are plotted against the cut-off frequency and presented in Figure 12. Peak reduction of Hilbert-transformed signal results reduced PAPR of the modulator output signal. PAPR reaches unity around the cut-off frequency of 3 GHz.

Because of the filtering of Hilbert-transformed signal, residual bandwidth of modulator output signal increases with increasing cut-off frequency. Spectral changes of high-pass Hilbert transform-based OSSB-SC signal are evaluated using 20-dB bandwidth of the optical spectrum. 20-dB bandwidth is defined as the spectral bandwidth at where the power spectral density becomes −20 dB relative to the maximum power spectral density of the modulator output signal spectrum. Because high-pass Hilbert transform filters out the lower frequencies of the Hilbert-transformed signal spectrum, sideband suppression deteriorates. Consequently, the 20-dB bandwidth increases almost linearly with the cut-off frequency. However, even at a cut-off frequency of 3 GHz, 20-dB bandwidth remains within 65% of double sideband modulation bandwidth giving spectral efficiency of 0.77 b/s/Hz.

6. Fiber Transmission of PAPR Reduced OSSB-SC Signal

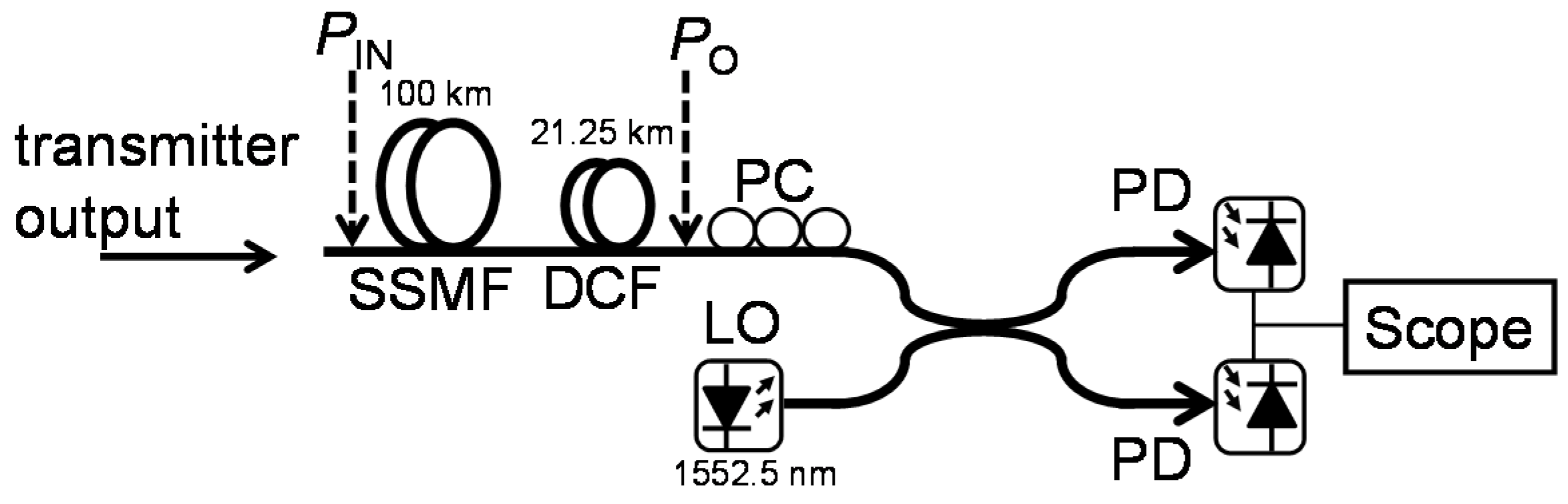
To study the effect of PAPR reduction on transmission characteristics of the OSSB-SC signal by the proposed methods, a 100-km transmission simulation was carried out. OSSB-SC signal was generated as described in Section 3, Section 4 and Section 5. The modulator output signal was launched into the fiber link shows in Figure 13 and transmitted.

We assumed ideal phase-diversity homodyne detection at the receiver instead of KK relation-based direct detection. This allows us to clarify the effect of PAPR reduction on nonlinear signal distortions during transmission, without bothering to optimize the DSP parameters required for the KK receiver, which is out of the scope of this paper. For the same reason, we used dispersion compensating fiber (DCF) in our simulation model to compensate fiber dispersion instead of frequency-domain equalization (FDE). Chromatic dispersion of standard single-mode fiber (SSMF) was compensated using 21.5-km long DCF. We found no waveform degradations during the transmission of DCF. Because of the superior sensitivity characteristics of coherent detection [23,35,36], we did not employ any optical amplifiers in our transmission simulations. Here P_IN and P_O represent average fiber input and output power, respectively. We simulated fiber transmission by solving the nonlinear Schrödinger equation using the split-step Fourier method [37]. Fiber parameters used in our calculations are given in

Table 1. Fiber Parameters.

Parameter		SMF	DCF	Unit
Loss coefficient	α	0.2	0.45	dB/km
Dispersion coefficient	D	+17.0	−80.0	ps/nm/km
Dispersion slope	S	0.057	−0.22	ps/nm2/km
Effective core cross-section	Aeff	80	14	μm2
Nonlinear index coefficient	n2	2.9 × 10−20	4.3 × 10−20	m2/W

. At the receiver, the transmitted signal was detected using a phase-diversity homodyne detector. The receiver consisted of a balanced detector and local oscillator (LO) laser. Here, we assumed ideal phase-matching between the LD and LO for the sake of simplicity.

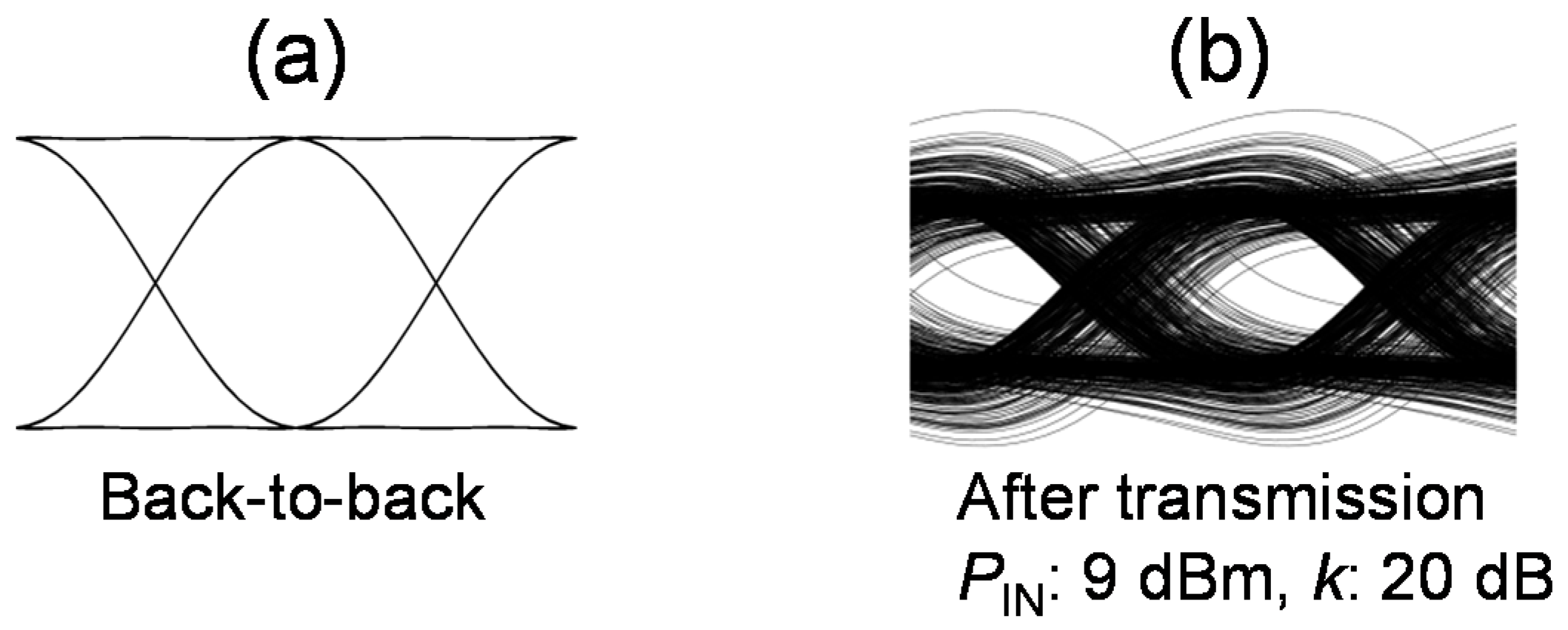
As our primary intention is to evaluate the reduction of the SPM effect during transmission, we neglect all the electrical and optical noises in the system. Since PAPR is closely related to waveform degradation, eye diagrams of the received signal were used to evaluate the transmitted signal. OSSB-SC signal eye diagrams of before and after transmission at a modulation depth of 0.1 are compared in Figure 14. Figure 14a depicts the back-to-back eye diagram, and the eye diagram of the received signal is presented in Figure 14b. We define the parameter k as the ratio of LO power to received signal power. k was set to 20 dB and P_IN to 9 dBm for the calculations of transmitted signal eye diagrams. Very obviously, high PAPR of OSSB-SC degrades the received signal eye diagrams due to the nonlinear phase-shifts by SPM. Figure 15 compares the eye diagrams of the transmitted signal whose PAPR is reduced using the techniques introduced in Section 3, Section 4 and Section 5.

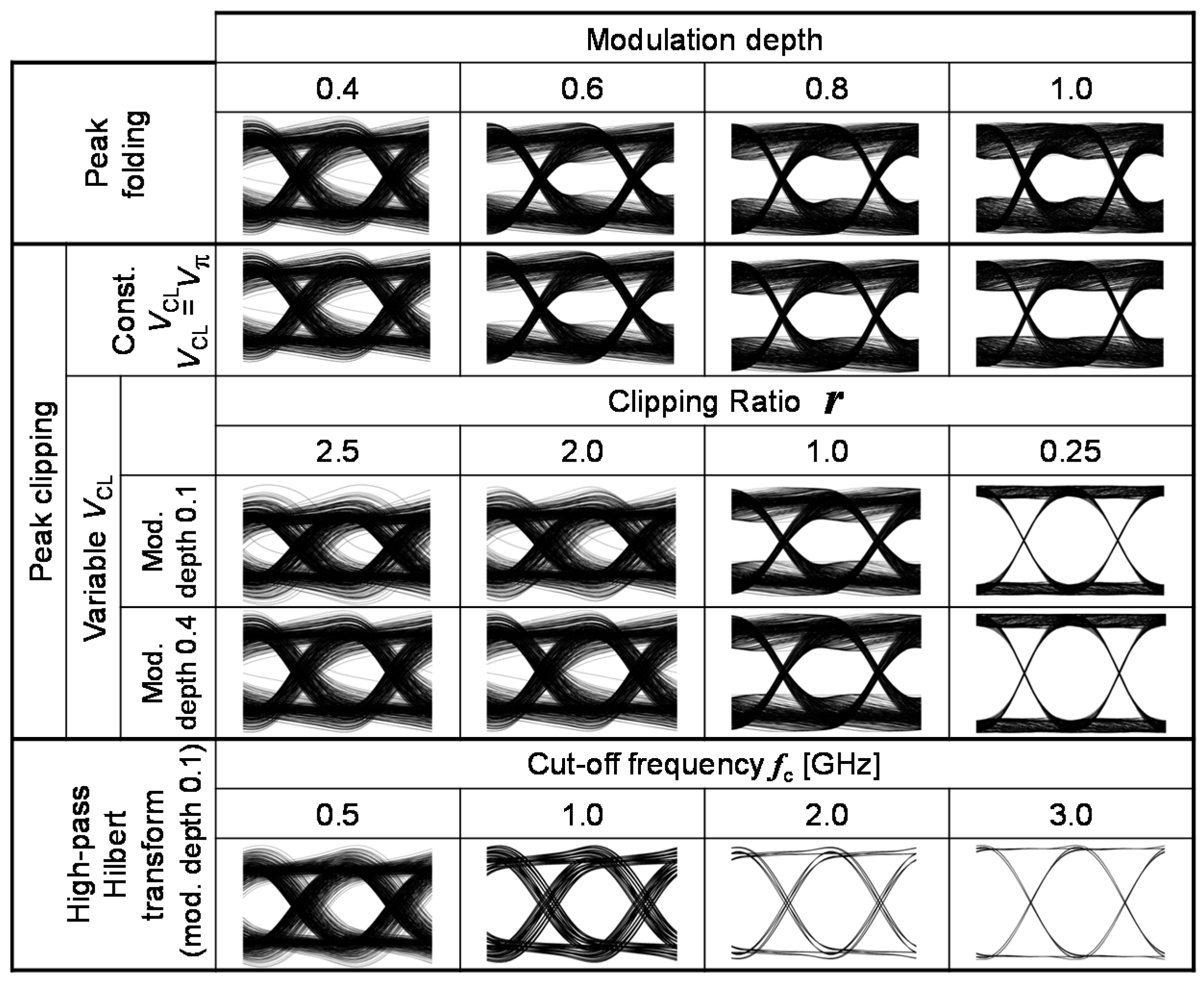
Eye diagrams of the peak-folded OSSB-SC signal are shown at the top of Figure 15 when modulation depth is varied. Eye-opening becomes larger with increasing modulation depth in peak-folded OSSB-SC signal. Because the peak-to-peak voltage of Hilbert-transformed signal becomes larger than 2V_π for modulation depths greater than 0.4, peak-folding of Hilbert-transformed signal component occurs which effectively increases the eye-opening.

The next row of Figure 15 displays the transmitted signal eye diagrams of peak-clipped OSSB-SC signal. V_CL was set to be V_π and modulation depth was varied. Compared with peak-folding, the eye-opening of the peak-clipped signal slightly increase. The reason for this slight increase of eye-opening is the reduction of high order harmonics during the modulation, by peak clipping.

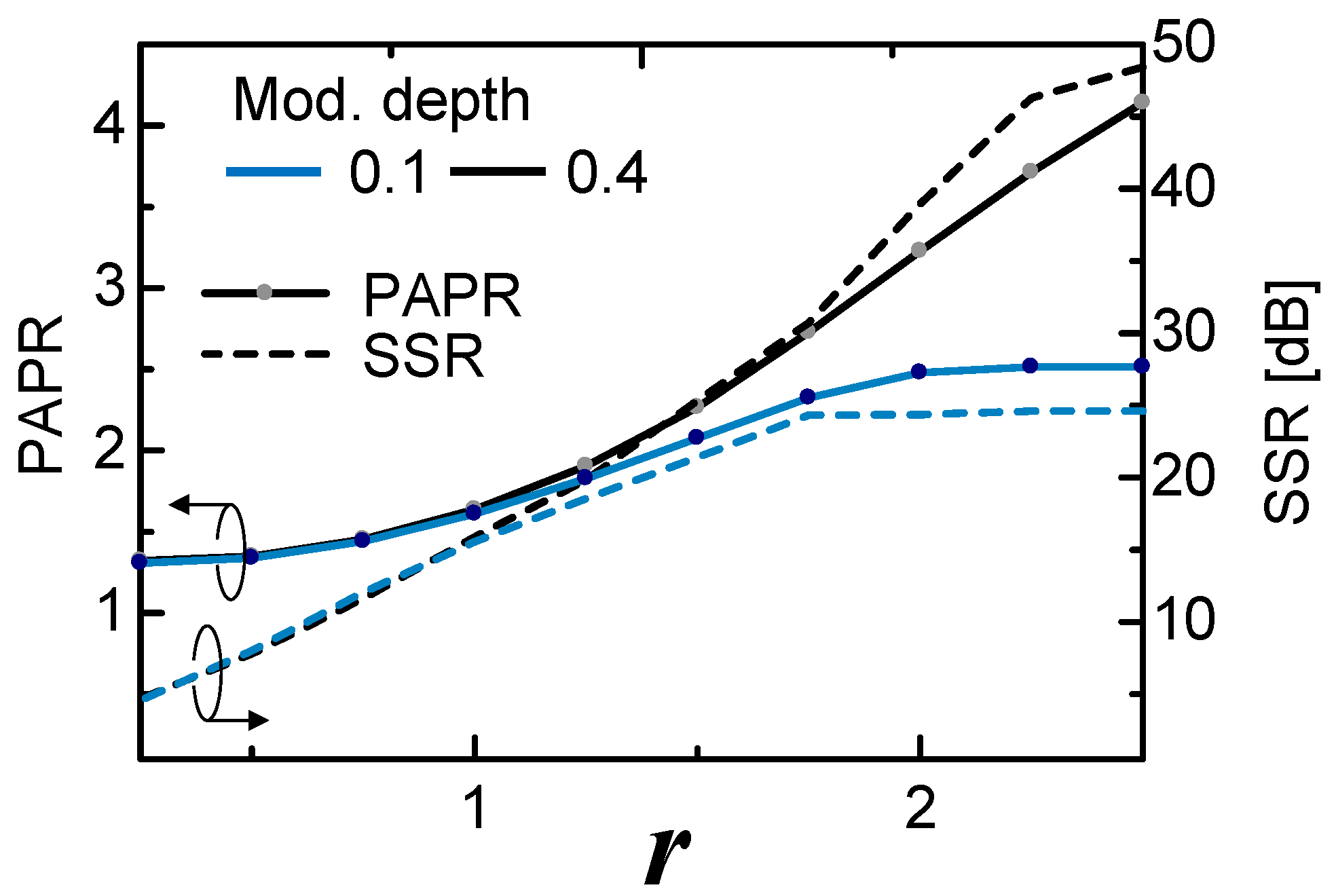
Peak-clipped signal eye diagrams with variable clipping voltage are also shown. When r is large, eye diagrams of modulation depth 0.1 show less eye-opening than that of modulation depth 0.4. This is because of the nonlinearity of the modulator. For small modulation depths, the modulator operates in its linear region. Hence, the PAPR of the OSSB-SC signal becomes high due to the linearly transformed peaks of Hilbert-transformed from the electrical domain to the optical domain. For larger modulation depths, PAPR becomes less since modulator nonlinearity folds the peaks of Hilbert-transformed signal. For smaller values of r, the clipping amount of the Hilbert-transformed waveform increases. As a result, the baseband signal component becomes dominant. The effect of modulation depth on the transmitted signal eye degradations disappears giving similar eye openings in both modulation depths.

The most opened eyes are archived in high-pass Hilbert-transformed OSSB-SC signal. Despite higher PAPR, high-pass Hilbert transform gives less degraded eyes compared to peak-folding and peak-clipping methods. This can be found comparing the eye diagrams of Figure 15. One can compare the eye diagrams of peak-folded and peak-clipped (V_CL = V_π) signal of modulation depths of 0.4 (PAPR = 2.51) and 0.6 (PAPR = 1.86) with the eye diagrams of high-pass Hilbert transform at cut-off frequencies of 0.5 GHz (PAPR = 3.05) and 1.0 GHz (PAPR = 2.18). Degradations of high-pass Hilbert-transformed OSSB-SC signal become less due to the deficiency of high order harmonics in the modulated signal spectrum. Since there are no waveform degradations of Hilbert-transformed signal during the PAPR reduction process, broadened mark, space levels are seen in peak-folding and peak-clipping do not appear in high-pass Hilbert-transformed eye diagrams. Along with increasing cut-off frequency of the high-pass Hilbert transformer, eye-opening increases due to the reduction of PAPR.

To evaluate the improvement of eye-opening by proposed techniques, eye-opening penalty (EOP) is defined as follows

$$EOP=\frac{E_R}{\left({\alpha }_{SMF}{L}_{SMF}\times {\alpha }_{DCF}{L}_{DCF}\right)E_T},$$

(4)

where E_R is the eye-opening (EO) of transmitted signal and E_T is the eye-opening of the back-to-back eye diagram when modulation depth is 0.1. EO is defined as the ratio of ΔI_r to (ΔI_r)_max where ΔI_r and (ΔI_r)_max are inside and outside eye openings as shown in the inset of Figure 16. α and L denote loss coefficients and fiber lengths of SMF and DCF of the transmission link, respectively.

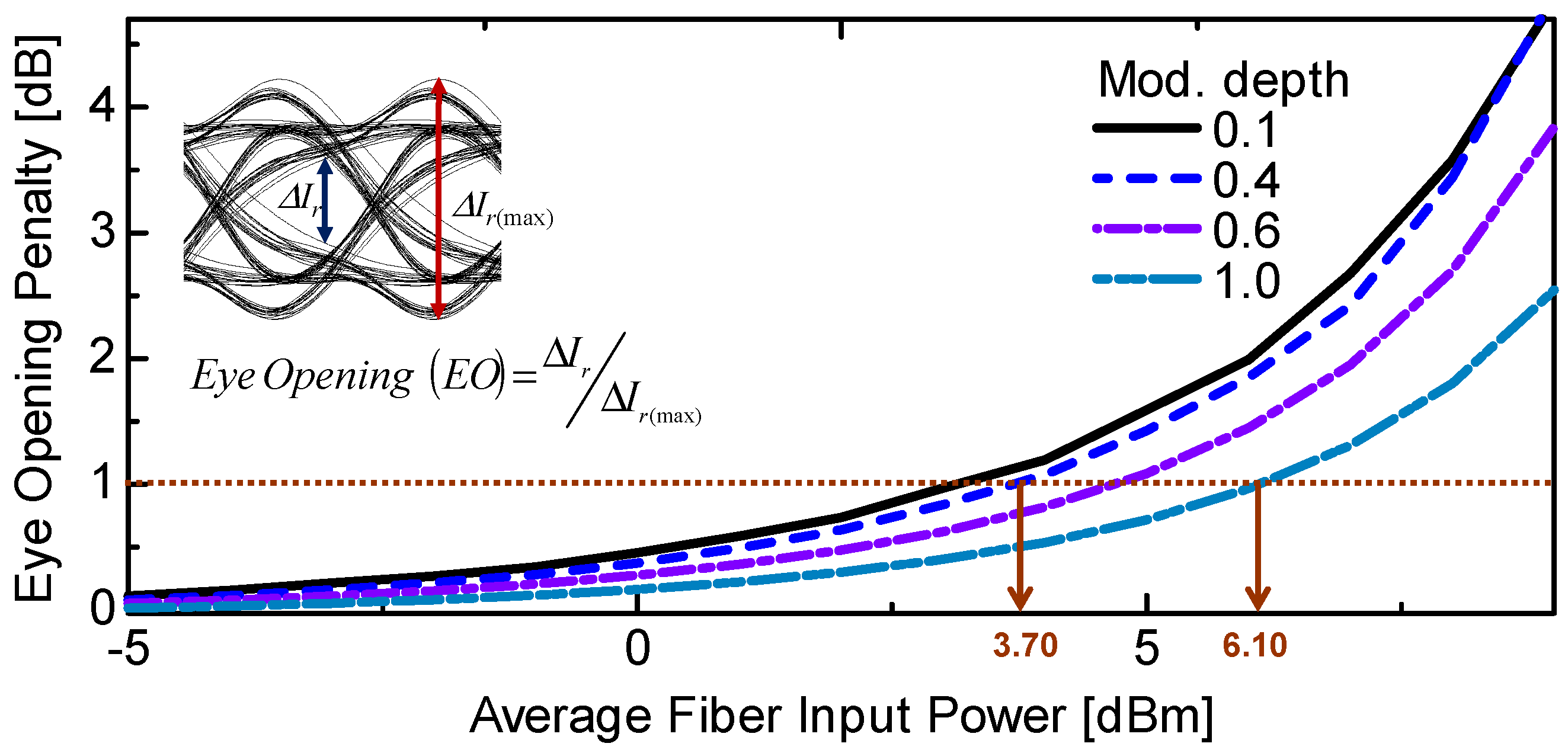
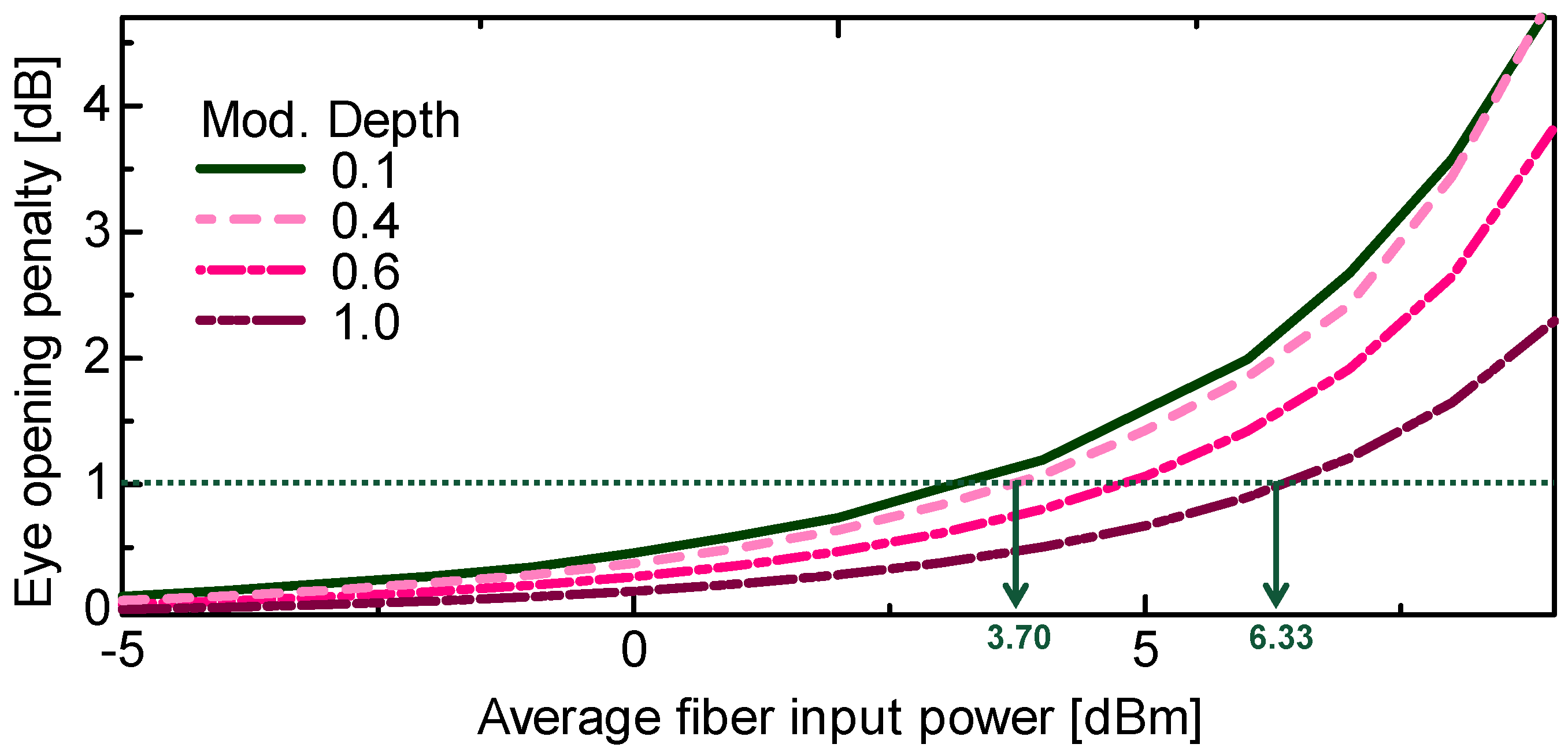
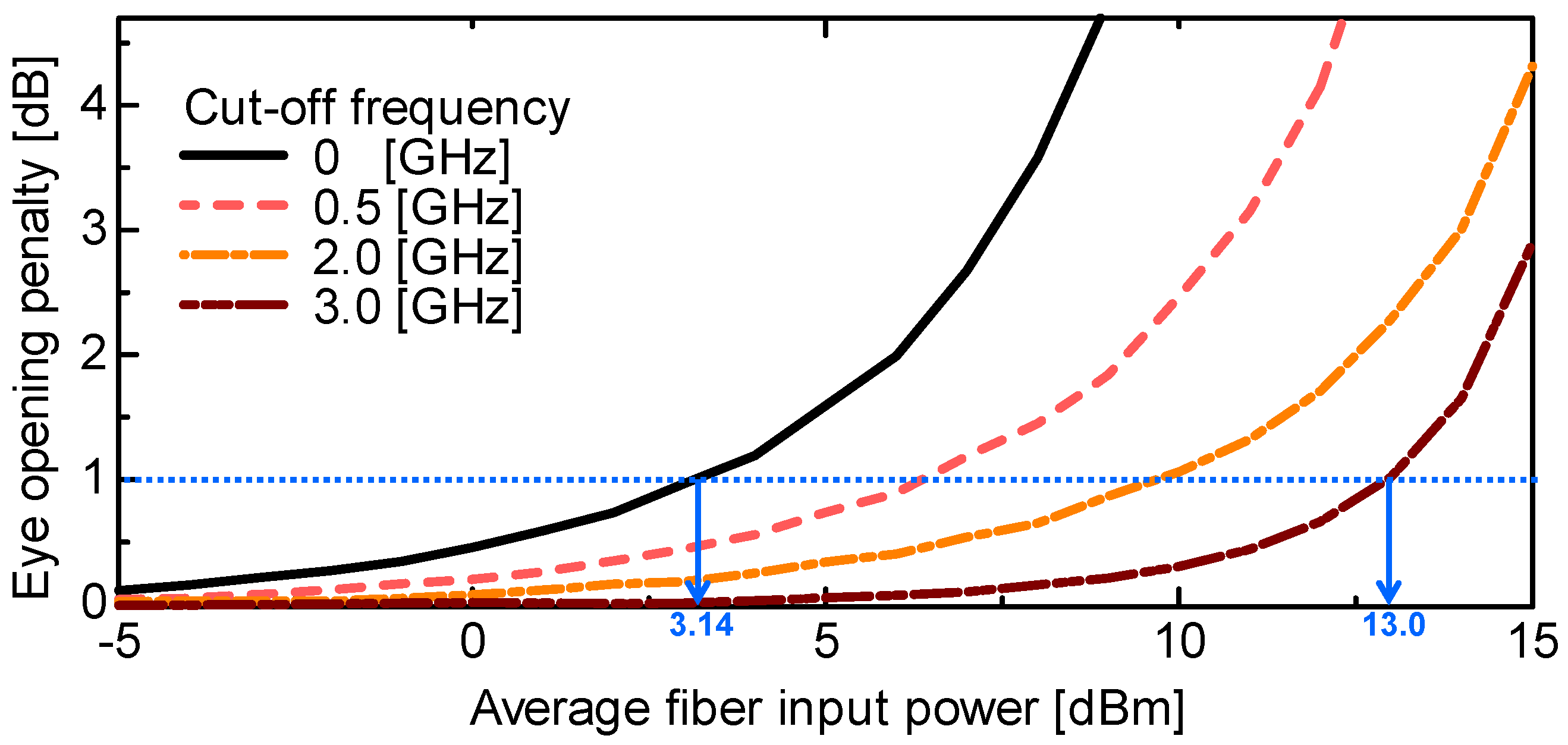
Figure 16, Figure 17 and Figure 18 show the EOP of the three methods introduced in Section 3, Section 4 and Section 5, respectively. In each case, EOP increases exponentially with P_IN. This increase in EOP is due to the waveform degradations caused by SPM. As noted with the eye diagrams, the increase in EOP was alleviated at higher modulation depths for peak folded and peak clipped OSSB-SC signal. This is because of the peak reduction of the Hilbert-transformed signal component by peak folding and peak clipping at greater modulation depths, respectively. In the high-pass Hilbert transform method, the average fiber input power which EOP starts to increase exponentially becomes higher with increasing cut-off frequency.

We defined the value of the average fiber input power that EOP becomes 1 dB as the SPM threshold. We found the SPM threshold of our system for the OSSB-SC transmission as 3.14 dBm when the modulation depth is 0.1. Peak-folding starts to occur for modulation depths larger than 0.4. SPM threshold becomes 3.99 dBm at the modulation depth of 0.4 where peak-folding just started. In the case of peak clipping, peak clipping also starts to occur for modulation depths larger than 0.4 since V_CL = V_π. The SPM threshold of the peak-clipped OSSB-SC signal at a modulation depth of 0.4 is 3.70 dBm. In peak folding and peak clipping methods, the SPM threshold can be improved up to 2.40 dB and 2.63 dB respectively, comparing to the situation where peak folding or clipping is not used. In the high-pass Hilbert transformed method, an SPM threshold of 9.86 dB is achieved at the cut-off frequency of 3 GHz for 10 Gbit/s NRZ-coded signals.

7. Discussion

Even though OSSB transmission is attracting the interest of researchers’ as a cost-effective solution for short-reach links, high PAPR of OSSB-SC transmission becomes a major drawback during the transmission. PAPR reduction has been substantially studied in wireless transmission. However, PAPR reduction methods for optical links have to be investigated.

We previously proposed three techniques to reduce the PAPR of optical SSB-SC signal using both time and frequency-domain signal processing. Peak folding using the nonlinearity of optical modulator was originally studied to suppress the noise of driving signals [38]. Later, we reported the capability of PAPR reduction of OSSB-SC signal using the same property of the LN modulator. In the peak-folding method, peaks of the Hilbert-transformed signal are folded back using the sinusoidal transfer function of the LN modulator. The Peak power was approximately halved while maintaining 20-dB spectral suppression. An SPM threshold improvement of 2.40 dB is reported.

PAPR reduction by peak clipping has been studied extensively for OFDM transmission in wireless communication [32,33]. We investigated PAPR reduction of OSSB-SC signal by clipping peaks of the Hilbert-transformed signal in the electrical domain. Reduction in spectral suppression is noticed during PAPR reduction. Peak power of the optical SSB-SC signal was reduced to about one-half of the original value with a spectral suppression of 20 dB. Using peak-clipping, the SPM threshold is improved by 2.63 dB.

To the best of our knowledge for the first time, we proposed a PAPR reduction method for OSSB-SC transmission using frequency-domain signal processing. Peaks of Hilbert-transformed signal are suppressed by reducing the power of low-frequency components of the spectrum where the energy is concentrated. The all-pass amplitude response of the Hilbert transformer was modified to a high-pass response to reduce the power of lower frequency components of the spectrum. The high-pass Hilbert transform method reduces the PAPR of the optical SSB-SC signal from 4.17 to 1.65. Bandwidth saving of over 30% was achieved relative to double-sideband modulation. As a result of PAPR reduction, the SPM threshold was improved by 9.86 dB.

In this study, we chose 10G-class BPSK modulation for the sake of simplicity. However, the proposed concepts can be extended to other modulation formats and higher transmission rates.

8. Conclusions

We compared the performances of three previously proposed methods to reduce the PAPR of OSSB-SC signal in a repeater-less 100-km transmission link. The effectiveness of the proposed methods was confirmed by the analysis of the transmitted signal. SPM threshold of the studied system can be improved by 2.40 dB and 2.63 by peak folding and peak clipping of Hilbert-transformed signal respectively. Besides reducing PAPR, the peak-folding method brings the benefit of driving signal noise suppression. (In this study, we focused on a noise-free signal for the sake of simplicity). Among the proposed methods, the high-pass Hilbert-transform method makes OSSB-SC signal most tolerant to SPM-based signal degradations. SPM threshold can be adjusted according to the demand by choosing the appropriate cut-off frequency in the high-pass Hilbert transform method. For 10 Gbit/s NRZ-coded baseband signal, the SPM threshold of 13 dBm could be achieved by setting the cut-off frequency to 3 GHz.

It is seen that the reduction of spectral efficiency cannot be avoided during PAPR reduction. Almost similar spectral characteristics were noticed in peak clipping and peak folding methods. Different from the other two methods, spectral bandwidth increase is noticed in the high-pass Hilbert-transform method during PAPR reduction. Hence, a technique to reduce PAPR should be chosen after taking the available bandwidth into account.

Chromatic dispersion of optical fibers has been identified as a limiting factor of next-generation radio over fiber (RoF) systems [39]. The reach limitation caused by the fiber dispersion is predicted to be severe in radio access networks where capacity improvements are planned to achieve using higher frequencies such as millimeter waves. Different methods such as optical-domain and electrical-domain compensation and O-band transmission have been studied to circumvent this issue of chromatic dispersion [40]. Among those, SSB transmission becomes a strong candidate because of the colorless operation capability and the simple configuration of the receiver. In combination with the proposed PAPR reduction methods, OSSB-SC transmission can increase the transmission power efficiency other than extending the reach.