Comparing Performance of Deep Convolution Networks in Reconstructing Soliton Molecules Dynamics from Real-Time Spectral Interference
Abstract
1. Introduction
2. Methods
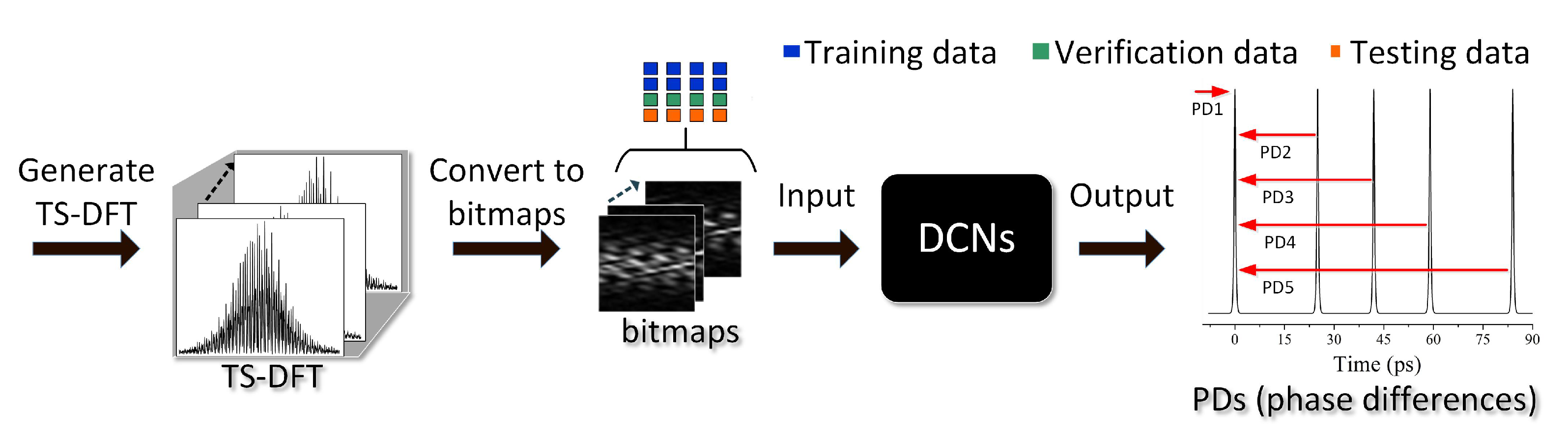
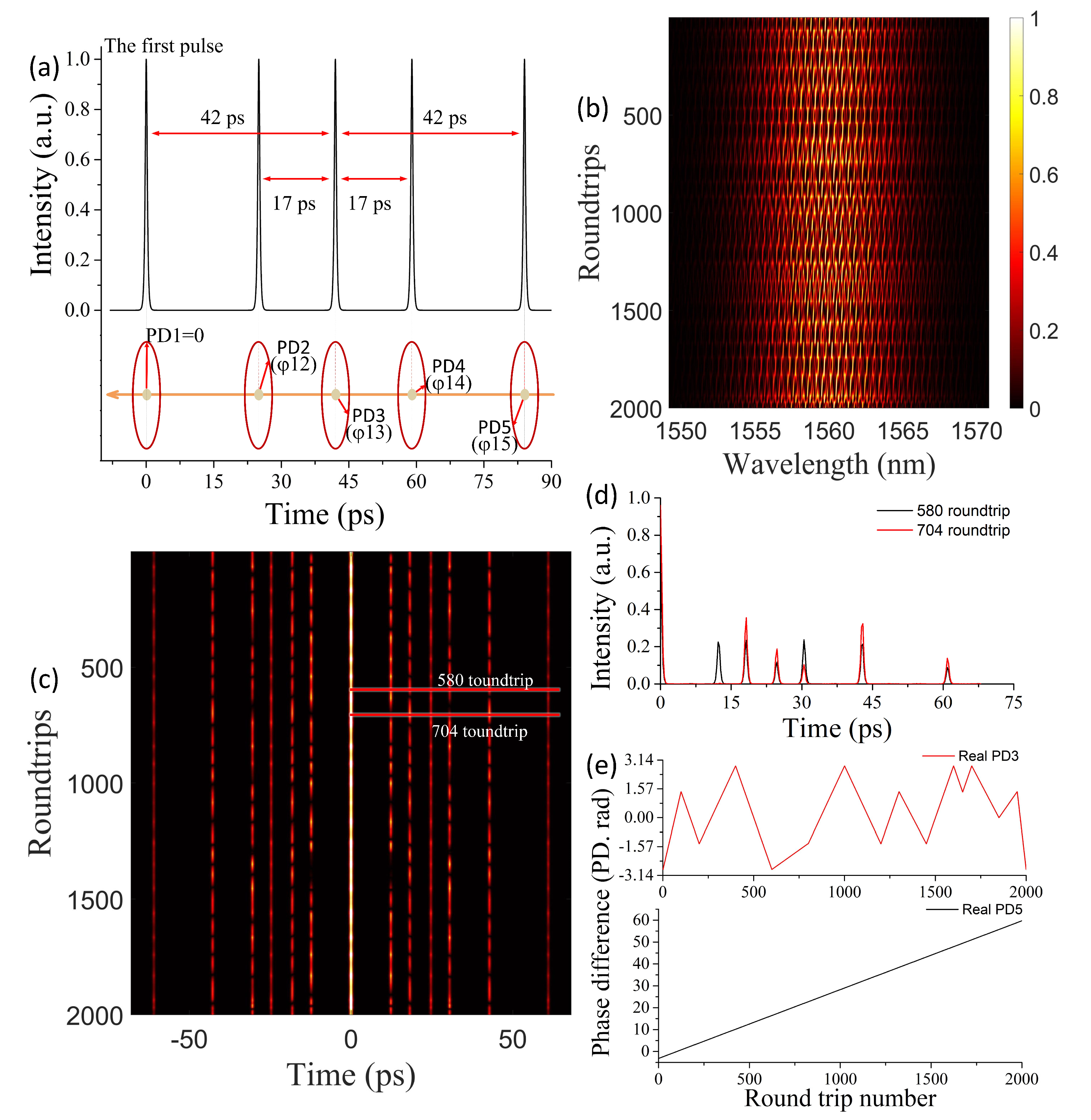
2.1. Generate Simulated TS-DFT Data of Soliton Molecules
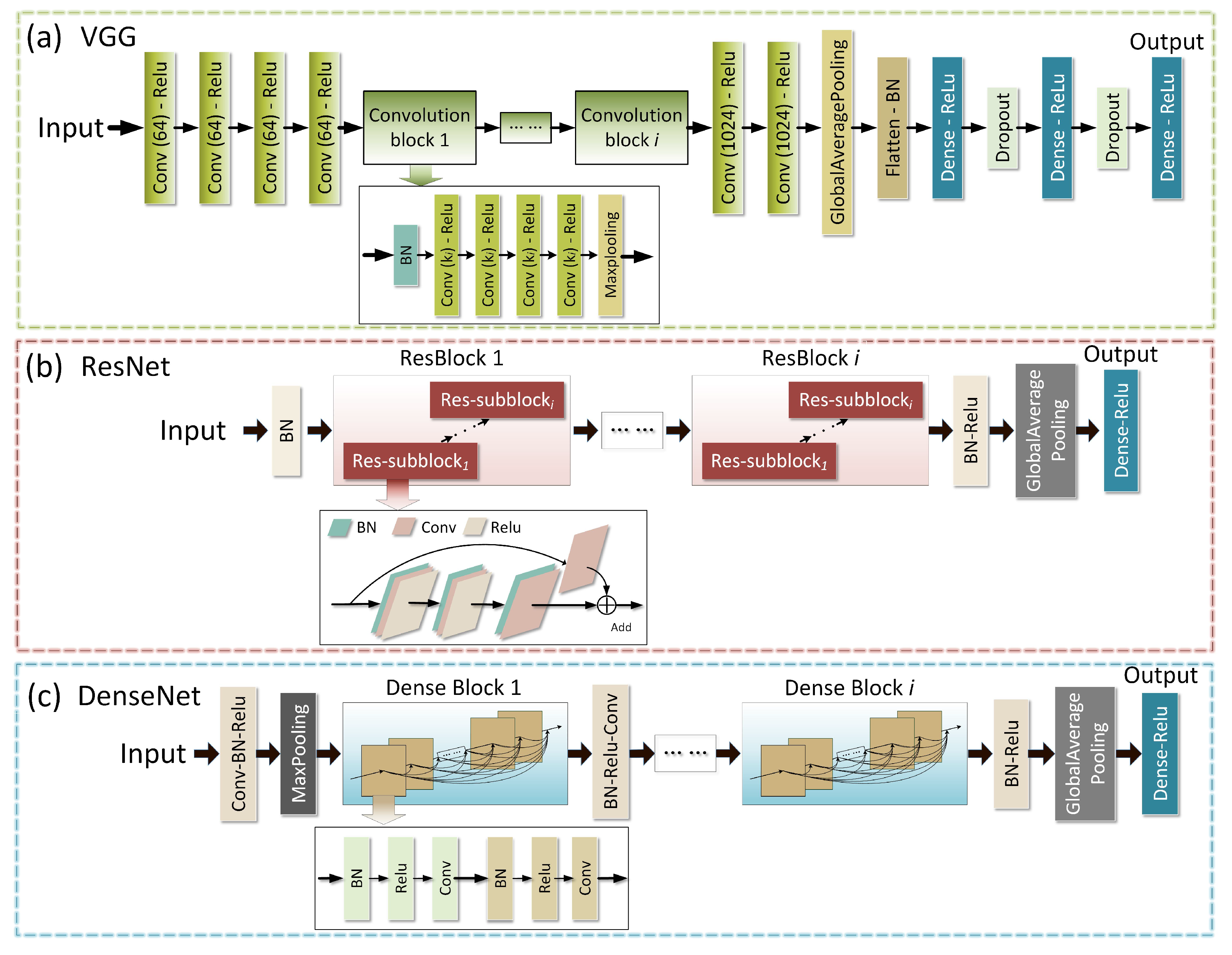
2.2. Structures of Deep Convolution Networks (DCNs)
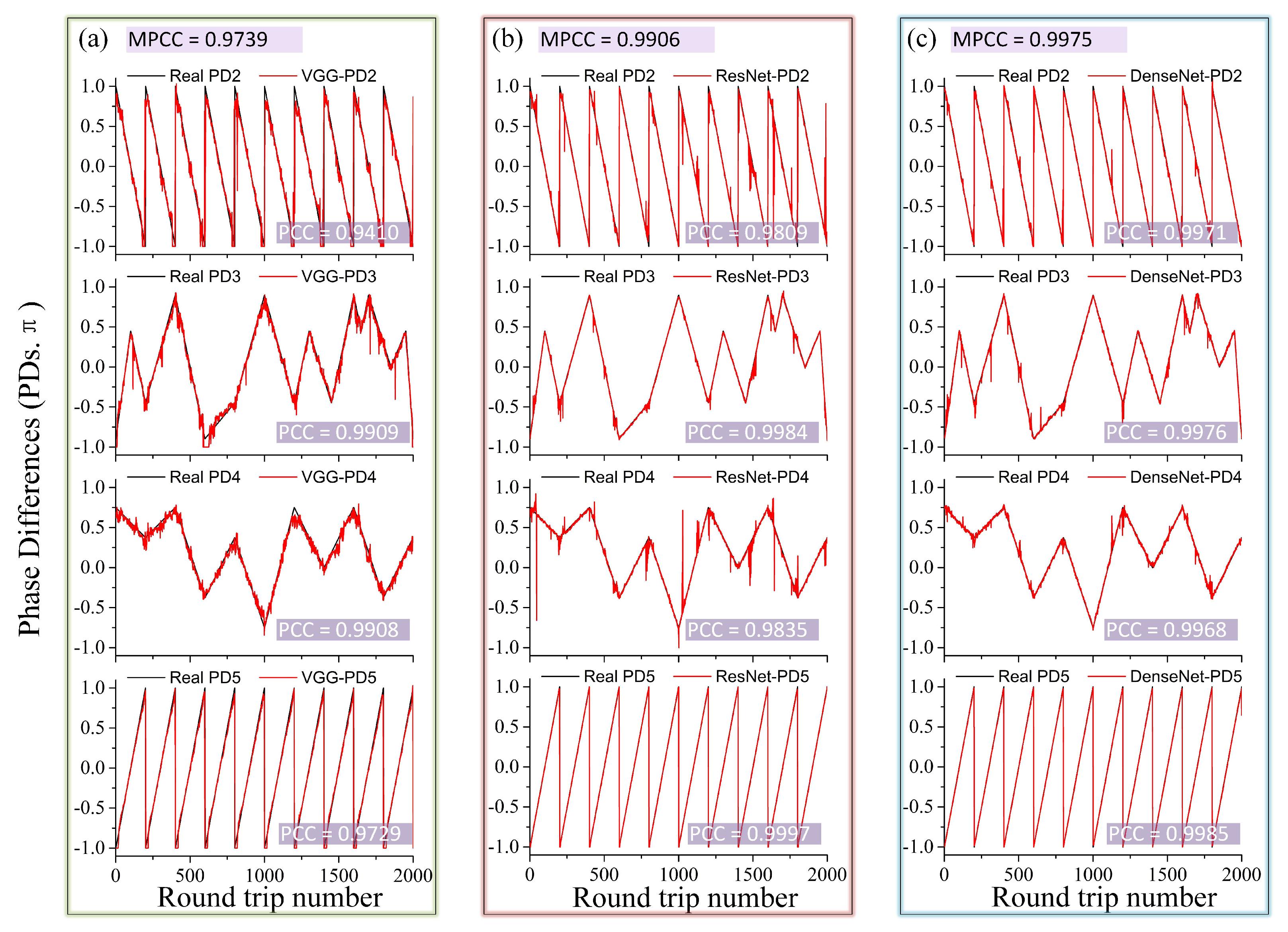
3. Results and Discussion
3.1. Soliton Molecular Structure of Test Set
3.2. Perform Three DCNs on TS-DFT Datasets of Five-Soliton Molecules
3.3. Pearson Correlation Analysis of Real and Predicted Values
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TS-DFT | time-stretch dispersive Fourier transformation |
| DCNs | deep convolution networks |
| MPCC | mean Pearson correlation coefficient |
| PDs | relative phase differences |
References
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Stratmann, M.; Pagel, T.; Mitschke, F. Experimental observation of temporal soliton molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef] [PubMed]
- Zavyalov, A.; Iliew, R.; Egorov, O.; Lederer, F. Dissipative soliton molecules with independently evolving or flipping phases in mode-locked fiber lasers. Phys. Rev. A 2009, 80, 043829. [Google Scholar] [CrossRef]
- Herink, G.; Kurtz, F.; Jalali, B.; Solli, D.R.; Ropers, C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 2017, 356, 50–53. [Google Scholar] [CrossRef] [PubMed]
- Krupa, K.; Nithyanandan, K.; Andral, U.; Tchofo-Dinda, P.; Grelu, P. Real-Time Observation of Internal Motion within Ultrafast Dissipative Optical Soliton Molecules. Phy. Rev. Lett. 2017, 118, 243901. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Yao, X.; Cui, Y. Real-Time Observation of the Buildup of Soliton Molecules. Phy. Rev. Lett. 2018, 121, 023905. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Zeng, H. Build-Up of Dissipative Optical Soliton Molecules via Diverse Soliton Interactions. Laser Photonics Rev. 2018, 12, 1800009. [Google Scholar] [CrossRef]
- He, W.; Pang, M.; Yeh, D.H.; Huang, J.; Menyuk, C.R.; Russell, P.S.J. Formation of optical supramolecular structures in a fibre laser by tailoring long-range soliton interactions. Nat. Commun. 2019, 10, 5756. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.Q.; Nithyanandan, K.; Coillet, A.; Tchofo-Dinda, P.; Grelu, P. Optical soliton molecular complexes in a passively mode-locked fibre laser. Nat. Commun. 2019, 10, 830. [Google Scholar] [CrossRef]
- Kurtz, F.; Ropers, C.; Herink, G. Resonant excitation and all-optical switching of femtosecond soliton molecules. Nat. Photonics 2020, 14, 9–13. [Google Scholar] [CrossRef]
- Luo, Y.; Xia, R.; Shum, P.; Ni, W.; Ys, L.; Lam, H.; Sun, Q.; Tang, X.; Zhao, L. Real-time dynamics of soliton triplets in fiber lasers. Photonics Res. 2020, 8, 884–891. [Google Scholar] [CrossRef]
- Liang, H.; Zhao, X.; Liu, B.; Yu, J.; Liu, Y.; He, R.; He, J.; Li, H.; Wang, Z. Real-time dynamics of soliton collision in a bound-state soliton fiber laser. Nanophotonics 2020, 9, 1921–1929. [Google Scholar] [CrossRef]
- Peng, J.; Boscolo, S.; Zhao, Z.; Zeng, H. Breathing dissipative solitons in mode-locked fiber lasers. Sci. Adv. 2019, 5, eaax1110. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Liu, Y.; He, R.; Zhao, J.; Wang, G.; Yang, G. Self-organized compound pattern and pulsation of dissipative solitons in a passively mode-locked fiber laser. Opt. Lett. 2018, 43, 478–481. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Broderick, N.G.R.; Erkintalo, M. Observation of soliton explosions in a passively mode-locked fiber laser. Optica 2015, 2, 36–39. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.G.; Wang, Z.; Yue, Y.; He, J.; Mao, B.; He, R.; Hu, J. Transient behaviors of pure soliton pulsations and soliton explosion in an L-band normal-dispersion mode-locked fiber laser. Opt. Express 2019, 27, 17729–17742. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; He, J.; He, R.; Liu, Y.; Yue, Y.; Liu, W.; Zhang, L.; Zhu, L.; Zhou, M.; Zhu, K.; et al. Analysis of real-time spectral interference using a deep neural network to reconstruct multi-soliton dynamics in mode-locked lasers. APL Photonics 2020, 5, 116101. [Google Scholar] [CrossRef]
- Närhi, M.; Salmela, L.; Toivonen, J.; Billet, C.; Dudley, J.M.; Genty, G. Machine learning analysis of extreme events in optical fibre modulation instability. Nat. Commun. 2018, 9, 4923. [Google Scholar] [CrossRef]
- Boscolo, S.; Finot, C. Artificial neural networks for nonlinear pulse shaping in optical fibers. Opt. Laser Technol. 2020, 131, 106439. [Google Scholar] [CrossRef]
- Kokhanovskiy, A.; Bednyakova, A.; Kuprikov, E.; Ivanenko, A.; Dyatlov, M.; Lotkov, D.; Kobtsev, S.; Turitsyn, S. Machine learning-based pulse characterization in figure-eight mode-locked lasers. Opt. Lett. 2019, 44, 3410–3413. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Baumeister, T.; Brunton, S.L.; Kutz, J.N. Deep learning and model predictive control for self-tuning mode-locked lasers. J. Opt. Soc. Am. B Opt. Phys. 2018, 35, 617–626. [Google Scholar] [CrossRef]
- An, Y.; Huang, L.; Li, J.; Leng, J.; Yang, L.; Zhou, P. Learning to decompose the modes in few-mode fibers with deep convolutional neural network. Opt. Express 2019, 27, 10127–10137. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yan, S.; Liu, H.; Chen, X. Superhigh-Resolution Recognition of Optical Vortex Modes Assisted by a Deep-Learning Method. Phys. Rev. Lett. 2019, 123, 183902. [Google Scholar] [CrossRef] [PubMed]
- Zibar, D.; Piels, M.; Jones, R.; Schaeeffer, C.G. Machine Learning Techniques in Optical Communication. J. Lightwave Technol. 2016, 34, 1442–1452. [Google Scholar] [CrossRef]
- Genty, G.; Salmela, L.; Dudley, J.M.; Brunner, D.; Kokhanovskiy, A.; Kobtsev, S.; Turitsyn, S.K. Machine learning and applications in ultrafast photonics. Nat. Photonics 2020, 15, 91–101. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J.Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. arXiv 2017, arXiv:1608.06993. [Google Scholar]
- Yu, D.; Seltzer, M.L.; Li, J.; Huang, J.T.; Seide, F. Feature Learning in Deep Neural Networks—Studies on Speech Recognition Tasks. arXiv 2013, arXiv:1301.3605. [Google Scholar]
- Huang, G.; Liu, Z.; Pleiss, G.; van der Maaten, L.; Weinberger, K.Q. Convolutional Networks with Dense Connectivity. arXiv 2020, arXiv:2001.02394. [Google Scholar] [CrossRef]
- Lee, C.Y.; Xie, S.; Gallagher, P.W.; Zhang, Z.; Tu, Z. Deeply-Supervised Nets. In Proceedings of the Artificial Intelligence and Statistics (AISTATS), San Diego, CA, USA, 9–12 May 2015; Volume 38, pp. 562–570. [Google Scholar]
- Wang, Z.; Wang, Z.; Liu, Y.; He, R.; Wang, G.; Yang, G.; Han, S. Generation and time jitter of the loose soliton bunch in a passively mode-locked fiber laser. Chin. Opt. Lett. 2017, 15, 080605. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity Mappings in Deep Residual Networks. In Proceedings of the 14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2016; Volume 9908, pp. 630–645. [Google Scholar] [CrossRef]
- Machrisaa, C. tensorflow-vgg: VGG19 and VGG16 on Tensorflow. Available online: https://github.com/machrisaa/tensorflow-vgg (accessed on 10 February 2021).
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Li, Y.; Yuan, Y. Convergence Analysis of Two-layer Neural Networks with ReLU Activation. Adv. Neural Inf. Process. Syst. 2017, 30, 597–607. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the OSDI’16: 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Meng, F.; Lapre, C.; Billet, C.; Genty, G.; Dudley, J.M. Instabilities in a dissipative soliton-similariton laser using a scalar iterative map. Opt. Lett. 2020, 45, 1232–1235. [Google Scholar] [CrossRef]
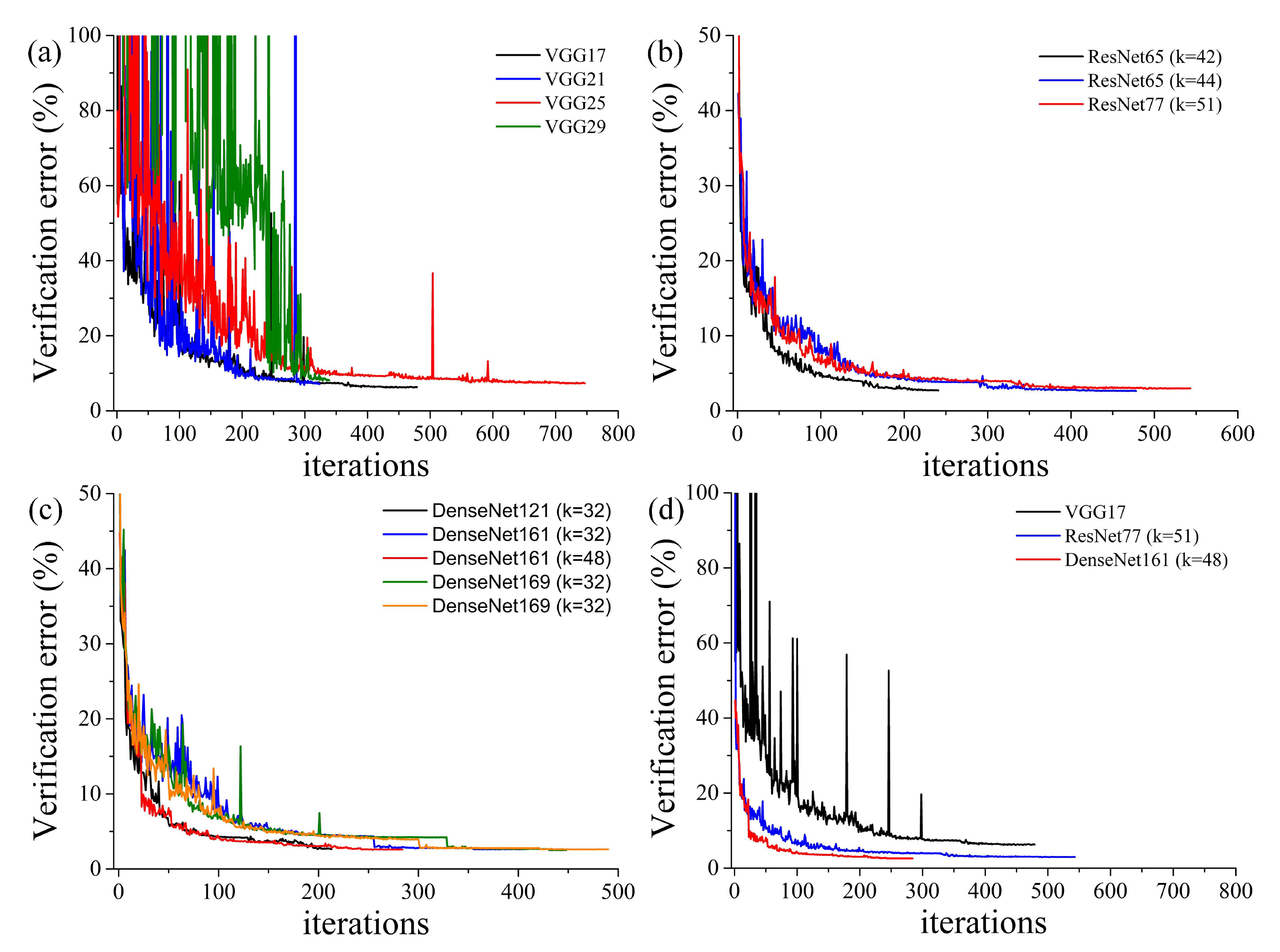
| Model-Layers | Params | Iterations | Verification Error (%) | Testing Error (%) |
|---|---|---|---|---|
| VGG17 | 268 M | 479 | 6.2891 | 5.2528 |
| VGG21 | 272 M | 324 | 7.1810 | 6.5479 |
| VGG25 | 320 M | 747 | 7.3101 | 6.8600 |
| VGG29 | 332 M | 339 | 8.1265 | 7.3815 |
| ResNet65 (k = 42) | 122 M | 241 | 2.7159 | 2.9438 |
| ResNet65 (k = 44) | 426 M | 543 | 2.6445 | 2.8491 |
| ResNet77 (k = 51) | 187 M | 478 | 2.9573 | 2.6260 |
| DenseNet121 (k = 32) | 68.1 M | 213 | 2.6361 | 2.6155 |
| DenseNet161 (k = 32) | 112 M | 405 | 2.6057 | 2.5037 |
| DenseNet161 (k = 48) | 246 M | 284 | 2.5917 | 2.2355 |
| DenseNet169 (k = 32) | 126 M | 448 | 2.5088 | 2.7286 |
| DenseNet169 (k = 48) | 278 M | 490 | 2.6103 | 2.8331 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; He, J.; Liu, Y.; Yue, Y.; Zhang, L.; Zhu, L.; Zhou, M.; Liu, C.; Zhu, K.; Wang, Z. Comparing Performance of Deep Convolution Networks in Reconstructing Soliton Molecules Dynamics from Real-Time Spectral Interference. Photonics 2021, 8, 51. https://doi.org/10.3390/photonics8020051
Li C, He J, Liu Y, Yue Y, Zhang L, Zhu L, Zhou M, Liu C, Zhu K, Wang Z. Comparing Performance of Deep Convolution Networks in Reconstructing Soliton Molecules Dynamics from Real-Time Spectral Interference. Photonics. 2021; 8(2):51. https://doi.org/10.3390/photonics8020051
Chicago/Turabian StyleLi, Caiyun, Jiangyong He, Yange Liu, Yang Yue, Luhe Zhang, Longfei Zhu, Mengjie Zhou, Congcong Liu, Kaiyan Zhu, and Zhi Wang. 2021. "Comparing Performance of Deep Convolution Networks in Reconstructing Soliton Molecules Dynamics from Real-Time Spectral Interference" Photonics 8, no. 2: 51. https://doi.org/10.3390/photonics8020051
APA StyleLi, C., He, J., Liu, Y., Yue, Y., Zhang, L., Zhu, L., Zhou, M., Liu, C., Zhu, K., & Wang, Z. (2021). Comparing Performance of Deep Convolution Networks in Reconstructing Soliton Molecules Dynamics from Real-Time Spectral Interference. Photonics, 8(2), 51. https://doi.org/10.3390/photonics8020051






