Determination of Optic Axes by Corneal Topography among Italian, Brazilian, and Chinese Populations
Abstract
1. Introduction
2. Materials and Methods
2.1. Clinical Data
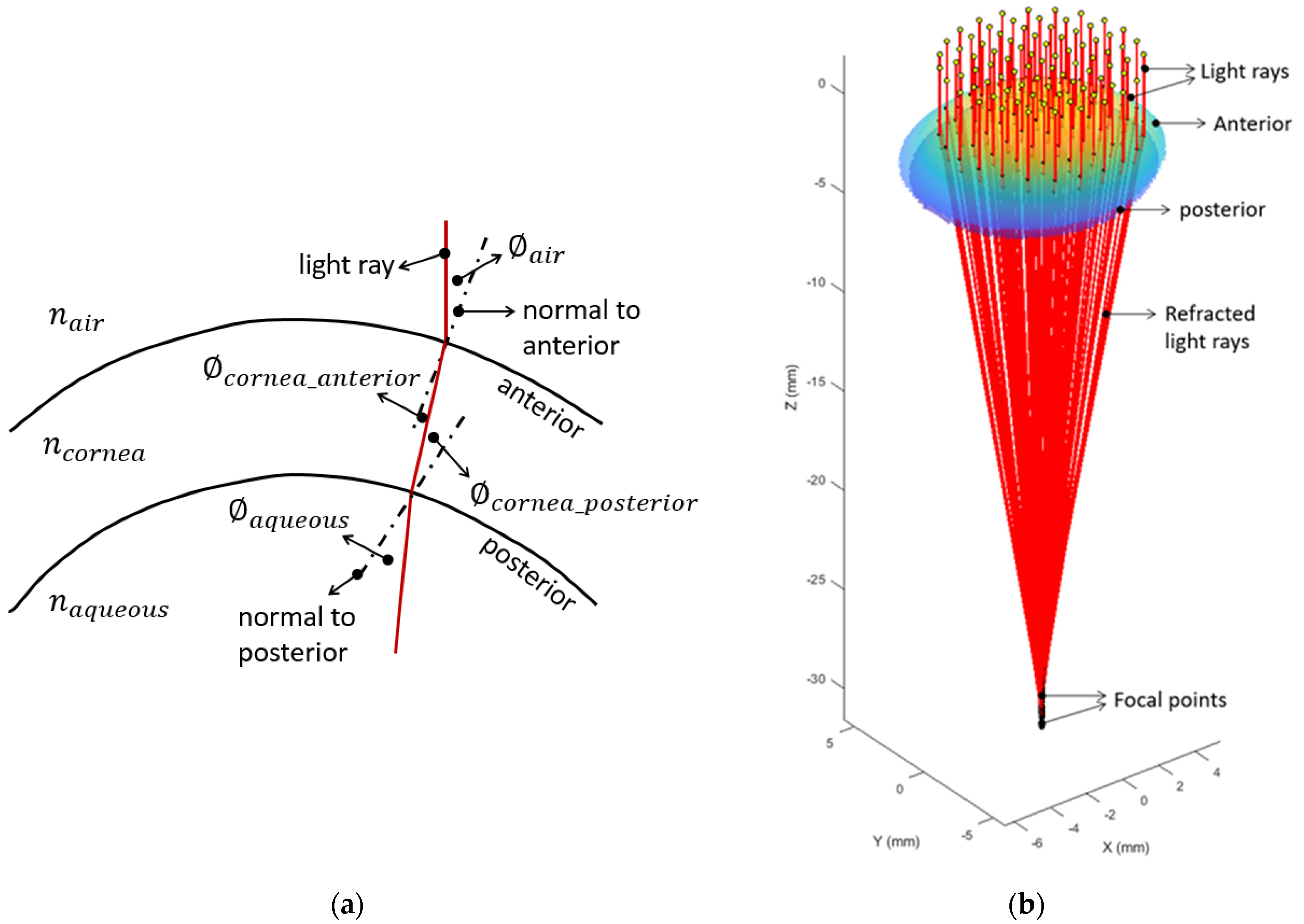
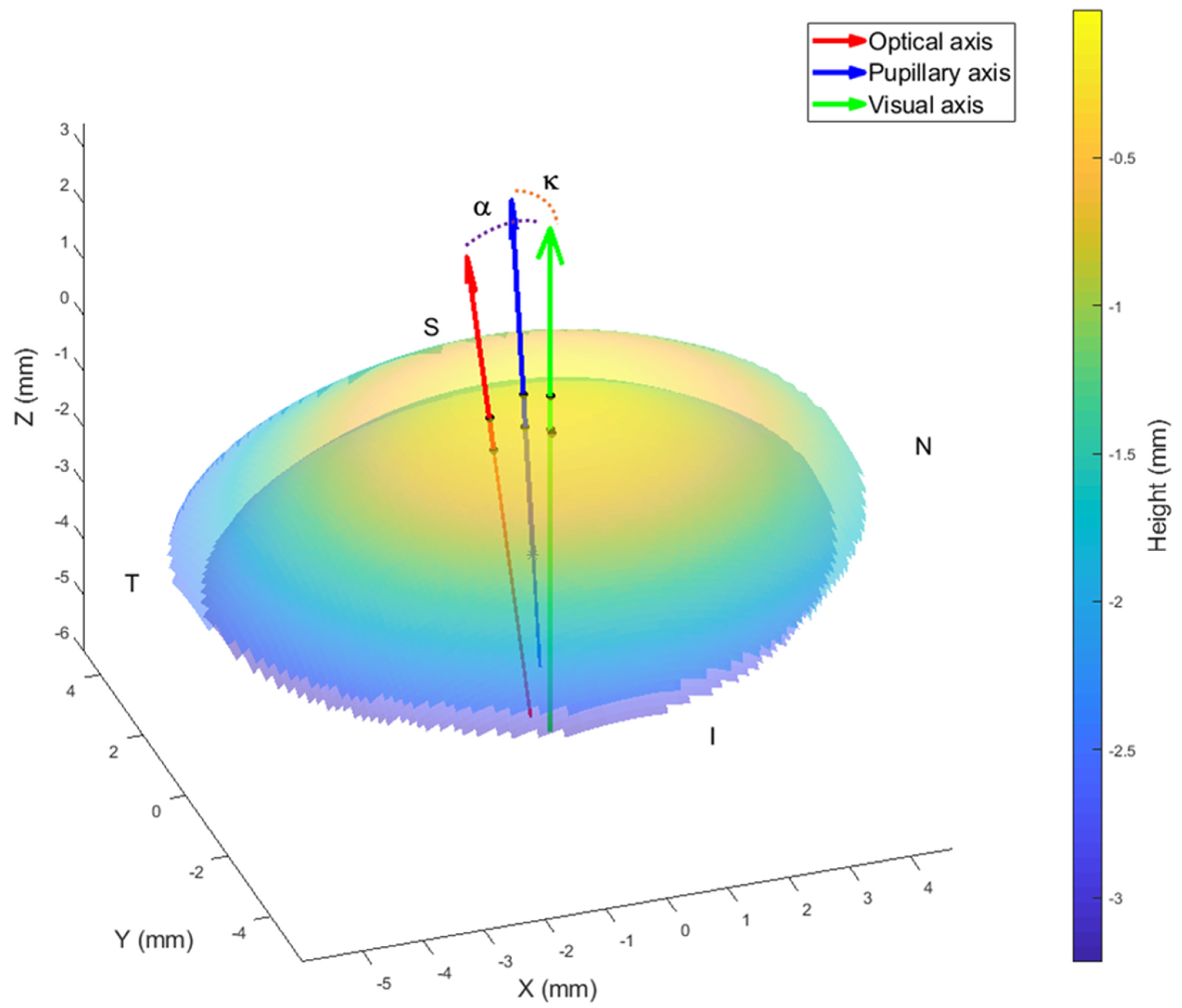
2.2. Determination of the Optical Axis
2.3. Determination of the Pupillary Axis
2.4. Determination of the Visual Axis
2.5. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Berrio, E.; Tabernero, J.; Artal, P. Optical aberrations and alignment of the eye with age. J. Vis. 2010, 10. [Google Scholar] [CrossRef] [PubMed]
- Keller, P.R.; Saarloos, P.P. Perspectives on corneal topography: A review of videokeratoscopy. Clin. Exp. Optom. 1997, 80, 18–30. [Google Scholar] [CrossRef]
- Douthwaite, W.A.; Pardhan, S. Surface tilt measured with the EyeSys videokeratoscope: Influence on corneal asymmetry. Investig. Ophthalmol. Vis. Sci. 1998, 39, 1727–1735. [Google Scholar]
- Pande, M.; Hillman, J.S. Optical zone centration in keratorefractive surgery. Entrance pupil center, visual axis, coaxially sighted corneal reflex, or geometric corneal center? Ophthalmology 1993, 100, 1230–1237. [Google Scholar] [CrossRef]
- Harris, W.F. Nodes and nodal points and lines in eyes and other optical systems. Ophthalmic Physiol. Opt. 2010, 30, 24–42. [Google Scholar] [CrossRef]
- Schwiegerling, J.T. Eye axes and their relevance to alignment of corneal refractive procedures. J. Refract. Surg. 2013, 29, 515–516. [Google Scholar] [CrossRef]
- Arba Mosquera, S.; Verma, S.; McAlinden, C. Centration axis in refractive surgery. Eye Vis. 2015, 2, 4. [Google Scholar] [CrossRef]
- Moshirfar, M.; Hoggan, R.N.; Muthappan, V. Angle Kappa and its importance in refractive surgery. Oman J. Ophthalmol. 2013, 6, 151–158. [Google Scholar] [CrossRef]
- Espinosa, J.; Mas, D.; Kasprzak, H.T. Corneal primary aberrations compensation by oblique light incidence. J. Biomed. Opt. 2009, 14, 044003. [Google Scholar] [CrossRef]
- Reinstein, D.Z.; Gobbe, M.; Archer, T.J. Coaxially sighted corneal light reflex versus entrance pupil center centration of moderate to high hyperopic corneal ablations in eyes with small and large angle kappa. J. Refract. Surg. 2013, 29, 518–525. [Google Scholar] [CrossRef] [PubMed]
- Prakash, G.; Prakash, D.R.; Agarwal, A.; Kumar, D.A.; Agarwal, A.; Jacob, S. Predictive factor and kappa angle analysis for visual satisfactions in patients with multifocal IOL implantation. Eye 2011, 25, 1187–1193. [Google Scholar] [CrossRef] [PubMed]
- Van Buskirk, E.M. The anatomy of the limbus. Eye 1989, 3 Pt 2, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Consejo, A.; Llorens-Quintana, C.; Radhakrishnan, H.; Iskander, D.R. Mean shape of the human limbus. J. Cataract Refract. Surg. 2017, 43, 667–672. [Google Scholar] [CrossRef]
- Yang, Q.; Cho, K.-S.; Chen, H.; Yu, D.; Wang, W.-H.; Luo, G.; Pang, I.-H.; Guo, W.; Chen, N.F. Microbead-induced ocular hypertensive mouse model for screening and testing of aqueous production suppressants for glaucoma. Investig. Ophthalmol. Vis. Sci. 2012, 53, 3733–3741. [Google Scholar] [CrossRef]
- Thibos, L.N.; Bradley, A.; Still, D.L.; Zhang, X.; Howarth, P.A. Theory and measurement of ocular chromatic aberration. Vis. Res. 1990, 30, 33–49. [Google Scholar] [CrossRef]
- Dominguez-Vicent, A.; Monsalvez-Romin, D.; Perez-Vives, C.; Ferrer-Blasco, T.; Montes-Mico, R. Measurement of angle Kappa with Orbscan II and Galilei G4: Effect of accommodation. Graefes Arch. Clin. Exp. Ophthalmol. 2014, 252, 249–255. [Google Scholar] [CrossRef]
- Basmak, H.; Sahin, A.; Yildirim, N.; Papakostas, T.D.; Kanellopoulos, A.J. Measurement of angle kappa with synoptophore and Orbscan II in a normal population. J. Refract. Surg. 2007, 23, 456–460. [Google Scholar] [CrossRef]
- Qi, H.; Jiang, J.J.; Jiang, Y.M.; Wang, L.Q.; Huang, Y.F. Kappa angles in different positions in patients with myopia during LASIK. Int. J. Ophthalmol. 2016, 9, 585–589. [Google Scholar] [CrossRef]
- Roop Roop, P. Optimizing optical outcomes of intraocular lens implantation by achieving centration on visual axis. Indian J. Ophthalmol. 2017, 65, 1425–1427. [Google Scholar] [CrossRef]
- Hubbe, R.E.; Foulks, G.N. The effect of poor fixation on computer-assisted topographic corneal analysis. Ophthalmology 1994, 101, 1745–1748. [Google Scholar]
- Doyle, S.J.; Hynes, E.; Naroo, S.; Shah, S. PRK in patients with a keratoconic topography picture. The concept of a physiological ‘displaced apex syndrome’. Br. J. Ophthalmol. 1996, 80, 25–28. [Google Scholar] [CrossRef][Green Version]
- Smit, G.; Atchison, D.A. The eye and visual optical instruments; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Smith, D.A.G. Optics of the Human Eye; Reed Educational and Professional Publishing Ltd.: Edinburgh, UK, 2000; 261p. [Google Scholar]
- Vojnikovi, B.; Tamajo, E. Gullstrand’s Optical Schematic System of the Eye Modified by Vojnikovi & Tamajo. Coll. Antropol. 2013, 37, 41–45. [Google Scholar]
- Wang, L.; Mahmoud, A.M.; Anderson, B.L.; Koch, D.D.; Roberts, C.J. Total corneal power estimation: Ray tracing method versus gaussian optics formula. Investig. Ophthalmol. Vis. Sci. 2011, 52, 1716–1722. [Google Scholar] [CrossRef]
- Welford, W.T. Aberrations of Optical Systems; CRC Press: Boca Raton, FL, USA; Taylor & Francis: Abingdon, UK, 1986. [Google Scholar]
- Guyon, F.; Riche, R.L. Least Squares Parameter Estimation and the Levenberg-Marquardt Algorithm: Deterministic Analysis; Sensitivities and Numerical Experiments; INSA de Rouen: Saint-Étienne-du-Rouvray, France, 1999. [Google Scholar]
- BjÓrck, A. Numerical Methods for Least Squares Problems. Philadelphia: Society for Industrial and Applied Mathematics. Available online: https://doi.org/10.1137/1.9781611971484 (accessed on 15 February 2021).
- Arvo, J. Fast Random Rotation Matrices. In Graphics Gems III; David, K., Ed.; Academic Press Professional, Inc.: Cambridge, MA, USA, 1992; pp. 117–120. [Google Scholar]
- Mrochen, M.; Kaemmerer, M.; Mierdel, P.; Seiler, T. Increased higher-order optical aberrations after laser refractive surgery: A problem of subclinical decentration. J. Cataract Refract. Surg. 2001, 27, 362–369. [Google Scholar] [CrossRef]
- Everitt, B.S.; Skrondal, A. The Cambridge Dictionary of Statistics, 4th ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Chan, J.S.; Mandell, R.B.; Burger, D.S.; Fusaro, R.E. Accuracy of videokeratography for instantaneous radius in keratoconus. Optom. Vis. Sci. 1995, 72, 793–799. [Google Scholar] [CrossRef]
- Park, C.Y.; Oh, S.Y.; Chuck, R.S. Measurement of angle kappa and centration in refractive surgery. Curr. Opin. Ophthalmol. 2012, 23, 269–275. [Google Scholar] [CrossRef]
- Choi, S.R.; Kim, U.S. The correlation between angle kappa and ocular biometry in Koreans. Korean J. Ophthalmol. 2013, 27, 421–424. [Google Scholar] [CrossRef]
- Gharaee, H.; Shafiee, M.; Hoseini, R.; Abrishami, M.; Abrishami, Y.; Abrishami, M. Angle Kappa Measurements: Normal Values in Healthy Iranian Population Obtained With the Orbscan II. Iran. Red Crescent Med. J. 2015, 17, e17873. [Google Scholar] [CrossRef]
- Hashemi, H.; KhabazKhoob, M.; Yazdani, K.; Mehravaran, S.; Jafarzadehpur, E.; Fotouhi, A. Distribution of angle kappa measurements with Orbscan II in a population-based survey. J. Refract. Surg. 2010, 26, 966–971. [Google Scholar] [CrossRef]
| Italian Participants | Brazilian Participants | Chinese Participants | ||||
|---|---|---|---|---|---|---|
| Participants (eyes) | 347 (694) | 181 (362) | 500 (1000) | |||
| Age in years; mean ± SD (min: max) | 37.6 ± 13.5 (6: 106) | 35.6 ± 15.8 (10: 87) | 24.2 ± 5.7 (17: 48) | |||
| Clinical features and angles | ||||||
| Minimum corneal thickness (µm) | 531 ± 420 | 404:706 | 550 ± 33 | 492:660 | 535 ± 290 | 453:620 |
| Flat curvature in the central 3 mm zone K1 (D) | 42.3 ± 1.9 | 36.6:47.8 | 42.6 ± 1.4 | 39.4:46.6 | 42.8 ± 1.4 | 38.2:48.1 |
| Steep curvature in the central 3 mm zone K2 (D) | 44.3 ± 2.9 | 37.1:51.4 | 43.8 ± 1.5 | 40.3:47.9 | 43.9 ± 1.6 | 38.6:49.5 |
| Index of Bad D | 1.2 ± 0.8 | −0.7:3.0 | 0.4 ± 0.5 | −0.9:1.4 | 1.0 ± 0.6 | −0.8:3.0 |
| Kappa angle (ϰ) | 3.33 ± 1.97 | 0.09:12.99 | 2.60 ± 1.52 | 0.27:10.26 | 2.09 ± 1.23 | 0.07:8.68 |
| Alpha angle (α) | 5.60 ± 2.48 | 0.57:18.77 | 5.38 ± 1.74 | 0.57:11.22 | 4.34 ± 1.30 | 0.81:8.45 |
| Italian Participants | Brazilian Participants | Chinese Participants | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Eye side | Right eye | Left eye | p-value | Right eye | Left eye | p-value | Right eye | Left eye | p-value |
| Mean ± SD Min:Max | Mean ± SD Min:Max | Mean ± SD Min:Max | Mean ± SD Min:Max | Mean ± SD Min:Max | Mean ± SD Min:Max | ||||
| ϰ (degree) | 3.80 ± 2.04 | 2.85 ± 1.76 | < 0.001 | 2.70 ± 1.41 | 2.49 ± 1.62 | 0.087 | 2.03 ± 1.24 | 2.15 ± 1.22 | 0.022 |
| 0.36:9.58 | 0.09:12.99 | 0.34:7.31 | 0.27:10.27 | 0.07:8.17 | 0.12:8.68 | ||||
| α (degree) | 5.64 ± 2.30 | 5.55 ± 2.65 | 0.518 | 5.40 ± 1.74 | 5.37 ± 1.75 | 0.646 | 4.31 ± 1.28 | 4.37 ± 1.31 | 0.284 |
| 0.57:14.92 | 0.57:18.77 | 1.03:11.22 | 0.57:11.18 | 0.81:8.45 | 0.85:8.20 | ||||
| Age Strata | < 20 years | 20–40 years | p-value | < 20 years | 20–40 years | < 20 years | 20–40 years | ||
| (n = 38) | (n = 356) | (n = 28) | (n = 230) | (n = 328) | (n = 652) | ||||
| Mean ± SD | Mean ± SD | Mean ± SD | Mean ± SD | p-value | Mean ± SD | Mean ± SD | p-value | ||
| Min:Max | Min:Max | Min:Max | Min:Max | Min:Max | Min:Max | ||||
| ϰ (degree) | 3.58 ± 1.93 | 3.31 ± 1.97 | 0.409 | 2.22 ± 1.53 | 2.63 ± 1.52 | 0.391 | 2.00 ± 1.16 | 2.14 ± 1.26 | 0.501 |
| 0.94:7.95 | 0.09:12.99 | 0.32:7.55 | 0.27:10.27 | 0.13:7.81 | 0.07:8.68 | ||||
| α (degree) | 5.95 ± 2.72 | 5.57 ± 2.46 | 0.418 | 5.67 ± 1.84 | 5.36 ± 1.73 | 0.187 | 4.38 ± 1.25 | 4.32 ± 1.32 | 0.085 |
| 1.92:14.92 | 0.57:18.77 | 2.23:9.39 | 0.57:11.22 | 0.81:7.81 | 0.81:8.45 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, B.T.; Eliasy, A.; Elhalwagy, M.; Vinciguerra, R.; Bao, F.; Vinciguerra, P.; Ambrósio, R., Jr.; Elsheikh, A.; Abass, A. Determination of Optic Axes by Corneal Topography among Italian, Brazilian, and Chinese Populations. Photonics 2021, 8, 61. https://doi.org/10.3390/photonics8020061
Lopes BT, Eliasy A, Elhalwagy M, Vinciguerra R, Bao F, Vinciguerra P, Ambrósio R Jr., Elsheikh A, Abass A. Determination of Optic Axes by Corneal Topography among Italian, Brazilian, and Chinese Populations. Photonics. 2021; 8(2):61. https://doi.org/10.3390/photonics8020061
Chicago/Turabian StyleLopes, Bernardo T., Ashkan Eliasy, Mohamed Elhalwagy, Riccardo Vinciguerra, Fangjun Bao, Paolo Vinciguerra, Renato Ambrósio, Jr., Ahmed Elsheikh, and Ahmed Abass. 2021. "Determination of Optic Axes by Corneal Topography among Italian, Brazilian, and Chinese Populations" Photonics 8, no. 2: 61. https://doi.org/10.3390/photonics8020061
APA StyleLopes, B. T., Eliasy, A., Elhalwagy, M., Vinciguerra, R., Bao, F., Vinciguerra, P., Ambrósio, R., Jr., Elsheikh, A., & Abass, A. (2021). Determination of Optic Axes by Corneal Topography among Italian, Brazilian, and Chinese Populations. Photonics, 8(2), 61. https://doi.org/10.3390/photonics8020061









