Abstract
Biodegradable and low-toxic silicon nanoparticles (SiNPs) have potential in different biomedical applications. Previous experimental studies revealed the efficiency of some types of SiNPs in tumor hyperthermia. To analyse the feasibility of employing SiNPs produced by the laser ablation of silicon nanowire arrays in water and ethanol as agents for laser tumor hyperthermia, we numerically simulated effects of heating a millimeter-size nodal basal-cell carcinoma with embedded nanoparticles by continuous-wave laser radiation at 633 nm. Based on scanning electron microscopy data for the synthesized SiNPs size distributions, we used Mie theory to calculate their optical properties and carried out Monte Carlo simulations of light absorption inside the tumor, with and without the embedded nanoparticles, followed by an evaluation of local temperature increase based on the bioheat transfer equation. Given the same mass concentration, SiNPs obtained by the laser ablation of silicon nanowires in ethanol (eSiNPs) are characterized by smaller absorption and scattering coefficients compared to those synthesized in water (wSiNPs). In contrast, wSiNPs embedded in the tumor provide a lower overall temperature increase than eSiNPs due to the effect of shielding the laser irradiation by the highly absorbing wSiNPs-containing region at the top of the tumor. Effective tumor hyperthermia (temperature increase above 42 °C) can be performed with eSiNPs at nanoparticle mass concentrations of 3 mg/mL and higher, provided that the neighboring healthy tissues remain underheated at the applied irradiation power. The use of a laser beam with the diameter fitting the size of the tumor allows to obtain a higher temperature contrast between the tumor and surrounding normal tissues compared to the case when the beam diameter exceeds the tumor size at the comparable power.
1. Introduction
Hyperthermia is a treatment modality based on the local heating of pathological tissue volumes to temperatures exceeding 42 °C. The heat effect produced by these temperatures can damage or kill pathological cells or make them more vulnerable to other therapy modalities, such as radiation therapy or chemotherapy, with minimal damage to surrounding normal tissues [1,2]. In practice, hyperthermia protocols aim at concentrating the heating primarily in the tumor area [3,4]. A promising direction to improve hyperthermia performance is photohyperthermia utilizing laser sources owing to the wide possibilities in configuring the beam geometry and, hence, the light intensity distribution within tissue. The employment of laser wavelengths within the so-called tissue transparency window (600–1300 nm) ensures low light absorption in superficial tissue layers, thus providing deeper light penetration into the treated volume [5]. It is worth noting that light is highly scattered in tissue and becomes diffusive within approximately a millimeter of depth [6]. In this region, the therapeutic effect might be induced by excessive tumor heating caused by light energy absorption [7,8], which was demonstrated to be efficient against skin cancer [9,10]. In hyperthermia, an additional absorption contrast between healthy and pathological tissues can be achieved by the targeted delivery of nanoagents to treatment areas [11,12,13]. Since nanoparticle (NP) shape and material determine its absorption spectra, the nanoparticles could be customized to provide additional absorption at the applied laser wavelength, thus enhancing the absorption contrast upon target delivery. Gold-based nanostructures constitute one of the most popular objects for therapeutic applications and were shown to be efficient both in experiments [14,15,16] and in numerical simulations [16,17,18]. Owing to plasmon resonance properties, these structures were demonstrated to provide a pronounced contrast in both optical scattering and absorption, even at relatively low concentrations [19,20,21]. To simulate laser heating of the tissues with embedded gold NPs, the Monte Carlo technique [16,17] is often employed, providing good agreement of calculated temperature distributions and experimental results for nanorods [16] and core-shell [17] gold nanostructures.
However, gold nanoparticles may exhibit strong toxicity, which limits their applications [22,23]. Being injected in the organism, gold nanoparticles readily interact with proteins, which finally makes the effect of gold NPs in vivo unpredictable [24]. Additionally, the toxicity is often caused by the presence of undesirable impurities due to the application of such chemicals as chloroauric acid, cetrimonium bromide, silver nitrate, sodium borohydride, ascorbic acid, and other reagents necessary for synthesizing the gold nanoparticles [25,26]. This so-called secondary toxicity can be sufficiently reduced via surface functionalization or by employing the laser ablation technique [27,28,29,30].
A possible solution of the toxicity problem consists in employing silicon nanoparticles (SiNPs), which are less expensive in production as compared to gold NPs. For example, the NPs based on porous silicon were shown to be biocompatible, biodegradable and have no cytotoxicity [31,32,33]. The SiNPs of moderate concentrations may be easily fully transformed to orthosilicic acid and removed from living organisms with urine [32] without accumulation effects, unlike gold nanoparticles.
Fabricating SiNPs by pulsed laser ablation of silicon nanowires [34] or porous silicon [35] in liquids represents a way to control SiNPs size through the selection of buffer liquid (water, ethanol, liquid helium) and pulse duration [36]. Additionally, the wavelength of ablating radiation affects the SiNPs size, insofar as the scattering and absorption properties of an ablation target depend on it.
SiNPs were additionally found to be promising as thermal coupling agents for hyperthermia [37,38,39]. In vitro experiments on a cell culture exposed to near-infrared laser irradiation demonstrated a significant reduction of tumor cell viability in the presence of SiNPs [37]. Experiments in vivo demonstrated that porous silicon in combination with laser irradiation allows for the selective destruction of cancer cells without damaging surrounding healthy cells [38]. Numerical simulations of laser tumor hyperthermia [39] demonstrated the increase of maximum tumor temperature by 4 °C due to SiNPs presence in the tumor site.
Potential SiNPs for photohyperthermia enhancement applications should be in the order of tens nanometer in diameter to ensure both efficient delivery to target tissues and reasonable light absorption. However, SiNPs in ready-to-use substances formed by means of mechanical milling or ultrasonic grinding of porous silicon layers are characterized by larger sizes [33,37,38]. High-energy grinding of porous silicon films in water by a planetary mill was demonstrated to result in the formation of SiNPs with diameters of 2–5 nm agglomerated into big particles of sizes ranging from 40 to 300 nm [33]. SiNPs of diameter less than 220 nm were reported to be formed with the help of fracturing porous silicon by ultrasonication in water [37] and ethanol [38] followed by membrane filtration.
The laser ablation of silicon or silicon nanostructures in liquids opens up a promising way to manufacture almost ready-to-use suspensions of SiNPs of the desired size free of any chemical impurities [40,41,42]. For example, SiNPs of mean size of 20–30 nm formed by the laser ablation of porous silicon were employed as agents for photohyperthermia: irradiation of the SiNP aqueous suspension (0.4 mg/mL) containing unicellular Paramecium caudatum organisms by continuous-wave laser radiation with the intensity of 25 kW/cm2 at a wavelength of 808 nm was found to result in temperature rise up to 20 °С and death of the living cells [43].
Employing arrays of silicon nanowires (SiNWs) as ablation targets seems to have various advantages for producing the SiNPs for biophotonics applications, including satisfactory stability of water- and ethanol-based suspensions with an absolute value of the zeta potential up to 30 mV [44]. This value indicates the typical time scale of spontaneous agglomeration as tens of hours, and the sonification of the SiNPs suspension prior to application allows to exclude the effect of agglomeration in the course of the procedure. Stability can be potentially increased via coating with biocompatible and biodegradable polymers as it has been done for porous silicon [45].
SiNW arrays fabricated via a metal-assisted chemical etching technique [46] contain SiNWs of about 100 nm in diameter and up to 100 µm in length which demonstrate strong scattering and high absorption of visible and near-infrared light [47,48]. Ablation threshold of SiNWs is up to eight times lower than in crystalline silicon [34,35], which increases product yield and reduces the estimated production cost. However, to our knowledge, the laser-ablated SiNWs have not been reported to be used in photohyperthermia.
In this work, we aimed at estimating the potential of SiNPs fabricated by the laser ablation of the SiNW arrays in water and ethanol as thermal coupling agents for hyperthermia. We performed a numerical simulation of heating a millimeter-sized nodular basal cell carcinoma (nBCC), which is the most common form of human skin cancer, located in human facial skin tissue [49] using continuous-wave (cw) laser irradiation. The choice of cw laser radiation for hyperthermia is determined by limits of laser radiation intensity for safe laser treatment of biotissues (below 200 mW/cm2 [50]), especially for healthy tissues surrounding the tumor. Employing pulsed irradiation has no advantages due to the decrease of safety energy density limits with shortening pulse duration [50,51]. Although silicon possesses significant cubic nonlinear susceptibility responsible for the light self-action [52], simple estimations demonstrate that for a laser pulse energy of the order of safety threshold [51], the relative variation of absorption for bulk silicon is in the order of 10−4.
We considered two configurations of the beam: (1) beam width corresponds to tumor transversal size to avoid excessive surrounding tumor heating, and (2) beam width exceeds it to ensure tumor heating at transversal boundaries. The considered beam power range was 60–200 mW. A systematic analysis of the effect of SiNPs concentration and beam configuration of hyperthermia performance was conducted. Optimal irradiation parameters providing hyperthermia of the entire tumor without significant overheating of surrounding healthy tissues were found.
2. Materials and Methods
The developed numerical model of laser-induced tumor hyperthermia with the embedded SiNPs consists of three parts. In the first step, we calculated the partial scattering and absorption coefficients of the nanoparticles embedded in biotissue using Mie theory based on the measured size distributions of the two types of employed nanoparticles. In the second step, we simulated light absorption distribution in a biotissue model mimicking skin with a superficial nBCC upon laser irradiation with a particular beam configuration using optical parameters accounting for the SiNPs presence in the tumor. In the third step, a bioheat transfer equation was employed to evaluate the temperature distribution in the tumor and the surrounding tissues. Several configurations of laser beam and power, as well as various SiNPs concentrations, have been considered in order to analyse hyperthermia efficiency and ensure the heating of healthy tissues below the damaging threshold.
2.1. Geometry and Optical Parameters of the Model
Figure 1 shows histology images of normal skin (Figure 1a) and typical nBCC (Figure 1b). The histology images were obtained from the institutional database and were fully anonymized. In the case of nBCC, stratum corneum and upper epidermis layers have normal morphology, while the tumor node has a shape close to the ellipsoidal one. To reproduce the observed morphological structure in the simulations, we modeled human facial skin by a three-layered medium consisting of epidermis, dermis, and subcutaneous fat. The nBCC is represented by a spheroid located at a depth of 0.02 mm below the skin surface, with semiaxes of 2.5 mm in the two directions parallel to the skin surface and 1 mm in the direction normal to skin surface, which is in agreement with the morphological observations.
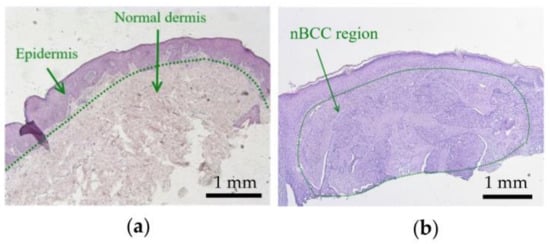
Figure 1.
Histological images of (a) normal skin and (b) nodular basal cell carcinoma.
Figure 2 demonstrates the layout of the nBCC hyperthermia scheme with the position of the laser beam at the skin surface. We considered cw laser irradiation with the circular homogeneous intensity distribution. The radius of the circle is r, and the laser beam axis coincides with the axial symmetry axis of the tumor. Laser radiation is assumed to be non-polarized. This beam shape is typical for hyperthermia carried out by light-emitting diodes [53] or lasers generating in multimode regime [54]. In these cases, circular homogeneous intensity distribution can be achieved with the help of laser radiation homogenizers, enabling a spatially flat-top laser spot of non-polarized laser radiation (see, e.g., [55]). Applying a homogeneous beam seems to be more practical due to the more homogeneous transversal distribution of the intensity as compared to alternatively employed Gaussian beams.
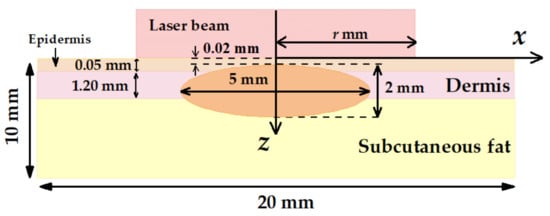
Figure 2.
Schematic of multilayer human skin model with an embedded tumor node employed in Monte Carlo simulations.
To ensure deep penetration of the laser radiation into the treated biotissue region, a wavelength from the optical transparency window (600–1300 nm) should be used. At the same time, in this wavelength range, the absorption of light by silicon decreases with the increase in wavelength [56]. Our previous study [39] compared the application of the wavelengths of 633 and 800 nm for nanoparticle-mediated tumor hyperthermia. It was shown that at equal intensities the wavelength of 633 nm provides higher local heating, which determined the choice of this wavelength for this study. Typical thicknesses of the simulated biotissue layers and their optical parameters at 633 nm are shown in Table 1 in accordance with Refs. [57,58,59].

Table 1.
Thicknesses and optical properties of tumor and healthy human skin tissue layers at wavelength of 633 nm [57,58,59].
2.2. Optical Characteristics of SiNPs Employed in the Simulations
In simulations, we considered the SiNPS obtained via the ablation of SiNW arrays by picosecond laser at wavelength of 1064 nm in water and ethanol (wSiNPs and eSiNPs, correspondingly) and reported in our earlier work [44]. According to previous studies of similar laser-ablated SiNPs, they may have a thin oxide shell [36,60] as well as a small fraction of amorphous phase [61]. Besides, eSiNPs undergo surface carbonization due to high power laser action to ethanol [36]. However, these effects may be excluded from the following consideration in our calculations due to their negligible contribution to SiNPs optical properties, and pure crystalline silicon particles are considered in the study.
Based on scanning electron microscopy data, a normalized size distribution function was obtained for wSiNPs (Figure 3a) and eSiNPs (Figure 3b) where index value i corresponds to the i-th size fraction with step of 4 nm, is the number of particles in a unit of volume (partial volume concentration) for i-th size fraction, and is the number of all SiNPs in the unit of volume (total volume concentration). In practice, the number of nanoparticles in the tumor is characterized by the mass concentration Cm (in mg/mL), given by the relation:
where is the silicon density () [62] and is the average volume of a single particle with the diameter corresponding to i-th size fraction. Therefore, the concentration ni of particles with diameter di can be expressed via the known size distribution function fi and mass concentration Cm as follows:
Assuming the spherical shapes and high crystallinity of both synthesized wSiNPs and eSiNPs, Mie theory [63] can be employed to calculate scattering cross-section σs,i, absorption cross-section σa,i (Figure 3c), and anisotropy factor gi for i-th size fraction of silicon nanocrystals.
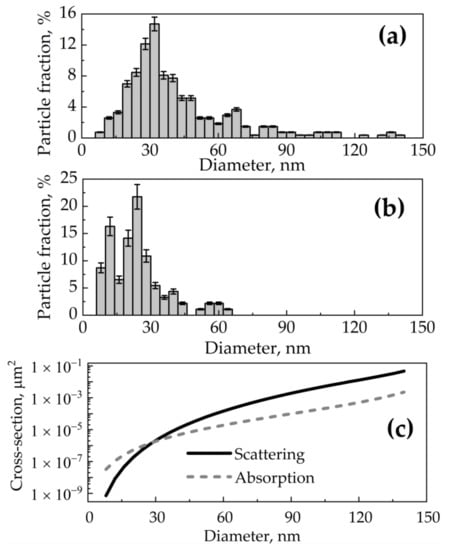
Figure 3.
(a,b) Size distributions fi for SiNPs obtained by ablation of SiNW arrays in water (a) and in ethanol (b) [44]; (c) dependencies of scattering and absorption cross-section of a spherical SiNP at wavelength of 633 nm on its diameter calculated by Mie theory.
Due to the small SiNP volume fraction, which does not exceed 0.003 for the maximal SiNP concentration, scattering () and absorption () coefficients of the tumor with the embedded SiNPs can be found by adding the scattering and absorption coefficient of all nanoparticles ( and , respectively) to scattering () and absorption () coefficients of the tumor without SiNPs, respectively [19]:
The relation between scattering anisotropy factor for the tumor with the SiNPs, scattering anisotropy factor of the tumor without SiNPs, and scattering anisotropy factor of i-th SiNP fraction is given by the expression [19]:
and the effective attenuation coefficient of diffusive light () for the tumor with the embedded SiNPs [64] is:
Given that the considered SiNP size exceeds 8 nm, whereas quantum-confinement effects in silicon resulting in variations of band gap and optical parameters could be detected for SiNP diameter below 5 nm [65], to calculate the SiNP optical parameters we used refractive index nNP = 3.8823 and extinction coefficient kNP = 0.0196 for crystalline silicon [66]. Relative variations of these values with temperature increase up to 10 °С for bulk silicon are 10−3 and 10−5, respectively [67,68]. Hence, the thermooptical effect on the SiNPs embedded into the tumor is expected to be negligible. Thermooptical effects in the biotissue are also extremely small. According to Ref. [69], the value of dμa/dT for biotissues does not exceed 0.02 cm−1 K−1. Considering the typical temperature increase in the treated biotissues and their absorption coefficients (see Table 1 and Table 2), the possible relative variation in absorption is estimated to not exceed 7% for tumor with embedded 1 mg/mL of eSiNPs and an order of magnitude smaller for tumor with 7 mg/mL wSiNPs. The refractive index for tumor tissue at the wavelength of 633 nm is assumed to be equal to ntum = 1.4 [57,70,71]. Optical properties of skin layers and tumor tissue are presented in Table 1. It is worth nothing that all optical parameters values were measured for a non-polarized light source [57].

Table 2.
Optical properties of nBCC in the presence of SiNPs with mass concentrations Сm = 1–7 mg/mL at wavelength of 633 nm.
We expect that the mass concentration of SiNPs required for hyperthermia should be rather high due to the comparatively low absorption of red light. This excludes any possibility of intravenous injection due to low accumulation efficiency [72,73]. Meanwhile, intratumoral injection allows up to 15% of all injected NPs to be concentrated inside the tumor, and NPs can be contained in a tumor in a concentration of up to 9 mg/mL [74]. To reveal the effect of SiNP concentration on the result of hyperthermia, the mass concentration of SiNPs employed in the simulations varied from 1 to 7 mg/mL within the tumor. We expect that during laser hyperthermia the tissue temperature does not significantly exceed 42 °C, and therefore SiNP agglomeration would not occur.
Optical parameters for a tumor containing SiNPs of various types and mass concentrations calculated using formulas (1)–(6) are presented in Table 2. In the calculations, it was assumed that after injection the SiNPs are contained only in the tumor area. The errors for μа, μs, and g of the tumor with SiNPs originate from the error of size distribution measurement that were estimated as 6.0% and 10.4% for wSiNPs and eSiNPs, respectively. This yields an estimated error of 2% in scattering and absorption characteristics evaluated by Mie formulas, which caused no relevant change in the obtained results.
According to Table 1 and Table 2, light absorption in nBCC without SiNPs is lower than that in healthy skin and human subcutaneous fat. The injection of SiNPs into the tumor at a concentration of 7 mg/mL increases the absorption coefficient of the tumor site 15 times for wSiNPs and 5.5 times for eSiNPs at the wavelength of 633 nm. However, an increase in scattering occurs upon SiNP injection, which yields a decrease of radiation penetration depth in biotissue. The effect of scattering increase is more pronounced for wSiNPs characterized by the maximum diameter of 140 nm compared to eSiNPs characterized by the maximum diameter of 80 nm.
2.3. Simulations of Light Absorption Distribution
The Monte Carlo method for light transport in tissues [75,76,77] was employed to calculate the absorption map, i.e., 3D spatial distribution of the power density absorbed by biological tissue upon its irradiation by a continuous-wave laser beam at the wavelength of 633 nm, as shown in Figure 2. Simulations were performed for N = 107 photons uniformly distributed within the circle of radius r at the biotissue surface. All photons enter the tissue normal to its surface. The computational grid for the absorption map consisted of 200 × 200 × 500 voxels (the voxel size was = 0.1 mm × 0.1 mm × 0.02 mm).
To study the effect of the irradiation area size on tumor heating efficiency, the calculations were performed for two laser beam sizes: r = 2.5 mm and r = 5 mm (Figure 2). In the first case, the laser beam size coincides with the width of the tumor, whereas in the latter case the laser beam covers a larger area, which may simulate hyperthermia on account of the safety margins.
At each step of Monte Carlo trajectory tracing, the absorbed part of the photon packet energy was added to the current value of the absorption map element B(x,y,z) corresponding to the coordinates (x,y,z) of the center of the voxel in which the current trajectory node was located. The resulting absorption map was normalized for the volume of the voxel and for the intensity of probing radiation expressed in photon weight per area unit to calculate the normalized volumetric density of absorbed energy:
To derive the discrete dimensional volumetric density of heat generation rate Qext (x,y,z) within the medium, the normalized volumetric density of absorbed energy should be multiplied by the beam intensity:
where P is the laser beam power.
The laser power P and the beam radius r were varied in the simulations in order to evaluate the range of optimal parameters to perform SiNPs mediated hyperthermia of nBCC. The range of the irradiation power was limited to ensure healthy biotissue is not heated to temperatures exceeding 42 °С to avoid damaging effects, such as tissue thermal destruction [78,79].
2.4. Calculation of Volumetric Temperature Distribution
At the next stage of simulations, the obtained discrete functions of heat sources were used to calculate temperature distribution within the biotissue during the laser treatment by means of solving a bioheat transfer equation. The standard way to obtain a temperature distribution within the tissues during a hyperthermia procedure is solving the bioheat transfer equation, which was initially proposed by Pennes in the following form [80,81]:
where is the biotissue temperature, is the biotissue density, Cp is the biotissue heat capacity at a constant pressure; k is the thermal conductivity, Qmet is the speed of metabolic heat generation the per unit volume, Qext is the external source power density, which in our case is a result of the laser radiation absorption, and Qperf is power density of the heat loss caused by perfusion (blood transfer through capillaries and extracellular spaces in tissue [82]). Despite great progress achieved during more than 70 years since its first proposal and various improvements and refinements of the equation (see, e.g., [83,84,85]), the Pennes equation is, nevertheless, applicable for the stationary case of continuous-wave irradiation of the biotissue [83]:
We solved Equation (10) using a finite-difference approach, taking the absorption map simulated by the Monte Carlo approach as the external source power density. In its stationary form, the Pennes Equation (9) does not depend on biotissue density and heat capacity:
Here, k is the thermal conductivity coefficient, Qmet = 420 W/cm3 is the volumetric rate of metabolic heat generation [86], and the last term of Equation (11) describes the perfusion heat loss power density, with ρbl = 1060 kg/m3, Cbl = 3770 J/(kg∙К) [87,88], Tbl = 37.2 °С [89,90], ωbl (Table 3) being the blood density, heat capacity, temperature, and perfusion coefficient (transfer of blood through capillaries and extracellular spaces [82]), respectively. The values of thermal conductivity coefficient k for different biotissues are presented in Table 3. Generally, the thermal parameters of nanoparticles can differ from those for bulk material due to the variation of the phonon spectrum and well-developed surface [91]. However, previously, we have shown that Raman spectra of the employed SiNPs coincide with the spectrum for crystalline silicon [34], while in the current study the volume fraction of the SiNPs does not exceed 0.003 and SiNP heating is expected to occur at several degrees. Based on this, we consider no variations of thermal parameters both for the SiNPs and for the tumor with embedded SiNPs.

Table 3.
Thermophysical properties of the biological media under interest [85,86].
In our preliminary studies, we demonstrated that a stationary temperature distribution is achieved in less than 400 s of cw irradiation [39]. It is worth noting that, according to the requirements of the hyperthermia procedure, the irradiation time in cw regime may take up to 60 min [92]. Thus, for therapeutic procedures longer than 400 s, employing a stationary bioheat transfer equation is reasonable.
Equation (11) was solved using COMSOL Multiphysics® software package using the finite element method [93,94,95]. The computational grid was tetrahedral with the minimum and maximum element sizes of 0.15 mm and 1 mm, respectively. Tetrahedral mesh allows accounting for the complicated shape of the ellipsoidal tumor boundaries when solving the equation. It also significantly reduces the calculation time by varying the grid voxel size depending on the typical scale of the simulated structure (larger voxels for subcutaneous fat and smaller voxels for skin and tumor) compared to the grid with rectangular voxels.
To translate previously calculated distributed heat sources to COMSOL Multiphysics® environment, we used linear interpolation of the discrete function Qext(x,y,z) on the tetrahedral grid nodes. Constant temperature of 37.0 °С was set at the rear boundary of the medium located within the biological tissue (z = 10 mm), while at the skin–air interface convection was taken into account [96]:
where convective heat transfer coefficient h = 18 W/(m2∙K) and air temperature Tair = 25.0 °С. Temperature distribution at the lateral boundaries Tsides(z) was evaluated from the solution of the 1D stationary bioheat transfer equation in the infinitely wide medium containing no tumor and in the absence of heat sources in biotissue:
Boundary conditions for Equation (11) were = 37.0 °C at the lower boundary (z = 10 mm) and the convection condition at the skin–air interface (z = 0 mm):
The values of bioheat transfer equation coefficients employed in the simulation are presented in Table 3. It is worth noting that blood perfusion in a tumor is greater than that in healthy tissue owing to a more developed network of small blood vessels [97,98].
As a result of the performed modeling, thermal fields in tissues containing nBCC tumor without and with embedded SiNPs were calculated. We aim to determine the conditions (nanoparticles concentration and the irradiation parameters) at which the employment of SiNPs allows to heat the tumor over 42 °C completely with the area of overheated healthy tissue being insignificant, which cannot be achieved in the absence of SiNPs in the treated tissue.
3. Results and Discussion
3.1. The Effect of eSiNPs and wSiNPs on Radiation Absorption Efficiency
Figure 4 shows the in-depth profiles of normalized volumetric density of absorbed energy at the beam axis q(x = 0,y = 0,z) in the biotissue with and without different types of SiNPs. The profile for the case without SiNPs shows that the maximum in the absorbed energy is located in the superficial tissue layer above the tumor. This is caused by a lower absorption coefficient of the tumor compared to that of the remaining biotissue together with the in-depth attenuation of the irradiation intensity. The embedding of SiNPs into the tumor leads to a shift of the absorption profile maximum to the tumor region. On the other hand, all profiles corresponding to presence of SiNPs demonstrate lower energy absorption in normal tissue layers underlying the tumor. Since wSiNPs are characterized by a higher absorption coefficient as compared to eSiNPs for the same mass concentration, for them the absorption maximum is located in the upper layer of the tumor, and they shield the penetration of the radiation into deeper tumor regions. For the eSiNPs, the maximum is shifted to the tumor center, and the density of absorbed energy in deeper tumor regions (z ≥ 1 mm) is higher than that for wSiNPs due to weaker shielding. Note that with the increase of the SiNPs concentration the maximum shifts towards tissue surface due to the higher extinction of radiation coming from the top of the tissue. Note that embedding SiNPs into the tumor reduces light absorption in epidermis, since the light is partially absorbed by SiNPs in the tumor, which results in a decrease of backscattering from this area.
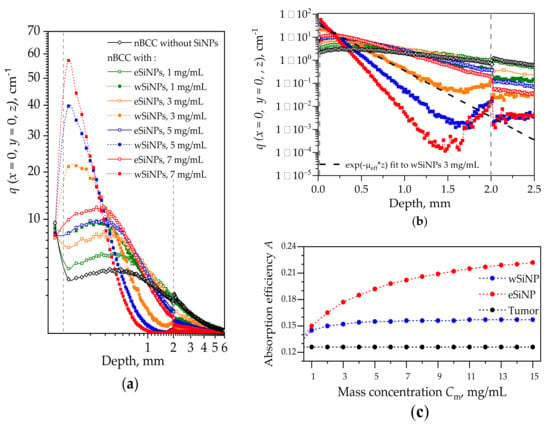
Figure 4.
(a) Distributions of normalized volumetric density of absorbed energy q(x = 0, y = 0, z) along the laser beam axis z for different types of SiNPs and their different concentrations for the beam of radius r = 5 mm. Dashed vertical lines depict the tumor edges. (b) Distribution of q(x = 0, y = 0, z) in the tumor with the exponential fit to the curve for wSiNP at mass concentration of 3 mg/mL. The fitting is shown with a dashed black line. Plots designations are the same for (a) and (b) fragments. (c) Dependence of the absorption efficiency parameter A on the concentration for wSiNPs and eSiNPs in the tumor.
Assessing the dependence of function q(x = 0, y = 0, z) on the scattering and absorption parameters of the medium may assist in designing SiNPs with the optimal optical properties to ensure sufficient absorption over the whole tumor region. Note that the in-depth decay rate of q(x = 0, y = 0, z) within the tumor up to the depths of z = 1.5 mm is strongly related to the value of the effective attenuation coefficient µeff (see Table 2). Moreover, the dependencies q(x = 0, y = 0, z) for eSiNPs with the mass concentration Cm = 5 mg/mL and for wSiNPs with the mass concentration Cm = 1 mg/mL are characterized by quite similar behavior, while the values of µeff are very close for these two cases.
We found out that the function qfit(z) ∝ exp(−µeff z), which describes attenuation of light in diffusive regime [75], provides a good fit to the simulated dependencies q(x = 0, y = 0, z) within the tumor region (Figure 4b). The exponential fit is shown for one curve in Figure 4b using the corresponding value of µeff taken from Table 2. Note that the slope of the function q(x = 0, y = 0, z) increases with the concentration of SiNPs as well as its amplitude defined by the absorption coefficient µa. Therefore, the effect of the concentration increase on the absorption efficiency is not obvious at first sight: the higher the concentration, the more pronounced are both the absorption and the signal drop. Assuming both the amplitude and the longitudinal scale of the function q(x = 0, y = 0, z), we propose the parameter A for the estimation of the light absorption efficiency within the whole tumor node with the embedded SiNPs that is defined as the product of the absorption coefficient in the tumor over the thickness of the “skin layer” of radiation penetration into the tumor:
The dependencies of the absorption efficiency A on the concentration for the two types of SiNPs are presented in Figure 4c. One can see that in the given range of mass concentrations Cm, the absorption efficiency almost does not depend on Cm for wSiNPs, while for eSiNPs the increase in concentration provides a noticeable rise of the parameter A. However, at very large eSiNPs concentrations (Cm > 10 mg/mL) the growth of A(Cm) slows down and obviously tends to saturate. In general, the increase in absorption efficiency obtained by embedding wSiNPs does not exceed 25% at their highest concentration compared to that for the tumor solely, and it is about 40% and 60% for eSiNPs at concentrations of 3 mg/mL and 7 mg/mL, respectively.
The cross-sections q(x, y = 0, z) of the normalized volumetric density of absorbed energy for a beam radius of 5 mm in the absence of SiNPs in nBCC and with SiNPs at concentrations of 3 and 7 mg/mL are shown in Figure 5. As already demonstrated in Figure 4, radiation absorption in nBCC without SiNPs is significantly lower than that of surrounding healthy tissue, which in particular results in discontinuity at the rear border of the tumor (Figure 4a,b). Embedding nanoparticles in the nBCC node significantly enhances absorption efficiency in it, resulting in a higher density of absorbed energy as compared to healthy tissue in superficial tumor region (Figure 5b,e). The presence of wSiNPs in nBCC at a concentration of 7 mg/mL increases the absorption efficiency on the upper tumor boundary for up to 20 times. However, the shielding effect originating from both enhanced absorption and scattering leads to primary energy absorption in the upper layer of the tumor (solid squares in Figure 4а,b and Figure 5c,e). For the eSiNPs at concentration of 7 mg/mL, the maximal increase is about four times (open squares in Figure 4а,b). However, the shielding effect is significantly weaker, resulting in a more uniform in-depth distribution of additional absorption in the tumor, thus confirming higher potential of these particles for hyperthermia.
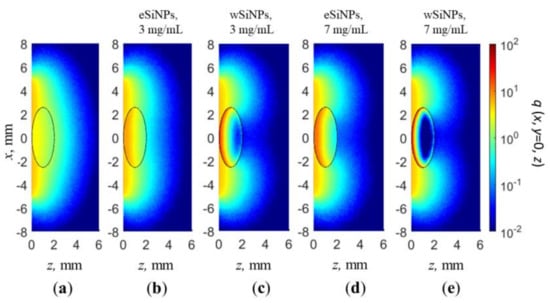
Figure 5.
Cross-section x, y = 0 of normalized volumetric density of absorbed energy q(x,y,z) for beam radius of 5 mm: (a) in absence of SiNPs in nBCC; (b,c) BCC with eSiNPs (b) and wSiNPs (c) at concentration of 3 mg/mL; (d,e) BCC with eSiNPs (d) and wSiNPs (e) at concentration of 7 mg/mL.
An increase in the absorbed energy close to the rear tumor boundary in the tumor (nearby z = 2 mm) with the embedded wSiNPs (Figure 4b and Figure 5c,e), manifested by the deviation from exponential decay for z > 1.5 mm, is caused by the inflow of backscattered diffusive light from the surrounding normal tissues where the fluence level is considerably higher with respect to the tumor due to smaller absorption and scattering. Such an effect is hardly noticed with eSiNPs because of smaller differences in the absorption and scattering coefficients between the tumor with embedded nanoparticles and the surrounding tissues (Figure 5b,d).
3.2. The Effect of eSiNPs and wSiNPs on Tumor Heating
The obtained absorption map values were used to calculate Qext, the volumetric heating rate from inner heat sources, in the bioheat transfer equation. For therapeutic applications, it is important to initiate tissue thermal destruction as a result of irradiation only in the tumor, not in surrounding normal tissues. In this context, the laser power P was varied to obtain temperatures above the threshold of T42 = 42 °C in the entire tumor volume while trying to minimize the temperature increase in surrounding healthy tissue above T42. Such a situation is referred to as optimal heating. The analysis of the choice of P ensuring tumor hyperthermia with minimal overheated normal tissue volume was performed for two beam sizes: one corresponding to the transversal tumor size and one exceeding it for two times aiming to ensure sufficient heating of the tumor boundary region.
3.2.1. Beam Size Equals the Tumor Transversal Size
Figure 6 shows axial and transversal profiles of the temperature distribution for r = 2.5 mm and power 110 mW (corresponding intensity I = 560 mW/cm2 [50]) in biotissue with and without SiNPs. This combination of r and I parameters ensures heating of the entire tumor volume to temperatures above T42 in the presence of eSiNPs at concentrations higher than 5 mg/mL, although it is worth mentioning that, besides quite a high value of intensity itself, it requires longer than 400 s to reach the stationary heating mode considered in simulations [5,39].
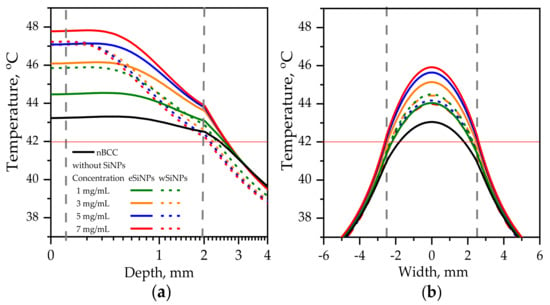
Figure 6.
Temperature distribution in biotissue with SiNPs embedded in the tumor at the indicated mass concentrations upon irradiation by laser beam with radius of 2.5 mm and power of 110 mW: (a) in-depth temperature dependence at the beam axis T(x = 0, y = 0, z); (b) transversal temperature dependencies at the depth z = 1 mm corresponding to the tumor center. Red horizontal line indicates the hyperthermia threshold temperature; grey vertical lines show the tumor edges.
For the tumor without SiNPs, the employed beam intensity allows reaching T42 at the beam axis through the whole tumor length (Figure 6a). However, the side regions of the tumor are left underheated, which can be seen from the transversal temperature profiles at depth z = 1 mm (Figure 6b, black solid line). The profiles have the bell shape owing to high tumor thermal conductivity, which smooths the temperature distribution despite the size of the beam exactly fitting the tumor width, and the intensity distribution is uniform.
Embedding eSiNPs in nBCC provides additional temperature increase up to 4.6 °C at the laser beam axis for a maximum mass concentration of 7 mg/mL (Figure 6a, solid red line) and broadens the transversal and longitudinal sizes of the region heated above T42, thus providing sufficient heating of the entire tumor for all considered concentrations (Figure 6b). The application of wSiNPs results in less efficient additional heating of the tumor: though the whole volume is heated over T42, the maximal temperature is reached only within a few hundred microns at the tumor top, and the back half of the tumor is sufficiently less heated compared to the front part. Note that the maximal temperature value obtained with the largest concentration of wSiNPs (7 mg/mL) is almost the same as for the eSiNPs at a concentration of 5 mg/mL. These results can be explained by the increase of absorption efficiency of eSiNPs with their concentration while the increase of Cm has almost no effect on the absorption efficiency in the presence of wSiNPs (Figure 4c).
It is worth noting that it is impossible to avoid overheating of surrounding normal tissues. However, it primarily occurs in the superficial layer above the tissue. Despite the decrease in absorption in this region owing to the presence of SiNPs in the tumor (see Figure 4a), a thermal flow from the tumor region results in its overheating (Figure 6). Nevertheless, the overheating of the normal tissues underlying the tumor does not exceed 2 degrees and quickly decays in-depth, while in the transversal direction the overheating of normal tissue is negligible (Figure 6b).
3.2.2. Beam Size Exceeds the Tumor Transversal Size
The previous considered case for r = 2.5 mm demonstrated the potential of employing SiNPs for the enhancement of laser hyperthermia. However, the required intensity of 560 mW/cm2 seems to be extremely high from the point of view of the safety requirements which demands intensities of about 200 mW/cm2 or less [50]. Obviously, the increase in beam radius allows to deliver the same energy to the tissue with lower intensity. Figure 7 depicts the temperature profiles for beam with radius of 5 mm and laser power of 165 mW. The corresponding intensity is 210 mW/cm2, which is significantly lower than the maximum permissible radiation intensity in the order of 500 mW/cm2 for only heating effects to occur.
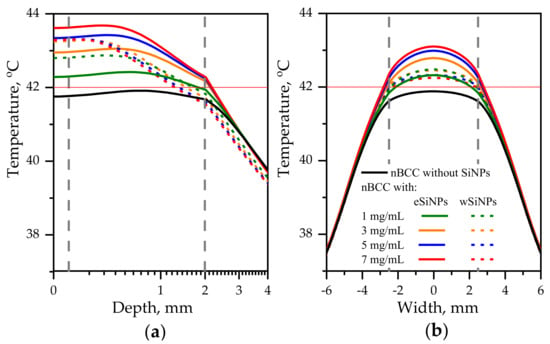
Figure 7.
Temperature distribution in biotissue with SiNPs embedded in the tumor at the indicated mass concentrations upon irradiation by laser beam with radius of 5 mm and power of 165 mW: (a) in-depth temperature dependence at the beam axis T(x = 0, y = 0, z); (b) transversal temperature dependencies at the depth z = 1 mm corresponding to the tumor center. Red horizontal line indicates the hyperthermia threshold temperature; grey vertical lines show the tumor edges.
In this case, the maximal additional temperature increase due to embedding SiNPs is 1.9 °C achieved when adding eSiNPs at concentration of 7 mg/mL. Figure 7a shows that the presence of SiNPs in tumor volume allows to reach temperatures higher than T42 in the entire tumor volume given that without SiNPs this threshold temperature is not reached. However, it can be expected that due to the complex structure of biotissue the temperatures in real tissue may vary, and the obtained increase is not so significant as compared to the value of 4.5 °C obtained in the case of a narrow beam. A comparison with Figure 6 shows that employing the beam with the diameter exceeding the tumor width allows to arrange more uniform transversal temperature distribution in the tumor region.
Figure 8 shows the dependency of temperature in the center of the tumor (x = 0, y = 0, z = 1 mm) and in healthy tissue at the same depth neighboring the tumor (x = 0, y = 3 mm, z = 1 mm) for both considered beam sizes on laser beam power. A smaller beam size allows to reach a more pronounced temperature contrast between tumor tissue and healthy tissue of up to 5 °C compared to 1.5 °C for the larger beam at comparable beam power. We stress that in the case of anti-tumor treatment the ANSI requirements for maximum permissible intensity (200 mW/cm2) [50] can be violated in the tumor region provided that the surrounding healthy tissues are not over-exposed.
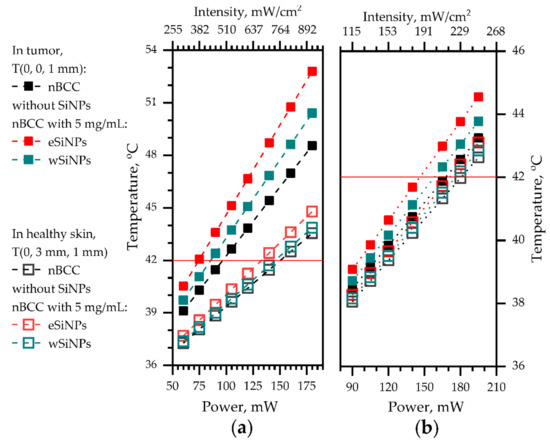
Figure 8.
The dependencies of temperature at (x = 0, y = 0, z = 1 mm), at the center of tumor (filled markers) and at (x = 0, y = 3 mm, z = 1 mm), in healthy skin neighboring the tumor at the same depth (hollow markers) on the laser power: (a) beam radius 2.5 mm; (b) beam radius 5 mm. Red horizontal line depicts the hyperthermia threshold temperature.
Therefore, higher mismatch between temperatures in tumor and normal tissue in the case of smaller beams provides wider opportunities for choosing a beam power for fulfilling optimal heating conditions. Note that the smaller temperature mismatch in the wide beam case is conditioned by the choice of the location in healthy skin within the area of direct laser irradiation by the 5-mm radius beam, while in the case of a narrow beam the temperature increase in healthy skin is caused by thermal conductivity.
3.2.3. Comparison of Flat Beam and Gaussian Beam Irradiation
The Gaussian beam is a widely used alternative to a flat intensity distribution in tissue irradiation configuration. The inhomogeneity of intensity distribution is considered as a drawback in laser hyperthermia due to possible hot spots in the target area [92]. A comparison of these two irradiation regimes evidences the longer time necessary for cancer cell necrosis in the latter case [99]. Nevertheless, Gaussian laser beams are often employed for cancer theranostics (e.g., [100]). To compare effects for both cases, we carried out simulations for the Gaussian laser beam with the same parameters as were employed for the flat beam.
In these simulations, the laser beam axis coincides with the axis of the tumor. Incident laser radiation power depends on x аnd y coordinates as:
where r is the beam radius at 1/e level and is the total laser power. In Monte Carlo simulations, to obtain Gaussian beam intensity distribution, the Box–Muller transform [101] was employed. The obtained cross-sections q(x, y = 0, z) of the normalized volumetric density of absorbed energy is presented in Figure 9.
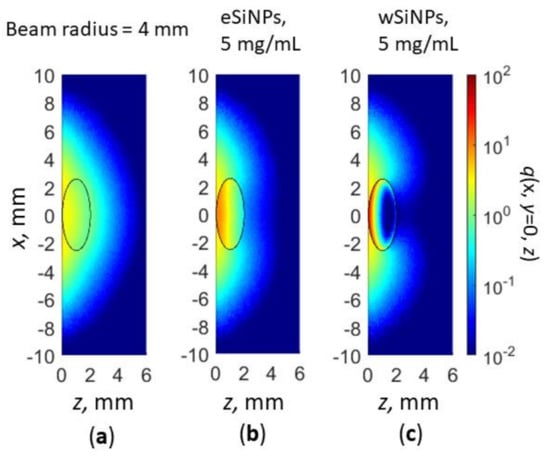
Figure 9.
Cross-section x,y = 0 of normalized volumetric density of absorbed energy q(x,y,z) for Gaussian beam radius of 4 mm: in absence of SiNPs in nBCC (a); BCC with eSiNPs (b) and wSiNPs (c) at SINP mass concentration of 5 mg/mL.
As one can see, qualitatively, the absorption distribution for the Gaussian beam does not differ significantly (cf. Figure 5a,d,e and Figure 9a–c) from the one for the flat beam, except for the region outside the tumor. Embedding in tumor eSiNPs with smaller absorption results in heating the entire tumor, whereas in the case of wSiNP the rear tumor part is underheated. Detailed calculations of the temperature distribution inside the tissue (Figure 10) evidence that at equal power the Gaussian laser beam enables heating up to lower temperature than the flat one: the tumor is not completely heated up to 42 °C at P0 = 110 mW and r = 2.5 mm (precisely of the tumor diameter) (cf. Figure 6 and Figure 10a,b) and precisely up to 42 °C at P0 = 165 mW and r = 4 mm (cf. Figure 7 and Figure 10c,d, note that the beam radius for uniform circular beam is larger than that for the Gaussian beam, which indicates even less tumor heating efficiency in the latter case). The reasons for this effect are obvious: (i) more than 37% of the laser radiation is absorbed outside the tumor if the beam radius exceeds the tumor radius, and (ii) due to a strongly non-uniform heat rate the heat flux is more prominent than in the case of a uniform intensity distribution. Thus, the simulation of the hyperthermia by Gaussian beam evidences that the circular flat laser beam has certain advantages over the Gaussian one.
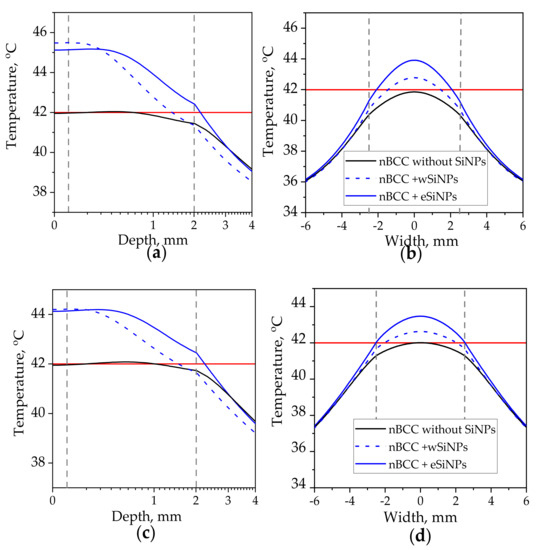
Figure 10.
Temperature distribution in biotissue with SiNPs embedded in the tumor at the mass concentrations of 5 mg/mL upon irradiation by Gaussian laser beam with radius of 2.5 mm and power of 110 mW (a,b), radius of 4 mm and power of 165 mW: (a,c) axial temperature profile at the beam axis T(x = 0, y = 0, z); (b,d) transversal temperature profile at the depth z = 1 mm corresponding to the tumor center. Red horizontal line indicates the hyperthermia threshold temperature of 42 °C; dashed vertical lines show the tumor edges.
Since no experimental results are available to assess the validity of the calculations performed, we analysed similar simulation studies. Refs. [37,38,43] report on the numerical simulation of heating water suspensions of SiNPs. However, such studies do not account for the effect of surrounding biotissues both in light transport and heat transfer aspects.
Recently, various inorganic metallic compounds were tested for their effectiveness as thermal coupling agents. In [102], CuFeSe2 nanosheets with a mean hydrodynamic diameter of 200 nm were experimentally shown to be able to heat water to 30 °C within 600 s. In [103], palladium hydride nanoparticles suspended in water gained additional heating at 10 °C during 180 s at NIR laser power of 154 mW. However, they require a sophisticated fabrication technique, while the pulsed laser ablation of silicon nanostructures in liquids seems to be a promising, scalable technology. As for inert material studies, gold nanoparticles irradiated with NIR light permit selective tumor hyperthermia at 42−43 °C without side effects to surrounding healthy tissues due to the spatial and temporal control of heat generation (selective accumulation and irradiation of heat nanosources) [104]. Nevertheless, silicon demonstrates more prominent biodegradation compared to gold, since silicon presents in living organisms as a natural trace compound.
4. Conclusions
This paper reports on the results of numerical simulations of human skin tumor hyperthermia mediated by the targeted delivery of SiNPs. Two types of SiNPs formed by the laser ablation of silicon nanowire arrays in water (wSiNPs) and ethanol (eSiNPs) are considered as potential enhancement agents. The simulations were performed for two radii of irradiation beam (one fitting the tumor size and second exceeding it) in order to reveal the optimal conditions of heating the tumor above the threshold temperature while minimizing excessive heating of surrounding normal tissues. A parameter for the evaluation of volume absorption efficiency depending on the optical properties of biotissue and SiNPs was proposed as a measure of NPs efficiency for hyperthermia performance, and the influence of SiNPs concentration on the light absorbance by the tumor was analyzed for both wSiNPs and eSiNPs. The effect of shielding deeper tumor regions from radiation by embedded SiNPs with high absorption coefficient was demonstrated, indicating the requirement for a careful selection of SiNPs concentration in tumor. It was demonstrated that irradiation by the beam with a smaller radius allows to obtain a higher temperature contrast between the tumor and surrounding normal tissues (about 5 °C) than in case of a larger beam radius (1.5 °C) for the comparable beam power at which healthy tissue neighboring the tumor remains underheated, while eSiNPs provide a higher additional heating effect as compared to wSiNPs for the same concentration of nanoparticles in the tumor.
As a result, the laser-ablated SiNPs seem to be promising for the enhancement of photohyperthermia. In comparison to gold nanoparticles, widely discussed as hyperthermia agents, the SiNPs are less expensive in terms of raw material and are shown to be biodegradable. However, laser ablation technology remains relatively expensive for use in mass production. This problem may be solved by using silicon targets with a reduced ablation threshold, e.g., the SiNWs discussed in this article, as well as by the optimization of laser source parameters. In the latter case, relatively cheap, high-power nanosecond lasers have high potential to produce a high yield of SiNPs with desirable sizes and properties, which can be considered as an alternative for the more expensive femto- and picosecond lasers that are currently widely used. Additionally, it will be necessary to carry out experiments with real biological tissues by the photohyperthermia technique to confirm our calculations.
Author Contributions
Conceptualization, E.A.S., L.A.G. and M.Y.K.; methodology, L.A.G. and M.Y.K.; software, O.I.S.; validation, E.A.S.; formal analysis, E.A.S., L.A.G. and M.Y.K.; investigation, O.I.S., A.V.K., D.A.K., N.Y.O. and S.V.Z.; resources, P.K.K.; data curation, O.I.S., A.V.K., D.A.K., N.Y.O. and S.V.Z.; writing—original draft preparation, O.I.S.; writing—review and editing, E.A.S., L.A.G., S.V.Z. and M.Y.K.; visualization, O.I.S.; supervision, P.K.K.; project administration, L.A.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 19-12-00192.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this research is available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, J.H.; Hahn, E.W. Clinical and Biological Studies of Localized Hyperthermia. Cancer Res. 1979, 39, 2258–2261. [Google Scholar]
- Song, C.W.; Kang, M.S.; Rhee, J.G.; Levitt, S.H. Vascular Damage and Delayed Cell Death in Tumours after Hyperthermia. Br. J. Cancer 1980, 41, 309–312. [Google Scholar] [CrossRef]
- Szasz, A.; Szasz, N.; Szasz, O. Hyperthermia Results and Challenges. In Oncothermia: Principles and Practices; Springer: Dordrecht, The Netherlands, 2010; pp. 17–88. ISBN 978-90-481-9497-1. [Google Scholar]
- Chatterjee, D.K.; Diagaradjane, P.; Krishnan, S. Nanoparticle-Mediated Hyperthermia in Cancer Therapy. Ther. Deliv. 2011, 2, 1001–1014. [Google Scholar] [CrossRef]
- Tuchin, V.V. Volume 1: Light-Tissue Interaction. In Handbook of Optical Biomedical Diagnostics, 2nd ed.; SPIE: Bellingham, WA, USA, 2016. [Google Scholar]
- Ntziachristos, V.; Ripoll, J.; Wang, L.V.; Weissleder, R. Looking and Listening to Light: The Evolution of Whole-Body Photonic Imaging. Nat. Biotechnol. 2005, 23, 313–320. [Google Scholar] [CrossRef]
- Hu, Q.; Huang, Z.; Duan, Y.; Fu, Z.; Liu, B. Reprogramming Tumor Microenvironment with Photothermal Therapy. Bioconjugate Chem. 2020, 31, 1268–1278. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Lovell, J.F.; Yoon, J.; Chen, X. Clinical Development and Potential of Photothermal and Photodynamic Therapies for Cancer. Nat. Rev. Clin. Oncol. 2020, 17, 657–674. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.; Jin, J.-O. Attachable Hydrogel Containing Indocyanine Green for Selective Photothermal Therapy against Melanoma. Biomolecules 2020, 10, 1124. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.P.; Alvi, S.B.; Pemmaraju, D.B.; Singh, A.D.; Manda, S.V.; Srivastava, R.; Rengan, A.K. NIR Triggered Liposome Gold Nanoparticles Entrapping Curcumin as in Situ Adjuvant for Photothermal Treatment of Skin Cancer. Int. J. Biol. Macromol. 2018, 110, 375–382. [Google Scholar] [CrossRef] [PubMed]
- Nomura, S.; Morimoto, Y.; Tsujimoto, H.; Arake, M.; Harada, M.; Saitoh, D.; Hara, I.; Ozeki, E.; Satoh, A.; Takayama, E.; et al. Highly Reliable, Targeted Photothermal Cancer Therapy Combined with Thermal Dosimetry Using a Near-Infrared Absorbent. Sci. Rep. 2020, 10, 9765. [Google Scholar] [CrossRef]
- Vervald, A.M.; Burikov, S.A.; Scherbakov, A.M.; Kudryavtsev, O.S.; Kalyagina, N.A.; Vlasov, I.I.; Ekimov, E.A.; Dolenko, T.A. Boron-Doped Nanodiamonds as Anticancer Agents: En Route to Hyperthermia/Thermoablation Therapy. ACS Biomater. Sci. Eng. 2020, 6, 4446–4453. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, N.; Rodrigues, C.F.; Moreira, A.F.; Correia, I.J. Overview of the Application of Inorganic Nanomaterials in Cancer Photothermal Therapy. Biomater. Sci. 2020, 8, 2990–3020. [Google Scholar] [CrossRef]
- Hu, J.-J.; Cheng, Y.-J.; Zhang, X.-Z. Recent Advances in Nanomaterials for Enhanced Photothermal Therapy of Tumors. Nanoscale 2018, 10, 22657–22672. [Google Scholar] [CrossRef]
- Yao, C.; Zhang, L.; Wang, J.; He, Y.; Xin, J.; Wang, S.; Xu, H.; Zhang, Z. Gold Nanoparticle Mediated Phototherapy for Cancer. J. Nanomater. 2016, 2016, 5497136. [Google Scholar] [CrossRef]
- Maksimova, I.L.; Akchurin, G.G.; Khlebtsov, B.N.; Terentyuk, G.S.; Akchurin, G.G.; Ermolaev, I.A.; Skaptsov, A.A.; Soboleva, E.P.; Khlebtsov, N.G.; Tuchin, V.V. Near-Infrared Laser Photothermal Therapy of Cancer by Using Gold Nanoparticles: Computer Simulations and Experiment. Med. Laser Appl. 2007, 22, 199–206. [Google Scholar] [CrossRef]
- Jeynes, J.C.G.; Wordingham, F.; Moran, L.J.; Curnow, A.; Harries, T.J. Monte Carlo Simulations of Heat Deposition During Photothermal Skin Cancer Therapy Using Nanoparticles. Biomolecules 2019, 9, 343. [Google Scholar] [CrossRef]
- Dimitriou, N.M.; Pavlopoulou, A.; Tremi, I.; Kouloulias, V.; Tsigaridas, G.; Georgakilas, A.G. Prediction of Gold Nanoparticle and Microwave-Induced Hyperthermia Effects on Tumor Control via a Simulation Approach. Nanomaterials 2019, 9, 167. [Google Scholar] [CrossRef] [PubMed]
- Kirillin, M.; Shirmanova, M.; Sirotkina, M.; Bugrova, M.; Khlebtsov, B.; Zagaynova, E. Contrasting Properties of Gold Nanoshells and Titanium Dioxide Nanoparticles for Optical Coherence Tomography Imaging of Skin: Monte Carlo Simulations and In Vivo Study. J. Biomed. Opt. 2009, 14, 021017. [Google Scholar] [CrossRef] [PubMed]
- Zagainova, E.V.; Sirotkina, M.A.; Shirmanova, M.V.; Elagin, V.V.; Kirillin, M.; Agrba, P.; Kamensky, V.A.; Nadtochenko, V.A. Plasmon Resonance Gold Nanoparticles for Improving Optical Diagnostics and Photothermal Therapy of Tumor. In Proceedings of the Plasmonics in Biology and Medicine VII, San Francisco, CA, USA, 23–28 January 2010; Vo-Dinh, T., Lakowicz, J.R., Eds.; SPIE: Bellingham, WA, USA, 2010; p. 75770. [Google Scholar] [CrossRef]
- Zagaynova, E.V.; Shirmanova, M.V.; Kirillin, M.Y.; Khlebtsov, B.N.; Orlova, A.G.; Balalaeva, I.V.; Sirotkina, M.A.; Bugrova, M.L.; Agrba, P.D.; Kamensky, V.A. Contrasting Properties of Gold Nanoparticles for Optical Coherence Tomography: Phantom, in Vivo studies and Monte Carlo Simulation. Phys. Med. Biol. 2008, 53, 4995–5009. [Google Scholar] [CrossRef]
- Singh, P.; Pandit, S.; Mokkapati, V.R.S.S.; Garg, A.; Ravikumar, V.; Mijakovic, I. Gold Nanoparticles in Diagnostics and Therapeutics for Human Cancer. Int. J. Mol. Sci. 2018, 19, 1979. [Google Scholar] [CrossRef]
- Sani, A.; Cao, C.; Cui, D. Toxicity of Gold Nanoparticles (AuNPs): A Review. Biochem. Biophys. Rep. 2021, 26, 100991. [Google Scholar] [CrossRef]
- Liu, J.; Peng, Q. Protein-Gold Nanoparticle Interactions and Their Possible Impact on Biomedical Applications. Acta Biomater. 2017, 55, 13–27. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Cao, Z.; Panwar, N.; Hu, R.; Wang, X.; Qu, J.; Tjin, S.C.; Xu, G.; Yong, K.-T. Functionalized Gold Nanorods for Nanomedicine: Past, Present and Future. Coord. Chem. Rev. 2017, 352, 15–66. [Google Scholar] [CrossRef]
- Liu, A.; Wang, G.; Wang, F.; Zhang, Y. Gold Nanostructures with Near-Infrared Plasmonic Resonance: Synthesis and Surface Functionalization. Coord. Chem. Rev. 2017, 336, 28–42. [Google Scholar] [CrossRef]
- Simakin, A.V.; Baimler, I.V.; Smirnova, V.V.; Uvarov, O.V.; Kozlov, V.A.; Gudkov, S.V. Evolution of the Size Distribution of Gold Nanoparticles under Laser Irradiation. Phys. Wave Phenom. 2021, 29, 102–107. [Google Scholar] [CrossRef]
- Simakin, A.V.; Astashev, M.E.; Baimler, I.V.; Uvarov, O.V.; Voronov, V.V.; Vedunova, M.V.; Sevost’yanov, M.A.; Belosludtsev, K.N.; Gudkov, S.V. The Effect of Gold Nanoparticle Concentration and Laser Fluence on the Laser-Induced Water Decomposition. J. Phys. Chem. B 2019, 123, 1869–1880. [Google Scholar] [CrossRef] [PubMed]
- Al-Kattan, A.; Nirwan, V.; Popov, A.; Ryabchikov, Y.; Strelkov, G.; Sentis, M.; Fahmi, A.; Kabashin, A. Recent Advances in Laser-Ablative Synthesis of Bare Au and Si Nanoparticles and Assessment of Their Prospects for Tissue Engineering Applications. Int. J. Mol. Sci. 2018, 19, 1563. [Google Scholar] [CrossRef] [PubMed]
- Braguer, D.; Correard, F.; Maximova, K.; Villard, C.; Roy, M.; Al-Kattan, A.; Sentis, M.; Gingras, M.; Kabashin, A.; Esteve, M.-A. Gold Nanoparticles Prepared by Laser Ablation in Aqueous Biocompatible Solutions: Assessment of Safety and Biological Identity for Nanomedicine Applications. Int. J. Nanomed. 2014, 9, 5415. [Google Scholar] [CrossRef] [PubMed]
- Canham, L. Handbook of Porous Silicon; Springer: New York, NY, USA, 2014; ISBN 978-3-319-05743-9. [Google Scholar]
- Ksenofontova, O.I.; Vasin, A.V.; Egorov, V.V.; Bobyl’, A.V.; Soldatenkov, F.Y.; Terukov, E.I.; Ulin, V.P.; Ulin, N.V.; Kiselev, O.I. Porous Silicon and Its Applications in Biology and Medicine. Tech. Phys. 2014, 59, 66–77. [Google Scholar] [CrossRef]
- Osminkina, L.A.; Tamarov, K.P.; Sviridov, A.P.; Galkin, R.A.; Gongalsky, M.B.; Solovyev, V.V.; Kudryavtsev, A.A.; Timoshenko, V.Y. Photoluminescent Biocompatible Silicon Nanoparticles for Cancer Theranostic Applications. J. Biophotonics 2012, 5, 529–535. [Google Scholar] [CrossRef]
- Zabotnov, S.V.; Skobelkina, A.V.; Kashaev, F.V.; Kolchin, A.V.; Popov, V.V.; Presnov, D.E.; Sergeeva, E.A.; Kirillin, M.Y.; Golovan, L.A. Pulsed Laser Ablation of Silicon Nanowires in Water and Ethanol. SSP 2020, 312, 200–205. [Google Scholar] [CrossRef]
- Skobelkina, A.V.; Kashaev, F.V.; Kolchin, A.V.; Shuleiko, D.V.; Kaminskaya, T.P.; Presnov, D.E.; Golovan, L.V.; Kashkarov, P.K. Silicon Nanoparticles Formed via Pulsed Laser Ablation of Porous Silicon in Liquids. Tech. Phys. Lett. 2020, 46, 687–690. [Google Scholar] [CrossRef]
- Kuzmin, P.G.; Shafeev, G.A.; Bukin, V.V.; Garnov, S.V.; Farcau, C.; Carles, R.; Warot-Fontrose, B.; Guieu, V.; Viau, G. Silicon Nanoparticles Produced by Femtosecond Laser Ablation in Ethanol: Size Control, Structural Characterization, and Optical Properties. J. Phys. Chem. C 2010, 114, 15266–15273. [Google Scholar] [CrossRef]
- Lee, C.; Kim, H.; Hong, C.; Kim, M.; Hong, S.S.; Lee, D.H.; Lee, W.I. Porous Silicon as an Agent for Cancer Thermotherapy Based on Near-Infrared Light Irradiation. J. Mater. Chem. 2008, 18, 4790. [Google Scholar] [CrossRef]
- Hong, C.; Lee, J.; Zheng, H.; Hong, S.-S.; Lee, C. Porous Silicon Nanoparticles for Cancer Photothermotherapy. Nanoscale Res. Lett. 2011, 6, 321. [Google Scholar] [CrossRef] [PubMed]
- Sokolovskaya, O.I.; Zabotnov, S.V.; Golovan, L.A.; Kashkarov, P.K.; Kurakina, D.A.; Sergeeva, E.A.; Kirillin, M.Y. Prospects for Using Silicon Nanoparticles Fabricated by Laser Ablation in Hyperthermia of Tumours. Quantum Electron. 2021, 51, 64–72. [Google Scholar] [CrossRef]
- Martínez-Carmona, M.; Vallet-Regí, M. Advances in Laser Ablation Synthesized Silicon-Based Nanomaterials for the Prevention of Bacterial Infection. Nanomaterials 2020, 10, 1443. [Google Scholar] [CrossRef]
- Serrano-Ruz, J.A.; Quiñones-Galván, J.G.; Santos-Cruz, J.; de Moure-Flores, F.; Campos-González, E.; Chavez Chavez, A.; Gómez-Rosas, G. Synthesis of Silicon Nanoparticles by Laser Ablation at Low Fluences in Water and Ethanol. Mater. Res. Express 2020. [Google Scholar] [CrossRef]
- Al-Kattan, A.; Ryabchikov, Y.V.; Baati, T.; Chirvony, V.; Sánchez-Royo, J.F.; Sentis, M.; Braguer, D.; Timoshenko, V.Y.; Estève, M.-A.; Kabashin, A.V. Ultrapure Laser-Synthesized Si Nanoparticles with Variable Oxidation States for Biomedical Applications. J. Mater. Chem. B 2016, 4, 7852–7858. [Google Scholar] [CrossRef] [PubMed]
- Oleshchenko, V.A.; Kharin, A.Y.; Alykova, A.F.; Karpukhina, O.V.; Karpov, N.V.; Popov, A.A.; Bezotosnyi, V.V.; Klimentov, S.M.; Zavestovskaya, I.N.; Kabashin, A.V.; et al. Localized Infrared Radiation-Induced Hyperthermia Sensitized by Laser-Ablated Silicon Nanoparticles for Phototherapy Applications. Appl. Surf. Sci. 2020, 516, 145661. [Google Scholar] [CrossRef]
- Zabotnov, S.V.; Skobelkina, A.V.; Sergeeva, E.A.; Kurakina, D.A.; Khilov, A.V.; Kashaev, F.V.; Kaminskaya, T.P.; Presnov, D.E.; Agrba, P.D.; Shuleiko, D.V.; et al. Nanoparticles Produced via Laser Ablation of Porous Silicon and Silicon Nanowires for Optical Bioimaging. Sensors 2020, 20, 4874. [Google Scholar] [CrossRef] [PubMed]
- Gongalsky, M.B.; Kharin, A.Y.; Osminkina, L.A.; Timoshenko, V.Y.; Jeong, J.; Lee, H.; Chung, B.H. Enhanced Photoluminescence of Porous Silicon Nanoparticles Coated by Bioresorbable Polymers. Nanoscale Res. Lett. 2012, 7, 446. [Google Scholar] [CrossRef]
- Huang, Z.; Geyer, N.; Werner, P.; de Boor, J.; Gösele, U. Metal-Assisted Chemical Etching of Silicon: A Review. Adv. Mater. 2011, 23, 285–308. [Google Scholar] [CrossRef] [PubMed]
- Osminkina, L.A.; Gonchar, K.A.; Marshov, V.S.; Bunkov, K.V.; Petrov, D.V.; Golovan, L.A.; Talkenberg, F.; Sivakov, V.A.; Timoshenko, V.Y. Optical Properties of Silicon Nanowire Arrays Formed by Metal-Assisted Chemical Etching: Evidences for Light Localization Effect. Nanoscale Res. Lett. 2012, 7, 524. [Google Scholar] [CrossRef]
- Efimova, A.; Eliseev, A.; Georgobiani, V.; Kholodov, M.; Kolchin, A.; Presnov, D.; Tkachenko, N.; Zabotnov, S.; Golovan, L.; Kashkarov, P. Enhanced Photon Lifetime in Silicon Nanowire Arrays and Increased Efficiency of Optical Processes in Them. Opt. Quantum Electron. 2016, 48, 232. [Google Scholar] [CrossRef]
- Cigna, E.; Tarallo, M.; Maruccia, M.; Sorvillo, V.; Pollastrini, A.; Scuderi, N. Basal Cell Carcinoma: 10 Years of Experience. J. Ski. Cancer 2011, 2011, 476362. [Google Scholar] [CrossRef]
- ANSI Z136.1–2014—American National Standard for Safe Use of Lasers; Laser Institute of America: Orlando, FL, USA, 2014.
- Jean, M.; Schulmeister, K. Laser-Induced Injury of the Skin: Validation of a Computer Model to Predict Thresholds. Biomed. Opt. Express 2021, 12, 2586. [Google Scholar] [CrossRef]
- Bristow, A.D.; Rotenberg, N.; van Driel, H.M. Two-Photon Absorption and Kerr Coefficients of Silicon for 850–2200 nm. Appl. Phys. Lett. 2007, 90, 191104. [Google Scholar] [CrossRef]
- Costa-Almeida, R.; Bogas, D.; Fernandes, J.R.; Timochenco, L.; Silva, F.A.L.S.; Meneses, J.; Gonçalves, I.C.; Magalhães, F.D.; Pinto, A.M. Near-Infrared Radiation-Based Mild Photohyperthermia Therapy of Non-Melanoma Skin Cancer with PEGylated Reduced Nanographene Oxide. Polymers 2020, 12, 1840. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, W.; Zhao, J.; Wu, C.; Ye, C.; Huang, M.; Wang, S. Preparation of injectable temperature-sensitive chitosan-based hydrogel for combined hyperthermia and chemotherapy of colon cancer. Carbohydr. Polym. 2019, 222, 115039. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Xu, C.; Xue, L.; Pang, H.; Cao, A.; Fu, Y.; Deng, Q. Integrated Double-Sided Random Microlens Array Used for Laser Beam Homogenization. Micromachines 2021, 12, 673. [Google Scholar] [CrossRef] [PubMed]
- Green, M.A.; Keevers, M.J. Optical Properties of Intrinsic Silicon at 300 K. Prog. Photovolt. Res. Appl. 1995, 3, 189–192. [Google Scholar] [CrossRef]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical Properties of Normal and Cancerous Human Skin in the Visible and Near-Infrared Spectral Range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef] [PubMed]
- Chopra, K.; Calva, D.; Sosin, M.; Tadisina, K.K.; Banda, A.; De La Cruz, C.; Chaudhry, M.R.; Legesse, T.; Drachenberg, C.B.; Manson, P.N.; et al. A Comprehensive Examination of Topographic Thickness of Skin in the Human Face. Aesthet. Surg. J. 2015, 35, 1007–1013. [Google Scholar] [CrossRef] [PubMed]
- Oltulu, P.; Ince, B.; Kokbudak, N.; Findik, S.; Kilinc, F. Measurement of Epidermis, Dermis, and Total Skin Thicknesses from Six Different Body Regions with a New Ethical Histometric Technique. Turk. J. Plast. Surg. 2018, 26, 56. [Google Scholar] [CrossRef]
- Gongalsky, M.B.; Osminkina, L.A.; Pereira, A.; Manankov, A.A.; Fedorenko, A.A.; Vasiliev, A.N.; Solovyev, V.V.; Kudryavtsev, A.A.; Sentis, M.; Kabashin, A.V.; et al. Laser-Synthesized Oxide-Passivated Bright Si Quantum Dots for Bioimaging. Sci. Rep. 2016, 6, 24732. [Google Scholar] [CrossRef] [PubMed]
- Zabotnov, S.V.; Kolchin, A.V.; Kashaev, F.V.; Skobelkina, A.V.; Nesterov, V.Y.; Presnov, D.E.; Golovan, L.A.; Kashkarov, P.K. Structural Analysis of Nanoparticles Formed via Laser Ablation of Porous Silicon and Silicon Microparticles in Water. Tech. Phys. Lett. 2019, 45, 1085–1088. [Google Scholar] [CrossRef]
- Hull, R. Properties of Crystalline Silicon; INSPEC: London, UK, 1999. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Barbagiovanni, E.G.; Lockwood, D.J.; Simpson, P.J.; Goncharova, L.V. Quantum Confinement in Si and Ge Nanostructures. J. Appl. Phys. 2012, 111, 034307. [Google Scholar] [CrossRef]
- Aspnes, D.E.; Studna, A.A. Dielectric Functions and Optical Parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV. Phys. Rev. B 1983, 27, 985. [Google Scholar] [CrossRef]
- Jellison, G.E.; Modine, F.A. Optical absorption of silicon between 1.6 and 4.7 eV at elevated temperatures. Appl. Phys. Lett. 1982, 41, 180–182. [Google Scholar] [CrossRef]
- Jellison, G.E.; Burke, H.H. The temperature dependence of the refractive index of silicon at elevated temperatures at severed laser wavelengths. J. Appl. Phys. 1986, 60, 841–843. [Google Scholar] [CrossRef]
- Iorizzo, T.W.; Jermain, P.R.; Salomatina, E.; Muzikansky, A.; Yaroslavsky, A.N. Temperature induced changes in the optical properties of skin in vivo. Sci. Rep. 2021, 11, 754. [Google Scholar] [CrossRef] [PubMed]
- Lihong, W. Scattering and Its Biological Origins. Ch. 1.5 Pp 8. Biomedical Optics; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Bolin, F.P.; Preuss, L.E.; Taylor, R.C.; Ference, R.J. Refractive Index of Some Mammalian Tissues. Appl. Opt. 1989, 28, 2297–2303. [Google Scholar] [CrossRef]
- Brocato, T.A.; Coker, E.N.; Durfee, P.N.; Lin, Y.-S.; Townson, J.; Wyckoff, E.F.; Cristini, V.; Brinker, C.J.; Wang, Z. Understanding the Connection between Nanoparticle Uptake and Cancer Treatment Efficacy Using Mathematical Modeling. Sci. Rep. 2018, 8, 7538. [Google Scholar] [CrossRef]
- Wilhelm, S.; Tavares, A.J.; Dai, Q.; Ohta, S.; Audet, J.; Dvorak, H.F.; Chan, W.C.W. Analysis of Nanoparticle Delivery to Tumours. Nat. Rev. Mater. 2016, 1, 16014. [Google Scholar] [CrossRef]
- Krylov, I.V.; Akasov, R.A.; Rocheva, V.V.; Sholina, N.V.; Khochenkov, D.A.; Nechaev, A.V.; Melnikova, N.V.; Dmitriev, A.A.; Ivanov, A.V.; Generalova, A.N.; et al. Local Overheating of Biotissue Labeled with Upconversion Nanoparticles Under Yb3+ Resonance Excitation. Front. Chem. 2020, 8, 295. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo Modeling of Light Transport in Multi-Layered Tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Loginova, D.; Sergeeva, E.; Fiks, I.; Kirillin, M. Probing Depth in Diffuse Optical Spectroscopy and Structured Illumination Imaging: A Monte Carlo Study. JBPE 2017, 3, 010303. [Google Scholar] [CrossRef]
- Manuchehrabadi, N.; Chen, Y.; Lebrun, A.; Ma, R.; Zhu, L. Computational Simulation of Temperature Elevations in Tumors Using Monte Carlo Method and Comparison to Experimental Measurements in Laser Photothermal Therapy. J. Biomech. Eng. 2013, 135, 121007. [Google Scholar] [CrossRef] [PubMed]
- Kurakina, D.; Khilov, A.; Shakhova, M.; Orlinskaya, N.; Sergeeva, E.; Meller, A.; Turchin, I.; Kirillin, M. Comparative Analysis of Single- and Dual-Wavelength Photodynamic Therapy Regimes with Chlorin-Based Photosensitizers: Animal Study. J. Biomed. Opt. 2019, 25, 063804. [Google Scholar] [CrossRef]
- Mironycheva, A.M.; Kirillin, M.Y.; Khilov, A.V.; Malygina, A.S.; Kurakina, D.A.; Gutakovskaya, V.N.; Turchin, I.V.; Orlinskaya, N.Y.; Shlivko, I.L.; Klemenova, I.A.; et al. Combined Application of Dual-Wavelength Fluorescence Monitoring and Contactless Thermometry during Photodynamic Therapy of Basal Cell Skin Cancer. Sovrem. Tehnol. Med. 2020, 12, 47. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Tunç, M.; Çamdali, Ü.; Parmaksizoğlu, C.; Çikrikçi, S. The Bio-heat Transfer Equation and Its Applications in Hyperthermia Treatments. Eng. Comput. 2006, 23, 451–463. [Google Scholar] [CrossRef]
- Ricketts, P.L.; Mudaliar, A.V.; Ellis, B.E.; Pullins, C.A.; Meyers, L.A.; Lanz, O.I.; Scott, E.P.; Diller, T.E. Non-Invasive Blood Perfusion Measurements Using a Combined Temperature and Heat Flux Surface Probe. Int. J. Heat Mass Transf. 2008, 51, 5740–5748. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Ogale, A.A.; Das, C.; Mitra, K.; Subramanian, C. Temperature Distribution in Different Materials Due to Short Pulse Laser Irradiation. Heat Transf. Eng. 2005, 26, 41–49. [Google Scholar] [CrossRef]
- Wang, X.; Qi, H.; Yang, X.; Xu, H. Analysis of the Time-Space Fractional Bioheat Transfer Equation for Biological Tissues during Laser Irradiation. Int. J. Heat Mass Transf. 2021, 177, 121555. [Google Scholar] [CrossRef]
- Liu, K.-C.; Chen, T.-M. Comparative Study of Heat Transfer and Thermal Damage Assessment Models for Hyperthermia Treatment. J. Therm. Biol. 2021, 98, 102907. [Google Scholar] [CrossRef]
- Xu, F.; Lu, T.J.; Seffen, K.A.; Ng, E.Y.K. Mathematical Modeling of Skin Bioheat Transfer. Appl. Mech. Rev. 2009, 62, 050801. [Google Scholar] [CrossRef]
- Cheng, T.-Y.; Herman, C. Optimization of Skin Cooling for Thermographic Imaging of Near-Surface Lesions. In Proceedings of the ASME 2011 International Mechanical Engineering Congress and Exposition, Denver, CO, USA, 11–17 November 2011; ASMEDC: New York, NY, USA, 2012; Volume 2, pp. 351–360. [Google Scholar] [CrossRef]
- Carberry, P.A.; Shepherd, A.M.; Johnson, J.M. Resting and Maximal Forearm Skin Blood Flows Are Reduced in Hypertension. Hypertension 1992, 20, 349–355. [Google Scholar] [CrossRef]
- Suleman, M.; Riaz, S. 3D in Silico Study of Magnetic Fluid Hyperthermia of Breast Tumor Using Fe3O4 Magnetic Nanoparticles. J. Therm. Biol. 2020, 91, 102635. [Google Scholar] [CrossRef]
- Patil, H.M.; Maniyeri, R. Finite Difference Method Based Analysis of Bio-Heat Transfer in Human Breast Cyst. Therm. Sci. Eng. Prog. 2019, 10, 42–47. [Google Scholar] [CrossRef]
- Qiu, L.; Zhu, N.; Feng, Y.; Michaelides, E.E.; Żyła, G.; Jing, D.; Zhang, X.; Norris, P.M.; Markides, C.N.; Mahian, O. A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids. Phys. Rep. 2020, 843, 1–81. [Google Scholar] [CrossRef]
- Priester, M.I.; Curto, S.; van Rhoon, G.C.; ten Hagen, T.L.M. External Basic Hyperthermia Devices for Preclinical Studies in Small Animals. Cancers 2021, 13, 4628. [Google Scholar] [CrossRef]
- Bass, L.; Nikolaeva, O.; Bykov, A.; Kirillin, M. Finite Difference Methods for Solving the Transport Equation in the Problems of Optical Biomedical Diagnostics. JBPE 2017, 3, 010311. [Google Scholar] [CrossRef]
- Deng, Z.-S.; Liu, J. Numerical Simulation of 3-D Freesing and Heating Problems for Combined Cryosurgery and Hyperthermia Therapy. Numer. Heat Transf. Part A Appl. 2004, 46, 587–611. [Google Scholar] [CrossRef]
- Gnyawali, S.C.; Chen, Y.; Wu, F.; Bartels, K.E.; Wicksted, J.P.; Liu, H.; Sen, C.K.; Chen, W.R. Temperature Measurement on Tissue Surface during Laser Irradiation. Med. Biol. Eng. Comput. 2008, 46, 159–168. [Google Scholar] [CrossRef] [PubMed]
- Ng, E.Y.K.; Tan, H.M.; Ooi, E.H. Boundary Element Method with Bioheat Equation for Skin Burn Injury. Burns 2009, 35, 987–997. [Google Scholar] [CrossRef] [PubMed]
- Torvi, D.A.; Dale, J.D. A Finite Element Model of Skin Subjected to a Flash Fire. J. Biomech. Eng. 1994, 116, 250–255. [Google Scholar] [CrossRef] [PubMed]
- Kengne, E.; Mellal, I.; Hamouda, M.B.; Lakhssassi, A. A Mathematical Model to Solve Bio-Heat Transfer Problems through a Bio-Heat Transfer Equation with Quadratic Temperature-Dependent Blood Perfusion under a Constant Spatial Heating on Skin Surface. J. Biomed. Sci. Eng. 2014, 7, 721–730. [Google Scholar] [CrossRef][Green Version]
- Akula, S.C.; Maniyeri, R. Numerical simulation of bioheat transfer: A comparative study on hyperbolic and parabolic heat conduction. J Braz. Soc. Mech. Sci. Eng. 2020, 42, 62. [Google Scholar] [CrossRef]
- Santos, O.; Cancino-Bernardi, J.; Pincela Lins, P.M.; Sampaio, D.; Pavan, T.; Zucolotto, V. Near-Infrared Photoactive Theragnostic Gold Nanoflowers for Photoacoustic Imaging and Hyperthermia. ACS Appl. Bio Mater. 2021, 4, 6780–6790. [Google Scholar] [CrossRef]
- Box, G.E.P.; Muller, M.E. A Note on the Generation of Random Normal Deviates. Ann. Math. Stat. 1958, 29, 610–611. [Google Scholar] [CrossRef]
- Liu, M.; Radu, D.R.; Selopal, G.S.; Bachu, S.; Lai, C.-Y. Stand-Alone CuFeSe2 (Eskebornite) Nanosheets for Photothermal Cancer Therapy. Nanomaterials 2021, 11, 2008. [Google Scholar] [CrossRef] [PubMed]
- Cruz, C.C.R.; da Silva, N.P.; Castilho, A.V.; Favre-Nicolin, V.A.; Cesar, C.L.; Orlande, H.R.B.; Dos Santos, D.S. Synthesis, Characterization and Photothermal Analysis of Nanostructured Hydrides of Pd and PdCeO2. Sci. Rep. 2020, 10, 17561. [Google Scholar] [CrossRef] [PubMed]
- Mulens-Arias, V.; Nicolás-Boluda, A.; Pinto, A.; Balfourier, A.; Carn, F.; Silva, A.K.A.; Pocard, M.; Gazeau, F. Tumor-Selective Immune-Active Mild Hyperthermia Associated with Chemotherapy in Colon Peritoneal Metastasis by Photoactivation of Fluorouracil–Gold Nanoparticle Complexes. ACS Nano 2021, 15, 3330–3348. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).