1. Introduction
Astronomical and planetary scientific observations performed using space telescopes have received more and more attention in recent years. Telescopes are used to observe planetary atmospheres in near-space. Near-space exploration has a bright future in the fields of military strategy and scientific observation. The European and American space agencies have numerous successful telescope observation missions [
1,
2,
3]. A mirror assembly collects light energy, and photoelectric conversion is performed by the detector to complete optical imaging. The mirror assembly studied in this paper is an important optical element in the space optical telescope. As the core component of the telescope, the space mirror assembly is important and must have good optical performance, be lightweight, and have strong temperature adaptability [
4]. The goal of a space mirror is to satisfy the requirements of the mirror surface accuracy under several load conditions, and the requirements of the mass [
5]. More and more methods for designing a space telescope’s mirrors are being adopted. At the beginning, many researchers designed the mirror assembly by experience. Subsequently, the optimization of mirrors has developed as a trend, such as topology optimization, size optimization, parametric design, and so on. The topology optimization of a large telescope’s lightweight primary mirror considering cast constraints under self-weight and polishing pressure was carried out by Liu et al. [
6]. Its objective function and constraint are to the minimum structural compliance and mass. After optimization, the performance of the new primary mirror has great superiority. To minimize the value of the root mean square (RMS) of surface accuracy and mass, a parametric optimization method based on topology optimization was proposed by Liu et al. [
7]. Jiang et al. created a SiC primary mirror using the topology optimization method to solve the axial support position sensitivity problem of the primary mirror. The resulting design not only had reduced sensitivity of the axial support position, but the lightweight ratio and the fundamental frequency were also improved [
8]. As mentioned above, many scholars have optimized the design of the mirror body to improve the mirror surface shape error of the assembly. The axial mount position for space mirror plays a key role in reducing optical distortion and obtaining good image quality [
9]. Liu et al. studied an adjustable bipod flexure (ABF) for a large-aperture mirror, adjusting the rotation center by means of ABF to optimize the mirror surface accuracy RMS at 8.1 nm [
10]. An optimum lightweight design for a Zerodur primary mirror and optimum bipod flexure was studied by Chen et al. [
11]. In this reference, the value of the RMS of surface accuracy was decreased in the optimization of primary mirror and flexure. Hu et al. [
12] used the compromise programming method to the parametric design of the primary mirror, and its design values all meet the index requirements. In addition, computer automation can be realized in the design process, but the tetrahedron mesh needs to be re-divided for the parametric design model, and so the calculation time is long.
From the analysis mentioned above, we can see that optimizing the mirror and flexure can obtain good mirror surface accuracy RMS, and some researchers have also built an integrated link to achieve automation, but the optimal design is time consuming. We present fast optimal design of a flexure based on mesh deformation to solve the problem of long parameterization time. There are many kinds of mesh deformation software, such as hypermorph, depmeshworks, primer, ansa, and so on, due to the software’s consistency, and so we apply hypermorph here. In this paper, the fast optimization method using mesh deformation is presented to enhance the optimization efficiency of a space mirror assembly. First, the space mirror body was created using topology optimization and size optimization to achieve a high mirror surface accuracy RMS. Then, a three-leaf flexure is created, and its size parameters and axial mount position are optimized using mesh deformation, and the optimization time of the method in this study compared with other methods is shorter; the optimization results, including the mirror surface accuracy RMS under lateral gravity, axial gravity, 4 °C temperature change and 0.01 mm assembly error and frequency, are presented to verify the feasibility and validity of the fast optimization method. Ultimately, mechanical tests and optical tests of the mirror assembly are performed, and the test results meet the engineering requirements.
3. The Fast Optimization of the Space Mirror Assembly
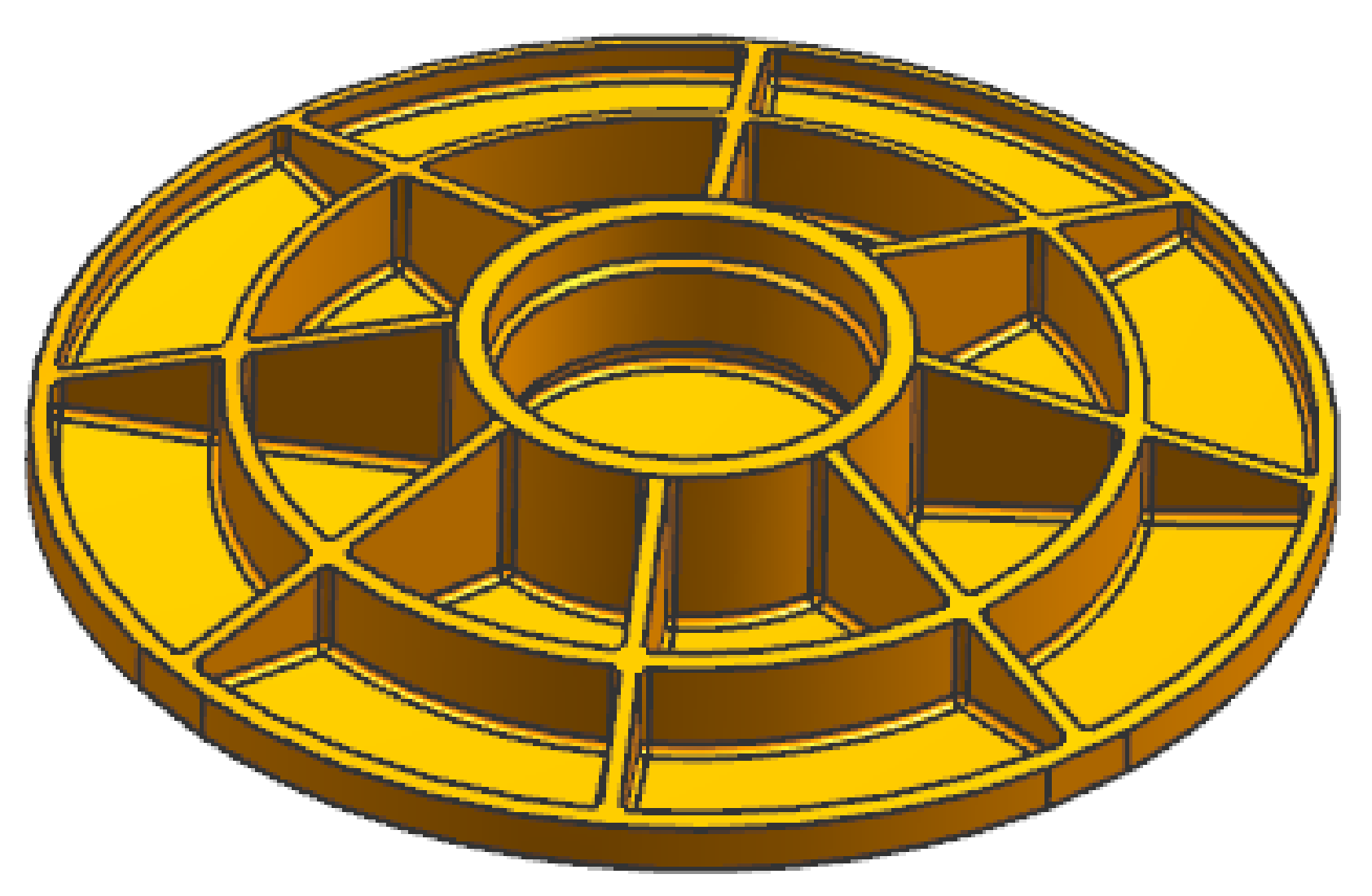
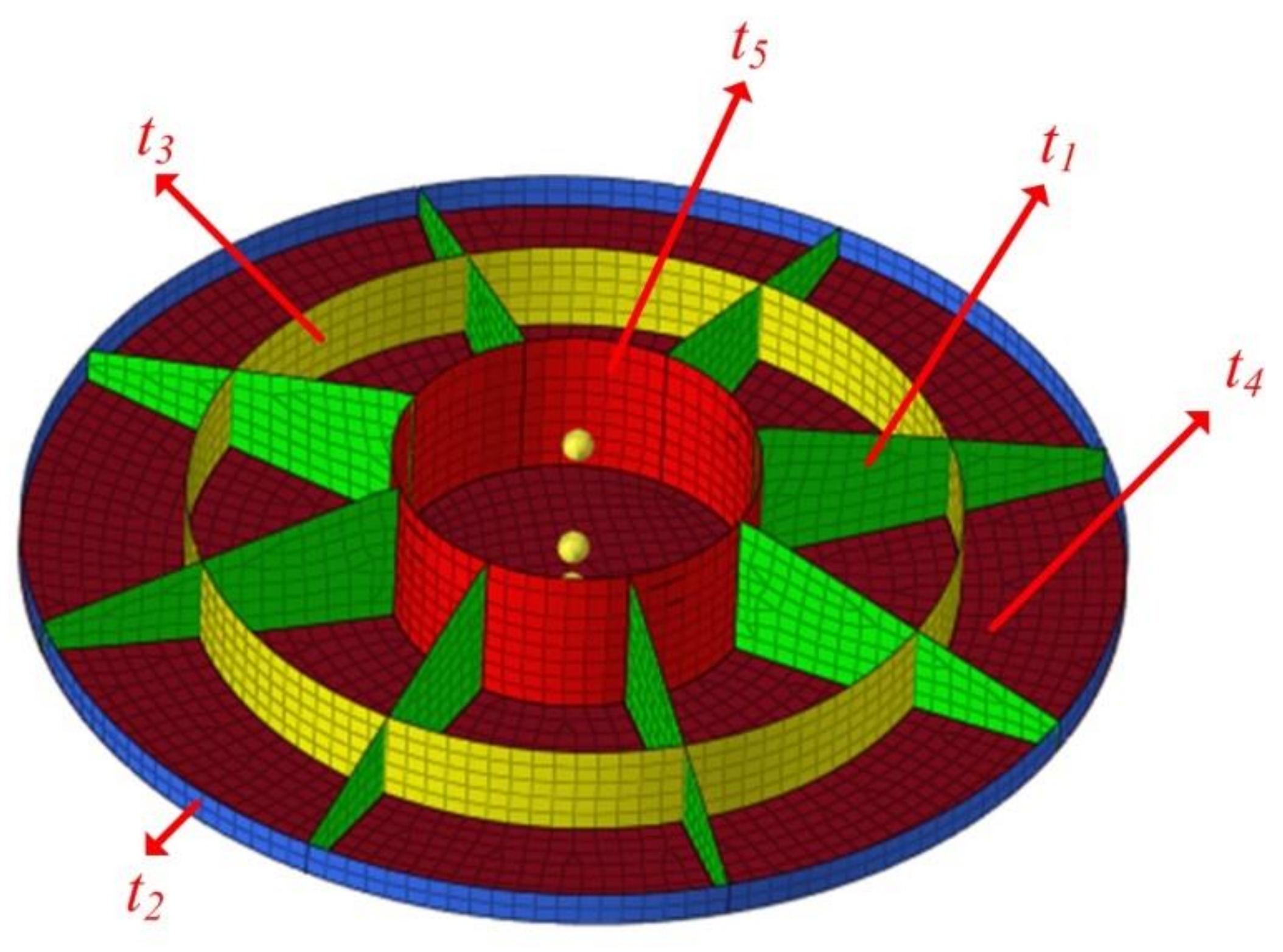
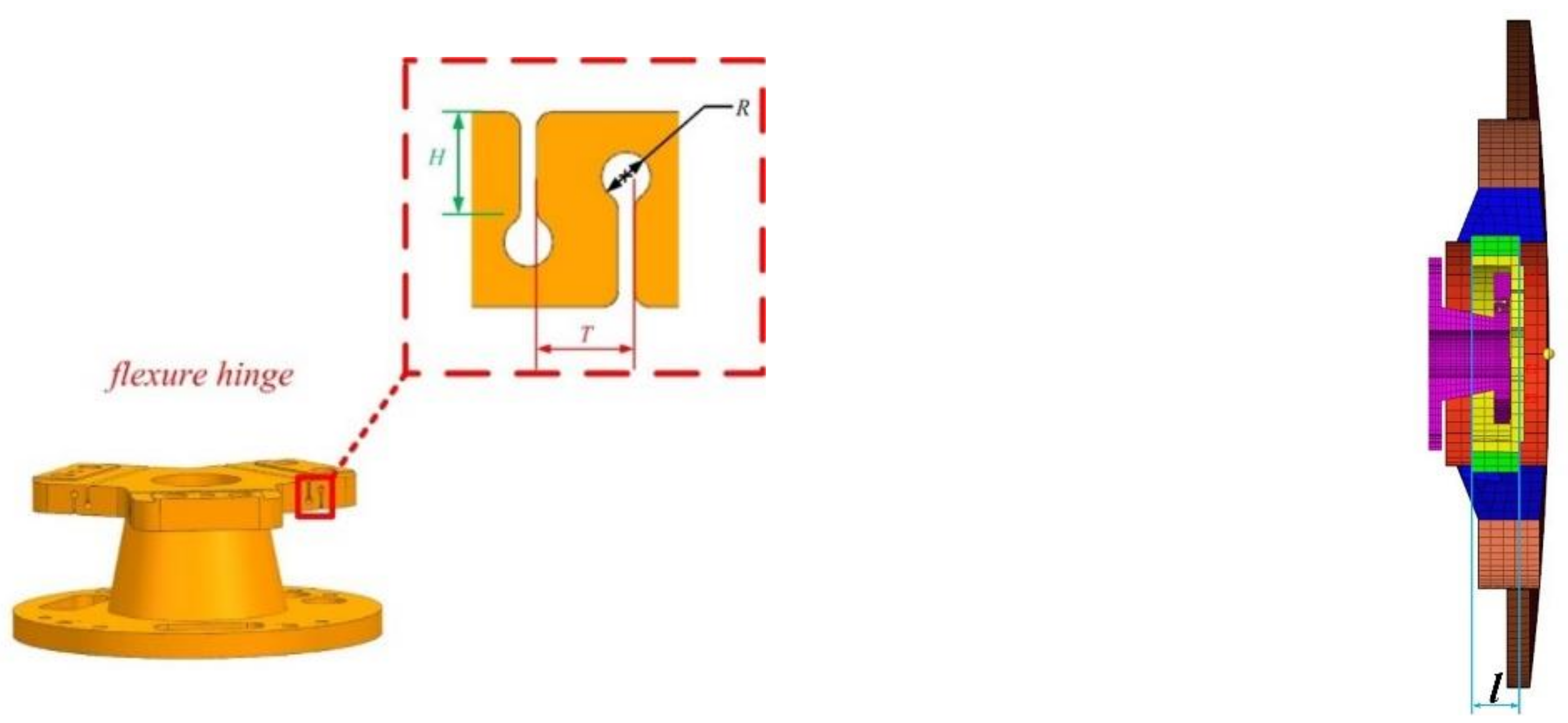
The space mirror assembly is composed of a mirror, a sleeve, and a flexure, and the form of the flexure is shown in
Figure 5b. The traditional design method of a mirror assembly is to modify the geometric model through experience, and then apply FEA to optimize it iteratively. The mirror assembly produced by this method depends on the experience of the designer; however, this method is time-consuming. Subsequently, Hu et al. [
9] achieved primary mirror assembly optimization by using the connection of UG, Hypermesh, Ansys, Matlab. Their goal was to connect several pieces of software and save the time of manual operation, but the elements of flexure in their model are also a second-order tetrahedron mesh, and the calculation time is also very long. As shown in
Figure 6, we establish the Hexahedral FE model by using Hypermesh. The total number of elements is 30,923, and the total number of nodes is 37,815. We alter the parameters of the flexure through the mesh deformation technology by using the Hypermorph module. Three parameters of flexure and axial mount position are shown in
Figure 7, namely R, H, T, and l, respectively.
This paper uses Hypermesh for meshing and morph, Optistruct for FEA, and Sigfit to calculate the mirror surface shape error. The automatic optimization design platform for the space mirror is established based on the multidisciplinary optimization software Isight. The computer used in this paper is a Lenovo computer, which has eight CPU cores (i7-6700) and 8 GB of memory. The multi-objective optimization is carried out 1001 times in an optimization routine. The flow of fast optimization of the space mirror assembly is represented in
Figure 8. In
Figure 8, the flexure size parameters are changed in the tcl script, the tcl script submitted to Hypermesh can generate a fem file, Optistruct calculates a fem file and outputs the mirror surface node deformation, fundamental frequency (f1) and mass, and then Sigfit calculates the RMS. After multiple optimizations, it can be output to meet the optimization mathematical model. Finally, the flexure axial installation position is optimized, and the optimization process ends. The analysis time for the space mirror assembly FEA model under four load cases using a second-order tetrahedron mesh is 10 min, whereas that of the flexure FEA model using the fast optimization method is 40 s. This advantage of less analysis time is more obvious, especially when performing multi-objective optimization.
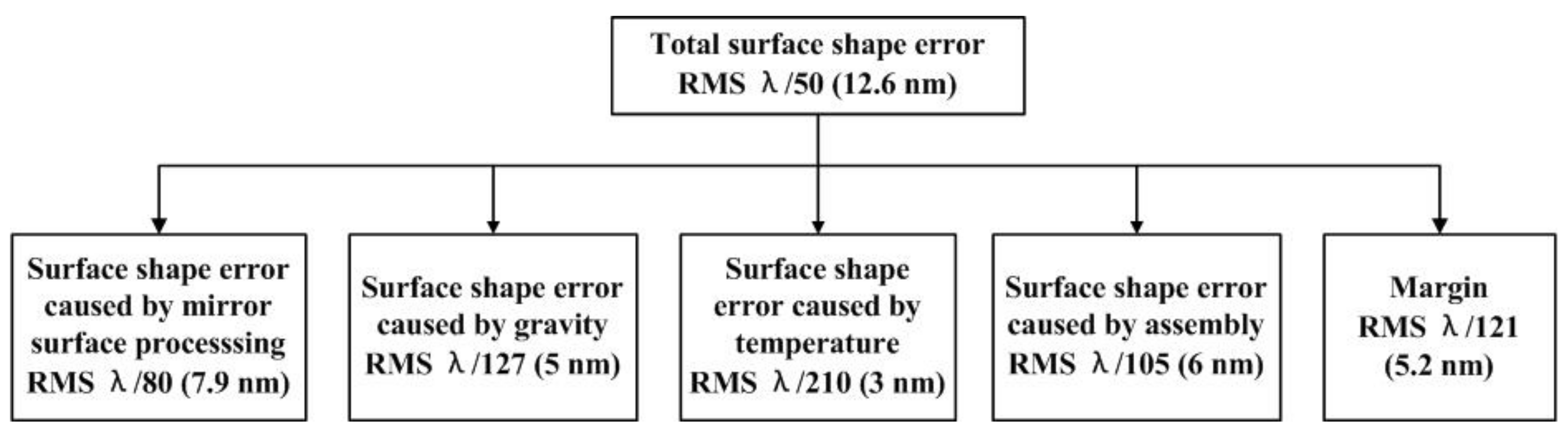
Due to the RMS under axial gravity being basically unaffected, it is not considered in the multi-objective optimization. The mirror assembly is used in space telescopes, and the space environment experiences temperature changes. The telescope takes temperature control measures, but there is still temperature change after temperature control, and so the RMS value caused by temperature change needs to be considered. Surface shape error caused by temperature is very complex. The complex temperature distribution will cause the temperature gradient to affect the surface shape error of the mirror. The aperture of the mirror is small and it is made of SiC material, which has a fast heat conduction speed and thus can reduce the temperature gradient. Our telescope has a special thermal control team for thermal design to ensure that the mirror works at a temperature of 20 ± 0.1 °C through various means, such as a temperature sensor, a heating plate and thermal coating. Even so, there is still a temperature gradient. We use a large 4 °C uniform temperature change to evaluate the temperature adaptability of the mirror.
According to Equation (5), the multi-objective multi-island genetic algorithm (MIGA) is adopted to optimize the space mirror assembly. RMSt, RMSy, and RMS0.01 represent the RMS value of the mirror surface shape error under 4 °C temperature change, lateral gravity, and 0.01 mm assembly error, respectively. A 0.01 mm assembly error indicates 0.01 mm of non-flatness on the flexible mounting surface. The radius of the flexure mounting surface is 37 mm, and non-flatness can reach 5 microns during traditional grinding, thus a certain margin is required, and we take 0.01 mm for the purposes of simulation. OPI is an optical performance index which represents the weighted value of the surface error under three working conditions. OPI and f1 are the objectives, while the RMS in three loads and mass are the constraints.
The value range, initial value, optimal value, and design value of the space mirror flexure parameters are presented in
Table 3. The RMSy of the initial design cannot meet the requirement (5 nm). According to the design values in
Table 3, a FEA is conducted by adjusting the axial position of the flexure, and the final results are provided in
Table 4. The RMS values under lateral gravity, axial gravity, a 4 °C temperature change and a 0.01 mm assembly error are 3.44, 1, 1.48, and 4.84 nm, respectively, and these values satisfy the requirements in
Figure 1. The tilt value under lateral gravity of the mirror has a value of 2.63″, which is better than the optimization constraint of 5″. The fundamental frequency of the mirror is 274.4 Hz, which is higher than the design requirement of 120 Hz. The mass of the space mirror assembly is 1.8 kg, which is lower than 2 kg. Compared with the initial design, the OPI reduces by 32.9%, and the fundamental frequency increases by 24.7%. The results show that the multi-objective optimization effect is obvious.
Here, OPI, which is the weighted mirror surface shape error; the RMSy cannot meet the index requirement, the RMS with a 0.01 mm assembly error can be reduced by grinding, and so the corresponding weight factors were set to , respectively. f1 represents the fundamental frequency, m denotes the mass of the space mirror assembly, and RMSt, RMSy, and RMS0.01 represent the optimization constraints of mirror surface shape error in three loads, respectively.
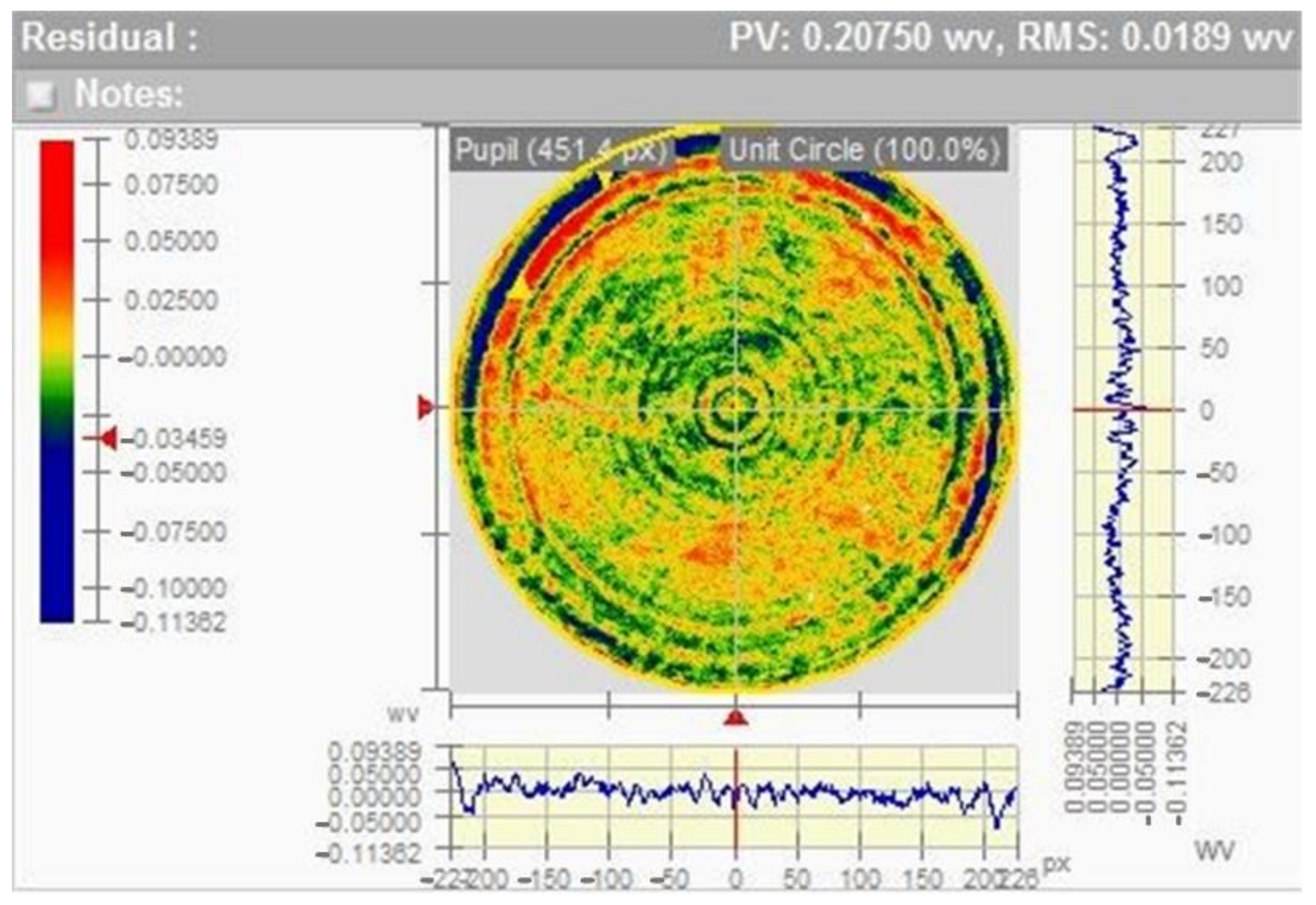
The final result obtained from the space mirror assembly is shown in
Figure 9. As shown in
Figure 9, the optimization results satisfy the designed error allocation. The total surface shape error RMS meets λ/50. As shown in
Figure 9a,c, the remaining primary spherical aberration is the main surface shape error. As shown in
Figure 9b,d, the remaining primary astigmatism is the main surface shape error. The astigmatism cannot be removed, while most of the spherical aberration can be removed during installation and adjustment when detecting system wave aberration.
5. Discussion
A fast optimization method of flexure based on mesh deformation is proposed in this paper, which can improve optimization efficiency compared with other design methods.
In this research, the mesh deformation is completed by adjusting the handle and domain, reduced the time required to change the model and remesh. Compared with the traditional method of calculating the finite element model to obtain the parameters of the flexure [
19] and establishing an optimization link to optimize the parametric model of the flexure [
11,
12], the fast optimization based on mesh deformation in this paper improves the optimization efficiency and saves the optimization time. The larger the diameter of the mirror, the more effective the fast optimization method based on mesh deformation is. Mesh deformation is more suitable for regular size and shape, as complex parameters are difficult to change.
A new frame-type support structure was proposed by Wang [
20], and compared with the rectangular mirror supported by a frame the size of the mirror assembly in this paper is small and the support structure is simple. Compared with the back three-point support mirror [
21], it has the advantages of a simple structure, being lightweight, and being able to avoid surface shape errors caused by non-flatness. The mirror assembly in this paper and those presented by previous scholars meet the requirements of force-thermal stability and application.
6. Conclusions
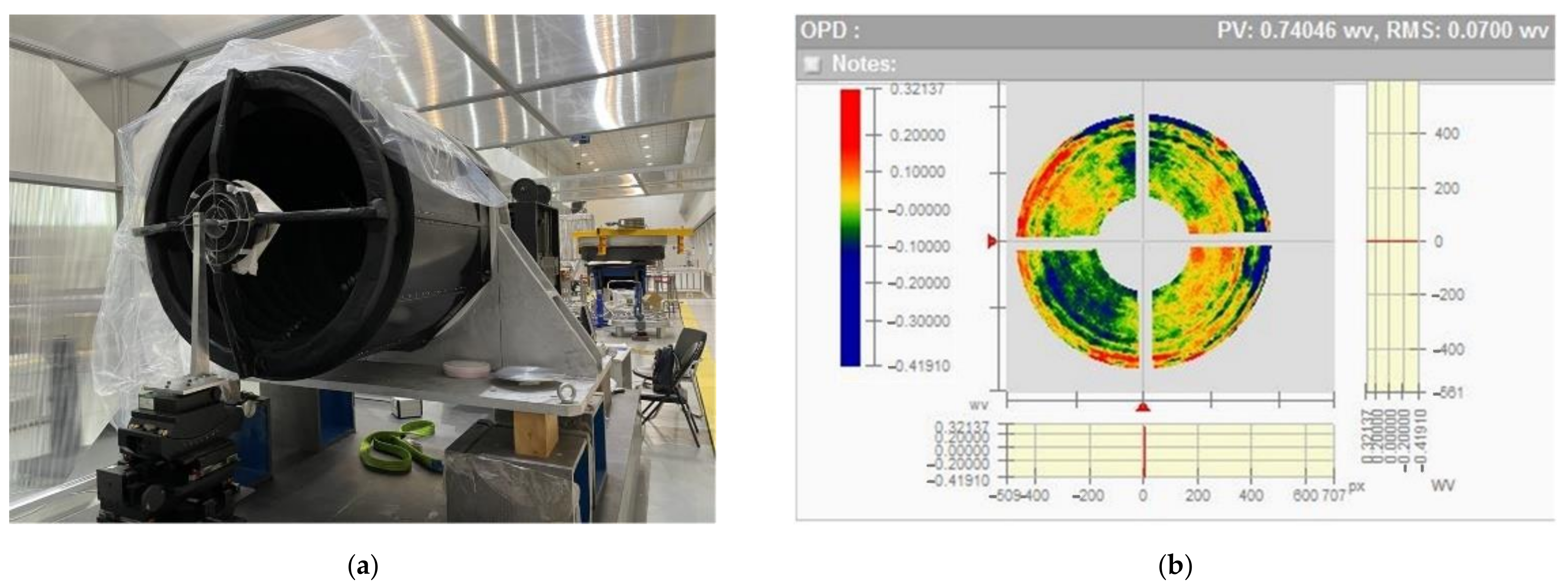
In this paper, the fast optimization method was carried out to improve optimization efficiency. The mirror is created using topology optimization and size optimization; moreover, the flexure with a flexible groove is designed. The flexible groove can release the rotational and translational degrees of freedom, which can minimize the effects of temperature change and assembly tolerance. The size parameters and axial mount position of the flexure were obtained by means of optimization using mesh deformation. This method can significantly improve optimization efficiency. The optimization results of the multi-objective show that the RMS under lateral gravity, axial gravity, 4 °C temperature change and 0.01 mm assembly error are 3.44, 1, 1.48, and 4.84 nm. Moreover, the inclination angle under lateral gravity is 2.63″, and the fundamental frequency is 274.4 Hz, which demonstrates that all indexes satisfy the design requirement. The space mirror assembly is fabricated and assembled for a mechanical test, optical test and stability test. In these tests, the fundamental frequency is 270 Hz, the mirror surface accuracy RMS is λ/50, and the inclination angle under lateral gravity is 3″, and the error of the FEA and tests satisfies the requirements of engineering. The wave aberration of the telescope system is less than λ/14, which satisfies the imaging quality requirements of the optical system. This research provides a meaningful method for improving the optimization efficiency of space mirror assemblies.