Towards Ultimate High-Power Scaling: Coherent Beam Combining of Fiber Lasers
Abstract
1. Introduction
1.1. Power Scaling Limitations of Fiber Lasers and Amplifiers
1.1.1. Nonlinear Effects (NLEs)
- Stimulated Raman Scattering effect
- Stimulated Brillouin Scattering effect:
- Self-phase modulation effect
- Self-focusing effect
- Four-wave mixing effect
- Transverse mode instability effect
1.1.2. Thermal Issues
1.1.3. Optical Damage
1.1.4. Pumping Limitations
1.2. Methods for Power Scaling
1.2.1. Tandem Pumping
1.2.2. Beam Combining
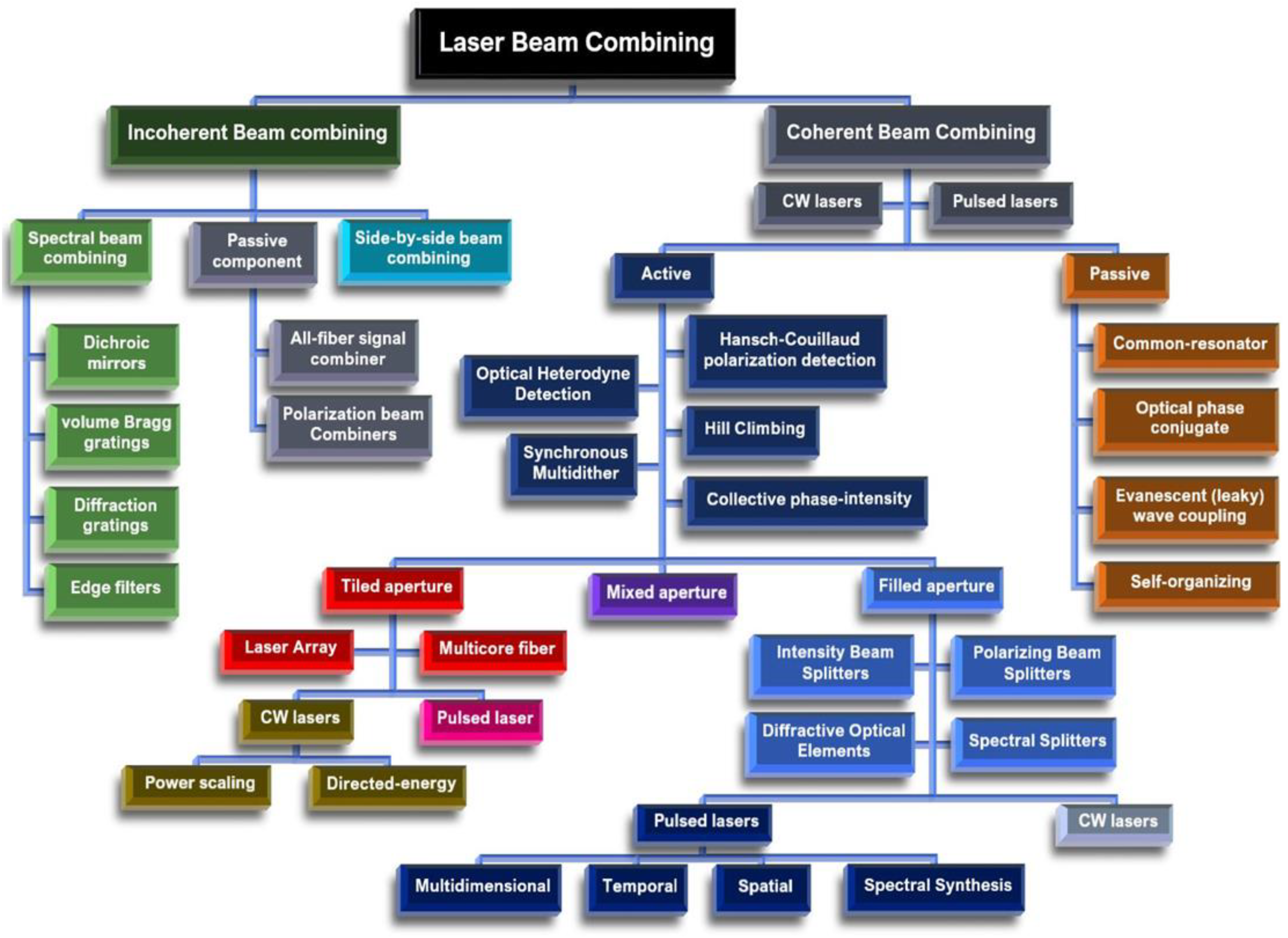
2. Incoherent Beam Combining
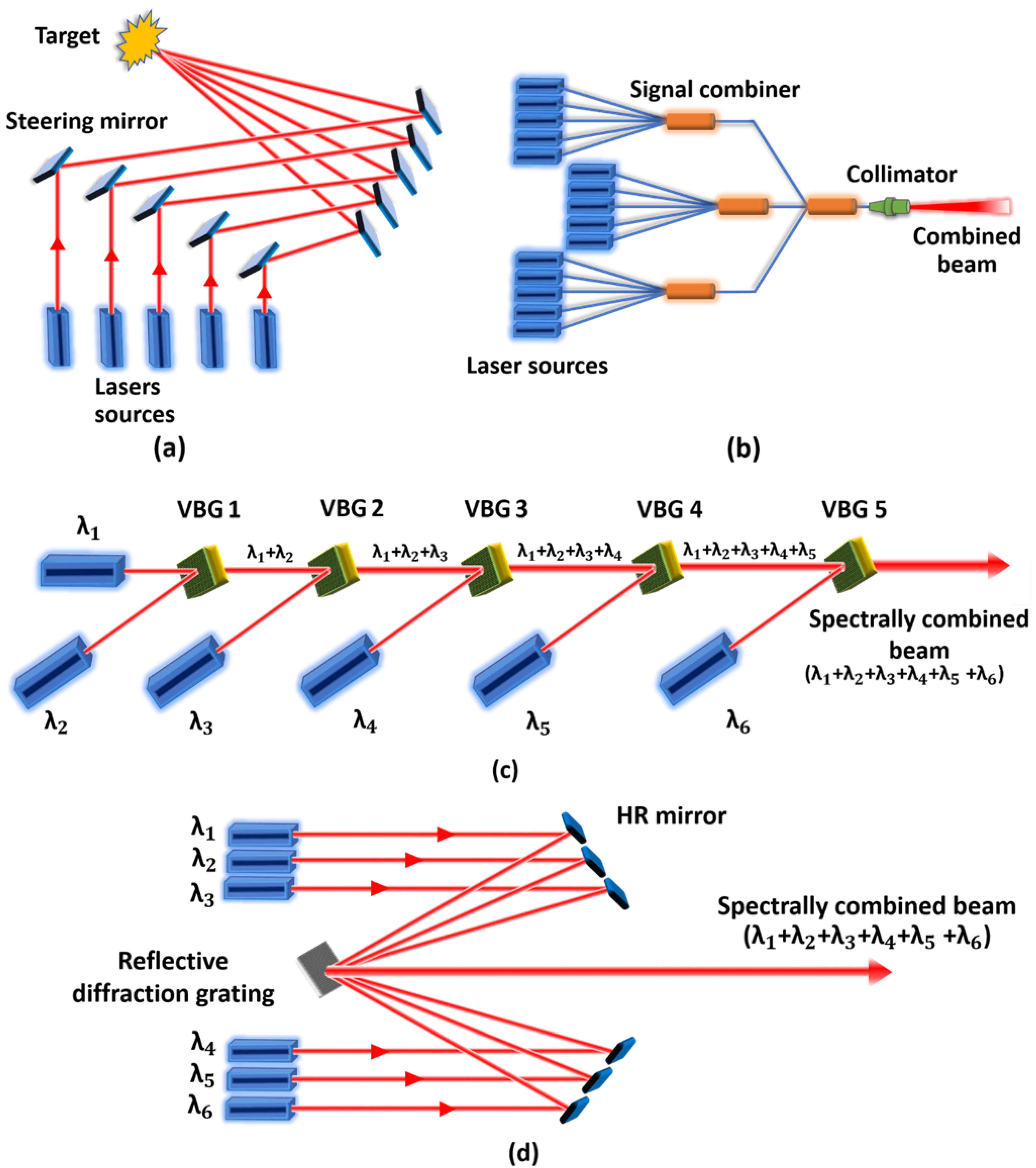
2.1. Side-by-Side Beam Combining
2.2. Passive Components
2.3. Spectral Beam Combining (SBC)
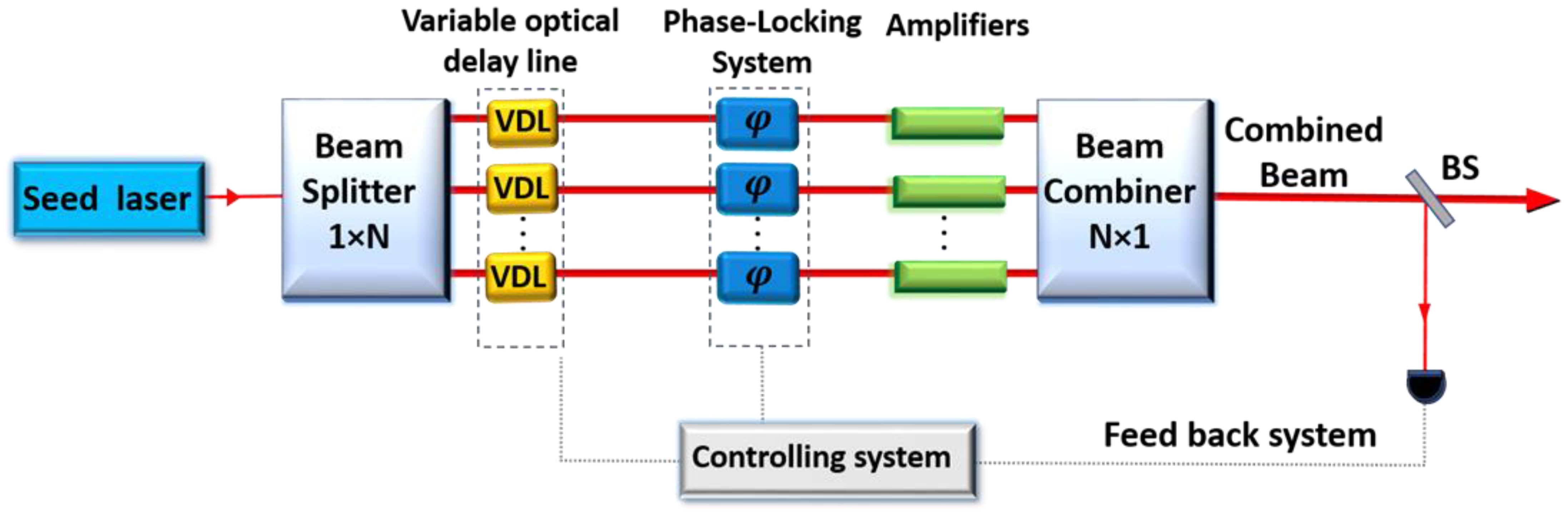
3. Coherent Beam Combining (CBC)
3.1. The Geometry of Combining/Splitting in Space and Time
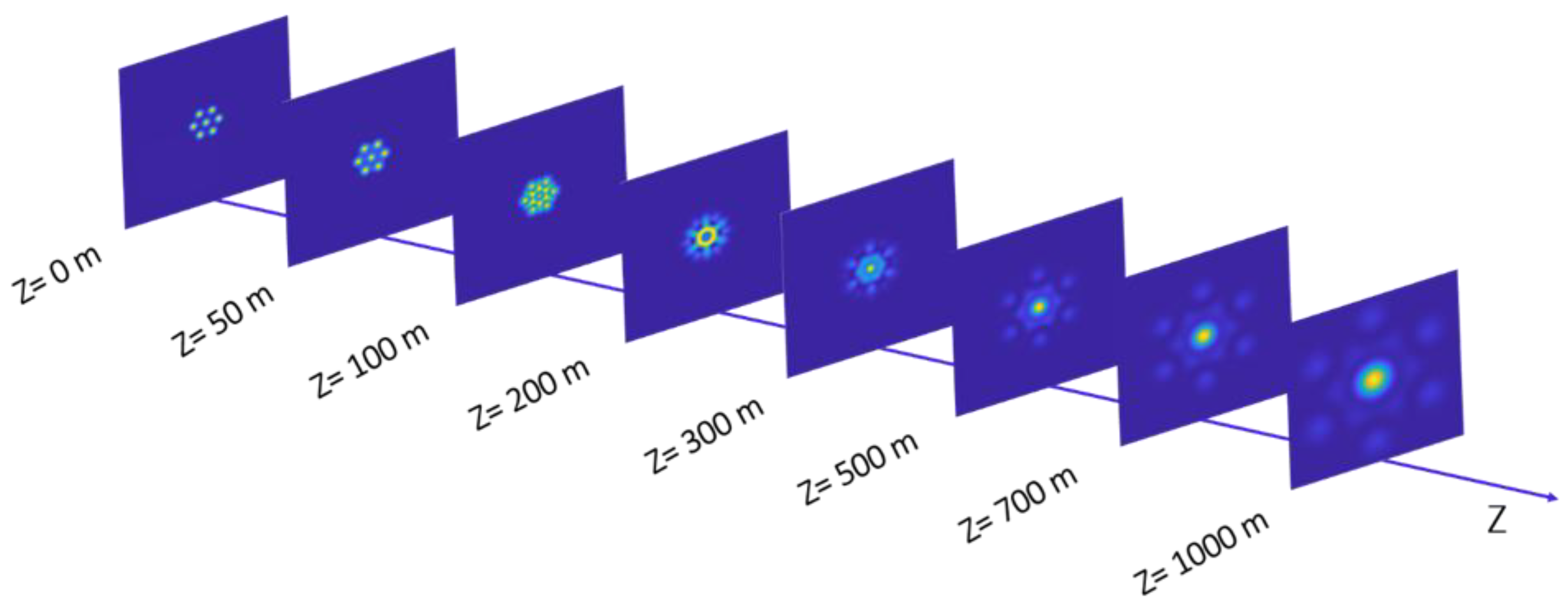
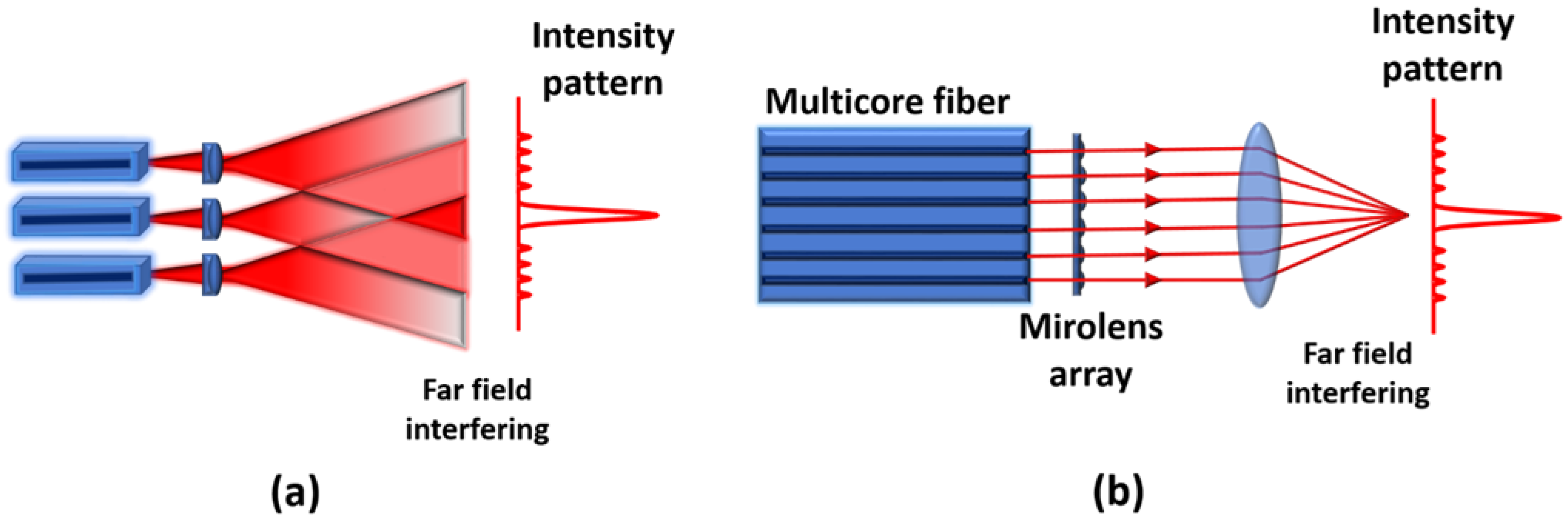
3.1.1. Tiled Aperture (TA)
- Multicore fibers and photonic crystal fibers (MCFs and MC-PCFs);
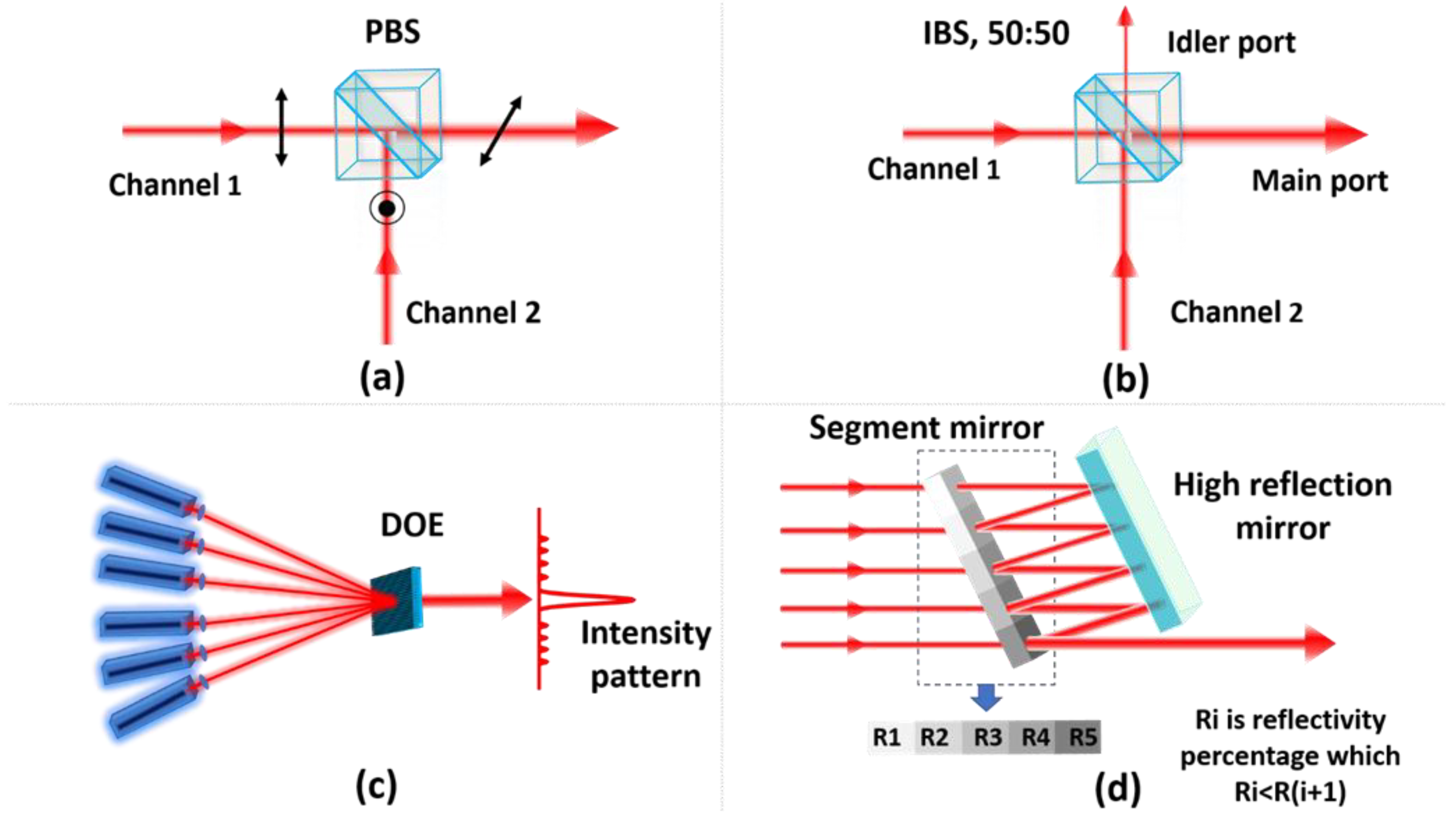
3.1.2. Filled Aperture (FA)
- Polarization beam combiners and thin-film polarizer
- Intensity beam combiners
- Diffractive optical elements
- Segment mirrors (SM)
3.1.3. Mixed Aperture (MA)
3.2. Laser Sources and Amplifiers
3.2.1. Seed Lasers
3.2.2. Laser Amplifiers
- Large mode area (LMA) fibers
- Photonic crystal fibers (PCFs)
- Taper double-clad fibers (T-DCF)
3.3. Phase-Locking Systems
3.3.1. Passive Phase Control
- Common resonator
- Optical phase conjugate
- Evanescent (leaky) wave coupling
- Self-organized
3.3.2. Active Phase Control
- Hansch–Couillaud (HC) polarization detection
- Hill Climbing
- Optical Heterodyne Detection (OHD)
- Frequency dithering
- Collective phase-intensity technique
- Collective phase measurement technique
- 2.
- Phase-intensity mapping (PIM)
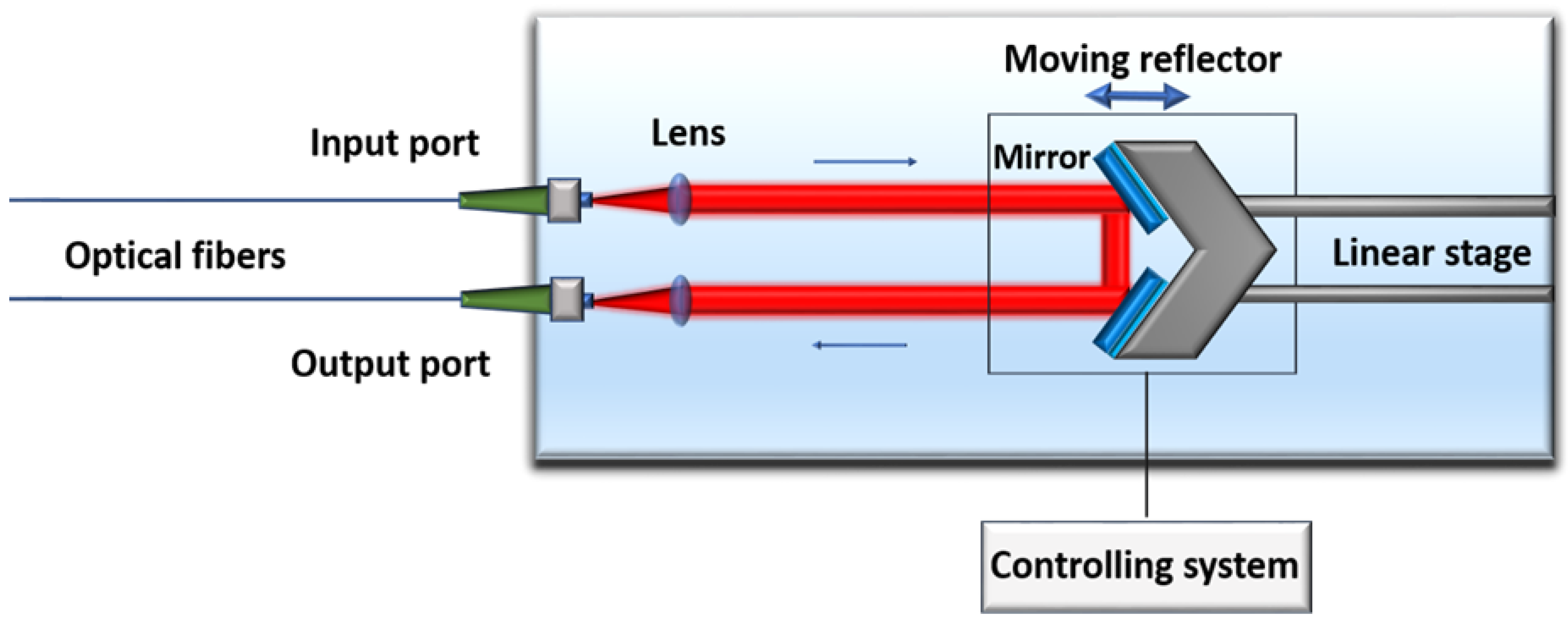
3.4. Optical Path Difference Control
3.5. Channel Scaling
4. Coherent Beam Combining of Ultrafast Fiber Lasers
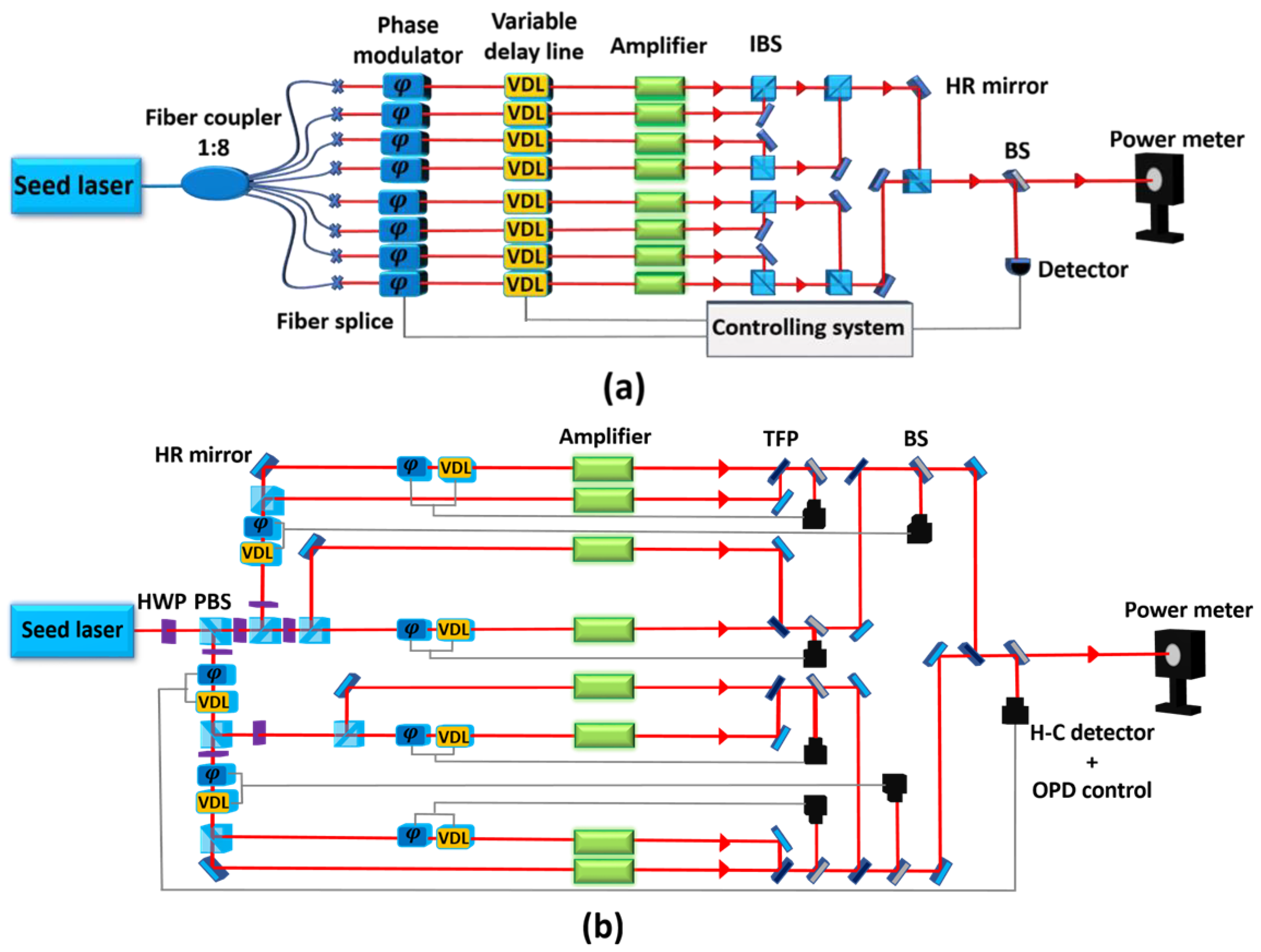
4.1. Spatial CBC
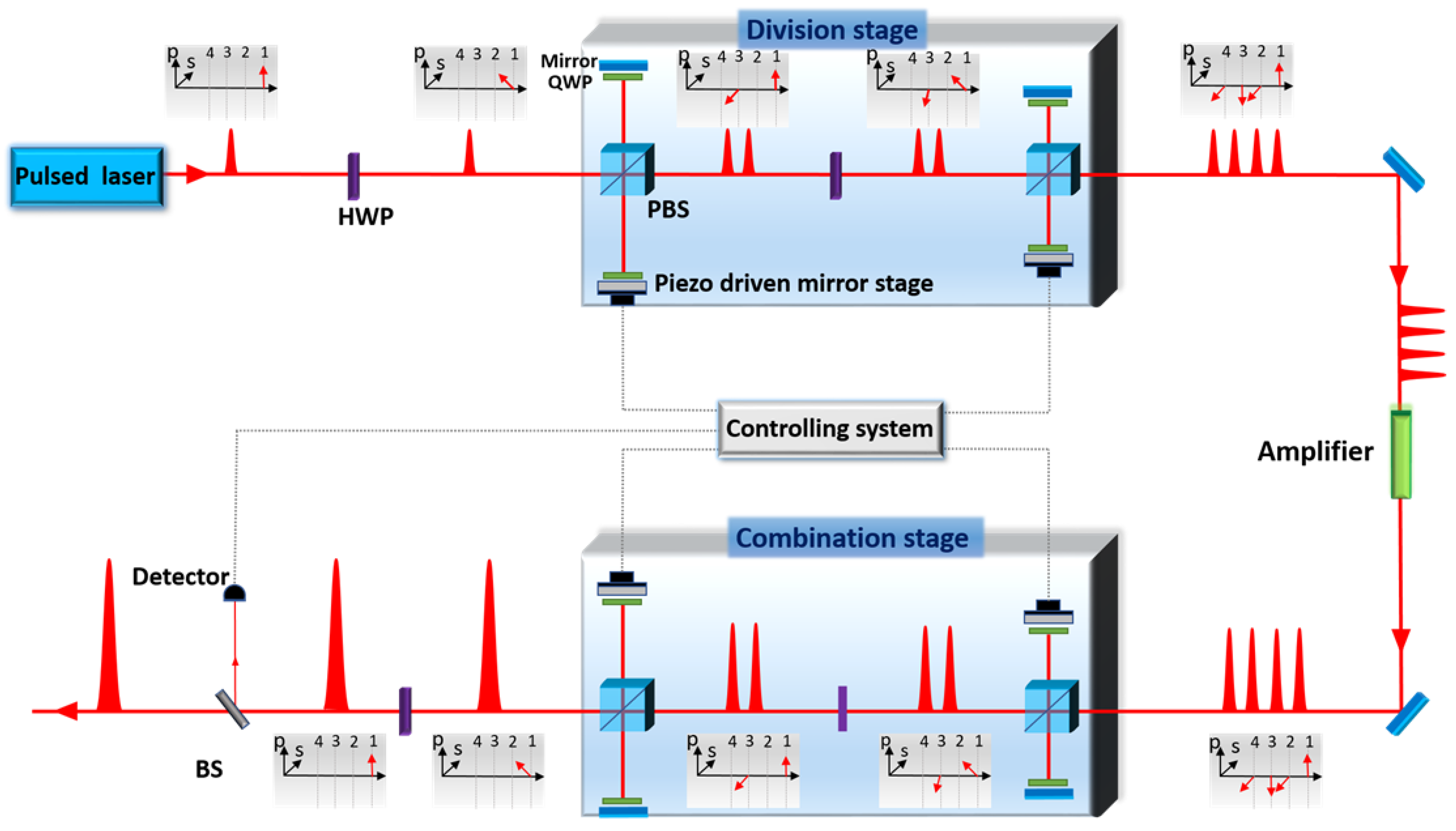
4.2. Temporal CBC
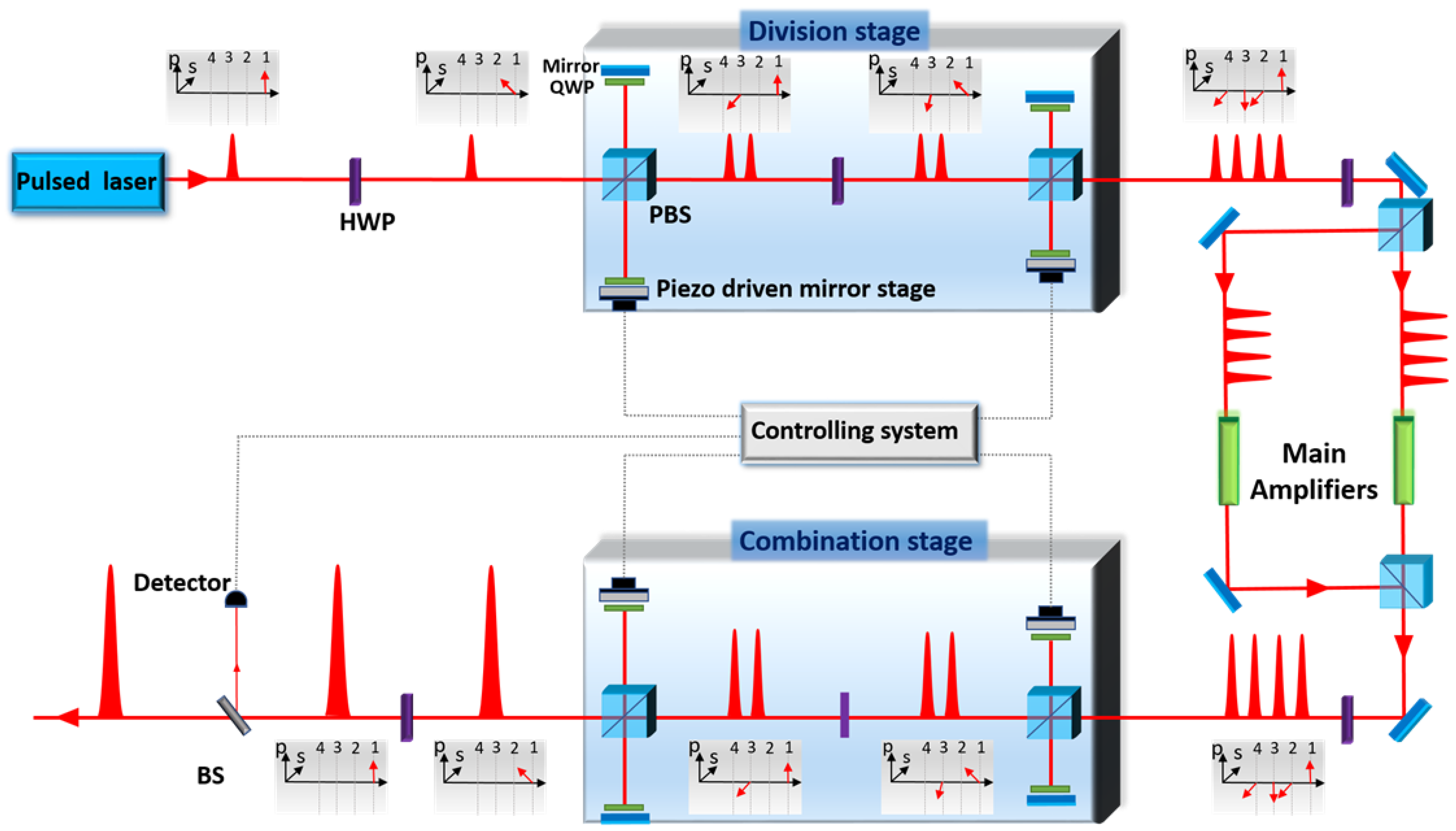
4.3. Multidimensional (Spatial + Temporal) CBC
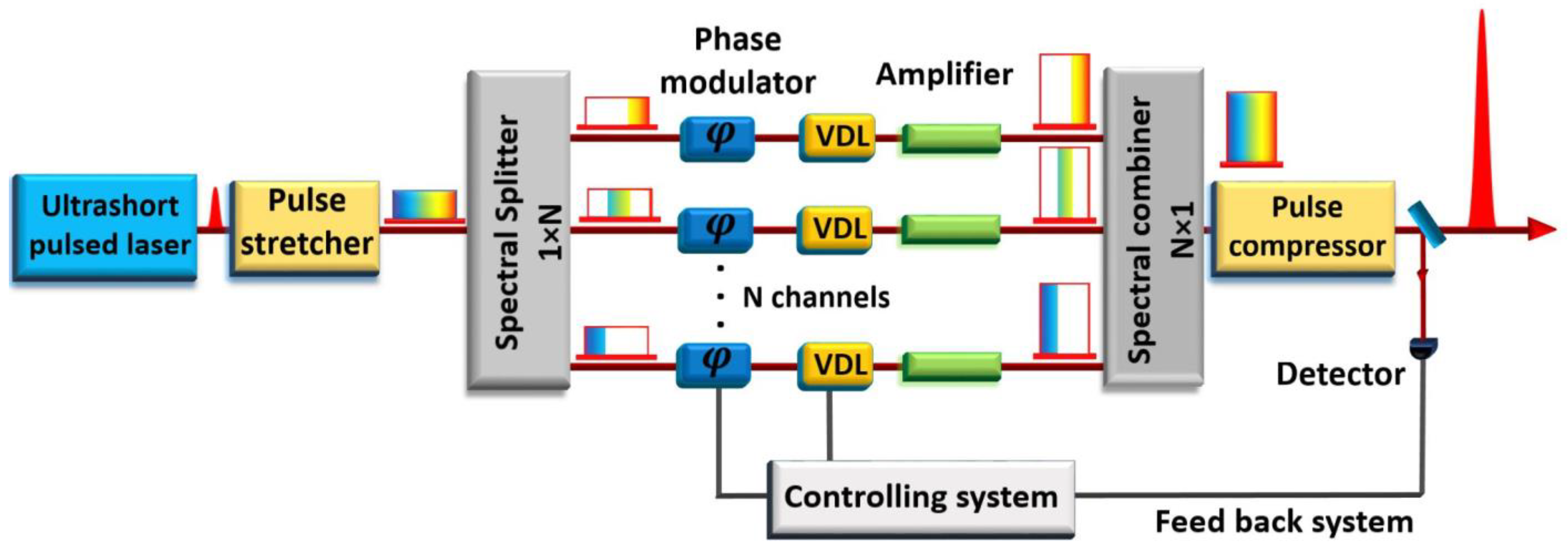
4.4. Spectral CBC (Spectral Pulse Synthesis)
5. Coherent Beam Combining of CW Fiber Lasers
5.1. Tiled Aperture
- Directed-energy applications
- Power scaling
5.2. Filled Aperture
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zervas, M.N.; Codemard, C.A. High Power Fiber Lasers: A Review. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 219–241. [Google Scholar] [CrossRef]
- Moulton, P.F.; Rines, G.A.; Slobodtchikov, E.V.; Wall, K.F.; Frith, G.; Samson, B.; Carter, A.L.G. Tm-Doped Fiber Lasers: Fundamentals and Power Scaling. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 85–92. [Google Scholar] [CrossRef]
- Richardson, D.J.; Nilsson, J.; Clarkson, W.A. High power fiber lasers: Current status and future perspectives [Invited]. J. Opt. Soc. Am. B 2010, 27, B63. [Google Scholar] [CrossRef]
- Jauregui, C.; Limpert, J.; Tünnermann, A. High-power fibre lasers. Nat. Photonics 2013, 7, 861–867. [Google Scholar] [CrossRef]
- Fang, Q.; Li, J.; Shi, W.; Qin, Y.; Xu, Y.; Meng, X.; Norwood, R.A.; Peyghambarian, N. 5 kW near-Diffraction-limited and 8 kW High-Brightness Monolithic Continuous Wave Fiber lasers Directly Pumped by laser Diodes. IEEE Photonics J. 2017, 9, 1–7. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, X.; Su, R.; Ma, P.; Zhou, P. Development status of high power fiber lasers and their coherent beam combination. Sci. China Inf. Sci. 2019, 62, 41301. [Google Scholar] [CrossRef]
- Chang, G.; Wei, Z. Ultrafast Fiber Lasers: An Expanding Versatile Toolbox. iScience 2020, 23, 101101. [Google Scholar] [CrossRef]
- Fermann, M.E.; Hartl, I. Ultrafast Fiber Laser Technology. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 191–206. [Google Scholar] [CrossRef]
- Lim, J.J.; Sujecki, S.; Lang, L.; Zhang, Z.; Paboeuf, D.; Pauliat, G.; Lucas-Leclin, G.; Georges, P.; MacKenzie, R.; Bream, P.; et al. Design and Simulation of Next-Generation High-Power, High-Brightness Laser Diodes. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 993–1008. [Google Scholar] [CrossRef]
- Snitzer, E.; Po, H.; Hakimi, F.; Tumminelli, R.; McCollum, B.C. Double Clad, Offset Core Nd Fiber Laser. In Proceedings of the Optical Fiber Sensors, OSA, New Orleans, LO, USA, 27 January 1988; p. PD5. [Google Scholar]
- Yang, B.; Wang, P.; Zhang, H.; Xi, X.; Shi, C.; Wang, X.; Xu, X. 6 kW single mode monolithic fiber laser enabled by effective mitigation of the transverse mode instability. Opt. Express 2021, 29, 26366. [Google Scholar] [CrossRef]
- Shcherbakov, E.A.; Fomin, V.V.; Abramov, A.A.; Ferin, A.A.; Mochalov, D.V.; Gapontsev, V.P. Industrial Grade 100 kW Power CW Fiber Laser. In Proceedings of the Advanced Solid-State Lasers Congress, OSA, Paris, France, 27 October–1 November 2013; Volume 5, p. ATh4A.2. [Google Scholar]
- Shiner, B. The Impact of Fiber Laser Technology on the World Wide Material Processing Market. In Proceedings of the CLEO, OSA, San Jose, CA, USA, 9–14 June 2013; p. AF2J.1. [Google Scholar]
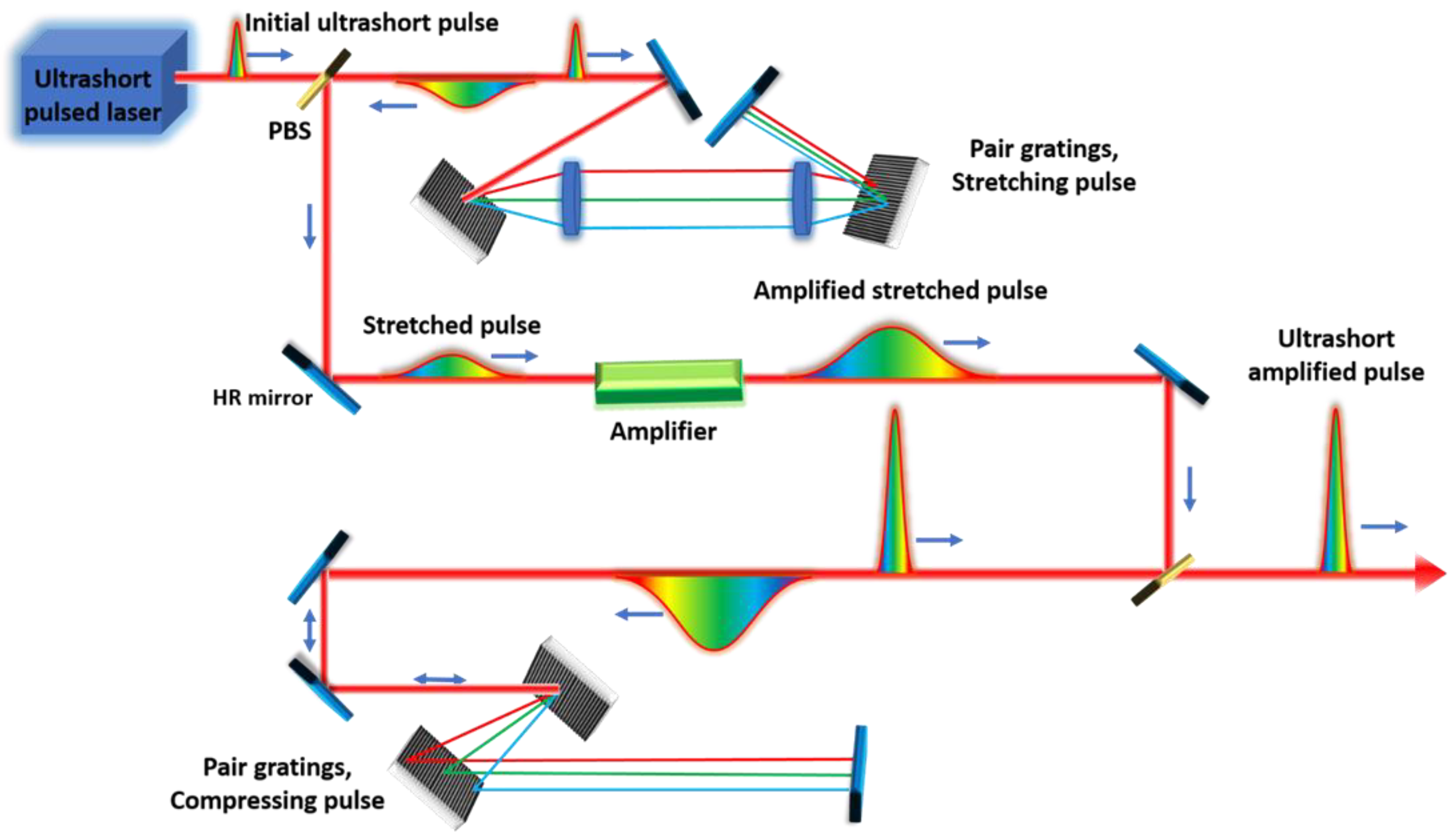
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Eidam, T.; Hanf, S.; Seise, E.; Andersen, T.V.; Gabler, T.; Wirth, C.; Schreiber, T.; Limpert, J.; Tünnermann, A. Femtosecond fiber CPA system emitting 830 W average output power. Opt. Lett. 2010, 35, 94. [Google Scholar] [CrossRef]
- Klenke, A.; Hädrich, S.; Eidam, T.; Rothhardt, J.; Kienel, M.; Demmler, S.; Gottschall, T.; Limpert, J.; Tünnermann, A. 22 GW peak-power fiber chirped-pulse-amplification system. Opt. Lett. 2014, 39, 6875. [Google Scholar] [CrossRef]
- Dawson, J.W.; Messerly, M.J.; Beach, R.J.; Shverdin, M.Y.; Stappaerts, E.A.; Sridharan, A.K.; Pax, P.H.; Heebner, J.E.; Siders, C.W.; Barty, C.P.J. Analysis of the scalability of diffraction-limited fiber lasers and amplifiers to high average power. Opt. Express 2008, 16, 13240. [Google Scholar] [CrossRef]
- Zervas, M.N. Power Scaling Limits in High Power Fiber Amplifiers due to Transverse Mode Instability, Thermal Lensing, and Fiber Mechanical Reliability. In Fiber Lasers XV: Technology and Systems; SPIE LASE 10512; SPIE Digital Library: San Francisco, CA, USA, 2018; p. 1051205. [Google Scholar]
- Zhu, J.; Zhou, P.; Ma, Y.; Xu, X.; Liu, Z. Power scaling analysis of tandem-pumped Yb-doped fiber lasers and amplifiers. Opt. Express 2011, 19, 18645. [Google Scholar] [CrossRef]
- Zervas, M.N. Transverse mode instability, thermal lensing and power scaling in Yb3+ -doped high-power fiber amplifiers. Opt. Express 2019, 27, 19019. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G. Nonlinear Fiber Optics, 6th ed.; Academic Press: London, UK, 2019; ISBN 9780128170427. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 4th ed.; Academic Press: Cambrigde, MA, USA, 2020; ISBN 9780128110027. [Google Scholar]
- Jauregui, C.; Stihler, C.; Limpert, J. Transverse mode instability. Adv. Opt. Photonics 2020, 12, 429. [Google Scholar] [CrossRef]
- Hejaz, K.; Shayganmanesh, M.; Rezaei-Nasirabad, R.; Roohforouz, A.; Azizi, S.; Abedinajafi, A.; Vatani, V. Modal instability induced by stimulated Raman scattering in high-power Yb-doped fiber amplifiers. Opt. Lett. 2017, 42, 5274. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Jing, F.; Li, C.; Liu, Y.; Luo, Q.; Lin, H.; Huang, Z.; Xu, S.; Yang, Z.; Wang, J. Impact of Stimulated Raman Scattering on the Transverse Mode Instability Threshold. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Kim, J.; Dupriez, P.; Codemard, C.; Nilsson, J.; Sahu, J.K. Suppression of stimulated Raman scattering in a high power Yb-doped fiber amplifier using a W-type core with fundamental mode cut-off. Opt. Express 2006, 14, 5103. [Google Scholar] [CrossRef] [PubMed]
- Jansen, F.; Nodop, D.; Jauregui, C.; Limpert, J.; Tünnermann, A. Modeling the inhibition of stimulated Raman scattering in passive and active fibers by lumped spectral filters in high power fiber laser systems. Opt. Express 2009, 17, 16255. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Jiang, M.; Shi, C.; Zhou, P.; Zhao, G.; Gu, X. Spectral shaping for suppressing stimulated-Raman-scattering in a fiber laser. Appl. Opt. 2017, 56, 3538. [Google Scholar] [CrossRef]
- Shi, C.; Su, R.T.; Zhang, H.W.; Yang, B.L.; Wang, X.L.; Zhou, P.; Xu, X.J.; Lu, Q.S. Experimental Study of Output Characteristics of Bi-Directional Pumping High Power Fiber Amplifier in Different Pumping Schemes. IEEE Photonics J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Zenteno, L.A.; Wang, J.; Walton, D.T.; Ruffin, B.A.; Li, M.J.; Gray, S.; Crowley, A.; Chen, X. Suppression of Raman gain in single-transverse-mode dual-hole-assisted fiber. Opt. Express 2005, 13, 8921. [Google Scholar] [CrossRef]
- Liu, A.; Chen, X.; Li, M.-J.; Wang, J.; Walton, D.T.; Zenteno, L.A. Suppressing nonlinear effects for power scaling of high power fiber lasers. Passiv Compon. Fiber-Based Devices IV 2007, 6781, 67810H. [Google Scholar] [CrossRef]
- Li, T.; Ke, W.; Ma, Y.; Sun, Y.; Gao, Q. Suppression of stimulated Raman scattering in a high-power fiber amplifier by inserting long transmission fibers in a seed laser. J. Opt. Soc. Am. B 2019, 36, 1457. [Google Scholar] [CrossRef]
- Jiao, K.; Shen, H.; Guan, Z.; Yang, F.; Zhu, R. Suppressing stimulated Raman scattering in kW-level continuous-wave MOPA fiber laser based on long-period fiber gratings. Opt. Express 2020, 28, 6048. [Google Scholar] [CrossRef] [PubMed]
- Hadjifotiou, A.; Hill, G.A. Suppression of stimulated brillouin backscattering by psk modulation for high-power optical transmission. IEE Proc. J Optoelectron. 1986, 133, 256. [Google Scholar] [CrossRef]
- Willems, F.W.; Muys, W.; Leong, J.S. Simultaneous suppression of stimulated Brillouin scattering and interferometric noise in externally modulated lightwave AM-SCM systems. IEEE Photonics Technol. Lett. 1994, 6, 1476–1478. [Google Scholar] [CrossRef]
- Broderick, N.G.R.; Offerhaus, H.L.; Richardson, D.J.; Sammut, R.A.; Caplen, J.; Dong, L. Large Mode Area Fibers for High Power Applications. Opt. Fiber Technol. 1999, 5, 185–196. [Google Scholar] [CrossRef]
- Koyamada, Y.; Sato, S.; Nakamura, S.; Sotobayashi, H.; Chujo, W. Simulating and designing Brillouin gain spectrum in single-mode fibers. J. Light. Technol. 2004, 22, 631–639. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.H.; Jeong, H.; Park, M.; Seung, J.H.; Lee, J.H. 2.05 kW all-fiber high-beam-quality fiber amplifier with stimulated Brillouin scattering suppression incorporating a narrow-linewidth fiber-Bragg-grating-stabilized laser diode seed source. Appl. Opt. 2019, 58, 6251. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Zhao, X.; Wang, M.; Wang, Z. Suppression of stimulated Brillouin scattering in optical fibers by tilted fiber Bragg gratings. Opt. Lett. 2020, 45, 4802. [Google Scholar] [CrossRef] [PubMed]
- Prakash, R.; Vikram, B.S.; Supradeepa, V.R. Polarization Maintaining, Narrow Linewidth Fiber Laser with >1 kW Output Power Using a Novel Dual Sine and Noise Modulation for Enhanced SBS Suppression. In Fiber Lasers XVIII Technology and Systems; Zervas, M.N., Jauregui-Misas, C., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11665, p. 3. [Google Scholar]
- Anderson, B.M.; MacDonald, K.; Taliaferro, A.; Flores, A. SBS Suppression Techniques in High-Power, Narrow-Linewidth Fiber Amplifiers. In Fiber Lasers XVIII: Technology and Systems; Zervas, M.N., Jauregui-Misas, C., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11665, p. 12. [Google Scholar]
- Zeringue, C.; Dajani, I.; Naderi, S.; Moore, G.T.; Robin, C. A theoretical study of transient stimulated Brillouin scattering in optical fibers seeded with phase-modulated light. Opt. Express 2012, 20, 21196. [Google Scholar] [CrossRef] [PubMed]
- Flores, A.; Robin, C.; Lanari, A.; Dajani, I. Pseudo-random binary sequence phase modulation for narrow linewidth, kilowatt, monolithic fiber amplifiers. Opt. Express 2014, 22, 17735. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, B.; Liu, M.; Huang, X.; Feng, Y.; Cheng, D.; He, B.; Zhou, J.; Nilsson, J. Optimization and visualization of phase modulation with filtered and amplified maximal-length sequence for SBS suppression in a short fiber system: A theoretical treatment. Opt. Express 2021, 29, 16781. [Google Scholar] [CrossRef]
- Beier, F.; Hupel, C.; Kuhn, S.; Hein, S.; Nold, J.; Proske, F.; Sattler, B.; Liem, A.; Jauregui, C.; Limpert, J.; et al. Single mode 43 kW output power from a diode-pumped Yb-doped fiber amplifier. Opt. Express 2017, 25, 14892. [Google Scholar] [CrossRef]
- Kobyakov, A.; Kumar, S.; Chowdhury, D.Q.; Ruffin, A.B.; Sauer, M.; Bickham, S.R.; Mishra, R. Design concept for optical fibers with enhanced SBS threshold. Opt. Express 2005, 13, 5338. [Google Scholar] [CrossRef]
- Ruffin, A.B.; Li, M.-J.; Chen, X.; Kobyakov, A.; Annunziata, F. Brillouin gain analysis for fibers with different refractive indices. Opt. Lett. 2005, 30, 3123. [Google Scholar] [CrossRef]
- Fini, J.M. Bend-resistant design of conventional and microstructure fibers with very large mode area. Opt. Express 2006, 14, 69. [Google Scholar] [CrossRef]
- Liu, A. Novel SBS Suppression Scheme for High-Power Fiber Amplifiers. In Fiber Lasers III: Technology, Systems, and Applications; SPIE: San Jose, CA, USA, 2006; Volume 6102, p. 61021R. [Google Scholar]
- Li, M.-J.; Chen, X.; Wang, J.; Gray, S.; Liu, A.; Demeritt, J.A.; Ruffin, A.B.; Crowley, A.M.; Walton, D.T.; Zenteno, L.A. Al/Ge co-doped large mode area fiber with high SBS threshold. Opt. Express 2007, 15, 8290. [Google Scholar] [CrossRef]
- Mermelstein, M.D.; Andrejco, M.J.; Fini, J.; Yablon, A.; Headley, C., III; DiGiovanni, D.J.; McCurdy, A.H. 11.2 dB SBS Gain Suppression in a Large Mode Area Yb-Doped Optical Fiber. In Fiber Lasers V: Technology, Systems, and Applications; Broeng, J., Headley, C., III, Eds.; SPIE: San Jose, CA, USA, 2008; Volume 6873, p. 68730N. [Google Scholar]
- Harish, A.V.; Nilsson, J. Suppression of Stimulated Brillouin Scattering in Single-Frequency Fiber Raman Amplifier Through Pump Modulation. J. Light. Technol. 2019, 37, 3280–3289. [Google Scholar] [CrossRef]
- Huang, Y.; Yan, P.; Wang, Z.; Tian, J.; Li, D.; Xiao, Q.; Gong, M. 2.19 kW narrow linewidth FBG-based MOPA configuration fiber laser. Opt. Express 2019, 27, 3136. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Ma, Y.; Chang, Z.; Peng, W.; Sun, Y.; Gao, Q.; Zhu, R.; Tang, C. 2.5 kW Narrow Linewidth Linearly Polarized All-Fiber MOPA With Cascaded Phase-Modulation to Suppress SBS Induced Self-Pulsing. IEEE Photonics J. 2020, 12, 1–15. [Google Scholar] [CrossRef]
- Wang, Y.; Ke, W.; Peng, W.; Chang, Z.; Feng, Y.; Sun, Y.; Gao, Q.; Ma, Y.; Zhu, R.; Tang, C. 3 kW, 0.2 nm narrow linewidth linearly polarized all-fiber laser based on a compact MOPA structure. Laser Phys. Lett. 2020, 17, 075101. [Google Scholar] [CrossRef]
- Lin, H.; Tao, R.; Li, C.; Wang, B.; Guo, C.; Shu, Q.; Zhao, P.; Xu, L.; Wang, J.; Jing, F.; et al. 3.7 kW monolithic narrow linewidth single mode fiber laser through simultaneously suppressing nonlinear effects and mode instability. Opt. Express 2019, 27, 9716. [Google Scholar] [CrossRef] [PubMed]
- Stolen, R.H.; Lin, C. Self-phase-modulation in silica optical fibers. Phys. Rev. A 1978, 17, 1448–1453. [Google Scholar] [CrossRef]
- Shimizu, F. Frequency Broadening in Liquids by a Short Light Pulse. Phys. Rev. Lett. 1967, 19, 1097–1100. [Google Scholar] [CrossRef]
- Hasegawa, A.; Tappert, F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl. Phys. Lett. 1973, 23, 142–144. [Google Scholar] [CrossRef]
- Farrow, R.L.; Kliner, D.A.V.; Hadley, G.R.; Smith, A.V. Peak-power limits on fiber amplifiers imposed by self-focusing. Opt. Lett. 2006, 31, 3423. [Google Scholar] [CrossRef]
- Dong, L. Approximate Treatment of the Nonlinear Waveguide Equation in the Regime of Nonlinear Self-Focus. J. Light. Technol. 2008, 26, 3476–3485. [Google Scholar] [CrossRef]
- Schimpf, D.N.; Eidam, T.; Seise, E.; Hädrich, S.; Limpert, J.; Tünnermann, A. Circular versus linear polarization in laser-amplifiers with Kerr-nonlinearity. Opt. Express 2009, 17, 18774. [Google Scholar] [CrossRef]
- Smith, A.V.; Do, B.T.; Hadley, G.R.; Farrow, R.L. Optical Damage Limits to Pulse Energy from Fibers. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 153–158. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, W.; Zhao, B.; Li, Z.; Li, G.; Gao, Q.; Ju, P.; Gao, W.; She, S.; Wu, P. Four-wave mixing effect on high-power continuous-wave all-fiber lasers. Mod. Phys. Lett. B 2018, 32, 1850275. [Google Scholar] [CrossRef]
- Eidam, T.; Wirth, C.; Jauregui, C.; Stutzki, F.; Jansen, F.; Otto, H.-J.; Schmidt, O.; Schreiber, T.; Limpert, J.; Tünnermann, A. Experimental observations of the threshold-like onset of mode instabilities in high power fiber amplifiers. Opt. Express 2011, 19, 13218. [Google Scholar] [CrossRef]
- Smith, A.V.; Smith, J.J. Influence of pump and seed modulation on the mode instability thresholds of fiber amplifiers. Opt. Express 2012, 20, 24545. [Google Scholar] [CrossRef]
- Smith, A.V.; Smith, J.J. Mode instability in high power fiber amplifiers. Opt. Express 2011, 19, 10180. [Google Scholar] [CrossRef] [PubMed]
- Jauregui, C.; Eidam, T.; Otto, H.-J.; Stutzki, F.; Jansen, F.; Limpert, J.; Tünnermann, A. Physical origin of mode instabilities in high-power fiber laser systems. Opt. Express 2012, 20, 12912. [Google Scholar] [CrossRef] [PubMed]
- Ward, B.; Robin, C.; Dajani, I. Origin of thermal modal instabilities in large mode area fiber amplifiers. Opt. Express 2012, 20, 11407. [Google Scholar] [CrossRef] [PubMed]
- Hejaz, K.; Shayganmanesh, M.; Azizi, S.; Abedinajafi, A.; Roohforouz, A.; Rezaei-Nasirabad, R.; Vatani, V. Transverse mode instability of fiber oscillators in comparison with fiber amplifiers. Laser Phys. Lett. 2018, 15, 055102. [Google Scholar] [CrossRef]
- Roohforouz, A.; Eyni Chenar, R.; Rezaei-Nasirabad, R.; Azizi, S.; Hejaz, K.; Hamedani Golshan, A.; Abedinajafi, A.; Vatani, V.; Nabavi, S.H. The effect of population inversion saturation on the transverse mode instability threshold in high power fiber laser oscillators. Sci. Rep. 2021, 11, 21116. [Google Scholar] [CrossRef] [PubMed]
- Ke, W.-W.; Wang, X.-J.; Bao, X.-F.; Shu, X.-J. Thermally induced mode distortion and its limit to power scaling of fiber lasers. Opt. Express 2013, 21, 14272. [Google Scholar] [CrossRef]
- Zervas, M.N. Power Scalability in High Power Fibre Amplifiers. In Proceedings of the 2017 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 25–29 June 2017; Volume 82, p. 1. [Google Scholar]
- Brown, D.C.; Hoffman, H.J. Thermal, stress, and thermo-optic effects in high average power double-clad silica fiber lasers. IEEE J. Quantum Electron. 2001, 37, 207–217. [Google Scholar] [CrossRef]
- Lapointe, M.-A.; Chatigny, S.; Piché, M.; Cain-Skaff, M.; Maran, J.-N. Thermal Effects in High-Power CW Fiber Lasers. In Fiber Lasers VI: Technology, Systems, and Applications; Gapontsev, D.V., Kliner, D.A., Dawson, J.W., Tankala, K., Eds.; SPIE: San Jose, CA, USA, 2009; Volume 7195, p. 71951U. [Google Scholar]
- Stuart, B.C.; Feit, M.D.; Rubenchik, A.M.; Shore, B.W.; Perry, M.D. Laser-Induced Damage in Dielectrics with Nanosecond to Subpicosecond Pulses. Phys. Rev. Lett. 1995, 74, 2248–2251. [Google Scholar] [CrossRef]
- Smith, A.; Do, B.; Soderlund, M. Deterministic Nanosecond Laser-Induced Breakdown Thresholds in Pure and Yb 3+ Doped Fused Silica. In Fiber Lasers IV: Technology, Systems and Applications; SPIE: San Jose, CA, USA, 2007; Volume 6453, p. 645317. [Google Scholar] [CrossRef]
- Gapontsev, V.; Gapontsev, D.; Platonov, N.; Shkurikhin, O.; Fomin, V.; Mashkin, A.; Abramov, M.; Ferin, S. 2 kW CW Ytterbium Fiber Laser with Record Diffraction-Limited Brightness. In Proceedings of the CLEO/Europe Conference on Lasers and Electro-Optics Europe, Munich, Germany, 12–17 June 2005; Volume 12, p. 508. [Google Scholar]
- Jain, D.; Jung, Y.; Barua, P.; Alam, S.; Sahu, J.K. Demonstration of ultra-low NA rare-earth doped step index fiber for applications in high power fiber lasers. Opt. Express 2015, 23, 7407. [Google Scholar] [CrossRef]
- Midilli, Y.; Ortaç, B. An All-Fiber Ultra-Low Numerical Aperture High Power Fiber MOPA System with an Output Power above 500 W. In Proceedings of the European Conference on Lasers and Electro-Optics, Munich, Germany, 23–27 June 2019; Volume 140, p. 14892. [Google Scholar]
- Lim, K.-J.; Kai-Wen Seah, S.; Yong’En Ye, J.; Lim, W.W.; Seah, C.-P.; Tan, Y.-B.; Tan, S.; Lim, H.; Sidharthan, R.; Prasadh, A.R.; et al. High absorption large-mode area step-index fiber for tandem-pumped high-brightness high-power lasers. Photonics Res. 2020, 8, 1599. [Google Scholar] [CrossRef]
- Paschotta, R.; Nilsson, J.; Barber, P.R.; Caplen, J.E.; Tropper, A.C.; Hanna, D.C. Lifetime quenching in Yb-doped fibres. Opt. Commun. 1997, 136, 375–378. [Google Scholar] [CrossRef]
- Huang, L.; Yao, T.; Leng, J.; Guo, S.; Tao, R.; Zhou, P.; Cheng, X. Mode instability dynamics in high-power low-numerical-aperture step-index fiber amplifier. Appl. Opt. 2017, 56, 5412. [Google Scholar] [CrossRef] [PubMed]
- Midilli, Y.; Ortac, B. Demonstration of an All-Fiber Ultra-Low Numerical Aperture Ytterbium-Doped Large Mode Area Fiber in a Master Oscillator Power Amplifier Configuration Above 1 kW Power Level. J. Light. Technol. 2020, 38, 1915–1920. [Google Scholar] [CrossRef]
- Lin, H.; Xu, L.; Li, C.; Shu, Q.; Chu, Q.; Xie, L.; Guo, C.; Zhao, P.; Li, Z.; Wang, J.; et al. 10.6 kW high-brightness cascade-end-pumped monolithic fiber lasers directly pumped by laser diodes in step-index large mode area double cladding fiber. Results Phys. 2019, 14, 102479. [Google Scholar] [CrossRef]
- Codemard, C.A.; Sahu, J.K.; Nilsson, J. Tandem Cladding-Pumping for Control of Excess Gain in Ytterbium-Doped Fiber Amplifiers. IEEE J. Quantum Electron. 2010, 46, 1860–1869. [Google Scholar] [CrossRef]
- Dai, J.; Li, F.; Liu, N.; Shen, C.; Zhang, L.; Li, H.; Li, Y.; Sun, S.; Li, Y.; Lv, J.; et al. Extraction of More than 10 kW from Yb-Doped Tandem-Pumping Aluminophosphosilicate Fiber. In Global Intelligent Industry Conference 2020; Wang, L., Ed.; SPIE: Bellingham, WA, USA, 2021; Volume 11780, p. 76. [Google Scholar]
- Zhou, P.; Xiao, H.; Leng, J.; Xu, J.; Chen, Z.; Zhang, H.; Liu, Z. High-power fiber lasers based on tandem pumping. J. Opt. Soc. Am. B 2017, 34, A29. [Google Scholar] [CrossRef]
- Glick, Y.; Sintov, Y.; Zuitlin, R.; Pearl, S.; Shamir, Y.; Feldman, R.; Horvitz, Z.; Shafir, N. Single-mode 230 W output power 1018 nm fiber laser and ASE competition suppression. J. Opt. Soc. Am. B 2016, 33, 1392. [Google Scholar] [CrossRef]
- Khitrov, V.; Samson, B.; Machewirth, D.; Tankala, K. 242W Single-Mode CW Fiber Laser Operating at 1030nm Lasing Wavelength and with 0.35 nm Spectral Width. In Proceedings of the Advanced Solid-State Photonics, OSA, Incline Village, NV, USA, 29 January–1 February 2006; p. WD5. [Google Scholar]
- Ottenhues, C.; Theeg, T.; Hausmann, K.; Wysmolek, M.; Sayinc, H.; Neumann, J.; Kracht, D. Single-mode monolithic fiber laser with 200 W output power at a wavelength of 1018 nm. Opt. Lett. 2015, 40, 4851. [Google Scholar] [CrossRef]
- Wang, X.; Yan, P.; Wang, Z.; Huang, Y.; Tian, J.; Li, D.; Xiao, Q. The 5.4 kW Output Power of the Ytterbium-Doped Tandem-Pumping Fiber Amplifier. In Proceedings of the Conference on Lasers and Electro Optics, San Jose, CA, USA, 13–18 May 2018; pp. 4–5. [Google Scholar]
- Lafouti, M.; Latifi, H.; Sarabi, H.; Fathi, H.; Ebrahimzadeh, S.; Sarikhani, S. 407 W specially-designed fiber laser at 1018 nm using a gain fiber with a low core/cladding ratio of 20/400 μ m. Laser Phys. 2018, 28, 115102. [Google Scholar] [CrossRef]
- Lafouti, M.; Latifi, H.; Fathi, H.; Ebrahimzadeh, S.; Sarikhani, S.; Sarabi, H. Experimental investigation of a high-power 1018 nm fiber laser using a 20/400 μm ytterbium-doped fiber. Appl. Opt. 2019, 58, 729. [Google Scholar] [CrossRef] [PubMed]
- Yan, P.; Wang, X.; Wang, Z.; Huang, Y.; Li, D.; Xiao, Q.; Gong, M. A 1150-W 1018-nm Fiber Laser Bidirectional Pumped by Wavelength-Stabilized Laser Diodes. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–6. [Google Scholar] [CrossRef]
- Fomin, V.; Abramov, M.; Ferin, A.; Abramov, A.; Mochalov, D.; Platonov, N.V.G. 10 kW Single-Mode Fiber Laser. In Proceedings of the 5th International Symposium on High-Power Fiber Lasers and Their Applications, St. Petersburg, Russia, 28 July 2010. [Google Scholar]
- Ferin, A.; Gapontsev, V.; Fomin, V.; Abramov, A.; Avramov, M.; Mochalov, D. 17 kW CW Laser with 50 µm Delivery Fiber. In Proceedings of the 15th Internation Conference on Laser Optics, St. Petersburg, Russia, 25–29 June 2012; p. 12AD. [Google Scholar]
- Yao, T.; Ji, J.; Nilsson, J. Ultra-Low Quantum-Defect Heating in Ytterbium-Doped Aluminosilicate Fibers. J. Light. Technol. 2014, 32, 429–434. [Google Scholar] [CrossRef]
- Naderi, S.; Dajani, I.; Grosek, J.; Madden, T.; Dinh, T.-N. Theoretical Analysis of Effect of Pump and Signal Wavelengths on Modal Instabilities in Yb-Doped Fiber Amplifiers. In Nonlinear Frequency Generation and Conversion: Material, Devices and Applications XIII; SPIE: San Francisco, CA, USA, 2014; Volume 8964, pp. 264–270. [Google Scholar] [CrossRef]
- Fu, S.; Feng, X.; Si, L.; Guo, Z.; Jia, X.; Zhao, Y.; Yuan, S.; Dong, X. Self-pulsing dynamics of high-power Yb-doped fiber lasers. Microw. Opt. Technol. Lett. 2006, 48, 2282–2285. [Google Scholar] [CrossRef]
- Limpert, J.; Klenke, A.; Kienel, M.; Breitkopf, S.; Eidam, T.; Hadrich, S.; Jauregui, C.; Tunnermann, A. Performance Scaling of Ultrafast Laser Systems by Coherent Addition of Femtosecond Pulses. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 268–277. [Google Scholar] [CrossRef]
- Klenke, A.; Muller, M.; Stark, H.; Kienel, M.; Jauregui, C.; Tunnermann, A.; Limpert, J. Coherent Beam Combination of Ultrafast Fiber Lasers. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–9. [Google Scholar] [CrossRef]
- Klenke, A.; Seise, E.; Limpert, J.; Tünnermann, A. Basic considerations on coherent combining of ultrashort laser pulses. Opt. Express 2011, 19, 25379. [Google Scholar] [CrossRef] [PubMed]
- Uberna, R.; Bratcher, A.; Tiemann, B.G. Coherent Polarization Beam Combination. IEEE J. Quantum Electron. 2010, 46, 1191–1196. [Google Scholar] [CrossRef]
- Fan, T.Y. Laser beam combining for high-power, high-radiance sources. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 567–577. [Google Scholar] [CrossRef]
- Augst, S.J.; Ranka, J.K.; Fan, T.Y.; Sanchez, A. Beam combining of ytterbium fiber amplifiers. J. Opt. Soc. Am. B 2007, 24, 1707. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Xu, X.; Wang, X.; Ma, Y. Coherent beam combining of high power fiber lasers: Progress and prospect. Sci. China Technol. Sci. 2013, 56, 1597–1606. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, P.; Su, R.; Tao, R.; Ma, Y.; Wang, X.; Zhou, P. High-power coherent beam polarization combination of fiber lasers: Progress and prospect. J. Opt. Soc. Am. B 2017, 34, A7. [Google Scholar] [CrossRef]
- Bourdon, P.; Le Gouet, J.; Goular, D.; Lombard, L.; Durecu, A. Coherent Combining with Active Phase Control: A Practical Tool for Adaptive and Nonlinear Optics. In Proceedings of the 2017 Conference on Lasers and Electro-Optics Pacific Rim (CLEO-PR), Singapore, 31 July–4 August 2017; Volume 122, pp. 1–3. [Google Scholar]
- Hanna, M.; Guichard, F.; Zaouter, Y.; Papadopoulos, D.N.; Druon, F.; Georges, P. Coherent combination of ultrafast fiber amplifiers. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 062004. [Google Scholar] [CrossRef]
- Sprangle, P.; Ting, A.; Penano, J.; Fischer, R.; Hafizi, B. Incoherent Combining and Atmospheric Propagation of High-Power Fiber Lasers for Directed-Energy Applications. IEEE J. Quantum Electron. 2009, 45, 138–148. [Google Scholar] [CrossRef]
- Sprangle, P.; Hafizi, B.; Ting, A.; Fischer, R. High-power lasers for directed-energy applications. Appl. Opt. 2015, 54, F201. [Google Scholar] [CrossRef]
- Lockheed Martin Demonstrates 30 kW Weapons-Grade Fiber Laser. Available online: https://www.laserfocusworld.com/lasers-sources/article/16564243/lockheed-martin-demonstrates-30-kw-weaponsgrade-fiber-laser (accessed on 30 January 2014).
- Zhu, Y.; Li, P.; Li, C.; Wang, L.; Yao, C.; Zhang, X.; Li, S.; Zhou, Y. Quantizing the Coherent Polarization Beam Combination from Temporal, Spatial, and Spectral Domains. In Fourth International Symposium on High Power Laser Science and Engineering (HPLSE 2021); Zhu, J., Ed.; SPIE: Bellingham, WA, USA, 2021; Volume 11849, p. 18. [Google Scholar]
- Lei, C.; Gu, Y.; Chen, Z.; Wang, Z.; Zhou, P.; Ma, Y.; Xiao, H.; Leng, J.; Wang, X.; Hou, J.; et al. Incoherent beam combining of fiber lasers by an all-fiber 7 × 1 signal combiner at a power level of 14 kW. Opt. Express 2018, 26, 10421. [Google Scholar] [CrossRef]
- Goodno, G.D.; Asman, C.P.; Anderegg, J.; Brosnan, S.; Cheung, E.C.; Hammons, D.; Injeyan, H.; Komine, H.; Long, W.H.; McClellan, M.; et al. Brightness-Scaling Potential of Actively Phase-Locked Solid-State Laser Arrays. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 460–472. [Google Scholar] [CrossRef]
- Augst, S.J.; Goyal, A.K.; Aggarwal, R.L.; Fan, T.Y.; Sanchez, A. Wavelength beam combining of ytterbium fiber lasers. Opt. Lett. 2003, 28, 331. [Google Scholar] [CrossRef] [PubMed]
- Sevian, A.; Andrusyak, O.; Ciapurin, I.; Smirnov, V.; Venus, G.; Glebov, L. Efficient power scaling of laser radiation by spectral-beam combining: Erratum. Opt. Lett. 2008, 33, 760. [Google Scholar] [CrossRef]
- Zhu, Z.; Gou, L.; Jiang, M.; Hui, Y.; Lei, H.; Li, Q. High Beam Quality in Two Directions and High Efficiency Output of a Diode Laser Array by Spectral-Beam-Combining. Opt. Express 2014, 22, 17804. [Google Scholar] [CrossRef]
- Sanchez-Rubio, A.; Fan, T.Y.; Augst, S.J.; Goyal, A.K.; Creedon, K.J.; Gopinath, J.T.; Daneu, V.; Chann, B.; Hung, R. Wavelength Beam Combining for Power and Brightness Scaling of Laser Systems. MIT-Lincoln Lab. J. 2014, 20, 52–66. [Google Scholar]
- Wirth, C.; Schmidt, O.; Tsybin, I.; Schreiber, T.; Eberhardt, R.; Limpert, J.; Tünnermann, A.; Ludewigt, K.; Gowin, M.; ten Have, E.; et al. High average power spectral beam combining of four fiber amplifiers to 82 kW. Opt. Lett. 2011, 36, 3118. [Google Scholar] [CrossRef]
- Schmidt, O.; Rekas, M.; Wirth, C.; Rothhardt, J.; Rhein, S.; Kliner, A.; Strecker, M.; Schreiber, T.; Limpert, J.; Eberhardt, R.; et al. High power narrow-band fiber-based ASE source. Opt. Express 2011, 19, 4421. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Liu, W.; Leng, J.; Xiao, H.; Guo, S.; Zhou, P.; Chen, J. Power scaling of narrowband high-power all-fiber superfluorescent fiber source to 1.87 kW. Opt. Lett. 2015, 40, 2973. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, Y.; Wang, J.; Hu, M.; Liu, G.; Zhao, X.; Chen, X.; Liu, K.; Zhao, C.; He, B.; et al. 10.8 kW spectral beam combination of eight all-fiber superfluorescent sources and their dispersion compensation. Opt. Express 2016, 24, 12063. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, Z.; Liu, X.; Yu, M.; Li, S.; Zhang, L.; Ni, Q.; Wang, J.; Wang, X. High-power, high-beam-quality spectral beam combination of six narrow-linewidth fiber amplifiers with two transmission diffraction gratings. Appl. Opt. 2019, 58, 8339. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Ma, J.; Wei, C.; Zhu, R.; Zhou, W.; Yuan, Q.; Pan, S.; Zhang, J.; Wen, Y.; Dou, J. 10 kW-level spectral beam combination of two high power broad-linewidth fiber lasers by means of edge filters. Opt. Express 2017, 25, 32783. [Google Scholar] [CrossRef]
- Wirth, C.; Schmidt, O.; Tsybin, I.; Schreiber, T.; Peschel, T.; Brückner, F.; Clausnitzer, T.; Limpert, J.; Eberhardt, R.; Tünnermann, A.; et al. 2 kW incoherent beam combining of four narrow-linewidth photonic crystal fiber amplifiers. Opt. Express 2009, 17, 1178. [Google Scholar] [CrossRef] [PubMed]
- Madasamy, P.; Loftus, T.; Thomas, A.; Jones, P.; Honea, E. Comparison of Spectral Beam Combining Approaches for High Power Fiber Laser Systems. In Laser Source Technology for Defense and Security IV; Dubinskii, M., Wood, G.L., Eds.; SPIE: Orlando, FL, USA, 2008; Volume 6952, p. 695207. [Google Scholar]
- Shi, C.; Zhang, H.; Wang, X.; Zhou, P.; Xu, X. kW-class high power fiber laser enabled by active long tapered fiber. High Power Laser Sci. Eng. 2018, 6, e16. [Google Scholar] [CrossRef]
- Ma, J.; Chen, F.; Wei, C.; Zhu, R. Modeling and Analysis of the Influence of an Edge Filter on the Combining Efficiency and Beam Quality of a 10-kW-Class Spectral Beam-Combining System. Appl. Sci. 2019, 9, 2152. [Google Scholar] [CrossRef]
- Lockheed Martin to Deliver World Record-Setting 60kW Laser to U.S. Army. 2017. Available online: https://news.lockheedmartin.com/2017-03-16-Lockheed-Martin-to-Deliver-World-Record-Setting-60kW-Laser-to-U-S-Army (accessed on 28 May 2021).
- Honea, E.; Afzal, R.S.; Savage-Leuchs, M.; Henrie, J.; Brar, K.; Kurz, N.; Jander, D.; Gitkind, N.; Hu, D.; Robin, C.; et al. Advances in Fiber Laser Spectral Beam Combining for Power Scaling. In Components and Packaging for Laser Systems II; Glebov, A.L., Leisher, P.O., Eds.; SPIE: San Francisco, CA, USA, 2016; Volume 9730, p. 97300Y. [Google Scholar]
- Team Dynetics Receives Contract for Next Phase of 100 KW-Class Laser Weapon System for U.S. Army. 2018. Available online: https://news.lockheedmartin.com/2018-08-06-Team-Dynetics-Receives-Contract-for-Next-Phase-of-100-kW-Class-Laser-Weapon-System-for-U-S-Army (accessed on 4 December 2021).
- Brignon, A. Coherent Laser Beam Combining. Wiley-VCH: Veinheim, Germany, 2013; p. 481. [Google Scholar]
- Ripper, J.E.; Paoli, T.L. Optical coupling of adjacent stripe-geometry junction lasers. Appl. Phys. Lett. 1970, 17, 371–373. [Google Scholar] [CrossRef]
- Kozlov, V.A.; Hernández-Cordero, J.; Morse, T.F. All-fiber coherent beam combining of fiber lasers. Opt. Lett. 1999, 24, 1814. [Google Scholar] [CrossRef]
- Cheung, E.C.; Weber, M.; Rice, R.R. Phase Locking of a Pulsed Fiber Amplifier. In Proceedings of the Advanced Solid-State Photonics, OSA, Nara, Japan, 27–30 January 2008; p. WA2. [Google Scholar]
- McNaught, S.J.; Asman, C.P.; Injeyan, H.; Jankevics, A.; Johnson, A.M.F.; Jones, G.C.; Komine, H.; Machan, J.; Marmo, J.; McClellan, M.; et al. 100-kW Coherently Combined Nd:YAG MOPA Laser Array. In Proceedings of the Frontiers in Optics 2009/Laser Science XXV/Fall 2009 OSA Optics & Photonics Technical Digest, San Jose, CA, USA, 11–15 October 2009; p. FThD2. [Google Scholar]
- Goodno, G.D.; Shih, C.; Rothenberg, J.E. Perturbative analysis of coherent combining efficiency with mismatched lasers. Opt. Express 2010, 18, 25403. [Google Scholar] [CrossRef] [PubMed]
- Leshchenko, V.E. Coherent combining efficiency in tiled and filled aperture approaches. Opt. Express 2015, 23, 15944. [Google Scholar] [CrossRef]
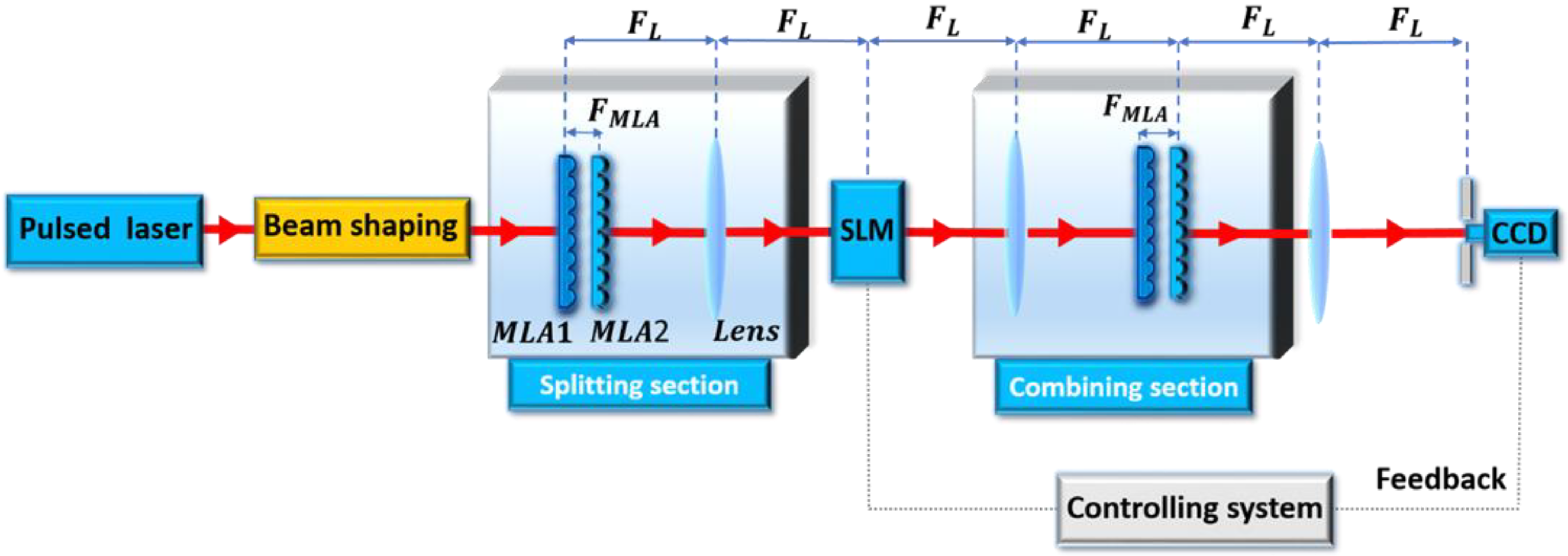
- Prossotowicz, M.; Heimes, A.; Flamm, D.; Jansen, F.; Otto, H.-J.; Budnicki, A.; Killi, A.; Morgner, U. Coherent beam combining with micro-lens arrays. Opt. Lett. 2020, 45, 6728. [Google Scholar] [CrossRef] [PubMed]
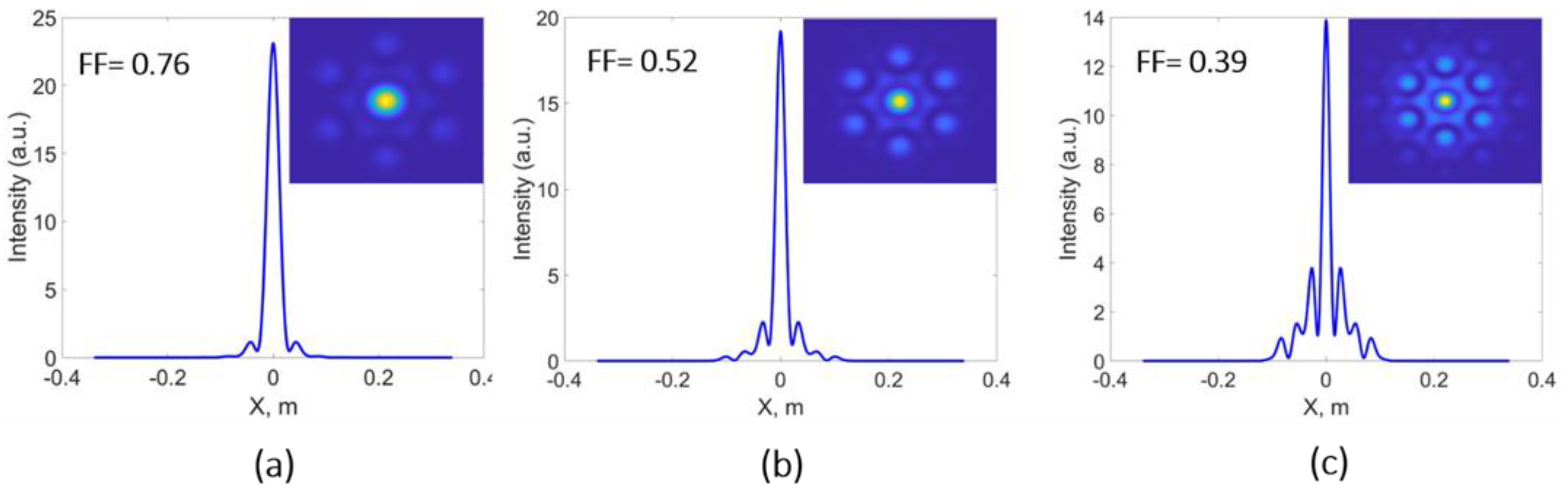
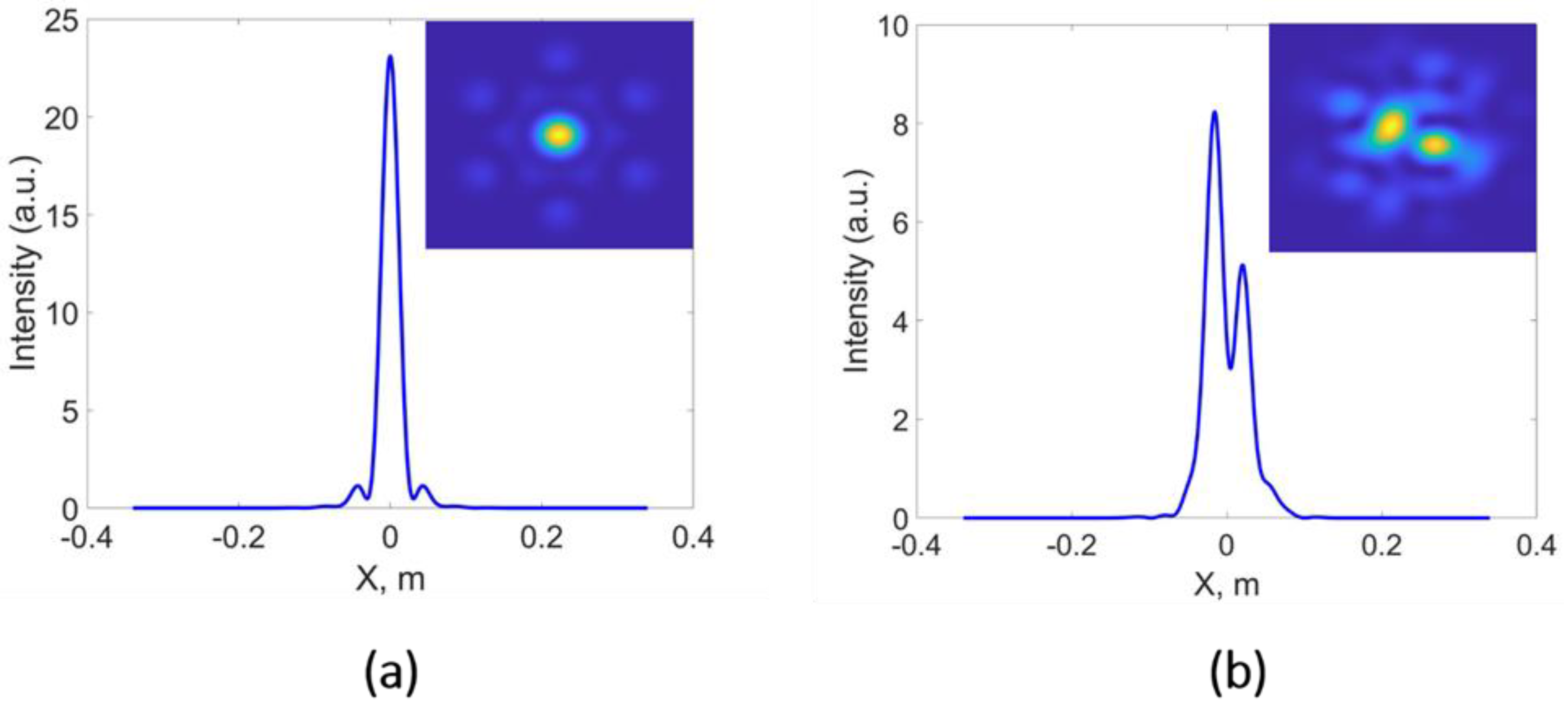
- Zhi, D.; Zhang, Z.; Ma, Y.; Wang, X.; Chen, Z.; Wu, W.; Zhou, P.; Si, L. Realization of large energy proportion in the central lobe by coherent beam combination based on conformal projection system. Sci. Rep. 2017, 7, 2199. [Google Scholar] [CrossRef]
- Scifres, D.R.; Streifer, W.; Burnham, R.D. High-power coupled-multiple-stripe phase-locked injection laser. Appl. Phys. Lett. 1979, 34, 259–261. [Google Scholar] [CrossRef]
- Tan, Y.; Li, X. Impact of Filling Factor on Correction of Piston and Tip/Tilt in Coherent Beam Combination. In 14th National Conference on Laser Technology and Optoelectronics (LTO 2019); Xu, H.-L., Chen, F., Ji, L., Li, B., Xie, X., Leng, Y., Sheng, Z., Yang, Y., Zhao, J., Zhu, J., Eds.; SPIE: Shanghai, China, 2019; Volume 11170, p. 215. [Google Scholar]
- Lachinova, S.L.; Vorontsov, M.A. Laser beam projection with adaptive array of fiber collimators II Analysis of atmospheric compensation efficiency. J. Opt. Soc. Am. A 2008, 25, 1960. [Google Scholar] [CrossRef] [PubMed]
- Le Dortz, J.; Heilmann, A.; Antier, M.; Bourderionnet, J.; Larat, C.; Fsaifes, I.; Daniault, L.; Bellanger, S.; Simon Boisson, C.; Chanteloup, J.-C.; et al. Highly scalable femtosecond coherent beam combining demonstrated with 19 fibers. Opt. Lett. 2017, 42, 1887. [Google Scholar] [CrossRef]
- Yu, C.X.; Augst, S.J.; Redmond, S.M.; Goldizen, K.C.; Murphy, D.V.; Sanchez, A.; Fan, T.Y. Coherent combining of a 4 kW, eight-element fiber amplifier array. Opt. Lett. 2011, 36, 2686. [Google Scholar] [CrossRef]
- Bourderionnet, J.; Bellanger, C.; Primot, J.; Brignon, A. Coherent Phase Combining of 64 Fibers. In Proceedings of the Conference on Lasers and Electro-Optics Europe and 12th European Quantum Electronics Conference (CLEO EUROPE/EQEC), Munich, Germany, 22–26 May 2011; Volume 19, p. 1. [Google Scholar]
- Weyrauch, T.; Vorontsov, M.A.; Carhart, G.W.; Beresnev, L.A.; Rostov, A.P.; Polnau, E.E.; Liu, J.J. Experimental demonstration of coherent beam combining over a 7 km propagation path. Opt. Lett. 2011, 36, 4455. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Tang, X.; Luo, Y.; Liu, C.; Li, J.; Zhang, D.; Wang, X.; Chen, T.; Han, M. Active phase locking of thirty fiber channels using multilevel phase dithering method. Rev. Sci. Instrum. 2016, 87, 033109. [Google Scholar] [CrossRef] [PubMed]
- Kabeya, D.; Kermène, V.; Fabert, M.; Benoist, J.; Saucourt, J.; Desfarges-Berthelemot, A.; Barthélémy, A. Efficient phase-locking of 37 fiber amplifiers by phase-intensity mapping in an optimization loop. Opt. Express 2017, 25, 13816. [Google Scholar] [CrossRef]
- Fsaifes, I.; Daniault, L.; Bellanger, S.; Veinhard, M.; Bourderionnet, J.; Larat, C.; Lallier, E.; Durand, E.; Brignon, A.; Chanteloup, J.-C. Coherent beam combining of 61 femtosecond fiber amplifiers. Opt. Express 2020, 28, 20152. [Google Scholar] [CrossRef] [PubMed]
- Du, Q.; Wang, D.; Zhou, T.; Li, D.; Wilcox, R. Characterization and Control of 81-beam Diffractive Coherent Combining. In Proceedings of the Laser Congress 2020 (ASSL, LAC), Washington, DC, USA, 13–16 October 2020; p. ATu4A.5. [Google Scholar]
- Chang, H.; Chang, Q.; Xi, J.; Hou, T.; Su, R.; Ma, P.; Wu, J.; Li, C.; Jiang, M.; Ma, Y.; et al. First experimental demonstration of coherent beam combining of more than 100 beams. Photonics Res. 2020, 8, 1943. [Google Scholar] [CrossRef]
- Klenke, A.; Müller, M.; Stark, H.; Stutzki, F.; Hupel, C.; Schreiber, T.; Tünnermann, A.; Limpert, J. Coherently combined 16-channel multicore fiber laser system. Opt. Lett. 2018, 43, 1519. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, L.P.; Hanna, M.; Bouwmans, G.; El Hamzaoui, H.; Bouazaoui, M.; Labat, D.; Delplace, K.; Pouysegur, J.; Guichard, F.; Rigaud, P.; et al. Coherent beam combining with an ultrafast multicore Yb-doped fiber amplifier. Opt. Express 2015, 23, 5406. [Google Scholar] [CrossRef] [PubMed]
- Elkin, N.N.; Napartovich, A.P.; Sukharev, A.G.; Troschieva, V.N.; Vysotsky, D.V. Direct numerical simulation of radiation propagation in a multicore fiber. Opt. Commun. 2000, 177, 207–217. [Google Scholar] [CrossRef]
- Wrage, M.; Glas, P.; Fischer, D.; Leitner, M.; Vysotsky, D.V.; Napartovich, A.P. Phase locking in a multicore fiber laser by means of a Talbot resonator. Opt. Lett. 2000, 25, 1436. [Google Scholar] [CrossRef]
- Gorton, E.K.; Jenkins, R.M. Theory of 1-N-way phase-locked resonators. Appl. Opt. 2001, 40, 916. [Google Scholar] [CrossRef]
- Vysotsky, D.V.; Napartovich, A.P. Coherent beam combining in optically coupled laser arrays. Quantum Electron. 2019, 49, 989–1007. [Google Scholar] [CrossRef]
- Michaille, L.; Bennett, C.R.; Taylor, D.M.; Shepherd, T.J.; Broeng, J.; Simonsen, H.R.; Petersson, A. Phase locking and supermode selection in multicore photonic crystal fiber lasers with a large doped area. Opt. Lett. 2005, 30, 1668. [Google Scholar] [CrossRef]
- Fang, X.-H.; Hu, M.-L.; Liu, B.-W.; Chai, L.; Wang, C.-Y.; Zheltikov, A.M. Generation of 150 MW, 110 fs pulses by phase-locked amplification in multicore photonic crystal fiber. Opt. Lett. 2010, 35, 2326. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Paurisse, M.; Hanna, M.; Druon, F.; Georges, P. Wavefront Control by Digital Holography in an Yb-Doped Multi-Core Fiber Amplifier. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 16–21 May 2010; Volume 35, p. CThO4. [Google Scholar]
- Steinkopff, A.; Jauregui, C.; Aleshire, C.; Klenke, A.; Limpert, J. Optimizing the Design of Coherently Combined Multicore Fiber Amplifiers. In Fiber Lasers XVIII: Technology and Systems; Zervas, M.N., Jauregui-Misas, C., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11665, p. 58. [Google Scholar]
- Lin, D.; Carpenter, J.; Feng, Y.; Jain, S.; Jung, Y.; Feng, Y.; Zervas, M.N.; Richardson, D.J. Reconfigurable structured light generation in a multicore fibre amplifier. Nat. Commun. 2020, 11, 3986. [Google Scholar] [CrossRef]
- Weyrauch, T.; Vorontsov, M.; Mangano, J.; Ovchinnikov, V.; Bricker, D.; Polnau, E.; Rostov, A. Deep turbulence effects mitigation with coherent combining of 21 laser beams over 7 km. Opt. Lett. 2016, 41, 840. [Google Scholar] [CrossRef] [PubMed]
- Shekel, E.; Vidne, Y.; Urbach, B. 16 kW Single Mode CW Laser with Dynamic Beam for Material Processing. In Fiber Lasers XVII: Technology and Systems; Dong, L., Zervas, M.N., Eds.; SPIE: San Francisco, CA, USA, 2020; Volume 11260, p. 73. [Google Scholar]
- Ma, P.; Chang, H.; Ma, Y.; Su, R.; Qi, Y.; Wu, J.; Li, C.; Long, J.; Lai, W.; Chang, Q.; et al. 7.1 kW coherent beam combining system based on a seven-channel fiber amplifier array. Opt. Laser Technol. 2021, 140, 107016. [Google Scholar] [CrossRef]
- Müller, M.; Aleshire, C.; Klenke, A.; Haddad, E.; Légaré, F.; Tünnermann, A.; Limpert, J. 10.4 kW coherently combined ultrafast fiber laser. Opt. Lett. 2020, 45, 3083. [Google Scholar] [CrossRef]
- Regelskis, K.; Gavrilinas, N.; Trusovas, R.; Račiukaitis, G. Coherent addition of orthogonally polarized fibre lasers with high combining efficiency. Lith. J. Phys. 2010, 50, 209–214. [Google Scholar] [CrossRef]
- Seise, E.; Klenke, A.; Limpert, J.; Tünnermann, A. Coherent addition of fiber-amplified ultrashort laser pulses. Opt. Express 2010, 18, 27827. [Google Scholar] [CrossRef] [PubMed]
- Klenke, A.; Breitkopf, S.; Kienel, M.; Gottschall, T.; Eidam, T.; Hädrich, S.; Rothhardt, J.; Limpert, J.; Tünnermann, A. 530 W, 13 mJ, four-channel coherently combined femtosecond fiber chirped-pulse amplification system. Opt. Lett. 2013, 38, 2283. [Google Scholar] [CrossRef]
- Kienel, M.; Müller, M.; Klenke, A.; Limpert, J.; Tünnermann, A. 12 mJ kW-class ultrafast fiber laser system using multidimensional coherent pulse addition. Opt. Lett. 2016, 41, 3343. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.; Kienel, M.; Klenke, A.; Gottschall, T.; Shestaev, E.; Plötner, M.; Limpert, J.; Tünnermann, A. 1 kW 1 mJ eight-channel ultrafast fiber laser. Opt. Lett. 2016, 41, 3439. [Google Scholar] [CrossRef] [PubMed]
- Stark, H.; Buldt, J.; Müller, M.; Klenke, A.; Tünnermann, A.; Limpert, J. 23 mJ high-power fiber CPA system using electro-optically controlled divided-pulse amplification. Opt. Lett. 2019, 44, 5529. [Google Scholar] [CrossRef]
- Stark, H.; Buldt, J.; Müller, M.; Klenke, A.; Limpert, J. 1 kW, 10 mJ, 120 fs coherently combined fiber CPA laser system. Opt. Lett. 2021, 46, 969. [Google Scholar] [CrossRef]
- Müller, M.; Aleshire, C.; Buldt, J.; Stark, H.; Grebing, C.; Klenke, A.; Limpert, J. Scaling potential of beam-splitter-based coherent beam combination. Opt. Express 2021, 29, 27900. [Google Scholar] [CrossRef]
- Veldkamp, W.B.; Leger, J.R.; Swanson, G.J. Coherent summation of laser beams using binary phase gratings. Opt. Lett. 1986, 11, 303. [Google Scholar] [CrossRef]
- Ehbets, P.; Gale, M.T.; Herzig, H.P.; Prongué, D. High-efficiency continuous surface-relief gratings for two-dimensional array generation. Opt. Lett. 1992, 17, 908. [Google Scholar] [CrossRef]
- Coherent Laser Beam Combining. Available online: https://books.google.fi/books/about/Coherent_Laser_Beam_Combining.html?id=OccZAgAAQBAJ&source=kp_book_description&redir_esc=y (accessed on 8 June 2021).
- Flores, A.; Dajani, I.; Holten, R.; Ehrenreich, T.; Anderson, B. Multi-kilowatt diffractive coherent combining of pseudorandom-modulated fiber amplifiers. Opt. Eng. 2016, 55, 096101. [Google Scholar] [CrossRef]
- Hebling, J. Derivation of the pulse front tilt caused by angular dispersion. Opt. Quantum Electron. 1996, 28, 1759–1763. [Google Scholar] [CrossRef]
- Zhou, T.; Sano, T.; Wilcox, R. Coherent combination of ultrashort pulse beams using two diffractive optics. Opt. Lett. 2017, 42, 4422. [Google Scholar] [CrossRef]
- Cheung, E.C.; Ho, J.G.; Goodno, G.D.; Rice, R.R.; Rothenberg, J.; Thielen, P.; Weber, M.; Wickham, M. Diffractive-optics-based beam combination of a phase-locked fiber laser array. Opt. Lett. 2008, 33, 354. [Google Scholar] [CrossRef] [PubMed]
- Redmond, S.M.; Ripin, D.J.; Yu, C.X.; Augst, S.J.; Fan, T.Y.; Thielen, P.A.; Rothenberg, J.E.; Goodno, G.D. Diffractive coherent combining of a 25 kW fiber laser array into a 19 kW Gaussian beam. Opt. Lett. 2012, 37, 2832. [Google Scholar] [CrossRef]
- Thielen, P.A.; Ho, J.G.; Burchman, D.A.; Goodno, G.D.; Rothenberg, J.E.; Wickham, M.G.; Flores, A.; Lu, C.A.; Pulford, B.; Robin, C.; et al. Two-dimensional diffractive coherent combining of 15 fiber amplifiers into a 600 W beam. Opt. Lett. 2012, 37, 3741. [Google Scholar] [CrossRef] [PubMed]
- McNaught, S.J.; Thielen, P.A.; Adams, L.N.; Ho, J.G.; Johnson, A.M.; Machan, J.P.; Rothenberg, J.E.; Shih, C.-C.; Shimabukuro, D.M.; Wacks, M.P.; et al. Scalable Coherent Combining of Kilowatt Fiber Amplifiers Into a 2.4-kW Beam. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 174–181. [Google Scholar] [CrossRef]
- Wilcox, R.; Dahlen, D.; Sano, T. Femtosecond Beam Combination Using Diffractive Optic Pairs. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 14–19 May 2017; Volume 2017, p. SM4I.2. [Google Scholar]
- Zhou, T.; Du, Q.; Sano, T.; Wilcox, R.; Leemans, W. Two-dimensional combination of eight ultrashort pulsed beams using a diffractive optic pair. Opt. Lett. 2018, 43, 3269. [Google Scholar] [CrossRef]
- Du, Q.; Zhou, T.; Doolittle, L.R.; Huang, G.; Li, D.; Wilcox, R. Deterministic stabilization of eight-way 2D diffractive beam combining using pattern recognition. Opt. Lett. 2019, 44, 4554. [Google Scholar] [CrossRef]
- Liu, M.; Shen, H.; Yang, Y.; Xian, Y.; Zhang, J.; Wang, H.; Li, B.; Niu, X.; He, B. Investigation of combining-efficiency loss induced by a diffractive optical element in a single-aperture coherent beam combining system. Opt. Express 2021, 29, 5179. [Google Scholar] [CrossRef]
- Klenke, A.; Müller, M.; Stark, H.; Tünnermann, A.; Limpert, J. Sequential phase locking scheme for a filled aperture intensity coherent combination of beam arrays. Opt. Express 2018, 26, 12072. [Google Scholar] [CrossRef]
- Aleshire, C.; Steinkopff, A.; Jauregui, C.; Klenke, A.; Tünnermann, A.; Limpert, J. Simplified design of optical elements for filled-aperture coherent beam combination. Opt. Express 2020, 28, 21035. [Google Scholar] [CrossRef]
- Harder, I.; Lano, M.; Lindlein, N.; Schwider, J. Homogenization and Beam Shaping with Microlens Arrays. In Photon Management; Photonics Europe: Strasbourg, France, 2004; Volume 5456, p. 99. [Google Scholar]
- Zimmermann, M.; Lindlein, N.; Voelkel, R.; Weible, K.J. Microlens laser beam homogenizer: From theory to application. Laser Beam Shap. VIII 2007, 6663, 666302. [Google Scholar] [CrossRef]
- Jin, Y.; Hassan, A.; Jiang, Y. Freeform microlens array homogenizer for excimer laser beam shaping. Opt. Express 2016, 24, 24846. [Google Scholar] [CrossRef]
- Streibl, N.; Nölscher, U.; Jahns, J.; Walker, S. Array generation with lenslet arrays. Appl. Opt. 1991, 30, 2739. [Google Scholar] [CrossRef]
- Prossotowicz, M.; Heimes, A.; Flamm, D.; Jansen, F.; Otto, H.-J.; Budnicki, A.; Morgner, U.; Killi, A. Dynamic Coherent Beam Combining based on a Setup of Microlens Arrays. In Laser Resonators, Microresonators, and Beam Control XXII; Armani, A.M., Kudryashov, A.V., Paxton, A.H., Ilchenko, V.S., Eds.; SPIE: San Francisco, CA, USA, 2020; Volume 1126612, p. 38. [Google Scholar]
- Prossotowicz, M.; Flamm, D.; Heimes, A.; Jansen, F.; Otto, H.-J.; Budnicki, A.; Killi, A.; Morgner, U. Dynamic focus shaping with mixed-aperture coherent beam combining. Opt. Lett. 2021, 46, 1660. [Google Scholar] [CrossRef]
- Kringlebotn, J.T.; Archambault, J.-L.; Reekie, L.; Payne, D.N. Er3+:Yb3+-codoped fiber distributed-feedback laser. Opt. Lett. 1994, 19, 2101. [Google Scholar] [CrossRef]
- Yelen, K.; Zervas, M.N.; Hickey, L.M.B. Fibre DFB lasers with ultimate efficiency. OSA Trends Opt. Photonics Ser. 2004, 95, 703–705. [Google Scholar]
- Bjarklev, A.; Broeng, J.; Bjarklev, A.S. Photonic Crystal Fibres; Springer: Boston, MA, USA, 2003; ISBN 9781461350958. [Google Scholar]
- Limpert, J.; Liem, A.; Reich, M.; Schreiber, T.; Nolte, S.; Zellmer, H.; Tunnermann, A.; Broeng, J.; Petersson, A.; Jakobsen, C. Low-nonlinearity single-transverse-mode ytterbium-doped photonic crystal fiber amplifier. Opt. Express 2004, 12, 1313. [Google Scholar] [CrossRef]
- Kawamura, T.; Shirakawa, A.; Saito, K. Phase-locked and mode-locked multicore photonic crystal fiber laser with a saturable absorber. Opt. Express 2021, 29, 17023. [Google Scholar] [CrossRef]
- Limpert, J.; Stutzki, F.; Jansen, F.; Otto, H.-J.; Eidam, T.; Jauregui, C.; Tünnermann, A. Yb-doped large-pitch fibres: Effective single-mode operation based on higher-order mode delocalisation. Light Sci. Appl. 2012, 1, e8. [Google Scholar] [CrossRef]
- Filippov, V.; Chamorovskii, Y.; Kerttula, J.; Golant, K.; Pessa, M.; Okhotnikov, O.G. Double clad tapered fiber for high power applications. Opt. Express 2008, 16, 1929. [Google Scholar] [CrossRef] [PubMed]
- Filippov, V.; Chamorovskii, Y.K.; Golant, K.M.; Vorotynskii, A.; Okhotnikov, O.G. Optical Amplifiers and Lasers based on Tapered Fiber Geometry for Power and Energy Scaling with Low Signal Distortion. In Fiber Lasers XIII: Technology, Systems, and Applications; Ballato, J., Ed.; SPIE: San Francisco, CA, USA, 2016; Volume 9728, p. 97280V. [Google Scholar]
- Kerttula, J.; Filippov, V.; Chamorovskii, Y.; Ustimchik, V.; Golant, K.; Okhotnikov, O.G. Principles and performance of tapered fiber lasers: From uniform to flared geometry. Appl. Opt. 2012, 51, 7025. [Google Scholar] [CrossRef]
- Huang, L.; Ma, P.; Su, R.; Lai, W.; Ma, Y.; Zhou, P. Comprehensive investigation on the power scaling of a tapered Yb-doped fiber-based monolithic linearly polarized high-peak-power near-transform-limited nanosecond fiber laser. Opt. Express 2021, 29, 761. [Google Scholar] [CrossRef] [PubMed]
- Bobkov, K.K.; Aleshkina, S.S.; Khudyakov, M.M.; Lipatov, D.S.; Likhachev, M.E. Active Tapered Fibers for High Peak Power Fiber Lasers. In Micro-structured and Specialty Optical Fibres VII; Peterka, P., Kalli, K., Mendez, A., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11773, p. 7. [Google Scholar]
- Guesmi, K.; Mugnier, A.; Canat, G.; Canal, C.; Maine, P. Simple Design for High Energy Femtosecond Tapered Double Clad Fiber Amplifier. In Fiber Lasers XVIII: Technology and Systems; Zervas, M.N., Jauregui-Misas, C., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11665, p. 39. [Google Scholar]
- Ye, Y.; Xi, X.; Shi, C.; Yang, B.; Wang, X.; Zhang, H.; Zhou, P.; Xu, X. Comparative study on transverse mode instability of fiber amplifiers based on long tapered fiber and conventional uniform fiber. Laser Phys. Lett. 2019, 16, 085109. [Google Scholar] [CrossRef]
- Fedotov, A.; Noronen, T.; Gumenyuk, R.; Ustimchik, V.; Chamorovskii, Y.; Golant, K.; Odnoblyudov, M.; Rissanen, J.; Niemi, T.; Filippov, V. Ultra-large core birefringent Yb-doped tapered double clad fiber for high power amplifiers. Opt. Express 2018, 26, 6581. [Google Scholar] [CrossRef] [PubMed]
- Filippov, V.; Chamorovskii, Y.; Kerttula, J.; Kholodkov, A.; Okhotnikov, O.G. 600 W power scalable single transverse mode tapered double-clad fiber laser. Opt. Express 2009, 17, 1203. [Google Scholar] [CrossRef]
- Filippov, V.; Kerttula, J.; Chamorovskii, Y.; Golant, K.; Okhotnikov, O.G. Highly efficient 750 W tapered double-clad ytterbium fiber laser. Opt. Express 2010, 18, 12499. [Google Scholar] [CrossRef]
- An, Y.; Yang, H.; Chen, X.; Xiao, H.; Huang, L.; Ma, P.; Xi, X.; Wang, X.; Zhou, P.; Pan, Z.; et al. 4 kW Single-Mode Laser Output Assisted by a Double-Tapered Double-Clad Fiber. In Fiber Lasers XVIII: Technology and Systems; Zervas, M.N., Jauregui-Misas, C., Eds.; SPIE: Bellingham, WA, USA, 2021; Volume 11665, p. 2. [Google Scholar]
- Zeng, L.; Pan, Z.; Xi, X.; Yang, H.; Ye, Y.; Huang, L.; Zhang, H.; Wang, X.; Wang, Z.; Zhou, P.; et al. 5 kW monolithic fiber amplifier employing homemade spindle-shaped ytterbium-doped fiber. Opt. Lett. 2021, 46, 1393. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, H.; Shi, C.; Wang, X.; Pan, Z.; Wang, Z.; Zhou, P.; Xu, X. High power monolithic tapered ytterbium-doped fiber laser oscillator. Opt. Express 2019, 27, 7585. [Google Scholar] [CrossRef] [PubMed]
- Patokoski, K.; Rissanen, J.; Noronen, T.; Gumenyuk, R.; Chamorovskii, Y.; Filippov, V.; Toivonen, J. Single-frequency 100 ns/05 mJ laser pulses from all-fiber double clad ytterbium doped tapered fiber amplifier. Opt. Express 2019, 27, 31532. [Google Scholar] [CrossRef]
- Kerttula, J.; Filippov, V.; Chamorovskii, Y.; Golant, K.; Okhotnikov, O.G. Actively Q-switched 16-mJ tapered double-clad ytterbium-doped fiber laser. Opt. Express 2010, 18, 18543. [Google Scholar] [CrossRef]
- Ustimchik, V.E.; Stoliarov, D.A.; Korobko, D.A.; Chamorovskii, Y.K.; Filippov, V.N. Passively Q-switched 0.24 mJ ring laser based on anisotropic tapered fiber. Results Phys. 2021, 20, 103640. [Google Scholar] [CrossRef]
- Bobkov, K.; Levchenko, A.; Kashaykina, T.; Aleshkina, S.; Bubnov, M.; Lipatov, D.; Laptev, A.; Guryanov, A.; Leventoux, Y.; Granger, G.; et al. Scaling of average power in sub-MW peak power Yb-doped tapered fiber picosecond pulse amplifiers. Opt. Express 2021, 29, 1722. [Google Scholar] [CrossRef]
- Petrov, A.; Odnoblyudov, M.; Gumenyuk, R.; Minyonok, L.; Chumachenko, A.; Filippov, V. Picosecond Yb-doped tapered fiber laser system with 1.26 MW peak power and 200 W average output power. Sci. Rep. 2020, 10, 17781. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Kim, A.V.; Anashkina, E.A.; Meyerov, I.B.; Lebedev, S.A.; Sergeev, A.M.; Koenig, K.; Mourou, G. Modeling of coherent beam combining from multimillijoule chirped pulse tapered fiber amplifiers. Eur. Phys. J. Spec. Top. 2015, 224, 2579–2583. [Google Scholar] [CrossRef]
- Bruesselbach, H.; Jones, D.C.; Mangir, M.S.; Minden, M.; Rogers, J.L. Self-organized coherence in fiber laser arrays. Opt. Lett. 2005, 30, 1339. [Google Scholar] [CrossRef]
- Rothenberg, J.E. Passive coherent phasing of fiber laser arrays. In Lasers and Applications in Science and Engineering; SPIE: San Jose, CA, USA, 2008; Volume 6873, p. 6873151-9. [Google Scholar]
- Wang, B.; Sanchez, A. All-fiber Passive Coherent Beam Combining of Fiber Lasers and Challenges. In Proceedings of the Lasers, Sources, and Related Photonic Devices, San Diego, CA, USA, 29 January–1 February 2012; p. FTh3A.2. [Google Scholar]
- Wu, T.; Chang, W.; Galvanauskas, A.; Winful, H.G. Dynamical, bidirectional model for coherent beam combining in passive fiber laser arrays. Opt. Express 2010, 18, 25873. [Google Scholar] [CrossRef]
- Jeux, F.; Desfarges-Berthelemot, A.; Kermène, V.; Barthelemy, A. Experimental demonstration of passive coherent combining of fiber lasers by phase contrast filtering. Opt. Express 2012, 20, 28941. [Google Scholar] [CrossRef] [PubMed]
- Napartovich, A.P.; Vysotsky, D.V. Phase-locking of multicore fibre laser due to talbot self-reproduction. J. Mod. Opt. 2003, 50, 2715–2725. [Google Scholar] [CrossRef]
- Huo, Y.; Cheo, P.K.; King, G.G. Fundamental mode operation of a 19-core phase-locked Yb-doped fiber amplifier. Opt. Express 2004, 12, 6230. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Lou, Q.; Wang, W.; Zhou, J.; Zheng, Y.; Dong, J.; Wei, Y.; Chen, W. Experimental demonstration of phase locking of a two-dimensional fiber laser array using a self-imaging resonator. Appl. Phys. Lett. 2008, 92, 251115. [Google Scholar] [CrossRef]
- Corcoran, C.J.; Durville, F. Experimental demonstration of a phase-locked laser array using a self-Fourier cavity. Appl. Phys. Lett. 2005, 86, 201118. [Google Scholar] [CrossRef]
- Kong, H.J.; Yoon, J.W.; Shin, J.S.; Beak, D.H. Long-term stabilized two-beam combination laser amplifier with stimulated Brillouin scattering mirrors. Appl. Phys. Lett. 2008, 92, 021120. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, Z.; Wang, X.; Ma, Y.; Ma, H.; Xu, X.; Guo, S. Coherent Beam Combining of Fiber Amplifiers Using Stochastic Parallel Gradient Descent Algorithm and Its Application. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 248–256. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, M.; He, B.; Zhou, J.; Liu, H.; Dai, S.; Wei, Y.; Lou, Q. Passive coherent beam combining of four Yb-doped fiber amplifier chains with injection-locked seed source. Opt. Lett. 2013, 38, 854. [Google Scholar] [CrossRef]
- Fridman, M.; Nixon, M.; Davidson, N.; Friesem, A.A. Passive phase locking of 25 fiber lasers. Opt. Lett. 2010, 35, 1434. [Google Scholar] [CrossRef]
- Cao, J.; Hou, J.; Lu, Q.; Xu, X. Numerical research on self-organized coherent fiber laser arrays with circulating field theory. J. Opt. Soc. Am. B 2008, 25, 1187. [Google Scholar] [CrossRef]
- Chang, W.-Z.; Wu, T.-W.; Winful, H.G.; Galvanauskas, A. Array size scalability of passively coherently phased fiber laser arrays. Opt. Express 2010, 18, 9634. [Google Scholar] [CrossRef] [PubMed]
- Bruesselbach, H.; Minden, M.; Rogers, J.L.; Jones, D.C.; Mangir, M.S. 200 W Self-Organized Coherent Fiber Arrays. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 22–27 May 2005; Volume CMDD, pp. 532–534. [Google Scholar]
- Loftus, T.H.; Thomas, A.M.; Norsen, M.; Minelly, J.D.; Jones, P.; Honea, E.; Shakir, S.A.; Hendow, S.; Culver, W.; Nelson, B.; et al. Four-Channel, High Power, Passively Phase Locked Fiber Array. In Proceedings of the Advanced Solid-State Photonics, Nara, Japan, 27–30 January 2008; p. WA4. [Google Scholar]
- Jeux, F.; Desfarges-Berthelemot, A.; Kermene, V.; Barthelemy, A. Passive Coherent Combining of 15 Fiber Lasers by Phase Contrast Filtering. In Proceedings of the 2013 Conference on Lasers & Electro-Optics Europe & International Quantum Electronics Conference CLEO EUROPE/IQEC, Munich, Germany, 12–16 May 2013; p. 1. [Google Scholar]
- Zaouter, Y.; Daniault, L.; Hanna, M.; Papadopoulos, D.N.; Morin, F.; Hönninger, C.; Druon, F.; Mottay, E.; Georges, P. 2 GW Peak Power Ultrafast Fiber System Using Passive Coherent Beam Combining. In Proceedings of the Lasers, Sources, and Related Photonic Devices, San Diego, CA, USA, 29 January–1 February 2012; p. AM6A.1. [Google Scholar]
- Daniault, L.; Hanna, M.; Papadopoulos, D.N.; Zaouter, Y.; Mottay, E.; Druon, F.; Georges, P. Coherent Combining of Two Femtosecond Chirped-Pulse Amplifiers in a Passive Architecture. In Proceedings of the Lasers, Sources, and Related Photonic Devices, San Diego, CA, USA, 29 January–1 February 2012; p. AT4A.29. [Google Scholar]
- Zaouter, Y.; Daniault, L.; Hanna, M.; Papadopoulos, D.N.; Morin, F.; Hönninger, C.; Druon, F.; Mottay, E.; Georges, P. Passive coherent combination of two ultrafast rod type fiber chirped pulse amplifiers. Opt. Lett. 2012, 37, 1460. [Google Scholar] [CrossRef]
- Bai, G.; Shen, H.; Liu, M.; Liu, K.; Zhang, H.; Niu, X.; Yang, Y.; He, B.; Zhou, J. Single-Aperture Passive Coherent Beam Combining of Fiber Lasers Based on Diffractive Optical Element. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 5–10 May 2019; p. JW2A.95. [Google Scholar]
- Tilseth, E.; Kunkel, W.M.; Leger, J.R. Demonstration of Spatial Mode Selection in a Coherently Combined Fiber Laser. In Proceedings of the 2019 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 23–27 June 2019; p. 1. [Google Scholar]
- Liu, H.; He, B.; Zhou, J.; Yang, Y.; Zheng, Y.; Hu, M.; Lou, Q. Experiments and Perturbative Analysis of Dammann-Grating-Based Aperture Filling in a Passive Coherent Beam Combination. J. Light. Technol. 2014, 32, 2220–2227. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, Y.; Hu, M.; Zhao, C.; Chen, X.; Liu, K.; He, B.; Zhou, J. Coherent Beam Combining of Fiber Amplifiers by means of Dammann Grating Spatial Filter. In Proceedings of the Advanced Solid State Lasers, Shanghai, China, 16–21 November 2014; p. AM5A.51. [Google Scholar]
- Jain, A.; Spiegelberg, C.; Smirnov, V.; Bochove, E.; Glebov, L. Efficient Coherent Beam Combining of Fiber Lasers Using Multiplexed Volume Bragg Gratings. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 6–11 May 2012; p. CF2N.8. [Google Scholar]
- Bochove, E.J.; Shakir, S.A. Analysis of a Spatial-Filtering Passive Fiber Laser Beam Combining System. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 320–327. [Google Scholar] [CrossRef]
- Shakir, S.A.; Culver, B.; Nelson, B.; Starcher, Y.; Bates, G.M.; Hedrick, J.W., Jr. Power Scaling of Passively Phased Fiber Amplifier Arrays. In Optical Technologies for Arming, Safing, Fuzing, and Firing IV; Dickey, F.M., Beyer, R.A., Eds.; SPIE: San Diego, CA, USA, 2008; Volume 7070, p. 70700N. [Google Scholar]
- Li, L.; Schülzgen, A.; Chen, S.; Temyanko, V.L.; Moloney, J.V.; Peyghambarian, N. Phase locking and in-phase supermode selection in monolithic multicore fiber lasers. Opt. Lett. 2006, 31, 2577. [Google Scholar] [CrossRef]
- Steinhausser, B.; Brignon, A.; Lallier, E.; Huignard, J.P.; Georges, P. High energy, single-mode, narrow-linewidth fiber laser source using stimulated Brillouin scattering beam cleanup. Opt. Express 2007, 15, 6464. [Google Scholar] [CrossRef]
- Chiang, H.-S.; Leger, J.R.; Nilsson, J.; Sahu, J. Passive Coherent Beam Combining of Fiber Lasers: Accurate Measurements of Phase Error Tolerance. In Proceedings of the CLEO, San Jose, CA, USA, 9–14 June 2013; p. CW3M.6. [Google Scholar]
- Wu, T.; Chang, W.; Galvanauskas, A.; Winful, H.G. Model for passive coherent beam combining in fiber laser arrays. Opt. Express 2009, 17, 19509. [Google Scholar] [CrossRef]
- Wang, B.; Mies, E.; Minden, M.; Sanchez, A. All-fiber 50 W coherently combined passive laser array. Opt. Lett. 2009, 34, 863. [Google Scholar] [CrossRef] [PubMed]
- Bloom, G.; Larat, C.; Lallier, E.; Lehoucq, G.; Bansropun, S.; Lee-Bouhours, M.-S.L.; Loiseaux, B.; Carras, M.; Marcadet, X.; Lucas-Leclin, G.; et al. Passive coherent beam combining of quantum-cascade lasers with a Dammann grating. Opt. Lett. 2011, 36, 3810. [Google Scholar] [CrossRef]
- Corcoran, C.J.; Durville, F. Passive Phasing in a Coherent Laser Array. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 294–300. [Google Scholar] [CrossRef]
- Bloom, G.; Larat, C.; Lallier, E.; Carras, M.; Marcadet, X. Coherent combining of two quantum-cascade lasers in a Michelson cavity. Opt. Lett. 2010, 35, 1917. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Dong, Z.; Zhang, J.; Lin, X. Passive coherent beam combination of three Nd:YAG lasers using cascaded Michelson-type compound cavities. Opt. Express 2018, 26, 18019. [Google Scholar] [CrossRef]
- Golubentsev, A.A.; Likhanskii, V.V.; Napartovich, A.P. Theory of Phase Locking of an Array of Lasers. In proceding of High-Power Multibeam Lasers and Their Phase Locking; SPIE: St. Petersburg, Russian, 7 October 1993; Volume 2109, pp. 205–218. [Google Scholar]
- Rockwell, D.A.; Giuliano, C.R. Coherent coupling of laser gain media using phase conjugation. Opt. Lett. 1986, 11, 147. [Google Scholar] [CrossRef] [PubMed]
- Carroll, D.L.; Johnson, R.; Pfeifer, S.J.; Moyer, R.H. Experimental investigations of stimulated Brillouin scattering beam combination. J. Opt. Soc. Am. B 1992, 9, 2214. [Google Scholar] [CrossRef]
- Eggleston, J. Steady-state coherent Raman beam combining with multiaxial mode lasers. IEEE J. Quantum Electron. 1986, 22, 1942–1952. [Google Scholar] [CrossRef]
- Park, S.; Cha, S.; Oh, J.; Lee, H.; Ahn, H.; Churn, K.S.; Kong, H.J. Coherent beam combination using self-phase locked stimulated Brillouin scattering phase conjugate mirrors with a rotating wedge for high power laser generation. Opt. Express 2016, 24, 8641. [Google Scholar] [CrossRef]
- Botez, D. Monolithic Phase-Locked Semiconductor Laser Arrays. In Diode Laser Arrays; Cambridge University Press: Cambridge, UK, 1994; pp. 1–71. [Google Scholar]
- Bochove, E.J.; Cheo, P.K.; King, G.G. Self-organization in a multicore fiber laser array. Opt. Lett. 2003, 28, 1200. [Google Scholar] [CrossRef]
- Cheo, P.K.; Liu, A.; King, G.G. A high-brightness laser beam from a phase-locked multicore Yb-doped fiber laser array. IEEE Photonics Technol. Lett. 2001, 13, 439–441. [Google Scholar] [CrossRef]
- Cheo, P.K. Clad Pumped, Eye-Safe and Multi-Core Phase-Locked Fiber Lasers. U.S. Patent 6,031,850, 29 February 2000. [Google Scholar]
- Minden, M.L.; Bruesselbach, H.W.; Rogers, J.L.; Mangir, M.S.; Jones, D.C.; Dunning, G.J.; Hammon, D.L.; Solis, A.J.; Vaughan, L. Self-Organized Coherence in Fiber Laser Arrays. In Fiber Lasers: Technology, Systems, and Applications; Durvasula, L.N., Ed.; SPIE: San Jose, CA, USA, 7 June 2004; Volume 5335, p. 89. [Google Scholar]
- Zhou, P.; Chen, Z.; Xu, X.; Hou, J.; Liu, Z. Modeling Self-Organized Coherent Fiber Laser Array. In Proceedings of the High-Power Lasers and Applications IV, Beijing, China, 6 February 2008; SPIE: Beijing, China, 2008; Volume 6823, p. 68230G. [Google Scholar]
- Chen, Z.; Hou, J.; Zhou, P.; Wang, X.; Xu, X.; Jiang, Z.; Liu, Z. Mutual injection locking and coherent combining of three individual fiber lasers. Opt. Commun. 2009, 282, 60–63. [Google Scholar] [CrossRef]
- Chen, Z.; Hou, J.; Wang, Z.; Chen, S. Self-Organized Coherence in Fiber Laser Arrays by Mutual Injection Locking. In Laser Optics 2010; Rosanov, N.N., Venediktov, V.Y., Eds.; SPIE: St. Petersburg, Russian, 22 March 2011; Volume 7822, p. 7822031-7. [Google Scholar]
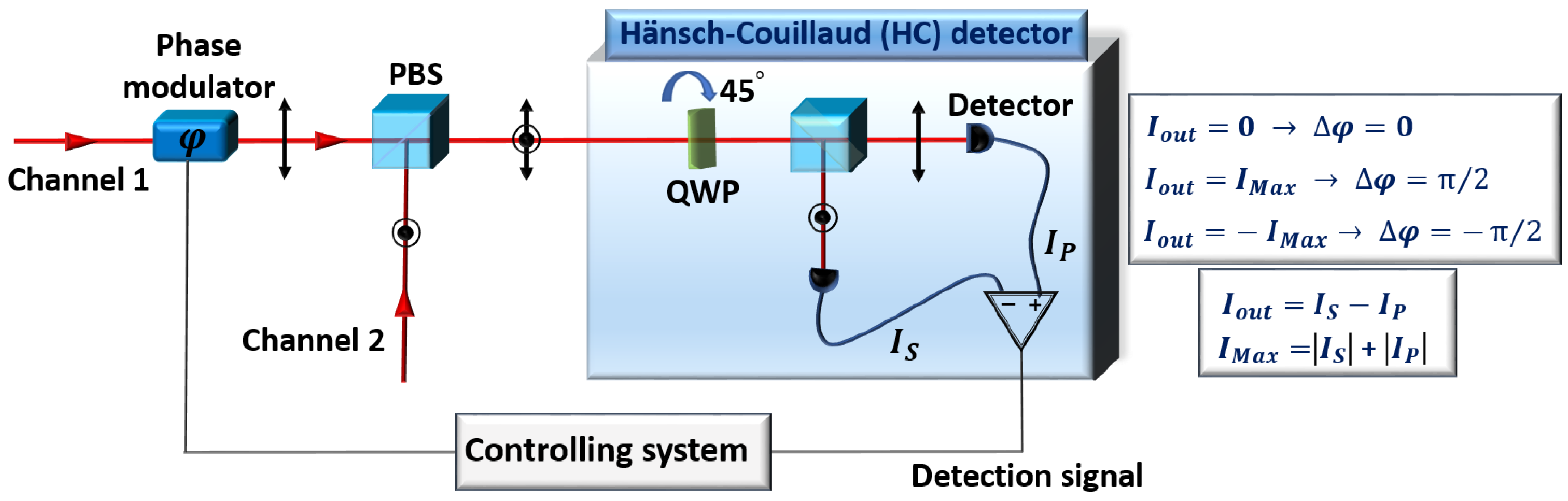
- Hansch, T.W.; Couillaud, B. Laser frequency stabilization by polarization spectroscopy of a reflecting reference cavity. Opt. Commun. 1980, 35, 441–444. [Google Scholar] [CrossRef]
- Anderegg, J.; Brosnan, S.; Cheung, E.; Epp, P.; Hammons, D.; Komine, H.; Weber, M.; Wickham, M. Coherently Coupled High-Power Fiber Arrays. In Fiber Lasers III: Technology, Systems and Applications; Brown, A.J.W., Nilsson, J., Harter, D.J., Tünnermann, A., Eds.; SPIE: San Jose, CA, USA, 2006; Volume 6102, p. 61020U. [Google Scholar]
- O’Meara, T.R. The multidither principle in adaptive optics. J. Opt. Soc. Am. 1977, 67, 306. [Google Scholar] [CrossRef]
- Ma, Y.; Zhou, P.; Wang, X.; Ma, H.; Xu, X.; Si, L.; Liu, Z.; Zhao, Y. Coherent beam combination with single frequency dithering technique. Opt. Lett. 2010, 35, 1308. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, X.; Leng, J.; Xiao, H.; Dong, X.; Zhu, J.; Du, W.; Zhou, P.; Xu, X.; Si, L.; et al. Coherent beam combination of 1.08 kW fiber amplifier array using single frequency dithering technique. Opt. Lett. 2011, 36, 951. [Google Scholar] [CrossRef]
- Ma, P.F.; Zhou, P.; Su, R.T.; Ma, Y.X.; Liu, Z.J. Coherent polarization beam combining of eight fiber lasers using single-frequency dithering technique. Laser Phys. Lett. 2012, 9, 456–458. [Google Scholar] [CrossRef][Green Version]
- Tang, X.; Huang, Z.; Zhang, D.; Wang, X.; Li, J.; Liu, C. An active phase locking of multiple fiber channels via square wave dithering algorithm. Opt. Commun. 2014, 321, 198–204. [Google Scholar] [CrossRef]
- Shay, T.M.; Benham, V.; Baker, J.T.; Sanchez, A.D.; Pilkington, D.; Lu, C.A. Self-Synchronous and Self-Referenced Coherent Beam Combination for Large Optical Arrays. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 480–486. [Google Scholar] [CrossRef]
- Shay, T.M. Theory of electronically phased coherent beam combination without a reference beam. Opt. Express 2006, 14, 12188. [Google Scholar] [CrossRef] [PubMed]
- Daniault, L.; Hanna, M.; Lombard, L.; Zaouter, Y.; Mottay, E.; Goular, D.; Bourdon, P.; Druon, F.; Georges, P. Coherent beam combining of two femtosecond fiber chirped-pulse amplifiers. Opt. Lett. 2011, 36, 621. [Google Scholar] [CrossRef]
- Wagner, T.J. Fiber Laser Beam Combining and Power Scaling Progress: Air Force Research Laboratory Laser Division. In Fiber Lasers IX: Technology, Systems, and Applications; SPIE: San Francisco, CA, USA, 15 February 2012; Volume 8237, p. 823718. [Google Scholar]
- Bourdon, P.; Jacqmin, H.; Augère, B.; Durécu, A.; Goular, D.; Rouzé, B.; Domel, R.; Fleury, D.; Planchat, C.; Lombard, L. Target-in-the-Loop Frequency-Tagging Coherent Combining of 7 Fiber Lasers up to 1 km Range. In Fiber Lasers XVIII: Technology and Systems; Zervas, M.N., Jauregui-Misas, C., Eds.; SPIE: Bellingham, WA, USA, 2021; p. 50. [Google Scholar]
- Kabeya, D.; Kermene, V.; Fabert, M.; Benoist, J.; Desfarges-Berthelemot, A.; Barthelemy, A. Active coherent combining of laser beam arrays by means of phase-intensity mapping in an optimization loop. Opt. Express 2015, 23, 31059. [Google Scholar] [CrossRef]
- Wang, D.; Du, Q.; Zhou, T.; Li, D.; Wilcox, R. Stabilization of the 81-channel coherent beam combination using machine learning. Opt. Express 2021, 29, 5694. [Google Scholar] [CrossRef]
- Du, Q.; Wang, D.; Zhou, T.; Li, D.; Wilcox, R. 81-beam coherent combination using a programmable array generator. Opt. Express 2021, 29, 5407. [Google Scholar] [CrossRef] [PubMed]
- Su, R.; Zhou, P.; Wang, X.; Zhang, H.; Xu, X. Impact of temporal and spectral aberrations on coherent beam combination of nanosecond fiber lasers. Appl. Opt. 2013, 52, 2187. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.L.; Ma, P.F.; Wang, X.L.; Su, R.T.; Zhou, P.; Chen, J.B. Influence of temporal–spectral effects on ultrafast fiber coherent polarization beam combining system. Laser Phys. Lett. 2015, 12, 105301. [Google Scholar] [CrossRef]
- Ma, P.; Tao, R.; Wang, X.; Ma, Y.; Su, R.; Zhou, P. Coherent polarization beam combination of four mode-locked fiber MOPAs in picosecond regime. Opt. Express 2014, 22, 4123. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.X.; Kansky, J.E.; Shaw, S.E.J.; Murphy, D.V.; Higgs, C. Coherent beam combining of large number of PM fibres in 2-D fibre array. Electron. Lett. 2006, 42, 1024. [Google Scholar] [CrossRef]
- Lombard, L.; Azarian, A.; Cadoret, K.; Bourdon, P.; Goular, D.; Canat, G.; Jolivet, V.; Jaouën, Y.; Vasseur, O. Coherent beam combination of narrow-linewidth 15μm fiber amplifiers in a long-pulse regime. Opt. Lett. 2011, 36, 523. [Google Scholar] [CrossRef]
- Siiman, L.A.; Chang, W.; Zhou, T.; Galvanauskas, A. Coherent femtosecond pulse combining of multiple parallel chirped pulse fiber amplifiers. Opt. Express 2012, 20, 18097. [Google Scholar] [CrossRef]
- Müller, M.; Klenke, A.; Steinkopff, A.; Stark, H.; Tünnermann, A.; Limpert, J. 3.5 kW coherently combined ultrafast fiber laser. Opt. Lett. 2018, 43, 6037. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Wise, F.W.; Ouzounov, D.G. Divided-pulse amplification of ultrashort pulses. Opt. Lett. 2007, 32, 871. [Google Scholar] [CrossRef]
- Stark, H.; Müller, M.; Kienel, M.; Klenke, A.; Limpert, J.; Tünnermann, A. Electro-optically controlled divided-pulse amplification. Opt. Express 2017, 25, 13494. [Google Scholar] [CrossRef]
- Guichard, F.; Lavenu, L.; Hanna, M.; Zaouter, Y.; Georges, P. Coherent combining efficiency in strongly saturated divided-pulse amplification systems. Opt. Express 2016, 24, 25329. [Google Scholar] [CrossRef] [PubMed]
- Zaouter, Y.; Guichard, F.; Daniault, L.; Hanna, M.; Morin, F.; Hönninger, C.; Mottay, E.; Druon, F.; Georges, P. Femtosecond fiber chirped- and divided-pulse amplification system. Opt. Lett. 2013, 38, 106. [Google Scholar] [CrossRef] [PubMed]
- Kienel, M.; Klenke, A.; Eidam, T.; Hädrich, S.; Limpert, J.; Tünnermann, A. Energy scaling of femtosecond amplifiers using actively controlled divided-pulse amplification. Opt. Lett. 2014, 39, 1049. [Google Scholar] [CrossRef]
- Guichard, F.; Zaouter, Y.; Hanna, M.; Mai, K.-L.; Morin, F.; Hönninger, C.; Mottay, E.; Georges, P. High-energy chirped- and divided-pulse Sagnac femtosecond fiber amplifier. Opt. Lett. 2015, 40, 89. [Google Scholar] [CrossRef]
- Daniault, L.; Hanna, M.; Papadopoulos, D.N.; Zaouter, Y.; Mottay, E.; Druon, F.; Georges, P. High peak-power stretcher-free femtosecond fiber amplifier using passive spatio-temporal coherent combining. Opt. Express 2012, 20, 21627. [Google Scholar] [CrossRef] [PubMed]
- Kienel, M.; Müller, M.; Klenke, A.; Eidam, T.; Limpert, J.; Tünnermann, A. Multidimensional coherent pulse addition of ultrashort laser pulses. Opt. Lett. 2015, 40, 522. [Google Scholar] [CrossRef]
- Loftus, T.H.; Liu, A.; Hoffman, P.R.; Thomas, A.M.; Norsen, M.; Royse, R.; Honea, E. 522 W average power, spectrally beam-combined fiber laser with near-diffraction-limited beam quality. Opt. Lett. 2007, 32, 349. [Google Scholar] [CrossRef]
- Andrusyak, O.; Smirnov, V.; Venus, G.; Vorobiev, N.; Glebov, L. Applications of Volume Bragg Gratings for Spectral Control and Beam Combining of High Power Fiber Lasers. In Fiber Lasers VI: Technology, Systems, and Applications; Gapontsev, D.V., Kliner, D.A., Dawson, J.W., Tankala, K., Eds.; SPIE: San Jose, CA, USA, 19 February 2009; Volume 7195, p. 71951Q. [Google Scholar]
- Regelskis, K.; Hou, K.-C.; Raciukaitis, G.; Galvanauskas, A. Spatial-Dispersion-Free Spectral Beam Combining of High Power Pulsed Yb-Doped Fiber Lasers. In Proceedings of the 2008 Conference on Lasers and Electro-Optics, San Jose, CA, USA, 4–9 May 2008; pp. 1–2. [Google Scholar]
- Chang, W.-Z.; Zhou, T.; Siiman, L.A.; Galvanauskas, A. Femtosecond pulse spectral synthesis in coherently-spectrally combined multi-channel fiber chirped pulse amplifiers. Opt. Express 2013, 21, 3897. [Google Scholar] [CrossRef]
- Guichard, F.; Hanna, M.; Lombard, L.; Zaouter, Y.; Hönninger, C.; Morin, F.; Druon, F.; Mottay, E.; Georges, P. Two-channel pulse synthesis to overcome gain narrowing in femtosecond fiber amplifiers. Opt. Lett. 2013, 38, 5430. [Google Scholar] [CrossRef] [PubMed]
- Rigaud, P.; Kermene, V.; Bouwmans, G.; Bigot, L.; Desfarges-Berthelemot, A.; Labat, D.; Le Rouge, A.; Mansuryan, T.; Barthélémy, A. Spatially dispersive amplification in a 12-core fiber and femtosecond pulse synthesis by coherent spectral combining. Opt. Express 2013, 21, 13555. [Google Scholar] [CrossRef]
- Guichard, F.; Hanna, M.; Lombard, L.; Zaouter, Y.; Hönninger, C.; Morin, F.; Druon, F.; Mottay, E.; Georges, P. Spectral pulse synthesis in large-scale ultrafast coherent combining systems. Eur. Phys. J. Spec. Top. 2015, 224, 2545–2549. [Google Scholar] [CrossRef]
- Goodno, G.D.; McNaught, S.J.; Rothenberg, J.E.; McComb, T.S.; Thielen, P.A.; Wickham, M.G.; Weber, M.E. Active phase and polarization locking of a 1.4 kW fiber amplifier. Opt. Lett. 2010, 35, 1542. [Google Scholar] [CrossRef]
- Prieto, C.; Vaamonde, E.; Diego-Vallejo, D.; Jimenez, J.; Urbach, B.; Vidne, Y.; Shekel, E. Dynamic laser beam shaping for laser aluminium welding in e-mobility applications. Procedia CIRP 2020, 94, 596–600. [Google Scholar] [CrossRef]
- Montoya, J.; Hwang, C.; Martz, D.; Aleshire, C.; Fan, T.Y.; Ripin, D.J. Photonic lantern kW-class fiber amplifier. Opt. Express 2017, 25, 27543. [Google Scholar] [CrossRef] [PubMed]
- Uberna, R.; Bratcher, A.; Alley, T.G.; Sanchez, A.D.; Flores, A.S.; Pulford, B. Coherent combination of high power fiber amplifiers in a two-dimensional re-imaging waveguide. Opt. Express 2010, 18, 13547. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, E. Extreme light. Nat. Mater. 2016, 15, 1. [Google Scholar] [CrossRef]
| Year | Channel | Geometry | Operation Mode | Combining Efficiency | Controlling System | Institution | Ref. |
|---|---|---|---|---|---|---|---|
| 2006 | 48 | Tiled | CW | RMS erorr < λ/30 | SPGD | MIT | [293] |
| 2011 | 64 | Tiled | CW | RMS erorr < λ/10 | PIM | TRT | [148] |
| 2017 | 37 | Tiled | CW | 96% | PIM | UNILIM | [151] |
| 2020 | 61 | Tiled | Pulsed | 50%, RMS erorr < λ/10 | SPGD | IPP | [152] |
| 2020 | 81 | Filled | Pulsed | RMS error < 1% | PIM | LBNL | [153] |
| 2020 | 107 | Tiled | CW | 96% * | SPGD | NUDT | [154] |
| Combining Configuration | Year | Average Power | Peak Power | Pulse Energy | Pulse Duration | Beam Quality (M2) | Combining Efficiency (%) | Channel Number/Replicas | Configuration | Institution | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spatial | 2014 | 230 W | 22 GW | 5.7 mJ | 200 fs | ≤1.3 | 88 | 4 | CPA, HC detection, PBS | Jena | [16] |
| 2020 | 10.4 kW | 0.5 GW | 130 µJ | 254 fs | ≤1.2 | 96 | 12 | CPA, LOCSET, IBS | Jena | [169] | |
| 2021 | 1 kW | 68 GW | 10 mJ | 120 fs | ≤1.2 | 94 | 16 | CPA, HC detection, PBS and TFP | Jena | [176] | |
| Temporal | 2013 | 77 W | 1.3 GW | 430 µJ | 320 fs | ≤1.3 | 97 | 2 | CPA + DPA, TFP, passive | Amplitude &CNRS | [300] |
| 2014 | 37.5 W | 2.9 GW | 1.25 mJ | 380 fs | NA | 75 | 4 | DPA, LOCSET, PBS | Jena | [301] | |
| Spatio-temporal | 2015 | 55 W | 3.1 GW | 1.1 mJ | 300 fs | ≤1.3 | 90 | 2×2 | CPA + DPA, passive | Amplitude &CNRS | [302] |
| 2015 | NA | NA | 37 µJ | 50 ps | NA | 75 | 2 × 4 | DPA, LOCSET, PBS | Jena | [304] | |
| 2016 | 700 W | 45 GW | 12 mJ | 262 fs | ≤1.2 | 78 | 8 × 4 | CPA + DPA, LOCSET, PBS and TFP | Jena | [173] | |
| 2019 | 674 W | 80 GW | 23 mJ | 235 fs | NA | 71 | 12 × 8 | CPA + DPA, LOCSET, PBS and TFP | Jena | [175] | |
| Spectral synthesis | 2013 | 273 mW | NA | NA | 403 fs | NA | 85.8 | 3 | Spectral filters, LOCSET | UMich | [308] |
| 2013 | 10 W | 2 MW | 0.29 µJ | 130 fs | ≤1.4 | 86 | 3 | LMA fiber, dichroic mirror | CNRS | [309] | |
| 2013 | 370 mW | NA | NA | 290fs | NA | NA | 12 | MCF, Grating and MLA twin pulses with 1.75 ps separation | CNRS | [310] |
| Tiled aperture | Directed Energy | Year | Distance | Channel number | Tip/Tilt Correction | Phase Control Method | Institution | Ref. |
| 2011 | 7 km | 7 | √ | SPGD | UD | [149] | ||
| 2015 | 7 km | 21 | √ | SPGD | UD | [166] | ||
| Power scaling | Year | Power (kW) | Channel number | Combining efficiency (%) | Phase control method | Institution | Ref. | |
| 2011 | 1.08 | 9 | 85 * | SFD | NUDT | [279] | ||
| 2011 | 4 | 8 | 78 | SPGD | MIT | [147] | ||
| 2020 | 16 | 32 | >95 | OPA | CIVAN | [167] | ||
| 2021 | 7.1 | 7 | 86 * | SPGD | NUDT | [168] | ||
| Filled aperture | Combining technique | Year | Power (kW) | Channel number | Combining efficiency (%) | Phase control method | Institution | Ref. |
| DOE | 2016 | 5 | 5 | 82 | LOCSET | AFRL | [181] | |
| PBS | 2017 | 2.16 | 4 | 94.5 | SFD | NUDT | [108] | |
| AFPL | 2017 | 1.27 | 3 | NA | SPGD | MIT | [314] | |
| RIW | 2010 | 0.1 | 4 | 80 | LOCSET | LM Corp | [315] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathi, H.; Närhi, M.; Gumenyuk, R. Towards Ultimate High-Power Scaling: Coherent Beam Combining of Fiber Lasers. Photonics 2021, 8, 566. https://doi.org/10.3390/photonics8120566
Fathi H, Närhi M, Gumenyuk R. Towards Ultimate High-Power Scaling: Coherent Beam Combining of Fiber Lasers. Photonics. 2021; 8(12):566. https://doi.org/10.3390/photonics8120566
Chicago/Turabian StyleFathi, Hossein, Mikko Närhi, and Regina Gumenyuk. 2021. "Towards Ultimate High-Power Scaling: Coherent Beam Combining of Fiber Lasers" Photonics 8, no. 12: 566. https://doi.org/10.3390/photonics8120566
APA StyleFathi, H., Närhi, M., & Gumenyuk, R. (2021). Towards Ultimate High-Power Scaling: Coherent Beam Combining of Fiber Lasers. Photonics, 8(12), 566. https://doi.org/10.3390/photonics8120566




