Abstract
Quantum key distribution (QKD) has gained a lot of attention over the past few years, but the implementation of quantum security applications is still challenging to accomplish with the current technology. Towards a global-scale quantum-secured network, satellite communications seem to be a promising candidate to successfully support the quantum communication infrastructure (QCI) by delivering quantum keys to optical ground terminals. In this research, we examined the feasibility of satellite-to-ground QKD under daylight and nighttime conditions using the decoy-state BB84 QKD protocol. We evaluated its performance on a hypothetical constellation with 10 satellites in sun-synchronous Low Earth Orbit (LEO) that are assumed to communicate over a period of one year with three optical ground stations (OGSs) located in Greece. By taking into account the atmospheric effects of turbulence as well as the background solar radiance, we showed that positive normalized secure key rates (SKRs) up to (bps/pulse) can be obtained, which implies that satellite-to-ground QKD can be feasible for various conditions, under realistic assumptions in an existing infrastructure.
1. Introduction
The advent of quantum computing may affect classical key cryptography in the next decades, setting a large part of cryptosystems insecure. Quantum computers are constantly gaining computational power with the manipulation of more and more qubits [1], while at the same time Shor’s algorithm ensures that today’s classical public key algorithms will become obsolete [2]. While data content is constantly becoming more vital and its security is getting compromised more frequently, the need for resilient schemes in cryptography is of high importance. Quantum cryptography promises unconditional security based on the laws of nature rather than computational security, providing a combat to the threat of quantum computers [3,4,5]. Quantum key distribution (QKD) protocols can establish a private key encryption between two remote parties, ensuring the generation of a shared key, which can be used in symmetric cryptographic algorithms, such as the Advanced Encryption Standard (AES).
Since the emergence of the first QKD protocol in 1984 [6], rapid progress has been made in the last decade, resulting in increases of transmission distances and key rates [3]. Fiber links have been realized and scaled up to the network size, as in SECOQC [7]. Despite the great progress, this technology has to overcome a major limitation. The lack of efficient quantum repeaters results in unamplified signals [8], thus leaving weak single-photon pulses extremely exposed to the induced attenuation due to the propagation. Therefore, serious limitations occur regarding the distance reach of such links, especially in fiber media. Currently, the maximum ground-based communication range achieved is 509 km in fiber [9] and this limitation for repeaterless links sets a major obstacle in the way towards a quantum-secured global mesh network. Even though QKD deployments over terrestrial free-space optics (FSO) links have been studied as a potential candidate for short-reach point-to-point QKD link connections [10], the maximum ground-based QKD link range that has been achieved is 144 km in free space [11].
Recently, satellite QKD has proved to be able to overcome the above range limits, thereby enabling secure communication globally [12]. Moreover, satellite QKD can enable secure network communication between multiple nodes on Earth, based on an efficient scheduling of communication with a set of ground stations [13].
Satellite QKD has been demonstrated for both prepare and measure and entangled-based protocols. Entangled-based QKD does not require the satellite to act as a trusted node and therefore can offer direct inter-optical ground station (OGS) connection. However, the satellite needs to be able to communicate with the two OGSs at the same time, and since the necessary quantum correlations are reduced from loss in the two satellite-to-ground channels, the resultant key rates are relatively low [14,15]. On the other hand, even though they require the use of a trusted satellite as a relay station, prepare and measure protocol implementations do not face these obstacles and at the same time they can be more practical at the moment. In addition, the technical complexity for the generation of single photons can be significantly reduced by employing attenuated coherent laser sources. In this respect, laser-light QKD schemes are more controllable, require less complex sources and can be used more efficiently to extend the distance of secure QKD to the global scale.
Optical satellite communication links are strongly dependent on free-space channel conditions [16]. Among the atmospheric phenomena that degrade optical satellite links, cloud coverage is the dominant one, which causes the blockage of the link [17]. For the mitigation of cloud coverage, the OGS diversity technique is employed [18,19,20], taking advantage of the spatial inhomogeneity of clouds. Even under the cloud-free line of sight conditions, optical satellite links are mainly affected by atmospheric turbulence, absorption and scattering, high background solar noise, and pointing losses [16,21,22,23]. To cope with the above channel-induced limitations, highly efficient photon detection systems combined with large aperture telescopes and narrow-band filters can be used among others for OGSs [24]. This approach can be easily combined with QKD sender stations featuring narrow beam divergences. Following the above methodology to cope with the challenges of optical-satellite-based links, numerous satellite-to-ground QKD experiments have been successfully demonstrated. Low-Earth-orbit (LEO) satellite-to-ground QKD links have been demonstrated to reach distances up to 1200 km and key rates up to kbps [25,26]. Moreover, both satellite uplink and downlink QKD feasibility has been thoroughly examined under daylight and nighttime conditions [24,27]. Another 53 km FSO link that exhibits high loss has been realized, examining the feasibility of QKD in daylight aiming towards inter-satellite QKD communication [28]. Finally, Bedington et al. have summarized the progress in satellite QKD in [29].
One step beyond the successful demonstration of QKD over optical-satellite-based links is that infrastructure initiatives are targeting the integration of these space-based QKD links with the existing terrestrial fiber segments. In this context, European Quantum Communication Infrastructure (EuroQCI)—the quantum communication infrastructure initiative in Europe—aims to integrate QKD-based systems into conventional communication infrastructures [30]. In this path, the observatories have been selected as the suitable gateways for interconnecting QKD satellite sender stations with terrestrial fiber-based segments fibers [30].
We aimed to contribute to this implementation path by presenting a thorough feasibility analysis for Greek QCI [31]. The results of our study went further from a feasibility analysis in the physical layer and the investigation of satellite-to-ground link availability. QKD-based security architectures were introduced to maximize the availability of quantum key resources. More specifically, our research focused on the feasibility analysis of an LEO satellite-to-ground prepare and measured the decoy-state BB84 QKD link over a turbulent atmospheric channel under daytime and nighttime conditions. For QKD transmitter stations, we considered a satellite constellation consisting of 10 LEO satellites flying at an orbital height of about 600 km. We assumed that each satellite can communicate with up to three OGSs at the same time. These ground stations are hosted in astronomical observatories located across Greece, and they were selected to support three different segments of Greek QCI. In order to model the atmospheric link, we took into account the position, height, and receiver’s telescope diameter of each OGS. By examining a period of one year, we reported secure key rates (SKRs) up to kbps and total distilled key bits per ground station up to Gbits. Finally, we described how the trusted satellites could share keys with the OGS in order to establish inter-OGS communication, and we examined if the distilled key rates can meet the demands for AES 256-bit key refresh time necessary to keep the attack success probability as low as possible.
The paper is structured as follows. Section 2 briefly describes the BB84 QKD protocol and its system architecture in the proposed satellite QKD network of ground stations located at Greek territory. Section 3 describes the methodology for the modeling of the atmospheric downlink channel, by taking into account the OGSs’ positions and altitudes. Finally, Section 4 provides the results of this study, and Section 5 and Section 6 discuss and conclude this work, respectively.
2. QKD Protocol and Architecture Assumptions in the LEO
2.1. System Architecture, Satellite, and Ground Stations
The presented work focuses on the use of LEO satellite-to-ground QKD links for delivering quantum keys on the ground segment of the network. The orbit altitude of LEO satellites is lower than 2000 km, thereby allowing for much higher signal-to-noise ratio (SNR) values and lower free-space loss compared to geostationary Earth orbit (GEO) satellites, which are positioned in a height of about 35,000 km. On the other hand, in contrast with GEO satellites that are at a fixed position in the sky, LEO satellites are visible by OGSs only a few minutes each day, if the atmospheric conditions allow it.
Through our analysis, we considered the satellite-to-ground scenario (downlink) assuming the cloud-free line of sight conditions and links with elevation angle higher than 20 degrees. In the case of downlink transmission, the attenuation caused by atmospheric turbulence is lower compared to that of the uplink, since the laser beam has already expanded before it comes into contact with the atmosphere [23,32]. Aside from the attractive transmission features, the downlink scenario is compatible with the strict requirements of satellite system architectures. More specifically, it allows the implementation of a compact quantum sender station based on a highly attenuated coherent source and simple optics for the encoding of quantum information, being also controlled by simple electronics [33]. In this way, complex single-photon counters which require advanced cooling mechanisms are located at the ground stations where there are not any strict requirements on footprint and energy consumption. Moreover, by implementing the satellite-to-ground scenario, large apertures for the single-photon detection can be placed in astronomical observatories. In this way, smaller, lighter apertures can be employed on board in space.
Through our analysis, we assumed that three astronomical observatories in Greece communicate with the LEO satellite constellation. The first is located in Skinakas (South, longitude: °, latitude: 24.8981°) at a height of 1750 m, the second in Helmos (Middle, longitude: 37.9855°, latitude: 22.1984°) is at a height of 2340 m, and the third in Cholomondas (North, longitude: 40.3419°, latitude: 23.5060°) is at a height of 850 m. These three observatories are involved in Greek QCI, which aims to build a secure communication infrastructure by exploiting the terrestrial fiber segments for quantum key delivery in users [31]. The location of each OGS is shown in Figure 1.
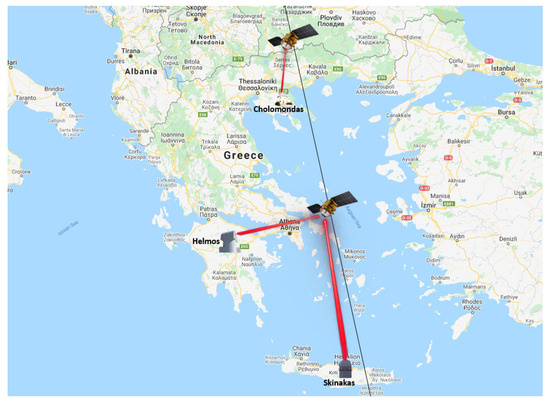
Figure 1.
Positions of the three optical ground stations (OGSs) of Skinakas, Helmos, and Cholomondas in Greece. The black line corresponds to a random passage of one of the 10 satellites of the constellation over Greece.
The quantum key sifting is assumed to be implemented via a public optical channel. For this purpose, different wavelengths within the standard bands will be available for classical data channel and quantum channel. Uplink beacon and other service channels for the QKD link establishment can be also implemented within the available bands [34].
2.2. Weak + Vacuum Decoy-State BB84 Protocol
In our simulation, we used the most well-known variation of the BB84 protocol [6], the weak + vacuum decoy-state BB84 protocol [35]. The concept behind the BB84 protocol is that Alice encodes bit sequences into different polarization states of single photons. Its security generally relies on the fact that Eve’s presence cannot remain undetected due to the quantum nature of single photons and will therefore inevitably introduce errors in the bit sequences. The only thing Alice and Bob have to do is to sacrifice a part of the exchanged bits to estimate the error rate. If the bit error rate is lower than a specific threshold, they proceed to the procedure of the secure key distillation. Despite that the unconditional security of the BB84 protocol has been proven [5,6,36], security loopholes may arise when moving on its practical implementations. For example, due to the hardness of engineering on-demand single-photon sources, most QKD implementations and experiments rely on the use of highly attenuated laser sources which emit probabilistically photons, including also multi-photon pulses. In order not to compromise security by the presence of these multi-photon pulses, the selected intensity level leads to an average photon number much smaller than one, thereby leading to lower detection rates. Even in that case, there exist a non-zero probability of emitting multi-photon states, which can open the possibility of photon-number-splitting (PNS) attacks. The need to counter the PNS attack [37] triggers the invention of the decoy-state protocol [35,38,39], which allows the efficient distillation of secure keys using weak coherent pulse-based QKD systems that were once vulnerable [8]. In the weak + vacuum state modification, this kind of attacks is encountered using decoy and vacuum states in order to precisely measure the attenuation of the channel, the background noise, and detector’s dark counts. It has been shown that, with the decoy modification, higher key rates and longer communication distances can be achieved [40,41].
For the reasons mentioned above, we adopted the weak + vacuum decoy-state BB84 protocol [35]. The introduction of the decoy states enhances the detection of eavesdropping via PNS attacks, thus allowing Alice to transmit a higher mean photon number per pulse, improving key rates and reaching longer distances. It is important to mention here that this protocol is suitable for free-space transmission, since experimental results have already shown very good polarization stability in the satellite-to-ground transmission [42,43]. The normalized SKR (bps/pulse) is lower bounded by the following inequation according to [35], as described in Appendix A:
where is the transmitters pulse repetition rate, q is the protocol efficiency, subscript µ is the average photon number per signal in signal states, and are the gain and the quantum bit error rate (QBER) of signal states, respectively, and are the gain and the error rate of the single-photon state in signal states, respectively, f(x) is the bi-directional error correction rate, and is the binary entropy function.
3. FSO Channel Modeling
Atmospheric conditions have a serious impact on the performance of the link. In the following subsections, the atmospheric losses under the cloud-free line of sight conditions, link losses, and setup losses are summarized [16,21,22,23,44].
3.1. Received Power
The received power after the receiver telescope and before the photo detector (watt) can be estimated as [16,22,23]:
where and are the transmitted and received intensities respectively, is the atmospheric transmittance, is the pointing loss factor, is the scintillation loss factor, is the free-space loss, and and are the transmitter and receiver gains, respectively.
3.2. Free-Space Loss
The free-space loss of the optical signal is due to the optical wave propagation from the transmitter to the receiver and is calculated as [32]:
where λ (m) is the wavelength of the signal and is the distance between the satellite and the OGS, which depends on the elevation angle of the satellite and can be given by [45]:
where is the satellite attitude above Earth’s surface, is the Earth’s radius, and is the elevation angle.
3.3. Transmitter and Receiver Gains
The gains of the transmitter and the receiver can be calculated according to [23]:
where Dr (m) is the receiver’s aperture diameter and is the half-width beam divergence angle (rad), which depends on the transmitter’s aperture diameter Dt (m) and can calculated as follows [32]:
3.4. Atmospheric Attenuation
The atmospheric transmittance of the laser beam under clear sky conditions (absence of clouds, rain etc.) is also dependent on the elevation angle and can be given by Equation (7) [46]:
where is the vertical link transmittance and is the zenith angle of the link. It is evident that, for low elevation angles, atmospheric attenuation is higher, since the light has to travel a longer path through the atmosphere to reach the receiver.
3.5. Pointing Error Loss
The pointing error loss is usually estimated for a specific probability from the probability density function (PDF) of the normalized intensity as follows [47]:
where is the divergence pointing ratio and can be written as:
where is the pointing error variance in rad and is the half-width divergence angle of the transmitted beam commuted for Gaussian beams. For a given outage probability , the pointing error loss is calculated as follows [47]:
3.6. Scintillation Loss
Scintillation can heavily affect an FSO communication link by causing intensity fluctuations in the receiver [32]. These fluctuations are caused by thermal changes that lead to changes in the refractive indices in small air cells, resulting in beam diffraction and beam wander [23,32]. In the case of satellite downlink, the beam front is usually much larger than the size of these air cells; therefore, the effect of scintillation in the receiver is small but should be taken into consideration.
The intensity of the scintillation is often described as weak, moderate and strong, depending on the value of the refractive index structure parameter , which strongly depends on the atmospheric conditions such as temperature and pressure. In this analysis, the modified expression of Hufnagel–Valley model was used [23,32], which takes into account the altitude of the ground station and the elevation angle. The value of can be calculated as follows [22,23]:
where is the refractive index structure parameter at the ground level, (m/s) is the average wind speed along the slant path using the Bufton model, is the OGS altitude height, and is the height above the ground station altitude.
For a plane wave approximation and assuming the Kolmogorov model, the scintillation index for weak, mean, and strong turbulences can be given by the following expression [16,32]:
where is the Rytov index which when taking into account the OGS’s height and can be calculated as [16,32]:
where is the wavenumber, is the zenith angle, and is the turbulence altitude which is considered negligible for altitudes higher than 20 km. To continue, we also considered the aperture-averaging effect in order to take the receiver’s aperture diameter into account. The aperture-averaging factor was expressed as [32,48]:
where is the scintillation index for a receiving telescope and is described as: . The aperture-averaging factor is calculated according to the following expression [32,49]:
where is intensity structure size parameter [32,49]:
where (deg) is the elevation angle of the link and is 12,000 m.
Finally, for modeling the signal fluctuation due to the scintillation effect, we used the log-normal distribution that suits for weak- and moderate-turbulence regimes. The log-normal normalized PDF is calculated as [32,49]:
where .
Given the PDF, we can now calculate the loss (dB) that is introduced by scintillation for a given probability (e.g., 1%) threshold as follows [49]:
3.7. Background Solar Radiance
Since single-photon detectors are extremely sensitive to noise, solar radiance is a major limitation in the implementation of a QKD FSO link under daylight conditions. The background noise power level in watt reaching the receiver can be given by the following equation [50]:
where corresponds to the background radiance energy density, is the field of view of the receiver’s aperture) is the receiver’s capture area, and ∆λ (µm) is the receiver’s band pass optical filter width. To insert this value to the QBER, we expressed the solar background noise power level in watt reaching the receiver in counts per second. Therefore, the probability of the detector firing due to a background noise photon can be expressed as:
where h × f corresponds to the energy of a single photon and therefore /(h × f) denotes the photon flux arriving at the receiver measured in counts per second. It is clear that a narrow bandpass filter combined with a limited receiver’s field of view (FOV) is necessary to keep the background noise to acceptable levels.
4. Simulation Results
4.1. System Parameters
To begin with, the wavelength of 1550 nm was selected. At this wavelength, we observed low atmospheric loss and decreased solar radiance [51,52]. Through this study, only the satellite downlink scenario was examined, while only satellite elevation angle over was considered. Considering the atmospheric parameters, the value of the refractive index structure parameter at the ground level was set to , and the average wind speed was set to 10 m/s. The pointing error variance was set to 0.75 μrad, and the pointing loss was calculated for an outage probability of 1%.
Considering the satellites components, we assumed an aperture of 0.15 m [24] for all three transmitters that the satellites are equipped with, providing a small beam divergence of about 13 μrad. On the receiver side, we assumed that every OGS is equipped with a different telescope aperture. Specifically, the OGSs of Skinakas, Helmos, and Cholomondas are equipped with a receiver telescope aperture of 1.3 m, 2.3 m and 0.75 m, respectively. To continue, in order to minimize the effects of strong daylight radiance, we assumed a narrow FOV of 100 μrad [27] and a narrow band-pass filter of 0.2 nm with an insertion loss of 3 dB. Concerning the detectors, we assumed two superconducting nanowires single-photon detectors (SNSPDs), which offer high detection efficiencies and low timing jitter [53]. Specifically, in our analysis, we assumed SNSPDs with quantum efficiencies of 85% at 1550 nm, dark count rates of 300 counts per second (cps), timing jitter of 50 ps, dead time of 30 ns, and no after-pulsing effect. The detector’s gate duration time was set to 1 ns. These values correspond to the typical performance of SNSPDs modules photon counters for single-photon detection at telecom wavelengths [53]. Finally, the Bob’s receiver loss was set to 2.65 dB [54], Bob’s interferometer visibility was set to 98%, and the polarization decoherence loss of the link was set to 0.3 dB [43].
Considering the mean photon number values of the signal and decoy states, we proceeded with a numerical optimization in order to provide the possible highest key rates. Specifically, the quantum signal mean value was set to μ = 0.56, the decoy mean value was set to ν = 0.11, and the protocol efficiency was set to about q = 2/5 (signal:decoy:vacuum ratio = 4:1:16, and ½ due to the BB84 protocol; Appendix A) [35]. Finally, the bi-direction error correction efficiency f (e) was set to 1.22, corresponding to the CASCADE error correction algorithm [55].
4.2. Feasibility of LEO Satellite-to-Ground QKD in Daytime and Nighttime
In this subsection, we analyzed the performance of the satellite FSO downlink considering one LEO satellite and one OGS. For the evaluation studies included in this subsection, the receiver’s telescope aperture diameter was set to be 0.75 m (if not stated otherwise).
4.2.1. Distance Reach
As we have already discussed in the introduction section, fiber QKD links are limited to few hundreds of kilometers due to the photon loss imposed by the fiber medium. When light propagates through empty space, none attenuation mechanism is present and therefore longer distances can be reached. On the other hand, other factors should be considered that lead to increased transmission losses, such as free-space loss. In order to minimize the geometrical loss, narrow beam divergences and large receiver apertures can be used. Aside from the loss mechanisms, the effect of the solar background noise during the day can significantly degrade the transmission performance. To combat this effect, ultra-narrow band-pass filters can be used to minimize the background noise to acceptable levels and isolate the quantum passband. Following the above approach and by using state-of-the-art equipment in both the satellite and the ground station, links up to GEO distances can be achieved [56]. Figure 2a shows the total downlink loss of the link including the quantum efficiency of the detectors, the setup loss of Bob station, the absorption and geometrical loss, the scintillation effect loss, pointing loss, and polarization decoherence loss. Figure 2b shows the SKR as a function of receiving telescope aperture and link distance under nighttime conditions.
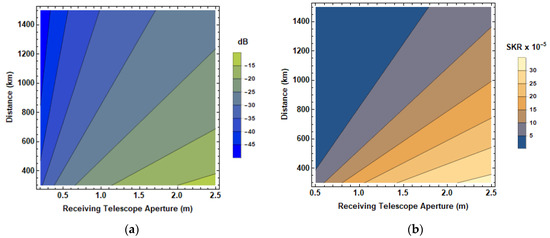
Figure 2.
(a) Total downlink loss (dB) over distance (km) and over receiving telescope aperture (m). (b) Normalized secure key rate (SKR; bps/pulse) over link distance (km) and over receiving telescope aperture (m) under nighttime conditions.
It is evident from the contour plots in Figure 2 that the total link loss for a 600 km link distance can get as low as 20 dB in total. To achieve this loss performance, a large enough telescope in the receiver is required. It should be also noted that this value would be the lowest for the link for an orbital height of 600 km that corresponds only to the point when the satellite is exactly above the station.
4.2.2. QKD under Different Background Noise Levels
The detection of single-photon signals buried in the intent background noise stemming from the solar radiance could be practically a very challenging task. Therefore, specific techniques are required to alleviate the presence of noise photons in QKD links, such as narrow spectral filtering and short detector gate time opening at Bob station. Even in this case, the presence of solar daylight radiance still affects drastically the performance of the link. The values of the solar background radiance during the day depend on the position of the satellite relative to the sun azimuth as well as on the OGS’s location. In addition, weather conditions such as cloud presence may further deteriorate the situation, enhancing the strength of the effect of solar radiance. Typical values for (watt/srμm) at 1550 nm for clear sky daylight conditions may vary between 0.1 and 6 (watt/srμm) [24,52,57]. In Figure 3, the effect of the solar radiance over the normalized secure key rate is presented. It can be observed that the background noise is a limiting factor not only in the distance reach, but also in the angle of view. This leads to a smaller view cone, which in turn reduces the satellite–OGS communication time.
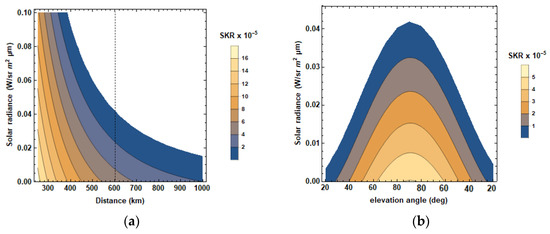
Figure 3.
(a) Normalized SKR (bps/pulse) over solar radiance (watt/srμm) over distance (km). (b) Normalized SKR (bps/pulse) over solar radiance (watt/srμm) over elevation angle (deg) for a satellite orbit altitude of 600 km.
In Figure 3, it is evident that strong limitations are imposed on the key establishment due to background radiance in daylight. More specifically, under our assumptions (0.2 nm filter passband, 1 ns detector gate opening, and 100 μrad FOV), the noise levels even for low solar radiance values are over the acceptable threshold, and therefore, no QKD link can be established. Further narrowing the quantum passband is a candidate solution, but state-of-the-art equipment with increased optical loss will be required. In general, it is uncertain if such a link could be operating under full daylight conditions [57].
In nighttime, the main source of background radiance is the moonlight. In addition, the night sky and city lights can also generate an amount of noise photons in the detectors. Typical values nighttime radiance () at 1550 nm may vary from (watt/srμm) (moonless clear night) to (watt/srμm) (full moon clear night) [24,52,57]. Even in the case of full moon, the background radiance corresponds to 10 kcps in the photon counter at most.
In the next subsections, we assumed that the link is always interrupted during daylight, and therefore, communication is only established during nighttime. The nighttime solar radiance was set to an average value of and was kept constant for the needs of the numerical study.
4.3. QKD Link Performance of an LEO Satellite Constellation over Greek QCI
The satellite constellation considered in this study consists of 10 LEO sun synchronous satellites at an orbital altitude of about 600 km with an inclination angle of . Each satellite flies over Greece approximately twice a day. The initial step towards the satellite QKD link modeling involves the estimation of time instances when each one of the ground stations views each satellite with an elevation angle greater than . For this estimation, we used the latitude, longitude, and orbital height data of each satellite that are obtained every 10 s employing the AGI/STK system tool [58].
By having all the time instances when the satellites are visible by the OGSs, we considered only nighttime communication, as discussed in the previous subsection. The time period between 6:00 am to 6:00 pm was considered as the daylight period; therefore, no key rates could be distilled during this time. In Figure 4 the satellites route during 24 h is depicted.
Figure 4.
Path of one out of 10 satellites during a single day of the year. The route lines slowly drift to the left day by day. Note that the satellite can be seen coming with the direction, either from South to North or from North to South. In the faint red circle, a single pass of the satellite over Greece is depicted.
4.3.1. Single Satellite Pass over a Single OGS
As the first step, a single pass of a satellite over the OGS of Helmos was examined. In Figure 5, the normalized SKR and the satellite–OGS distance are depicted as a function of time for one LEO satellite pass over the Helmos OGS.
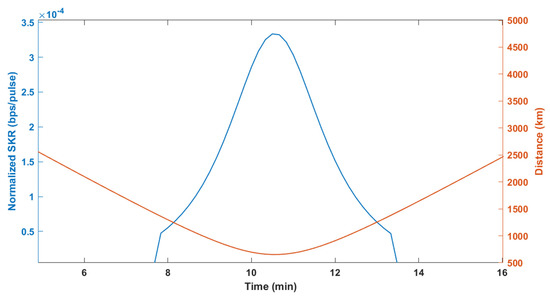
Figure 5.
Normalized SKR (bps/pulse) of one out of 10 satellites (left) and distance (km) (right) over time for a single pass over the observatory in Helmos with a receiver’s telescope aperture of 2.3 m. The link is considered available, if the elevation angle exceeds 20°.
The duration of this single pass was found to be 340 s or 5.7 min. The maximum SKR value that was obtained was bps/pulse, which corresponded to the maximum elevation angle of . The total number of key bits that were distilled from this single pass, assuming a 100 MHz Alice’s repetition rate [25,26], was about 1.99 Mbits. It should be mentioned that the elevation angle of the satellite may differ from day to day, since the satellite does not always follow the exact same path over the OGS. Therefore, the satellite can be visible for either shorter or longer time lapses.
4.3.2. Satellite Full Constellation Pass over a Single OGS
Every satellite passes over a ground station approximately twice a day (24 h). Therefore, 10 constellations are visible around 20 times a day by every station. A single station can establish 10 different quantum links, each one with a different satellite. In Figure 6, the passes of the constellation over the observatory of Helmos over a period of one month and over two days are shown. Again, the time instances when the sun is up were filtered out, as it can be clearly seen in Figure 6b.
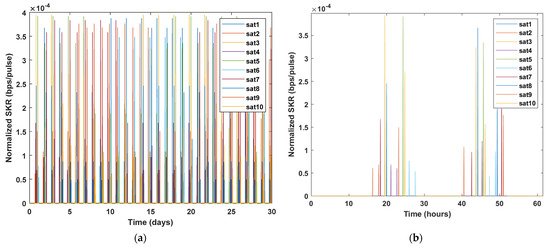
Figure 6.
(a) Normalized SKR (bps/pulse) over time for a period of 1 month between the satellite constellation and the OGS of Helmos. (b) Normalized SKR (bps/pulse) over time for a period of 60 h between the satellite constellation and the OGS of Helmos.
The total daily time contact for a single pass of the constellation over the OGS of Helmos can be found to be 2010 s or 33.5 min, thereby allowing for a longer quantum communication window. Aside from the increase of the overall key rates, the LEO satellite constellation increases the QKD link availability, since it is more likely that an OGS establishes a link to at least one satellite. Since the weather conditions and specifically clouds may interrupt the satellite downlink, the employment more satellites can increase the QKD link availability within the day. It is worth mentioning that the constellation satellites are placed in such a way to achieve the maximum availability. This means that no more than one satellite is visible by an OGS at the same time.
4.3.3. Satellite Full Constellation Pass over Greek QCI
The QKD link availability can be significantly enhanced by considering that each QKD satellite payload can communicate with a number of OGSs that are geographically distributed across the territory [18,19]. Assuming that each LEO satellite is equipped with three independent QKD Alice stations, three independent QKD links can be established with the three OGSs simultaneously for a period when they are all visible and only if the weather conditions allow it. Therefore, based on the link study in the above paragraphs, these three QKD links can be efficiently established for less than 10 min each day. During the rest of the period, the links could be used for classical communication or for other functions (e.g., imaging). Figure 7 illustrates the downlink normalized SKR between the satellite constellation and the three OGSs across Greece.
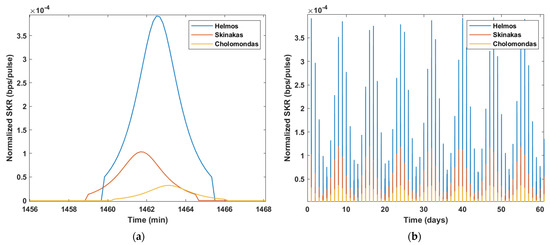
Figure 7.
(a) Normalized SKR (bps/pulse) over time for a random pass of one satellite over three OGSs. (b) Normalized SKR (bps/pulse) over time for a period of two months between one satellite and three OGSs.
The differences in the maximum value of the normalized SKRs depicted in Figure 8a were estimated due to the different aperture diameters of the telescopes installed in the three OGSs. Larger aperture diameters lead to lower free-space loss and scintillation loss, and therefore, higher key rates can be distilled from the QKD links. In our study, Helmos OGS, equipped with the largest telescope in Greece with a diameter of 2.3 m, can offer SKRs up to (bps/pulse), which is about four times higher SKRs compared to that offered by Skinakas OGS and more than eight times higher SKRs compared to that offered by Cholomondas OGS.
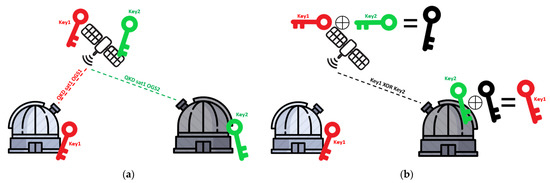
Figure 8.
(a) Key exchange between the satellite and two optical ground stations (OGSs). The satellite establishes two QKD links for each OGS. (b) The satellite sends Key1 ⊕ Key2 to OGS2 with classical data communication. OGS2 uses Key2 to acquire Key1.
In Table 1, the estimated total distilled key bits between each satellite and each ground station for a period of one year are presented, assuming nighttime communication and no link interruption due to clouds and a quantum signal repetition rate of 100 MHz [25,26]. It is worth mentioning that despite the fast repetition rate at Alice station, the photon loss due to link attenuation is also high. This combination prevents the detectors of Bob station to be saturated due to their dead time, since only a limited number of photons go to reach OGSs’ detectors. Higher repetition rates values have been also assumed in other publications [56], but this comes at the cost of further reducing the detectors gate time opening, possibly resulting in high time jitter loss and difficulties in synchronization [59].

Table 1.
Distilled key bits (Gbits) per satellite per ground station over a period of one year.
As expected, the OGSs with bigger apertures are able to distill more key bits. We assumed that these key bits are stored in a memory and can be used to encrypt classical communication data when necessary. Appropriate key management is necessary to assure that the keys are properly stored and their cryptoperiod while they are either stored or in use does not exceed the standard limits set by the National Institute of Standards and Technology (NIST) [60].
4.4. Practical Exploitation of Distilled Key Bits
Beyond the QKD link performance evaluation, the use of quantum keys as part of the symmetric-key cryptography systems is discussed in this subsection. In our proposed scheme, the quantum keys distilled by the QKD satellite link are fed into an AES-256 encryption engine, providing ultra-secure protection for data flows in Gbps rates. When sufficient key bits can be distilled, the OGS is able to use them to securely communicate with a single satellite. In practice, this is not very useful, since every satellite is visible by the OGS only for a few minutes daily. To overcome this limitation, an alternative security scheme is proposed, where the satellites are considered as trusted nodes that share identical keys between two OGSs. The security levels of the AES-256 for the above security architectures are studied, focusing on the AES-256 key refresh time.
4.4.1. Satellite as a Trusted Node
In the security architecture where the satellite can be used as a trusted node, one key that is shared between a satellite and an OGS can be also securely transmitted to another OGS as depicted in Figure 8 [61]. It is assumed that the satellite has already established quantum links between two different OGSs and two key strings of 256 bits distilled by these QKD links have been stored in its memory. By using the method of one-time pad (OTP), the satellite can send the 256-bit string result of the exclusive OR (XOR) operation between Key1 and Key2 (Key1 ⊕ Key2) to the OGS2. Given that Key1 and Key2 are only known by the satellite and each of the OGSs, the transmission of Key1 ⊕ Key2 through a classical channel is proven to be completely secure by the theory of OTP. Finally, OGS2 performs (Key1 ⊕ Key2) ⊕ Key2 to obtain Key1. Similarly, OGS1 obtains Key2; therefore, no quantum-distributed key bits are sacrificed in this chain.
4.4.2. AES-256 Key Refresh Time
The cryptographic algorithm of AES is most frequently supposed to be used as the encryption algorithm using the distilled keys of a QKD link. AES is proven to be quantum-resistant and therefore can be effectively combined with QKD to offer high security in the post-quantum world [62]. In order to further enforce the security of the encryption, a key size of 256 bits, instead of the classical size of 128 bits, was proposed to be used in AES-based methods. Besides the size of the AES key, the amount of the data encrypted by the same key is essential for guaranteeing the algorithm’s security [60,63]. Therefore, it is of high importance that the keys that will support the AES-256 engines are frequently refreshed. Different quantum key rotation times can be selected, depending on the attack surface that we need to pursue in the link, as well the classical data rates fed into AES-256 cryptographic engines [64].
In the presented satellite QKD scheme, we assumed that the trusted node communicates between all three OGSs with a single shared key used for encryption of data flows at 10 Gbps data speeds. The lifespan of a single key is depended on many factors [60], with the amount of data encrypted by the same key to be the most crucial parameter. According to [63], the maximum volume of data that can be encrypted by a single key in order to achieve an ultra-low attack success probability of is calculated to be about 0.3887 terabytes. Therefore, the keys should be frequently refreshed in order not to exceed this threshold. The maximum refresh time that can ensure this constraint for the given data speed was calculated in Appendix B to be 103.65 s or approximately 1.72 min. According to Table 1 and the method described in Section 4.4.1, every ground station is able to share up to 1.43 Gbits over a period of one year with each other. In Appendix C, these calculated bits are sufficient for refresh times down to about 5.64 s. This value is much less than the maximum refresh threshold of 1.72 min, corresponding to attack success probability threshold of . Consequently, this would mean that the security levels of all three OGSs would not be compromised even if the link had an availability as low as low as 5.4% during nighttime and the key rates would still support the threshold refresh time value of 1.72 min (Appendix C).
5. Discussion
Satellite communication networks have been declared as a strong candidate to support QKD blocks towards global-scale quantum-secured networks. This strategy for global-scale interconnection segments is going to be implemented through national-scale infrastructures, allowing for the enhanced feasibility of delivering satellite QKD across OGSs. Contributing in this direction, this research attempted to evaluate a satellite QKD downlink under realistic clear sky conditions for Greek QCI. Assuming a sufficient number of bits stored to be able to refresh the AES-256 keys, even with very low-key rates or frequent link interruption, the QKD-enabled communication link would still be practical, as it was presented in the results section. Beyond this proof-of-concept key distillation, a feasibility analysis investigating other atmospheric effects such as cloud coverage and the impact of the background radiance in the QKD link is the next research step. More specifically, studying on solar radiance under different sun and moon positions in the sky as well as the satellite’s position would be an interesting research extension.
It should also me mentioned that the finite size effect of key bits is an important parameter, especially in LEO satellite-to-ground QKD links. Due to the limited transmission time windows between the satellite and the OGS, this design parameter is taken into account in QKD studies [65,66]. Usually, the finite size effect is considered and examined in the optimization of QKD protocols. In our case, the finite size effect of key bits was not taken into consideration in the feasibility analysis, since the amount of exchanged key bits is big enough to exceed the lower bounds set in [67], therefore allowing positive key rates. Under a scenario where the link gets frequently interrupted (e.g., due to the cloud presence), thus leading to shorter communication time windows, this effect should be taken into consideration.
Besides the feasibility of the satellite-to-ground QKD link, the distribution of the quantum keys across terrestrial fiber segments is also an essential block of the future QCI. Observatories may be able to host state-of-the-art equipment that will grant higher key rates, but the support of the demanding needs of a terrestrial environment requires a closer investigation in both the physical layer and the security architecture. Under the Greek QCI initiative, dark fiber segments are planned to interconnect OGSs with nearby cities. By establishing QKD links between OGSs and the nearest cities and at the same time using the OGS as trusted relays, key delivery can be supported to distant fiber terminals. QKD protocols with proven performance in real-world circumstances can be considered as a deployment option [68]. Aside from the state-of-the-art QKD protocols allowing for outstanding distance-rate performance metrics, advanced quantum key management strategies can be implemented, based on collaboration with quantum-resistant algorithms (QRAs) [69].
6. Conclusions
We presented a thorough design study and a feasibility analysis on QKD satellite deployment devoted for Greek QCI. Using the installation parameters of OGSs hosted in Greek observatories, a decoy-state BB84 QKD link between a satellite constellation consisting of 10 LEO satellites and three OGSs was discussed. Realistic protocol implementation parameters have been considered for the QKD layer, and the QKD link performance was studied, considering the key atmospheric processes affecting the wireless optical link. Based on the set of the reported numerical results, the establishment of the QKD downlink is hard to accomplish in daylight conditions, but a sufficient amount of quantum keys can be distilled during nighttime. During the time instances when the satellites are visible to the OGSs at nighttime, the normalized SKR up to (bps/pulse) can be distilled. Over a period of one year, an amount of up to 1.435 Gbits of secret keys can be generated per ground station, and by using the trusted node architecture, these bits can be shared between the OGSs. It has been shown that this value of distilled bits is sufficient to support the AES-256 refresh times that keep an ultra-low attack success probability, ensuring high levels of security in data encryption/decryption. The reported results contribute towards the deployment discussions on Greek QCI based on the telescopes hosted in the observatories placed in South, Central, and North sectors of Greek territory. The successful quantum key delivery in the three OGSs via LEO satellite QKD links can be combined with terrestrial fiber segments to distribute securely optical data flows via terrestrial QKD systems, thereby allowing for end-to-end quantum-secured connectivity scenarios.
Author Contributions
Conceptualization, A.N., N.K.L., D.Z. and G.G.; data curation, A.N., N.K.L., D.Z. and G.G.; investigation, A.N., N.K.L., D.Z. and G.G.; methodology, A.N., N.K.L., D.Z. and G.G.; supervision, A.D.P. and H.A.; writing—the original draft, A.N., N.K.L., D.Z. and G.G.; writing—review and editing, A.D.P. and H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by H2020-funded Flagship project UNIQORN (820474).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Part of the research leading to this work was also supported by the ESA SKYLIGHT QUARTZ, Contract 4000123878/18/NL/MM.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Decoy-State BB84 Protocol Equation
Equation (1) gives the lower bound of the normalized SKR value and was written according to [35]. In this equation, q denotes the protocol efficiency factor, which depends on the implementation and can be calculated as:
where ½ occurs due to the selection of the BB84 protocol, since half of the received bit are shifted; , , and correspond to the numbers of emitted signal, decoy, and vacuum states, respectively; and correspond to the gain and the error rate of the single-photon states, respectively, and are upper bounded and lower bounded according to the following equations:
where μ and ν denote the mean photon numbers of the signal and decoy states, respectively; and correspond to the gains of the signal and decoy states, respectively; and corresponds to the overall quantum bit error rate. The values of and can be calculated as:
where η corresponds to the overall link transmittance, corresponds to the baseline system error rate and is equal to (1 − V)/2, where V is the detectors interferometer visibility, corresponds to the error rate of the background noise, is set to ½ by assuming that the background noise is random, and corresponds to the chance probability of the detector firing due to dark counts or background noise and is calculated as:
Appendix B. Maximum Refresh Time Calculation
According to [63], an attack success probability of can be achieved, if a single AES key encrypts no more than 0.3887 terabytes of data. Assuming that all three OGSs share the same AES-256 key and also that hey communicate at a data rate of 10 Gbps, the maximum key refresh time that bounds the attack success probability to can be calculated as follows:
Appendix C. Minimum Refresh Time Calculation
The total amount of distilled bits per station according to Table 1 can be up to 1.43 Gbits in a period of one year. Therefore, the minimum refresh time that is possible with a key size of 256 can be calculated as:
This value is times faster than the minimum refresh time. This means that even 18 times less distilled key bits (i.e., ~94.6% link interruption or ~5.4% link availability during nighttime) are sufficient to support the threshold of 103.65 s.
References
- Wu, Y.; Bao, W.-S.; Cao, S.; Chen, F.; Chen, M.-C.; Chen, X.; Chung, T.-H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photonics 2020, 12, 1012. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.-K.; Chau, H.F. Unconditional Security of Quantum Key Distribution over Arbitrarily Long Distances. Science 1999, 283, 2050–2056. [Google Scholar] [CrossRef] [Green Version]
- Shor, P.W.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bennett, C.H.; Gilles, B. Proceedings of the IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; IEEE: Piscataway, NJ, USA, 1984. [Google Scholar]
- Peev, M.; Pacher, C.; Alléaume, R.; Barreiro, C.; Bouda, J.; Boxleitner, W.; Debuisschert, T.; Diamanti, E.; Dianati, M.; Dynes, J.F.; et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 2009, 11, 075001. [Google Scholar] [CrossRef] [Green Version]
- Diamanti, E.; Lo, H.-K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. NPJ Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.-P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.; Hu, X.-L.; Guan, J.-Y.; Yu, Z.-W.; Xu, H.; Lin, J.; et al. Sending-or-Not-Sending with Independent Lasers: Secure Twin-Field Quantum Key Distribution over 509 km. Phys. Rev. Lett. 2020, 124, 070501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ntanos, A.; Zavitsanos, D.; Lyras, N.K.; Giannoulis, G.; Avramopoulos, H. On the Availability of the Decoy State BB84 QKD over a Terrestrial FSO Link. In Proceedings of the 2021 International Conference on Optical Network Design and Modeling (ONDM), Gothenburg, Sweden, 28 June–1 July 2021. [Google Scholar]
- Ursin, R.; Tiefenbacher, F.; Schmitt-Manderbach, T.; Weier, H.; Scheidl, T.; Lindenthal, M.; Blauensteiner, B.; Jennewein, T.; Perdigues, J.M.; Trojek, P.; et al. Entanglement-based quantum communication over 144 km. Nat. Phys. 2007, 3, 481–486. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.-K.; Cai, W.-Q.; Handsteiner, J.; Liu, B.; Yin, J.; Zhang, L.; Rauch, D.; Fink, M.; Ren, J.-G.; Liu, W.-Y.; et al. Satellite-Relayed Intercontinental Quantum Network. Phys. Rev. Lett. 2018, 120, 030501. [Google Scholar] [CrossRef] [Green Version]
- Polnik, M.; Mazzarella, L.; Di Carlo, M.; Oi, D.; Riccardi, A.; Arulselvan, A. Scheduling of space to ground quantum key distribution. EPJ Quantum Technol. 2020, 7, 3. [Google Scholar] [CrossRef]
- Khan, I.; Heim, B.; Neuzner, A.; Marquardt, C. Satellite-Based QKD. Opt. Photonics News 2018, 29, 26–33. [Google Scholar] [CrossRef]
- Yin, J.; Cao, Y.; Li, Y.-H.; Liao, S.-K.; Zhang, L.; Ren, J.-G.; Cai, W.-Q.; Liu, W.-Y.; Li, B.; Dai, H.; et al. Satellite-based entanglement distribution over 1200 kilometers. Science 2017, 356, 1140–1144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef] [Green Version]
- Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D. Cloud Attenuation Statistics Prediction from Ka-Band to Optical Frequencies: Integrated Liquid Water Content Field Synthesizer. IEEE Trans. Antennas Propag. 2016, 65, 319–328. [Google Scholar] [CrossRef]
- Lyras, N.K.; Efrem, C.N.; Kourogiorgas, C.I.; Panagopoulos, A.D. Optimum Monthly Based Selection of Ground Stations for Optical Satellite Networks. IEEE Commun. Lett. 2018, 22, 1192–1195. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, Y.; Gao, J. Achieving Accountability in Smart Grid. IEEE Syst. J. 2014, 8, 493–508. [Google Scholar] [CrossRef] [Green Version]
- Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D. Cloud free line of sight prediction modeling for Low Earth Orbit optical satellite networks. In International Conference on Space Optics—ICSO 2018; SPIE: Bellingham, WA, USA, 2019; Volume 11180, p. 111801G. [Google Scholar]
- Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D.; Liolis, K.P.; Sodnik, Z. Long Term Irradiance Statistics for Optical GEO Satellite Feeder Links: Validation Against Experimental Data. Wirel. Pers. Commun. 2020, 114, 749–764. [Google Scholar] [CrossRef]
- Kapsis, T.T.; Lyras, N.K.; Kourogiorgas, C.I.; Panagopoulos, A.D. Time Series Irradiance Synthesizer for Optical GEO Satellite Downlinks in 5G Networks. Futur. Internet 2019, 11, 131. [Google Scholar] [CrossRef] [Green Version]
- Hemmati, H. Near-Earth Laser Communications, 71–73; CRC Press: Boca Raton, FL, USA; New York, NY, USA; London, UK, 2009. [Google Scholar]
- Bonato, C.; Tomaello, A.; Da Deppo, V.; Naletto, G.; Villoresi, P. Feasibility of satellite quantum key distribution. New J. Phys. 2009, 11, 045017. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.-K.; Cai, W.-Q.; Liu, W.-Y.; Zhang, L.; Li, Y.; Ren, J.-G.; Yin, J.; Shen, Q.; Cao, Y.; Li, Z.-P.; et al. Satellite-to-ground quantum key distribution. Nat. Cell Biol. 2017, 549, 43–47. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-A.; Zhang, Q.; Chen, T.-Y.; Cai, W.-Q.; Liao, S.-K.; Zhang, J.; Chen, K.; Yin, J.; Ren, J.-G.; Chen, Z.; et al. An integrated space-to-ground quantum communication network over 4600 kilometres. Nat. Cell Biol. 2021, 589, 214–219. [Google Scholar]
- Tomaello, A.; Bonato, C.; Da Deppo, V.; Naletto, G.; Villoresi, P. Link budget and background noise for satellite quantum key distribution. Adv. Space Res. 2011, 47, 802–810. [Google Scholar] [CrossRef]
- Liao, S.-K.; Yong, H.-L.; Liu, C.; Shentu, G.-L.; Li, D.-D.; Lin, J.; Dai, H.; Zhao, S.-Q.; Li, B.; Guan, J.-Y.; et al. Long-distance free-space quantum key distribution in daylight towards inter-satellite communication. Nat. Photonics 2017, 11, 509–513. [Google Scholar] [CrossRef]
- Bedington, R.; Arrazola, J.M.; Ling, A. Progress in satellite quantum key distribution. npj Quantum Inf. 2017, 3, 30. [Google Scholar] [CrossRef]
- All Member States Now Committed to Building An EU Quantum Communication Infrastructure. Available online: https://digital-strategy.ec.europa.eu/en/news/all-member-states-now-committed-building-eu-quantum-communication-infrastructure (accessed on 3 November 2021).
- Giannopappa, C. 5G, Fibre in the Sky and beyond. In Proceedings of the ScyLight Workshop on Optical and Quantum Communication, Online Event, 8–9 June 2021. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Optical Engineering Press: Bellingham, WA, USA, 1998; pp. 47–50. [Google Scholar]
- Auer, M.; Freiwang, P.; Baliuka, A.; Schattauer, M.; Knips, L.; Weinfurter, H. A portable and compact decoy-state QKD sender. In Proceedings of the 2021 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 21–25 June 2021; p. 1. [Google Scholar]
- Mazzarella, L.; Lowe, C.; Lowndes, D.; Joshi, S.K.; Greenland, S.; McNeil, D.; Mercury, C.; Macdonald, M.; Rarity, J.; Oi, D.K.L. QUARC: Quantum Research Cubesat—A Constellation for Quantum Communication. Cryptography 2020, 4, 7. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [Green Version]
- Mayers, D. Unconditional security in quantum cryptography. JACM 2001, 48, 351–406. [Google Scholar] [CrossRef]
- Huttner, B.; Imoto, N.; Gisin, N.; Mor, T. Quantum cryptography with coherent states. Phys. Rev. A 1995, 51, 1863–1869. [Google Scholar] [CrossRef] [Green Version]
- Hwang, W.-Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-B. Beating the Photon-Number-Splitting Attack in Practical Quantum Cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Chen, W.; Yin, Z.-Q.; Li, H.-W.; He, D.-Y.; Li, Y.-H.; Zhou, Z.; Song, X.-T.; Li, F.-Y.; Wang, D.; et al. Field and long-term demonstration of a wide area quantum key distribution network. Opt. Express 2014, 22, 21739–21756. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Qi, B.; Ma, X.; Lo, H.-K.; Qian, L. Simulation and Implementation of Decoy State Quantum Key Distribution over 60km Telecom Fiber. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 2094–2098. [Google Scholar]
- Carrasco-Casado, A.; Kunimori, H.; Takenaka, H.; Kubo-Oka, T.; Akioka, M.; Fuse, T.; Koyama, Y.; Kolev, D.; Munemasa, Y.; Toyoshima, M. LEO-to-ground polarization measurements aiming for space QKD using Small Optical TrAnsponder (SOTA). Opt. Express 2016, 24, 12254–12266. [Google Scholar] [CrossRef]
- Takenaka, H.; Carrasco-Casado, A.; Fujiwara, M.; Kitamura, M.; Sasaki, M.; Toyoshima, M. Satellite-to-ground quantum-limited communication using a 50-kg-class microsatellite. Nat. Photon. 2017, 11, 502–508. [Google Scholar] [CrossRef] [Green Version]
- Kolev, D.R.; Toyoshima, M. Satellite-to-ground optical communications using small optical transponder (SOTA)—received-power fluctuations. Opt. Express 2017, 25, 28319–28329. [Google Scholar] [CrossRef]
- Cakaj, S.; Kamo, B.; Lala, A.; Rakipi, A. The Coverage Analysis for Low Earth Orbiting Satellites at Low Elevation. Int. J. Adv. Comput. Sci. Appl. 2014, 5, 8. [Google Scholar] [CrossRef] [Green Version]
- Series, P. Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems. Recommendation ITU-R, 618–12; ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Kiasaleh, K. On the probability density function of signal intensity in free-space optical communications systems im-paired by pointing jitter and turbulence. Opt. Eng. 1994, 33, 3748–3757. [Google Scholar] [CrossRef]
- Yura, H.T.; McKinley, W.G. Aperture averaging of scintillation for space-to-ground optical communication applications. Appl. Opt. 1983, 22, 1608–1609. [Google Scholar] [CrossRef]
- Giggenbach, D.; Moll, F. Scintillation loss in optical Low Earth Orbit data downlinks with avalanche photodiode receivers. In Proceedings of the 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Naha, Japan, 14–16 November 2017; pp. 115–122. [Google Scholar]
- Rollins, D.; Baars, J.; Bajorins, D.P.; Cornish, C.S.; Fischer, K.W.; Wiltsey, T. Background light environment for free-space optical terrestrial communication links. In Optical Wireless Communications; SPIE: Bellingham, WA, USA, 2002; Volume 4873, pp. 99–111. [Google Scholar]
- Carrasco-Casado, A.; Sanchez-Pena, J.M.; Vergaz, R. CTA Telescopes as Deep-Space Lasercom Ground Receivers. IEEE Photonics J. 2015, 7, 1–14. [Google Scholar] [CrossRef]
- Recommendation ITU-R P. 1621, Propagation Data Required for the Design of Earth-Space Systems Operating between 20 THz and 375 THz; ITU: Geneva, Switzerland, 2003.
- Single Quantum Eos. Available online: https://singlequantum.com/products/single-quantum-eos/ (accessed on 3 November 2021).
- Mlejnek, M.; Kaliteevskiy, N.A.; Nolan, D.A. Reducing spontaneous Raman scattering noise in high quantum bit rate QKD systems over optical fiber. arXiv 2017, arXiv:1712.05891. [Google Scholar]
- Eraerds, P.; Walenta, N.; Legré, M.; Gisin, N.; Zbinden, H. Quantum key distribution and 1 Gbps data encryption over a single fibre. New J. Phys. 2010, 12, 063027. [Google Scholar] [CrossRef] [Green Version]
- Dirks, B.P.; Ferrario, I.; Le Pera, A.; Finocchiaro, D.V.; Desmons, M.; de Lange, D.; de Man, H.; Meskers, A.J.H.; Morits, J.; Neumann, N.M.M.; et al. GEOQKD: Quantum key distribution from a geostationary satellite. In Proceedings of the International Conference on Space Optics—ICSO 2020; SPIE: Bellingham, WA, USA, 2021; Volume 11852, p. 118520J. [Google Scholar]
- Er-Long, M.; Zheng-Fu, H.; Shun-Sheng, G.; Tao, Z.; Da-Sheng, D.; Guang-Can, G. Background noise of satellite-to-ground quantum key distribution. New J. Phys. 2005, 7, 215. [Google Scholar] [CrossRef]
- Available online: https://www.agi.com/products/stk (accessed on 3 November 2021).
- Migdall, A.; Polyakov, S.V.; Fan, J.; Bienfang, J.C. Single-Photon Generation and Detection: Physics and Applications; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Barker, E. Recommendation for Key Management Part 1: General; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016.
- Tajima, A.; Kondoh, T.; Ochi, T.; Fujiwara, M.; Yoshino, K.; Iizuka, H.; Sakamoto, T.; Tomita, A.; Shimamura, E.; Asami, S.; et al. Quantum key distribution network for multiple applications. Quantum Sci. Technol. 2017, 2, 034003. [Google Scholar] [CrossRef]
- Bonnetain, X.; Naya-Plasencia, M.; Schrottenloher, A. Quantum Security Analysis of AES. IACR Trans. Symmetric Cryptol. 2019, 2, 55–93. [Google Scholar] [CrossRef]
- Luykx, A.; Paterson, K.G. Limits on Authenticated Encryption Use in TLS. 2015. Available online: http://www.isg.rhul.ac.uk/~kp/TLS-AEbounds.pdf (accessed on 2 November 2021).
- Zavitsanos, D.; Ntanos, A.; Giannoulis, G.; Avramopoulos, H. On the QKD Integration in Converged Fiber/Wireless Topologies for Secured, Low-Latency 5G/B5G Fronthaul. Appl. Sci. 2020, 10, 5193. [Google Scholar] [CrossRef]
- Sun, X.; Djordjevic, I.B.; Neifeld, M.A. Secret Key Rates and Optimization of BB84 and Decoy State Protocols Over Time-Varying Free-Space Optical Channels. IEEE Photonics J. 2016, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Sidhu, J.S.; Brougham, T.; McArthur, D.; Pousa, R.G.; Oi, D.K. Finite key effects in satellite quantum key distribution. arXiv 2020, arXiv:2012.07829. [Google Scholar]
- Scarani, V.; Renner, R. Quantum cryptography with finite resources: Unconditional security bound for discrete-variable protocols with one-way postprocessing. Phys. Rev. Lett. 2008, 100, 200501. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Jiang, C.; Zhu, H.-T.; Zou, M.; Yu, Z.-W.; Hu, X.-L.; Xu, H.; Ma, S.; Han, Z.; Chen, J.-P.; et al. Field Test of Twin-Field Quantum Key Distribution through Sending-or-Not-Sending over 428 km. Phys. Rev. Lett. 2021, 126, 250502. [Google Scholar] [CrossRef]
- Community Response to the NCSC 2020 Quantum Security Technologies White Paper. Available online: https://www.quantumcommshub.net/news/community-response-to-the-ncsc-2020-quantum-security-technologies-white-paper/?site=industry-government-media (accessed on 3 November 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).