Remote Quantum-Safe Authentication of Entities with Physical Unclonable Functions

Abstract

Physical unclonable functions have been shown to be a useful resource of randomness for implementing various cryptographic tasks including entity authentication. All the related entity authentication protocols that have been discussed in the literature so far, either they are vulnerable to an emulation attack, or they are limited to short distances. Hence, quantum-safe remote entity authentication over large distances remains an open question. In the first part of this work, we discuss the requirements that an entity authentication protocol has to offer, to be useful for remote entity authentication in practice. Subsequently, we propose a protocol, which can operate over large distances, and offers security against both classical and quantum adversaries. The proposed protocol relies on standard techniques, it is fully compatible with the infrastructure of existing and future photonic networks, and it can operate in parallel with other quantum protocols, including QKD protocols.

1. Introduction

Entity authentication is one of the main pillars of our digital world, which is widely employed to control access of users to physical or virtual resources [1,2]. The typical scenario involves a human user (claimant) who must provide in real time evidence, of her identity to another human or non-human entity (verifier), to obtain access e.g., to a laboratory or to a bank account.

Entity authentication can be provided by means of various techniques, some of which are not inherently cryptographic. Among the cryptographic techniques, dynamic schemes with a challenge-response mechanism are of particular interest, because they offer high level of security for most everyday tasks [1,2]. This is, for instance, the case of smart cards (tokens) that are widely used e.g., in transactions through ATMs, as well as in e-commerce. To a large extent, their security relies on a short (typically four- to eight-digit) PIN, which is connected to the card, and it is known to the legitimate owner of the card, as well as an independent long numerical secret key, which is stored on the card, and the verifier has a matching counterpart of it. The PIN may also be stored on the token, and it provides an additional level of security in case the token is lost or stolen. A common technique is for the PIN to serve as a means for the verification of the user to the token, and subsequently the token (representing the user) authenticates itself to the system by means of the additional secret key stored on it (e.g., the token may be asked to encrypt a randomly chosen challenge with its key). Hence, we have a two-stage authentication, which requires the user to remember the short PIN, and to possess the token where the longer secret key is stored. There are cases where both stages take place (e.g., transactions through ATMs), and cases where the authentication of the user to the card suffices (e.g., e-commerce). In either case, the secrecy of the long numerical secret key is of vital importance, and there are various physical invasive and non-invasive attacks as well as software attacks, which aim at its extraction from the card [3,4,5,6].

Physical unclonable functions (PUFs) have been proposed as a means for developing entity authentication protocols (EAPs) [7,8], which do not require the storage of a secret numerical key, and thus they are resistant to the aforementioned attacks. Typically, a PUF relies on a physical token with internal randomness, which is introduced explicitly or implicitly during its fabrication, and it is considered to be technologically hard to clone (hence the term physical unclonable). The operation of PUF-based EAPs relies on a challenge-response mechanism, where the verifier accepts or rejects the identity of the claimant based on the responses of the token to one or more randomly chosen challenges. A list of challenge-response pairs is generated by the manufacturer, before the token is given to a user, and it is stored in a system database where the verifier has access over an authenticated classical channel.

The nature of the physical token essentially determines the nature of the challenges and the responses, as well as the operation of the PUF. One can find a broad range of PUFs in the literature [9,10,11], and electronic PUFs is the most well studied class, mainly because of their compatibility with existing technology and hardware. However, they are susceptible to various types of modeling and side-channel attacks [10,12,13,14,15], and current research is focused on the development of new schemes, which offer provable security against such attacks (e.g., see [16] and references therein). On the contrary, optical PUFs are not fully compatible with existing technology in ATMs, but they offer many advantages relative to electronic PUFs, including low cost, high complexity, and security against modeling attacks [10,17]. Typically, their operation relies on the response of a disordered optical multiple-scattering medium (token), when probed by light with randomly chosen parameters. In general, one can distinguish between two major classes of optical PUFs. In optical PUFs with classical readout, different numerical challenges are encoded on the parameters of laser light that is scattered by the token [7,8,18,19]. Typically, such encoding may involve the wavelength, the wavefront, the point and angle of incidence, or a combination thereof. In the second major class of optical PUFs, the token is interrogated by quantum states (quantum readout), and different numerical challenges are encoded on non-orthogonal quantum states of light [20,21,22,23,24,25].

To the best of our knowledge, all the known EAPs with classical readout of optical PUFs are susceptible to an emulation attack [20,21]. On the other hand, as explained below in more detail, all the known EAPs that rely on optical PUFs and offer security against an emulation attack [22,23,24], assume a tamper-resistant verification setup, while they are limited to short distances (typically $<10$ km). Moreover, none of the above EAPs (with classical [7,8,18,19] or quantum readout [20,21,22,23,24,25]) takes into account the possibility of the token to be stolen or lost, and thus they are not secure in a scenario where the token is possessed by the adversary. In the present work our aim is to propose a protocol which addresses all these issues, and it offers quantum-secure entity authentication over large distances (≳100 km). The proposed protocol does not require the storage of any secret key, apart from the short PIN which accompanies the token, and it must be memorized by the holder. Moreover, the protocol can be implemented with current technology, and it is fully compatible with existing and forthcoming quantum key distribution (QKD) infrastructure.

2. Materials and Methods

For the sake of completeness, in this section we summarize the main optical-PUF-based EAPs that have been discussed in the literature so far, focusing on their vulnerabilities in a remote authentication scenario, which is the main subject of the present work.

The general setting of an EAP involves two parties: the prover or claimant (Alice) and the verifier (Bob). Alice (A) presents evidence about her identity to Bob (B), and the main task of Bob is to confirm the claimed identity. Typically, an EAP may rely on something that the claimant knows (e.g., a password), something that the claimant possesses (e.g., a token), or on a combination of the two. To avoid any misunderstandings, throughout this work Alice is considered to be honest, whereas there is a third party (Eve), who intends to impersonate Alice to the verifier.

Depending on whether the optical challenges are formed by encoding numerical challenges on classical or quantum states of light, one can distinguish between optical PUFs with classical [7,8,18,19] and quantum readout [20,21,22,23,24]. In either case, all the related EAPs that have been proposed in the literature, rely on a challenge-response mechanism and the existence of a challenge-response database, which is generated by the manufacturer only once, before the token is given to the legitimate user. The database characterizes fully the response of the token with respect to all the possible challenges that may be chosen by the system, and thus the verifier may accept or reject the token-based solely on its response to a finite number of randomly chosen challenges. In a single authentication session, the token is inserted in a verification setup, where the verifier has remote access, and it is interrogated by randomly chosen optical challenges. The corresponding responses are returned to the verifier, and they are compared to the expected ones. The verifier accepts the identity of the claimant if the recorded responses are compatible with the expected ones, and rejects it otherwise.

To the best of our knowledge, besides the unclonability of the token, all of the known optical EAPs assume that the token is in possession of the legitimate user [7,8,18,19,21,22,23]. However, there is nothing in these protocols that binds the token to the legitimate owner, which means that whoever has the token can impersonate successfully the legitimate owner to the system [1]. In other words, none of the existing schemes is secure when the token is lost or stolen. In analogy to conventional smart cards, one way to prevent the use of the token by an unauthorized user is to introduce a PIN which is connected somehow to the token, and it is memorized by the legitimate owner of the token. Moreover, to facilitate remote entity authentication, it is desirable for the PIN verification to be possible without any access to a central database. In conventional smart cards this is achieved by storing the PIN on the chip of the card. However, the generalization of this approach to all-optical EAPs is not straightforward, and one must design judiciously the protocol.

Communication between the claimant and the verifier is inevitable for any EAP, irrespective of whether this is performed by means of classical or quantum resources. We are interested in EAPs which remain secure even when an adversary monitors this communication. One way to satisfy this requirement is to ask for Alice and Bob to be connected via a trusted communication line, which in turn imposes additional requirements (e.g., additional secret keys). The assumption of trusted communication line, safe from monitoring, may be reasonable for a local authentication scenario, where Alice and Bob are in the same building, but it is not suitable for remote entity authentication, where the information exchanged between them may travel hundreds of kilometers over open communication lines. In this case, the security of entity authentication requires guarding against potential adversaries who monitor the communications, and the development of secure protocols becomes rather challenging.

Schemes with classical readout [7,8,19], have an advantage over schemes with quantum readout, in the sense that they are not susceptible to inevitable losses and noise associated with the transmission of quantum states over large distances. As a result, they can operate over arbitrarily large distances, but they are vulnerable to emulation and replay attacks [1,21], if an adversary (Eve) obtains undetected access to the database of challenge-response pairs, or if she monitors the classical communication between Alice and Bob.

To prevent such attacks, various authors have proposed EAPs in which different numerical challenges are mapped onto non-orthogonal quantum states of light, and the authentication of the token involves one or more such states chosen at random and independently [20,21,22,23,24]. In this case, in order for Eve to successfully impersonate Alice (without access to her token), she must identify successfully each one of the transmitted states, and to send the right sequence of responses to the system. Fundamental laws of quantum physics limit the amount of information that can be extracted from each state, and it is inevitable for Eve to deduce the wrong challenge for some of them. In these cases she will send the wrong responses to the verifier, and her intervention will be revealed. These ideas are exploited by the protocols in Refs. [20,21,22,23,24], and the security of the protocols has been investigated against various types of intercept-resend attacks, where the adversary has obtained access to the database of challenge-response pairs, and the verification setup is tamper resistant. The latter assumption implies that all the components of the verification setup are controlled by the verifier, and the adversary has access to the optical challenge only immediately before it impinges on the token.

Unfortunately, for practical reasons, all these schemes are limited to short distances (<10 km). This is well below the distances that can be covered presently by standard QKD protocols, which employ single-mode fibers (SMFs) [26,27]. More precisely, extension of the protocol of Goorden et al. [21] to large distances requires the use of multimode fibers, which allow for the transmission of the modified wavefront from the verifier to the claimant and backwards. Inevitable time-dependent variations of the multimode fiber during the transmission of the optical signals will result in cross-mode coupling (e.g., see [28] and references therein), therefore limiting the distances over which secure entity authentication can be achieved. Moreover, integration of the authentication scheme of Goorden et al. in forthcoming quantum communications infrastructures, is complicated considerably by the necessity for reliable low-loss interfaces between multimode fibers and SMFs. On the other hand, although the scheme of Refs. [22,23,24] is fully compatible with existing QKD infrastructure, it relies on a Mach-Zehnder interferometric setup. As a result, it can operate reliably only if the relative length of the arms in the interferometer does not change by more than a fraction of a wavelength [26]. This is also possible for short distances (<10 km), but it is harder when the distance between the verifier and the claimant increases, because of inevitable environmental variations.

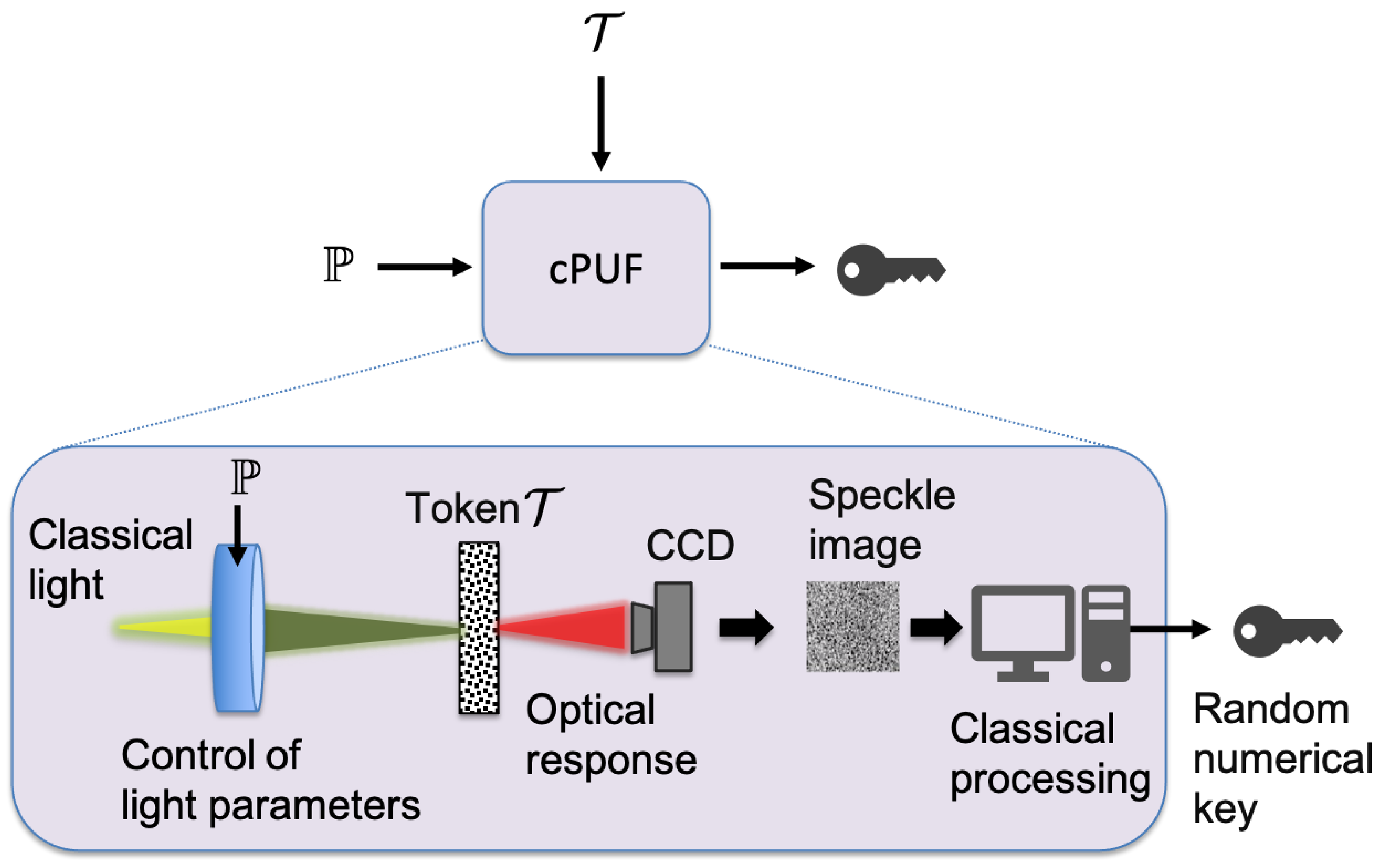
In the following sections we propose an EAP, which addresses all the above issues and it is suitable for remote authentication over arbitrary distances. At the core of our scheme there is a token $\mathcal{T}$, which is given to a user and it is used for her identification by the verifier. The token resembles a standard smart card in conventional EAPs, with a random multiple-scattering optical medium in place of the chip (see Figure 1). The faithful cloning of the token typically requires the exact positioning (on a nanometer scale) of millions of scatterers with the exact size and shape, which is considered to be a formidable challenge not only for current, but for future technologies as well. Hence, the internal disorder on the one hand renders the cloning of the token a formidable challenge, while on the other hand may serve as a physical source of randomness for the development of cryptographic primitives.

The optical response of the token $\mathcal{T}$ to classical light is a random interference pattern (speckle), which depends strongly on the internal disorder of $\mathcal{T}$, as well as on the parameters of scattered light (including the wavelength, the power, the wavefront, the point and angle of incidence). It has been shown that through a judicious classical processing of the speckle, one can obtain a random numerical key K [7,8,18,19], which passes successfully all the widely accepted tests for random-sequence certification (see Figure 2). This means that for all practical purposes such a key can be considered to be close to truly random [7,8,18,19], and there are no correlations between different elements or parts of the key, as well as between keys that have been generated from different tokens or from light with different parameters. Typically, the processing also involves error correction so that to ensure stability of the key with respect to inevitable innocent noise, thermal fluctuations, instabilities, etc. Therefore, the function

$$\begin{array}{c}\hfill \mathrm{cPUF}(\mathcal{T},\mathbb{P})=K,\end{array}$$

(1)

is essentially an optical pseudorandom number generator, which generates the random key K from the token $\mathcal{T}$, when seeded with light of parameters $\mathbb{P}$. The same token will yield the same random key when interrogated by classical light with parameters $\mathbb{P}$, and thus there is no need for storage of K, provided one has access to both of $\mathcal{T}$ and $\mathbb{P}$. The length of the keys that can be extracted in this way, ranges from hundreds to thousands of bits [7,8,18,19].

It is important to emphasize once more that the classical algorithm used for the extraction of the key from the speckle plays a pivotal role in the randomness of the key, and the wrong choice may result in keys which contain correlations, and they are far from uniform.

3. Results

The EAP we will consider relies on a judicious combination of the ideas discussed in Refs. [7,8,18,19]. At the core of the proposed protocol, there is the optical pseudorandom number generator discussed above.

3.1. Enrollment of the Token to the System

We consider a two-stage enrollment, which takes place only once, before the token ${\mathcal{T}}_{\mathrm{A}}$ is given to the legitimate user (Alice). The process in summarized in Figure 3.

Stage E1.—The first step aims at the generation of a short (typically four-digit) PIN, which is associated with the token. More precisely, the token is interrogated by classical light with a fixed and publicly known set of parameters ${\mathbb{P}}_{\mathrm{def}}$, which may include wavelength, wavefront, power, position and angle of incidence, etc. This is the default set of parameters for all the verification set-ups where the user may insert her token. To associate the token with a short random PIN we exploit the ideas discussed in Section 2. More precisely, Alice’s PIN is obtained by means of the pseudorandom number generator shown in Figure 2 (with the appropriate classical processing), and for all practical purposes it can be considered stable and close to truly random. The PIN is given to Alice together with the associated token ${\mathcal{T}}_{\mathrm{A}}$, and in analogy to conventional smart cards, Alice must memorize it. By contrast to conventional smart cards, in our case the PIN is not stored on the token or anywhere else.

Stage E2.—The second step of the enrollment stage also exploits the ideas discussed in Section 2, and aims at the creation of a database of challenge-response pairs for the token ${\mathcal{T}}_{\mathrm{A}}$, which will be used by the verifier for the authentication of Alice to the system (see below). Let $\{{\mathbb{P}}_j,j=1,2,\dots \}$ denote different challenges. Each challenge pertains to the parameters of the classical light to be used in the interrogation of the token, and by contrast to ${\mathbb{P}}_{\mathrm{def}}$ used above, it is not publicly known. These parameters may include wavelength, angle and position of incidence, wavefront, etc. In order to minimize the secret information that must be shared between the verifier and the user, we introduce a second token ${\mathcal{T}}_{\mathrm{B}}$ which is accessible by the verifier only. The two tokens are independent of each other, and thus their responses to the same challenge are also random and independent. Let ${\mathit{k}}_j^{\left(\mathrm{A}\right)}$ and ${\mathit{k}}_j^{\left(\mathrm{B}\right)}$ denote the numerical binary keys generated from tokens ${\mathcal{T}}_{\mathrm{A}}$ and ${\mathcal{T}}_{\mathrm{B}}$ respectively, for challenge ${\mathbb{P}}_j$. The joint key ${\mathit{k}}_j^{\left(\mathrm{A}\right)}\oplus {\mathit{k}}_j^{\left(\mathrm{B}\right)}$ (the symbol ⊕ denotes addition modulo 2), together with the corresponding challenge ${\mathbb{P}}_j$, are stored in the database, whereas the individual keys are never stored in plain text.

3.2. Verification

In analogy to entity authentication by means of conventional smart cards, we consider a two-stage verification process, which is summarized in Figure 4.

Stage V1.—Initially, the user is authenticated to the token by means of the short PIN, so that to ensure that the token has not been stolen, and it is possessed by the legitimate holder. By contrast to conventional smart cards, in our case the PIN is not stored on the token, but it can be produced from it easily. As depicted in Figure 4, the claimant inserts her token to the (un)secured terminal, and types in her secret PIN. The token is interrogated by classical light with parameters ${\mathbb{P}}_{\mathrm{def}}$, and the corresponding response (speckle) is processed classically to yield $\widetilde{\mathrm{PIN}}$, which is compared to the PIN that the claimant has typed in independently. The system accepts that the legitimate user is in possession of the token only if $\mathrm{PIN}=\widetilde{\mathrm{PIN}}$, and it is only in this case that the protocol proceeds to the second stage pertaining to the authentication of the token. It is also worth noting that stage V1 takes place locally and there is no need for communication with the verifier.

Stage V2.—Assuming that the verification of the user to the token has been successful, the token can represent the claimant and the remaining step is its authentication to the system.

Each authentication session pertains to a different row of the database, which is chosen at random by the verifier (Bob). For the sake of concreteness, we will consider the jth row. Bob uses a classical optical probe with parameters ${\mathbb{P}}_j$, in order to derive key ${\mathit{k}}_j^{\left(\mathrm{B}\right)}$ from token ${\mathcal{T}}_{\mathrm{B}}$, along the lines discussed in Section 2. Subsequently, he generates independently a random secret binary message ${\mathit{z}}^{\left(\mathrm{B}\right)}$ of the same length as ${\mathit{k}}_j^{\left(\mathrm{B}\right)}$, and sends to the verification setup the ciphertext

$$\begin{array}{c}\hfill {\mathit{w}}_j={\mathit{z}}^{\left(\mathrm{B}\right)}\oplus ({\mathit{k}}_j^{\left(\mathrm{A}\right)}\oplus {\mathit{k}}_j^{\left(\mathrm{B}\right)})\oplus {\mathit{k}}_j^{\left(\mathrm{B}\right)}={\mathit{z}}^{\left(\mathrm{B}\right)}\oplus {\mathit{k}}_j^{\left(\mathrm{A}\right)},\end{array}$$

(2)

together with the associated set of parameters ${\mathbb{P}}_j$. If the user is honest and has inserted the right token in the verification setup, then she should be able to decrypt the message of the verifier. Let us denote by ${\tilde{\mathcal{T}}}_{\mathrm{A}}$ the token that represents the user to the system, which may or may not be Alice’s true token. The token ${\tilde{\mathcal{T}}}_{\mathrm{A}}$ is interrogated by classical light with parameters ${\mathbb{P}}_j$, and the resulting speckle is processed classically to yield the numerical key ${\tilde{\mathit{k}}}_j^{\left(\mathrm{A}\right)}$. All the process takes place locally, and the derived key is XORed with the received ciphertext ${\mathit{w}}_j$. The resulting message ${\mathit{z}}^{\left(\mathrm{A}\right)}={\tilde{\mathit{k}}}_j^{\left(\mathrm{A}\right)}\oplus {\mathit{w}}_j$, is sent back to the verifier. Bob accepts the token (and thus the claimed identity of the user), if and only if ${\mathit{z}}^{\left(\mathrm{A}\right)}={\mathit{z}}^{\left(\mathrm{B}\right)}$. Assuming that innocent noise and imperfections have been taken care by the classical processing of the speckle through which the keys are derived, it is highly unlikely for the verifier and the honest user to derive keys which differ from the ones used in the encryption of ${\mathit{z}}^{\left(\mathrm{B}\right)}$ [7,8,18,19]. Hence, any discrepancies between ${\mathit{z}}^{\left(\mathrm{A}\right)}$ and ${\mathit{z}}^{\left(\mathrm{B}\right)}$ can be attributed to a wrong token, and/or some type of cheating.

At the end of the session, the jth entry of the database is erased, and it is never used again, irrespective of the outcome of the authentication session.

4. Discussion

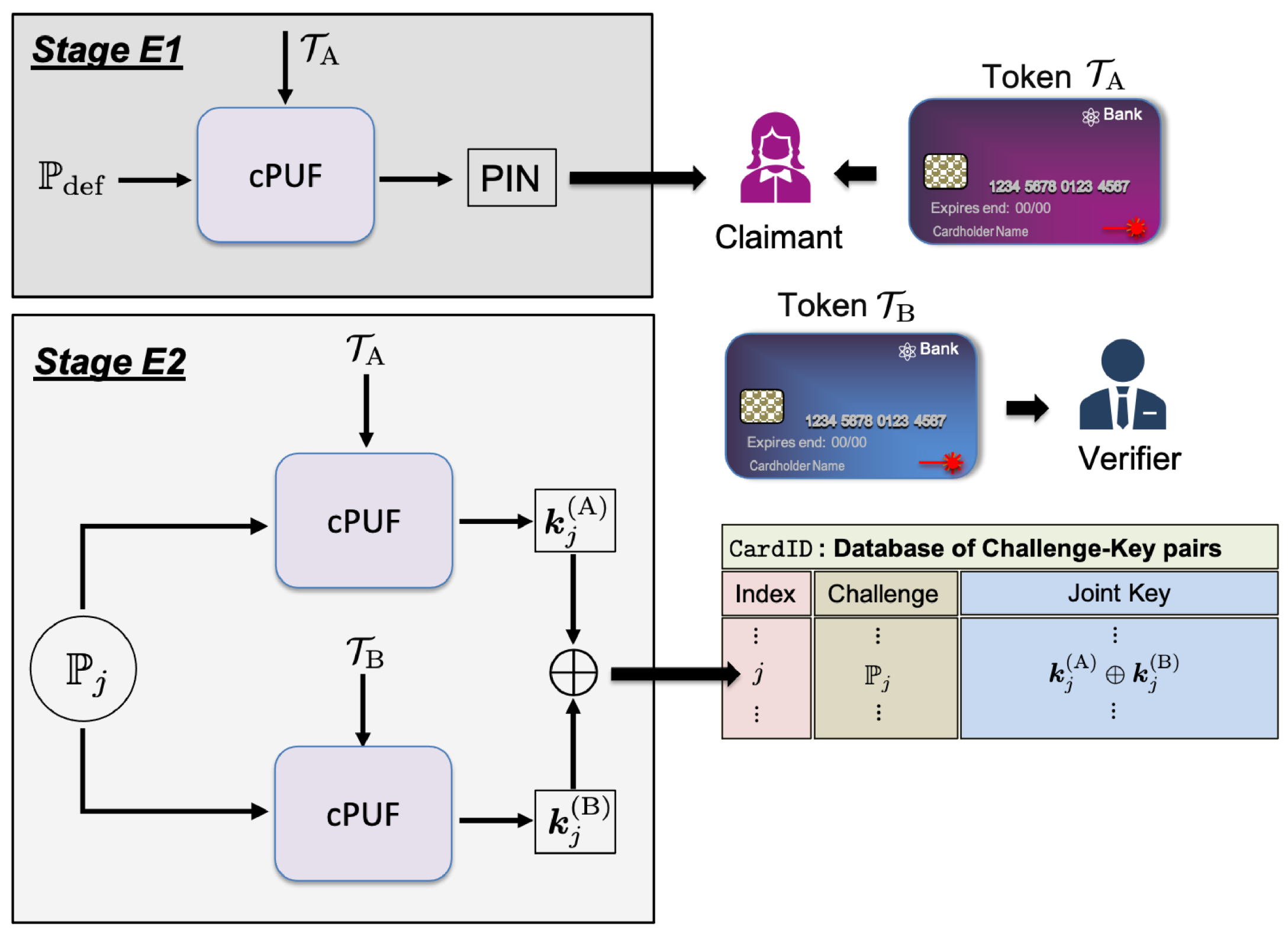
We emphasize that for Eve to successfully impersonate Alice, she must pass successfully both of the verification stages discussed in Section 3.

The security of the protocol stems directly from the security of the protocols discussed in Refs. [7,8,18,19]. For the sake of completeness it is worth summarizing here the three main cornerstones. The first one is the technological hardness of the cloning of the optical disordered token. This is a common prerequisite for any useful PUF-based cryptographic protocol, and there have been some attempts for the quantification of the hardness in the case of optical tokens [7,8,22,29]. The second cornerstone is the strong sensitivity of the speckle to the internal disorder of the token and to the parameters of the input light, which has been demonstrated in different experimental set-ups and for various combinations of parameters [7,8,18,19]. The third cornerstone pertains to the algorithms used for the conversion of the random speckle to a numerical key. These algorithms should be able to convert the random speckle into random numerical key, without introducing any correlations. Various algorithms have been discussed in the literature, and most of them achieve this goal.

Assuming that these three conditions are satisfied simultaneously, then it is highly unlikely for Eve to have both a clone of Alice’s token and the associated PIN, in order to impersonate her successfully. The unclonability of the token essentially implies that the creation of a nearly perfect clone, which produces the same challenge-response pairs as the actual token, is a formidable challenge for current as well as near-future technology. However, given that one cannot be sure about the technology of a potential adversary, it is very important for Alice not to leave her token unattended for a long period of time. The strong dependence of the speckle on the internal disorder of the token as well as on the details of the input light, implies that the speckle associated with different tokens and/or different parameters are random and independent. For judiciously chosen algorithms, these properties are transferred over to the derived numerical keys, which have been shown to pass successfully standard randomness tests [7,8,18,19] and thus, for all practical purposes, they can be considered to be close to truly random with uniform distribution.

A short 4-digit PIN extracted by truncation of a long random numerical key is also close to truly random with uniform distribution. It is worth noting that the PIN verification takes place locally, and the PIN never leaves the verification setup. In analogy to conventional smart cards, it is important for the legitimate user to cover the keypad of the setup while entering her PIN, so that to protect it from an adversary who has installed a camera that monitors the user’s actions, without being detected. Under these conditions, the best an adversary can do is to make a guess for the PIN, with the probability of successful guessing being ${10}^{-4}$.

The keys ${\mathit{k}}_j^{\left(\mathrm{A}\right)}$ and ${\mathit{k}}_j^{\left(\mathrm{B}\right)}$ that are used in the token authentication are never stored in plain text. Based on the above, they are uniformly distributed independent random strings, because they pertain to different independent tokens. Even if an adversary has obtained a copy of the database, the derivation of the individual keys from ${\mathit{k}}_j^{\left(\mathrm{A}\right)}\oplus {\mathit{k}}_j^{\left(\mathrm{B}\right)}$ is impossible by virtue of the one-time-pad encryption, unless he has also access to at least one of the tokens, either ${\mathcal{T}}_{\mathrm{A}}$ or ${\mathcal{T}}_B$. This implies that ${\mathit{k}}_j^{\left(\mathrm{A}\right)}$ is a secret random key, and thus the encryption of the random message ${\mathit{z}}^{\left(\mathrm{B}\right)}$ is information theoretically secure. An adversary who monitors the communication line that connects the verification setup to the verifier, cannot successfully impersonate the legitimate user, without access to ${\mathcal{T}}_{\mathrm{A}}$. The best she can do is to make a guess for ${\mathit{z}}^{\left(\mathrm{B}\right)}$ (or equivalently ${\mathit{k}}_j^{\left(\mathrm{A}\right)}$), and the probability for correct guessing drops exponentially with its length. For instance, when $|{\mathit{z}}^{\left(\mathrm{B}\right)}|\ge 100$ the probability of correct guessing is $2^{-100}\simeq {10}^{-30}$.

In closing, it should be emphasized that the protocol is not secure if the same row of the database is used in more than one authentication sessions. This is because an adversary who follows the communication between the legitimate user and the verifier, can extract ${\mathit{k}}_j^{\left(\mathrm{A}\right)}$ as follows ${\mathit{k}}_j^{\left(\mathrm{A}\right)}={\mathit{w}}_j\oplus {\mathit{z}}^{\left(\mathrm{A}\right)}$, which allows her to impersonate successfully the legitimate user later, if the same key is used again (replay attack). This is because ${\mathit{w}}_j$ and ${\mathit{z}}^{\left(\mathrm{A}\right)}$ are sent in plain text, whereas for the legitimate honest user ${\mathit{z}}^{\left(\mathrm{A}\right)}={\mathit{z}}^{\left(\mathrm{B}\right)}$. In order to prevent such an attack, and to ensure the security of the protocol for future authentication sessions, it is important for the entire jth row to be deleted permanently from the database at the end of the running session, irrespective of the outcome. The number of entries in the database is essentially limited by the number of different keys that can be extracted from a given token, and it is smaller after each session. Moreover, the precise number of entries depends strongly on the type of the optical token, as well as on the parameters of the input light that are exploited by the protocol. Related studies suggest that an optical PUF may support hundreds to thousands different challenge-response pairs [7,8,18,19]. When the entries in the database are exhausted, a new token must be assigned to the legitimate user. Finally, the protocol does not provide protection against privileged insiders or superusers, who have access to all the system’s files and resources, including the database of challenge-response pairs and the token ${\mathcal{T}}_{\mathrm{B}}$.

5. Conclusions

We have discussed remote authentication of entities with physical unclonable functions. The protocol we have presented offers security against both classical and quantum adversaries, it can be performed with today’s technology, and it is compatible with the infrastructure of standard QKD protocols. Only classical information is exchanged between the verifier and the verification setup, and thus there are no limitations on the distances over which entity authentication can be performed. However, the number of different authentication sessions that can be performed with the same random token is limited by the amount of randomness that can be extracted from the token, because the number of available challenge-response pairs grows smaller after each session, irrespective of the outcome. The removal of the used entries from the database is not important for the running authentication session, but it ensures the security of future sessions.

Throughout this work, we have assumed that the verifier is honest. To the best of our knowledge, all the optical PUF-based EAPs that have been discussed in the literature so far rely on the same assumption. One may relax this assumption, using quantum PUFs, which however are not compatible with today’s technology [30,31]. The development of practical schemes for remote entity authentication, which offer security even against privileged insiders or superusers, remains an open question.

Another cryptographic task, which has not been discussed adequately in the literature of PUFs is message authentication [1]. It has been shown recently for a large family of quantum message-authentication codes [32] that quantum resources do not offer any advantage relative to conventional unconditionally secure message-authentication codes. An interesting question therefore is whether optical PUFs can offer some advantage, therefore opening up the way to novel PUF-based message-authentication codes.