1. Introduction
Light-matter interaction permits modulating the properties of the materials by confining the light field to form exciton-polaritons coupled states. The extent of the light-matter coupling can be weak or strong; the strong one produces the hybrid polaritons [
1,
2,
3,
4]. The light by the hybrid polaritons is characterized by having a split dispersion with an upper and lower polariton branch, developed above and below the excitonic energy [
5]. The energy spectrum of the hybrid system results in new modes whose frequencies become different from those of the original oscillators, while the difference between the modes measures the strength of the coupling [
6,
7]. The outstanding aspect of strong coupling is the extensive control that is possible on the plasmon modes, which are generated in the plasmonic structures, and the impact on the matter behavior, which, then, becomes easily tunable. The manipulation of the polaritons or
dressed states permits the generation of non-classical photon states, opening the door toward exciting and unexpected applications [
8,
9]. The control of the plasmon modes occurs from a combination of impressive nano-fabrication techniques and a very good understanding of the relationship between the details of the nanostructure and the nature of the associated plasmon modes [
10,
11].
The strong coupling of light and molecules working as emitters has been studied, using planar microcavities, plasmonic nanostructures, and dielectric resonators, such as Mie resonators. The use of these structures has provided valuable insights into strong light-matter coupling but they are generally impractical for applications such as polaritonic chemistry [
12]. In 1974, it was reported that the surface plasmon polaritons work like the cavity polaritons in creating exciton−plasmon strong coupling [
13,
14]. This result had a significant impact on expediting the study of strong coupling because of the numerous planar platforms that became available with a moderate cost and labor time to the experimentalists.
The dye molecules and quantum dots have been demonstrated to be the most interesting systems for studying strong coupling. They have well-defined exciton transitions, which survive at room temperature in contrast to the conventional inorganic semiconductors that require to be cooled down at room temperature for observing the coupling. In this context, it is worth mentioning the 2D materials; they interact with the matter when the electrons are excited [
15,
16,
17]. These recent results consolidated the theory of strong coupling observable in cavity-free and very simple systems, like the coupling of the molecular resonances and confined electromagnetic fields in thin soft dielectric film, without any temperature pumping and under the condition of visible light [
18,
19]. The principle behind this coupling relies upon leaky modes due to the impedance mismatch between the dielectric thin film and a silicon substrate. To date, a smooth layer of plasmonic metals can be useful for molecular studies, even with bad coupling behavior (low
Q-factor).
The understanding of the physics allowing the strong coupling between exciton-plasmon polariton, observed at room temperature, is the aim of this study [
20]. A layer of Au generates the surface plasmon polariton (SPPs) while a dye of the family of the azo-molecules becomes the source of the excitons.
To study the chromophore−Au strong coupling, a simple Kretschmann–Raether configuration was employed, which has been previously pioneered in experiments with exciton−plasmon coupling [
21,
22]. However, this is one of the first works that apply the ATR configuration to study the strong plasmon coupling in 2D, at room temperature. This configuration allows the excitation of the surface plasmons in a planar thin film with a simple method, able to incorporate a tunable plasmon resonance and observe strong coupling.
The variation of the incident angle of light through the prism and detuning of the coupling allows one to attain the dispersion plots.
After an analysis based on the emission of the SPP/molecule system for discussing the coupling in terms of Rabi splitting, the impact of the strong enhancement of the emitted signal is discussed and explained as a consequence of the collective action of the molecules [
20,
23,
24,
25,
26]. Strong coupling phenomena have been extensively discussed for single atoms, but the experimental results have also evidenced that collective mechanisms are of utmost relevance. Quantum plasmonics, which relies upon the sub-wavelength plasmon volume for achieving the strong coupling regime, has been demonstrated to obtain a significant enhancement of the effect because of the collective action of the molecules. However, it is far more difficult to create strong coupling with a multi-molecular system than at the single-molecule level because the molecules have the behavior to form aggregates, which in theory must be avoided.
Then, based on the numerical and experimental findings, a hybrid model is proposed here for describing the collective molecular action and its role in the enhancement of the coupling.
A discussion about the impact of the measured enhancement on Raman scattering of the molecules is done to derive a model that explains the relationship between the observed spectral splitting and the Rabi splitting, and the mechanisms contributing to them.
In conclusion, the achieved results are important for the understanding of the properties of dyes and have potential implications in the design of polaritonic devices for quantum sensing by the generation of non-classical photon states, while learning the manipulation of the polaritons permits the control of chemical reactions and other unexpected applications.
2. Experimental Section
The Au deposition was realized in an ultra-high vacuum chamber (base 10
−9 Torr) using an electron gun. A 99.99% pure Au deposited was used. The thickness of the film of Au was controlled by a quartz micro-balance. The annihilation took 45 min at the deposition temperature, and the samples were cooled down to room temperature at a rate of 10 °C min
−1. The optimal thickness of the Au layer set for these measurements was set at 40 nm, according to the knowledge gained in previous investigations [
27].
For the measurement with the dye, the Au layer was coupled with an optical prism (UV Fused Silica 25 mm right-angle prism, n = 1.466 at λ = 650 nm, Thorlabs Inc.), by an index matching oil (refractive index n = 1.515, Shanghai Specimen and Model Factory, China) and once the alignment of the optical components was done, a selected volume of Congo red solution (0.1 mM aqueous solution, 2 μL) was dropped on the top of the layer.
The mechanical configuration and optical pathway are schematized in
Figure 1a. The system has been developed on the Kretschmann configuration concept, where the axes of all the optical elements are aligned in the vertical plane so that these lenses have power only in the horizontal plane, where the SPR absorption takes place. All measurements were recorded in a transversal magnetic TM configuration, in air, and at room temperature.
The SPR setup is housed on the back part of the prism. This consists of two moveable arms, one of which drives the beam of the laser (Shenzen Futhe Tech. Co. Ltd. with peak emission at λ = 650 nm and FWMH = 10 nm), after the noise is removed by an iris and the direction of the beam is p-polarized. A second arm collects into a multimode optical fiber the reflected signal before being sent to a high-resolution spectrometer (Ocean Optics HR4000, Custom), after being collimated by C1 (RC12FC-P01 Thorlabs Inc.) and polarized P1, a double Glan-Taylor Calcite Polarizer (Thorlabs Inc.). The emitted light is collected by a silicon photodiode (FDS 10 × 10 Thorlabs, λ = 340–1100 nm, peak λ0 = 960 nm), and the noise is reduced by a ceramic disk capacitor. A cable drives the signal to the photo-oscilloscope (Picotech, series 5000).
Two different experiments were performed. First, for detecting the minimum in the reflectivity curve, the p-polarized reflectivity at a fixed wavelength with angular scans was measured. Simultaneously, the emission curve as a function of the angle of incidence was recorded. The second set of experiments was carried out at the angle of resonance and the emitted spectrum in the range of frequency was recorded.
The transfer matrix method was used to model the dispersion of the coupled-mode system. The method relies upon the use of 4 × 4 matrices, one for each constituent layer in the single or multilayer slab, to relate the complex amplitudes of the electric field phasor of the reflected and transmitted plane waves to the complex-valued amplitude of the electric field phasor of the incident plane wave. The method assumes that the stuck layers are normal to the
z-axis and that the field within one layer can be represented by the overlapped left- and right-traveling wave with wave number
k,
Besides, because of the Maxwell equation, the continuity across the boundary must be respected and the following equation is valid:
Equations (1) and (2) correlate between the electric and magnetic field, E and H with and , the unimodular matrix represents the propagation over a distance L into the positive z-direction; . The M matrix represents the propagation through a layer if k is the wave number in the medium and L is the thickness of the layer.
The model consisted of the following layers, with the p-polarized light incident from the prism side: NBK7 substrate/40 nm Au/(2 nm, 6 nm) Congo red. Then, the system under consideration is a bilayer, then the matrix of the system is given by .
The refractive index for each layer was taken from the dedicated source: The fused silica refractive index was taken from the HJPDOC library, the Au from Palik [
28], the NBK7 glass from Schott, and Congo red from [
29]. Implementation of the transfer matrix method was done in MATLAB (Matlab 2021, MathWorks).
3. Results
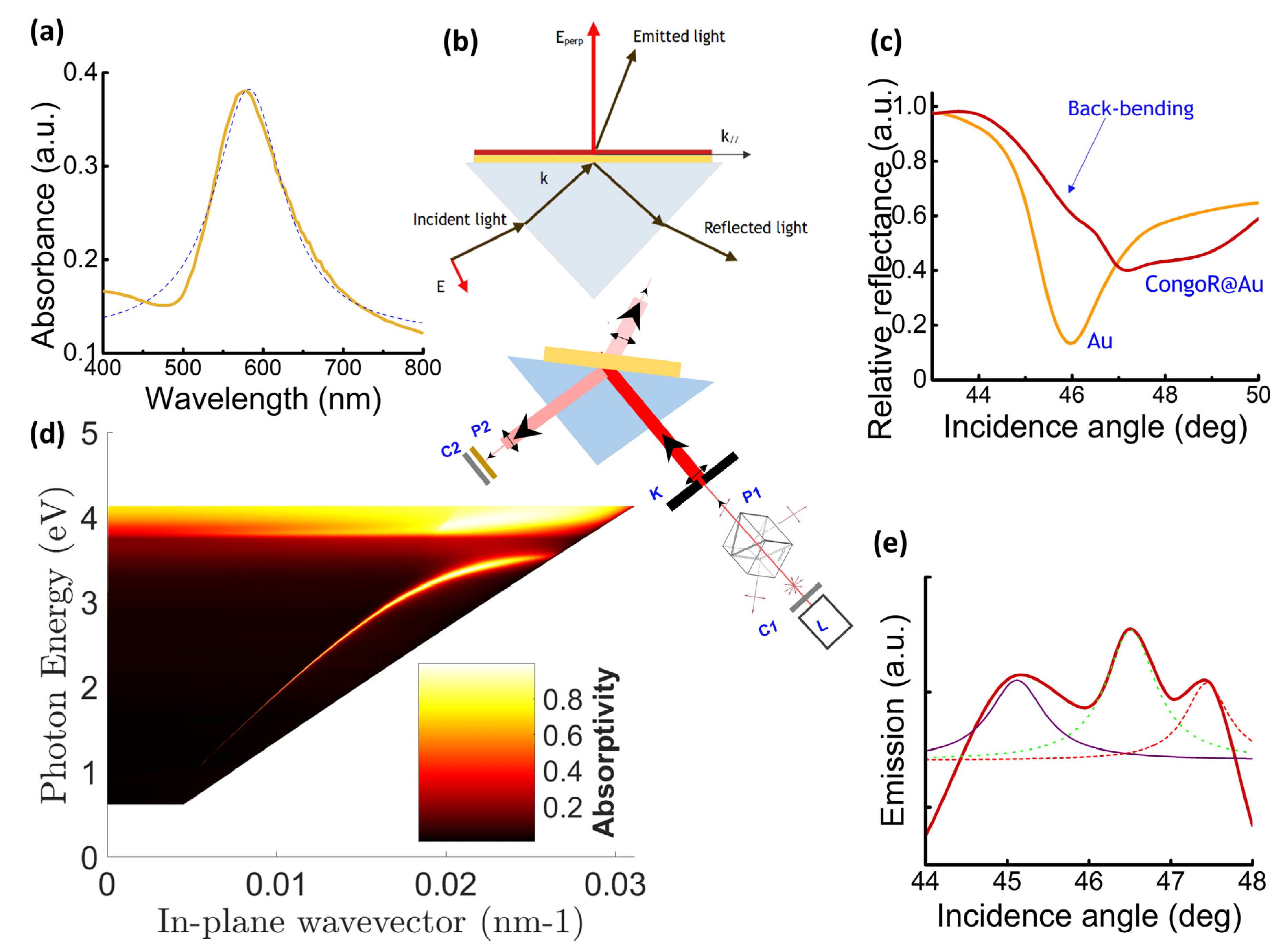
The Au was sputtered to a thickness of 40 nm on BK-7 glass slides. The thin layer has a resonant frequency of
and a decay rate of
, as derived from the full width at half maximum, FWHM, of the Lorentzian fit of the absorbance spectrum in
Figure 1a. The quality factor
Q, derived from
, is
, which classifies the layer as a bad substrate for the coupling. Indeed, to observe a strong coupling, there must be a combination of a large coupling rate,
g, and small line widths of the SPPs (large
Q-factor); then, it is expected that other conditions occur to promote the coupling.
To study the coupling, the reflected and emitted signals were measured according to the working principle displayed in
Figure 1b. In practice, when the angle of incidence of the beam, which impacts on the surface of the prism, is greater than the critical angle, total internal reflection occurs; from this point on, the surface plasmon resonance is measured. In contact with the surface of the prism, the Au layer permits that the
in-plane wavevector of the evanescent field extends beyond the base of the prism itself and couples to the surface plasmon polariton SPP mode. The
in-plane wavevector is estimated as
, where
is the incident photon wavelength,
is the index of refraction of the Au, and
is the incident angle of light inside the prism. An angle-resolved far-field measurement of the reflectance under transverse magnetic TM polarization is shown in
Figure 1c. The evolution of the wavevector-resolved spectrum (at
= 650 nm and in the air, at room temperature), with the incidence angle, scanned approaching and departing from the resonance, showed that the dip of the reflectance occurred at an angle of incidence
ϑres = 46.076 deg with a line width FWHM = (1.16 ± 0.48) deg; on the other hand, the numerical dispersion of the plain Au in the system prism/glass slide/Au/air provides the SPP excitation at an angle
ϑin =
ϑres = 46 deg (
Figure 1d), coherently with the experimental results.
With the adsorption of the chromophore, the surface plasmon resonance dip shifts to an angle
ϑinc =
ϑres = 47 deg, while the line width widens to (5.88 ± 1.18 deg) with the consequent broadening of the SPP. The reflection measurements have a slight back-bending of the minimum of the reflectance; this anomalous shape of the curve underlines that the system is either in the strong coupling regime or approaching it [
30].
An emission spectrum of the dye adsorbed to the Au and resolved to the angle of incidence (see
Figure 1e) strengthened the hypothesis of coupling between the two different modes; it displays a complex shape, which corresponds to the over-position of different modes, as highlighted by the deconvolution of the curve.
Aimed at the analysis of the mode coupling, the behavior of the system was modeled with a transfer matrix method and the energy of the system Congo red/Au according to the in-plane wavevector was studied. The investigation covered a range of two different concentrations and thicknesses of the Congo red while maintaining a constant Au layer thickness and excitation energy. However, the thickness of the chromophore did not yield a significant influence on the behavior of the system, while a significant effect of the concentration of the chromophore was observed.
The photonic dispersion (energy versus in-plane wavevector,
E versus
) is inferred from R(
ω,
θ) using the relationship
and
. Indeed, the dispersions were constructed by plotting the absorptivity, A, as a function of incident photon energy,
E, and in-plane wavevector,
, which is appropriate for studying strong coupling when the reflectance is collected as a function of angle. For the sake of clarity, the absorptivity was calculated as A = 1 − R − T, where R is the reflectance and T is the transmission [
31].
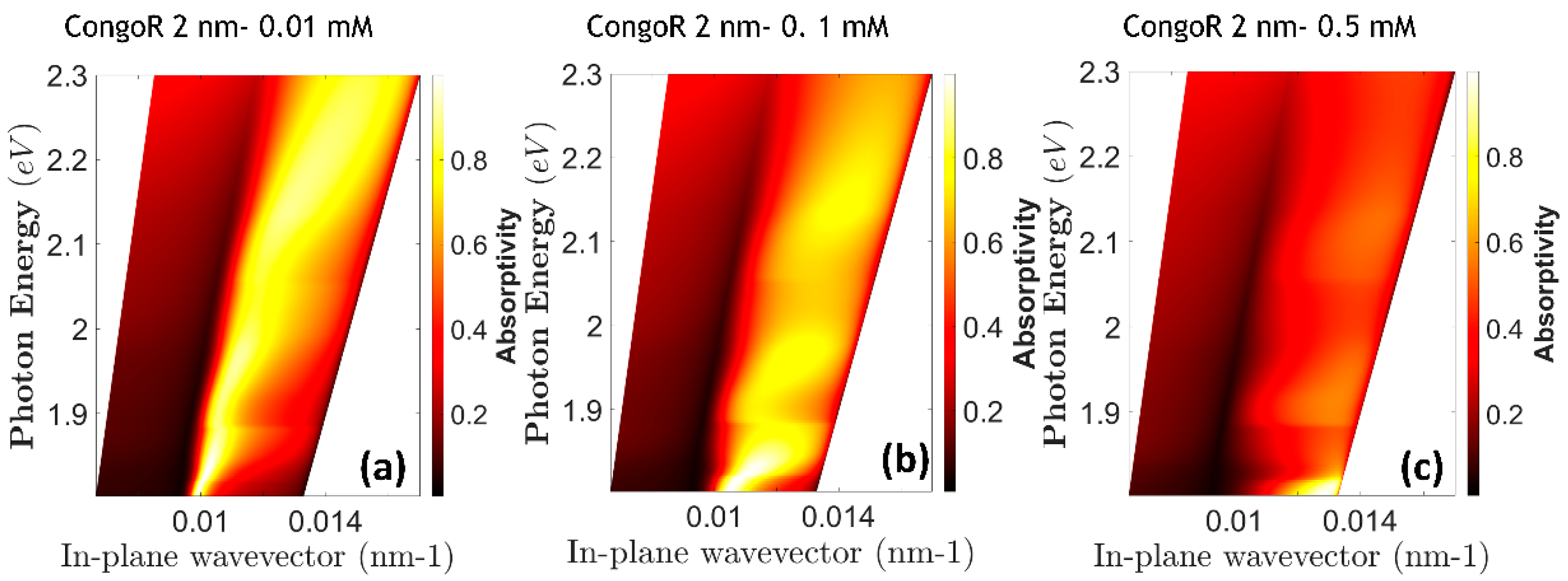
The dispersion of the samples measured at room temperature is shown in
Figure 2. Among the conditions taken under consideration, one can derive that upon raising the concentration, the strength of the coupling growths, and the system shows a typical level of anti-crossing, forming the upper and lower polariton branch (see
Figure 2a). In correspondence of a concentration set at 0.01 mM, the dispersive branches of the transverse magnetic mode folded in the first Brillouin zone are observable. At the 2nd-order Bragg scattering, they lie at approximately 2 eV (upper branch) and 1.7 eV (lower branch).
Figure 2b, which shows the result of a concentration set at 0.1 mM, reveals that the upper dispersive branch of the transverse magnetic mode is split into two branches related to the new eigenstates of the system, the lower polariton LP and the upper polariton UP modes and with each of them standing for the hybrid exciton−plasmon mode, coherently with the experimental measurement of the emission (see
Figure 1e). The anti-crossing with a minimum splitting of 0.1 eV has been measured. The minimum Rabi splitting that is gauged in the (
E,
) space is 0.4 at a normalized
At a higher concentration (see
Figure 2c), a less pronounced splitting is measured for an effect of saturation of the surface.
For making visible the anti-crossing in the dispersion, which is typical of the strong coupling, the line widths of the absorption/emission resonance and the optical/plasmonic mode should be smaller than the strength of the coupling. In other words, strong coupling is only possible for molecules with a narrow absorption spectrum. This definition excludes all dyes from forming strong coupling with the Au substrate. The Congo red has an absorbance spectrum with a typical molecule energy
while the decay corresponds to a rate of
[
18], which means that the line width of the spectrum is significantly broad and against the principle of strong coupling.
The low Q-factor of the Au layer and broad line width of the dye represents the premise for poor or weak coupling, but the numerical findings together with the result presented in
Figure 1 support the hypothesis of non-weak coupling and hence highlight that a different thickness of the Au and the Congo red slightly influences the strength of the coupling, but a variation of the chromophore concentrations offers a mean to tune the coupling.
At this point of the investigation, a possible explanation of these results is that the microscopic details like the vibrational level structure of the molecules play a crucial role, and despite the poor conditions of coupling, the matching between the phonons and the excitons reaches an outstanding strength.
For the microscopic molecular behavior insight and because they can represent the fingerprint of the coupling, the emission fast Fourier transform, FFT, spectra were studied [
15,
32,
33]. Then, the following section features an analysis of the emission spectra.
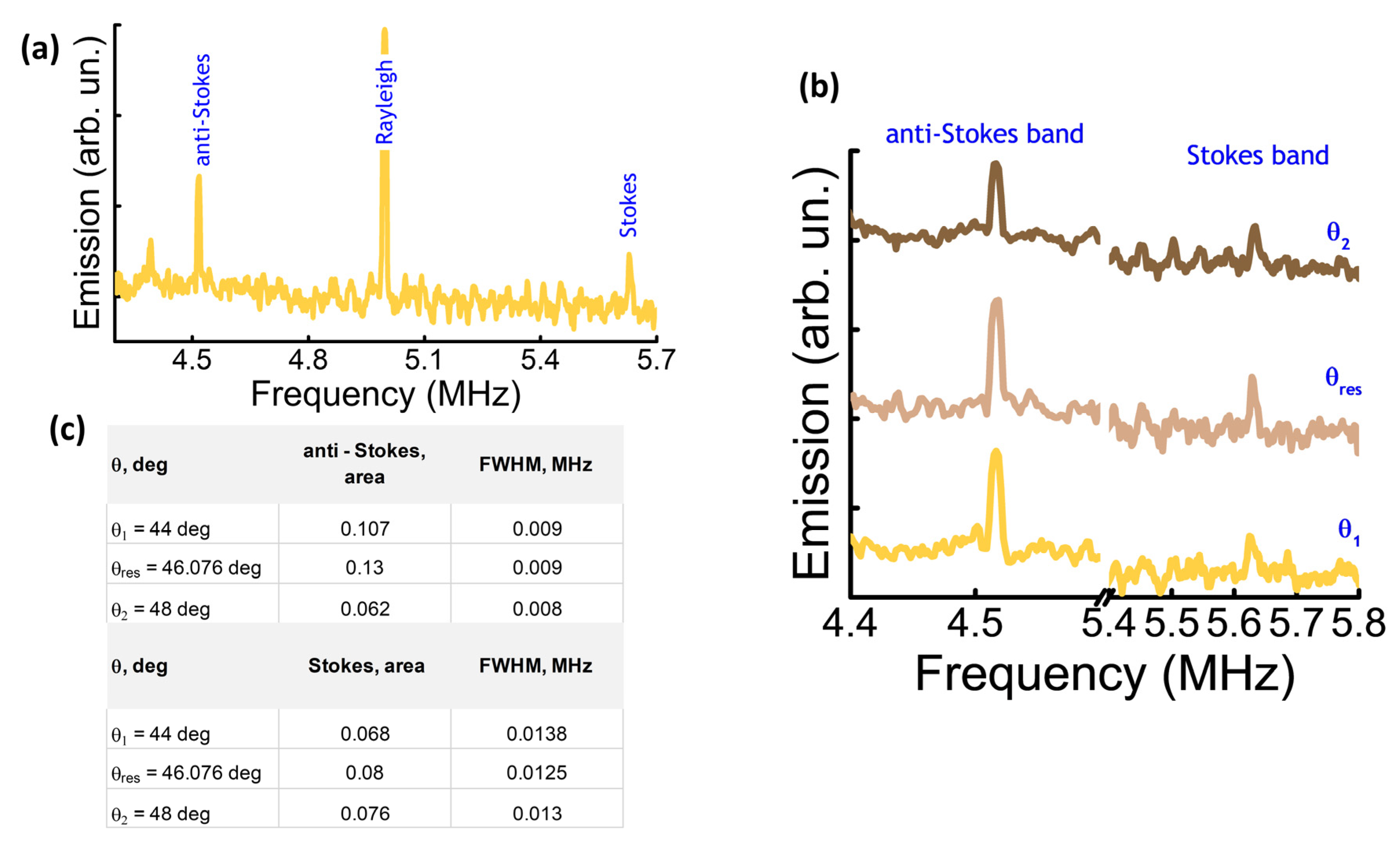
Figure 3a shows the band spectroscopy of the Au layer. The physical spectrum of emission is formed by three fundamental peaks: the elastic Rayleigh scattering and the inelastic Stokes and anti-Stokes bands. A comparison between the spectra measured under the condition of resonance and out of this condition displays that the typical elastic scattered Rayleigh peak at frequency
5 MHz, as well as the inelastic Stokes at
5.67 MHz and anti-Stokes at
4.39 MHz, are visible in three spectra (
Figure 3b); albeit, under-resonance, the intensity of Stokes and anti-Stokes peaks is higher, as summarized in
Figure 3c.
The spectra of the adsorbed dye were compared with the one of the plain Au (see
Figure 4a). Under-resonance, the anti-Stokes and Stokes peaks of the spectra of the red dye adsorbed on the Au displayed the highest intensity (results not shown), which agreed with the behavior of the plain Au.
The concept of coupling the light to a mechanical oscillator is old [
34] and it has been used for developing interferometers, and recently, it has been extended for describing Raman and SERS, upon considering the quantum-mechanical nature of the molecular vibration. For these systems, the shift is given by the relationship
[
34]. The vacuum optomechanical coupling rate is
g0 given by the product of the parameter of coupling
with the molecular polarizability
, (
), the zero-point motion and scales with the mode volume
[
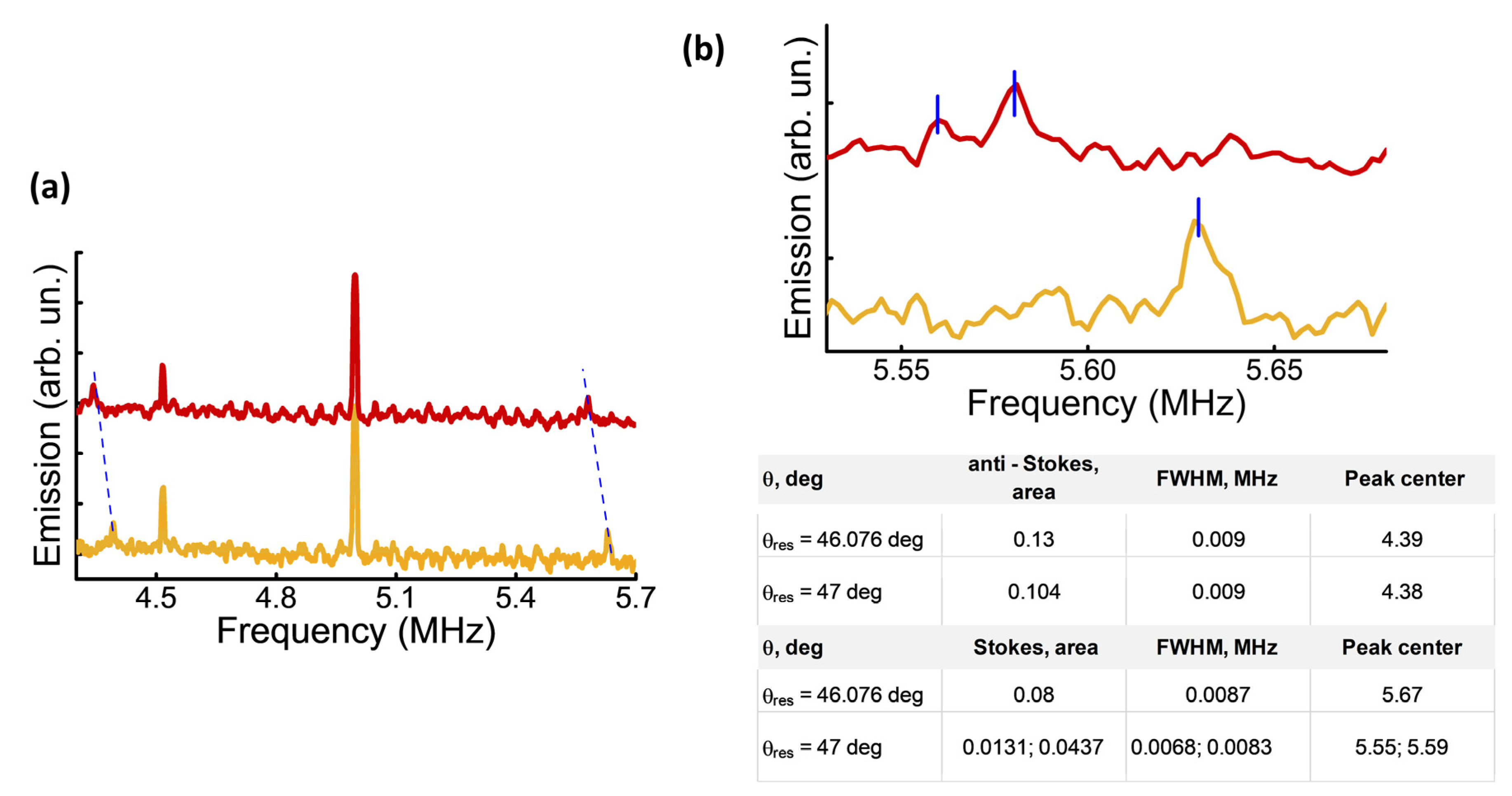
35]. The experimental results observed with the adsorption of the chromophore displays that the Stokes peaks frequency shifts (see
Figure 4b). Furthermore, a splitting of the peak with an upper and lower branch happens at
and
. The newly-formed polariton modes do split apart at a distance (distance
), which exceeds the polariton line width
(table embedded in the figure).
Since the strong-coupling regime is defined as the situation when the line width of coupled states is much smaller than the splitting, the results provide experimental evidence of the strong coupling between the dye and Au [
36].
Another key point related to the damping rate is given by the contribution of the split levels, which is lower than the one relative to the pure mechanical damping term of the rate (approximated by the line width of the frequency of the harmonic oscillator used for describing the molecule), then, it is expected that a negative contribution comes from the optomechanical damping rate, . The negative optomechanical contribution to the damping prospects the existence of a family of incoherent phonons, which destroy the equilibrium of the SPP/exciton system and bring the system to a decoherent level. The description of the decoherent level is outside the scope of this manuscript, nevertheless, the mechanism has been mentioned because it highlights that strong coupling requires a quantum mechanical approach and the quantization of both the SPPs and emitter.
The Hamiltonian
of the quantized system is
with the last term accounting for the coupling [
37], and the annihilation and creation operators
and
permitting the quantization of the molecular vibrational levels, while the annihilation and creation operators
and
describing the quantum behavior of the SPPs.
The eigenvalue problem for the Hamiltonian yields the eigenfrequencies that include the parameter
[
38], called the Rabi oscillating frequency, and the two polaritonic states are defined as the dressed light-matter states. The Rabi oscillations to which
is correlated represent the quantum-electrodynamic effect produced by atoms in cavities because of the vacuum of the radiation field. The vacuum-field Rabi oscillations lead to a splitting in the spontaneous-emission spectra of atoms in the cavity, like it has been shown in
Figure 1 and
Figure 2 [
39,
40].
The relationship between Rabi frequency splitting and the coupling rate enables the calculation of an analytical value of both
and
to determine the quantum mechanical coupling SPPs/exciton, whereas the excitons are related to the molecules. The coupling strength
is calculated by estimating the molecular dipole moment
and the vacuum field amplitude
. The expression of the vacuum field amplitude is
, while the dipole moment is given by
, assuming a parallel orientation of molecules to the electromagnetic field [
19].
The definition of the vacuum electric field includes the mode volume
; the estimation of the volume mode might need difficult calculations, but for systems supporting the plasmon resonances, because the field of the resonance is shaped by the geometry, the mode volume follows the geometrical one, like it was already prospected by Purcell in 1946 [
41]. Then, upon considering, surface area A equals 10
−5 μm
2 and a mode volume
≈ 1.5 × 10
−6 μm
3, in analogy with Zhu et al. [
42], two results can be derived, the amplitude of the vacuum field
and, interestingly, the number of molecules involved in the optomechanical interaction, namely N (with N = 100), for a molecular density
(
= 10
3 molecule/μm
2) [
20]. For calculating the dipole moment
, the absorption cross-section of the Congo red has been calculated from the absorbance using the Lambert–Beer law, finding that
, which permits the calculation of
, in combination with the experimental values relative to the molecular damping
.
According to the results above, the theoretical value of Rabi frequency is , which denotes a significant difference from the experimental value reported above (.
It remains to explain the reason for the discrepancy between the experimental and numerical results. The discrepancy existing between the experimental results and the quantum approach lies in the fact that the Rabi splitting theory is mainly valid for a single atom/molecule interacting with a common light field, but when the interaction takes place between a group of N = 100 molecules and the light field, then, the description of the physical problem becomes more complex [
43,
44]. Under these conditions, the optomechanical interaction couples N molecules through the plasmonic substrate, leading to a collective oscillator mode [
45].
There is an open debate regarding molecular strong coupling and whether the observed collective Rabi splitting generated by coupling simultaneously to N molecules occurs at the level of each molecule. A discussion about the collective action of the molecules must clarify the inconsistencies encountered above, and relative to a system having a low Q-factor and high , as well as the discrepancy between the experimental results and the quantum mechanical approach.
The light field tends to correlate the behavior between dipole moments, which, working in coordination with plasmon, broaden the spectral width , where each of the N molecule-emitter works and contributes to the enhancement of the signal. Then, compared to the single molecular Rabi splitting frequency, the spectral splitting can grow with the number of molecules rising. However, if this was the case, the effect of strong coupling on each molecule would be negligible and could not explain the significant changes in the system behavior.
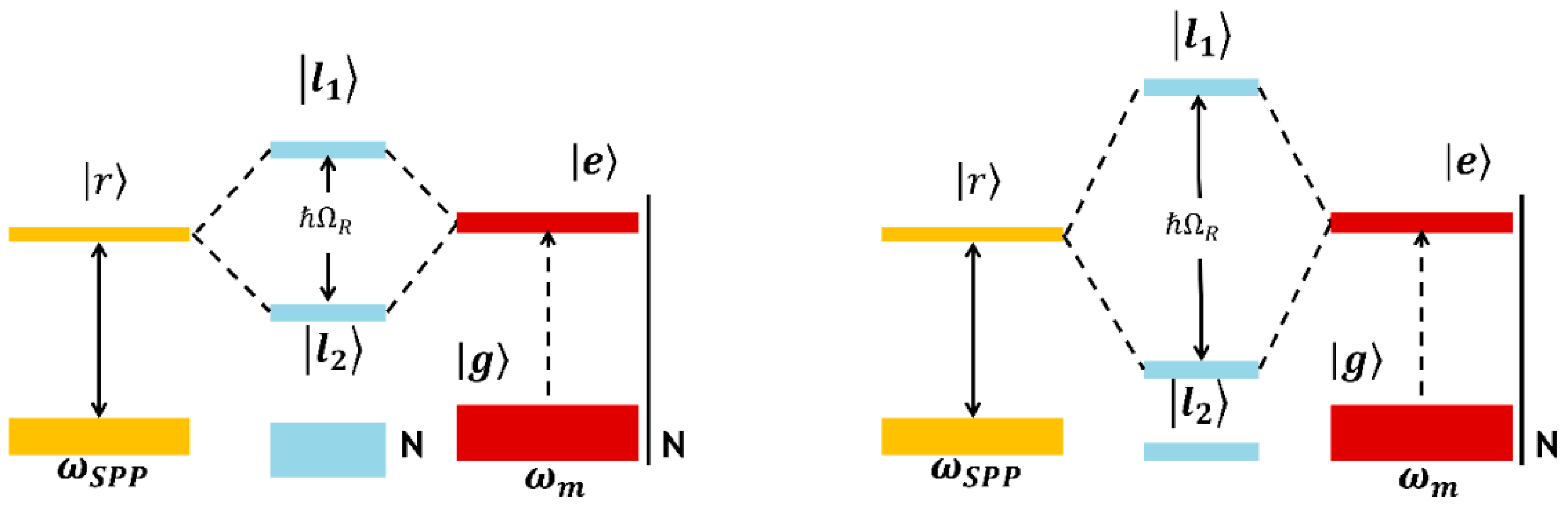
Then, for interpreting the results, an analogy with the collective polaritonic states can describe the delocalized molecular orbitals across all the contributing atoms. However, the translation of a pure quantum model from the single atom/molecule to several becomes complicated since the molecules could not form a single giant quantum emitter. More reasonably, a physical model includes two components. On the one hand, a quantum mechanical interaction between the single molecule and light is established; this generates a tiny Rabi oscillation. On the other side, the classical optical multiple scattering existing among different molecules and their collective strong coupling with plasmon induce a giant spectral splitting in the scattering spectrum. The Rabi hybrid model introduced for the multi-molecular system is illustrated in
Scheme 1; it displays the two models of the Rabi oscillations, the interaction single-molecule/SPP on the right, and the collective strong coupling molecule/SPP on the left. The regime of strong coupling is characterized by a coherent exchange of energy between the emitter and the metal at a rate faster than any decay process that is recorded by the oscillation of the emitter. The exchange of energy manifests itself in an energy splitting of the light matter-energy levels and includes a ground state that does not depend on the interaction.
Finally, evidence of the emission from the chromophore consists of the generation of a strong surface-enhanced Raman scattering, under vibrational strong coupling, as it probes the property at the level of each molecule from a spectral window outside that involved in strong coupling.
To explore the Raman properties in a regime of strong coupling, the azo-dye spectrum was measured at an excitation wavelength of 648 nm that is far from the typical stretching frequencies of the chromophore having a typical peak at 450 nm.
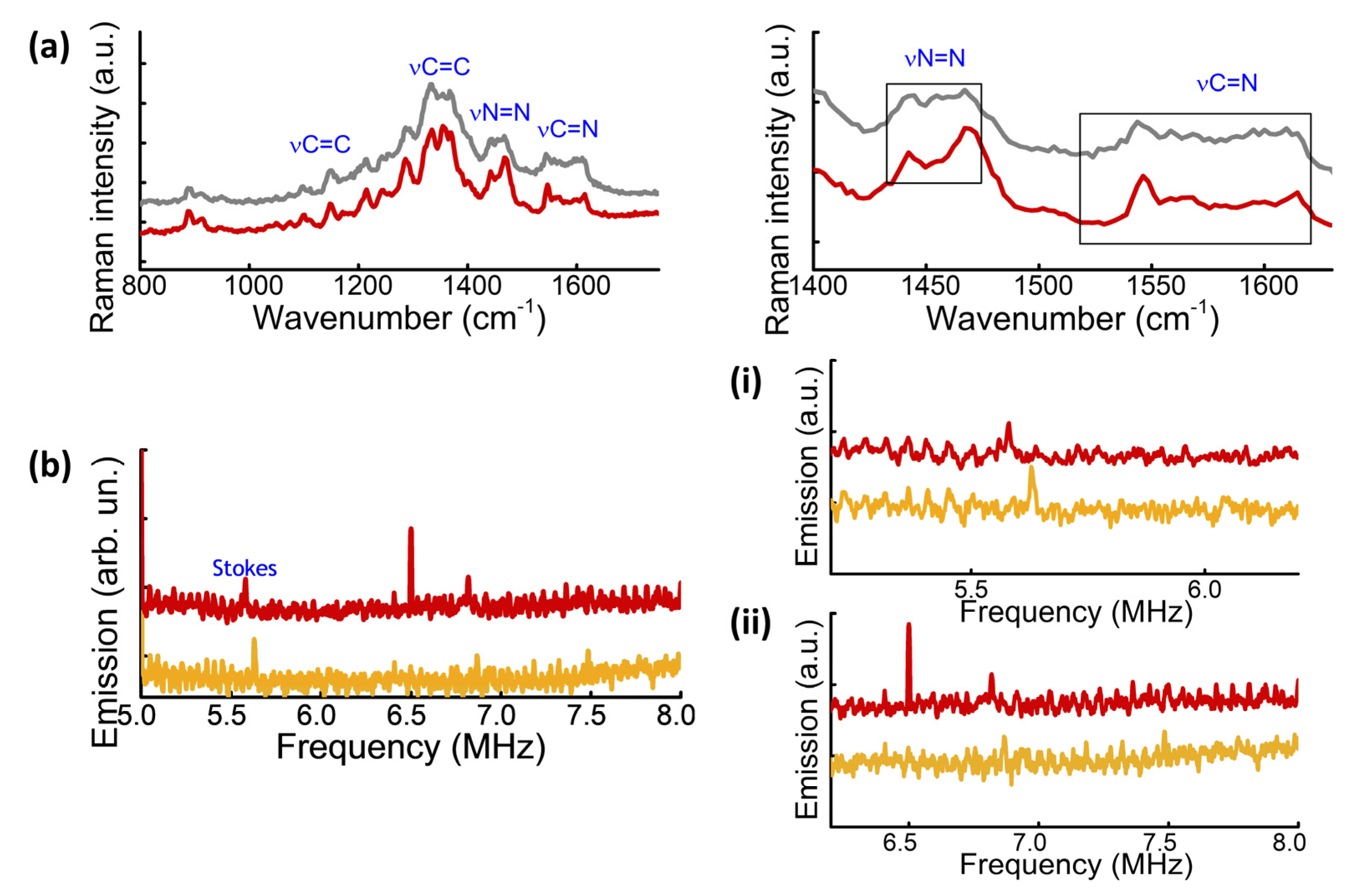
The Raman inspection shows the difference between the spectrum of the chromophore adsorbed on the Au layer (bottom spectrum in
Figure 5a) and the top of a
sans-Au glass slide (top spectrum in
Figure 5a). The typical vibrational bands are highlighted in the Raman pattern, and those together with the smaller peak at 1043 cm
−1, due to the symmetric stretching vibration of the sulfonate group, represent the fingerprint of the molecule. The two spectra differ in the intensity of the peaks associated with the vibration of the chemical groups, the adsorption on the Au seems to intensify the molecular vibration with consequent impact on the intensity. Besides, the peaks of the C=N and N=N split into two peaks (see
Figure 5a right).
Analogous consideration can be done when the FTT emission spectra are analyzed. The results in
Figure 5b refer to the vibrational FFT spectrum of the plain Au before and after the adsorption of the dye. For the sake of clarity, the range of frequency has been divided for identifying the low-frequency range and high-frequency range, respectively below and above the Rayleigh peak. The two plots are shown on the right side of
Figure 5b, (i) and (ii). The subplot (i) confirms the shift of the Stokes peak, but in the range of frequency just around this until
, insignificant differences between the spectra have been recorded. The subplot (ii) displays a more diversified scenario. At
and
, two new peaks are spiked. The new features can only originate from the formation of the two eigenvalues in the coupled system and depend on the vibration of the chromophore [
47].
For clarifying the collective mechanism, the intensity of the scattered Stokes photons has been accounted. The Stokes intensity is given by the following equation,
[
48] where
is the optical excitation distribution function related to the mode structure at the excitation wavelength,
represents that the matrix of the polarizability tensor for vibrational transition
i (with
) is the fixed coordinate system, and
account for the transmission through the system of the Stokes photon from the vibrating molecule to the detector. It is worth noting that while
and
depend on the optical structure and geometrical values of the Au layer, the tensor of the molecular polarizability only depends on the intrinsic property of the vibrating bond and then on the scattering state [
48,
49]. Those observations imply that the amplification factor is simply given by the ratio of the polarizability tensor elements in the coupled and uncoupled conditions
. Although this result needs to be addressed by a rigorous theoretical analysis of such a strongly coupled system, there is enough evidence to speculate on the origin of this surprising finding.
In a regime of strong light-matter coupling, the spatial coherence drives all the coupled resonators in phase with each other, and constructive interference is developed. However, the polarizability per molecule results is enhanced by the coherence of the polaritonic states, giving a relevant role to the matter contribution at the coupling.