Anisotropic Non-Kolmogorov Turbulence Spectrum with Anisotropic Tilt Angle

Abstract

With the in-depth study of atmospheric turbulence, scholars have identified that the anisotropy of turbulence cells should not be forgotten. The anisotropic non-Kolmogorov turbulence model can better characterize the actual situation of atmospheric turbulence. However, the results of recent experiments by Wang et al. and Beason et al. demonstrate that the turbulence cell has an anisotropic tilt angle, i.e., the long axis of turbulence cell may not be horizontal to the ground but has a certain angle with the ground. In this paper, we derive the anisotropic non-Kolmogorov turbulence spectra for the horizontal and satellite links with anisotropic tilt angle. Then by use of these spectra, the analytical expressions of scintillation index in the horizontal and satellite links are derived for the weak fluctuation condition. The calculation results display that the scintillation index for the horizontal and satellite links vary with the changes of anisotropic tilt angle and azimuth angle. Therefore, the anisotropic tilt angle is indispensable in the horizontal and satellite links.

1. Introduction

Despite the Kolmogorov turbulence model being currently the most generally used atmospheric turbulence model [1], as more and more atmospheric experimental results violate the Kolmogorov turbulence model, scholars have discovered that the anisotropic non-Kolmogorov turbulence model is more consistent with the actual situation of atmospheric turbulence [2,3,4,5,6,7,8]. The investigation on light wave transmission in anisotropic non-Kolmogorov atmospheric turbulence has become a research hotspot. Korotkova analyzed the polarization properties of deterministic or random light with isotropic source correlations propagating in anisotropic turbulence along horizontal paths [9]. Baykal et al. examined the scintillation index for higher order laser beams propagating through weak anisotropic non-Kolmogorov atmospheric turbulence along horizontal links [10]. We derived the fiber-coupling efficiency for a Gaussian-beam propagating horizontally through weak-to-strong anisotropic non-Kolmogorov turbulence in the presence of random angular jitter and bias error [11]. In addition, then considering the ellipsoid hypothesis of turbulence cell, we derived a new anisotropic non-Kolmogorov turbulence spectrum for the satellite links that is applicable to both vertical and slant links, and developed the fiber-coupling efficiency for a Gaussian-beam propagating through the weak-to-strong anisotropic non-Kolmogorov satellite-to-ground downlink [12]. So far almost all anisotropic non-Kolmogorov turbulence models established by scholars are based on the assumption that the long axis of turbulence cell should be horizontal to the ground. However, the results of recent experiments by Wang et al. and Beason et al. have obviously demonstrated that the turbulence cell has an anisotropic tilt angle, i.e., the long axis of turbulence cell may not be horizontal to the ground but has a certain angle with the ground [7,8]. Thus, it is vital to derive the anisotropic non-Kolmogorov turbulence spectra for the horizontal and satellite links with anisotropic tilt angle. In this paper, based on our previous research [12], the anisotropic non-Kolmogorov turbulence spectra for the horizontal and satellite links with anisotropic tilt angle are derived. By using these spectra, we develop the analytical expressions of scintillation index for the horizontal and satellite links in the weak fluctuation regime. In addition, then calculations are performed to investigate the effects of anisotropic tilt angle and azimuth angle on the scintillation index in the horizontal and satellite links. Our research will be advantageous for the construction of atmospheric turbulence model and the perception of light wave propagation along the anisotropic non-Kolmogorov links.

2. Formulation

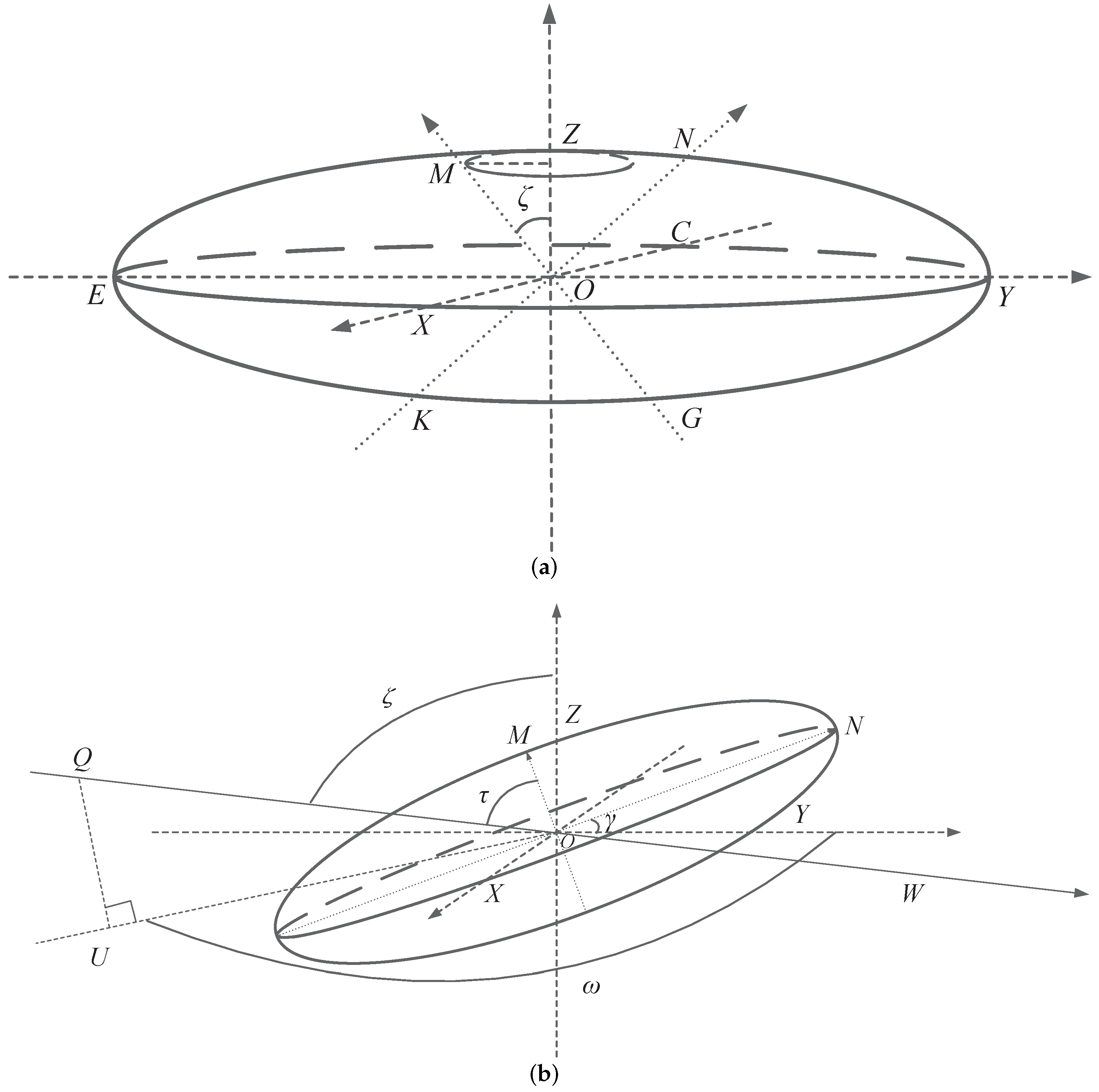
As exhibited in Figure 1, the anisotropy diagrams of turbulence cell without anisotropic tilt angle $\gamma$ and with anisotropic tilt angle $\gamma$ are displayed separately. In addition, they are applicable to both horizontal and satellite links. First, based on our previous research [12], we will briefly review the process of establishing the anisotropy model of turbulence cell without anisotropic tilt angle $\gamma$. To simplify the modeling, we only consider the existence of an anisotropic factor $\mu$ for the turbulence cell, i.e., assuming $OX=OY=\mu s$, $OZ=s$. As presented in Figure 1a, $\mu$ denotes the anisotropic factor that is the ratio of long axis to short axis for the turbulence cell, $OZ$ denotes the plumb line, $\zeta$ denotes the zenith angle, and the plane $XOY$ denotes the horizontal plane. By basic geometry, it can be simply found that when the propagation direction of laser beam is $MG$, we can definitely find a straight-line $NK$ in the plane $MOZ$, which passes through the point O, is perpendicular to $MG$, and intersects the ellipse $MOZ$ at points N and K. Based on the symmetry of ellipse, $ON=OK$, $OM=OG$. Because $OZ$ is perpendicular to $OX$, and $OZ$ is perpendicular to $OY$, the plane $MOZ$ is perpendicular to the plane $XOY$. Then we can definitely find a straight-line in the plane $XOY$ that is perpendicular to the plane $MOZ$ and passes through the point O. Through simple observation in Figure 1a, we can find that the straight-line is $XC$, and the symmetry of ellipse displays that $OX=OC$. In conclusion, when the propagation direction of laser beam $MG$ is provided, we can absolutely discover the corresponding straight lines $NK$ and $XC$ in the ellipsoid, which construct a rectangular coordinate system and meet $OM=OG$, $ON=OK$ and $OX=OC$. Thus, we can use the ratio between $OX$, $ON$ and $OM$ to evaluate the anisotropic factors of turbulence cell in the horizontal and satellite links, i.e., ${\mu }_x=OX/OM$, ${\mu }_y=ON/OM$. By use of the basic trigonometric function and the standard equation of ellipse, we can have that $OM=\mu s\sqrt{\left(1+{tan}^2\zeta \right)/\left({\mu }^2+{tan}^2\zeta \right)}$, $ON=\mu s\sqrt{\left(1+{tan}^2\zeta \right)/\left(1+{\mu }^2{tan}^2\zeta \right)}$. Then the anisotropy model of turbulence cell without anisotropic tilt angle $\gamma$ for the horizontal and satellite links is built, and the anisotropic factors ${\mu }_x$ and ${\mu }_y$ have the following expressions

$${\mu }_x=OX/OM=\sqrt{\frac{{\mu }^2+{tan}^2\zeta }{1+{tan}^2\zeta }},{\mu }_y=ON/OM=\sqrt{\frac{{\mu }^2+{tan}^2\zeta }{1+{\mu }^2{tan}^2\zeta }}.$$

(1)

Second, as presented in Figure 1b, let us introduce the definitions of anisotropic tilt angle $\gamma$ and azimuth angle $\omega$, which can help us better establish the anisotropy model of turbulence cell with anisotropic tilt angle $\gamma$. Because we only consider the existence of an anisotropic factor $\mu$ for the turbulence cell, an ellipsoid model can be used to demonstrate the actual turbulence cell. Then the anisotropic tilt angle $\gamma$ is the angle between the plane $XON$ where the long axes of ellipsoid are located and the horizontal plane $XOY$, counterclockwise is positive, and the value range is 0 degrees to 180 degrees. To simplify the modeling, we set the x-axis as the intersection of the two planes. Correspondingly, it can be simply derived from Figure 1b that the short axis of ellipsoid lies in the plane $YOZ$. Take the situation in Figure 1b as an example, the unit vector for the short axis of ellipsoid is $\left(0,-sin\gamma ,cos\gamma \right)$. The azimuth angle $\omega$ is the angle between the plane $QOU$ and the plane $YOZ$, clockwise is positive, the value range is 0 degrees to 360 degrees, and the z-axis is the intersection of the two planes. Furthermore, the plane $QOU$ is determined by the transmission direction of laser beam $QO$ and its horizontal projection $UO$, and the plane $YOZ$ is defined by the short axis of ellipsoid and the plumb line. By use of the zenith angle $\zeta$ and the azimuth angle $\omega$, we can define any transmission direction of laser beam in the three-dimensional space.

Finally, as shown in Figure 1b, let us introduce the angle $\tau$, which is the angle between the transmission direction of laser beam $QO$ and the short axis of ellipsoid. In fact, considering the symmetry of ellipsoid, the anisotropy model of turbulence cell should essentially depend on the value of angle $\tau$, not the value of zenith angle $\zeta$. By basic geometry, it can be simply derived from Figure 1b that for different transmission directions of laser beam with the same value of angle $\tau$, the anisotropic factors ${\mu }_x$ and ${\mu }_y$ should be equal. As for why the zenith angle $\zeta$ is used in the case of Figure 1a, it is just because the angle $\tau$ and the zenith angle $\zeta$ happen to be equal when the anisotropic tilt angle $\gamma$ is not considered. By obtaining the value of angle $\tau$, we can use the previous modeling process to develop the anisotropy model of turbulence cell with anisotropic tilt angle $\gamma$ for the horizontal and satellite links. Take the situation in Figure 1b as an example, the unit vector for the transmission direction of laser beam $QO$ is $\left(sin({180}^{\circ }-\omega )sin\zeta ,-cos({180}^{\circ }-\omega )sin\zeta ,cos\zeta \right)$. Based on simple spatial vector knowledge, the angle between the transmission direction of laser beam $QO$ and the short axis of ellipsoid is $\tau =arccos\left(cos\zeta cos\gamma -sin\zeta sin\gamma cos\omega \right)$. Then the anisotropy model of turbulence cell with anisotropic tilt angle $\gamma$ for the horizontal and satellite links is developed, and the anisotropic factors ${\mu }_x$ and ${\mu }_y$ have the following expressions

$${\mu }_x=\sqrt{\frac{{\mu }^2+{tan}^2\tau }{1+{tan}^2\tau }},{\mu }_y=\sqrt{\frac{{\mu }^2+{tan}^2\tau }{1+{\mu }^2{tan}^2\tau }}.$$

(2)

In addition, through theoretical derivation, we can confirm that no matter the transmission direction of laser beam is any direction in the three-dimensional space, the calculation formula for the angle $\tau$ always holds.

Inserting the anisotropy model of turbulence cell with anisotropic tilt angle $\gamma$ for the horizontal and satellite links Equation (2) into the existing anisotropic non-Kolmogorov turbulence spectrum model [5], the power spectrum model for the anisotropic non-Kolmogorov horizontal link with anisotropic tilt angle $\gamma$ can be expressed as

$${\mathsf{\Phi }}_n\left({\kappa }_x,{\kappa }_y\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2{\mu }_x{\mu }_y}{{\left({\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2\right)}^{\alpha /2}},3<\alpha <4,$$

(3)

and given that the anisotropic non-Kolmogorov structure constant for the satellite links is dependent on the value of altitude, the power spectrum model for the anisotropic non-Kolmogorov satellite links with anisotropic tilt angle $\gamma$ has the following expression

$${\mathsf{\Phi }}_n\left({\kappa }_x,{\kappa }_y,h\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2\left(h\right){\mu }_x{\mu }_y}{{\left({\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2\right)}^{\alpha /2}},3<\alpha <4,$$

(4)

where $\alpha$ represents the spectral power law, ${\mu }_x$ and ${\mu }_y$ represent the anisotropic factors applied to define the asymmetry of turbulence cells, ${\tilde{C}}_n^2$ represents the structure constant for the anisotropic non-Kolmogorov link in units of m${}^{3-\alpha }$, $\kappa$ represents the spatial wavenumber vector, ${\kappa }_x$ and ${\kappa }_y$ represent the x and y components of $\kappa$, $\kappa =\sqrt{{\mu }_x^2{\kappa }_x^2+{\mu }_y^2{\kappa }_y^2}$, $A\left(\alpha \right)=\mathsf{\Gamma }\left(\alpha -1\right)cos\left(\alpha \pi /2\right)/4{\pi }^2$, and $\mathsf{\Gamma }\left(x\right)$ represents the Gamma function. As displayed in [13,14], the ${\tilde{C}}_n^2$ of satellite links is altitude dependent and expressed as

$$\begin{array}{c}{\tilde{C}}_n^2\left(h\right)=\frac{0.033}{A\left(\alpha \right)}{\left(kcos\zeta /h\right)}^{\left(\alpha /2-11/6\right)}\left[0.00594{(\frac{w}{27})}^2{\left({10}^{-5}h\right)}^{10}exp\left(-\frac{h}{1000}\right)\right.\hfill \\ \left.+2.7\times {10}^{-16}exp\left(-\frac{h}{1500}\right)+C_n^2\left(0\right)exp\left(-\frac{h}{100}\right)\right],\hfill \end{array}$$

(5)

where $\zeta$ represents the zenith angle, h denotes the altitude in units of m, $C_n^2\left(0\right)$ represents the nominal value of $C_n^2$ when $h=0$ in units of m${}^{-2/3}$, w represents the rms wind speed in units of m/s, $k=2\pi /\lambda$, and $\lambda$ represents the wavelength. Because the zenith angle $\zeta$ for the horizontal link is 90 degrees, the calculation formula of angle $\tau$ for the horizontal link reduces to $\tau =arccos\left(-sin\gamma cos\omega \right)$. It should be noted that Equation (5) is based on non-Kolmogorov turbulence; however we suppose that it is also valid in the presence of anisotropic non-Kolmogorov turbulence, at least approximately.

For the weak Kolmogorov horizontal link, the scintillation index of a plane wave is given by [1]

$${\sigma }_{I,horizontal}^2=8{\pi }^2{k}^{2}L{\int }_0^1{\int }_0^{\infty }\kappa {\mathsf{\Phi }}_n\left(\kappa \right)\left[1-cos\left(\frac{L{\kappa }^2\xi }{k}\right)\right]d\kappa d\xi ,$$

(6)

where L denotes the link distance, $\xi$ denotes the normalized link coordinate which has a mathematical relationship with z, i.e., $\xi =1-z/L$. Inserting Equation (3) into Equation (6) results in

$$\begin{array}{c}{\sigma }_{I,horizontal}^2=4\pi k^{2}L{\int }_0^1{\int }_0^{\infty }{\int }_0^{\infty }{\mathsf{\Phi }}_n\left({\kappa }_x,{\kappa }_y\right)\left[1-cos\left(\frac{L{\kappa }^2\xi }{k}\right)\right]d{\kappa }_{x}d{\kappa }_{y}d\xi .\hfill \end{array}$$

(7)

The stretched coordinate system for ${\mathsf{\Phi }}_n\left({\kappa }_x,{\kappa }_y\right)$ can be transformed into an isotropic coordinate system by use of the following substitutions,

$${\kappa }_x=\frac{q_x}{{\mu }_x}=\frac{qcos\theta }{{\mu }_x},{\kappa }_y=\frac{q_y}{{\mu }_y}=\frac{qsin\theta }{{\mu }_y},q=\sqrt{q_x^2+q_y^2},$$

(8)

$$\kappa =q\sqrt{\frac{{cos}^2\theta }{{\mu }_x^2}+\frac{{sin}^2\theta }{{\mu }_y^2}},d{\kappa }_{x}d{\kappa }_y=\frac{d{q}_{x}d{q}_y}{{\mu }_x{\mu }_y}=\frac{qdqd\theta }{{\mu }_x{\mu }_y},$$

(9)

$${\mathsf{\Phi }}_n\left(q\right)=\frac{A\left(\alpha \right){\tilde{C}}_n^2{\mu }_x{\mu }_y}{q^{\alpha }}.$$

(10)

Inserting Equations (8)–(10) into Equation (7), we can obtain

$$\begin{array}{c}{\sigma }_{I,horizontal}^2=4\pi k^{2}L{\int }_0^1{\int }_0^{2\pi }{\int }_0^{\infty }A\left(\alpha \right){\tilde{C}}_n^2{q}^{1-\alpha }\hfill \\ \times \left\{1-cos\left[\frac{L{q}^2\xi }{k}\left(\frac{{cos}^2\theta }{{\mu }_x^2}+\frac{{sin}^2\theta }{{\mu }_y^2}\right)\right]\right\}dqd\theta d\xi .\hfill \end{array}$$

(11)

Then appraising this integral, the scintillation index of a plane wave in the weak anisotropic non-Kolmogorov horizontal link with anisotropic tilt angle $\gamma$ can be obtained,

$$\begin{array}{c}{\sigma }_{I,horizontal}^2=-\frac{2}{\alpha }\mathsf{\Gamma }\left(1-\frac{\alpha }{2}\right)\mathsf{\Gamma }\left(\alpha -1\right)sin\left(\frac{\alpha \pi }{4}\right)cos\left(\frac{\alpha \pi }{2}\right)\hfill \\ \times {\tilde{C}}_n^2{k}^{3-\frac{\alpha }{2}}{L}^{\frac{\alpha }{2}}\frac{1}{2\pi }{\int }_0^{2\pi }{\left(\frac{{cos}^2\theta }{{\mu }_x^2}+\frac{{sin}^2\theta }{{\mu }_y^2}\right)}^{\frac{\alpha }{2}-1}d\theta .\hfill \end{array}$$

(12)

In the case of downlink, the laser beam can be precisely approximated as a plane wave. For an uplink, where the atmosphere starts just outside the transmitter, the spherical wave approximation can be used. Therefore, the scintillation index for a plane wave propagating through the weak Kolmogorov downlink can be expressed as [1]

$$\begin{array}{c}{\sigma }_{I,downlink}^2=8{\pi }^2{k}^{2}sec\left(\zeta \right){\int }_{h_0}^H{\int }_0^{\infty }\kappa {\mathsf{\Phi }}_n\left(\kappa ,h\right)\hfill \\ \times \left\{1-cos\left[\frac{L{\kappa }^2}{k}\left(\frac{h-h_0}{H-h_0}\right)\right]\right\}d\kappa dh.\hfill \end{array}$$

(13)

The scintillation index for spherical wave uplink propagation in the weak fluctuation regime can be expressed as [1]

$$\begin{array}{c}{\sigma }_{I,uplink}^2=8{\pi }^2{k}^{2}sec\left(\zeta \right){\int }_{h_0}^H{\int }_0^{\infty }\kappa {\mathsf{\Phi }}_n\left(\kappa ,h\right)\hfill \\ \times \left\{1-cos\left[\frac{L{\kappa }^2}{k}\frac{\left(H-h\right)\left(h-h_0\right)}{{\left(H-h_0\right)}^2}\right]\right\}d\kappa dh,\hfill \end{array}$$

(14)

where $h_0$ denotes the altitude in units of m for the receiver of downlink or the transmitter of uplink, $H=h_0+Lcos\left(\zeta \right)$ denotes the satellite altitude in units of m. Inserting Equation (4) into Equations (13) and (14) lead to

$$\begin{array}{c}{\sigma }_{I,downlink}^2=4\pi k^{2}sec\left(\zeta \right){\int }_{h_0}^H{\int }_0^{\infty }{\int }_0^{\infty }{\mathsf{\Phi }}_n\left({\kappa }_x,{\kappa }_y,h\right)\hfill \\ \times \left\{1-cos\left[\frac{L{\kappa }^2}{k}\left(\frac{h-h_0}{H-h_0}\right)\right]\right\}d{\kappa }_{x}d{\kappa }_{y}dh,\hfill \end{array}$$

(15)

$$\begin{array}{c}{\sigma }_{I,uplink}^2=4\pi k^{2}sec\left(\zeta \right){\int }_{h_0}^H{\int }_0^{\infty }{\int }_0^{\infty }{\mathsf{\Phi }}_n\left({\kappa }_x,{\kappa }_y,h\right)\hfill \\ \times \left\{1-cos\left[\frac{L{\kappa }^2}{k}\frac{\left(H-h\right)\left(h-h_0\right)}{{\left(H-h_0\right)}^2}\right]\right\}d{\kappa }_{x}d{\kappa }_{y}dh.\hfill \end{array}$$

(16)

According to the same steps we have used in the derivation for the scintillation index of horizontal link, the scintillation index for a plane wave (a spherical wave) transmitting in the weak anisotropic non-Kolmogorov downlink (uplink) with anisotropic tilt angle $\gamma$ can be obtained,

$$\begin{array}{c}{\sigma }_{I,downlink}^2=-4{\pi }^2{k}^{3-\frac{\alpha }{2}}{L}^{\frac{\alpha }{2}-1}\mathsf{\Gamma }\left(1-\frac{\alpha }{2}\right)sin\left(\frac{\alpha \pi }{4}\right)sec\left(\zeta \right)\hfill \\ \times {\int }_{h_0}^{H}A\left(\alpha \right){\tilde{C}}_n^2\left(h\right){\left(\frac{h-h_0}{H-h_0}\right)}^{\frac{\alpha }{2}-1}dh\hfill \\ \times \frac{1}{2\pi }{\int }_0^{2\pi }{\left(\frac{{cos}^2\theta }{{\mu }_x^2}+\frac{{sin}^2\theta }{{\mu }_y^2}\right)}^{\frac{\alpha }{2}-1}d\theta ,\hfill \end{array}$$

(17)

$$\begin{array}{c}{\sigma }_{I,uplink}^2=-4{\pi }^2{k}^{3-\frac{\alpha }{2}}{L}^{\frac{\alpha }{2}-1}\mathsf{\Gamma }\left(1-\frac{\alpha }{2}\right)sin\left(\frac{\alpha \pi }{4}\right)sec\left(\zeta \right)\hfill \\ \times {\int }_{h_0}^{H}A\left(\alpha \right){\tilde{C}}_n^2\left(h\right){\left[\frac{\left(H-h\right)\left(h-h_0\right)}{{\left(H-h_0\right)}^2}\right]}^{\frac{\alpha }{2}-1}dh\hfill \\ \times \frac{1}{2\pi }{\int }_0^{2\pi }{\left(\frac{{cos}^2\theta }{{\mu }_x^2}+\frac{{sin}^2\theta }{{\mu }_y^2}\right)}^{\frac{\alpha }{2}-1}d\theta .\hfill \end{array}$$

(18)

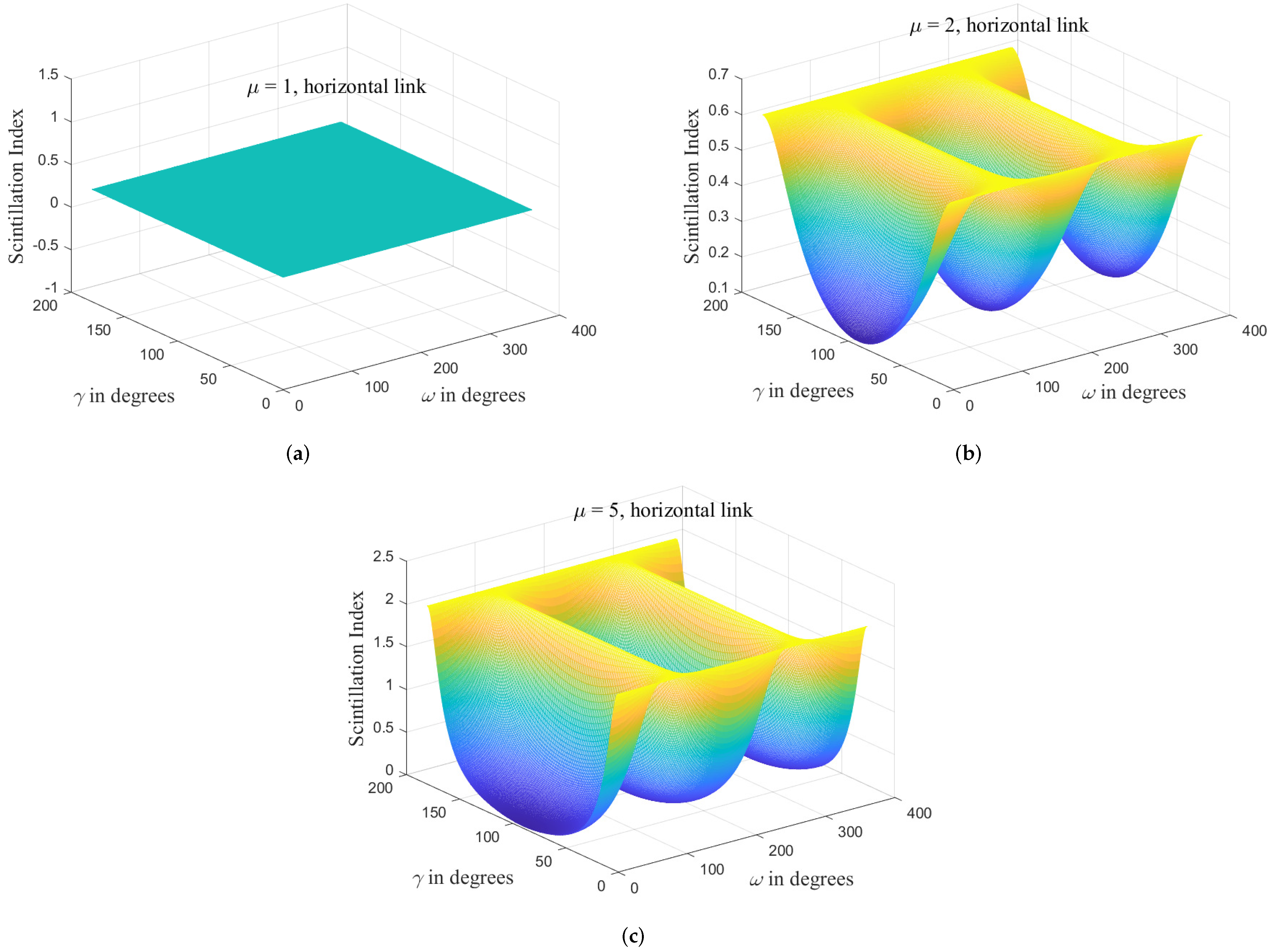
In Figure 2, the influences of anisotropic tilt angle $\gamma$, azimuth angle $\omega$, and anisotropic factor $\mu$ on the scintillation index of a plane wave in the weak anisotropic non-Kolmogorov horizontal link are numerically analyzed. Please note that in the calculation, we have $\lambda$ = 1.55 $\mathsf{\mu }$m, $\alpha$ = 3.5, ${\tilde{C}}_n^2=1\times {10}^{-14}{\mathrm{m}}^{3-\alpha }$, and L = 1 km. As shown in Figure 2, when the anisotropic factor $\mu =1$, anisotropic turbulence reduces to isotropic turbulence, so the variations of anisotropic tilt angle $\gamma$ and azimuth angle $\omega$ have no effect on the scintillation index of horizontal link, and our model is self-consistent for the horizontal link. When the anisotropic factor $\mu$ is greater than 1, the scintillation index of horizontal link varies with the changes of anisotropic tilt angle $\gamma$ and azimuth angle $\omega$. However, while the azimuth angle $\omega$ is equal to the specific values of 90 degrees and 270 degrees, the scintillation index of horizontal link remains unchanged. The physical explanation for this conclusion can be mentioned that the curvature for the anisotropic turbulence cells is different from the isotropic case, and anisotropic turbulence cells will make the focusing properties of the turbulence change. When a beam propagates along the long axis of the anisotropic turbulence cells (horizontal link), the radius of curvature for the interface between the beam and the anisotropic turbulence cells is small, and the beam will be more deviated from the transmission direction since these turbulence cells serve as lenses with a lower radius of curvature [4]. Correspondingly, while a beam propagates along the short axis of the anisotropic turbulence cells (vertical link), the radius of curvature for the interface between the beam and the anisotropic turbulence cells is large, and the beam will be less deviated from the transmission direction since these turbulence cells serve as lenses with a higher radius of curvature. Then based on basic spatial geometry, we can simply deduce that when the azimuth angle $\omega$ is equal to the specific values of 90 degrees and 270 degrees, as the anisotropic tilt angle $\gamma$ varies, the radius of curvature for the interface between the propagated beam and the anisotropic turbulence cells is basically unchanged in the horizontal link. Hence, the scintillation index of horizontal link remains unchanged. However, while the azimuth angle $\omega$ is not equal to the specific values of 90 degrees and 270 degrees, the radius of curvature for the interface between the propagated beam and the anisotropic turbulence cells varies with the changes of anisotropic tilt angle $\gamma$ and azimuth angle $\omega$. In addition, as the anisotropic factor $\mu$ increases, the variation range of scintillation index for the horizontal link increases.

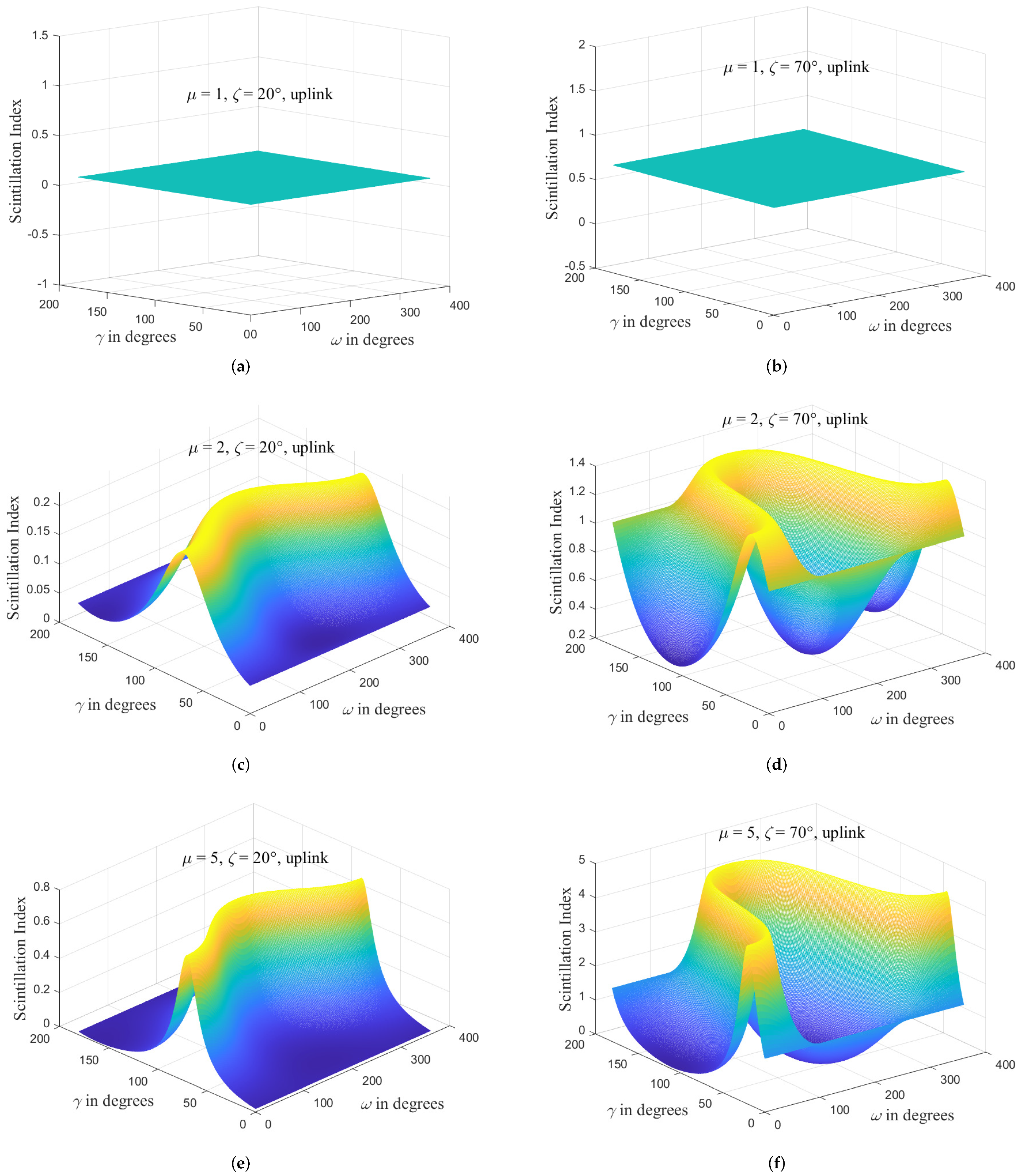
Figure 3 and Figure 4 present the variation of scintillation index for downlink and uplink against the function of anisotropic tilt angle $\gamma$ and azimuth angle $\omega$ with some fixed values of zenith angle $\zeta$ and anisotropic factor $\mu$. Please note that in the calculation, we have $\lambda$ = 1.55 $\mathsf{\mu }$m, $\alpha$ = 3.5, L = 1000 km, $C_n^2\left(0\right)=1\times {10}^{-14}{\mathrm{m}}^{-2/3}$, $h_0$ = 0 m, and w = 30 m/s. It can be observed from Figure 3 and Figure 4 that when the anisotropic factor $\mu =1$, anisotropic turbulence reduces to isotropic turbulence, so the variations of anisotropic tilt angle $\gamma$, azimuth angle $\omega$, and zenith angle $\zeta$ also have no effect on the scintillation index for downlink and uplink, and our model is self-consistent for the satellite links. When the anisotropic factor $\mu$ is greater than 1, the scintillation index for downlink and uplink vary with the changes of anisotropic tilt angle $\gamma$ and azimuth angle $\omega$. The change of zenith angle $\zeta$ will completely alter the trend of scintillation index for downlink and uplink with $\gamma$ and $\omega$. The physical interpretation of this result is the same as Figure 2, which can be attributed to the curvature difference between the anisotropic turbulence cells and the isotropic case. In addition, the radius of curvature for the interface between the propagated beam and the anisotropic turbulence cells varies with the changes of anisotropic tilt angle $\gamma$, azimuth angle $\omega$, and zenith angle $\zeta$. In addition, as the zenith angle $\zeta$ and the anisotropic factor $\mu$ increase, the variation range of scintillation index for the satellite links increases.

3. Conclusions

In this paper, the anisotropic non-Kolmogorov turbulence spectra with anisotropic tilt angle $\gamma$ are developed for the horizontal and satellite links. Then based on these spectra, the analytical expressions of scintillation index for the weak anisotropic non-Kolmogorov horizontal and satellite links are derived. The calculation results indicate that the scintillation index for the horizontal and satellite links vary with the changes of anisotropic tilt angle $\gamma$ and azimuth angle $\omega$. However, while the azimuth angle $\omega$ is equal to the specific values of 90 degrees and 270 degrees, the scintillation index of horizontal link remains unchanged. In addition, the variation of zenith angle $\zeta$ will completely alter the trend of scintillation index for downlink and uplink with $\gamma$ and $\omega$. Therefore, the anisotropic tilt angle $\gamma$ is necessary in the horizontal and satellite links. It should be noted that this work will benefit the construction of atmospheric turbulence model and the perception of light wave propagation in the anisotropic non-Kolmogorov links.