A Preliminary Assessment of an FBG-Based Hard Landing Monitoring System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hard Landing
2.2. Test Article: Leaf Spring Landing Gear
2.3. Fibre Optic Sensors
2.4. FBGs and SGs Arrays
2.5. Acquisition Systems
3. Results
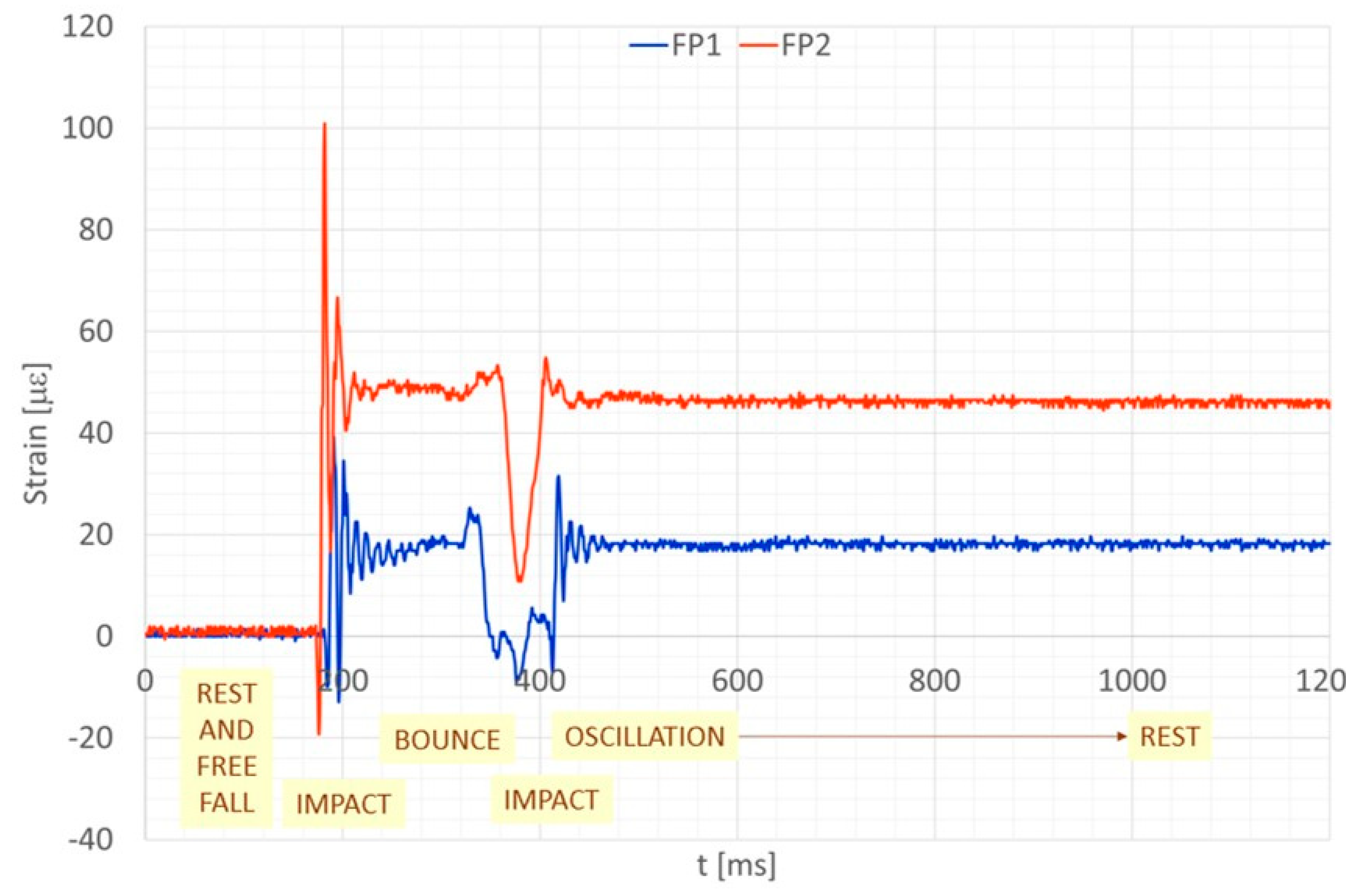
3.1. Generalities
3.2. Elementary Kinematics
3.3. Data Extraction
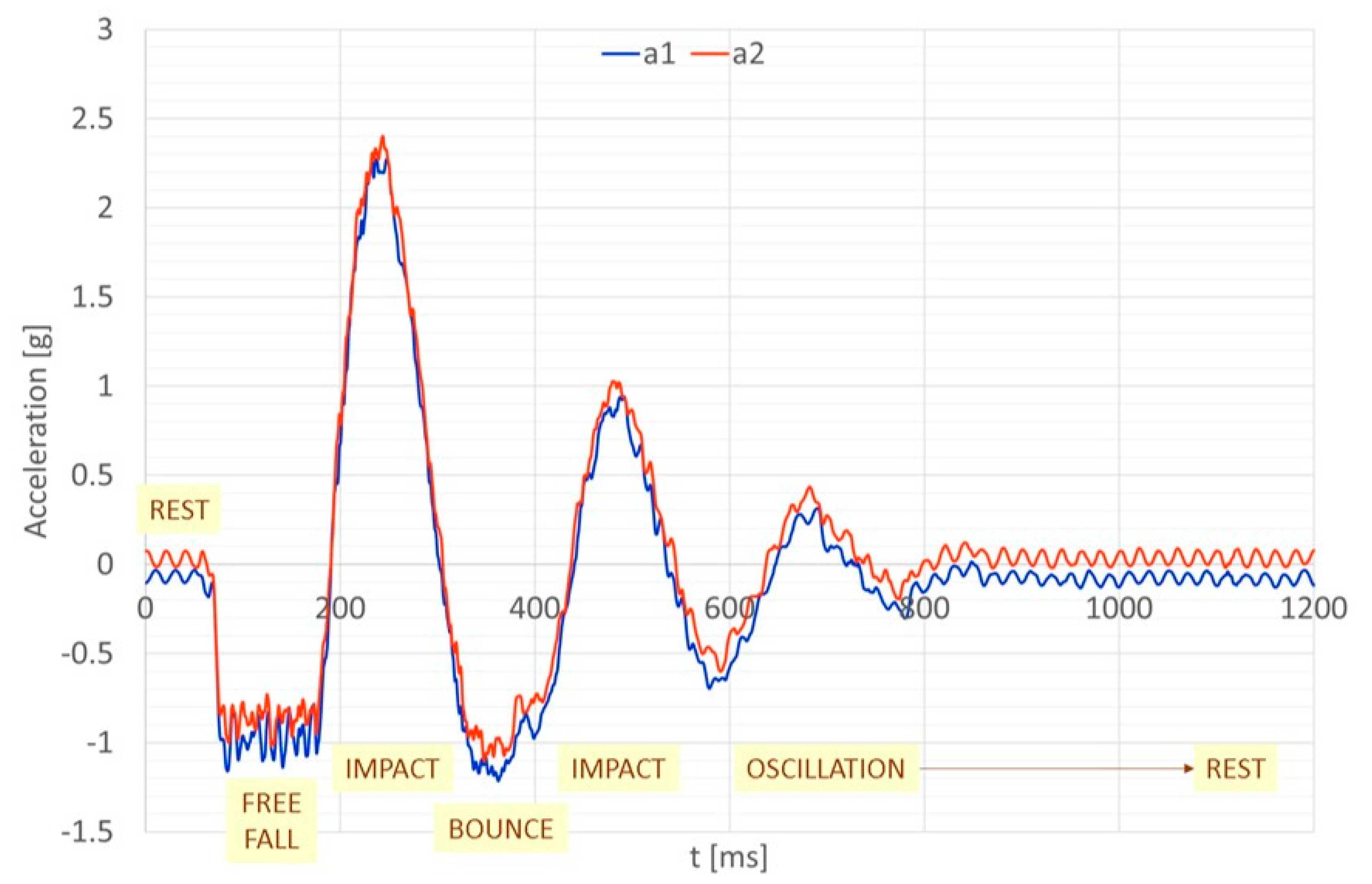
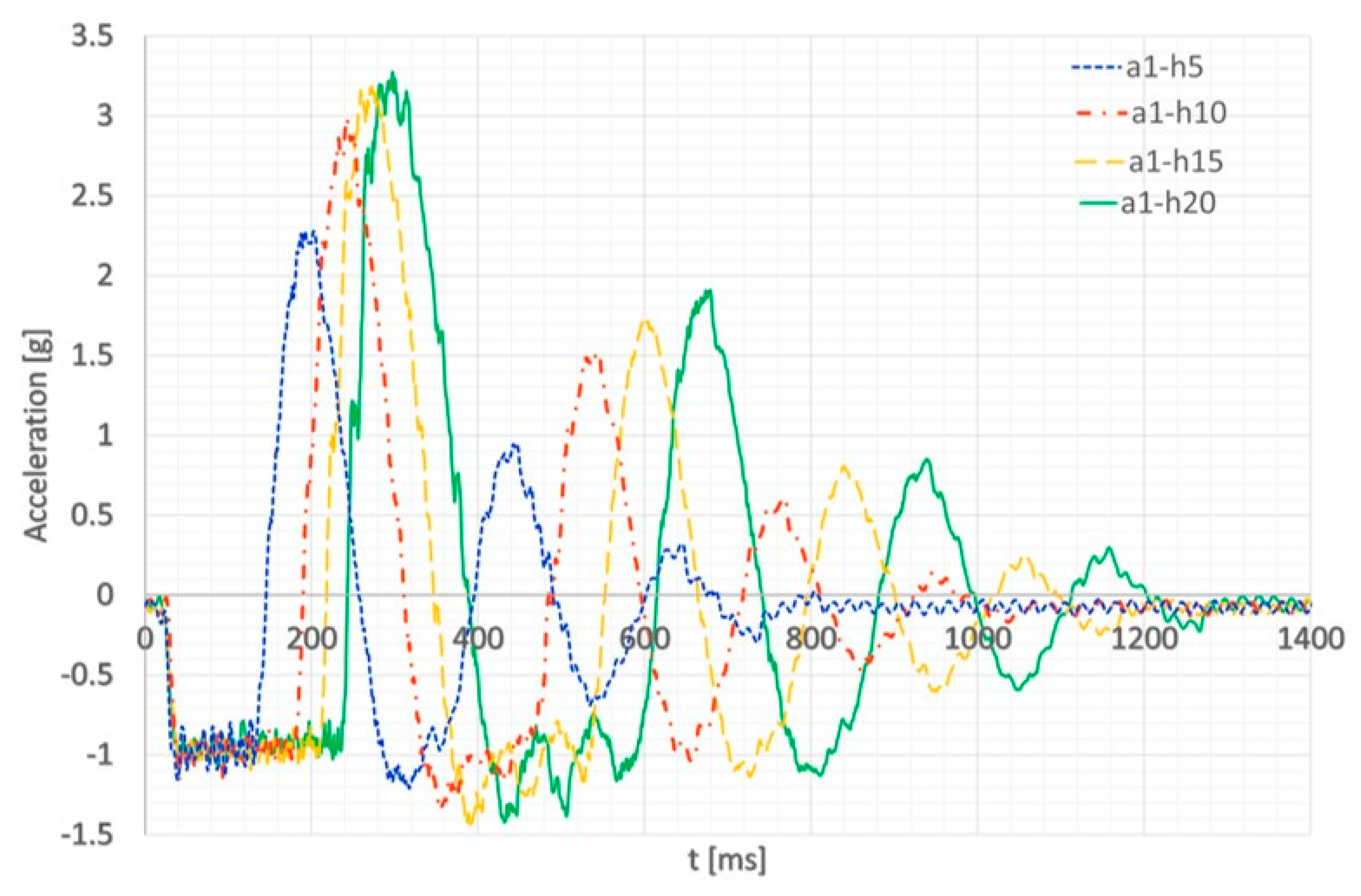
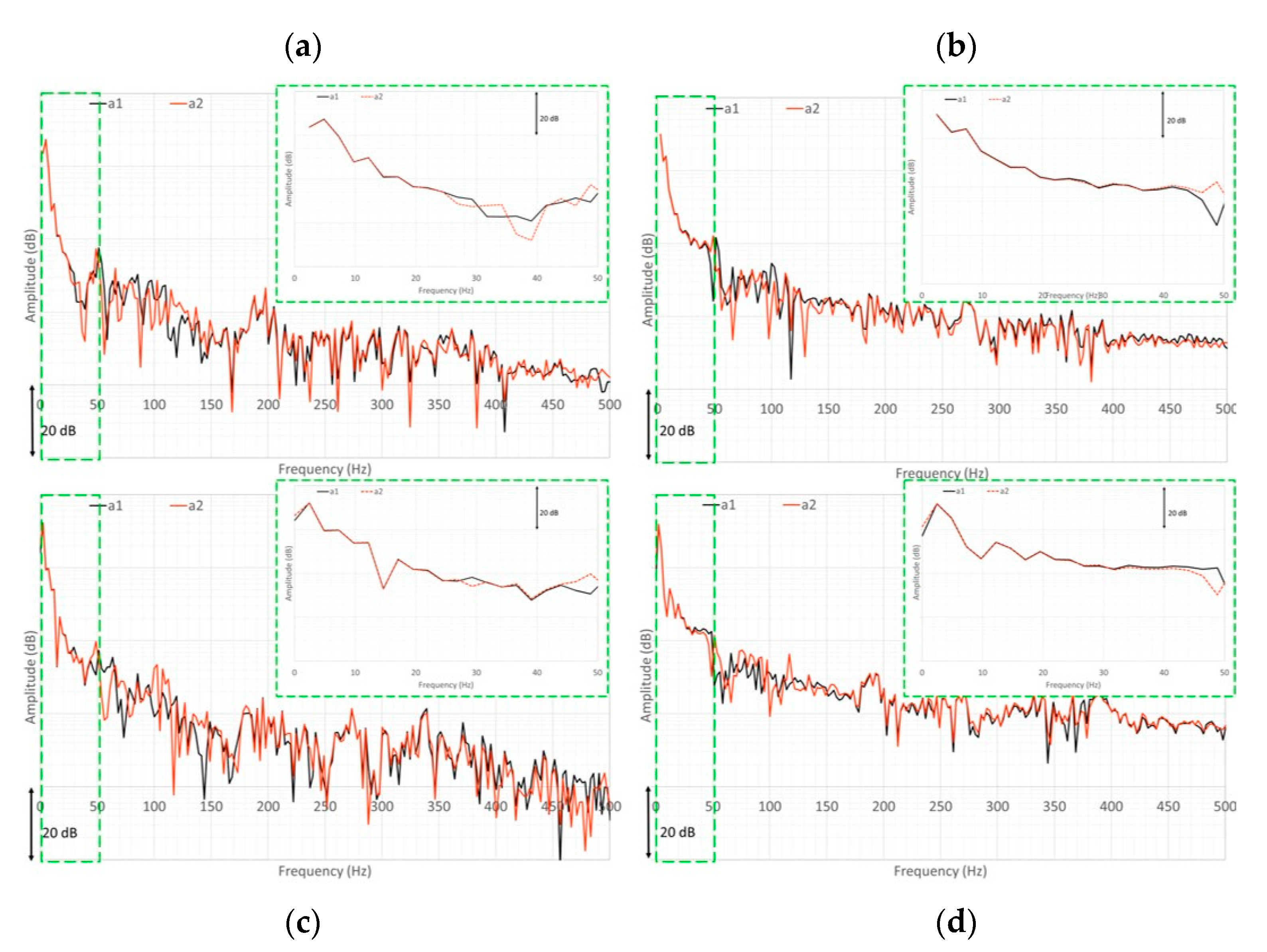
3.4. Accelerometer Signals
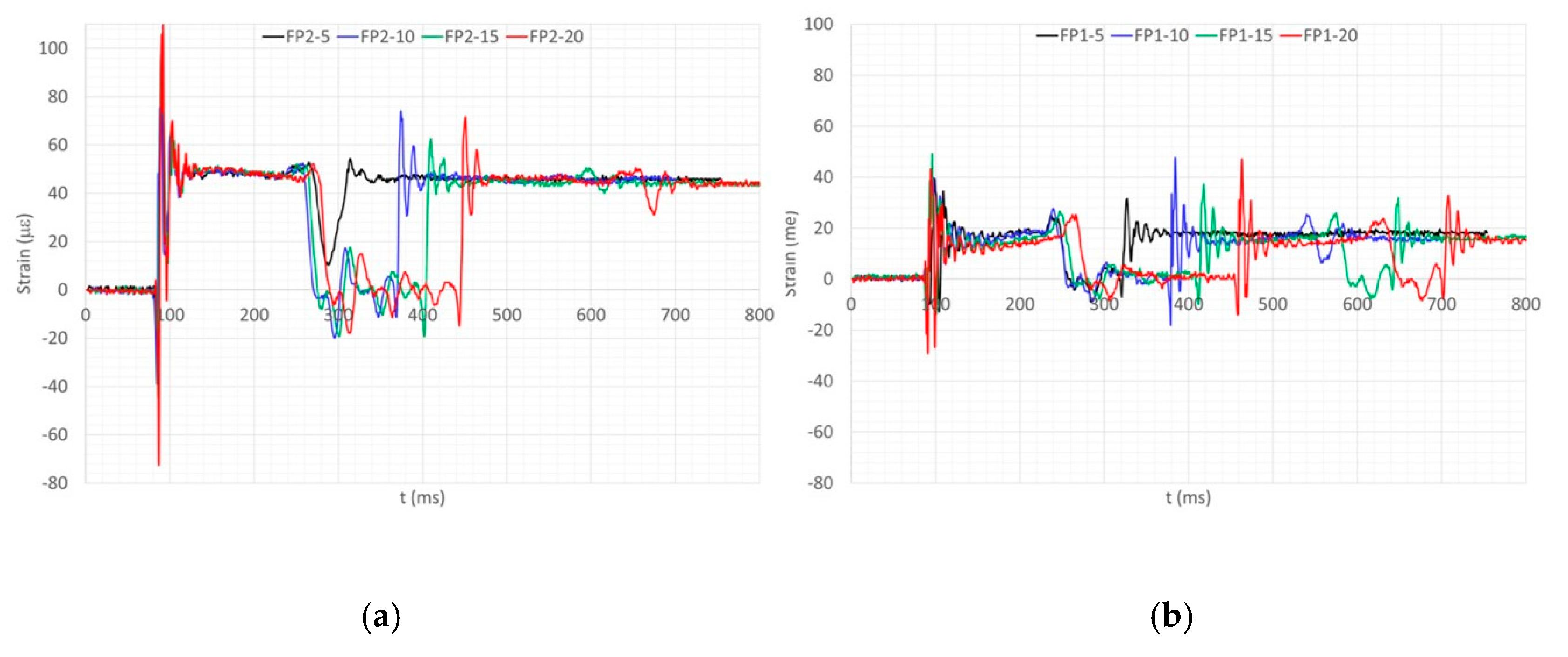
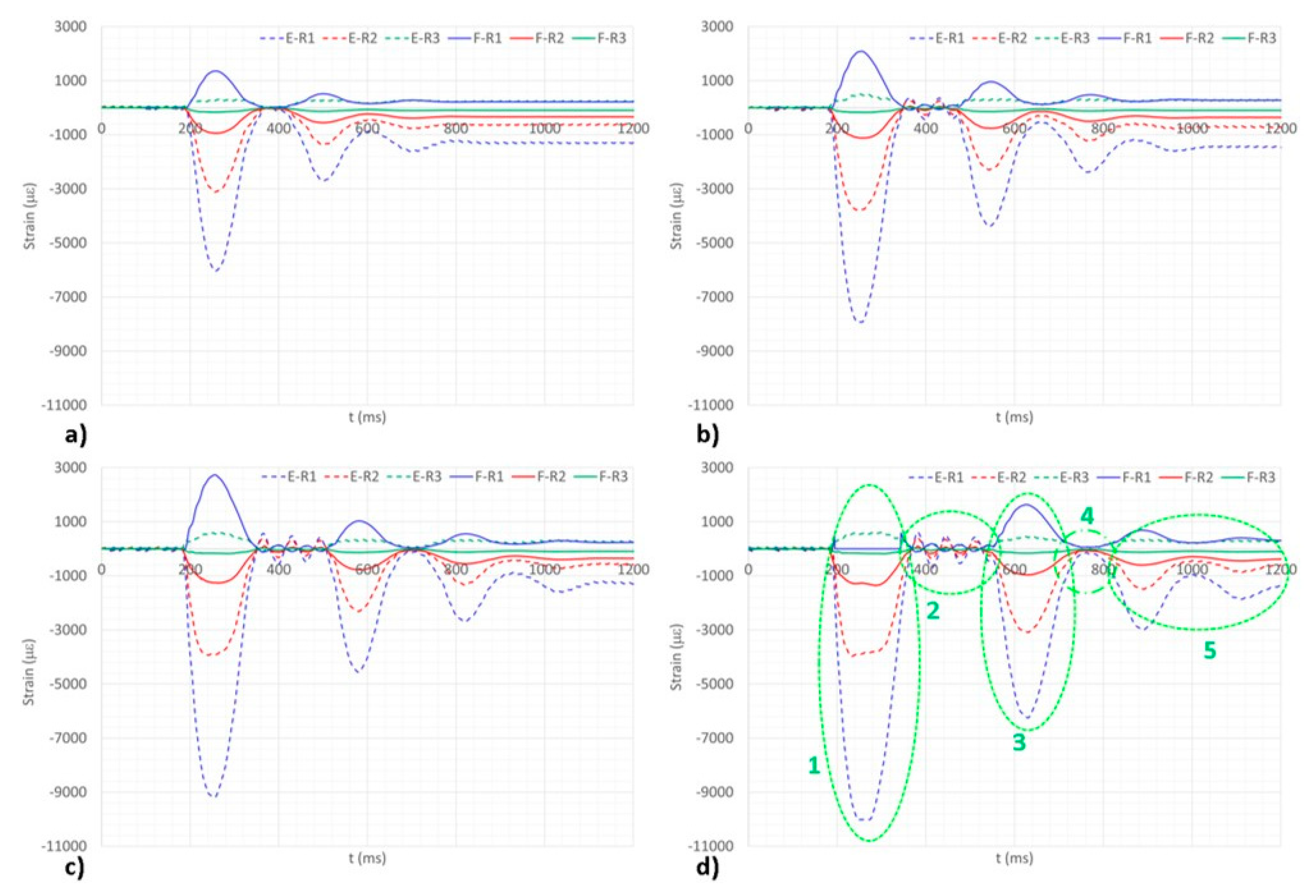
3.5. Plate-FBG Signals
- Region 1: It represents the signal history recorded while the wheel is in contact with the ground. The oscillation appears significantly dampened due to the effect of the inflated pneumatic absorption. It is relevant to note that the vibrations experience a homogeneous reduction, until the system starts to rebound and prepares to leave the plates.
- Regions 2: The effect of the rebound is seen as a novel, negative impulse for the plate, which starts to vibrate again in a different way. Two main differences are associated with this behavior: Damping is lower, because there is no damping generator on the plate, as the wheels are detached from it; frequency is considerably lower since the wheel absence determines a drastic diminution of the structural constraints.
- Region 3: It is analogous to region 1, with the relevant difference of a smaller vibration amplitude since the rebound is associated with reduced heights; therefore, the energy release is less than before. It is relevant to note that as the damping levels are substantially the same as before and, as already mentioned (it is associated with the first pinned mode of the system), the impact time is the same.
- Region 4: It is characterized by a very small time-segment. In this case, it is understood that the landing gear does experience just a partial rebound, not coming to a complete separation from the plate. It does manifest, then, into a relaxation of the vibration period between two full-contact configurations (regions 3 and 5) and a very short duration.
- Region 5: It does correspond to the very end part of the dynamic response history until vibration vanishes. After that period, the landing gear is at rest, and the FBG sensors record a strain that is proportional to the weight fraction that stands on it.
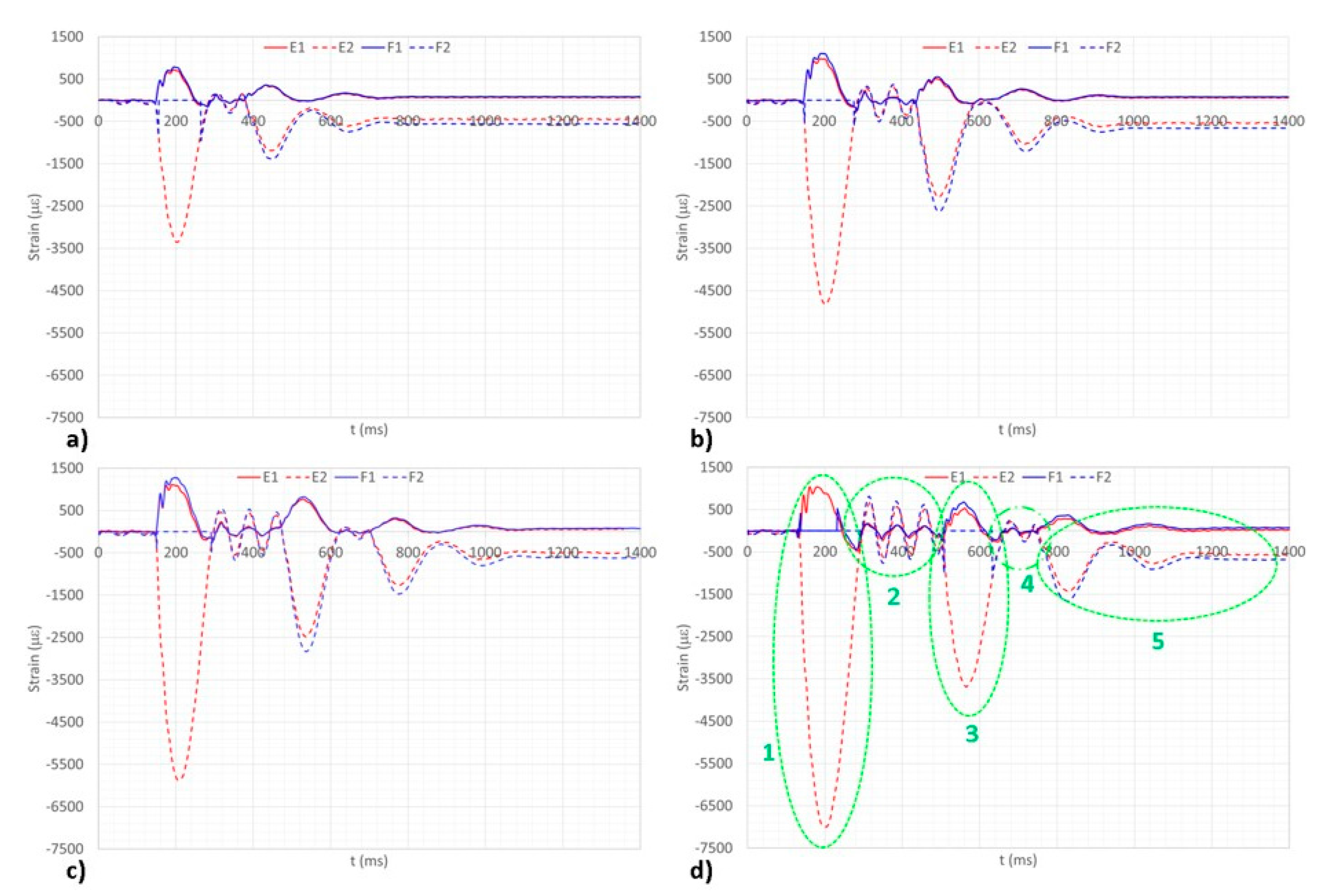
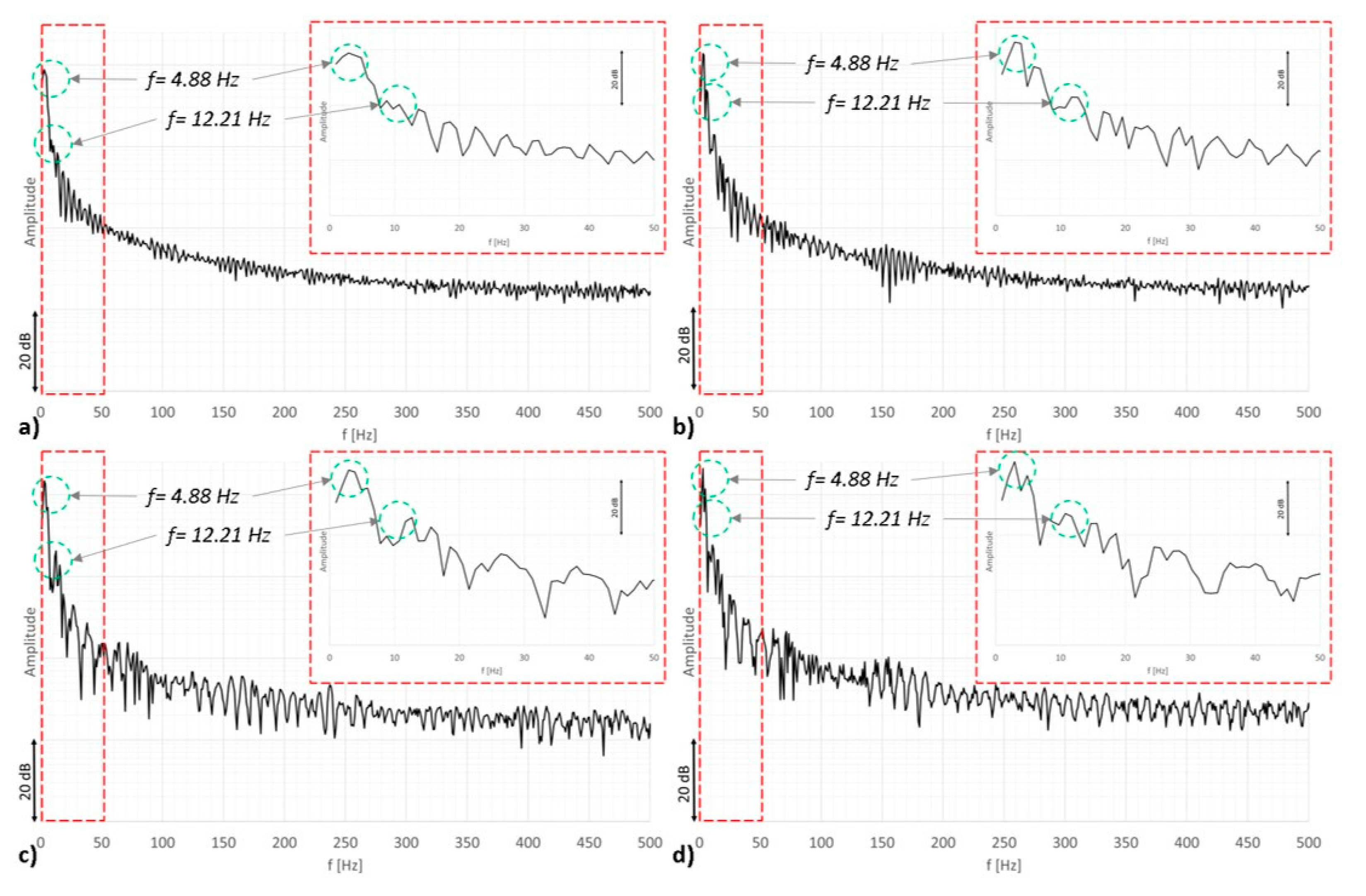
3.6. Test Article FBGs’ Arrays
- Region 1: The first impact is the one causing the largest deformation levels, as expected: All the fall energy is converted into elastic energy, partly transferred to the landing gear system and partly to the impact plates. The first mode of vibration of the LG is clearly detected and, as evident from the pictures, is equal for all the tested heights. This mode, as already stated, is the one characterized by a large displacement of the top interface plate and large straddle of the LG legs and is coherent with the outline of the system pinned at the wheels.
- Region 2: The structure detaches from the ground and moves freely in the air. The detected strain oscillations refer to the first mode of the free-free LG; it is characterized by a large motion of the two legs, behaving similar to a clamped beam with a concentrated mass at its free end. In both the cases, it is evident as the strain curve is much clearer than the previous acceleration graphs. This is a direct outcome of the filter imposed by the acquisition system at 1 kHz.
- Region 3: The LG strikes once again the ground (first rebound). The first pinned mode is again excited, for the same time interval but for a lower amplitude.
- Region 4: The system is shown to leave once again the ground, but just partially, according to the illustrated curves; this frame is somehow characterized by a mixed behavior between the pinned and the free motion and lasts for a very short time.
- Region 5: Pinned oscillations are evident: They correspond to a sort of structure relaxing around the first mode, whose amplitude slowly vanishes until rest. One of the two sensors (Figure 19) approaches zero again at the end of the dynamic history. This is just a case, indicating that the deformed shape of the system under its own weight, and for the cited boundary constraints, presents a node at the SG/FBG positions.
3.7. Spring Ties Effect
4. Conclusions
- The three sets of used sensors provide the same kind of information so that it is possible to state that the networks are exchangeable. The actual difference may be identified in the frequency bandwidth of the acquisition systems. Namely, the impact dynamics involve all the vibration modes of the system under investigation. Therefore, it shall be calibrated with reference to the specific landing gear. Generally, a good conservative target for structural systems may be set at 1 kHz. In this case, we shall state that an optical interrogator showing a 4 kHz band per channel can be sufficient to the scope.
- The vibration modes that shall be considered at that aim are both the pinned ones (representing the landing gear supported by the wheels) and the free-free configuration, as the complete system experiences rebounds and it detaches from the ground. However, this is a minimal requirement since in reality many other occurrences can be experienced (non-symmetrical landing with just one or two, out of the three legs on the ground and so on), making the assessment of this spec really hard to be defined.
- Accelerometers may provide excellent information on the system dynamics, being able for definition to provide data also for the free-fall state (gravity driven), something that strain sensors are only partially able to produce (static strain response to gravity load, usually very low). However, accelerometers have strong weaknesses that make their choice as point descriptors hardly feasible: For instance, their number should be excessive to catch the dynamics of the landing gear system, and the related cabling could be easily impracticable; also, the output data do not give direct information on the system stress state that shall be in turn extrapolated. The second point could be overcome by the use of strain gauges, which, however, are not suitable to bypass the first issue. Fibre optics are able to overcome both of these points and present the well-known advantages of being insensible to electromagnetic fields and having minimum intrusiveness and weight penalty, among the others.
- A further basic benefit comes directly for FBG and fibre optics’ minimal size, which allows the sensor system to be embeddable within the reference structure. This may faces some difficulties for metal structures but can be simple in a certain measure for composite structures, where a lot of activities have been presented in the literature [38,39]. This process, apart from the forecast cleanness of the resulting system, makes it more robust to external accidents, either due to normal operations or randomness. In that sense, the reported experience evidences once more the fibre optics as one of the showstoppers for actual aeronautic implementation.
- The sensor system, including the gauges network and the acquisition instrumentation, shall be flyable. FBG interrogators have owned this characteristic for a long time with respect to traditional architectures, while many other solutions have been recently presented, enlarging the number of sensors deployable on a single line, significantly. Other technologies, based on distributed architectures, do not have the maturity to be installed on-board aircrafts yet, but further developments are expected in the current decade as different proposals are being presented on the market.
- Since FBG networks allow just a limited number of sensors, namely, 64 for typical 4-channel interrogators, the retrieved information shall necessarily pass through some model of the reference structure that, combined with information allowing to reconstruct the landing conditions, can give a representation of the actual strain map and, therefore, of the mechanical energy entering the gear structure. It may be objected that, also currently, the number of channels may be simply enlarged by increasing the number of interrogators. This kind of solution, however, is accompanied by amplified safety, maintenance, cost and even architectural issues, as it is easy to imagine.
- Enrich the available tools with a detailed FEM of the system, including the instrumented Landing Gear, the plates and partially the sliding system;
- Introduce a denser network on the structure, in order to increase the accessible data, even using special measures to compact its outline and different optical sensors;
- Develop a correlation between the numerical model and the achieved data, trying to assess a tool for retrieving the overall configuration from the limited experimental info, for instance, based on Artificial Neural Networks;
- Develop, as a complement to the point above, an optimization tool for deploying the sensor networks in the most effective points, for instance, based on Genetic Algorithms, to maximize the strength of the extrapolation;
- Resume and expand some preliminary and independent engineering tools that the authors set and published in some recent work [30] to correlate strain information to energy directly to further augment the predictability power.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Howe, D. Aircraft Loading and Structural Layout; Professional Engineering Publishing Limited: London, UK, 2004; ISSN 1743-386X. [Google Scholar]
- MC Gehee, J.R.; Carden, H.D. Analytical Investigation of Landing Dynamics of a Large Airplane with a Load-control System in Main Landing Gear. NASA Tech. Pap. 1979, 1555, ADA078613. [Google Scholar]
- Gorinevsky, D.; Gordon, G.A.; Beard, S.; Kumar, A.; Chang, F.K. Design of Integrated SHM System for Commercial Aircraft Applications. In Proceedings of the 5th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2005. [Google Scholar]
- Forrest, C.; Wiser, D. Landing gear structural health monitoring (SHM). Procedia Struct. Integr. 2017, 5, 1153–1159. [Google Scholar] [CrossRef]
- Cowan, S.J.; Cox, R.L.; Slusher, H.W.; Jinadsa, S. Airplane Hard Landing Indication System. U.S. Patent 6,767,075, 13 January 2004. [Google Scholar]
- Pritchard, J. Overview of Landing Gear Dynamics. J. Aircr. 2001, 38. [Google Scholar] [CrossRef] [Green Version]
- Tripero, A.; Arevalo, J. Weight on wheel system based on strain gauges. In Proceedings of the ICAS, Brisbane, Australia, 23–28 September 2012; ISBN 978-0-9565333-1-9. [Google Scholar]
- Brindisi, A.; Ameduri, S.; Concilio, A.; Ciminello, M.; Leone, M.; Iele, A.; Consales, M.; Cusano, C. A multi-scaled demonstrator for aircraft weight and balance measurements based on FBG sensors: Design rationale and experimental characterization. Measurement 2019, 141, 113–123. [Google Scholar] [CrossRef]
- Iele, A.; Leone, M.; Consales, M.; Persiano, G.V.; Brindisi, A.; Ameduri, S.; Concilio, A.; Ciminello, M.; Apicella, A.; Bocchetto, F.; et al. A fiber optic sensor system for load monitoring on aircraft landing gears. In Proceedings of the SPIE 11199, 7th European Workshop on Optical Fibre Sensors, 111990L, Limassol, Cyprus, 1–4 October 2019. [Google Scholar] [CrossRef]
- Pytka, J.; Jozwik, J.; Lyszczyk, T. Embedded Wheel Force Sensor For Aircraft Landing Gear Testin. In Proceedings of the 5th IEEE International Workshop on Metrology for Aerospace, Rome, Italy, 20–22 June 2018. [Google Scholar]
- Jebacek, I.; Horak, M. Measuring of a Nose Landing Gear Load during Take-Off and Landing. In Proceedings of the 21st International Conference Engineering Mechanics, Svratka, Czech Republic, 11–14 May 2015; pp. 120–121. [Google Scholar]
- Baird, B.W. Overload Detection/Health Monitoring Landing Gear Sensor System Proposal. Master’s Thesis, Ryerson University, Toronto, ON, Canada, 2008. Paper 1157. [Google Scholar]
- Schmidt, R.K. Monitoring of aircraft landing gear structure. J. Aircr. 2008, 112, 275–278. [Google Scholar] [CrossRef]
- Schmidt, R.K.; El-Samid, N.A. Structural Deflection and Load Measuring Device. Patent WO 2006/024146 A1, 9 March 2006. [Google Scholar]
- Sagi, O.T.; Maynard, D.; Enikov, E. In Proceedings of the Capacitive Transducer for Condition Based Maintenance after Harsh Landing Events, Baltimore, MD, USA, 12–15 September 2011.
- Finance, R.J. Device for Detecting Hard Landings. USA Patent US4278219A, 14 July 1981. [Google Scholar]
- Anì, T.; Ting, Z.Z.; Tao, C.J. A technique of landing gear loads calibration with strain gauges. In Proceedings of the 27th International Congress of Aeronautical Sciences, Nice, France, 19–24 September 2010. [Google Scholar]
- Schmidt, R.K.; Sartor, P.N. Landing Gear. In Encyclopaedia of Structural Health Monitoring; Boller, C., Chang, K.F., Fujino, T., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 1983–1994. ISBN 978-0-470-05822-0. [Google Scholar]
- Schmidt, R.K. System and Method for Determining Aircraft Hard Landing Events from Inertial and Aircraft Reference Frame Data. U.S. Patent 7,589,645, 11 January 2009. [Google Scholar]
- Zhou, Y.; Liu, D.; Li, D.; Zhao, Y.; Zhang, M.; Zhang, W. Review on Structural Health Monitoring in Metal Aviation Based on Fiber Bragg Grating Sensing Technology. In Proceedings of the 2020 Prognostics and Health Management Conference (PHM-Besançon), Besancon, France, 4–7 May 2020; pp. 97–102. [Google Scholar] [CrossRef]
- Di Sante, R. Fibre Optic Sensors for Structural Health Monitoring of Aircraft Composite Structures: Recent Advances and Applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, G.; Sandberg, R.L.; Lalone, B.M.; Marshall, B.R.; Grover, M.; Stevens, G.; Udd, E. High pressure sensing and dynamics using high speed Fiber Bragg Grating interrogation systems. Fiber Opt. Sens. Appl. XI 2014. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, X. Fiber Bragg Gratings Sensors for Aircraft Wing Shape Measurement: Recent Applications and Technical Analysis. Sensors 2019, 19, 55. [Google Scholar] [CrossRef] [Green Version]
- Chandler, K.; Ferguson, S.; Graver, T.; Csipkes, A.; Mendez, A. On-line structural health and fire monitoring of a composite personal aircraft using an FBG sensing system. SPIE Proc. Smart Sens. Phenom. Technol. Netw. Syst. 2008, 6933. [Google Scholar] [CrossRef]
- Kressel, I.; Balter, J.; Mashiach, N.; Sovran, I.; Shapira, O.; Shemesh, N.Y.; Glamm, B.; Dvorjetski, A.; Yehoshua, T.; Tur, M. High Speed, In-Flight Structural Health Monitoring System for Medium Altitude Long Endurance Unmanned Air Vehicle. In Proceedings of the EWSHM 7th European Workshop on Structural Health Monitoring, IFFSTTAR, Inria, Université de Nantes, Nantes, France, 8–11 July 2014. hal-01020352. [Google Scholar]
- Briancourt, S.; Seymour, T. Aircraft Landing Gear Load Sensor. USA Patent US 8,235,326 B2, 7 August 2012. [Google Scholar]
- Petroneb, G.; Brunoa, M.; Bocchettoa, F.; Bregliob, G.; Puglieseb, M.; Caldarab, A.; Cavallaric, A.N.; Moriellod, S.S.L.; Capuano, G. An Innovative Health Monitoring System for Aircraft Landing Gears. In Proceedings of the 8th European Workshop On Structural Health Monitoring (EWSHM), Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Kwon, H.; Park, Y.; Shin, C.; Kim, J.-H.; Kim, C.-G. In-Flight Strain Monitoring of Aircraft Tail Boom Structure Using a Fiber Bragg Grating Sensor Based Health and Usage Monitoring System. Int. J. Aeronaut. Space Sci. 2021, 22, 567–577. [Google Scholar] [CrossRef]
- Iadicicco, A.; Natale, D.; Di Palma, P.; Spinaci, F.; Apicella, A.; Campopiano, S. Strain Monitoring of a Composite Drag Strut in Aircraft Landing Gear by Fiber Bragg Grating Sensors. Sensors 2019, 19, 2239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brindisi, A.; Vendittozzi, C.; Travascio, L.; Di Palma, L.; Concilio, A. Landing gear hard impact: Preliminary study on optic monitoring system. Proc. Inst. Mech. Eng. Part C 2020, 1–12. [Google Scholar] [CrossRef]
- Cordis, AlGeSMo (Advanced Landing Gear Sensing and Monitoring). Available online: https://cordis.europa.eu/project/id/717179/results (accessed on 30 September 2021).
- Technobis, Landing Gear Load Sensing. Available online: https://www.technobis.com/files/6315/3259/9099/5.pdf (accessed on 30 September 2021).
- EASA, CS23 Easy Access Rules for Normal-Category Aeroplanes (CS-23) (CS Amendment 5, AMC/GM Issue 2). Available online: https://www.easa.europa.eu/document-library/certification-specifications/cs-23-amendment-5 (accessed on 1 August 2021).
- EASA, CS25 CS-25 Amendment 24. Available online: https://www.easa.europa.eu/document-library/certification-specifications/cs-25-amendment-25 (accessed on 1 August 2021).
- Boeing, Conditional Inspections. Available online: https://www.boeing.com/commercial/aeromagazine/aero_14/conditional_story.html (accessed on 1 October 2021).
- Measures, R.M. Structural Monitoring with Fiber Optic Technology; Academic Press: San Diego, CA, USA, 2001; ISBN 0-12-487430-4. [Google Scholar]
- University of Maryland, Jim Hetrick’s Homepage, Oscillations. Available online: https://www-personal.umd.umich.edu/~jameshet/IntroLabs/IntroLabDocuments/150-11%20Oscillations%5b2%5d/Oscillations%5b2%5d%2012.0.pdf (accessed on 1 October 2021).
- Waite, S.R. Use of embedded optical fibre for significant fatigue damage detection in composite materials. Composites 1990, 21, 225–231. [Google Scholar] [CrossRef]
- Bednarska, K.; Sobotka, P.; Wolinski, T.R.; Zakrecka, O.; Pomianek, W.; Nocon, A.; Lesiak, P. Hybrid Fiber Optic Sensor Systems in Structural Health Monitoring in Aircraft Structures. Materials 2020, 13, 2249. [Google Scholar] [CrossRef] [PubMed]



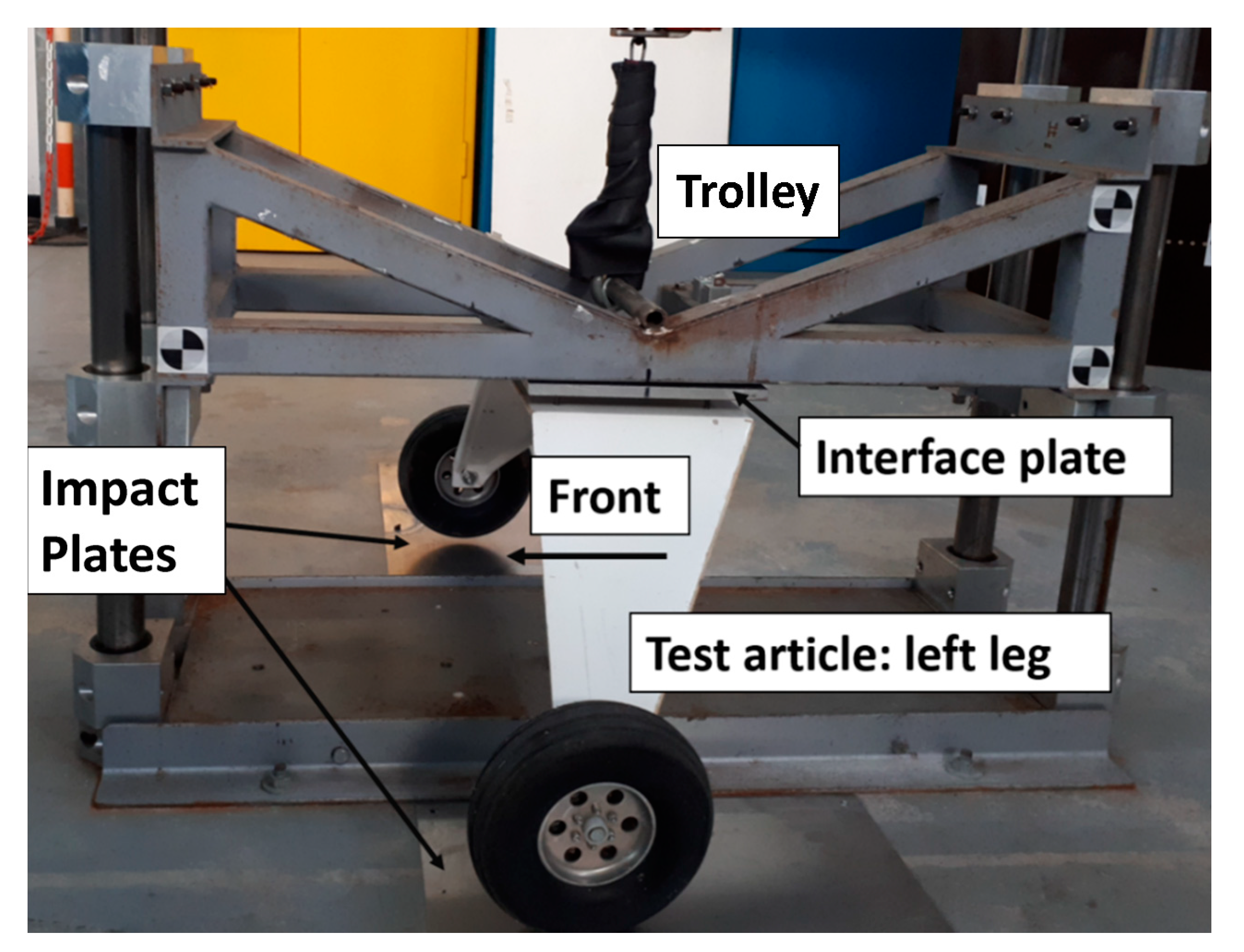

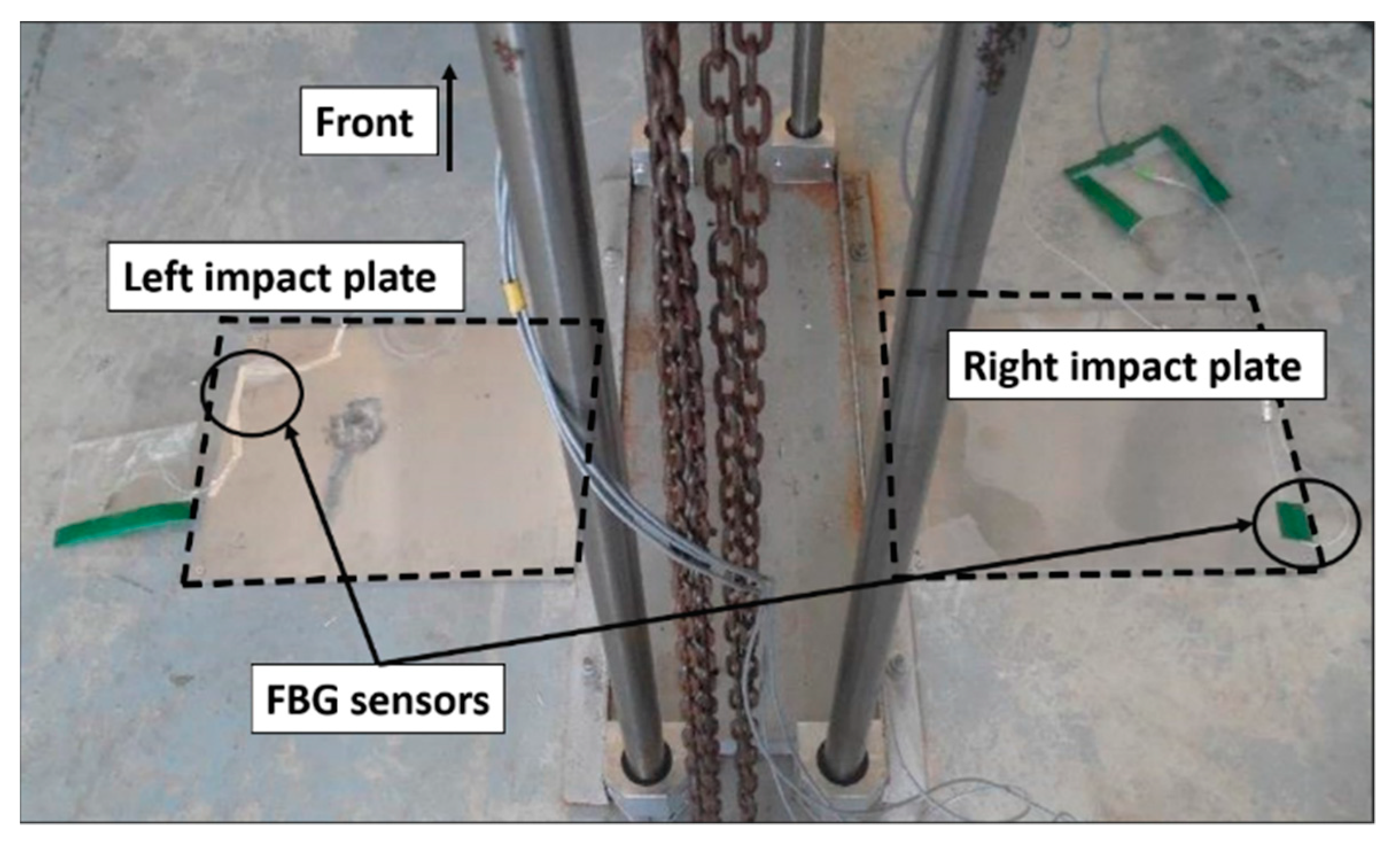
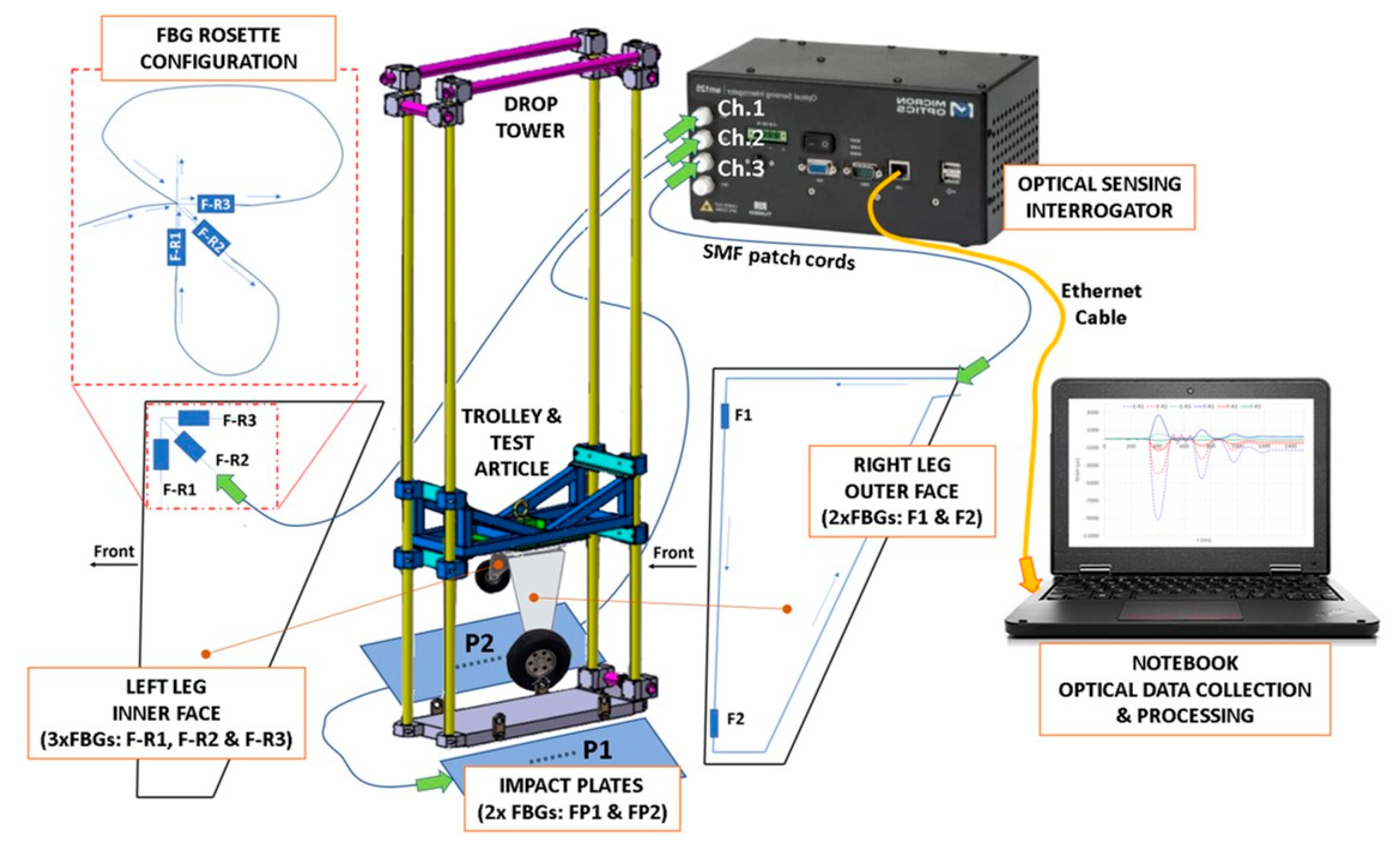








| Channel | Position | Sensor Name | λ (nm) |
|---|---|---|---|
| Ch 1 | Left Leg | F-R1 @ 0° F-R2 @ 45° F-R3 @ 90° | 1530.126 1550.011 1570.167 |
| Ch 2 | Impact Plates | FP1 (right) FP2 (left) | 1530.176 1570.003 |
| Ch 3 | Right Leg | F1 F2 | 1530.124 1570.001 |
| h (m) | v [m/s] | TTFFT (s) * | TEFFT (s) * | ε% ** |
|---|---|---|---|---|
| 0.05 | 0.990 | 0.101 | 0.106 | 4.99% |
| 0.10 | 1.401 | 0.143 | 0.153 | 6.94% |
| 0.15 | 1.716 | 0.175 | 0.190 | 8.59% |
| 0.20 | 1.981 | 0.202 | 0.221 | 9.30% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brindisi, A.; Vendittozzi, C.; Travascio, L.; Di Palma, L.; Ignarra, M.; Fiorillo, V.; Concilio, A. A Preliminary Assessment of an FBG-Based Hard Landing Monitoring System. Photonics 2021, 8, 450. https://doi.org/10.3390/photonics8100450
Brindisi A, Vendittozzi C, Travascio L, Di Palma L, Ignarra M, Fiorillo V, Concilio A. A Preliminary Assessment of an FBG-Based Hard Landing Monitoring System. Photonics. 2021; 8(10):450. https://doi.org/10.3390/photonics8100450
Chicago/Turabian StyleBrindisi, Angela, Cristian Vendittozzi, Lidia Travascio, Luigi Di Palma, Michele Ignarra, Vincenzo Fiorillo, and Antonio Concilio. 2021. "A Preliminary Assessment of an FBG-Based Hard Landing Monitoring System" Photonics 8, no. 10: 450. https://doi.org/10.3390/photonics8100450
APA StyleBrindisi, A., Vendittozzi, C., Travascio, L., Di Palma, L., Ignarra, M., Fiorillo, V., & Concilio, A. (2021). A Preliminary Assessment of an FBG-Based Hard Landing Monitoring System. Photonics, 8(10), 450. https://doi.org/10.3390/photonics8100450








