Abstract
All pseudo-Schell model sources have been shown to possess the same continuous set of circularly symmetric modes, all of them presenting a conical wavefront. For keeping energy at a finite level, the mode amplitude along the radial coordinate is modulated by a decreasing exponential function. A peculiar property of such modes is that they exist in the Laplace transform’s realm. After a brief discussion of the near-zone, we pass to the far-zone, where the field can be evaluated in closed form. The corresponding features of the intensity distribution are discussed.
1. Introduction
A partially coherent source whose degree of coherence between two points is shift-invariant (i.e., depends only on the difference between the position vectors of the two points) is said to be of the Schell-model type [1]. Sources of this class have found application in the study of the radiation emitted by many natural sources and, since they can always be synthesized starting from spatially incoherent sources, they have represented for a long time the main tool for experimentally validating results of the scalar theory of coherence.
More general sources, though, can be envisaged with different behaviors of the correlation function. In particular, since their coherence properties affect the features of the radiated beam [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18], this opens a new way to searching for particular light sources that best fit for specific applications, such as particle trapping [12,19], free space optical communications [20,21], or sub-Rayleigh imaging [22,23,24,25], among others.
Here we deal with a wide class of nonconventionally correlated partially coherent sources, the so called pseudo-Schell model sources [11] that are characterized by a degree of coherence that depends only on the difference of the radial coordinates between the involved points. The cross-spectral density (CSD) of the fields produced by such sources was found to possess several peculiar properties [11,12].
In the present paper, we investigate the structure of the modes underlying pseudo-Schell sources and study their behavior upon free propagation. It will be found that such modes have a universal conical form regardless of the particular function representing the degree of coherence, thus establishing a connection with the subject of circular gratings. This suggests the use of an exponentially decreasing window function on accounting for the finite radius of the grating instead of the Gaussian or rectangular windows typically used when utilizing circular gratings for light concentration (axicons [26]). This leads to the unusual occurrence of the Laplace transform as the proper mathematical tool to study free propagation.
The mode structure changes upon propagation. In the Fresnel region some analytic results can be obtained in closed form whereas, in general, they require numerical evaluation. In the far zone instead the propagation integrals are solved exactly and reveal the nature of the field. Contrary to many far-zone field distributions, which are real (except for simple factors, like curvature or twist-phase functions), we find intrinsically complex disturbances where the connection between real and imaginary parts will be investigated.
2. Mode Evaluation
Pseudo-Schell model sources have a CSD [1] of the form [11]
where (with ) are the position vectors of two arbitrary points across the source plane. While the transmission function can depend on the direction of the position vectors, the degree of coherence is assumed to depend only on the difference of the radial distances of the two points from the origin.
Whatever the specific form of the degree of coherence across the source we can assume that a Fourier expansion
holds. The degree of coherence is genuine if is non-negative [27]. This amounts to saying that we can always assume the field associated to to be the superposition of uncorrelated fields (pseudomodes) [28] belonging to a continuous family with conical wavefronts of the form
with real . The CSD associated to a single pseudomode (3) is
and, of course, specifies a coherent contribution [1]. The universal structure of the modes (3) for all pseudo-Schell model sources gives to such modes a peculiar importance. Hence it is of interest to study their features.
The right-hand side of Equation (3) can be read as the transmission function of a circular phase grating with constant radial period. This kind of object, as well as its variations, has been studied in numberless papers, which began almost a century ago and kept appearing up to the present (for a sample through decades see [26,29,30,31,32,33,34,35,36,37,38]).
Since modes (3) have a diverging norm an important role is played by the windowing function appearing in Equation (1) for which from now on a dependence on will be assumed. The need of a windowing function has been faced in various ways, a frequent choice in the literature being a Gaussian filter. Often the propagation integrals had to be treated numerically. It is to be noted that in previous studies major importance has been given to the near (Fresnel) region. This is because that is the region where energy concentration around the z-axis can occur, which is the aim of axicons [26], one of the most relevant applications of circular gratings. We are ultimately interested instead in coherence propagation, and we shall pay attention to the far-zone where closed form expressions for the propagated disturbance can be derived. Furthermore, in partially coherent light the so-called far-zone is known to be reached at shorter distances from the source than in the case of coherent light [39]. Nonetheless, we devote some space to the near-zone.
As for the windowing function we shall assume a circularly symmetric real decreasing exponential function. Accordingly, the complete field distribution across the source plane has the simple form
where A is a complex amplitude and
with positive and real . This kind of distribution does not seem to have been frequently used in previous research. Yet, in a sense, the real decreasing exponential function is the natural completion of the simple structure. In fact the complete form of Equation (5) shows that the spatial part of the pseudomode is ruled by a single complex number. When we look at Equation (5) as a function of we can generalize it by assuming A to be a function of . Furthermore, since is an analytic function [40], we can assume A to be an analytic function of , too, so that Equation (5) is replaced by an equation of the form
It will be noted that in this view Equation (2) could be replaced by an integral in the complex plane, done along the imaginary axis. In other words, the integral of (2) can be thought of as an inverse Laplace transform [41], i.e., by an integral along a suitable path in the plane. This type of superposition process is well known in coherence theory [28,42] and is mathematically specified in reproducing kernel Hilbert spaces [43]. In the following however, since we shall work at a fixed , we shall simply assume the amplitude to be constant. Then note that we can say the pseudomode to depend only on the angle that characterizes the complex number in the Argand–Gauss plane. The modulus can in fact be modified at will by using a suitable unit of length for r.
Let us begin our analysis about the expression of the propagated field. A relevant question is: does the structure in Equation (7) of the field keep holding upon free propagation? Let us assume the answer is positive. In particular, let us make the hypothesis that the field produced at a plane has the same form of that across the plane , possibly with different parameters. In other words, if the field at is
we assume the field at to be of the form
where and could differ from and , respectively.
Note that since we deal with circularly symmetric functions the two-dimensional Fourier transform goes over the Hankel transform of zero order. The Fourier Transforms (FT) of and , say and , respectively, are deducible from Formula (6.623.2) of [41], which gives
and
Then the FT and are equal to each other, apart from scale and proportionality factors. In fact from Equations (10) and (11) we have
with
Then, the ratio between and can be expressed as
Now, assuming paraxial propagation along the z axis (passing through the center of symmetry of the grating), is the convolution of with the Fresnel wavelet
where is the wavenumber. Then, by virtue of the convolution theorem, and are connected by the relation
where
is the FT of Equation (15).
Accordingly, from Equation (16) we have
Since the functional structures of the right-hand sides of Equations (14) and (18) are different the equality cannot hold for any . Then the hypothesis is false. Therefore, if a wavefront is conical across a certain plane, it cannot be conical in any other plane. Since we have shown that the modes of a pseudo-Schell source must be conical, the property of a partially coherent source of being of the pseudo-Schell model is not preserved during propagation.
3. Mode Propagation in Near Zone
The propagated field at the observation point can be evaluated in the paraxial approximation. Using the Fresnel integral and denoting the radial distance in the source plane by , we have [44]
which is seen to have the form of a (direct) Laplace transform [41]. If read as a function of , V turns out to be an analytic function. This could lead us to deduce some of its properties. Nonetheless, we shall use a more elementary approach.
Some general features can be deduced from integral (19). Note that the and parameters appearing in (see Equation (6)) have a clear physical meaning. In fact, we can let
where L is the decay length of the function and P is the radial period of the phase modulation (the positive and negative sign in corresponding to a converging or a diverging wavefront, respectively). We then give the form
with
and introduce the Fresnel number
In such a way, the integral in Equation (19) takes the form
where the normalized radial coordinates and have been used.
Although in general the integral in Equation (24) cannot be given a closed form, it shows that the shape of the propagated field depends only on two real parameters, namely, the Fresnel number and the ratio between and . As an example, Figure 1 shows the intensity calculated by means of numerical evaluation of Equation (24) at several planes for two different values of the grating periodicity P and a fixed value of the attenuation length L.
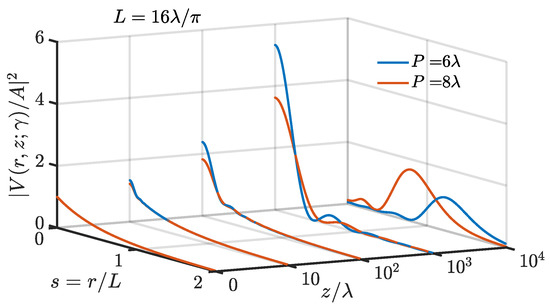
Figure 1.
Evolution of the field. The curves for are multiplied by a factor 100 and their s axis is compressed by a factor 5.
A closed form for the propagated field is obtained if we limit ourselves to points , i.e., points of the z-axis, in which case the propagated field takes the form
Here, for brevity, the unessential phase term has been omitted.
Solving Equation (25) with the aid of Equation (17.13.27) of [41] yields
where Erfc is the complementary error function [41]. Actually, Equation (17.13.27) of [41] would require the quadratic exponent in Equation (25) to include a real negative coefficient. According to symbolic evaluation software codes this condition can be omitted provided that the real coefficient of t in the first exponential function, 1 in our case, is (strictly) >0. As a matter of fact, numerical evaluations of Equation (26) coincide with numerical estimates of the integral (25).
Plots of the axial intensity are shown in Figure 2a (for positive ) and Figure 2b (for negative ) as a function of the normalized coordinate
for several values of .
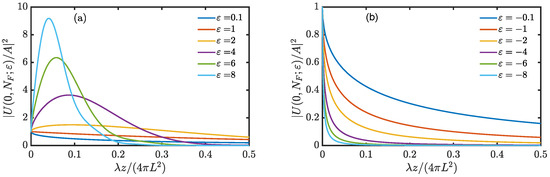
Figure 2.
Axial intensity for (a) positive and (b) negative values of .
Qualitatively different behaviors can be noticed, depending on the sign of . When is positive (Figure 2a), the diffracted wavefronts are inclined toward the z-axis and this produces an intensity increase along the axis itself (principle of axicons). Such an effect cannot be observed when the effective length of the beam (L) is small with respect to the grating period (P), i.e., when tends to zero. Changing sign to the wavefronts are inclined to outside and a drop of intensity is seen, as in Figure 2b (note the change of scale in the vertical axis).
4. Mode Propagation in Far Zone
Let us now pass to the far-zone. Using Equation (19), introducing the dimensionless coordinate, and disregarding proportionality and curvature terms, the far-field can be written as
with
Using Formula (17.13.104) of [41] we find
which corresponds to Equation (10) with different symbols. Equation (30) is fairly simple. At first it could even seem a trivial monotonically decreasing function of R. Actually, since is a complex function, its behavior is far richer than that. We begin by examining the intensity, which, up to a constant, is given by . We then find
Let us discuss the behavior of this expression as a function of R depending on the values of the parameter . When the maximum intensity is reached for , while if , the maximum intensity is reached at .
A few curves of , normalized to its maximum value are shown in Figure 3. Since the horizontal coordinate is proportional to r, the corresponding two-dimensional figures are annular rings (except for the first two values of ), whose radius increases with .
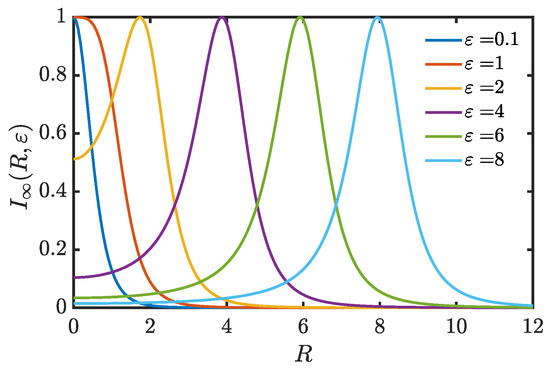
Figure 3.
Far-zone intensity (normalized to its maximum value) for several values of .
Using now physical quantities (L and P) we look at the intensity plots when P is kept fixed and L is varied. (see Figure 4).
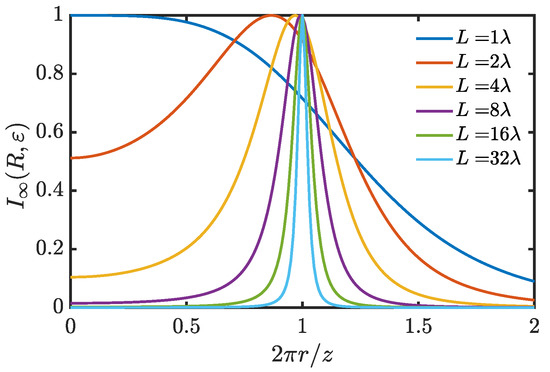
Figure 4.
Far-zone intensity (normalized to its maximum value) for and several values of L.
It is seen that on increasing L, i.e., the grating extent, the curves become slimmer and slimmer. We could think that when L tends to infinity the curve of the far-zone field tends to an (annular) Dirac delta function (use of half-integer order delta functions has been suggested in [35]). A moment’s thought however reveals that this cannot be true. An annular delta in the far-field in fact corresponds in the near-field to a Bessel function of zero order [45] and not to an exponential function as in Equation (7).
For a more complete description let us consider the real and imaginary parts of . We shall limit ourselves to the case in which is much greater than 1. Then, the most significant region for R in Equation (30) is around . Accordingly, we consider the function where . Neglecting and 1 with respect to , Equation (30) can be approximated by
where ± refers to the sign of .
Figure 5 shows the squares of the real and imaginary parts of separately. It is seen that the two functions are symmetrical with respect to the vertical axis. It will be also noted that (provided it is much greater than 1) only determines a proportionality factor, so that the shapes of the curves of Figure 5 do not depend on . It is to be stressed though that their width is to be compared with their mean abscissa, which equals . Hence the two curves become more and more narrow with respect to their mean abscissa when increases.
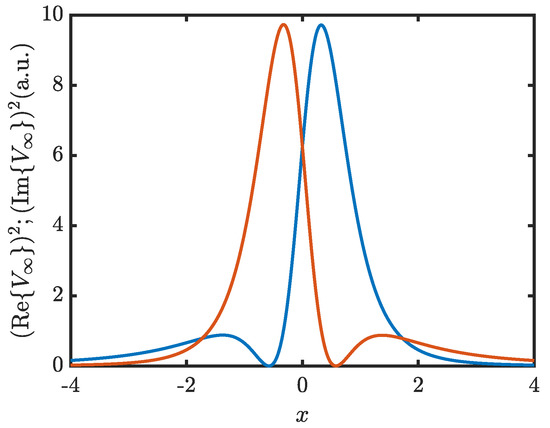
Figure 5.
Squared real (blue) and imaginary (red) parts of for large , in arbitrary units.
For , an interesting feature of the far-zone field is that its squared real and imaginary parts have clearly separated maxima and minima. This opens the way to experiments where the corresponding peaks can be altered in phase thus leading to additive or subtractive combinations. It can be further noticed that if the basic field is replaced by its real (or imaginary) part the same will occur to the far-zone field.
5. Discussion
We found that the modes of pseudo-Schell model sources form a continuous set. Differently from other cases, like that of plane or spherical waves though their analytical structure changes upon propagation until the rather simple asymptotic form of Equation (30) is reached. It could be expected that the latter would take on the form of an annular delta function, but this is not the case because, even for , the squared real and imaginary parts have maxima and minima at different positions.
The occurrence of the Laplace transform in the evaluation of propagated modes was evident even if slightly surprising. At the origin of its appearance there was indeed the kernel (5), but the other key element was the single sided integration domain (), implied by circular symmetry, but readable as a trademark of customary Laplace transform [41]. These elements make it likely that this type of mathematical tool can play a role in several other cases.
Author Contributions
Conceptualization, M.S., R.M.-H., G.P., J.C.G.d.S. and F.G.; Formal analysis, M.S., R.M.-H., G.P., J.C.G.d.S. and F.G.; Funding acquisition, R.M.-H.; Investigation, M.S., R.M.-H., G.P., J.C.G.d.S. and F.G.; Methodology, M.S., R.M.-H., G.P., J.C.G.d.S. and F.G.; Software, M.S., G.P., J.C.G.d.S. and F.G.; Supervision, M.S., R.M.-H., G.P., J.C.G.d.S. and F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Spanish Ministerio de Economía y Competitividad under grant number PID2019 104268GB-C21.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CSD | Cross spectral density |
| FT | Fourier Transform |
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Ponomarenko, S.A. A class of partially coherent beams carrying optical vortices. J. Opt. Soc. Am. A 2001, 18, 150–156. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Chen, Y.; Wang, F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review [Invited]. J. Opt. Soc. Am. A 2014, 31, 2083–2096. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Chen, Y.; Yu, J.; Liu, X.; Liu, L. Generation of Partially Coherent Beams. Prog. Opt. 2017, 62, 157–223. [Google Scholar] [CrossRef]
- Santarsiero, M.; Martínez-Herrero, R.; Maluenda, D.; de Sande, J.C.G.; Piquero, G.; Gori, F. Partially coherent sources with circular coherence. Opt. Lett. 2017, 42, 1512–1515. [Google Scholar] [CrossRef] [PubMed]
- Santarsiero, M.; Martínez-Herrero, R.; Maluenda, D.; de Sande, J.C.G.; Piquero, G.; Gori, F. Synthesis of circularly coherent sources. Opt. Lett. 2017, 42, 4115–4118. [Google Scholar] [CrossRef] [PubMed]
- Hyde, M.W., IV. Controlling the Spatial Coherence of an Optical Source Using a Spatial Filter. Appl. Sci. 2018, 8, 1465. [Google Scholar] [CrossRef]
- Piquero, G.; Santarsiero, M.; Martínez-Herrero, R.; de Sande, J.C.G.; Alonzo, M.; Gori, F. Partially coherent sources with radial coherence. Opt. Lett. 2018, 43, 2376–2379. [Google Scholar] [CrossRef]
- Wu, D.; Wang, F.; Cai, Y. High-order nonuniformly correlated beams. Opt. Laser Technol. 2018, 99, 230–237. [Google Scholar] [CrossRef]
- de Sande, J.C.G.; Martínez-Herrero, R.; Piquero, G.; Santarsiero, M.; Gori, F. Pseudo-Schell model sources. Opt. Express 2019, 27, 3963–3977. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Piquero, G.; de Sande, J.C.G.; Santarsiero, M.; Gori, F. Besinc Pseudo-Schell Model Sources with Circular Coherence. Appl. Sci. 2019, 9, 2716. [Google Scholar] [CrossRef]
- Hyde, M.W. Stochastic complex transmittance screens for synthesizing general partially coherent sources. J. Opt. Soc. Am. A 2020, 37, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Zhu, S.; Chen, Y.; Huang, H.; Li, Z.; Cai, Y. Experimental synthesis of partially coherent sources. Opt. Lett. 2020, 45, 1874–1877. [Google Scholar] [CrossRef]
- Dong, M.; Zhao, C.; Cai, Y.; Yang, Y. Partially coherent vortex beams: Fundamentals and applications. Sci. China Phys. Mech. Astron. 2020, 64, 224201. [Google Scholar] [CrossRef]
- Hyde, M.W. Independently Controlling Stochastic Field Realization Magnitude and Phase Statistics for the Construction of Novel Partially Coherent Sources. Photonics 2021, 8, 60. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Linear Combinations of the Complex Degrees of Coherence. Photonics 2021, 8, 146. [Google Scholar] [CrossRef]
- Li, P.; Yin, Y.; Zhu, S.; Wang, Q.; Li, Z.; Cai, Y. Constructing light with high precision using source coherence. Appl. Phys. Lett. 2021, 119, 041102. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, Y. Trapping two types of particles using a focused partially coherent elegant Laguerre-Gaussian beam. Opt. Lett. 2011, 36, 2251–2253. [Google Scholar] [CrossRef]
- Korotkova, O.; Andrews, L.C.; Phillips, R.L. Model for a partially coherent Gaussian beam in atmospheric turbulence with application in Lasercom. Opt. Eng. 2004, 43, 330–341. [Google Scholar] [CrossRef]
- Ma, L.; Ponomarenko, S.A. Free-space propagation of optical coherence lattices and periodicity reciprocity. Opt. Express 2015, 23, 1848–1856. [Google Scholar] [CrossRef]
- Tong, Z.; Korotkova, O. Beyond the classical Rayleigh limit with twisted light. Opt. Lett. 2012, 37, 2595–2597. [Google Scholar] [CrossRef]
- Liang, C.; Wu, G.; Wang, F.; Li, W.; Cai, Y.; Ponomarenko, S.A. Overcoming the classical Rayleigh diffraction limit by controlling two-point correlations of partially coherent light sources. Opt. Express 2017, 25, 28352–28362. [Google Scholar] [CrossRef]
- Liang, C.; Monfared, Y.E.; Liu, X.; Qi, B.; Wang, F.; Korotkova, O.; Cai, Y. Optimizing illumination’s complex coherence state for overcoming Rayleigh’s resolution limit. Chin. Opt. Lett. 2021, 19, 052601. [Google Scholar] [CrossRef]
- Martínez-Herrero, R.; Santarsiero, M.; Piquero, G.; González de Sande, J.C. A New Type of Shape-Invariant Beams with Structured Coherence: Laguerre-Christoffel-Darboux Beams. Photonics 2021, 8, 134. [Google Scholar] [CrossRef]
- McLeod, J.H. The Axicon: A New Type of Optical Element. J. Opt. Soc. Am. 1954, 44, 592–597. [Google Scholar] [CrossRef]
- Riesz, F.; Sz-Nagy, B. Functional Analysis; Dover Publications: Mignola, NY, USA, 1955. [Google Scholar]
- Martínez-Herrero, R.; Mejías, P.M.; Gori, F. Genuine cross-spectral densities and pseudo-modal expansions. Opt. Lett. 2009, 34, 1399–1401. [Google Scholar] [CrossRef] [PubMed]
- Ronchi, V. Das Okularinterferometer und das Objektivinterferometer bei der Auflösung der Doppelsterne. Z. Phys. 1926, 37, 732–757. [Google Scholar] [CrossRef]
- Dyson, J. Circular and spiral diffraction gratings. Proc. R. Soc. Lond. A 1958, 248, 93–106. [Google Scholar] [CrossRef]
- Tichenor, D.; Bracewell, R.N. Fraunhofer diffraction of concentric annular slits. J. Opt. Soc. Am. 1973, 63, 1620–1622. [Google Scholar] [CrossRef]
- Fedotowsky, A.; Lehovec, K. Far Field Diffraction Patterns of Circular Gratings. Appl. Opt. 1974, 13, 2638–2642. [Google Scholar] [CrossRef]
- Khonina, S.; Kotlyar, V.; Soifer, V.; Shinkaryev, M.; Uspleniev, G. Trochoson. Opt. Commun. 1992, 91, 158–162. [Google Scholar] [CrossRef]
- Friberg, A.T. Stationary-phase analysis of generalized axicons. J. Opt. Soc. Am. A 1996, 13, 743–750. [Google Scholar] [CrossRef]
- Amidror, I. Fourier spectrum of radially periodic images. J. Opt. Soc. Am. A 1997, 14, 816–826. [Google Scholar] [CrossRef]
- Topuzoski, S.; Janicijevic, L. Diffraction characteristics of optical elements designed as phase layers with cosine-profiled periodicity in the azimuthal direction. J. Opt. Soc. Am. A 2011, 28, 2465–2472. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, Y.; Yan, S.; Friberg, A.T.; Kuebel, D.; Visser, T.D. Electromagnetic diffraction theory of refractive axicon lenses. J. Opt. Soc. Am. A 2017, 34, 1201–1211. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Miao, C.; Wu, J.; Zhou, C. Circular Dammann gratings for enhanced control of the ring profile of perfect optical vortices. Photon. Res. 2020, 8, 648–658. [Google Scholar] [CrossRef]
- Gori, F. Far-zone approximation for partially coherent sources. Opt. Lett. 2005, 30, 2840–2842. [Google Scholar] [CrossRef]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Gradshteiin, I.S.; Ryzhik, I.M. Table of Integrals, Series, And Products, 4th ed.; Academic Press: Cambridge, MA, USA, 1965. [Google Scholar]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Gori, F.; Martínez-Herrero, R. Reproducing Kernel Hilbert spaces for wave optics: Tutorial. J. Opt. Soc. Am. A 2021, 38, 737–748. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 6th ed.; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Its Applications; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).