Precise RF Phase Measurement by Optical Sideband Generation Using Mach–Zehnder Modulators
Abstract
:1. Introduction
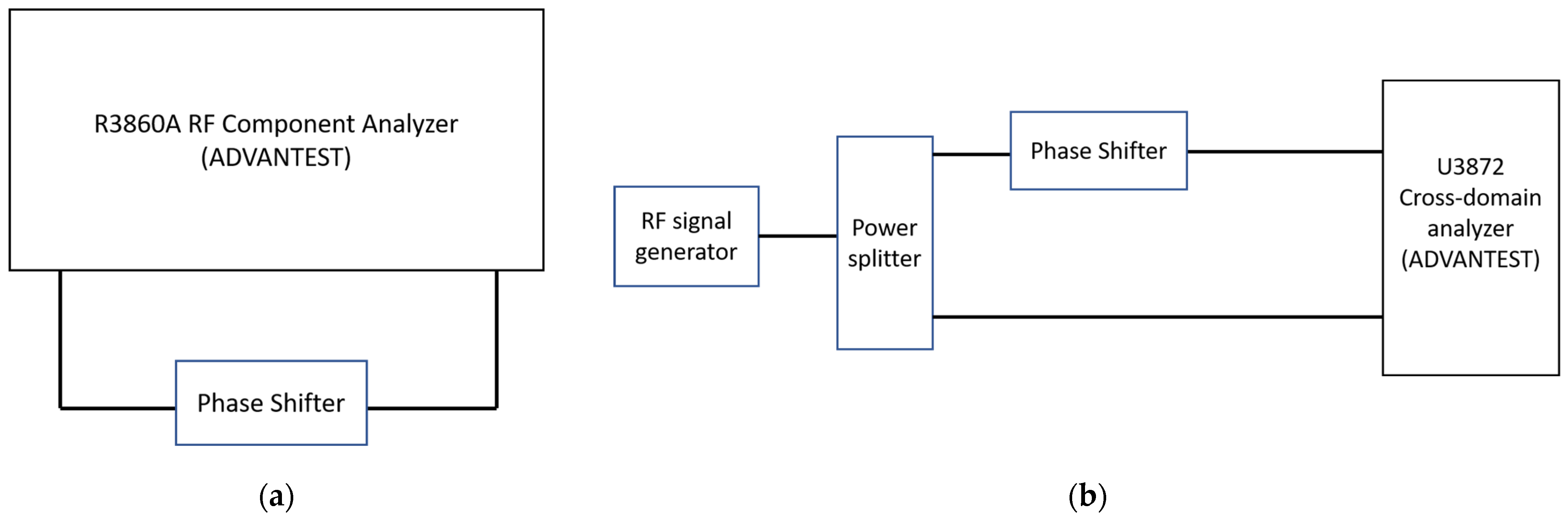
2. Methods
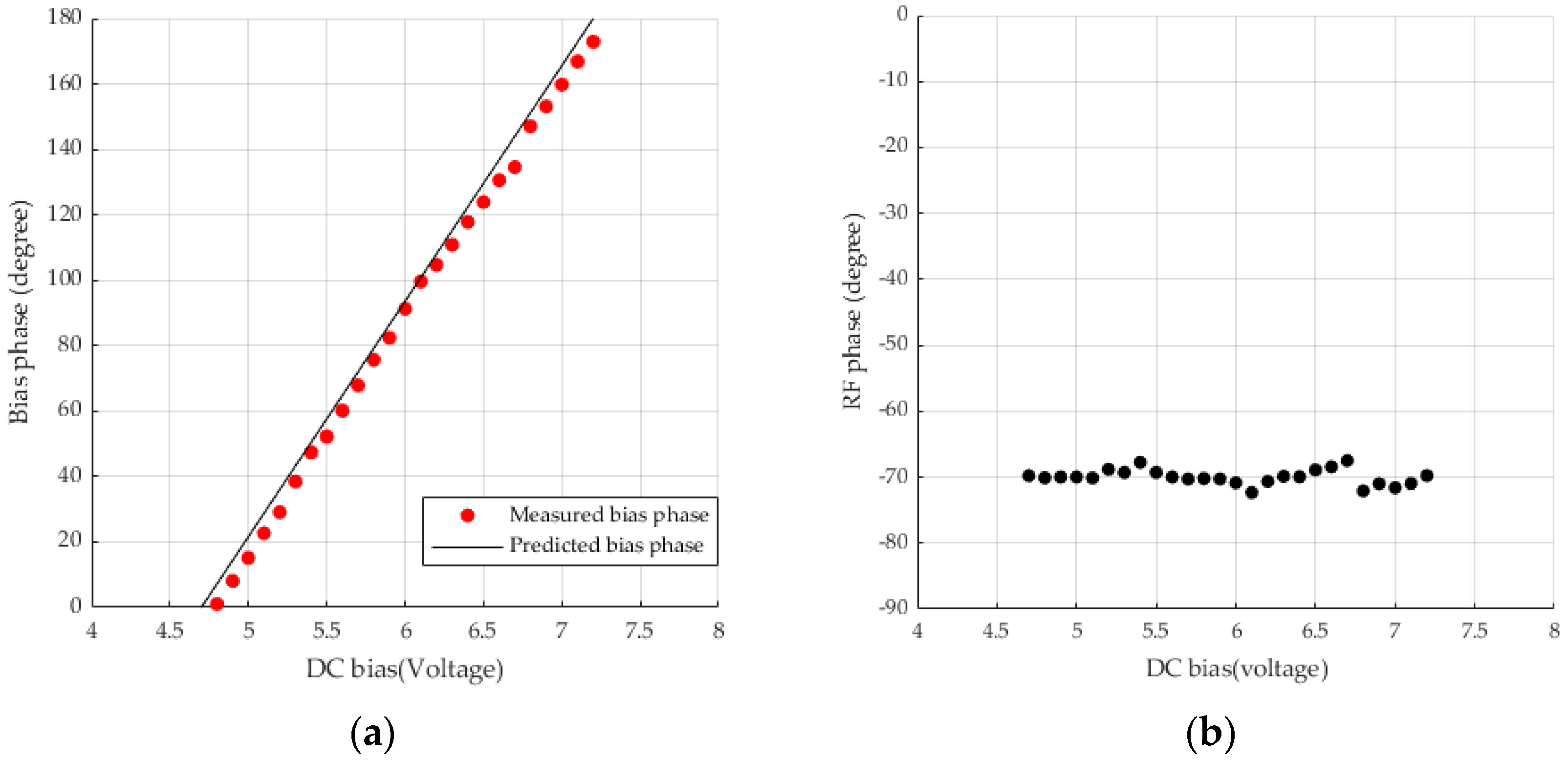
2.1. Characterization of Mach–Zehnder Modulator
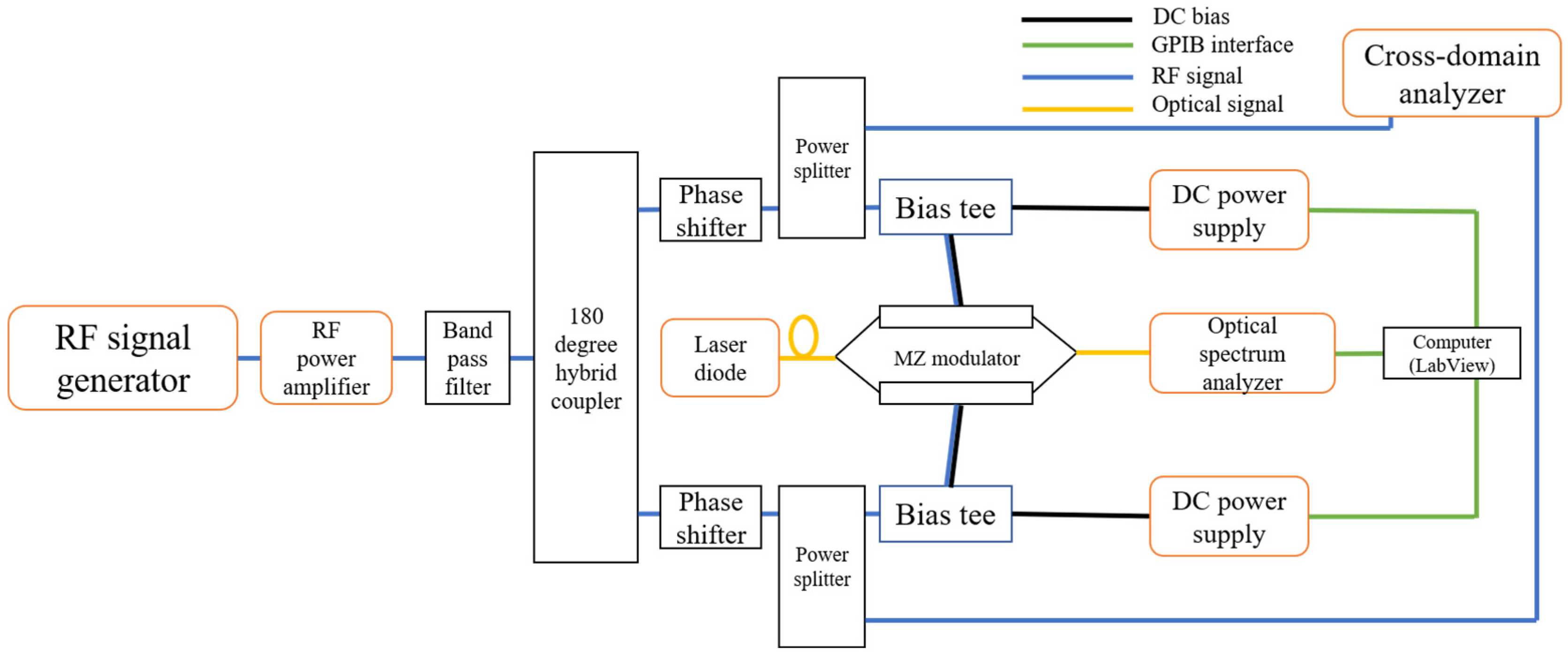
2.2. Experimental Setup
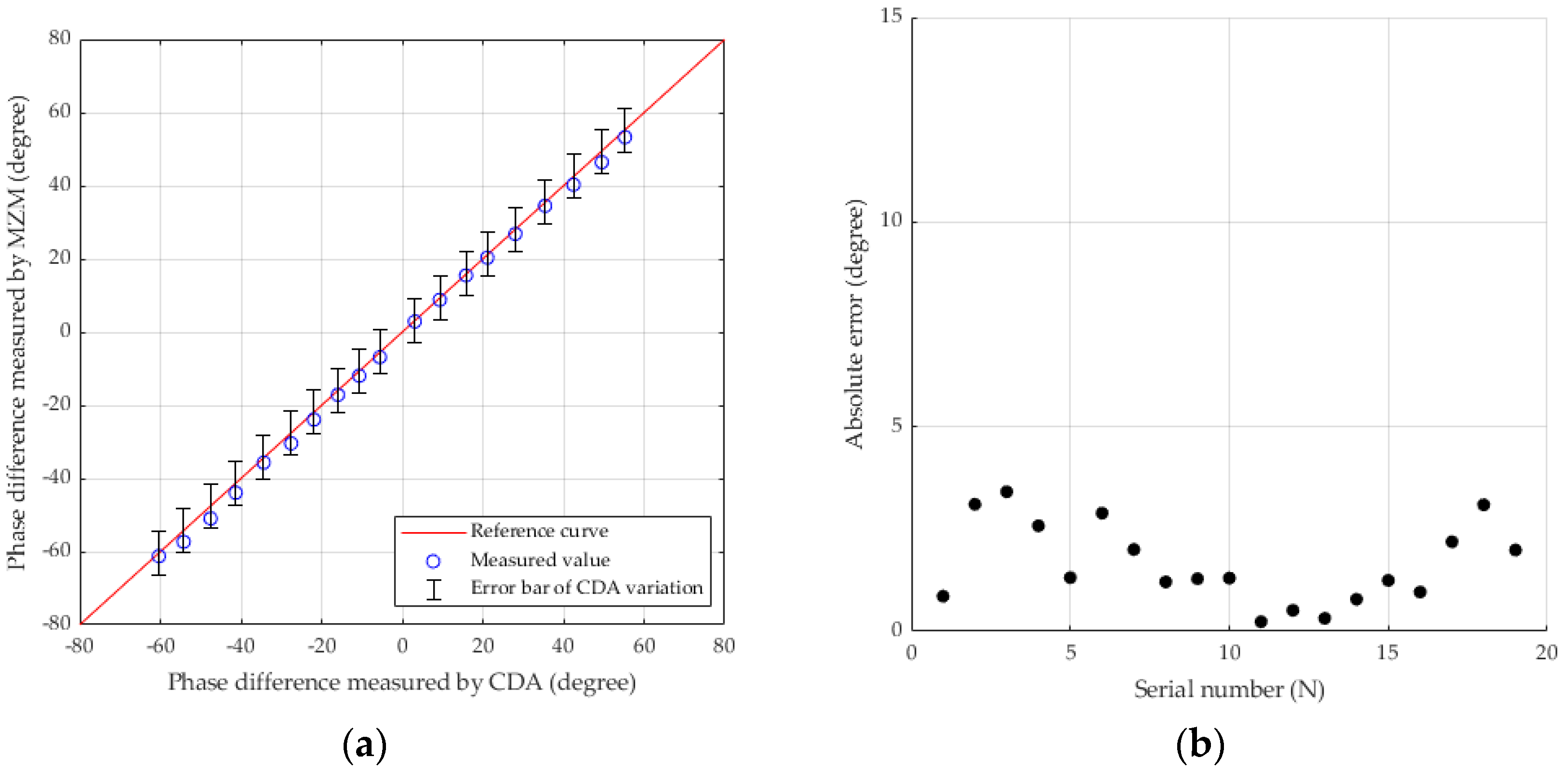
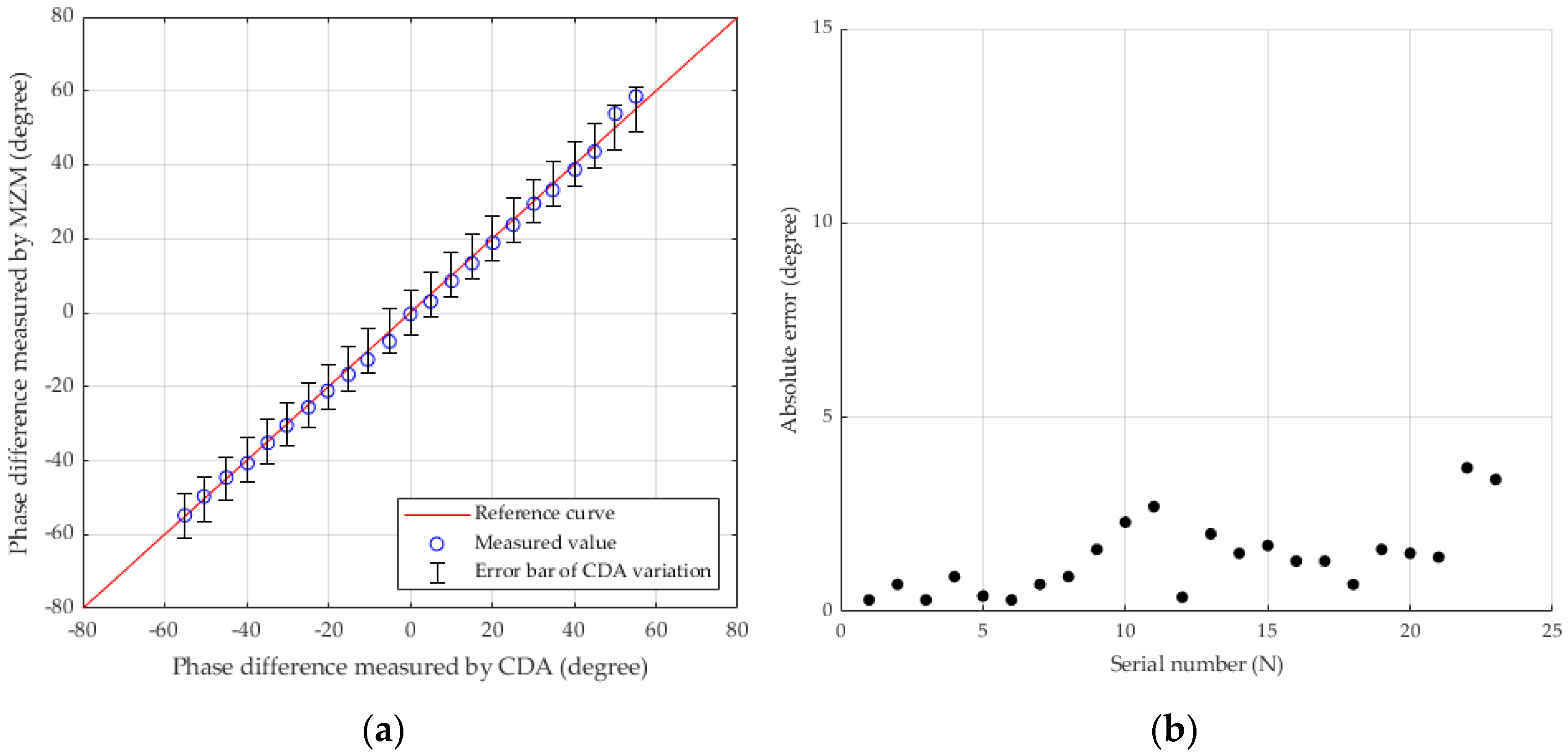
3. Results and Discussion
4. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- RF signal generator: ROHDE & SCHWARZ SMF 100A;
- Optical spectrum analyzer: YOKOGAWA AQ6370N;
- DC power supply: ROHDE & SCHWARZ HMC8043;
- Phase shifter: SAGE 6705K-2;
- Laser diode: YOKOGAWA AQ2211 frame controller with AQ2200-132 grid TLS module;
- Cross-domain analyzer: ADVANTEST U3872.
Appendix B
| Frequency | Phase A to Phase B | Phase B to Phase C |
|---|---|---|
| 12 GHz | ||
| 12.5 GHz | ||
| 13 GHz |
| Frequency | Phase A to Phase B | Phase B to Phase C |
|---|---|---|
| 12 GHz | ||
| 12.5 GHz | ||
| 13 GHz |
| Frequency | Phase A to Phase B | Phase B to Phase C |
|---|---|---|
| 12 GHz | ||
| 12.5 GHz | ||
| 13 GHz |
References
- Succeeded in the World’s First Bidirectional 300 GHz Terahertz Transmission. Available online: https://www.waseda.jp/top/news/81671 (accessed on 25 January 2023).
- Yu, J. Terahertz Signal MIMO Transmission. In Broadband Terahertz Communication Technologies; Springer: Berlin/Heidelberg, Germany, 2021; pp. 99–120. [Google Scholar]
- Amiri, I.S.; Alavi, S.E.; Fisal, N.; Supa’at, A.S.M.; Ahmad, H. All-Optical Generation of Two IEEE802.11n Signals for 2 × 2 MIMO-RoF via MRR System. IEEE Photonics J. 2014, 6, 1–11. [Google Scholar] [CrossRef]
- Raji, Y.M.; Dahawi, T.H.; Yusoff, Z.; Senior, J.M. 60GHZ MIMO-GFDM RoF Over OFDM-PON. In Proceedings of the 2022 IEEE 9th International Conference on Photonics (ICP), Kuala Lumpur, Malaysia, 8–10 August 2022. [Google Scholar]
- Kawanishi, T.; Sakamoto, T.; Chiba, A. High-speed vectorial lightwave modulation techniques. In Proceedings of the 2008 Digest of the IEEE/LEOS Summer Topical Meetings, Acapulco, Mexico, 21–23 July 2008. [Google Scholar]
- Kawanishi, T.; Kogo, K.; Oikawa, S.; Izutsu, M. Direct Measurement of chirp parameters of high-speed Mach-Zehnder type optical modulators. Opt. Commun. 2001, 195, 399–404. [Google Scholar] [CrossRef]
- Kawanishi, T. Estimation of Parallel Mach-Zehnder Modulators. In Electro-Optic Modulation for Photonic Networks: Precise and High-Speed Control of Lightwaves; Springer: Berlin/Heidelberg, Germany, 2022; pp. 205–211. [Google Scholar]
- Kawanishi, T. Basics of Electro-Optic Modulators. In Electro-Optic Modulation for Photonic Networks: Precise and High-Speed Control of Lightwaves; Springer: Berlin/Heidelberg, Germany, 2022; pp. 62–63. [Google Scholar]
- Hugo, S.C.; Freire; Yamaguchi, Y.; Kawanishi, T. High-Speed Characterization of Parallel Mach-Zehnder Optical Modulators. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019. [Google Scholar]
- U3841/3851/3872—Advantest. Available online: https://www3.advantest.com/documents/11348/146302/catalog_U3841_U3851_U3872_e.pdf/6a412e3e-fcd7-44ed-8ae0-5474865c4fe4 (accessed on 25 January 2023).
- Nagata, H.; Honda, H.; Akizuki, K. Initial bias dependency in dc drift of z-cut LiNbO3 optical intensity modulators. Opt. Eng. 2000, 39, 1103–1105. [Google Scholar]
- AQ2200 Series Multi Application Test System—Yokogawa. Available online: https://cdn.tmi.yokogawa.com/1/2474/files/BUAQ2200-20EN.pdf (accessed on 4 March 2023).
- R3860A RF Component Analyzer—Advantest. Available online: https://scdn.rohde-schwarz.com/ur/pws/dl_downloads/dl_common_library/dl_brochures_and_datasheets/pdf_1/R3860A_R3768_R3770.pdf (accessed on 3 March 2023).

| Modulating Frequency | Absolute Error | Absolute Error (Time Domain) |
|---|---|---|
| 12 GHz | <4 | <0.93 ps |
| 12.5 GHz | <7 | <1.56 ps |
| 13 GHz | <5 | <1.07 ps |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Q.; Kawanishi, T. Precise RF Phase Measurement by Optical Sideband Generation Using Mach–Zehnder Modulators. Photonics 2023, 10, 324. https://doi.org/10.3390/photonics10030324
Huang Q, Kawanishi T. Precise RF Phase Measurement by Optical Sideband Generation Using Mach–Zehnder Modulators. Photonics. 2023; 10(3):324. https://doi.org/10.3390/photonics10030324
Chicago/Turabian StyleHuang, Qingchuan, and Tetsuya Kawanishi. 2023. "Precise RF Phase Measurement by Optical Sideband Generation Using Mach–Zehnder Modulators" Photonics 10, no. 3: 324. https://doi.org/10.3390/photonics10030324
APA StyleHuang, Q., & Kawanishi, T. (2023). Precise RF Phase Measurement by Optical Sideband Generation Using Mach–Zehnder Modulators. Photonics, 10(3), 324. https://doi.org/10.3390/photonics10030324





