Full-Vectorial Fiber Mode Solver Based on a Discrete Hankel Transform
Abstract
:1. Introduction
2. Coupled Set of 1D Wave Equations
3. The Discrete Hankel Transform
4. Transformation of the Differential Operators
- 1.
- 2.
4.1. Transformation of the Bessel Operator
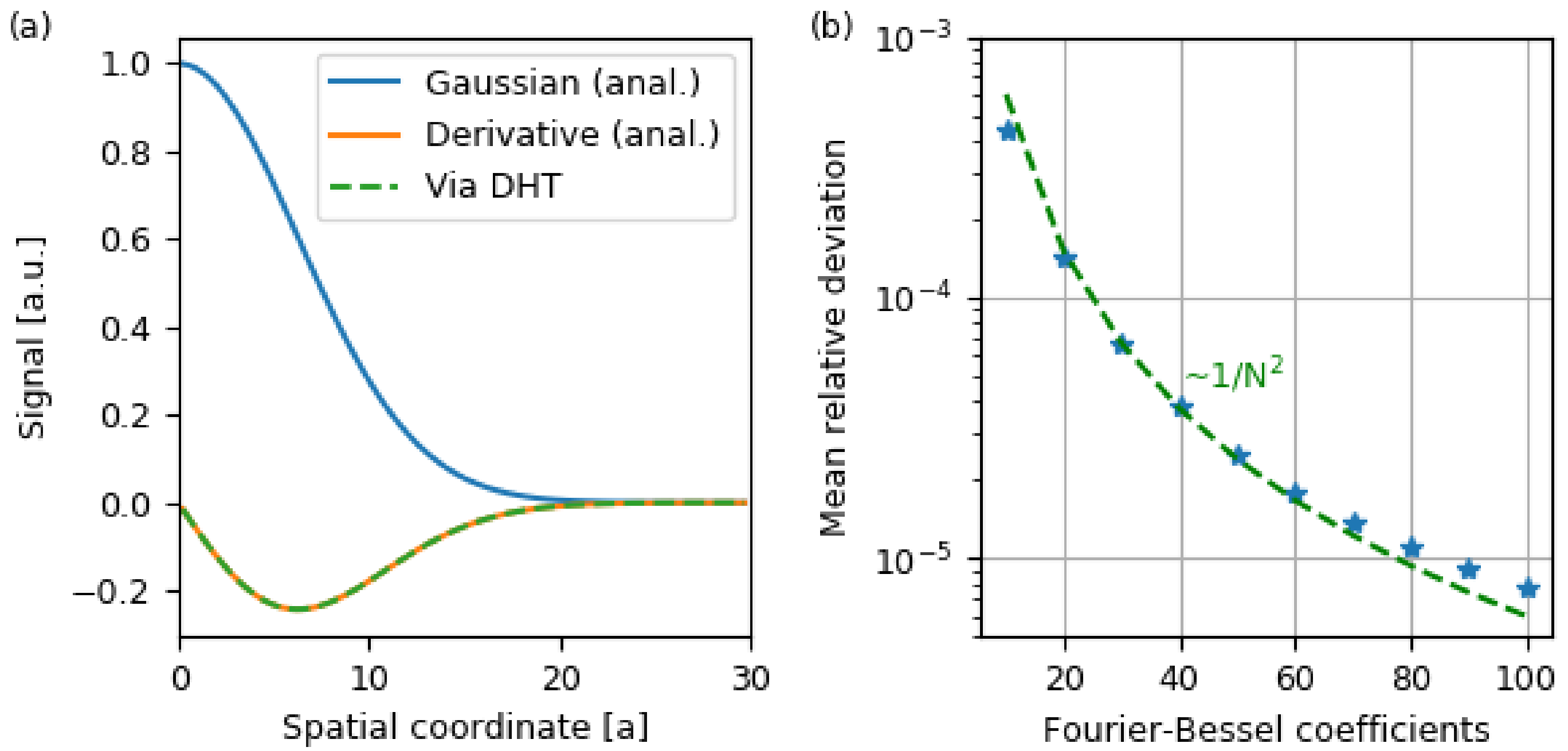
4.2. Transformation of the Derivative Operator
5. Implementation and Validation of the DHT-Based Mode Solver
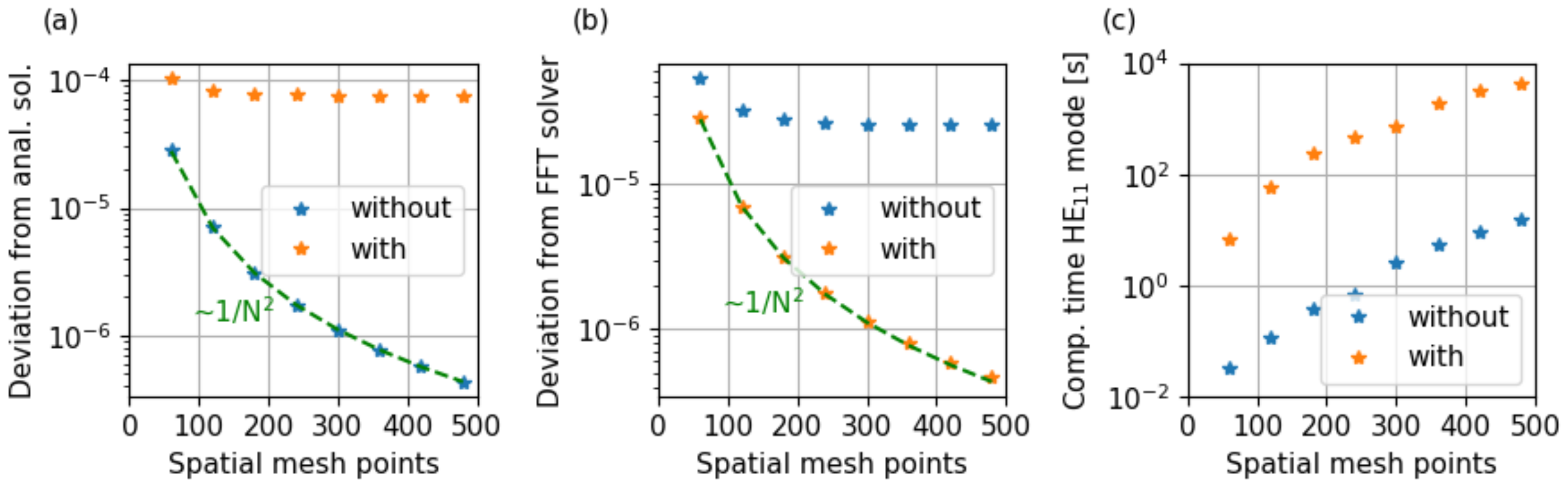
5.1. Step-Index Fiber Design
5.2. Graded-Index Fiber Design
6. Conclusions
7. Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agrawal, G.P. Nonlinear Fiber Optics, 6th ed.; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Hult, J. A Fourth-Order Runge–Kutta in the Interaction Picture Method for Simulating Supercontinuum Generation in Optical Fibers. J. Light. Technol. 2007, 25, 3770–3775. [Google Scholar] [CrossRef]
- Cherif, R.; Zghal, M.; Tartara, L.; Degiorgio, V. Supercontinuum Generation by Higher-Order Mode Excitation in a Photonic Crystal Fiber. Opt. Express 2008, 16, 2147–2152. [Google Scholar] [CrossRef] [PubMed]
- Gnauck, A.; Garrett, L.; Danziger, Y.; Levy, U.; Tur, M. Dispersion and Dispersion-Slope Compensation of NZDSF for 40 Gb/s Operation Over the Entire C Band. In Proceedings of the Optical Fiber Communication Conference, Baltimore, MD, USA, 7 March 2000; Technical Digest Postconference Edition; Trends in Optics and Photonics; (IEEE Cat. No. 00CH37079). Volume 4, pp. 190–192. [Google Scholar] [CrossRef]
- Cruz-Delgado, D.; Ramirez-Alarcon, R.; Ortiz-Ricardo, E.; Monroy-Ruz, J.; Dominguez-Serna, F.; Cruz-Ramirez, H.; Garay-Palmett, K.; U’Ren, A.B. Fiber-Based Photon-Pair Source Capable of Hybrid Entanglement in Frequency and Transverse Mode, Controllably Scalable to Higher Dimensions. Sci. Rep. 2016, 6, 27377. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wadsworth, W.J.; Birks, T.A. Ultraviolet Four-Wave Mixing in the LP02 Fiber Mode. Opt. Lett. 2013, 38, 3747–3750. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weng, Y.; He, X.; Pan, Z. Space Division Multiplexing Optical Communication Using Few-Mode Fibers. Opt. Fiber Technol. 2017, 36, 155–180. [Google Scholar] [CrossRef]
- Boonzajer Flaes, D.E.; Stopka, J.; Turtaev, S.; de Boer, J.F.; Tyc, T.; Čižmár, T. Robustness of Light-Transport Processes to Bending Deformations in Graded-Index Multimode Waveguides. Phys. Rev. Lett. 2018, 120, 233901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, Z.; Ramachandran, S. Propagation Stability in Optical Fibers: Role of Path Memory and Angular Momentum. Nanophotonics 2021, 10, 209–224. [Google Scholar] [CrossRef]
- He, Z.; Du, J.; Chen, X.; Shen, W.; Huang, Y.; Wang, C.; Xu, K.; He, Z. Machine Learning Aided Inverse Design for Few-Mode Fiber Weak-Coupling Optimization. Opt. Express 2020, 28, 21668–21681. [Google Scholar] [CrossRef]
- Nagel, S.; MacChesney, J.; Walker, K. An Overview of the Modified Chemical Vapor Deposition (MCVD) Process and Performance. IEEE J. Quantum Electron. 1982, 18, 459–476. [Google Scholar] [CrossRef]
- Ingerslev, K.; Gregg, P.; Galili, M.; Ros, F.D.; Hu, H.; Bao, F.; Castaneda, M.A.U.; Kristensen, P.; Rubano, A.; Marrucci, L.; et al. 12 mode, WDM, MIMO-Free Orbital Angular Momentum Transmission. Opt. Express 2018, 26, 20225–20232. [Google Scholar] [CrossRef]
- Wang, Q.K.; Wang, F.X.; Liu, J.; Chen, W.; Han, Z.F.; Forbes, A.; Wang, J. High-Dimensional Quantum Cryptography with Hybrid Orbital-Angular-Momentum States through 25 km of Ring-Core Fiber: A Proof-of-Concept Demonstration. Phys. Rev. Appl. 2021, 15, 064034. [Google Scholar] [CrossRef]
- Wangüemert-Pérez, J.; Molina-Fernández, I.; Luque-Nieto, M. Theory and Operational Rules for the Discrete Hankel Transform. Opt. Quantum Electron. 2004, 36, 285–301. [Google Scholar] [CrossRef]
- Koch, T.B.; Davies, J.B.; Wickramasinghe, D. A Finite Difference/Finite Element Propagation Algorithm for Integrated Optical Devices. In Proceedings of the IEE Colloquium on Integrated Optics, London, UK, 6 June 1989; pp. 14/1–14/12. [Google Scholar]
- Chung, Y.; Dagli, N. An Assessment of Finite Difference Beam Propagation Method. IEEE J. Quantum Electron. 1990, 26, 1335–1339. [Google Scholar] [CrossRef]
- Hu, B.; Sewell, P.; Wykes, J.G.; Vukovic, A.; Benson, T.M. Fourth-Order Accurate Sub-Sampling for Finite-Difference Analysis of Surface Plasmon Metallic Wwaveguides. Microw. Opt. Technol. Lett. 2008, 50, 995–1000. [Google Scholar] [CrossRef]
- Sujecki, S. Arbitrary Ttruncation Order Three-Point Finite Difference Method for Optical Waveguides with Stepwise Refractive Index Discontinuities. Opt. Lett. 2010, 35, 4115–4117. [Google Scholar] [CrossRef]
- Marcuse, D. Solution of the Vector Wave Equation for General Dielectric Waveguides by the Galerkin Method. IEEE J. Quantum Electron. 1992, 28, 459–465. [Google Scholar] [CrossRef]
- Wanguemert-Perez, J.G.; Molina-Fernandez, I. Analysis of Dielectric Waveguides by a Modified Fourier Decomposition Method with Adaptive Mapping Parameters. J. Light. Technol. 2001, 19, 1614–1627. [Google Scholar] [CrossRef]
- Henry, C.; Verbeek, B. Solution of the Scalar Wave Equation for Arbitrarily Shaped Dielectric Waveguides by two-dimensional Fourier Analysis. J. Light. Technol. 1989, 7, 308–313. [Google Scholar] [CrossRef]
- Ortega-Monux, A.; Wanguemert-Perez, J.G.; Molina-Fernandez, I.; Silvestre, E.; Andres, P. Fast-Fourier Based Full-Vectorial Mode Solver for Arbitrarily Shaped Dielectric Waveguides. In Proceedings of the MELECON 2006—2006 IEEE Mediterranean Electrotechnical Conference, Malaga, Spain, 16–19 May 2006; pp. 218–221. [Google Scholar] [CrossRef]
- Baddour, N.; Chouinard, U. Theory and Operational Rules for the Discrete Hankel Transform. J. Opt. Soc. Am. A 2015, 32, 611–622. [Google Scholar] [CrossRef]
- Guizar-Sicairos, M.; Gutiérrez-Vega, J.C. Computation of Quasi-Discrete Hankel Transforms of Integer Order for Propagating Optical Wave Fields. J. Opt. Soc. Am. A 2004, 21, 53–58. [Google Scholar] [CrossRef] [Green Version]
- Johnson, H. An Improved Method for Computing a Discrete Hankel Transform. Comput. Phys. Commun. 1987, 43, 181–202. [Google Scholar] [CrossRef]
- Lehoucq, R.B.; Sorensen, D.C.; Yang, C. ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Yariv, A.; Yeh, P. Optical Electronics in Modern Communications, 6th ed.; Oxford Series in Electrical and Computer Engineering; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Dai, D.; Sheng, Z. Numerical Analysis of Silicon-On-Insulator Ridge Nanowires by Using a Full-Vectorial Finite-Difference Method Mode Solver. J. Opt. Soc. Am. B 2007, 24, 2853–2859. [Google Scholar] [CrossRef]
- Wu, F.; Guo, S.; Ikram, K.; Albin, S.; Tai, H.; Rogowski, R.S. Numerical Analysis of Bragg Fibers Using a Compact 1D Finite-Difference Frequency-Domain Method. Opt. Commun. 2005, 249, 165–174. [Google Scholar] [CrossRef]
- Li, J.; Qu, H.; Wang, J. Photonic Bragg Waveguide Platform for Multichannel Resonant Sensing Applications in the THz Range. Biomed. Opt. Express 2020, 11, 2476–2489. [Google Scholar] [CrossRef] [PubMed]
- Chaisakul, P.; Vakarin, V.; Frigerio, J.; Chrastina, D.; Isella, G.; Vivien, L.; Marris-Morini, D. Recent Progress on Ge/SiGe Quantum Well Optical Modulators, Detectors, and Emitters for Optical Interconnects. Photonics 2019, 6, 24. [Google Scholar] [CrossRef] [Green Version]
- Baddour, N. Discrete Two-Dimensional Fourier Transform in Polar Coordinates Part I: Theory and Operational Rules. Mathematics 2019, 7, 698. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Nallappan, K. Optimization of Hollow-Core Photonic Bragg Fibers Towards Practical Sensing Implementations. Opt. Mater. Express 2019, 9, 1640–1653. [Google Scholar] [CrossRef]
- Ni, W.; Yang, C.; Luo, Y.; Xia, R.; Lu, P.; Hu, D.J.J.; Danto, S.; Shum, P.P.; Wei, L. Recent Advancement of Anti-Resonant Hollow-Core Fibers for Sensing Applications. Photonics 2021, 8, 128. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinke, M. Full-Vectorial Fiber Mode Solver Based on a Discrete Hankel Transform. Photonics 2021, 8, 439. https://doi.org/10.3390/photonics8100439
Steinke M. Full-Vectorial Fiber Mode Solver Based on a Discrete Hankel Transform. Photonics. 2021; 8(10):439. https://doi.org/10.3390/photonics8100439
Chicago/Turabian StyleSteinke, Michael. 2021. "Full-Vectorial Fiber Mode Solver Based on a Discrete Hankel Transform" Photonics 8, no. 10: 439. https://doi.org/10.3390/photonics8100439
APA StyleSteinke, M. (2021). Full-Vectorial Fiber Mode Solver Based on a Discrete Hankel Transform. Photonics, 8(10), 439. https://doi.org/10.3390/photonics8100439




