A Tip–Tilt and Piston Detection Approach for Segmented Telescopes

Abstract

Accurate segmented mirror wavefront sensing and control is essential for next-generation large aperture telescope system design. In this paper, a direct tip–tilt and piston error detection technique based on model-based phase retrieval with multiple defocused images is proposed for segmented mirror wavefront sensing. In our technique, the tip–tilt and piston error are represented by a basis consisting of three basic plane functions with respect to the x, y, and z axis so that they can be parameterized by the coefficients of these bases; the coefficients then are solved by a non-linear optimization method with the defocus multi-images. Simulation results show that the proposed technique is capable of measuring high dynamic range wavefront error reaching 7λ, while resulting in high detection accuracy. The algorithm is demonstrated as robust to noise by introducing phase parameterization. In comparison, the proposed tip–tilt and piston error detection approach is much easier to implement than many existing methods, which usually introduce extra sensors and devices, as it is a technique based on multiple images. These characteristics make it promising for the application of wavefront sensing and control in next-generation large aperture telescopes.

1. Introduction

In the past, the aperture size was the main factor that impeded the development of high-resolution telescopes. The segmented mirror scheme paves a new way to designing a very large aperture telescope, achieving diffraction-limited optical imaging. The deployment of the Keck telescope [1,2], in which the primary mirror consists of 36 hexagon mirrors and the diameter reaches 10 m, demonstrated the success of the solution of a segmented mirror in the application of a large aperture telescope. Nowadays, the James Web Space Telescope (JWST) [3,4], the successor of the Hubble Telescope built for deep space exploration, also employs a segmented mirror to design the primary mirror with an advanced accurate control device and algorithm.

Generally, cophasing contains several steps: segment searching, coarse alignment, coarse phasing, and fine phasing [5]. The Jet Propulsion Laboratory (JPL) developed a multi-step stacking process to realize cophasing for JWST based on combined techniques such as phase retrieval and dispersive fringe sensing. The wavefront is calculated by a multiple image-based phase retrieval algorithm [6], then the tip–tilt error is obtained by least-squares fitting with the Hexikes polynomials for each segment. The fine wavefront of the whole aperture is then measured by phase retrieval. Following the cophasing solution developed by JPL, more cophasing techniques were developed during the last decade. In 2013, Fernández-Valdivia et al. developed a tip–tilt detection technique based on the Van Dam and Lane algorithm with two defocus images measured by a geometric sensor [7]. In 2014, Cheetham et al. introduced Fizeau Interferometric Cophasing of Segmented Mirrors, which is capable of phasing mirror segments to interferometric precision without involving exceptional hardware in order to realize fine cophasing of the JWST with a single algorithm [8]. In 2016, Greenbaum et al. developed an in-focus wavefront sensing technique using non-redundant mask-induced pupil diversity for JWST cophasing, without introducing focus diversity [9]. In 2017, Potiron et al. realized the fine cophasing of segmented aperture telescopes based on an analysis scheme to the signal of a Zernike wavefront sensor, which enabled the sensor to retrieve a segment piston and tip–tilt unambiguously [10]. More recently, a focal-plane wavefront sensing technique was proposed for measuring and correcting the low-wind effect [11].

Nonetheless, among existing cophasing techniques, phase retrieval is considered to be one of the best options for wavefront sensing and control for next-generation large aperture telescopes for its high accuracy and simplicity of implementation [12]. Actually, the wavefront sensing with phase retrieval technique has drawn lots of attentions and became more and more mature since the success of its application with the Hubble Telescope aberration detection [13]. Due to its high performance and simplicity, JWST is also mainly based on phase retrieval for accurate wavefront sensing and control. Even though the phase retrieval algorithm developed by JPL has been validated much more robust than the classical phase retrieval techniques such as the Gesrchberg-Saxton (GS) [14] or hybrid input–output (HIO) algorithm [15], by introducing phase diversity [16], simulation has shown that the alternative projecting-based phase retrieval technique requires a very high signal-to-noise ratio (SNR) image to guarantee high accuracy and efficiency; in contrast, the model-based phase retrieval technique seems to be much more accurate and robust to noise in practice [17]. In this paper, we employ a model-based phase retrieval technique [18] to directly detect the tip–tilt error in a segmented mirror without introducing any extra sensor or device such as the abovementioned cophasing techniques. In Section 2, we review the model-based phase retrieval and show the implementation of the non-linear optimization-based phase retrieval algorithm with multiple defocused images for robust and efficient wavefront sensing. In Section 3, we apply the proposed multiple image-based phase retrieval algorithm for tip–tilt and piston detection for a segmented mirror with a basis consisting of three basic planes. In Section 4, the proposed technique is validated by simulation. Finally, we summarize our work in Section 5.

2. Model-Based Phase Retrieval Based on Multiple Defocus Images

The model-based method solves the phase retrieval problem with a parametrized method and optimization algorithm such as the Newton method or Gauss–Newton algorithm. Mathematically, a wavefront can be represented by an orthogonal basis such as Zernike polynomials [19,20], by which a phase can be parameterized so that the phase retrieval problem can be solved by a non-linear optimization method easily. The pupil function can be expressed as

$$P\left(x,y\right)=A·\exp (i{\displaystyle \sum }_{n=1}^N{q}_n·{\mathsf{\Psi }}_n)$$

(1)

where $q=\left(q_1,q_2,\cdots ,q_N\right)$ and $\mathsf{\Psi }={\left({\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2,\cdots ,{\mathsf{\Psi }}_N\right)}^T$ are a coefficient vector and an appropriate polynomial basis vector, respectively. According to diffraction theory, the formed image in the focal plane can be represented by

$$G\left(u,v\right)={\left|F\left[P\left(x,y\right)\right]\right|}^2$$

(2)

where $F$ denotes Fourier transformation. Based on the least-squares estimation method, the objective function with respect to $q$ can be written as

$$E\left(q\right)={\displaystyle \sum }_j^L{\{{\left|F\left[P\left(q\right)\right]\right|}_j^2-I_j\}}^2, j=1,2,\cdots ,L$$

(3)

where $I$ denotes the image measured by the detector, $j$ is the index of the pixel, and $L$ denotes the length of the data points.

In practice, the single image-based phase retrieval methods are very easy to stagnate and cannot guarantee global convergence. To avoid this problem, multiple images can be introduced, e.g., defocus images. Figure 1 shows the principle of multiple defocus image-based phase retrieval. It uses not only the focal plane image, but also several extra diverse images, i.e., defocused images. In this case, Equation (1) is rewritten as

$$P\left(x,y\right)=A·\exp (i{\displaystyle \sum }_{n=1}^N{q}_n\cdot {\mathsf{\Psi }}_n+\varphi )$$

(4)

where $\varphi$ denotes the introduced known diverse phase. For defocus diversity, the introduced phase can be approximated with the following:

$$\varphi =\pi \Delta z\frac{\left(x^2+y^2\right)}{\lambda f^2}$$

(5)

where $\lambda$ is the wavelength of the light, $\Delta z$ is the defocus distance, and $f$ is the focal length of the lens. As more images are utilized, the algorithm becomes much more effective and robust. Assuming $M$ images are used, then the total error can be written as

$$E=E_1\left(q\right)+E_2\left(q\right)+\cdots E_M\left(q\right)$$

(6)

Theoretically, minimizing the above objective function results in an optimal solution that satisfies Equation (2), with which the phase can be reconstructed with the corresponding basis. Basically, the minimization problem can be solved by existing non-linear optimization methods. However, many existing non-linear optimization techniques are very easy to stagnate due to the serious nonlinearity of the phase retrieval problem. We here employed the Levenberg–Marquardt (LM) algorithm, which is theoretically intended for solving least-squares problems and has been demonstrated as more accurate and robust to noise than a Fourier iteration method such as the Modified GS algorithm [17].

Assuming the least-squares based objective function is represented as

$$E\left(q\right)=r{\left(q\right)}^{T}r\left(q\right)={\displaystyle \sum }_j^L{r}_j^2\left(q\right)$$

(7)

where $j=1,2,\cdots ,L$ denotes the index of data points and $q=\left(q_1,q_2,\dots ,q_N\right)$, $r$ denotes the difference between the estimated result by the model function and the observed data, the iterative formula of the LM algorithm [21] can be written as

$$q_{k+1}=q_k-{\left(J^{T}J+\mu \Lambda \right)}^{-1}\cdot g_k$$

(8)

where $k$ denotes the index of iteration. The gradient with respect to the objective function is written as $g\left(q\right)=J{\left(q\right)}^{T}r\left(q\right)$, and the Jacobian matrix is defined as

$$J\left(q\right)=\left[\begin{array}{ccc}\frac{\partial r_1}{\partial q_1}& \cdots & \frac{\partial r_1}{\partial q_N}\\ ⋮& \ddots & ⋮\\ \frac{\partial r_L}{\partial q_1}& \cdots & \frac{\partial r_L}{\partial q_N}\end{array}\right]$$

(9)

For model-based phase retrieval problems, the residual error is written as $r=G\left(q\right)-I$, where $G\left(q\right)$ is the image calculated by Equation (2), and the partial derivative of $r$ with respect to $q$, i.e., the column vector in the Jacobian matrix, can be derived easily as

$$\begin{array}{ll}\frac{\partial r\left(q\right)}{\partial q}& =\frac{\partial \left[G\left(q\right)-I\right]}{\partial q}\\ & =\frac{\partial \left[F\left(P\right)F^{*}\left(P\right)\right]}{\partial q}\\ & =\frac{\partial \left[F\left(P\right)\right]}{\partial q}{F}^{*}\left(P\right)+F\left(P\right)\frac{\partial \left[F^{*}\left(P\right)\right]}{\partial q}\\ & =F\left(P·i\mathsf{\Psi }\right)F^{*}\left(P\right)+F\left(P\right)F^{*}\left(P·i\mathsf{\Psi }\right)\end{array}$$

(10)

with which LM can be implemented easily.

As mentioned above, single image-based phase retrieval usually suffers from the stagnation problem, especially for large dynamic range phase retrieval. Therefore, more images usually are introduced to improve robustness in practice, and the most convenient way would be to employ defocus images. We introduced a simple multi-LM algorithm to solve the phase retrieval problem with multiple defocus images. Namely, each LM algorithm calculates the parameter $q$ with an image independently and the results are then combined with a weighting technique to guarantee global convergence.

Assuming that $M$ defocused images are taken for phase retrieval by the proposed multi-LM algorithm, we propose an effective weighting technique as follows: First calculate the weight for each calculated parameter vector $q_m$ as

$$w_m=\frac{{\epsilon }_m^{\gamma }}{{{\displaystyle \sum }}_{m=1}^M{\epsilon }_m^{\gamma }}$$

(11)

where ${\epsilon }_m$ is a quantity used for calculating the weighting value, and $\gamma$ is the constant controlling the penalty degree. The simplest way to determine the weight for each resulting parameter by LM algorithm is to use the residual error calculated by each LM as $\epsilon$. However, the calculated images by algorithm may not match the measured ones in amplitude, which could result in faulty weight. To avoid this problem, we introduced the maximum of correlation between two images, which is written as

$$\epsilon =\max \left(I_{Est}\otimes I_{Det}\right)$$

(12)

where $I_{Est}$ is the image estimated by the algorithm, $I_{Det}$ denotes the detected image, and $\max$ means taking the maximum of the correlation map between two images. The correlation map could be calculated by a general image correlation technique, such as Pearson coefficients, but we employed cosine similarity, which can be calculated by fast Fourier transformation (FFT) for the sake of efficiency. In this case, the value $\gamma =2$ is good option empirically. When the value of all weights are determined, $q_k$ is updated as

$$q_{k+1}={{\displaystyle \sum }}_{m=1}^M{w}_m{q}_{k+1}^m$$

(13)

The principle of the algorithm is be described in Figure 2. The algorithm contains two loops: the inner loop and outer loop. In the inner loop, each LM algorithm calculates $q$ independently with a common input, i.e., $q_k$. Then the results output by all LM algorithms are combined to generate $q_{k+1}$ in the outer loop. This process is repeated until the stop condition is satisfied.

3. Model-Based Tip–Tilt and Piston Detection for Segmented Mirror

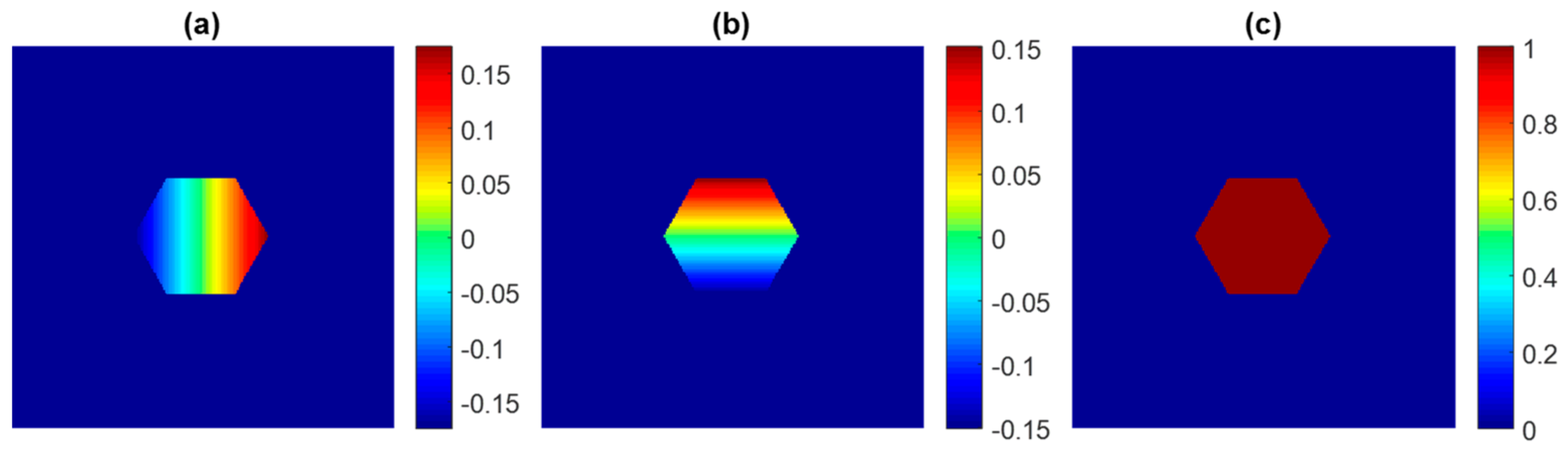
In practice, there are many forms of segmenting that actually share similar modeling in analysis. For simplicity, we took the hexagon segmented mirror, one of the most popular segmenting fashions. In the case of hexagon segmented mirror wavefront sensing, let us just consider tip–tilt and piston phase error retrieval. In this case, each segment of the phase can be represented as

$$\psi \left(a,b,c\right)=aX+bY+cZ$$

(14)

where $X$, $Y$, and $Z$ are the normalized bases of each phase segment, which are just as Figure 3 shows, and $a,b$, and $c$ are their respective coefficients. $X$ and $Y$ are defined by planes $x-z=0$ and $y-z=0$, respectively, and $Z$ is defined by plane $z=1$, with the support defined by a segment.

As there is no overlap between segments, the phase of the whole mirror is the sum of the phase of all segments. Thus, the whole wavefront can be written as

$$\mathsf{\Theta }\left(a,b,c\right)={\displaystyle \sum }_{n=1}^N\theta \left(a_n,b_n,c_n\right)$$

(15)

where $n$ is the index of the segment, $N$ is the total amount of segments, and $\left(a,b,c\right)$ is the vector of $\left[a_1,a_2,\cdots a_N,b_1,b_2,\cdots b_N,c_1,c_2,\cdots c_N\right]$, which contains all the parameters to be solved. From the above formula, it can be seen that the function of each segment has three parameters, and there are $3N$ parameters in total for the whole mirror that need to be calculated. Similar to Equation (3), the objective function for the case herein can be written as

$$E\left(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\right)={\displaystyle \sum }_{j=1}^L{\left[G\left(\psi \right)-I\right]}_j^2$$

(16)

$$={\displaystyle \sum }_{j=1}^L{\left(F^2\left[A·\exp \left(i\theta \left(a,b,c\right)\right)\right]-I\right)}_j^2$$

(17)

where $I$ denotes the image measured by the detector, and the sum is applied to all pixels with index $j$. Obviously, the process of solving Equation (17) is just the same as the case of model-based wavefront sensing analyzed above. Similar to the popular Zernike polynomial-based parameterized technique, a set of bases, i.e., the segmented tip–tilt and piston, is used to parameterize the wavefront of the whole segment mirror here. Therefore, the tip–tilt and piston error sensing for a segmented mirror also can be calculated like a general model-based phase retrieval algorithm with high accuracy.

4. Simulation

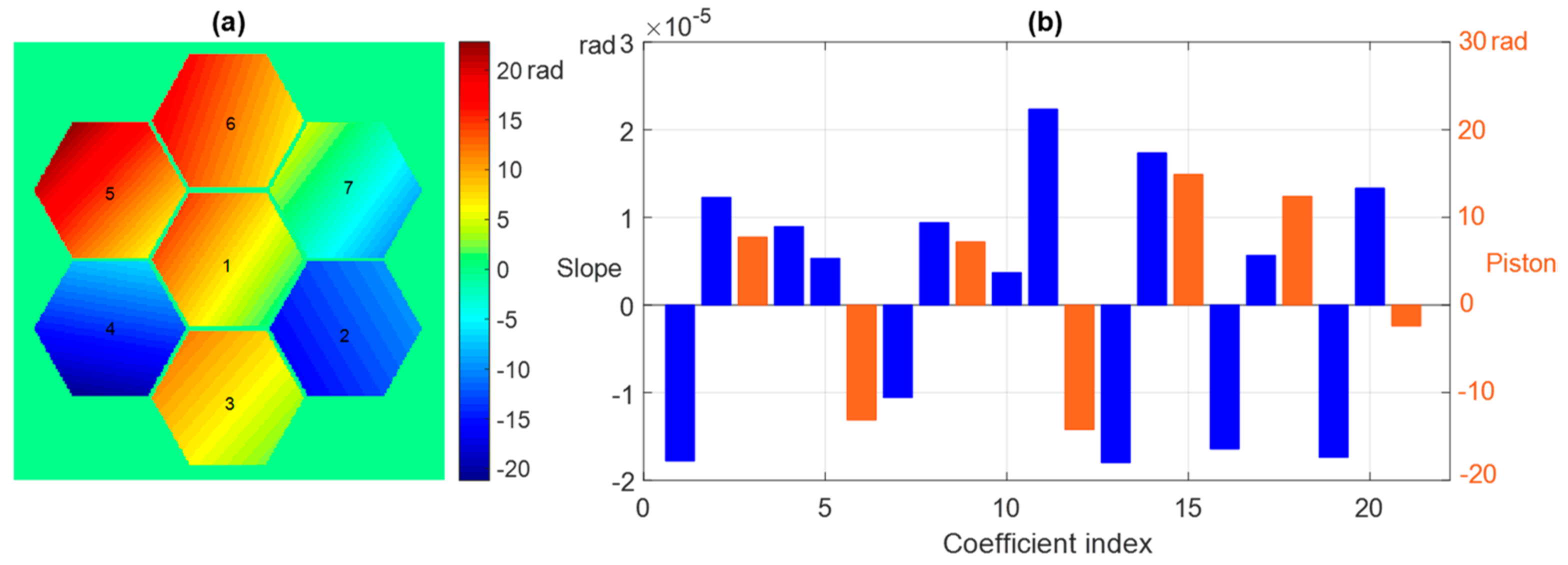
We validated the proposed algorithm by simulation with the case of hexagon segment mirror tip–tilt error detection. The ground truth wavefront and corresponding coefficients are just as Figure 4 shows. In this segmented mirror phase retrieval simulation, we consider a segmented mirror with 7 segments, just as Figure 4a shows. 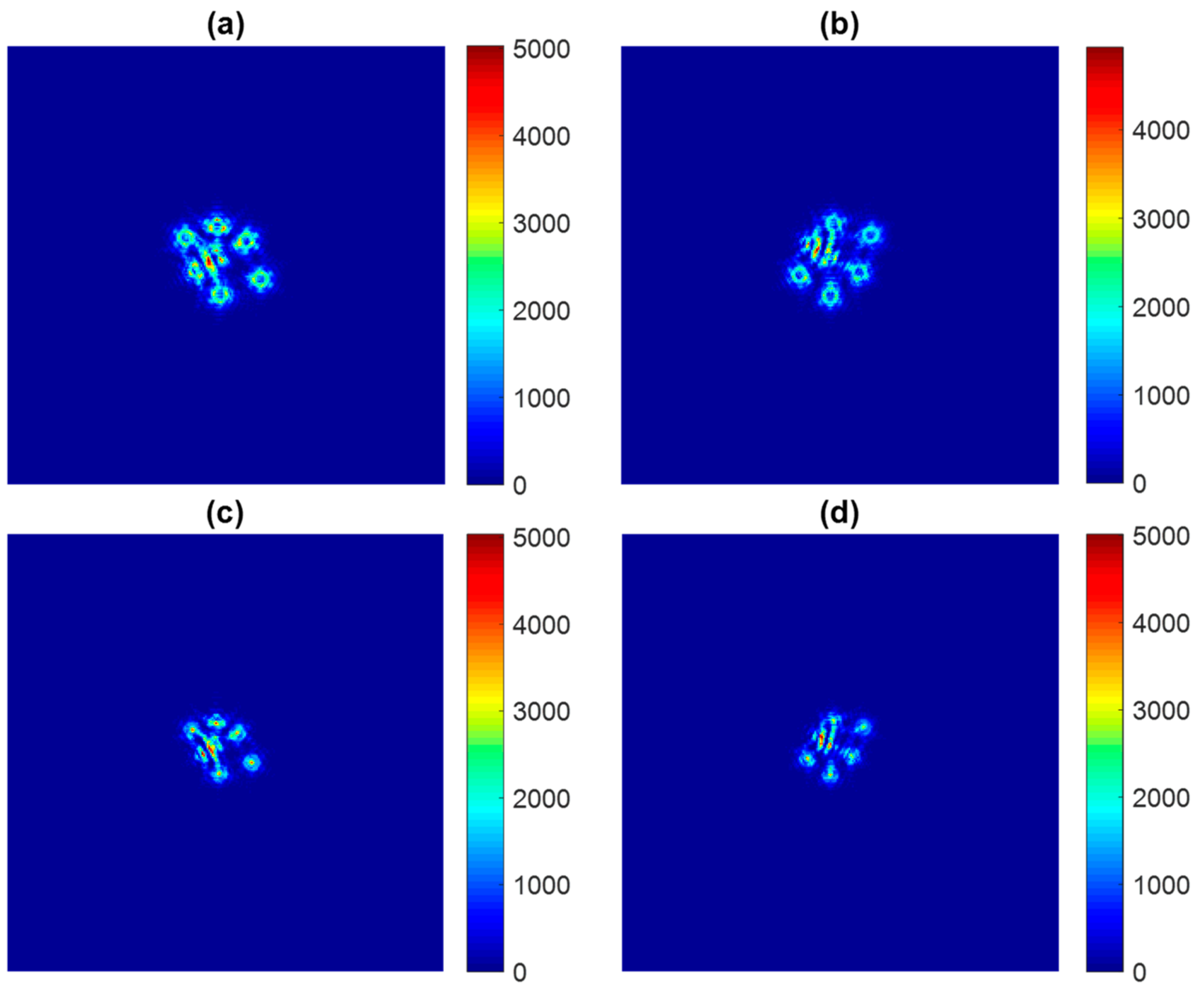The peak-to-valley (PV) value of the whole wavefront was set to 7$\lambda$, which contained tip–tilt error and piston error, just as Figure 4b shows. The slope and the piston error of each segment was generated randomly. Four out-of-focus images were simulated based on the model represented by Equation (2). Poisson noise was applied to all image data; the noisy images used for simulation are just as Figure 5 shows.

We then used our algorithm to retrieve the tip–tilt and piston error from the measured images shown in Figure 5, for which the image SNR was 30 dB on average. The simulation was implemented on the general computer without graphic card acceleration; the computer configuration was i7-6700HQ [email protected], 16 G RAM, 64-bit Windows 10 OS, and the platform for algorithm coding and testing was based on MATLAB R2018b. As Poisson noise is the dominant noise in modern digital cameras [22], it was applied to all simulated images for testing the algorithm’s performance, such as the efficiency and robustness to noise.

Figure 6 shows the performance of the proposed phase retrieval algorithm when used to retrieve the tip–tilt and piston error of the segmented mirror shown in Figure 4. The simulation shows very accurate results in tip–tilt error, but a completely different result in piston error. In fact, due to the 2$\pi$ ambiguity problem, the piston cannot be determined uniquely when the PV is larger than one wavelength for the image-based phase retrieval algorithm. Therefore, the phase retrieval method based on intensity can only retrieve the real piston error within one wavelength. Nonetheless, it shows that the proposed algorithm is still valuable for direct accurate tip–tilt and piston error detection without introducing extra complex sensors or devices, based on the result of the coarse cophasing step, in which the large initial tip–tilt and piston error is usually effectively corrected by another technique. Actually, combining the proposed image-based wavefront techniques with some existing techniques could be a good choice to realize fast and accurate large dynamic-range cophasing in practice.

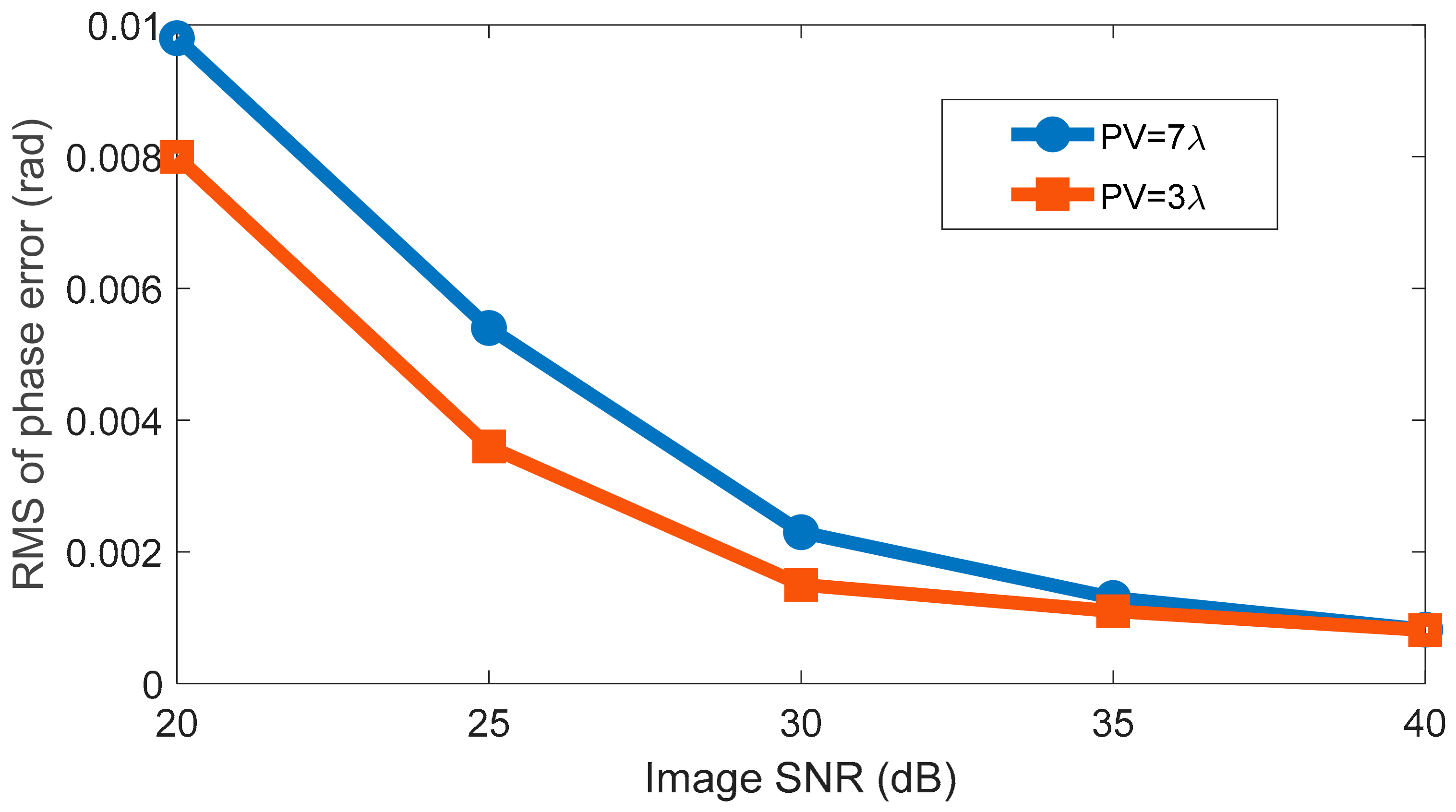
Figure 7 shows the performance of the proposed phase retrieval algorithm to noise. It shows that the wavefront error decreased with the increasing of image SNR. The retrieved wavefront was quite accurate even for low image SNR; for the image with SNR = 30 dB, which corresponds to a gray level of several thousand—a quite general signal amplitude level in practice—the resulting root mean square (RMS) of the wavefront already reached about 0.2% radian. This denotes that the model-based phase retrieval technique is able to achieve very high accuracy for wavefront sensing. It also shows that the lower dynamic range (PV $\le 3\mathsf{\lambda }$) resulted in higher accuracy, but the difference of resulting accuracies between the high dynamic range and the low dynamic range were not large, which indicates that noise level is the main factor that impacts accuracy. Therefore, the image SNR should be as high as possible to guarantee high performance wavefront sensing in practice.

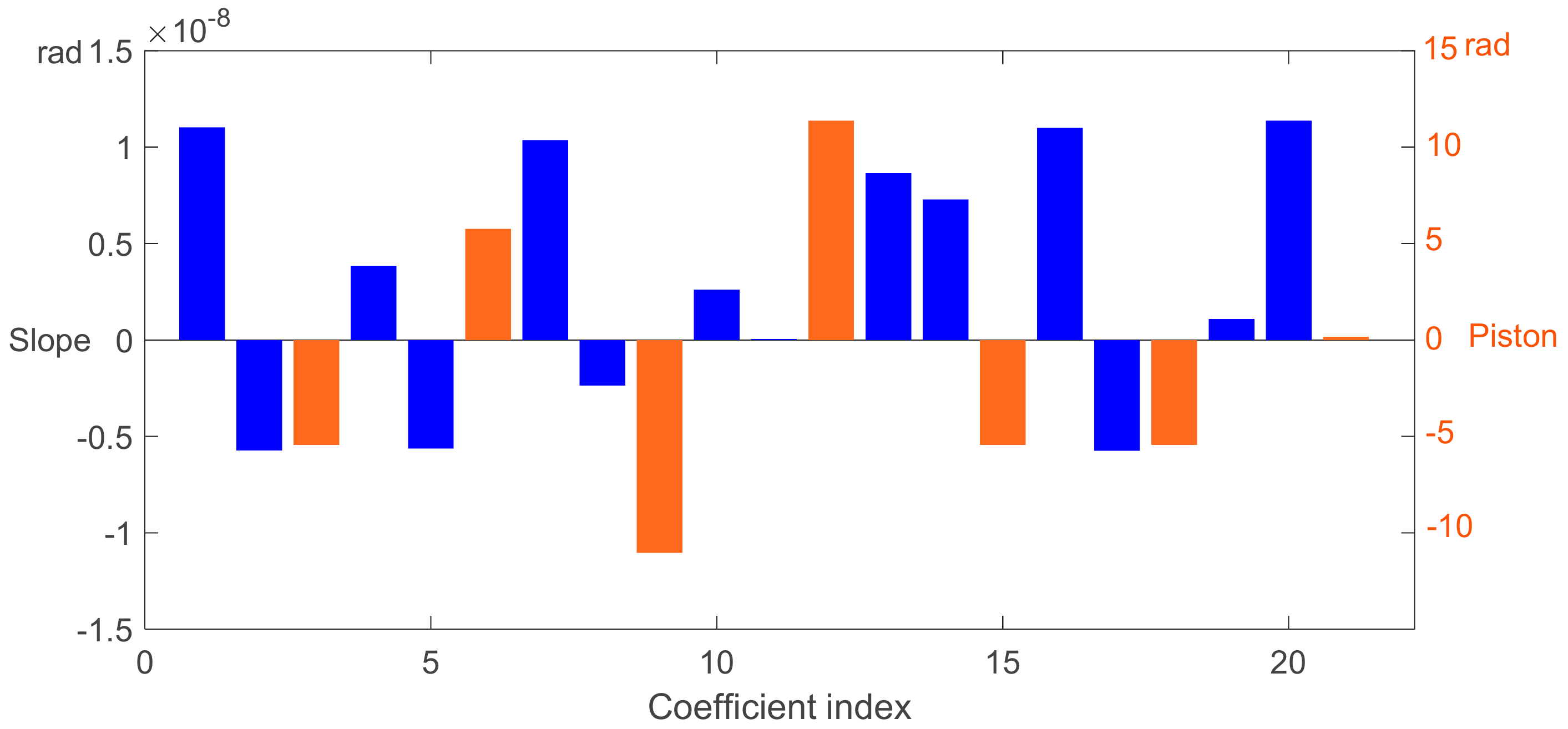
To clearly show the performance of piston detection by the proposed image-based phase retrieval technique, we also implemented simulations on small and large piston sensing. In simulation, all tip–tilt errors were set to zero, i.e., only pistons were taken into consideration. Then the same algorithm was used to calculate the values of all 21 coefficients. The initial value for all parameters was set to zero. Figure 8 and Figure 9 show the simulation results of the piston retrieval by the proposed phase retrieval algorithm.

Figure 8a shows that the piston could be retrieved successfully for small pistons, however, an extra background piston was introduced. This makes sense, since a background piston denotes all segments shift as a whole, namely, there is no relative shifting between them, which has no impact on the imaged Fourier modulus pattern. Figure 8b shows the comparison between the retrieved relative piston and the ground truth relative piston, which shows quite high accuracy. The simulations show that when the piston error was small, the piston errors could be retrieved correctly, otherwise the calculated pistons involved a 2$\pi$ phase ambiguity problem. It was found that the algorithm only worked well for relative pistons lower than half a wavelength with zero as the initial value. In fact, there was no guarantee that the exact piston could be retrieved by an image-based phase retrieval algorithm mathematically; however, for a small piston error with an appropriate initial value, the algorithm was still able to retrieve the real piston successfully.

Figure 9 shows the simulation result in the case of large piston retrieval. Similar to the case of small piston retrieval, the pistons were retrieved quite well. Figure 9a shows that the ground truth piston was quite high, where the PV reached 10$\lambda$, and the retrieved pistons were quite different from the ground truth due to the 2$\pi$ ambiguity problem. The retrieved pistons were constrained within a wavelength of dynamic range.

Even though it suffered from the 2$\pi$ ambiguity problem for large pistons, our simulation shows that the proposed algorithm was still capable of calculating an optimal solution, even for PV higher than 10$\lambda$, with high accuracy. The wrapped retrieved relative pistons were actually the same as those of the ground truth, just as Figure 9b shows. Therefore, the calculated piston value would be useful for large accurate detection within one measurement, combining the result with another piston detection technique, e.g., a piston detection sensor and the technique of sensor fusion. Therefore, it can believed that the proposed technique still has potential for fast, accurate large piston error detection.

5. Discussion

In this article, we proposed a direct tip–tilt and piston error detection approach for a segmented mirror in large-aperture telescope system design. We show that the tip–tilt and piston error can be represented by the combination of three basic plane functions, which are used as the basis for parameterizing the segmented mirror tip–tilt and piston error. The problem then is solved by the well-known LM algorithm with multiple defocus images. The simulation shows that the proposed technique results in accurate tip–tilt error detection, even for a low SNR image, and is able to retrieve a high dynamic range wavefront. Even though a large piston could not be retrieved successfully due to the ambiguity problem for the image-based phase retrieval problem when the PV of the wavefront is higher than one wavelength, it is still very valuable for accurate tip–tilt error detection and small piston detection in application, and we believe that the proposed technique still has potential for fast, accurate large piston detection. The advantage of the proposed phase retrieval algorithm is that it is precise, efficient, and very easy to implement. However, it should be pointed out that the complexity of the proposed algorithm will increase with the increasing of number of segments and the number of the bases used to represent the wavefront of a single segment. As the cost of computing is becoming cheaper and the power of computers is increasing, we believe that the proposed technique is a still a good solution for segmented mirror wavefront sensing with any amount of segments in the future. In future work, we will focus on a fast, accurate piston detection approach with the proposed technique and look for and use more appropriate basis to represent more phase error beyond tip–tilt and piston for each segment.