Abstract
Generally, the diffractive waveguide combiner and computer-generated hologram (CGH) technique have the potential to achieve compact head-mounted display (HMD) with a natural 3D display function. However, the diffractive waveguide combiner will degrade the image quality because of aberration. In order to resolve this issue, the complex analysis based on the ray-tracing method is necessary. Since the major aberration of the waveguide combiners is only astigmatism and anamorphic distortion, only these two aberrations were discussed in this paper. Furthermore, two common waveguide structures were discussed here. In total, four formulas were summarized to analyze aberration and anamorphic distortion in these two structures. Finally, the simplified formulas were verified with the commercial ray-tracing software Zemax. The calculated results of the proposed method match the simulation of Zemax software well. Therefore, the aberration of an arbitrary similar diffractive waveguide can be analyzed by the proposed method. This will make the designing process simpler and faster.
1. Introduction
Display technology has been developing for decades. In recent years, the HMD devices have received growing attention [1,2]. The HMDs are suitable to achieve the augmented reality (AR) function due to their portability. Furthermore, the HMDs can provide autostereoscopic images without viewing zone limit. However, the traditional stereoscopic imaging with two 2-D images is possibly causing the vergence–accommodation conflicts [3]. In order to resolve this issue, providing 3D images with depth information is necessary.
The holography technique is an ideal method to project natural 3D images [4]. However, the traditional holography technique records information optically and is difficult to achieve dynamic display function. In contrast, the CGH technique computes the holograms numerically, and makes the recording process become simpler [5,6,7]. Furthermore, the dynamic display function can be achieved by displaying the holograms on a spatial light modulator (SLM). Then, the HMDs with 3D information can be achieved utilizing the CGH techniques [8,9]. Since the general SLM can only modulate amplitude or phase distribution, the phase information or the amplitude information of the hologram must be eliminated. However, the elimination will degrade the image quality. In order to enhance the image quality, the iterative algorithm [10,11] and the complex-amplitude modulation method [12,13,14] were proposed successively.
Excluding the image quality issue, the weight is also an important issue in similar devices. In order to resolve this issue, the devices with waveguide combiner were also proposed [2]. In this method, the light is coupled into the waveguide and propagated inside the waveguide via total internal reflection (TIR) on the waveguide surface. The in-coupler can be a diffraction element or a geometric structure such as prism or wedge etc. Finally, the lights will be guided to the human eye by a diffraction element. The diffraction element of in-coupler or out-coupler could be Raman–Nath grating [15,16] or volume holographic element (VHOE) with Bragg grating [17,18,19]. The advantage of the former is that achieving a wide viewing angle is easier. However, enhancing diffraction efficiency is difficult. The VHOEs can achieve higher diffraction efficiency, but the rigorous angular selectivity will confine the viewing angle. No matter the type, the diffraction waveguides cause the aberration and blur the image. In order to correct the aberration, the aberration has to be analyzed in the waveguides with symmetric [20,21] and asymmetric structures [22]. Concerning the latter, a geometric structure was utilized as the in-coupler to reduce the power loss, and a VHOE was employed as the out-coupler. Both the geometric structure and the diffraction element change the propagation angle of the light along a single direction. It caused serious astigmatism and anamorphic distortion. On the contrary, the former utilized two symmetric VHOEs as the in-coupler and the out-coupler. Since the angle changes caused by two VHOEs are compensated to each other, the astigmatism becomes smaller, and the anamorphic distortion is almost ignorable.
In this paper, we propose a simplified method to analyze astigmatism and anamorphic distortion of the symmetric and asymmetric structure. When the specification of the waveguides and the diffraction angle of the normal incident ray on the HOE are known, astigmatism and anamorphic distortion can be calculated easily. According to the literature, the waveguides caused aberration in only one direction. The aberration for the different field perpendicular to this direction is almost constant. Considering the viewing angle of the current SLM devices, the proposed method was simplified based on the paraxial approximation. In the following sections, the symmetric and asymmetric structures similar to [21,22] were utilized to verify the proposed method. If the diffractive efficiency is not considered, the diffraction behavior of Raman–Nath grating and VHOE is the same. Therefore, the diffraction grating formula was employed to replace H. Kogelnik’s coupled wave theory. It makes the proposed formulas simpler. Furthermore, the formulas are also available for Raman–Nath grating—not only for VHOE.
2. Materials and Methods
The schematic diagrams of the holographic waveguide element were shown in Figure 1. The SLM provided object information, and the holographic waveguide combiners guide the information to the human eye, then the observer can obtain virtual images. The symmetric structure as shown as Figure 1a utilized two HOEs to couple optical information in and out the waveguide. The asymmetric structure as shown as Figure 1b utilized a wedge with a polished surface as an in-coupling surface and a HOE as an out-coupling element. The HOEs in these two structures are linear gratings in which the grating vectors are parallel to the x-axis. Since the diopter of the HOEs and the wedge in x-direction and y-direction is different, the waveguide element will cause astigmatism. Therefore, the human eye obtains astigmatism virtual images when the SLM provides aberration-free objects. On the other hand, the astigmatism objects will be obtained when the light of aberration-free images incident the out-coupling HOE inversely. Then, the device can provide images without aberration when the astigmatism objects are produced by the SLM.
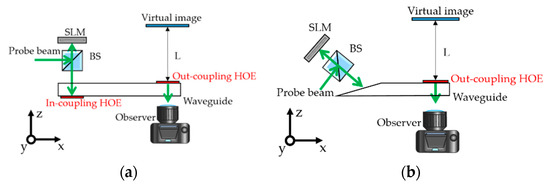
Figure 1.
The schematic diagrams of the holographic waveguide element: (a) symmetric waveguide structure; (b) asymmetric waveguide structure.
When the light of a virtual image was coupled into the waveguide at the Out-coupling HOE, the field curvature curve of the object is shown in Figure 2. The distance from the out-coupling HOE to the virtual image L is 250 mm. The diffraction angle for the normal incident light is 50 degrees. The tilt angle of the wedge-shape in Figure 1b is 17.7 degrees. The field curvature curves as shown in Figure 2 were simulated via the commercial ray-tracing software Zemax. The horizontal and vertical axis marks the viewing angle and the distance respect to the last surface of combiners, separately. The red curve shows the position of the imaging points in the y-z plane (Tangential plane), and the black one shows that in the x-z plane (Sagittal plane). The distance of black lines became shorter because of the holographic waveguides. The red lines in the two structures were located at the same distance because the holographic waveguide changed the effective distance for x fan only.
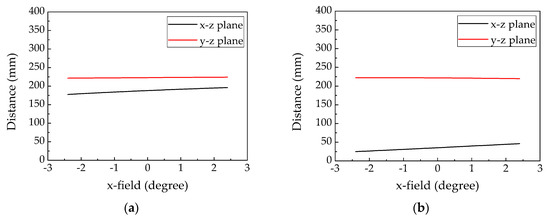
Figure 2.
The field curvature plot which exported by commercial ray-tracing software shows astigmatism caused by the waveguide elements: (a) symmetric waveguide structure; (b) asymmetric waveguide structure.
The holographic waveguides also cause anamorphic distortion as shown in Figure 3, which were simulated via Zemax. In this grid distortion diagram, the ideal object without aberration is a 4 by 4 grid as the solid grid. The crosses marked the real position of the grid intersection. In the asymmetric structure, the object with serious anamorphic distortion was enlarged in the x-direction as shown in Figure 3b. However, the distortion in the symmetric structure is not serious because the symmetric linear grating compensated it. In this section, the simplified formulas are proposed to predict astigmatism and anamorphic distortion.
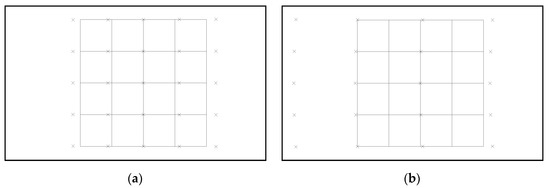
Figure 3.
The grid distortion diagram which exported by commercial ray-tracing software shows the anamorphic distortion caused by the waveguide elements: (a) symmetric waveguide structure; (b) asymmetric waveguide structure.
2.1. Astigmatism Analysis
Figure 4 shows the schematic when the incident light of an arbitrary image point pass-through the waveguides. The green line is the chief ray where the aperture stop is the human eye. The gray line is an arbitrary off-axis ray, which deviates from the chief ray by a small angle . Although both the off-axis rays in x-fan and y-fan were considered in this section, only the ray in x-fan was drawn in this figure. Here, we define and as the deviation angle of the off-axis rays in x-fan and y-fan; L is the distance from virtual images to the out-coupling HOE; is the eye-relief; t is the thickness of the waveguide; and are the incident angle of the chief ray at the out-coupling HOE in the x-direction and y-direction; and are the diffraction angle in the x-direction and y-direction, separately; and are the angle of the output light in air in the x-direction and y-direction, and is the tilt angel of the wedge-shape in Figure 4b. Notice that the angle respects the normal line of the last surface of the waveguides. The symbols and are defined as the separation of the chief ray and the off-axis rays at the last surface. The symbols and are the distance from the last surface to the focal point of x-fan and y-fan. In this case, the aberration varied with the incident angle in the y-direction not significantly. Therefore, only the image points on the x-axis (y = 0) were considered in this section.
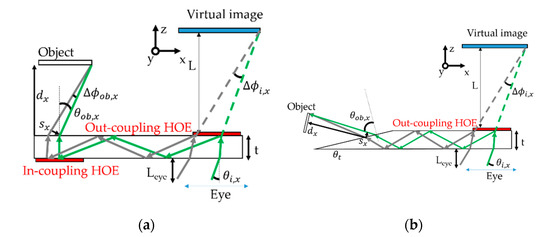
Figure 4.
The schematic diagrams of the ray track when the information light propagated inversely: (a) symmetric waveguide structure; (b) asymmetric waveguide structure.
2.1.1. Symmetric Structure
In the symmetric structure, the distance from the last surface to the object in the x-z plane (Sagittal plane) and y-z plane (Tangential plane) of the points on the x-axis can be described as
Then, the astigmatism can be defined as
The relationship between and can be described as
where is the period in the x-direction, is the wavelength, n is the refractive index of the waveguide and is the diffraction angle of the normal incident ray. Accordingly, when the incident angle is changed , the variation of diffraction angle is
Then, the separation s in x-direction can be described as
where is the TIR times and is the angle of output light in the waveguide considered Snell’s law. The first term is the separation parallel to the x-axis at the out-coupling HOE. The second term is the separation between two HOEs, and the third term is the separation from the in-coupling HOE to the last surface. The final term behind the square bracket is utilized to obtain the component which is perpendicular to the propagating direction. Since the angle of the incident ray and the output ray are equal, Formula (5) becomes
where is the angle of incident ray considering Snell’s law. Similarly, the separation in the y-direction can be described as
Finally, when Formulas (6) and (7) are inducted into Formula (2), the aberration becomes
Considering that the incident angle of the CGH systems is very small, Formula (8) can be simplified as
Here, the diffraction angle should be calculated according to Formula (3) for the arbitrary incident angle .
2.1.2. Asymmetric Structure
In the asymmetric structure with the wedge-shaped waveguide, the diffraction angle can be computed following Formula (3), and the output angle can be computed according to Snell’s law. The angle of the output ray can be described as
Furthermore, when the incident angle is changed , the change of the output ray is
According to the experience in the former paragraph, the separation in at the last surface can be described as
where is the distance from the out-coupling HOE to the wedge. For the x fan, the terms in the square brackets are the separation parallel to the x-axis. The final term behind the square brackets is utilized to obtain the component which is perpendicular to the propagating direction. Considering Formula (11) and (12), the distance from the last surface to the object can be described as
where is the angle of the output chief ray when the x-field is 0. Additionally, the astigmatism with paraxial approximation is
Here, the output angle should be calculated according to Formulas (3) and (10) for arbitrary incident angle .
2.2. Anamorphic Distortion
Assuming the chief ray of an image point nearby the reference point probes the Out-coupling HOE and the incident angle of the ray is
where and are equal. The chief rays of this point and the reference point will converge at the aperture stop. Since the position of the object can be predicted, the separation of these two rays at the object plane can also be analyzed. Then, the anamorphic distortion can be predicted via the ratio of the components of the separation in the x-direction and y-direction.
2.2.1. Symmetric Structure
In the symmetric structure, the component in the x-direction considers paraxial approximation is
The first term is the separation at the first surface. The second term is the total separation in the waveguide. The third term is the product of the deviation angle and the distance from the waveguide to the object . Furthermore, the former formula can be simplified as
where is the result of Formula (9). Similarly, the separation in the y-direction can be described as
Then we define the effective distance from the human eye to virtual images as
and the aspect ratio of the anamorphic object can be defined as
When the image distance L is far enough, the aspect ratio must be equal to one.
2.2.2. Asymmetric Structure
In the asymmetric structure, the separation in the x-direction can be described as
where can be calculated as
The first term is the separation at the wedge, and that term behind the square brackets is employed to obtain the component which is perpendicular to the propagating direction. The second term is the product of the deviation angle of output rays and distance of object . Similarly, the separation in the y-direction can be described as
Finally, the aspect ratio can be described as
When the image distance L is far enough, the aspect ratio can be approximated as
3. Results
In order to verify the proposed method, the calculated results of the formulas were compared to the simulation results of Zemax in this section. Since the simulation in Zemax software was verified so that results match the optical experiments in [21,22], the results of the proposed method should match the results of Zemax. In this section, the thicknesses of the waveguide t in these two structures were both 8 mm, and the refractive indexes were both 1.5195. The periods of three HOEs were equal to each other. The diffraction angle of the normal incident ray was 50 degrees. The TIR times n in the symmetric structure were 2. The tilt angle of the wedge-shape in the asymmetric structure was 17.7 degrees, and the distance from out-coupling HOE to the wedge D was about 45 mm. The field of view (FOV) of the virtual images was ±2.4 degrees considering that the maximum diffraction angle of the SLM with 6.4 um pixels was 2.38 degrees at 532 nm. When the image distance L was 250 mm, the astigmatism of the objects is shown in Figure 5. The horizontal axis is the viewing angle in the x-direction. Generally, the image distance L was much higher than the thickness and the eye-relief. Therefore, the viewing angle in the x-direction was approximated as the incident angle . The red plots in Figure 5a,b were calculated using Formulas (9) and (14), separately.
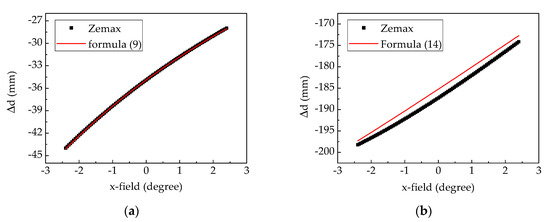
Figure 5.
The astigmatism with different x-field was predicted via Zemax software and the simplified formulas: (a) symmetric waveguide structure; (b) asymmetric waveguide structure.
In Figure 5a, the deviations between the results of the proposed method and Zemax were almost equal to 0, and the maximum deviation was 0.17 mm corresponding to −2.4° field. In Figure 5b, the results of the two methods were separated by about 2 mm because the Gaussian image plane slightly shifted in Zemax. The maximum deviation was 2.04 mm when x-field was 0°. However, the percentage error was smaller than 1.09% and was ignorable.
When the image distance L was a variation, the astigmatism of the central field is shown in Figure 6. In the symmetric structure, astigmatism related to L was a constant, as shown in Figure 6a. On the contrary, the astigmatism increased as the image distance L in the asymmetric structure. The phenomenon also matches the results in [22]. In Figure 6b, the deviations with different distances L between different methods were all about 2 mm. According to these results, the simplified Formulas (9) and (14) for astigmatism analysis were verified.
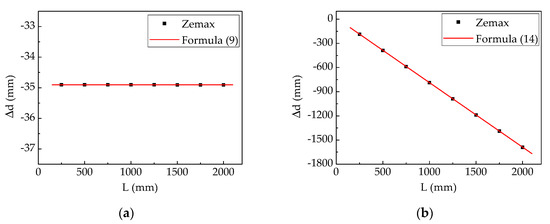
Figure 6.
The astigmatism of the central field with different image distance was predicted via Zemax software and the simplified formulas: (a) symmetric waveguide structure; (b) asymmetric waveguide structure.
The aspect raio of the anamorphic objects in these two structures are shown in Figure 7. The horizontal axis is the viewing angle and the vertical axis is the aspect ratio . The values simulated by Zemax were calculated based on the grid distortion diagram. The solid curves in Figure 7a,b were calculated by Formulas (20) and (24), separately. In these two structures, the anamorphic distortion became significant, corresponding to the reduction in the x-field, and the deviation increased as the reduction in distance L. In Figure 7a, the anamorphic distortion was not significant because the symmetric linear grating compensated the aberration. When the distance L was 250 mm, the aspect ratio of the central field was 1.13. The aspect ratio grew closer to 1 with the farther distance L. The maximum percentage error in this figure was 0.17%. In the asymmetric structure, the anamorphic was highly significant as shown in Figure 7b. The aspect ratio grew closer to Formula (25) with the farther distance L. In this case, the aspect ratio of the central field in Formula (25) was 2.25. Additionally, the ratio of the central field when L was 250 mm, 500 mm and infinity was 2.01, 2.12 and 2.25, separately. The maximum percentage error in this figure was 0.32%.
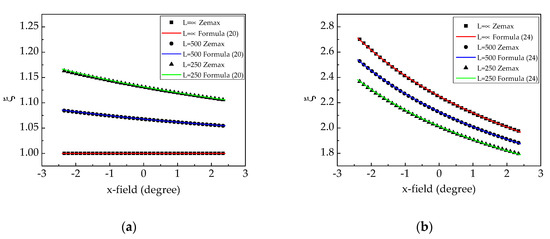
Figure 7.
The aspect ratio of the anamorphic object with different x-field was predicted via Zemax software and the simplified formulas: (a) symmetric waveguide structure; (b) asymmetric waveguide structure.
4. Discussion
In this study, the equations of astigmatism and anamorphic distortion of the diffractive waveguide combiner are presented for the CGH technique. Astigmatism of symmetric and asymmetric structures can be calculated via Formula (8) and (13). The formulas were simplified as Formulas (9) and (14) based on paraxial approximation. Furthermore, the anamorphic distortion of these two structures can be calculated based on Formulas (20) and (24). Considering the commercial SLM with a 6.4 um pixel size, the aberration was analyzed for ±2.4° FOV in this paper.
Dismissing the limitation of SLMs, we compared the proposed method to the simulation of Zemax with a larger field. In the simulation configuration employed in this paper, the maximum FOV of the symmetric structure was from −10° to 9.4°, and in the asymmetric structure was from −5.2° to 9.4°. The upper limit was limited by the TIR condition, and the lower limit was limited by the dimension of the in-coupling surface. Smaller than the lower limit, the chief ray exceeded the boundary of the in-coupling surface. The calculation results and the simulation results in this range when L was 250 mm are shown in Figure 8. In Figure 8a,b, the results of Formulas (8) and (13) match the results of Zemax. The maximum deviation between Formulas (8) and (9) was 6.18 mm, and the percentage error was 5.67% when the x-field was −10°. The maximum deviation between Formulas (13) and (14) was 6.92 mm, and the percentage error was 5.36% when the x-field was 9.4°. In Figure 8c,d, the maximum percentage error of the anamorphic analyzation based on Formula (20) was 2.53% when the x-field was −10°, and the maximum percentage error of Formula (24) was 2.23% when x-field was 9.4°.
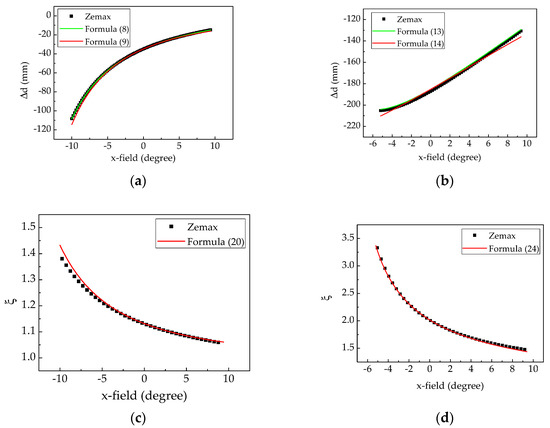
Figure 8.
The aberration analyzation for large x-field: (a) astigmatism of symmetric structure; (b) astigmatism of asymmetric structure; (c) anamorphic of symmetric structure; (d) anamorphic of asymmetric structure.
Considering the above information, we believe the proposed method is available for most diffractive waveguide HMDs, which is based on the current CGH technique. In fact, even whenemploying the SLM with the smallest pixel size (3.74 um for current commercial SLMs), the maximum FOV is about only ±4°. In the condition, the maximum deviation in Figure 8a was smaller than 0.54 mm, and the maximum deviation in Figure 8b was smaller than 2.04 mm. Furthermore, the percentage error of the anamorphic analyzation based on Formulas (20) and (24) was not larger than 0.64%.
5. Conclusions
In this paper, the aberration of two types of the holographic waveguide combiner are discussed. The major aberration caused by the holographic combiners is astigmatism and anamorphic distortion. In order to provide aberration-free images to the observer, producing an object with reverse aberration is necessary. For each field, astigmatism is predicted via tracing the crossing point of the x-fan and the y-fan separately, and the anamorphic distortion is predicted via tracing the position at the object plane of the chief rays of the nearby points. In the proposed method, the astigmatism and the anamorphic distortion can be calculated easily when the specification of the waveguides and the diffraction angle of the HOE for the normal incident ray are known. Formulas (9) and (14) were utilized to predict the astigmatism of the object in the symmetric waveguide and the asymmetric waveguide, separately. Formulas (20) and (24) were utilized to predict the anamorphic distortion of the objects in the symmetric waveguide and asymmetric waveguide, separately. The results of the proposed method are very close to the simulation of ray-tracing software Zemax, where the simulation of Zemax has been proved for aberration correcting. Therefore, the aberration of an arbitrary device with a similar holographic waveguide element can be corrected via the proposed method. It will make the designing process simpler and faster.
Author Contributions
Writing—original draft preparation, W.-K.L.; writing—review and editing, W.-C.S. and B.-S.L.; methodology, W.-K.L.; software, S.-K.Z.; funding acquisition, W.-C.S. supervision, W.-C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Ministry of Science and Technology of Taiwan under contract MOST 108-2221-E-018 -018 -MY3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shibata, T. Head mounted display. Displays 2002, 23, 57–64. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Shi, G.; Qu, H.; Wu, Y.; Zhang, J. Review and analysis of avionic helmet-mounted displays. Opt. Eng. 2013, 52, 110901. [Google Scholar] [CrossRef]
- Hoffman, D.M.; Girshick, A.R.; Akeley, K.; Banks, M.S. Vergence–accommodation conflicts hinder visual performance and cause visual fatigue. J. Vis. 2008, 8, 33. [Google Scholar] [CrossRef]
- Leith, E.N.; Upatnieks, J. Reconstructed wavefronts and communication theory. J. Opt. Soc. Am. 1962, 52, 1123–1130. [Google Scholar] [CrossRef]
- Ogihara, Y.; Sakamoto, Y. Fast calculation method of a CGH for a patch model using a point-based method. Appl. Opt. 2015, 54, A76–A83. [Google Scholar] [CrossRef]
- Shimobaba, T.; Matsushima, K.; Kakue, T.; Masuda, N.; Ito, T. Scaled angular spectrum method. Opt. Lett. 2012, 37, 4128–4130. [Google Scholar] [CrossRef]
- Matsushima, K. Computer-generated holograms for three-dimensional surface objects with shade and texture. Appl. Opt. 2005, 44, 4607–4614. [Google Scholar] [CrossRef]
- Moon, E.; Kim, M.; Roh, J.; Kim, H.; Hahn, J. Holographic head-mounted display with RGB light emitting diode light source. Opt. Express 2014, 22, 6526–6534. [Google Scholar] [CrossRef]
- Murakami, E.; Oguro, Y.; Sakamoto, Y. Study on Compact Head-Mounted Display System Using Electro-Holography for Augmented Reality. IEICE Trans. Electron. 2017, 100, 965–971. [Google Scholar] [CrossRef]
- Sypek, M.; Kolodziejczyk, A.; MikuĹ, G. Three-plane phase-only computer hologram generated with iterative Fresnel algorithm. Opt. Eng. 2005, 44, 125805–125807. [Google Scholar]
- Masuda, K.; Saita, Y.; Toritani, R.; Xia, P.; Nitta, K.; Matoba, O. Improvement of image quality of 3D display by using optimized binary phase modulation and intensity accumulation. J. Disp. Technol. 2016, 12, 472–477. [Google Scholar] [CrossRef]
- Gao, Q.; Liu, J.; Duan, X.; Zhao, T.; Li, X.; Liu, P. Compact see-through 3D head-mounted display based on wavefront modulation with holographic grating filter. Opt. Express 2017, 25, 8412–8424. [Google Scholar] [CrossRef]
- Mendoza-Yero, O.; Mínguez-Vega, G.; Lancis, J. Encoding complex fields by using a phase-only optical element. Opt. Lett. 2014, 39, 1740–1743. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Zhao, T.; Wang, Y. Color dynamic holographic display with wide viewing angle by improved complex amplitude modulation. Opt. Express 2018, 26, 2349–2358. [Google Scholar] [CrossRef]
- Eisen, L.; Meyklyar, M.; Golub, M.; Friesem, A.A.; Gurwich, I.; Weiss, V. Planar configuration for image projection. Appl. Opt. 2006, 45, 4005–4011. [Google Scholar] [CrossRef]
- Levola, T. Diffractive optics for virtual reality displays. J. Soc. Inf. Disp. 2006, 14, 467–475. [Google Scholar] [CrossRef]
- Piao, J.-A.; Li, G.; Piao, M.-L.; Kim, N. Full color holographic optical element fabrication for waveguide-type head mounted display using photopolymer. J. Opt. Soc. Korea 2013, 17, 242–248. [Google Scholar] [CrossRef]
- Han, J.; Liu, J.; Yao, X.; Wang, Y. Portable waveguide display system with a large field of view by integrating freeform elements and volume holograms. Opt. Express 2015, 23, 3534–3549. [Google Scholar] [CrossRef]
- Piao, M.-L.; Kim, N. Achieving high levels of color uniformity and optical efficiency for a wedge-shaped waveguide head-mounted display using a photopolymer. Appl. Opt. 2014, 53, 2180–2186. [Google Scholar] [CrossRef]
- Yeom, H.-J.; Kim, H.-J.; Kim, S.-B.; Zhang, H.; Li, B.; Ji, Y.-M.; Kim, S.-H.; Park, J.-H. 3D holographic head mounted display using holographic optical elements with astigmatism aberration compensation. Opt. Express 2015, 23, 32025–32034. [Google Scholar] [CrossRef]
- Lin, W.-K.; Matoba, O.; Lin, B.-S.; Su, W.-C. Astigmatism correction and quality optimization of computer-generated holograms for holographic waveguide displays. Opt. Express 2020, 28, 5519–5527. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.-K.; Matoba, O.; Lin, B.-S.; Su, W.-C. Astigmatism and deformation correction for a holographic head-mounted display with a wedge-shaped holographic waveguide. Appl. Opt. 2018, 57, 7094–7101. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).