Short Barriers for Lowering Current-Density in Terahertz Quantum Cascade Lasers
Abstract
:1. Introduction
2. Role of IR Scattering in Three-Well QCLs with Short and Tall Barriers
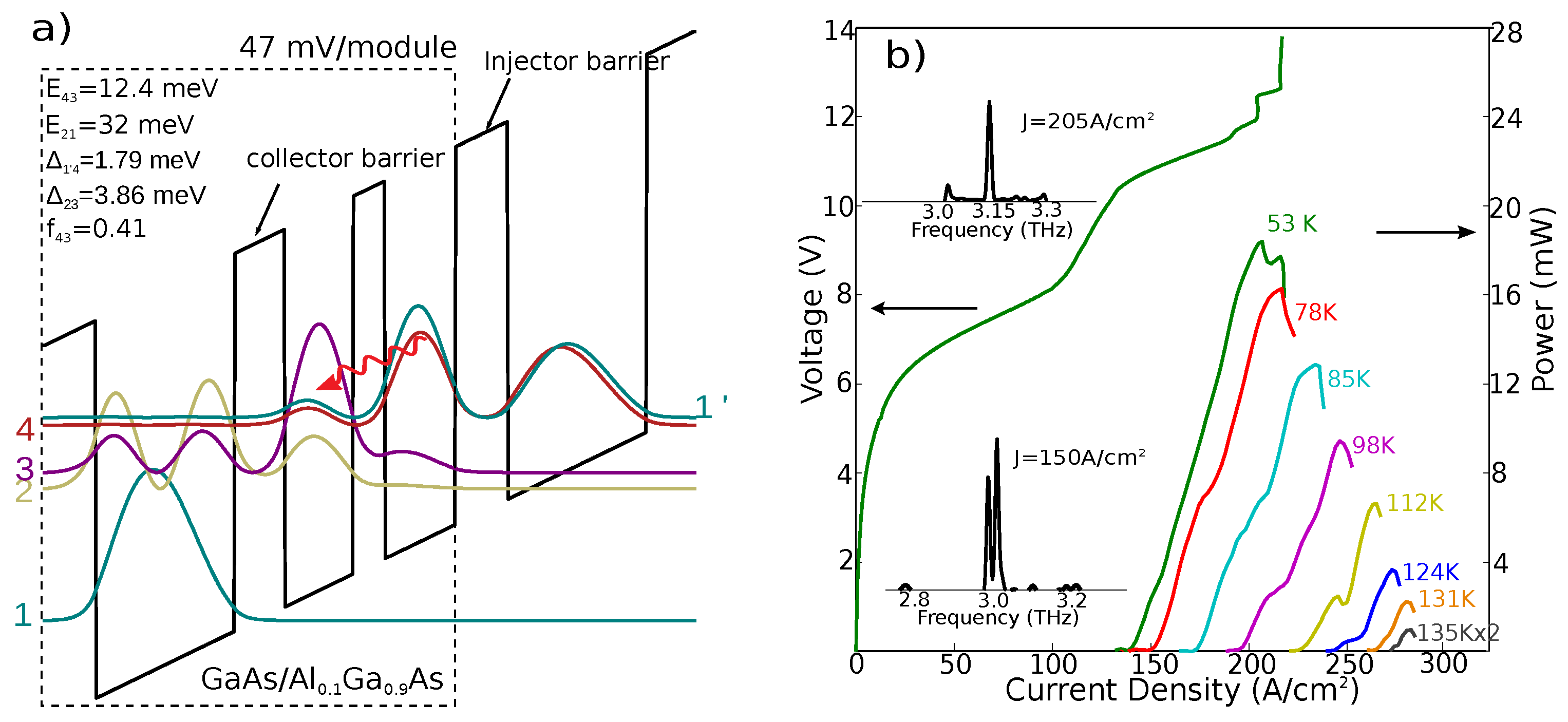
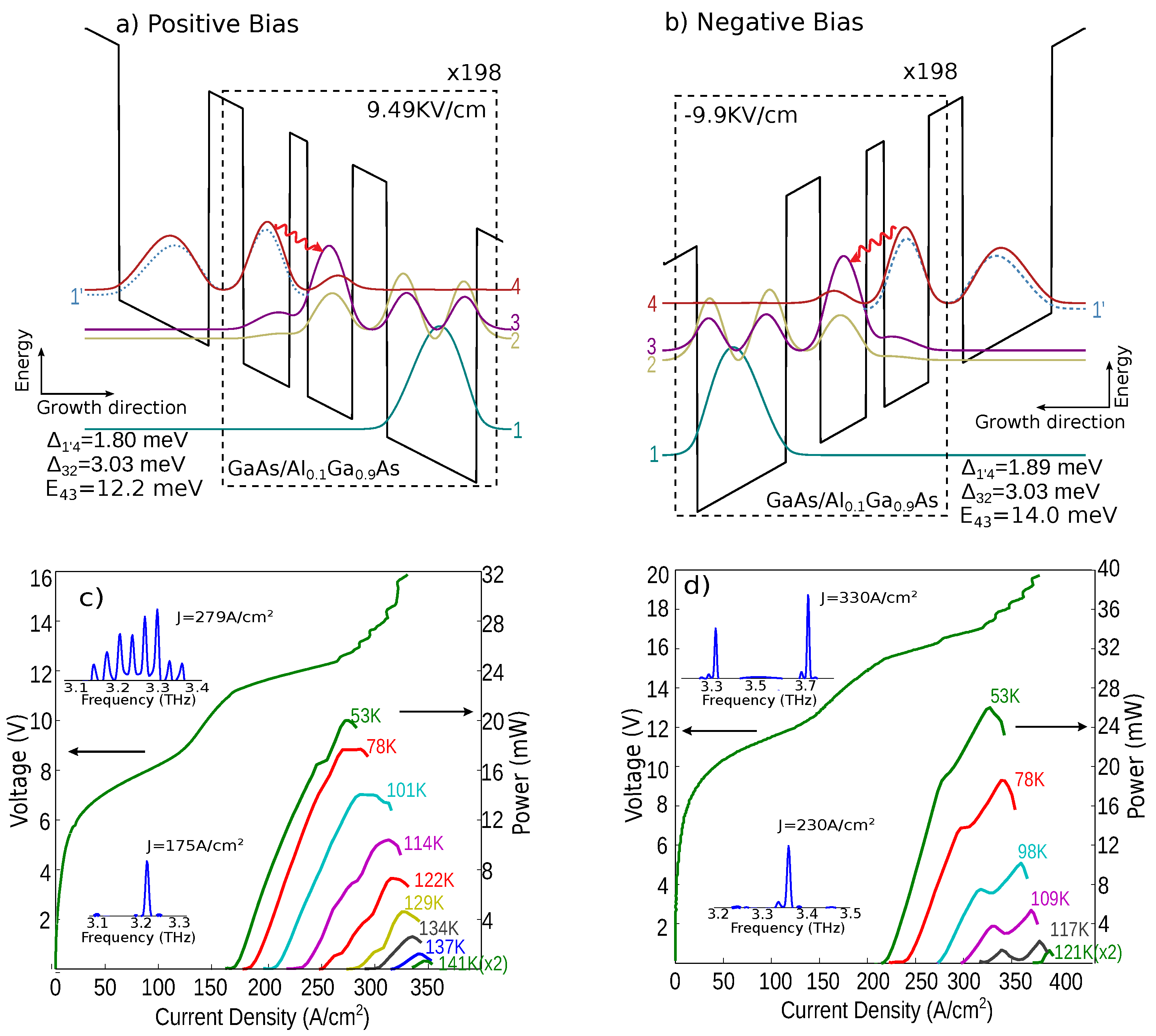
3. Experimental Results from Two Different QCLs
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Köhler, R.; Tredicucci, A.; Beltram, F.; Beere, H.E.; Linfield, E.H.; Davies, A.G.; Ritchie, D.A.; Iotti, R.C.; Rossi, F. Terahertz semiconductor-heterostructure laser. Nature 2002, 417, 156–159. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Qiang, B.; Wang, Q.J. Photonic Engineering Technology for the Development of Terahertz Quantum Cascade Lasers. Adv. Opt. Mater. 2019. [Google Scholar] [CrossRef]
- Kumar, S.; Hu, Q.; Reno, J.L. 186 K operation of terahertz quantum-cascade lasers based on a diagonal design. Appl. Phys. Lett. 2009, 94, 131105. [Google Scholar] [CrossRef]
- Kumar, S.; Chan, C.W.I.; Hu, Q.; Reno, J.L. A 1.8 THz quantum-cascade laser operating significantly above the temperature of ℏω/kB. Nat. Phys. 2011, 7, 166. [Google Scholar] [CrossRef]
- Fathololoumi, S.; Dupont, E.; Chan, C.W.I.; Wasilewski, Z.R.; Laframboise, S.R.; Ban, D.; Mátyás, A.; Jirauschek, C.; Hu, Q.; Liu, H.C. Terahertz quantum cascade lasers operating up to ∼200 K with optimized oscillator strength and improved injection tunneling. Opt. Express 2012, 20, 3866. [Google Scholar] [CrossRef]
- Bosco, L.; Franckié, M.; Scalari, G.; Beck, M.; Wacker, A.; Faist, J. Thermoelectrically cooled THz quantum cascade laser operating up to 210 K. Appl. Phys. Lett. 2019, 115, 010601. [Google Scholar] [CrossRef]
- Kainz, M.A.; Semtsiv, M.P.; Tsianos, G.; Kurlov, S.; Masselink, W.T.; Schönhuber, S.; Detz, H.; Schrenk, W.; Unterrainer, K.; Strasser, G.; et al. Thermoelectric-cooled terahertz quantum cascade lasers. Opt. Express 2019, 27, 20688. [Google Scholar] [CrossRef]
- Richter, H.; Greiner-Bär, M.; Pavlov, S.G.; Semenov, A.D.; Wienold, M.; Schrottke, L.; Giehler, M.; Hey, R.; Grahn, H.T.; Hübers, H.W. A compact, continuous-wave terahertz source based on a quantum-cascade laser and a miniature cryocooler. Opt. Express 2010, 18, 10177. [Google Scholar] [CrossRef]
- Richter, H.; Wienold, M.; Schrottke, L.; Biermann, K.; Grahn, H.T.; Hübers, H.W. 4.7-THz local oscillator for the GREAT heterodyne spectrometer on SOFIA. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 539. [Google Scholar] [CrossRef]
- Franckié, M.; Winge, D.O.; Wolf, J.; Liverini, V.; Dupont, E.; Trinité, V.; Faist, J.; Wacker, A. Impact of interface roughness distributions on the operation of quantum cascade lasers. Opt. Express 2015, 23, 5201–5212. [Google Scholar] [CrossRef]
- Krivas, K.; Winge, D.; Franckié, M.; Wacker, A. Influence of interface roughness in quantum cascade lasers. J. Appl. Phys. 2015, 118, 114501. [Google Scholar] [CrossRef] [Green Version]
- Deutsch, C.; Detz, H.; Zederbauer, T.; Andrews, A.M.; Klang, P.; Kubis, T.; Klimeck, G.; Schuster, M.E.; Schrenk, W.; Strasser, G.; et al. Probing scattering mechanisms with symmetric quantum cascade lasers. Opt. Express 2013, 21, 7209. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Laframboise, S.R.; Wasilewski, Z.R.; Aers, G.C.; Liu, H.C.; Cao, J.C. Terahertz quantum-cascade lasers based on a three-well active module. Appl. Phys. Lett. 2007, 90, 041112. [Google Scholar] [CrossRef]
- Williams, B.S.; Callebaut, H.; Kumar, S.; Hu, Q.; Reno, J.L. 3.4-THz quantum cascade laser based on longitudinal-optical-phonon scattering for depopulation. Appl. Phys. Lett. 2003, 82, 1015–1017. [Google Scholar] [CrossRef] [Green Version]
- Scalari, G.; Hoyler, N.; Giovannini, M.; Faist, J. Terahertz bound-to-continuum quantum-cascade lasers based on optical-phonon scattering extraction. Appl. Phys. Lett. 2005, 86, 181101. [Google Scholar] [CrossRef]
- Kumar, S.; Williams, B.S.; Hu, Q.; Reno, J.L. 1.9 THz quantum-cascade lasers with one-well injector. Appl. Phys. Lett. 2006, 88, 121123. [Google Scholar] [CrossRef]
- Benz, A.; Fasching, G.; Andrews, A.M.; Martl, M.; Unterrainer, K.; Roch, T.; Schrenk, W.; Golka, S.; Strasser, G. Influence of doping on the performance of terahertz quantum-cascade lasers. Appl. Phys. Lett. 2007, 90, 101107. [Google Scholar] [CrossRef]
- Scalari, G.; Amanti, M.I.; Fischer, M.; Terazzi, R.; Walther, C.; Beck, M.; Faist, J. Step well quantum cascade laser emitting at 3 THz. Appl. Phys. Lett. 2009, 94, 041114. [Google Scholar] [CrossRef]
- Amanti, M.I.; Scalari, G.; Terazzi, R.; Fischer, M.; Beck, M.; Faist, J.; Rudra, A.; Gallo, P.; Kapon, E. Bound-to-continuum terahertz quantum cascade laser with a single-quantum-well phonon extraction/injection stage. New J. Phys. 2009, 11, 125022. [Google Scholar] [CrossRef]
- Chan, C.W.I.; Hu, Q.; Reno, J.L. Tall-barrier terahertz quantum cascade lasers. Appl. Phys. Lett. 2013, 103, 151117. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Hu, Q. Coherence of resonant-tunneling transport in terahertz quantum-cascade lasers. Phys. Rev. B 2009, 80, 245316. [Google Scholar] [CrossRef] [Green Version]
- Sakaki, H.; Noda, T.; Hirakawa, K.; Tanaka, M.; Matsusue, T. Interface roughness scattering in GaAs/AlAs quantum wells. Appl. Phys. Lett. 1987, 51, 1934. [Google Scholar] [CrossRef]
- Walther, C.; Fischer, M.; Scalari, G.; Terazzi, R.; Hoyler, N.; Faist, J. Quantum cascade lasers operating from 1.2 to 1.6 THz. Appl. Phys. Lett. 2007, 91, 131122. [Google Scholar] [CrossRef]
- Beere, H.E.; Fowler, J.C.; Alton, J.; Linfield, E.H.; Ritchie, D.A.; Köhler, R.; Tredicucci, A.; Scalari, G.; Ajili, L.; Faist, J.; et al. MBE growth of terahertz quantum cascade lasers. J. Cryst. Growth 2005, 278, 756. [Google Scholar] [CrossRef]
- Li, L.H.; Zhu, J.X.; Chen, L.; Davies, A.G.; Linfield, E.H. The MBE growth and optimization of high performance terahertz frequency quantum cascade lasers. Opt. Express 2015, 23, 2720. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.B.; Kumar, S.; Hu, Q.; Reno, J.L. Operation of terahertz quantum-cascade lasers at 164 K in pulsed mode and at 117 K in continuous-wave mode. Opt. Express 2005, 13, 3331. [Google Scholar] [CrossRef]
- Belkin, A.M.; Fan, A.J.; Hormoz, S.; Capasso, F.; Khanna, S.; Lachab, M.; Davies, A.G.; Linfield, H.E. Terahertz quantum cascade lasers with copper metal-metal waveguides operating up to 178 K. Opt. Express 2008, 16, 3242. [Google Scholar] [CrossRef]
- Khanal, S.; Gao, L.; Zhao, L.; Reno, J.L.; Kumar, S. High-temperature operation of broadband bidirectional terahertz quantum-cascade lasers. Sci. Rep. 2016, 6, 32978. [Google Scholar] [CrossRef] [Green Version]
- Khanal, S.; Zhao, L.; Reno, J.L.; Kumar, S. Temperature performance of terahertz quantum-cascade lasers with resonant-phonon active-regions. J. Opt. 2014, 16, 094001. [Google Scholar] [CrossRef]
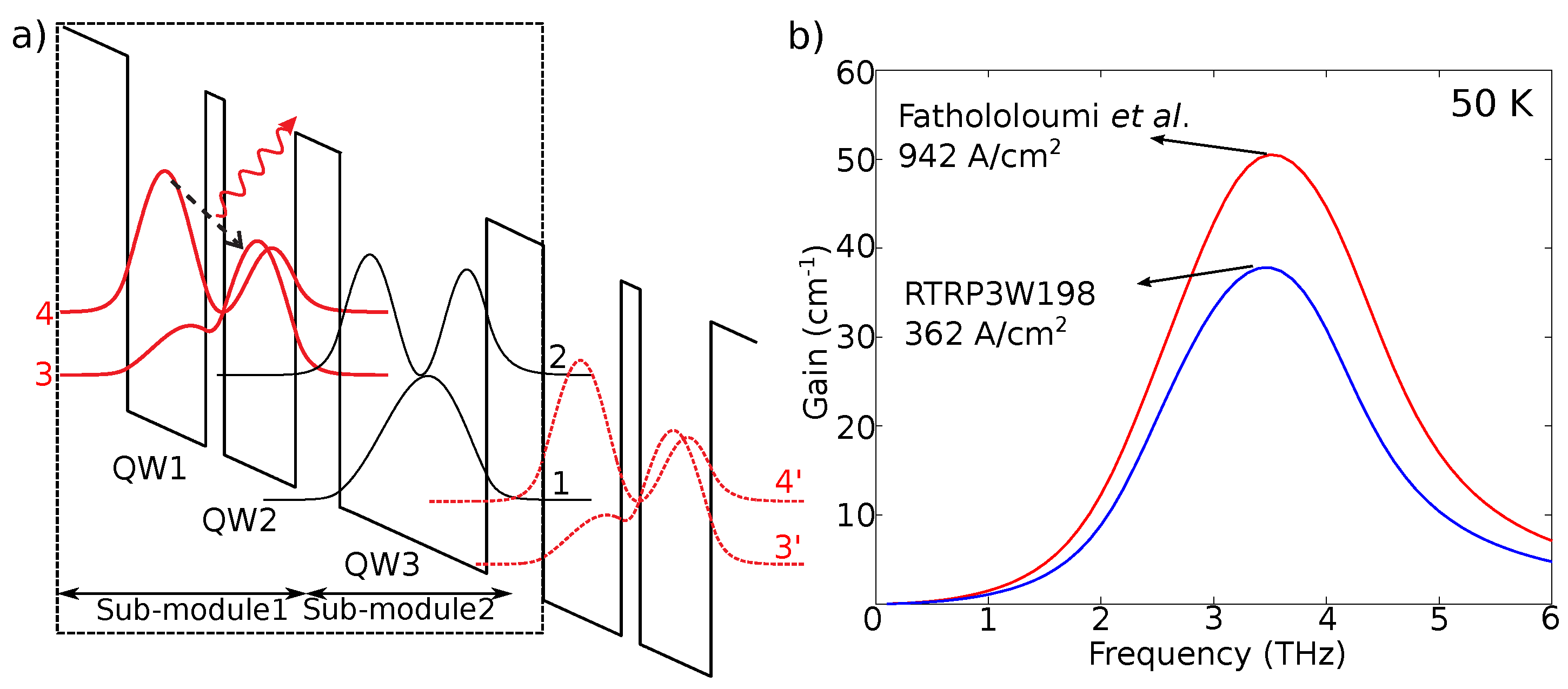
| Design | T (K) | J (A/cm2) | Peak Gain (cm−1) | ||||
|---|---|---|---|---|---|---|---|
| RTRP3W198 | 50 | 148 ps | 5.9 ps | 5.7 ps | 0.56 ps | 362 | 38 |
| Fathololoumi et al. [5] | 50 | 66 ps | 2.3 ps | 2.2 ps | 0.21 ps | 942 | 51 |
| RTRP3W198 | 150 | 4.0 ps | 7.3 ps | 2.6 ps | 0.28 ps | 666 | 31 |
| Fathololoumi et al. [5] | 150 | 2.3 ps | 2.8 ps | 1.3 ps | 0.20 ps | 1353 | 37 |
| Design Name | Wafer No. | Frequency | Jth (A/cm2) | Jmax (A/cm2) | Tmax | Doping Density |
|---|---|---|---|---|---|---|
| RTRP3W197 | VB0464 | 2.7 THz | 240 @77 K | 450 @77 K | 157 K | 2.8 × 1010 cm−2 |
| RTRP3W198 | VB0890 | 3.1 THz | 134 @53 K | 208 @53 K | 135 K | 2.8 × 1010 cm−2 |
| BIDR3W198 (pos. bias) | VB0891 | 3.2 THz | 167 @53 K | 270 @53 K | 141 K | 2.8 × 1010 cm−2 |
| BIDR3W198 (neg. bias) | VB0891 | 3.5 THz | 217 @53 K | 322 @53 K | 121 K | 2.8 × 1010 cm−2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, L.; Reno, J.L.; Kumar, S. Short Barriers for Lowering Current-Density in Terahertz Quantum Cascade Lasers. Photonics 2020, 7, 7. https://doi.org/10.3390/photonics7010007
Gao L, Reno JL, Kumar S. Short Barriers for Lowering Current-Density in Terahertz Quantum Cascade Lasers. Photonics. 2020; 7(1):7. https://doi.org/10.3390/photonics7010007
Chicago/Turabian StyleGao, Liang, John L. Reno, and Sushil Kumar. 2020. "Short Barriers for Lowering Current-Density in Terahertz Quantum Cascade Lasers" Photonics 7, no. 1: 7. https://doi.org/10.3390/photonics7010007
APA StyleGao, L., Reno, J. L., & Kumar, S. (2020). Short Barriers for Lowering Current-Density in Terahertz Quantum Cascade Lasers. Photonics, 7(1), 7. https://doi.org/10.3390/photonics7010007





