Electron Population Dynamics in Optically Pumped Asymmetric Coupled Ge/SiGe Quantum Wells: Experiment and Models
Abstract
1. Introduction
2. Materials and Methods
3. Results
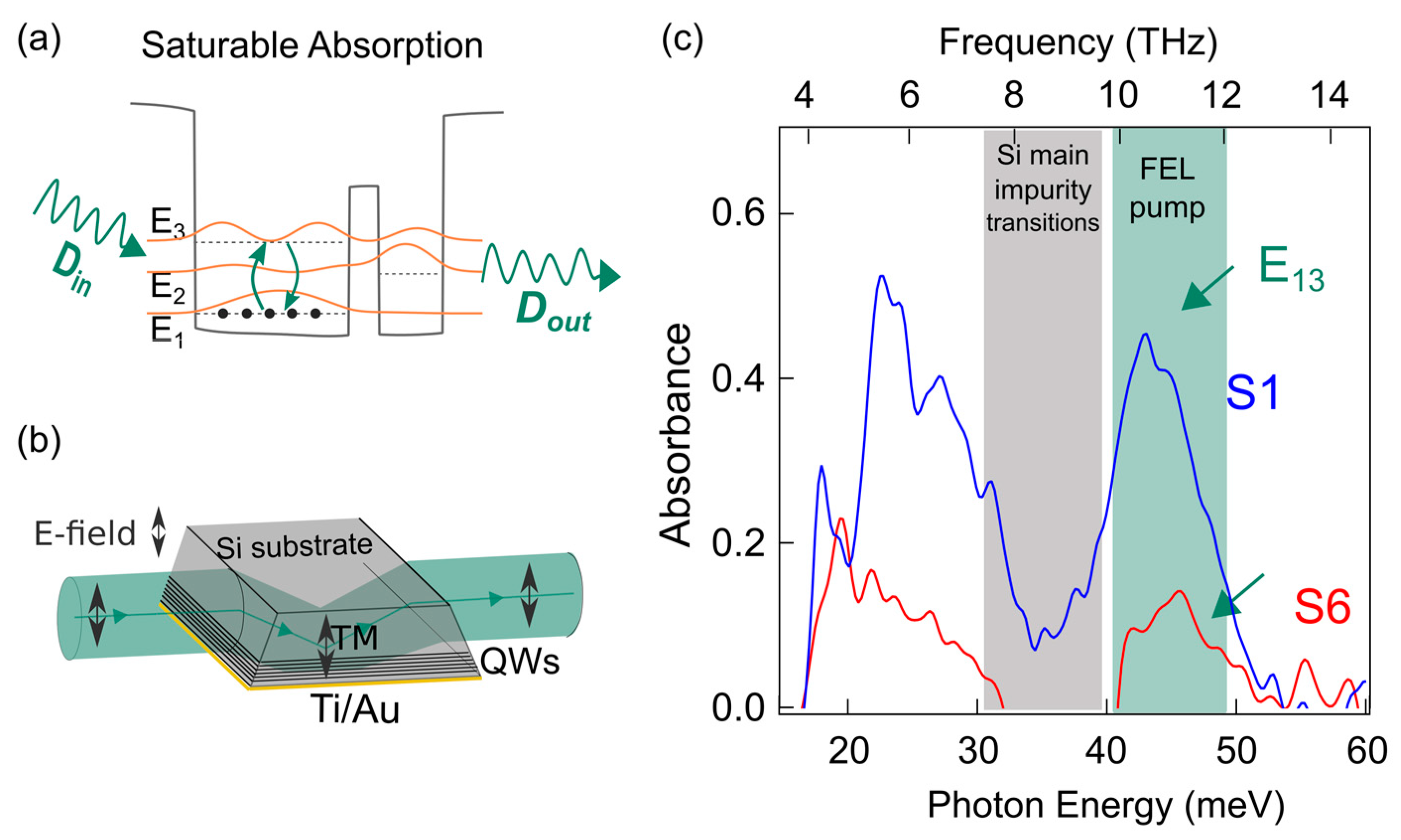
3.1. Spectroscopy at Equilibrium
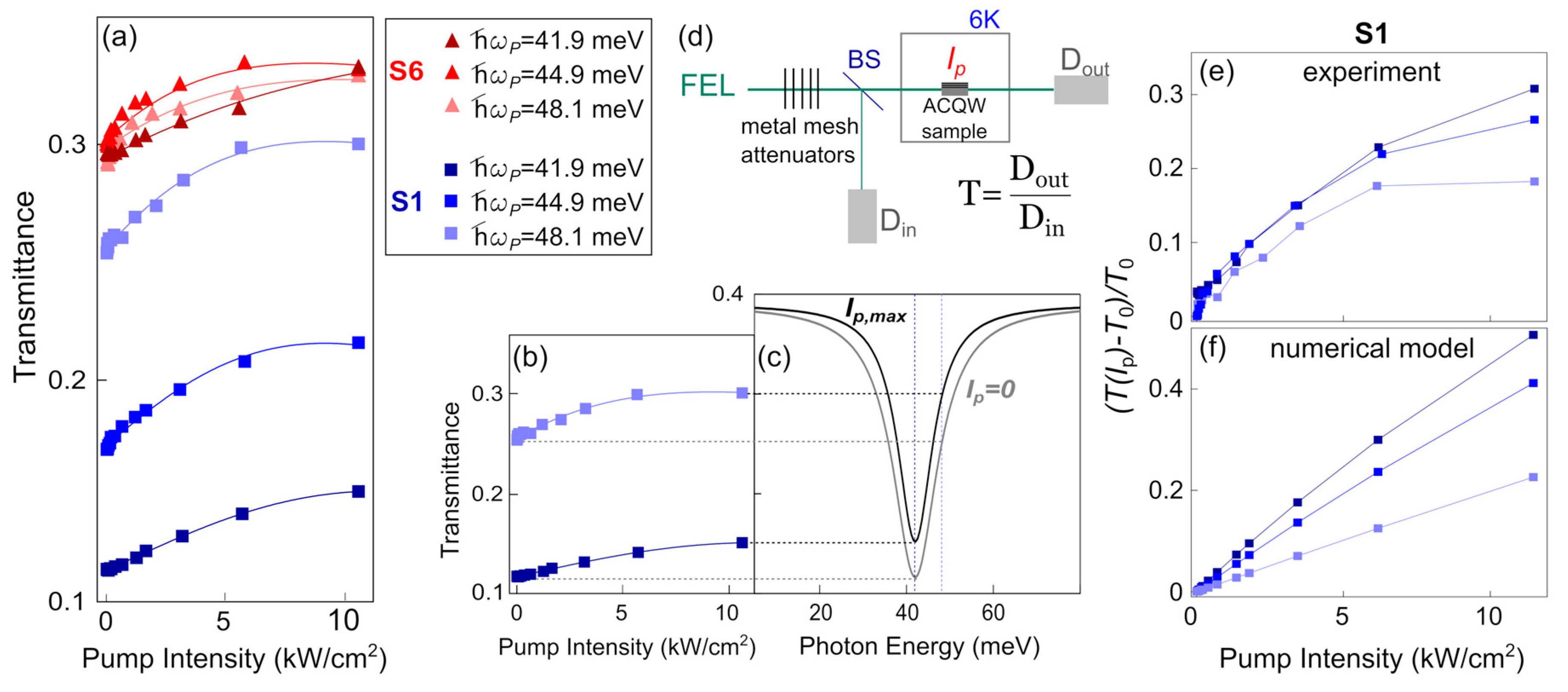
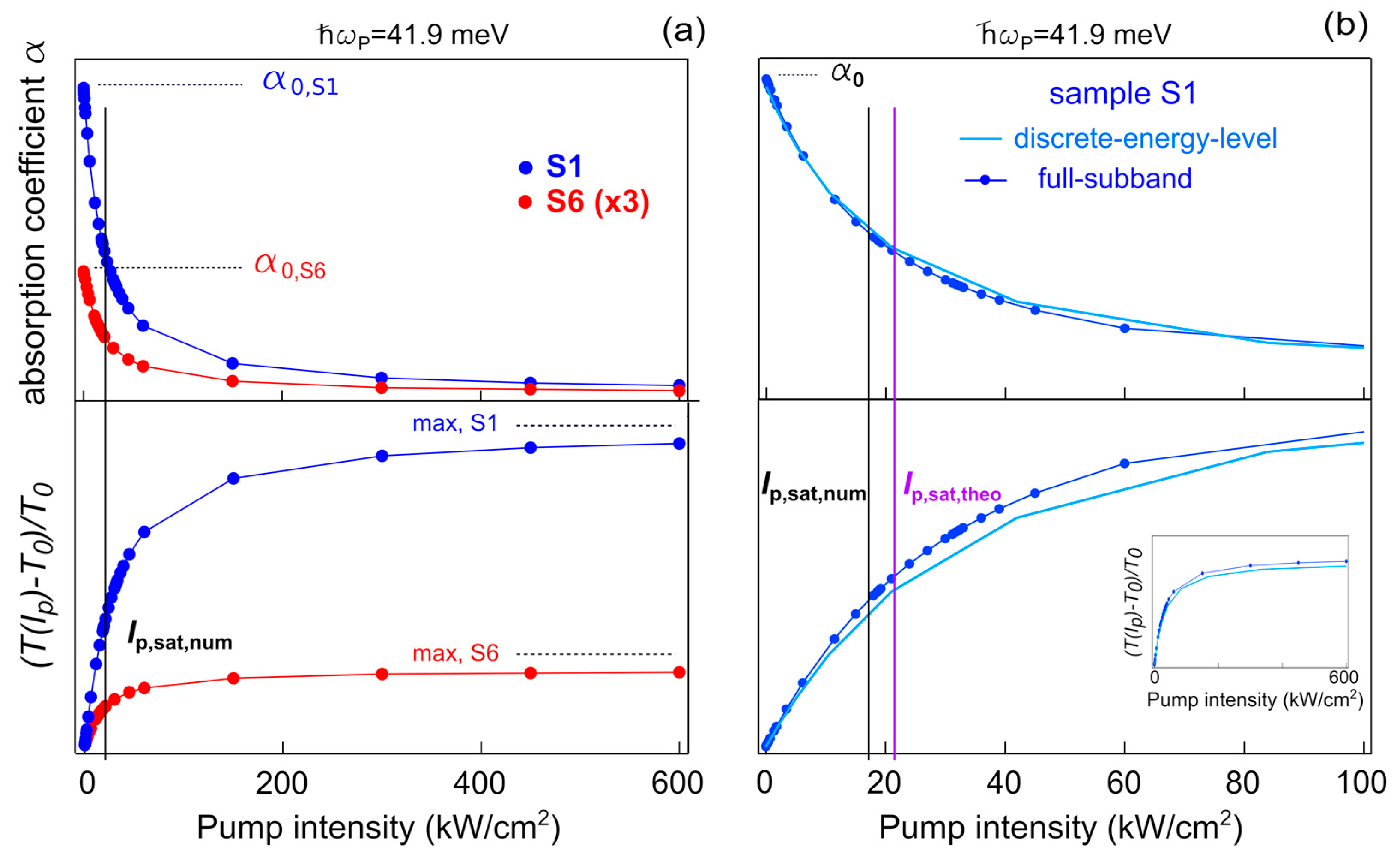
3.2. Absorption-Saturation Experiment
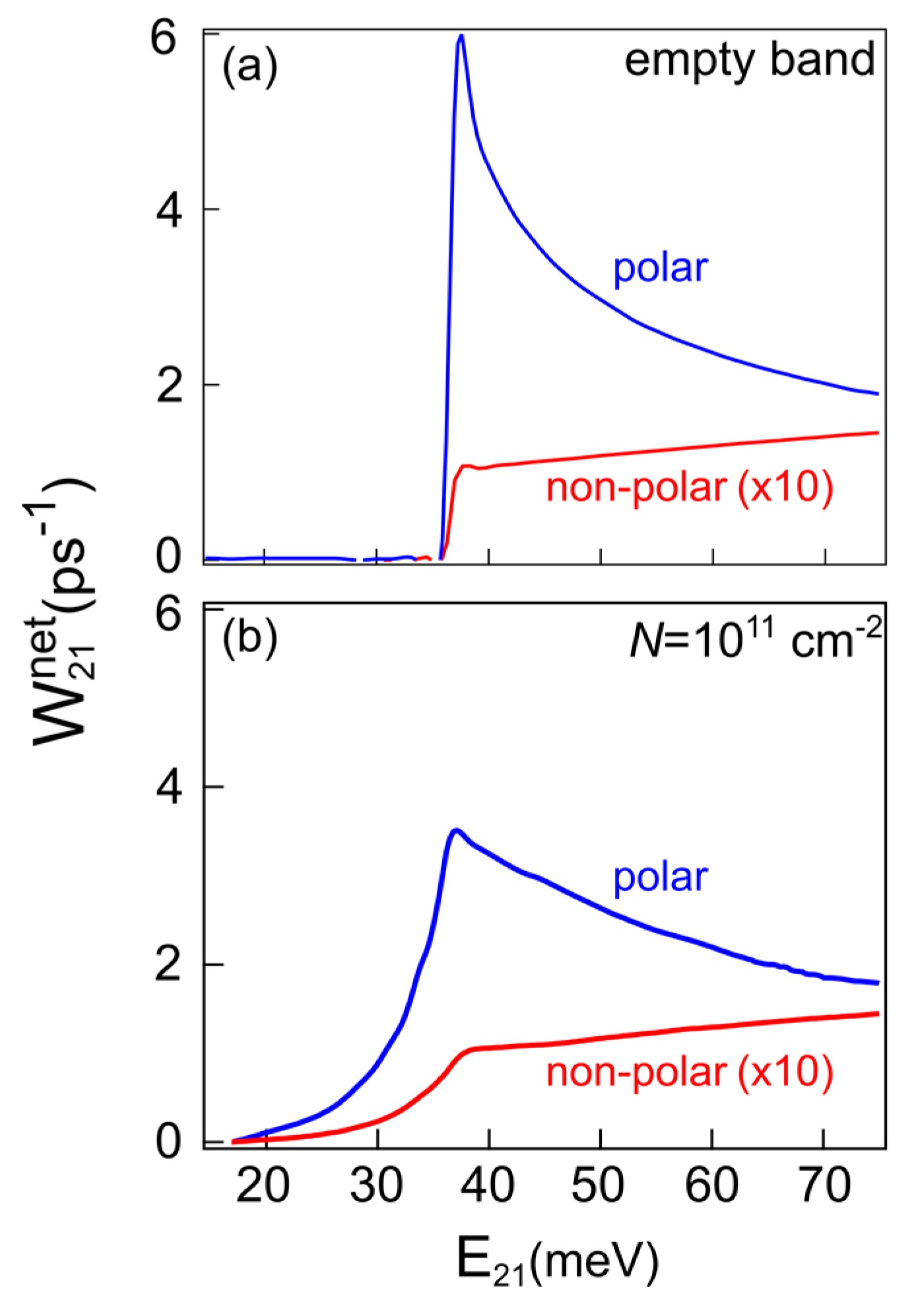
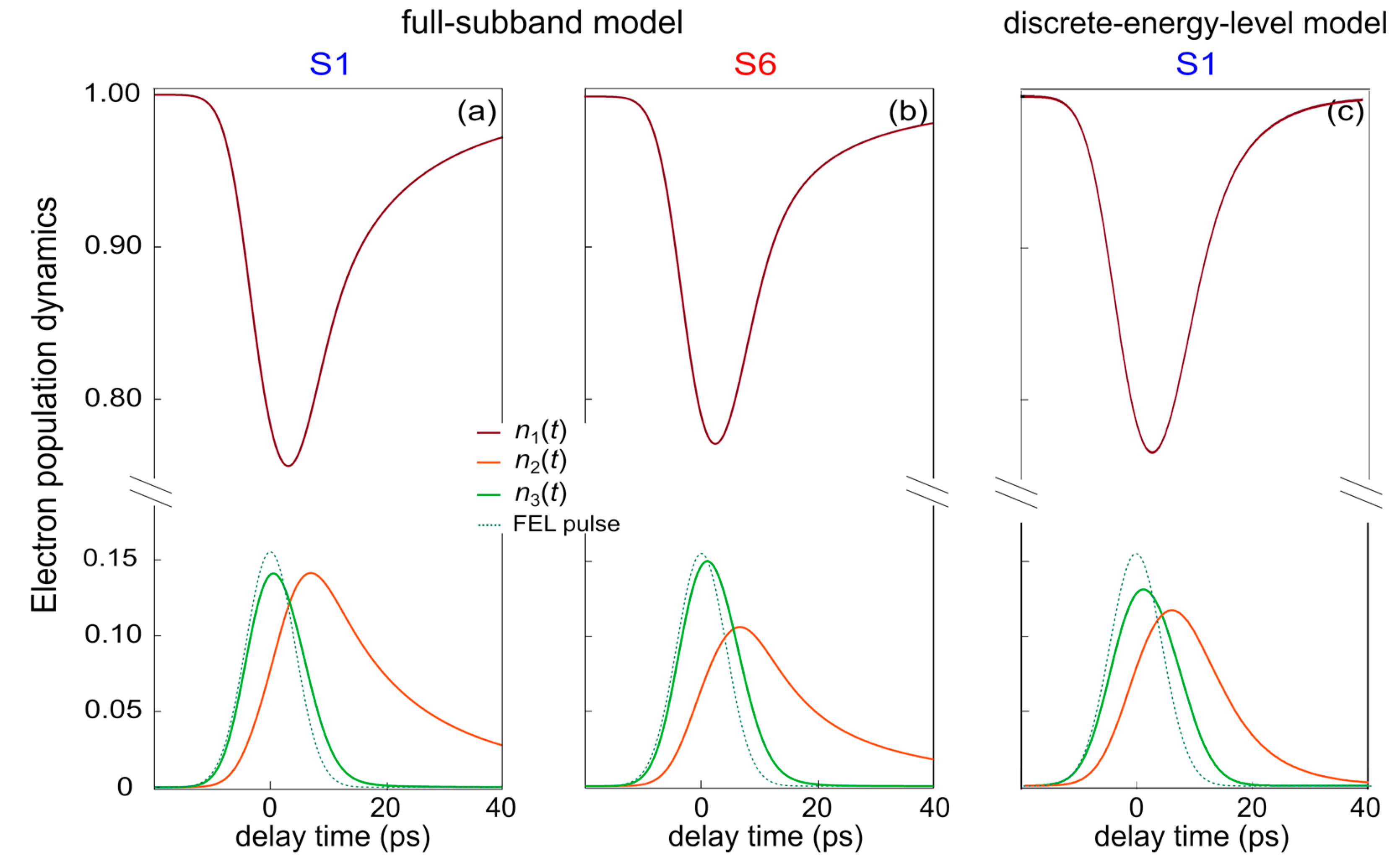
3.3. Numerical Simulations of Subband Population Dynamics
3.4. Analytic Solution of the Discrete-Energy-Level Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vitiello, M.S.; Scalari, G.; Williams, B.; De Natale, P. Quantum Cascade Lasers: 20 years of challenges. Opt. Express 2015, 23, 5167–5182. [Google Scholar] [CrossRef] [PubMed]
- Bashir, A.; Gallacher, K.; Millar, R.W.; Paul, D.J.; Ballabio, A.; Frigerio, J.; Isella, G.; Kriegner, D.; Ortolani, M.; Barthel, J.; et al. Interfacial sharpness and intermixing in a Ge-SiGe multiple quantum well structure. J. Appl. Phys. 2018, 123, 035703. [Google Scholar] [CrossRef]
- Frigerio, J.; Ortolani, M.; Ballabio, A.; Virgilio, M. Modeling of second harmonic generation in hole-doped silicon-germanium quantum wells for mid-infrared sensing. Opt. Express 2018, 26, 31861–31872. [Google Scholar] [CrossRef] [PubMed]
- Rauter, P.; Spindlberger, L.; Schaeffler, F.; Fromherz, T.; Freund, J.; Brehm, M. Room-temperature group-IV LED based on defect-enhanced Ge quantum dots. ACS Photonics 2018, 5, 431–438. [Google Scholar] [CrossRef]
- Failla, M.; Keller, J.; Scalari, G.; Maissen, C.; Faist, J.; Reichl, C.; Wegscheider, W.; Newell, O.J.; Leadley, D.R.; Myronov, M.; et al. Terahertz quantum Hall effect for spin-split heavy-hole gases in strained Ge quantum wells. New J. Phys. 2016, 18, 113036. [Google Scholar] [CrossRef]
- Montanari, M.; Virgilio, M.; Manganelli, C.L.; Zaumseil, P.; Zoellner, M.H.; Hou, Y.; Schubert, M.A.; Persichetti, L.; Di Gaspare, L.; De Seta, M.; et al. Photoluminescence study of interband transitions in few-layer, pseudomorphic, and strain-unbalanced Ge/GeSi multiple quantum wells. Phys. Rev. B 2018, 98, 195310. [Google Scholar] [CrossRef]
- Sun, G.; Cheng, H.H.; Menéndez, J.; Khurgin, J.B.; Soref, R.A. Strain-free Ge/GeSiSn quantum cascade lasers based on L-valley intersubband transitions. Appl. Phys. Lett. 2007, 90, 251105. [Google Scholar] [CrossRef]
- Sun, G.; Soref, R.A.; Cheng, H.H. Design of a Si-based lattice-matched room-temperature GeSn/GeSiSn multi-quantum-well mid-infrared laser diode. Opt. Express 2010, 18, 19957–19965. [Google Scholar] [CrossRef]
- Driscoll, K.; Paiella, R. Design of n-type silicon-based quantum cascade lasers for terahertz light emission. J. Appl. Phys. 2007, 102, 093103. [Google Scholar] [CrossRef]
- Driscoll, K.; Paiella, R. Silicon-based injection lasers using electronic intersubband transitions in the L valleys. Appl. Phys. Lett. 2006, 89, 191110. [Google Scholar] [CrossRef]
- Grange, T.; Stark, D.; Scalari, G.; Faist, J.; Persichetti, L.; Di Gaspare, L.; De Seta, M.; Ortolani, M.; Paul, D.J.; Capellini, G.; et al. Room temperature operation of n-type Ge/SiGe terahertz quantum cascade lasers predicted by non-equilibrium Green’s function. Appl. Phys. Lett. 2019, 114, 111102. [Google Scholar] [CrossRef]
- Grange, T.; Mukherjee, S.; Capellini, G.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; Birner, S.; Attiaoui, A.; Moutanabbir, O.; Virgilio, M.; et al. Atomic-scale insights into diffuse heterointerfaces: from three dimensional roughness analysis to a generalized theory of interface scattering. ACS Appl. Mater. Interfaces 2019. First Online. [Google Scholar]
- Wacker, A.; Bastard, G.; Carosella, F.; Ferreira, R.; Dupont, E. Unraveling of free carrier absorption for terahertz radiation in heterostructures. Phys. Rev. B 2011, 84, 205319. [Google Scholar] [CrossRef]
- Gauthier-Lafaye, O.; Julien, F.H.; Cabaret, S.; Lourtioz, J.M.; Strasser, G.; Gornik, E.; Helm, M.; Bois, P. High-power GaAs/AlGaAs quantum fountain unipolar laser emitting at 14.5 μm with 2.5% tunability. Appl. Phys. Lett. 1999, 74, 1537–1539. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Sun, G.; Friedman, L.R.; Soref, R.A. Comparative analysis of optically pumped intersubband lasers and intersubband Raman oscillators. J. Appl. Phys. 1995, 78, 7398–7400. [Google Scholar] [CrossRef]
- Virgilio, M.; et al. Numerical model of electron relaxation in optically pumped Ge/SiGe quantum wells, manuscript in preparation. Under Preparation.
- Sa’ar, A.; Lavon, Y.; Julien, F.H.; Boucaud, P.; Wang, J.; Leburton, J.-P.; Planel, R. Mid-infrared intersubband emission from optically pumped asymmetric coupled quantum wells. Superlattices Microst. 1997, 21, 517–525. [Google Scholar] [CrossRef]
- Choe, J.-W.; Perera, A.G.U.; Fracombe, M.H.; Coon, D.D. Estimates of infrared intersubband emission and its angular dependence in GaAs/AlGaAs multiquantum well structures. Appl. Phys. Lett. 1991, 59, 54–56. [Google Scholar] [CrossRef]
- Helm, M.; England, P.; Colas, E.; DeRosa, F.; Allen, S.J., Jr. Intersubband emission from semiconductor superlattices excited by sequential resonant tunneling. Phys. Rev. Lett. 1989, 63, 74–77. [Google Scholar] [CrossRef]
- Ortolani, M.; Stehr, D.; Wagner, M.; Helm, M.; Pizzi, G.; Virgilio, M.; Grosso, G.; Capellini, G.; De Seta, M. Long intersubband relaxation times in n-type germanium quantum wells. Appl. Phys. Lett. 2011, 99, 201101. [Google Scholar] [CrossRef]
- Sabbagh, D.; Schmidt, J.; Winnerl, S.; Helm, M.; Di Gaspare, L.; De Seta, M.; Virgilio, M.; Ortolani, M. Electron Dynamics in Silicon-Germanium Terahertz Quantum Fountain Structures. ACS Photonics 2016, 3, 403–414. [Google Scholar] [CrossRef]
- Ciano, C.; Virgilio, M.; Bagolini, L.; Baldassarre, L.; Pashkin, A.; Helm, M.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; Capellini, G.; et al. Terahertz absorption-saturation and emission in germanium quantum wells. Opt. Express 2019, submitted. [Google Scholar]
- Scheinert, M.; Sigg, H.; Tsujino, S.; Giovannini, M.; Faist, J. Intersubband Raman laser from GaInAs/AlInAs double quantum wells. Appl. Phys. Lett. 2007, 91, 131108. [Google Scholar] [CrossRef]
- Wang, J.; Leburton, J.-P.; Moussa, Z.; Julien, F.H.; Sa’ar, A. Simulation of optically pumped mid-infrared intersubband semiconductor laser structures. J. Appl. Phys. 1996, 80, 1970–1978. [Google Scholar] [CrossRef]
- Ciano, C.; Virgilio, M.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; Ortolani, M.; Baldassarre, L.; Zoellner, M.H.; Skibitzki, O.; Scalari, G.; et al. Control of electron-state coupling in asymmetric Ge/Si-Ge quantum wells. Phys. Rev. Appl. 2019, 11, 014003. [Google Scholar] [CrossRef]
- Virgilio, M.; Ortolani, M.; Teich, M.; Winnerl, S.; Helm, M.; Sabbagh, D.; Capellini, G.; De Seta, M. Combined effect of electron and lattice temperatures on the long intersubband relaxation times of Ge/SixGe1−x quantum wells. Phys. Rev. B 2014, 89, 045311. [Google Scholar] [CrossRef]
- Julien, F.H.; Lourtioz, J.M.; Hershkorn, N.; Delacourt, D.; Pocholle, J.P.; Papuchon, M.; Planel, R.; Le Roux, G. Optical saturation of intersubband absorption in GaAs-AlxGa1−xAs quantum wells. Appl. Phys. Lett. 1988, 53, 116. [Google Scholar] [CrossRef]
- Tribuzy, C.V.-B.; Ohser, S.; Winnerl, S.; Grenzer, J.; Schneider, H.; Helm, M.; Neuhaus, J.; Dekorsy, T.; Biermann, K.; Künzel, H. Femtosecond pump-probe spectroscopy of intersubband relaxation dynamics in narrow InGaAs/AlAsSb quantum well structures. Appl. Phys. Lett. 2006, 89, 171104. [Google Scholar] [CrossRef]
- Bianchi, V.; Carey, T.; Viti, L.; Li, L.; Linfield, E.H.; Davies, G.; Tredicucci, A.; Yoon, D.; Karagiannidis, P.G.; Lombardi, L.; et al. Terahertz saturable absorbers from liquid phase exfoliation of graphite. Nat. Commun. 2017, 8, 15763. [Google Scholar] [CrossRef]
- Haiml, M.; Grange, R.; Keller, U. Optical characterization of semiconductor saturable absorbers. Appl. Phys. B 2004, 79, 331–339. [Google Scholar] [CrossRef]
- Hoffmann, M.C.; Turchinovich, D. Semiconductor saturable absorbers for ultrafast terahertz signals. Appl. Phys. Lett. 2010, 96, 151110. [Google Scholar] [CrossRef]
- Hübers, H.-W.; Pavlov, S.G.; Shastin, V.N. Terahertz lasers based on germanium and silicon. Semicond. Sci. Technol. 2005, 20, S211–S221. [Google Scholar] [CrossRef]
- Vinh, N.Q.; Greenland, P.T.; Litvinenko, K.; Redlich, B.; van der Meer, A.F.G.; Lynch, S.A.; Warner, M.; Stoneham, A.M.; Aeppli, G.; Paul, D.J.; et al. Silicon as a model ion trap: time domain measurements of donor Rydberg states. Proc. Natl. Acad. Sci. USA 2008, 105, 10649. [Google Scholar] [CrossRef]
- Pavlov, S.G.; Zukavin, R.K.; Shastin, V.N.; Hübers, H.-W. The physical principles of terahertz silicon lasers based on intracenter transitions. Phys. Status Solidi B 2013, 250, 9–36. [Google Scholar] [CrossRef]
- Stroscio, M.A. Phonons in Nanostructures; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Lee, S.-C.; Galbraith, I.; Pidgeon, C.R. Influence of electron temperature and carrier concentration on electron-LO-phonon intersubband scattering in wide GaAs/AlxGa1−xAs quantum wells. Phys. Rev. B 1995, 52, 1874–1881. [Google Scholar] [CrossRef]
- Virgilio, M.; Grosso, G.; Pizzi, G.; De Seta, M.; Capellini, G.; Ortolani, M. Modeling picosecond electron dynamics of pump-probe intersubband spectroscopy in n-type Ge/SiGe quantum wells. Phys. Rev. B 2012, 86, 205317. [Google Scholar] [CrossRef]
- Mueller, T.; Parz, W.; Strasser, G.; Unterrainer, K. Influence of carrier-carrier interaction on time-dependent intersubband absorption in a semiconductor quantum well. Phys. Rev. B 2004, 70, 155324. [Google Scholar] [CrossRef]
- Lever, L.; Valavanis, A.; Ikonic, Z.; Kelsall, R.W. Simulated [111] Si-SiGe terahertz quantum cascade laser. Appl. Phys. Lett. 2008, 92, 021124. [Google Scholar] [CrossRef]
- Paul, D.J. The progress towards terahertz quantum cascade lasers on silicon substrates. Laser Photon. Rev. 2010, 4, 610–632. [Google Scholar] [CrossRef]
- Lever, L.; Valavanis, A.; Evans, C.A.; Ikonic, Z.; Kelsall, R.W. The importance of electron temperature in silicon-based terahertz quantum cascade lasers. Appl. Phys. Lett. 2009, 95, 131103. [Google Scholar] [CrossRef]
- Virgilio, M.; Sabbagh, D.; Ortolani, M.; Di Gaspare, L.; Capellini, G.; De Seta, M. Physical mechanisms of intersubband-absorption linewidth broadening in s-Ge/SiGe quantum wells. Phys. Rev. B 2014, 90, 155420. [Google Scholar] [CrossRef]
- Harrison, P.; Valavanis, A. Quantum Wells, Wires and Dots: Theoretical and Computational Physics of Semiconductor Nanostructures, 3rd ed.; John Wiley & Sons Ltd.: England, UK, 2011. [Google Scholar]
- Hercher, M. An analysis of Saturable Absorbers. Appl. Opt. 1967, 6, 947–954. [Google Scholar] [CrossRef] [PubMed]
- Scheinert, M. Optical Pumping: A Possible Approach towards a SiGe Quantum Cascade Laser? Ph.D. Thesis, University of Neuchatel, Neuchâtel, Switzerland, 2007. [Google Scholar]
- Bransden, B.H.; Joachin, C.J. Physics of Atoms and Molecules; Prentice Hall: Harlow, UK, 2003. [Google Scholar]
- Lutgen, S.; Kaindl, R.A.; Woerner, M.; Elsaesser, T.; Hase, A.; Künzel, H.; Gulia, M.; Meglio, D.; Lugli, P. Nonequilibrium dynamics in a quasi-two-dimensional electron plasma after ultrafast intersubband excitation. Phys. Rev. Lett. 1996, 77, 3657. [Google Scholar] [CrossRef] [PubMed]
- Julien, F.H.; Moussa, Z.; Boucaud, P.; Lavon, Y.; Sa’ar, A.; Wang, J.; Leburton, J.-P.; Berger, V.; Nagle, J.; Planel, R. Intersubband mid-infrared emission in optically pumped quantum wells. Superlattices Microst. 1996, 19, 70–79. [Google Scholar] [CrossRef]
| Sample | Ip,sat,theo (kW/cm2) | Ip,sat,num (kW/cm2) | Ip,sat,exp (kW/cm2) |
|---|---|---|---|
| S1 (Ntot = 7 × 1011 cm−2) | 21 | 17 ± 2 | 7.2 ± 2.0 |
| S6 (Ntot = 1 × 1011 cm−2) | 23 | 15 ± 2 | 7.2 ± 2.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciano, C.; Virgilio, M.; Bagolini, L.; Baldassarre, L.; Rossetti, A.; Pashkin, A.; Helm, M.; Montanari, M.; Persichetti, L.; Di Gaspare, L.; et al. Electron Population Dynamics in Optically Pumped Asymmetric Coupled Ge/SiGe Quantum Wells: Experiment and Models. Photonics 2020, 7, 2. https://doi.org/10.3390/photonics7010002
Ciano C, Virgilio M, Bagolini L, Baldassarre L, Rossetti A, Pashkin A, Helm M, Montanari M, Persichetti L, Di Gaspare L, et al. Electron Population Dynamics in Optically Pumped Asymmetric Coupled Ge/SiGe Quantum Wells: Experiment and Models. Photonics. 2020; 7(1):2. https://doi.org/10.3390/photonics7010002
Chicago/Turabian StyleCiano, Chiara, Michele Virgilio, Luigi Bagolini, Leonetta Baldassarre, Andrea Rossetti, Alexej Pashkin, Manfred Helm, Michele Montanari, Luca Persichetti, Luciana Di Gaspare, and et al. 2020. "Electron Population Dynamics in Optically Pumped Asymmetric Coupled Ge/SiGe Quantum Wells: Experiment and Models" Photonics 7, no. 1: 2. https://doi.org/10.3390/photonics7010002
APA StyleCiano, C., Virgilio, M., Bagolini, L., Baldassarre, L., Rossetti, A., Pashkin, A., Helm, M., Montanari, M., Persichetti, L., Di Gaspare, L., Capellini, G., Paul, D. J., Scalari, G., Faist, J., De Seta, M., & Ortolani, M. (2020). Electron Population Dynamics in Optically Pumped Asymmetric Coupled Ge/SiGe Quantum Wells: Experiment and Models. Photonics, 7(1), 2. https://doi.org/10.3390/photonics7010002








