Task-Independent Computational Abilities of Semiconductor Lasers with Delayed Optical Feedback for Reservoir Computing
Abstract
:1. Introduction
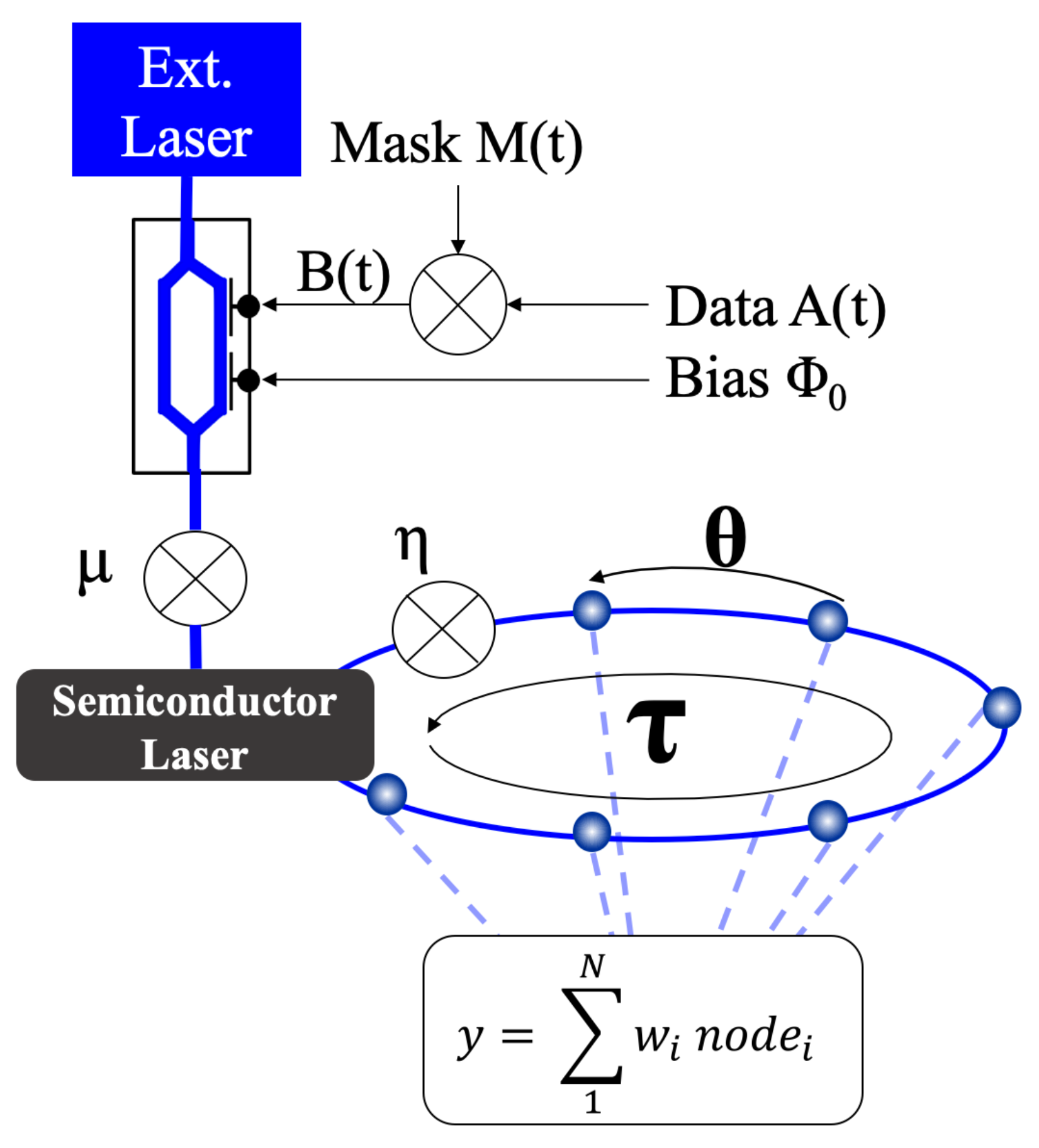
2. Reservoir Computing with a Semiconductor Laser and Delayed Feedback
2.1. Rate Equation Model
2.2. Pre- and Post-Processing
3. Timeseries Prediction
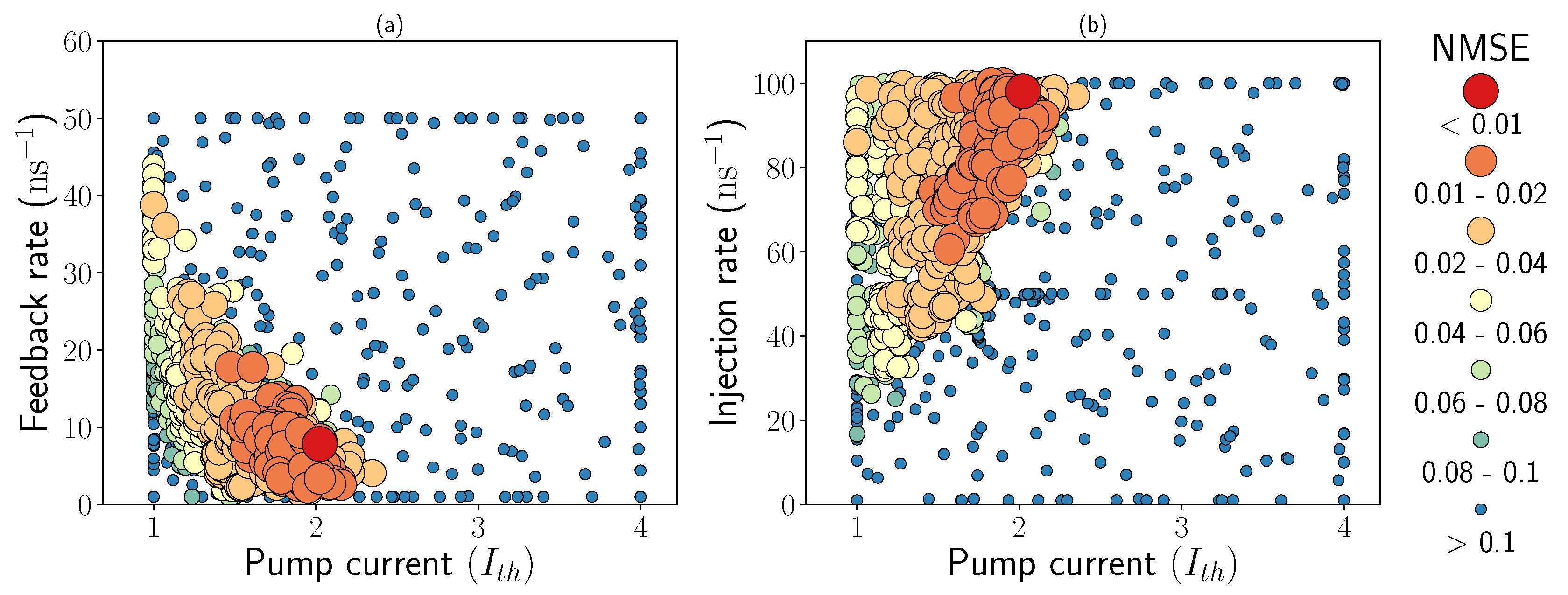
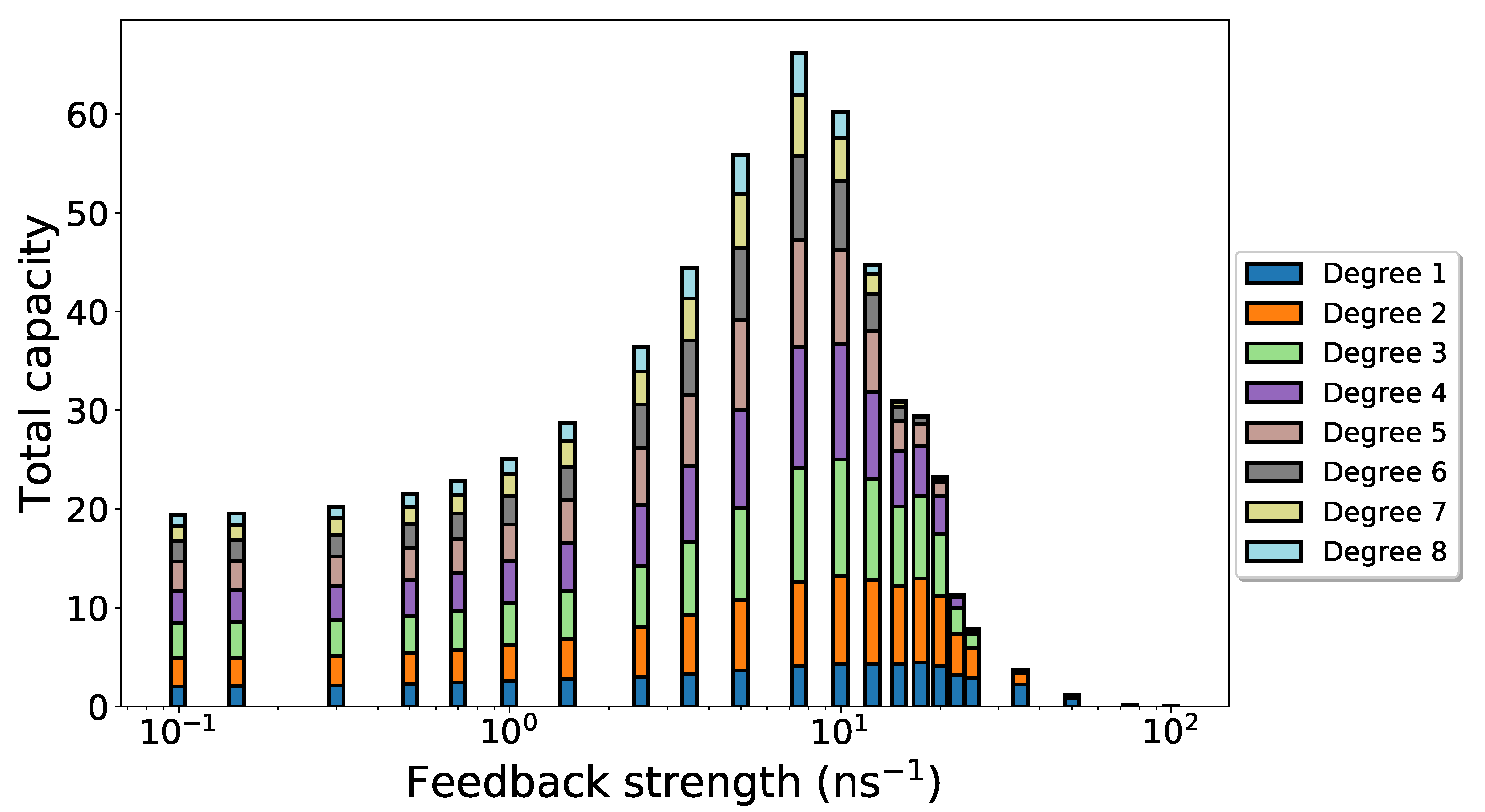
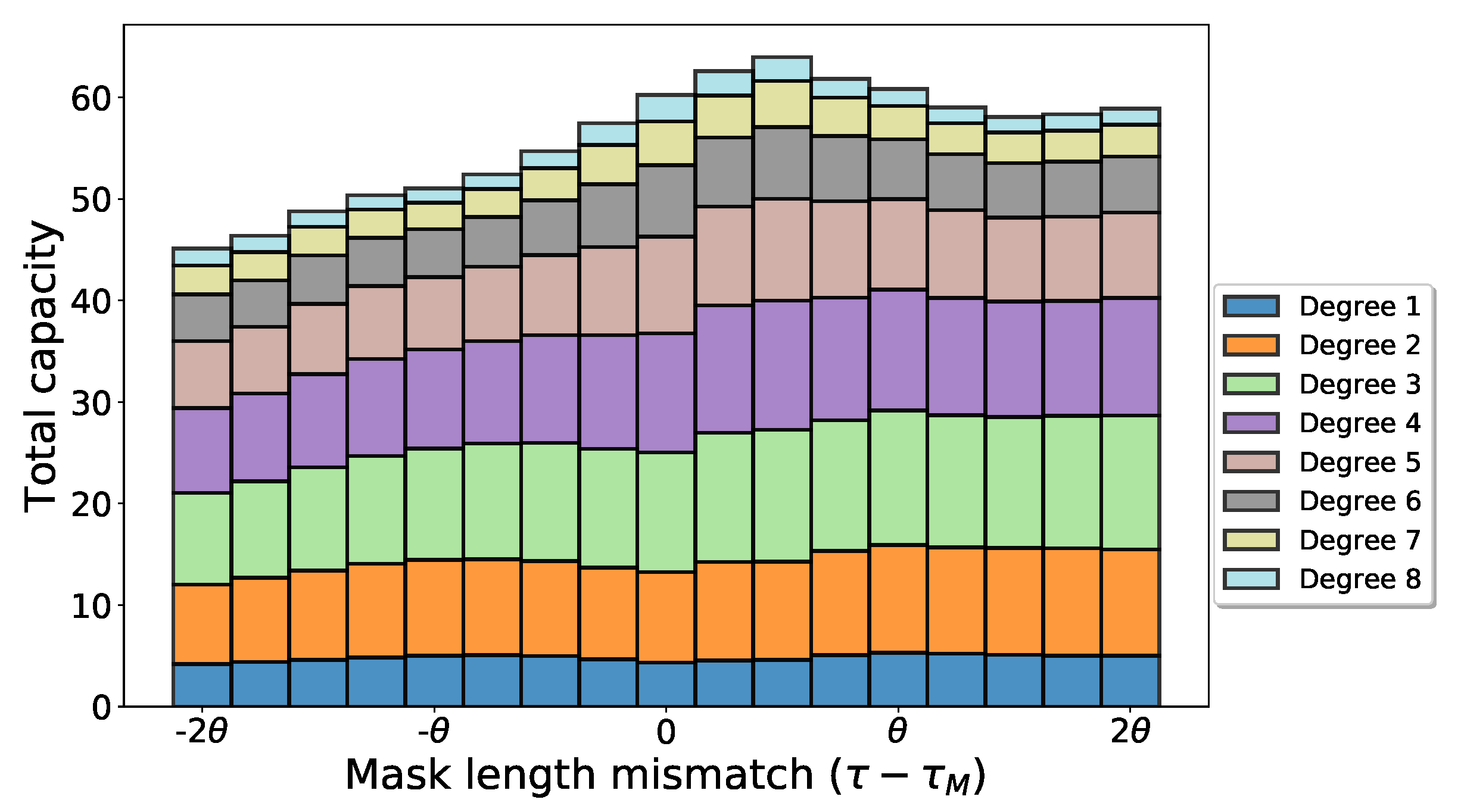
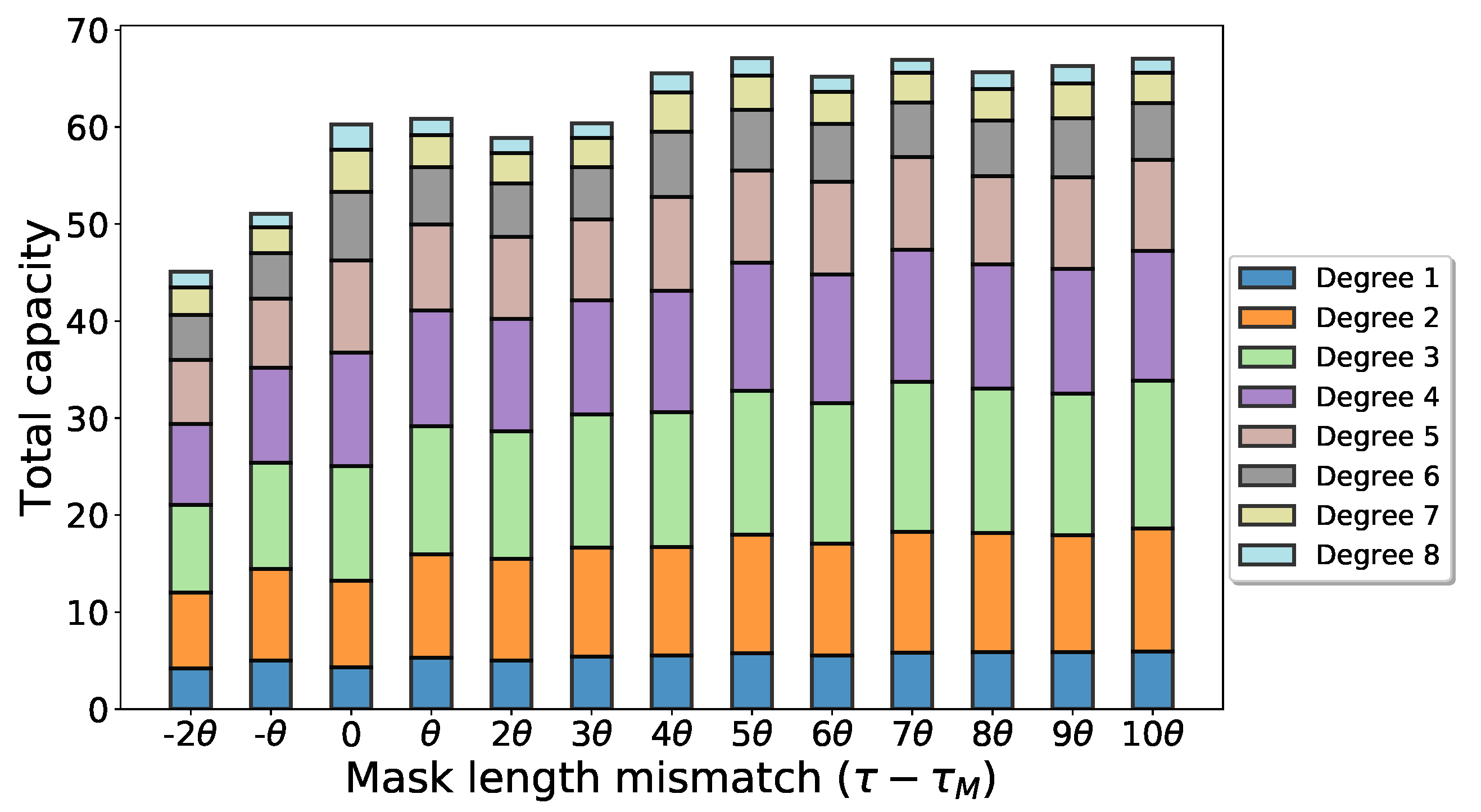
4. Task-Independent Computational Performance
Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 1097–1105. [Google Scholar] [CrossRef]
- Van der Sande, G.; Brunner, D.; Soriano, M.C. Advances in photonic reservoir computing. Nanophotonics 2017, 6, 561–576. [Google Scholar] [CrossRef]
- Vandoorne, K.; Dierckx, W.; Schrauwen, B.; Verstraeten, D.; Baets, R.; Bienstman, P.; Van Campenhout, J. Toward optical signal processing using photonic reservoir computing. Opt. Express 2008, 16, 11182–11192. [Google Scholar] [CrossRef] [PubMed]
- Vandoorne, K.; Dambre, J.; Verstraeten, D.; Schrauwen, B.; Bienstman, P. Parallel reservoir computing using optical amplifiers. IEEE Trans. Neural Netw. 2011, 22, 1469–1481. [Google Scholar] [CrossRef] [PubMed]
- Vandoorne, K.; Mechet, P.; Van Vaerenbergh, T.; Fiers, M.; Morthier, G.; Verstraeten, D.; Schrauwen, B.; Dambre, J.; Bienstman, P. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun. 2014, 5, 2541. [Google Scholar] [CrossRef] [PubMed]
- Brunner, D.; Fischer, I. Reconfigurable semiconductor laser networks based on diffractive coupling. Opt. Lett. 2015, 40, 3854–3857. [Google Scholar] [CrossRef] [PubMed]
- Appeltant, L.; Soriano, M.C.; Van der Sande, G.; Danckaert, J.; Massar, S.; Dambre, J.; Schrauwen, B.; Mirasso, C.R.; Fischer, I. Information processing using a single dynamical node as complex system. Nat. Commun. 2011, 2, 468. [Google Scholar] [CrossRef] [PubMed]
- Paquot, Y.; Dambre, J.; Schrauwen, B.; Haelterman, M.; Massar, S. Reservoir computing: A photonic neural network for information processing. In Proceedings of the SPIE Photonics Europe on International Society for Optics and Photonics, Brussels, Belgium, 12–16 April 2010; p. 77280B. [Google Scholar]
- Paquot, Y.; Duport, F.; Smerieri, A.; Dambre, J.; Schrauwen, B.; Haelterman, M.; Massar, S. Optoelectronic reservoir computing. Sci. Rep. 2012, 2, 287. [Google Scholar] [CrossRef] [PubMed]
- Brunner, D.; Soriano, M.C.; Mirasso, C.R.; Fischer, I. Parallel photonic information processing at gigabyte per second data rates using transient states. Nat. Commun. 2013, 4, 1364. [Google Scholar] [CrossRef] [PubMed]
- Takano, K.; Sugano, C.; Inubushi, M.; Yoshimura, K.; Sunada, S.; Kanno, K.; Uchida, A. Compact reservoir computing with a photonic integrated circuit. Opt. Express 2018, 26, 29424–29439. [Google Scholar] [CrossRef] [PubMed]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; Van der Sande, G. Simultaneous computation of two independent tasks using reservoir computing based on a single photonic nonlinear node with optical feedback. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 3301–3307. [Google Scholar] [CrossRef] [PubMed]
- Vatin, J.; Rontani, D.; Sciamanna, M. Enhanced performance of a reservoir computer using polarization dynamics in VCSELs. Opt. Lett. 2018, 43, 4497–4500. [Google Scholar] [CrossRef] [PubMed]
- Bueno, J.; Brunner, D.; Soriano, M.C.; Fischer, I. Conditions for reservoir computing performance using semiconductor lasers with delayed optical feedback. Opt. Express 2017, 25, 2401–2412. [Google Scholar] [CrossRef] [PubMed]
- Kuriki, Y.; Nakayama, J.; Takano, K.; Uchida, A. Impact of input mask signals on delay-based photonic reservoir computing with semiconductor lasers. Opt. Express 2018, 26, 5777–5788. [Google Scholar] [CrossRef] [PubMed]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; Van der Sande, G. Fast photonic information processing using semiconductor lasers with delayed optical feedback: Role of phase dynamics. Opt. Express 2014, 22, 8672–8686. [Google Scholar] [CrossRef] [PubMed]
- Duport, F.; Schneider, B.; Smerieri, A.; Haelterman, M.; Massar, S. All-optical reservoir computing. Opt. Express 2012, 20, 22783–22795. [Google Scholar] [CrossRef] [PubMed]
- Duport, F.; Smerieri, A.; Akrout, A.; Haelterman, M.; Massar, S. Fully analogue photonic reservoir computer. Sci. Rep. 2016, 6, 22381. [Google Scholar] [CrossRef] [PubMed]
- Weigend, A.S.; Gershenfeld, N.A. The Future of Time Series. In Time Series Prediction: Forecasting the Future and Understanding the Past; Addison-Wesley: Boston, MA, USA, 1993. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Jaeger, H. Short Term Memory in Echo State Networks; GMD-Report 152; GMD–German National Research Institute for Computer Science: Sankt Augustin, Germany, 2002; Available online: http://www.faculty.jacobs-university.de/hjaeger/pubs/STMEchoStatesTechRep.pdf (accessed on 8 September 2019).
- Dambre, J.; Verstraeten, D.; Schrauwen, B.; Massar, S. Information Processing Capacity of Dynamical Systems. Sci. Rep. 2012, 2, 514. [Google Scholar] [CrossRef] [PubMed]

| Parameters | Designation | Value Used in Bayesian Optimization |
|---|---|---|
| Linewidth enhancement factor | α | 3.0 |
| Loss | Γ | 1 ps−1 |
| Threshold gain | g | 1 ps−1 |
| Differential gain | ξ | 5000 s−1 |
| Spontaneous emission factor | β | 10−6 |
| Carrier-lifetime | T | 1 ns |
| Threshold pump-current | Ith | 16 mA |
| Pump-current | I | scanned over [Ith;3Ith] |
| Feedback rate | η | scanned over [0; 50 ns−1] |
| Injection rate | μ | scanned over [0; 100 ns−1] |
| Amplitude of injected field | 200 | |
| Bias voltage of the MZM | Φ0 | |
| Constant feedback phase | Ω | 0 |
| Node distance | θ | 20 ps |
| Number of nodes | N | 200 |
| Delay time | τ | 4 ns |
| Mask length | τM | 4 ns |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harkhoe, K.; Van der Sande, G. Task-Independent Computational Abilities of Semiconductor Lasers with Delayed Optical Feedback for Reservoir Computing. Photonics 2019, 6, 124. https://doi.org/10.3390/photonics6040124
Harkhoe K, Van der Sande G. Task-Independent Computational Abilities of Semiconductor Lasers with Delayed Optical Feedback for Reservoir Computing. Photonics. 2019; 6(4):124. https://doi.org/10.3390/photonics6040124
Chicago/Turabian StyleHarkhoe, Krishan, and Guy Van der Sande. 2019. "Task-Independent Computational Abilities of Semiconductor Lasers with Delayed Optical Feedback for Reservoir Computing" Photonics 6, no. 4: 124. https://doi.org/10.3390/photonics6040124
APA StyleHarkhoe, K., & Van der Sande, G. (2019). Task-Independent Computational Abilities of Semiconductor Lasers with Delayed Optical Feedback for Reservoir Computing. Photonics, 6(4), 124. https://doi.org/10.3390/photonics6040124






