Optical Image Encryption System Using Several Tilted Planes

Abstract

A well-known technique for optical image encryption is the double random phase encoding (DRPE) technique, which uses two random phase masks (RPMs), one RPM at the input plane of the encryption system and the other RPM at the Fourier plane of the optical system, in order to obtain the encrypted image. In this work, we propose to use tilted planes for the Fourier and the output planes of the optical DRPE encryption system with the purpose of adding two new security keys, which are the angles of the tilted planes. The optical diffraction on a tilted plane is computed using the angular spectrum of plane waves and the coordinate rotation in the Fourier domain. The tilted distributions at the intermediate and output planes of the optical DRPE encryption system are the second RPM and the encrypted image, respectively. The angles of the tilted planes allow improvement to the security of the encrypted image. We perform several numerical simulations with the purpose of demonstrating the validity and feasibility of the proposed image encryption system.

1. Introduction

The double random phase encoding (DRPE) technique is a very important technique for optical image encryption [1,2,3,4,5]. Initially, the DRPE technique was optically implemented using a 4f-processor in the Fourier domain [6]. Later, the DRPE was extended to the Fresnel [7,8] and the fractional Fourier domains [9], to increase the security level of the encryption and decryption systems.

We propose to use tilted planes for the optical DRPE technique in the Fresnel domain, with the purpose of encrypting and decrypting images. The proposed tilted planes for the optical DRPE encryption system are the intermediate and output planes. The tilted planes contain the second RPM used in the DRPE technique and the encrypted image, respectively. The use of the tilted planes for the optical DRPE technique allows to introduction of new security keys, given by the two tilt angles. The proposed DRPE encryption system of this work uses the free optical propagation on tilted planes and this propagation is computed by using the angular spectrum of plane waves and the coordinate rotation in the Fourier domain [10]. The two tilt angles and the propagations distances are security keys that permit improvements to the security of the encrypted image. The proposed security system is verified by using numerical simulations of the encryption and decryption systems.

2. Optical Diffraction on Tilted Planes

We use the technique based on the angular spectrum of plane waves and coordinate rotation in the Fourier domain described in reference [10] in order to compute the optical diffraction on tilted planes. Let $g(x,y)$ and $G(u,v)$ be a source field and its spectrum, in the source plane; the coordinates of the source plane are denoted by x and y. The distance between the source plane and the reference plane is $d>0$ and the optical propagation of the source field is along the z axis. Let $G_d(u,v)$ be the source spectrum in an intermediate plane or reference plane, which is parallel to the source plane, and that its coordinates share the origin with the reference coordinates; the coordinates of the reference plane are represented by $x^{\prime }$ and $y^{\prime }=\widehat{y}$. 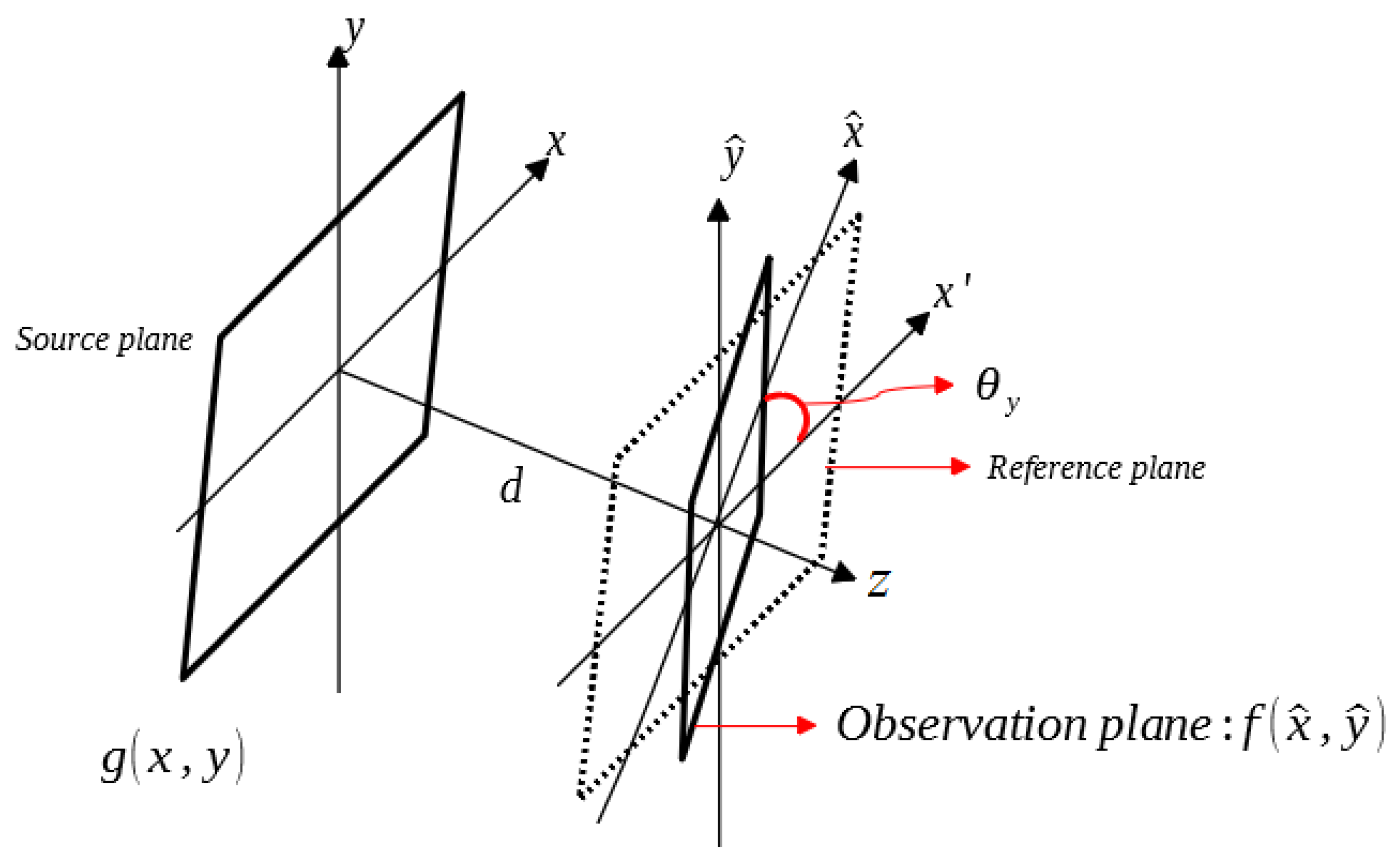Figure 1 shows the optical scheme for the diffraction on a tilted plane where the coordinates of the observation plane are denoted by $\widehat{x}$ and $\widehat{y}$. Using the standard formula of the angular spectrum of plane waves [6], we can obtain

$$\begin{array}{c}\hfill G_d(u,v)=G(u,v)exp\left\{i2\pi d{\left({\lambda }^{-2}-u^2-v^2\right)}^{1/2}\right\},\end{array}$$

(1)

where u and v are the spatial frequency coordinates and $\lambda$ is the wavelength. The rotation matrix $\mathbf{T}$ can be used to transform the reference coordinates into the observation coordinates. Therefore, the wave vectors of these coordinates can also be transformed into each other by

$$\begin{array}{c}\hfill \widehat{\mathit{k}}=\mathbf{T}\mathit{k},\mathit{k}={\mathbf{T}}^{-1}\widehat{\mathit{k}},\end{array}$$

(2)

with

$$\begin{array}{cc}\hfill \widehat{\mathit{k}}=& 2\pi \left[\begin{array}{ccc}\widehat{u}& \widehat{v}& \widehat{w}(\widehat{u},\widehat{v})\end{array}\right],\widehat{w}(\widehat{u},\widehat{v})={\left({\lambda }^{-2}-{\widehat{u}}^2-{\widehat{v}}^2\right)}^{1/2},\hfill \\ \hfill \mathit{k}=& 2\pi \left[\begin{array}{ccc}u& v& w(u,v)\end{array}\right],w(u,v)={\left({\lambda }^{-2}-u^2-v^2\right)}^{1/2},\hfill \\ \hfill {\mathbf{T}}^{-1}=& \left[\begin{array}{ccc}{a}_1& a_2& a_3\\ a_4& a_5& a_6\\ a_7& a_8& a_9\end{array}\right],\hfill \end{array}$$

(3)

where $2\pi w(u,v)$ represents the component in z direction of the wave vector. The spatial frequency coordinates $(u,v)$ and $(\widehat{u},\widehat{v})$ are related to the source spectrum in the reference (without tilt) and observation (with tilt) planes, respectively. The rotation matrices ${\mathbf{T}}^{-1}$ that produce a tilted plane for Figure 1 are

$$\begin{array}{c}\hfill {\mathbf{T}}_x^{-1}\left({\theta }_x\right)=\left[\begin{array}{ccc}1& 0& 1\\ 0& cos{\theta }_x& -sin{\theta }_x\\ 0& sin{\theta }_x& cos{\theta }_x\end{array}\right],{\mathbf{T}}_y^{-1}\left({\theta }_y\right)=\left[\begin{array}{ccc}cos{\theta }_y& 0& sin{\theta }_y\\ 0& 1& 0\\ -sin{\theta }_y& 0& cos{\theta }_y\end{array}\right],\end{array}$$

(4)

where the rotation matrix ${\mathbf{T}}_x^{-1}\left({\theta }_x\right)$ is a rotation around the x axis, which produces a tilted plane with respect to the y axis and the rotation matrix ${\mathbf{T}}_y^{-1}\left({\theta }_y\right)$ is a rotation around the y axis and this produces a tilted plane with respect to the x axis. The tilted plane of Figure 1 is described by the rotation matrix ${\mathbf{T}}_y^{-1}\left({\theta }_y\right)$.

The Fourier frequencies in the reference coordinates are related to those in the observation coordinates in the following form

$$\begin{array}{c}\hfill u=\alpha (\widehat{u},\widehat{v})=a_1\widehat{u}+a_2\widehat{v}+a_3\widehat{w}(\widehat{u},\widehat{v}),v=\beta (\widehat{u},\widehat{v})=a_4\widehat{u}+a_5\widehat{v}+a_6\widehat{w}(\widehat{u},\widehat{v}).\end{array}$$

(5)

The spectrum in the observation coordinate is given by the spectrum in the reference coordinate according to

$$\begin{array}{c}\hfill F(\widehat{u},\widehat{v})=G_d(\alpha (\widehat{u},\widehat{v}),\beta (\widehat{u},\widehat{v})).\end{array}$$

(6)

The complex amplitudes of the field in the observation coordinates with the same energy as the complex amplitudes of the field in the reference coordinates are given by

$$\begin{array}{c}\hfill f(\widehat{x},\widehat{y})=\underset{-\infty }{\overset{+\infty }{\int }}\underset{-\infty }{\overset{+\infty }{\int }}F(\widehat{u},\widehat{v})\left|J(\widehat{u},\widehat{v})\right|exp\left\{i2\pi (\widehat{x}\widehat{u}+\widehat{y}\widehat{v})\right\}\mathrm{d}\widehat{u}\mathrm{d}\widehat{v}={\mathcal{F}}^{-1}\left\{F(\widehat{u},\widehat{v})\left|J(\widehat{u},\widehat{v})\right|\right\},\end{array}$$

(7)

where the Jacobian is

$$\begin{array}{c}\hfill J(\widehat{u},\widehat{v})=\frac{\partial \alpha }{\partial \widehat{u}}\frac{\partial \beta }{\partial \widehat{v}}-\frac{\partial \alpha }{\partial \widehat{v}}\frac{\partial \beta }{\partial \widehat{u}}=\frac{1}{\widehat{w}(\widehat{u},\widehat{v})}\left[(a_2{a}_6-a_3{a}_5)\widehat{u}+(a_3{a}_4-a_1{a}_6)\widehat{v}\right]+(a_1{a}_5-a_2{a}_4).\end{array}$$

(8)

3. DRPE Using Tilted Plane: Optical Image Encryption and Decryption Systems

The DRPE technique uses two RPMs in order to encrypt the information of the original image $f(x_1,y_1)$; the values of $f(x_1,y_1)$ are in the interval of [0, 1]. The two RPMs are represented by

$$\begin{array}{c}\hfill r(x_1,y_1)=exp\left\{i2\pi s(x_1,y_1)\right\},h(x_2,y_2)=exp\left\{i2\pi n(x_2,y_2)\right\},\end{array}$$

(9)

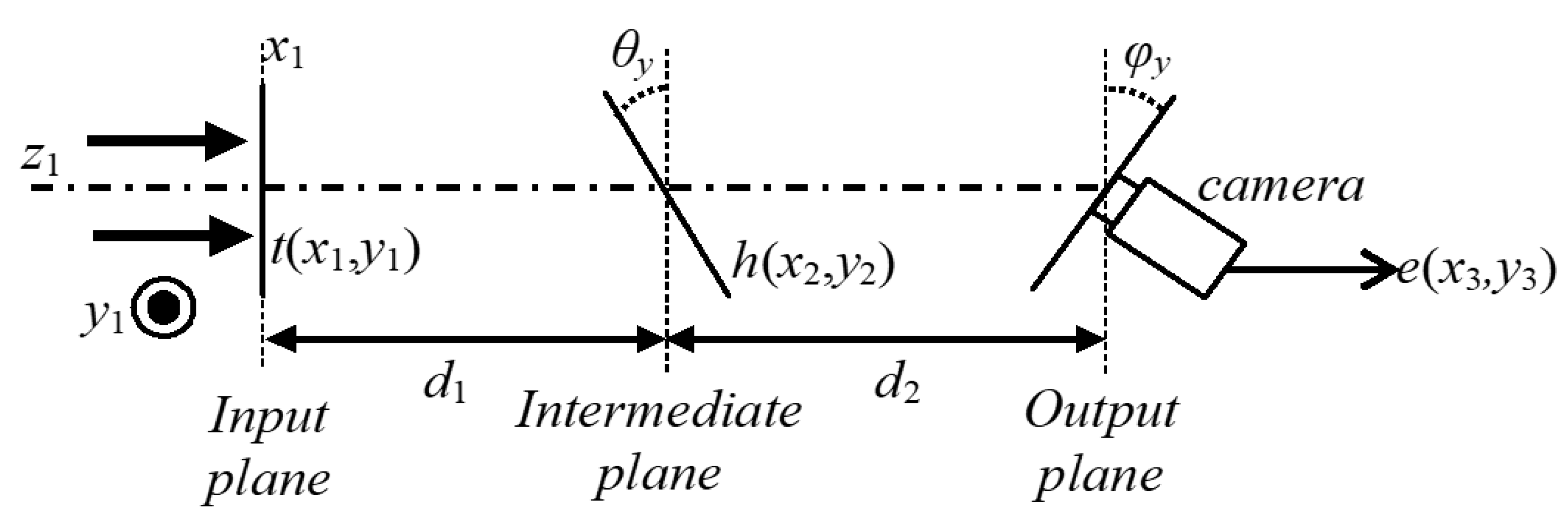
where $x_1$, $y_1$, $x_2$ and $y_2$ are spatial coordinates, $s(x_1,y_1)$ and $n(x_2,y_2)$ are normalized positive function generated randomly, independent statistically and their values are uniformly distributed in the interval of [0, 1] [1]. Figure 2 depicts the optical scheme based on the DRPE technique and the optical diffraction on two tilted planes.

The distribution $t(x_1,y_1)$ of the input plane of the encryption system of Figure 2 is composed by the original image $f(x_1,y_1)$ to encrypt placed against the RPM $r(x_1,y_1)$

$$\begin{array}{c}\hfill t(x_1,y_1)=f(x_1,y_1)r(x_1,y_1)=f(x_1,y_1)exp\left\{i2\pi s(x_1,y_1)\right\}.\end{array}$$

(10)

The optical diffraction of the distribution $t(x_1,y_1)$ on the tilted plane placed at the distance $d_1$ with respect to the input plane of the encryption system is given by the distribution $p(x_2,y_2)$ and it is computed using the procedure described in Section 2. We use the following parameters and functions to compute $p(x_2,y_2)$

$$T_{d_1}(u,v)=\mathcal{F}\left\{t(x_1,y_1)\right\}exp\left\{i2\pi d_1{\left({\lambda }^{-2}-u^2-v^2\right)}^{1/2}\right\},$$

(11)

$${\mathbf{T}}_y^{-1}\left({\theta }_y\right)=\left[\begin{array}{ccc}cos{\theta }_y& 0& sin{\theta }_y\\ 0& 1& 0\\ -sin{\theta }_y& 0& cos{\theta }_y\end{array}\right],$$

(12)

$$u=\alpha (\widehat{u},\widehat{v})=\widehat{u}cos{\theta }_y+\widehat{w}(\widehat{u},\widehat{v})sin{\theta }_y,v=\beta (\widehat{u},\widehat{v})=\widehat{v},\widehat{w}(\widehat{u},\widehat{v})={\left({\lambda }^{-2}-{\widehat{u}}^2-{\widehat{v}}^2\right)}^{1/2},$$

(13)

$$P(\widehat{u},\widehat{v})=T_d(\alpha (\widehat{u},\widehat{v}),\beta (\widehat{u},\widehat{v}))=T_d(\widehat{u}cos{\theta }_y+\widehat{w}(\widehat{u},\widehat{v})sin{\theta }_y,\widehat{v}),$$

(14)

$$p(x_2,y_2)=\underset{-\infty }{\overset{+\infty }{\int }}\underset{-\infty }{\overset{+\infty }{\int }}P(\widehat{u},\widehat{v})\left|J(\widehat{u},\widehat{v})\right|exp\left\{i2\pi (x_2\widehat{u}+y_2\widehat{v})\right\}\mathrm{d}\widehat{u}\mathrm{d}\widehat{v}={\mathcal{F}}^{-1}\left\{P(\widehat{u},\widehat{v})\left|J(\widehat{u},\widehat{v})\right|\right\},$$

(15)

$$J(\widehat{u},\widehat{v})=cos{\theta }_y-\frac{sin{\theta }_y}{\widehat{w}(\widehat{u},\widehat{v})}\widehat{u}.$$

(16)

The RPM $h(x_2,y_2)$ is multiplied by the image $p(x_2,y_2)$ with the purpose of obtaining the intermediate distribution $q(x_2,y_2)=h(x_2,y_2)p(x_2,y_2)$. The image $q(x_2,y_2)$ is optically tilted to the intermediate plane of the encryption system and the resulting image is the input for the second optical diffraction on the tilted plane placed at the distance $d_2$ with respect to the intermediate plane, which corresponds to the output plane of the encryption system. We apply again the approach described in Section 2 using the optically tilted distribution obtained from $q(x_2,y_2)$, the propagation distance $d_2$ and the rotation matrix ${\mathbf{T}}_y^{-1}\left({\phi }_y\right)$, in order to compute the encrypted image $e(x_3,y_3)$.

The RPM $h(x_2,y_2)$, the propagation distances $d_1$ and $d_2$, and the angles of the tilted planes ${\theta }_y$ and ${\phi }_y$, are the security keys of the encryption system and the RPM $r(x_1,y_1)$ is used to spread the information content of the original image $f(x_1,y_1)$ onto the encrypted image $e(x_3,y_3)$ [1]. When the angles of the tilted planes are equal to ${\theta }_y=0^{\circ }$ and ${\phi }_y=0^{\circ }$, the proposed encryption system in this work is reduced to the DRPE encryption system in the Fresnel domain [8].

The decryption system is performed by digital computations and it is computed in the reverse order of the encryption system using the encrypted image $e(x_3,y_3)$ and the method presented in Section 2 along with the following five security keys: the complex conjugated of the RPM $h(x_2,y_2)$, the propagation distances $d_1$ and $d_2$, and the two angles $-{\theta }_y$ and $-{\phi }_y$. For the decryption system, the input and intermediate planes are tilted at an angle of $-{\phi }_y$ and $-{\theta }_y$, respectively. The output plane of the decryption system is not tilted.

A second rotation around the x axis (${\theta }_x$ or ${\phi }_x$ for the intermediate and output planes of the encryption system, respectively) produces a tilted plane with respect to the y axis and the method of Section 2 can be used in order to obtain the optical diffraction over the final tilted plane. The two new tilt angles ${\theta }_x$ and ${\phi }_x$ can be considered to be new security keys of the proposed encryption and decryption systems.

The results of the numerical simulations for the security system proposed in this section are shown in Figure 3. The original image $f(x_1,y_1)$ to encrypt and the random code image $s(x_1,y_1)$ of the RPM $r(x_1,y_1)$ are depicted in Figure 3a,b, respectively. The random code image $n(x_2,y_2)$ of the RPM $h(x_2,y_2)$ has different values but the same appearance of the image shown in Figure 3b. The encrypted image $e(x_3,y_3)$ is presented in Figure 3c for the security keys: $d_1=200$ mm, $d_2=300$ mm, ${\theta }_y=14.5^{\circ }$, ${\phi }_y=12.7^{\circ }$ and the RPM $h(x_2,y_2)$. This encrypted image is a noisy pattern that does not reveal any information of the original image $f(x_1,y_1)$. When the decryption system is performed using the encrypted image $e(x_3,y_3)$ and the five correct security keys ($d_1$, $d_2$, ${\theta }_y$, ${\phi }_y$ and $h(x_2,y_2)$), the original image $f(x_1,y_1)$ is retrieved at the output plane of the decryption system. The decrypted image $\tilde{f}(x_1,y_1)$ is depicted in Figure 3d. We use the metric of the root mean square error (RMSE) between the decrypted images $\tilde{f}(x_1,y_1)$ and the original image $f(x_1,y_1)$

$$\mathrm{RMSE}={\left(\frac{{\sum }_{x_1=1}^M{\sum }_{y_1=1}^N{[f(x_1,y_1)-\tilde{f}(x,y)]}^2}{{\sum }_{x_1=1}^M{\sum }_{y_1=1}^N{\left[f(x_1,y_1)\right]}^2}\right)}^{\frac{1}{2}},$$

(17)

with the purpose of evaluating the image quality of the decrypted images. The values of the RMSE metric to evaluate the image quality are values between 0 and 1; when the value of the RMSE is near or equal to 0, the image quality of the decrypted image is very good while the values of the RMSE near or equal to 1 represent a worse image quality of the decrypted image. The RMSE between the original image of Figure 3a and the decrypted image of Figure 3d is $0.027$.

The noisy images presented in Figure 3e,f correspond to the decrypted images when the wrong tilt angle ${\theta }_y=14.4^{\circ }$ or ${\phi }_y=12.8^{\circ }$ are used in the decryption system, respectively. If the RPM $h(x_2,y_2)$ is wrong in the decryption system, the decrypted image obtained will be similar to the image shown in Figure 3e. The values of the RMSEs between the original image of Figure 3a and the decrypted images of Figure 3e,f are $0.91$ and $0.87$, respectively. When we use the correct values of the all five security keys in the decryption system, the properly retrieval of the original image at the output plane of the decryption system is possible.

We evaluate the sensitivity on the tilt angles ${\theta }_y$ and ${\phi }_y$ for the decrypted images by introducing small errors in these and leaving fixed the other three security keys ($d_1$, $d_2$ and $h(x_2,y_2)$) with their correct values in the decryption system. The RMSEs between the original image and the decrypted images are computed to measure the level of protection on the encrypted image. For this deviation test of the tilt angles on their correct values for the decryption process, it is introduced a small error that varies between $-1\times {10}^{-5}$ and $1\times {10}^{-5}$ and then, for each variation is calculated the RMSE. We use the right value for the tilt angle ${\phi }_y$ when a small error is introduced for the tilt angle ${\theta }_y$, and vice versa. From these numerical simulations, it was found that the tilt angles ${\phi }_y$ and ${\theta }_y$ are sensitive to a variation of $1\times {10}^{-4}$ and $1\times {10}^{-3.5}$, respectively. The tilt angle ${\phi }_y$ is more sensitive than the tilt angle ${\theta }_y$, because the first optical diffraction in the decryption system is from the tilted plane with a tilt angle $-{\phi }_y$.

4. Conclusions

We have proposed a new version of the DRPE encryption and decryption system using the optical diffraction on two tilted planes. The new security keys given by the angles of the tilted planes, permits increase in the security of the encrypted image. The security of the presented system was also increased due to the nonlinearity introduced by the tilt of the intermediate and output planes of the proposed encryption system. The encryption and decryption systems have five security keys represented by two propagation distances, two tilt angles, and one RPM. All these security keys allow improvement to the security of the encrypted image against to the brute force and plaintext attacks. Finally, the retrieval of the original image at the output plane of the decryption system is only possible when the values of the five security keys for the decryption system are the same that were used in the encryption system.