A Refractive Index Sensor Based on a Fabry–Perot Interferometer Manufactured by NIR Laser Microdrilling and Electric Arc Fusion †
Abstract
1. Introduction
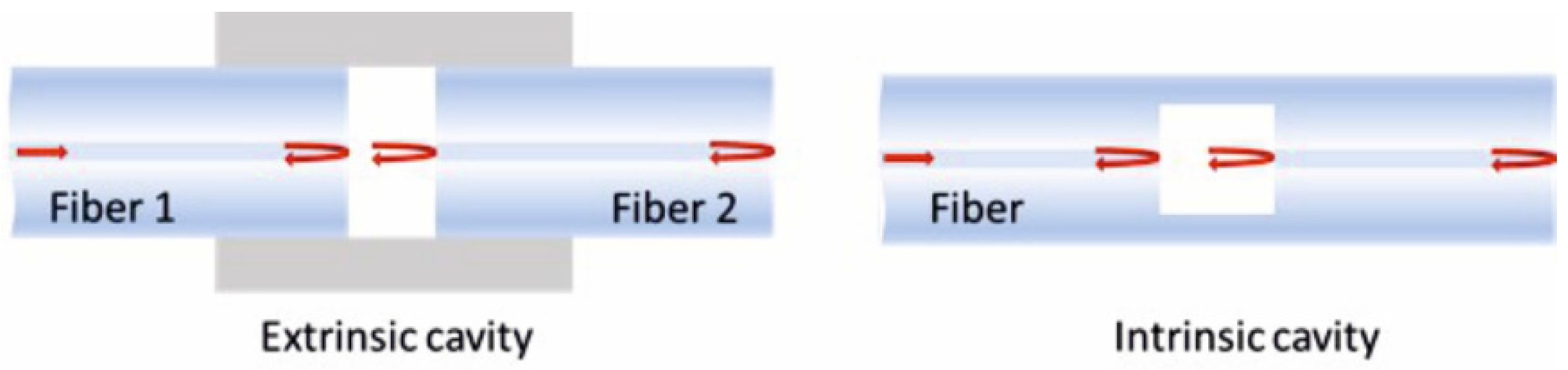
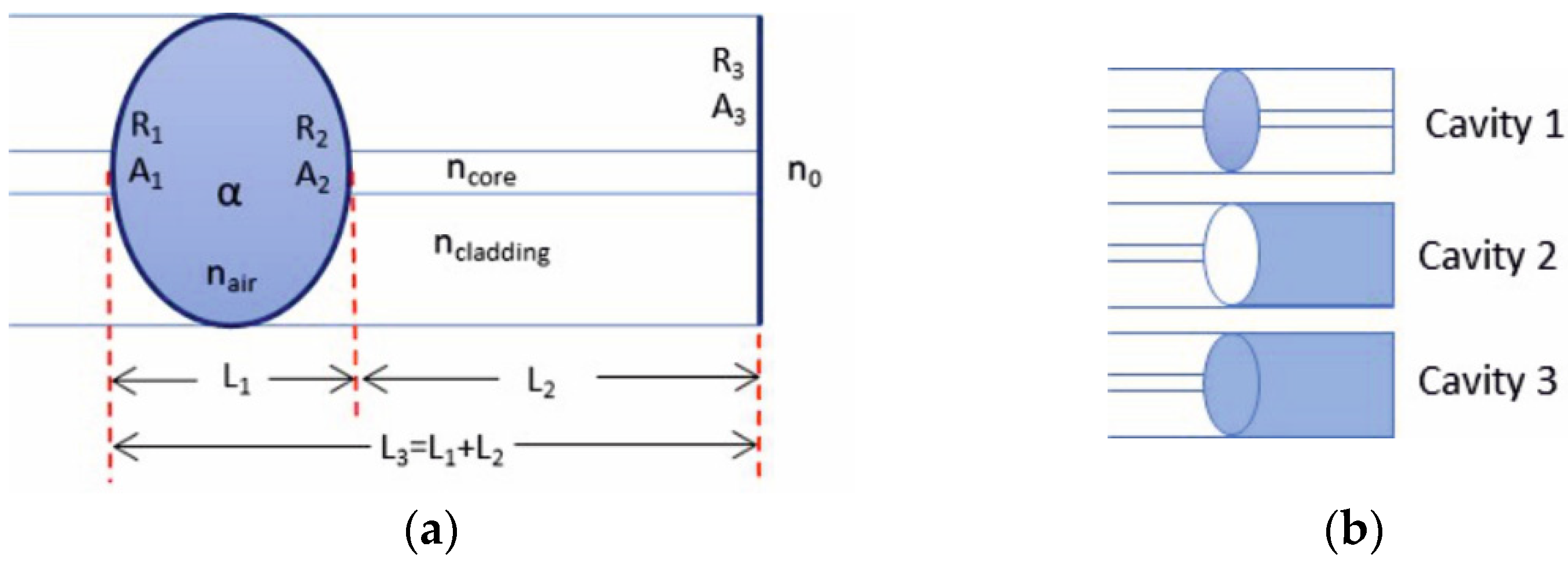
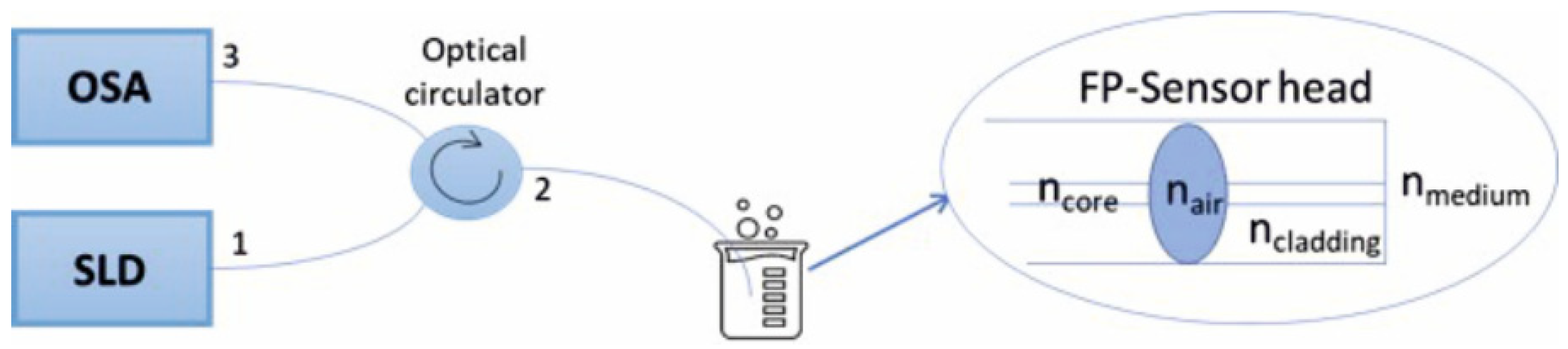
2. Operation Principles
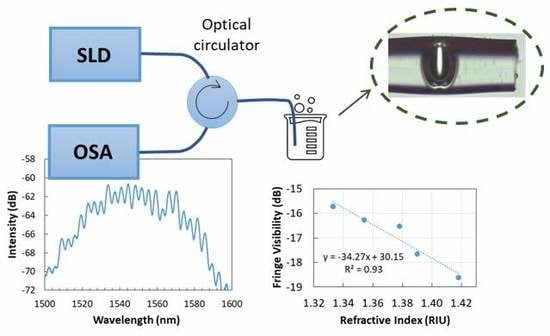
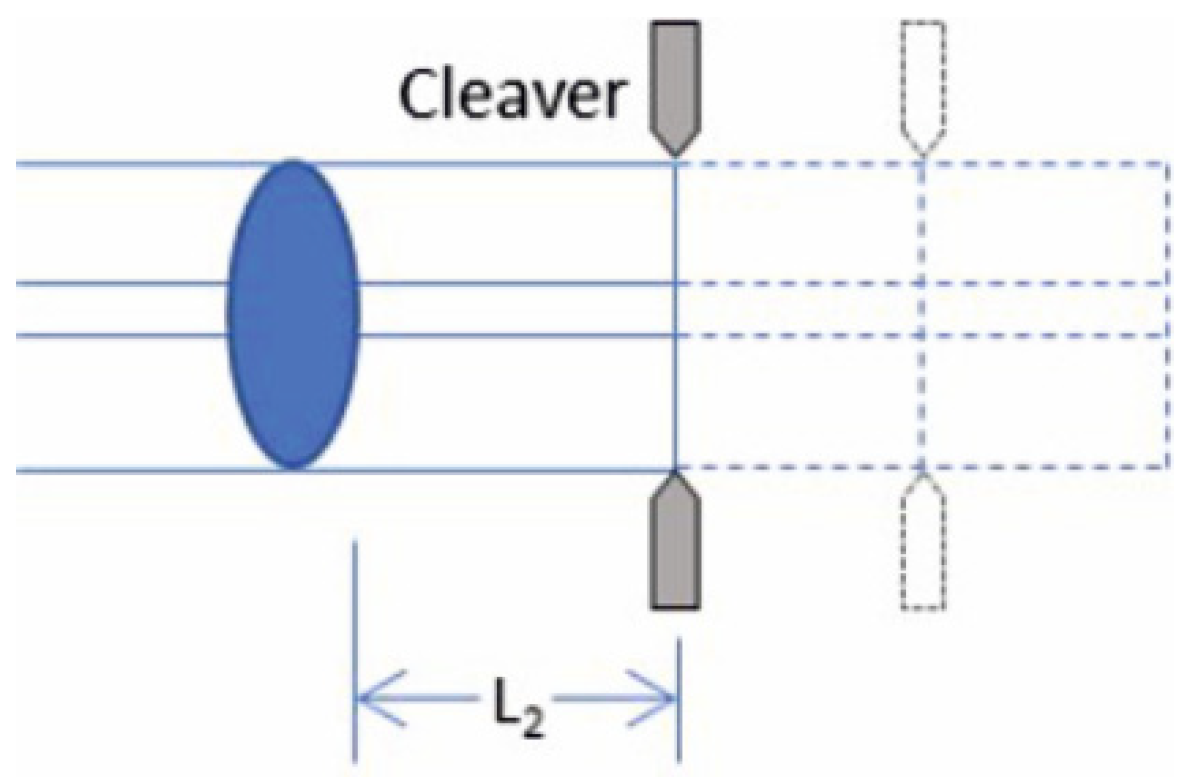
3. Experimental Procedures
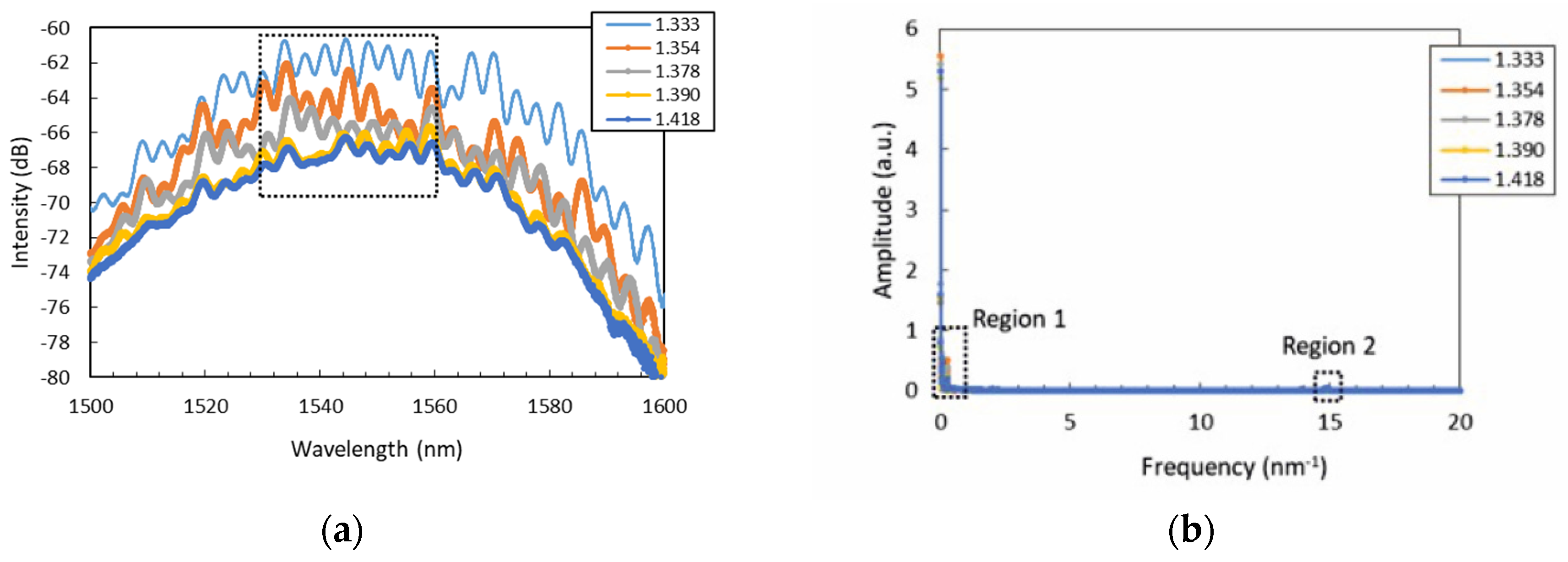
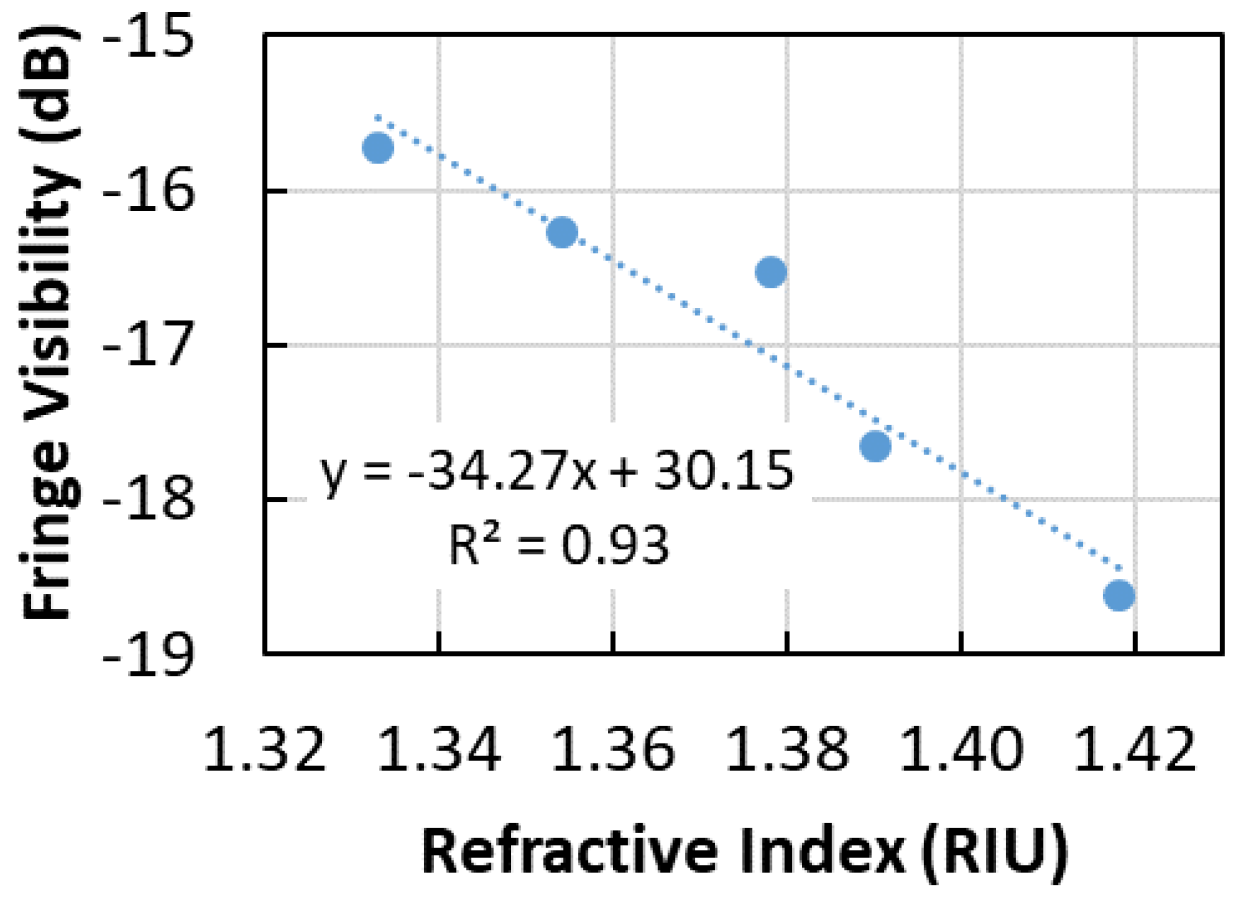
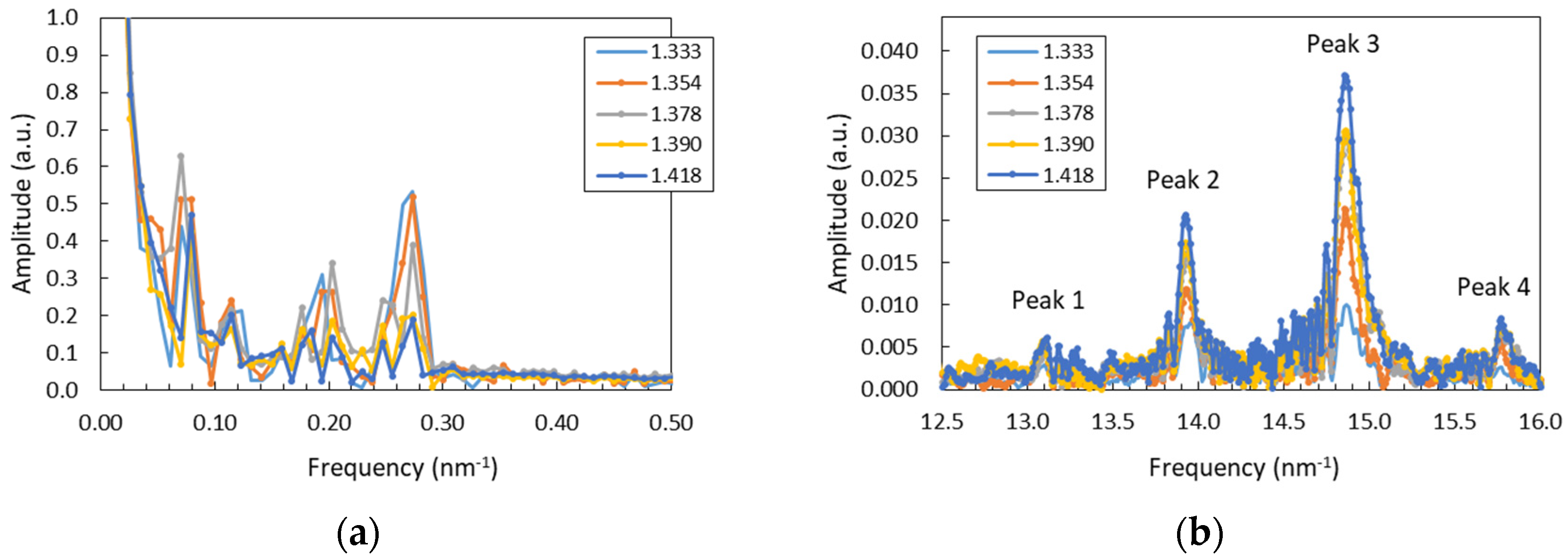
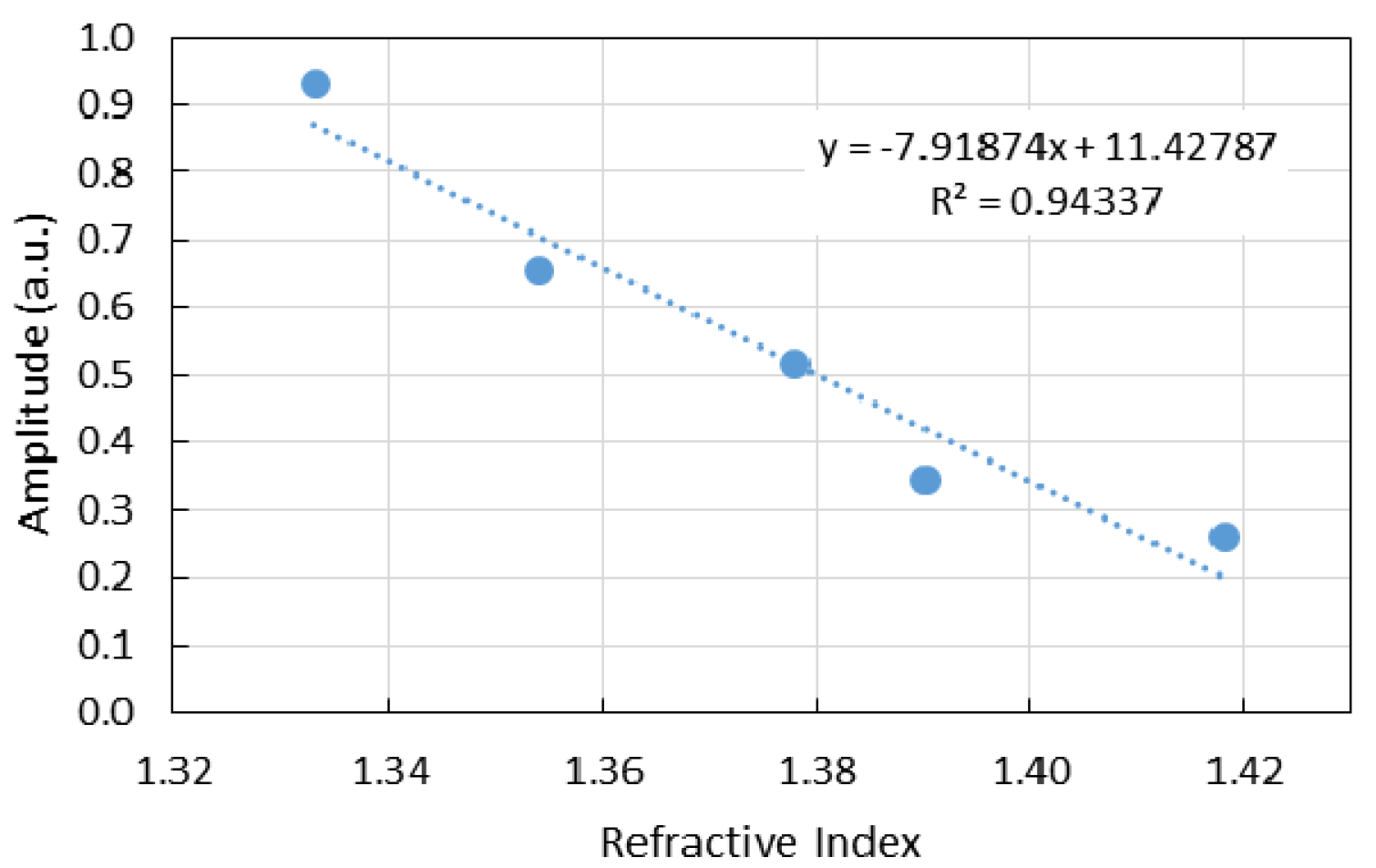
4. Results and Discussion
4.1. FP-Short Sensor
4.2. FP-Long Sensor
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Islam, M.; Ali, M.; Lai, M.H.; Lim, K.S.; Ahmad, H. Chronology of Fabry-Perot interferometer fiber-optic sensors and their applications: A review. Sensors 2014, 14, 7451–7488. [Google Scholar] [CrossRef] [PubMed]
- Javernik, A.; Donlagic, D. Miniature, micro-machined, fiber-optic Fabry-Perot voltage sensor. Opt. Express 2019, 27, 13280–13291. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Jia, P.; Liu, J.; Fang, G.; Li, Z.; Hong, Y.; Liang, T.; Xiong, J. Diaphragm-Free Fiber-Optic Fabry-Perot Interferometric Gas Pressure Sensor for High Temperature Application. Sensors 2018, 18, 1011. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Zhou, Y.; Zou, X. Fabry-Perot Cavity Sensing Probe with High Thermal Stability for an Acoustic Sensor by Structure Compensation. Sensors 2018, 18, 3393. [Google Scholar] [CrossRef] [PubMed]
- Flores, R.; Janeiro, R.; Viegas, J. Optical fibre Fabry-Pérot interferometer based on inline microcavities for salinity and temperature sensing. Sci. Rep. 2019, 9, 9556. [Google Scholar] [CrossRef] [PubMed]
- Budinski, V.; Donlagic, D.A. Miniature Fabry Perot Sensor for Twist/Rotation, Strain and Temperature Measurements Based on a Four-Core Fiber. Sensors 2019, 19, 1574. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.R.; Hu, T.Y.; Wang, D.N. Optical fiber Fabry-Perot interferometer cavity fabricated by femtosecond laser micromachining and fusion splicing for refractive index sensing. Opt. Express 2012, 20, 22813–22818. [Google Scholar] [CrossRef] [PubMed]
- Duan, D.W.; Rao, Y.J.; Hou, Y.S.; Zhu, T. Microbubble based fiber-optic Fabry–Perot interferometer formed by fusion splicing single-mode fibers for strain measurement. Appl. Opt. 2012, 51, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Gui, Z.; Wang, G.; An, Y.; Gu, J.; Zhang, M.; Liu, X.; Wang, Z.; Wang, G.; Jia, P. A micro bubble structure based Fabry–Perot optical fiber strain sensor with high sensitivity and low-cost characteristics. Sensors 2017, 17, 555. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, C.S.; Ferreira, M.S.; Silva, S.O.; Kobelke, J.; Schuster, K.; Bierlich, J.; Frazão, O. Fiber Fabry-Perot interferometer for curvature sensing. Photonic Sens. 2016, 6, 339–344. [Google Scholar] [CrossRef]
- Tan, X.; Li, X.; Geng, Y.; Yin, Z.; Wang, L.; Wang, W.; Deng, Y. Polymer microbubble-based Fabry–Perot fiber interferometer and sensing applications. IEEE Photonic Technol. Lett. 2015, 27, 2035–2038. [Google Scholar] [CrossRef]
- Chen, M.Q.; Zhao, Y.; Xia, F.; Peng, Y.; Tong, R.J. High sensitivity temperature sensor based on fiber air-microbubble Fabry-Perot interferometer with PDMS-filled hollow-core fiber. Sens. Actuator A Phys. 2018, 275, 60–66. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, L.H.; Dong, X.; Yang, J.; Long, H.Y.; So, P.L.; Chan, C.C. Miniature pH optical fiber sensor based on Fabry–Perot interferometer. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 331–335. [Google Scholar] [CrossRef]
- Tian, M.; Lu, P.; Chen, L.; Liu, D.; Yang, M.; Zhang, J. Femtosecond laser fabricated in-line micro multicavity fiber FP interferometers sensor. Opt. Commun. 2014, 316, 80–85. [Google Scholar] [CrossRef]
- Warren-Smith, S.C.; André, R.M.; Dellith, J.; Eschrich, T.; Becker, M.; Bartelt, H. Sensing with ultra-short Fabry-Perot cavities written into optical micro-fibers. Sens. Actuator B Chem. 2017, 244, 1016–1021. [Google Scholar] [CrossRef]
- Wu, S.; Yan, G.; Zhou, B.; Lee, E.H.; He, S. Open-cavity fabry-perot interferometer based on etched side-hole fiber for microfluidic sensing. IEEE Photonics Technol. Lett. 2015, 27, 1813–1816. [Google Scholar]
- Ran, Z.L.; Rao, Y.J.; Liu, W.J.; Liao, X.; Chiang, K.S. Laser-micromachined Fabry-Perot optical fiber tip sensor for high-resolution temperature-independent measurement of refractive index. Opt. Express 2018, 16, 2252–2263. [Google Scholar] [CrossRef] [PubMed]
- Nespereira, M.; Silva, C.; Coelho, J.; Rebordão, J. Nanosecond laser micropatterning of optical fibers. In Proceedings of the International Conference on Applications of Optics and Photonics, Braga, Portugal, 3–7 May 2011; Volume 8001, p. 800140. [Google Scholar]
- Nespereira, M.; Coelho, J.; Rebordão, J. In line Fabry-Perot cavities manufactured by electric arc fusion of NIR-laser micro-drilled optical fiber flat tips. In Proceedings of the Fourth International Conference on Applications of Optics and Photonics, Lisbon, Portugal, 31 May–4 June 2019; Volume 11207, p. 112072F. [Google Scholar]

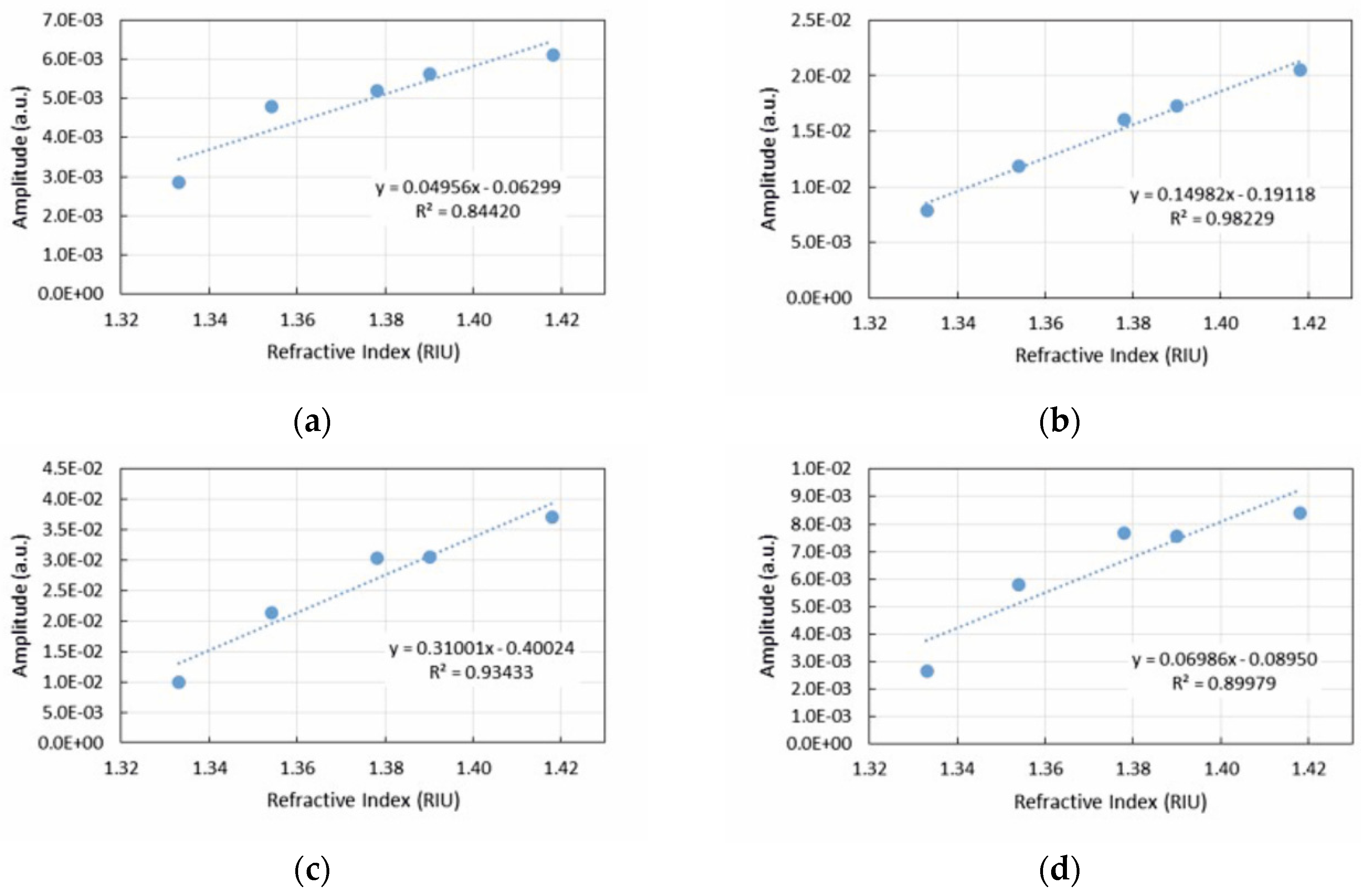
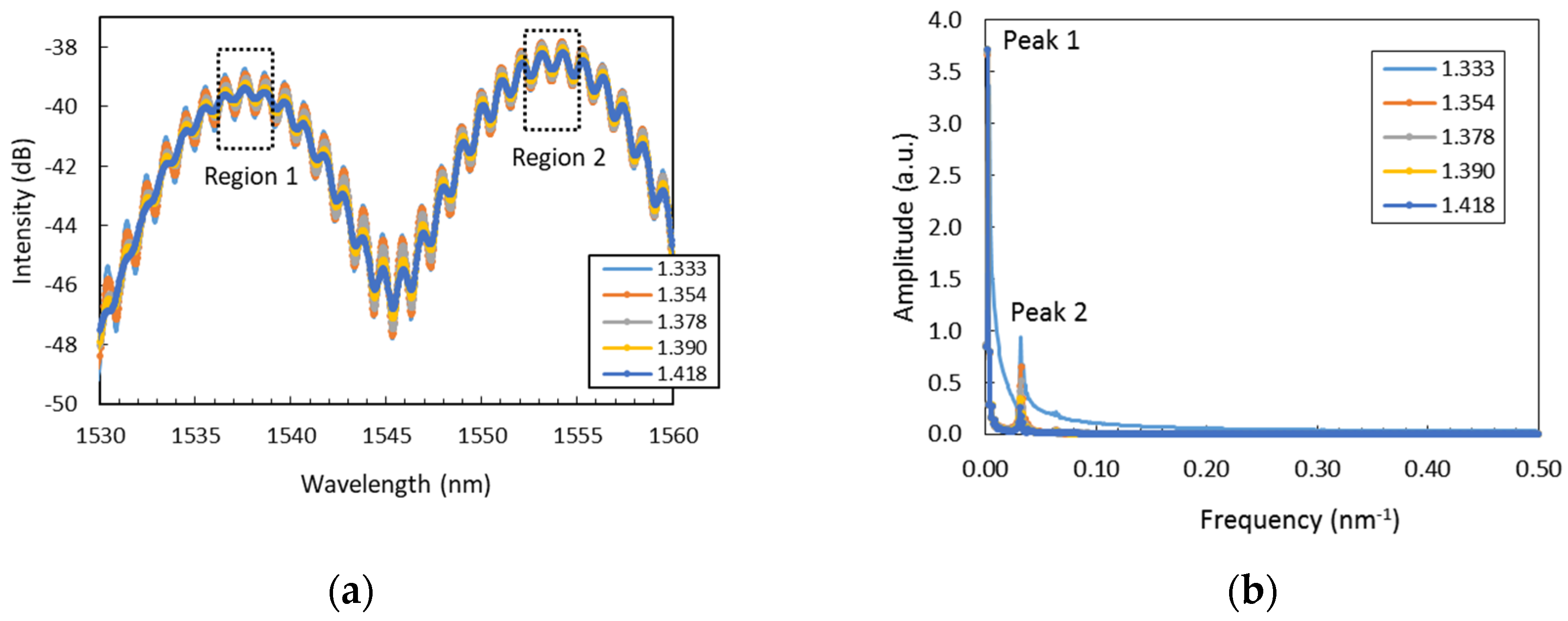
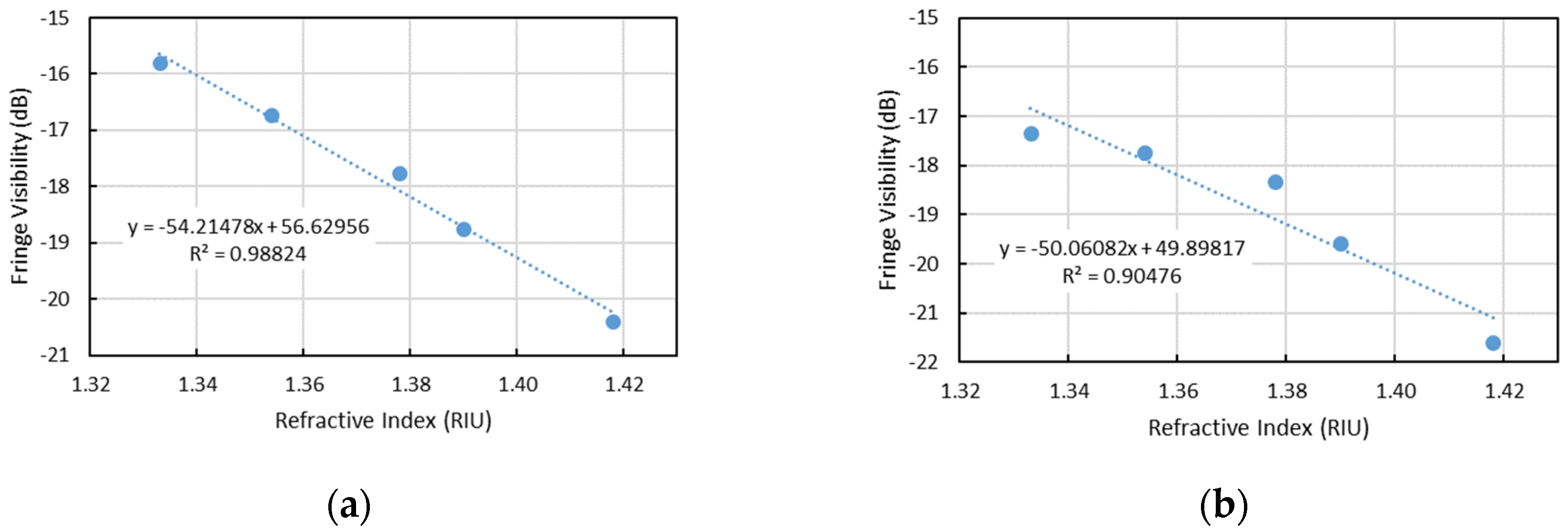
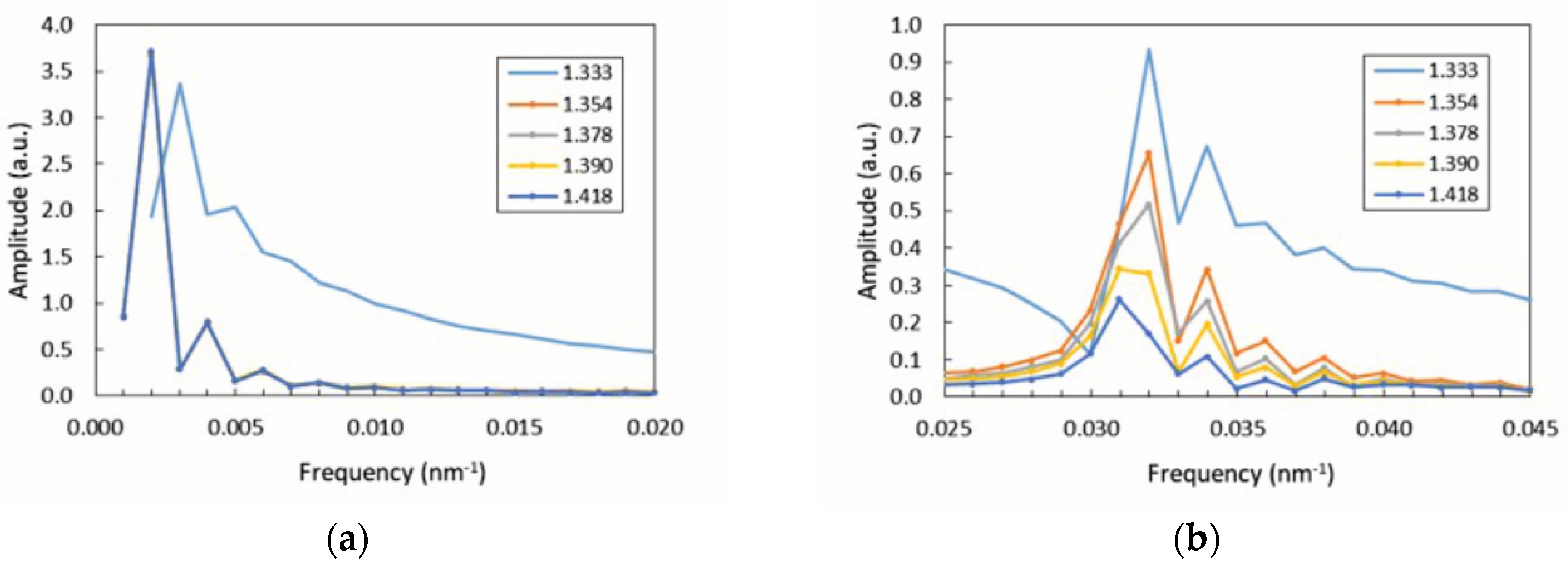
| Concentration (%) | Refractive Index (RIU) |
|---|---|
| 0 | 1.333 |
| 20 | 1.354 |
| 40 | 1.378 |
| 60 | 1.390 |
| 80 | 1.418 |
| FP-Short | FP-Long | |||||
|---|---|---|---|---|---|---|
| Fringe Visibility | FFT Amplitude | Fringe Visibility | FFT Amplitude | |||
| Analysis range | 1550–1560 nm | Peak 2 | Peak 3 | Region 1 | Region 2 | Peak 2 |
| Sensitivity | −34.3 * | 0.15 ** | 0.31 ** | −54.2 * | −50.1 * | −7.9 ** |
| R2 | 93% | 98% | 93% | 99% | 90% | 94% |
| FP-Short | FP-Long | |||||
|---|---|---|---|---|---|---|
| Fringe Visibility | FFT Amplitude | Fringe Visibility | FFT Amplitude | |||
| Analysis range | 1550–1560 nm | Peak 2 | Peak 3 | Region 1 | Region 2 | Peak 2 |
| 1.333 | 0.7% | 0.3% | 0.7% | 0.2% | 0.8% | 0.6% |
| 1.354 | 0.4% | 0.1% | 0.5% | 0.1% | 0.2% | 0.5% |
| 1.378 | 0.0% | 0.4% | 0.8% | 0.4% | 1.1% | 0.0% |
| 1.390 | 1.0% | 0.1% | 0.0% | 0.0% | 0.1% | 0.7% |
| 1.418 | 0.8% | 0.3% | 0.5% | 0.2% | 0.7% | 0.6% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nespereira, M.; Coelho, J.M.P.; Rebordão, J.M. A Refractive Index Sensor Based on a Fabry–Perot Interferometer Manufactured by NIR Laser Microdrilling and Electric Arc Fusion. Photonics 2019, 6, 109. https://doi.org/10.3390/photonics6040109
Nespereira M, Coelho JMP, Rebordão JM. A Refractive Index Sensor Based on a Fabry–Perot Interferometer Manufactured by NIR Laser Microdrilling and Electric Arc Fusion. Photonics. 2019; 6(4):109. https://doi.org/10.3390/photonics6040109
Chicago/Turabian StyleNespereira, Marta, João M. P. Coelho, and José M. Rebordão. 2019. "A Refractive Index Sensor Based on a Fabry–Perot Interferometer Manufactured by NIR Laser Microdrilling and Electric Arc Fusion" Photonics 6, no. 4: 109. https://doi.org/10.3390/photonics6040109
APA StyleNespereira, M., Coelho, J. M. P., & Rebordão, J. M. (2019). A Refractive Index Sensor Based on a Fabry–Perot Interferometer Manufactured by NIR Laser Microdrilling and Electric Arc Fusion. Photonics, 6(4), 109. https://doi.org/10.3390/photonics6040109