Hyperspectral Imaging Bioinspired by Chromatic Blur Vision in Color Blind Animals
Abstract
:1. Introduction
2. Materials and Methods
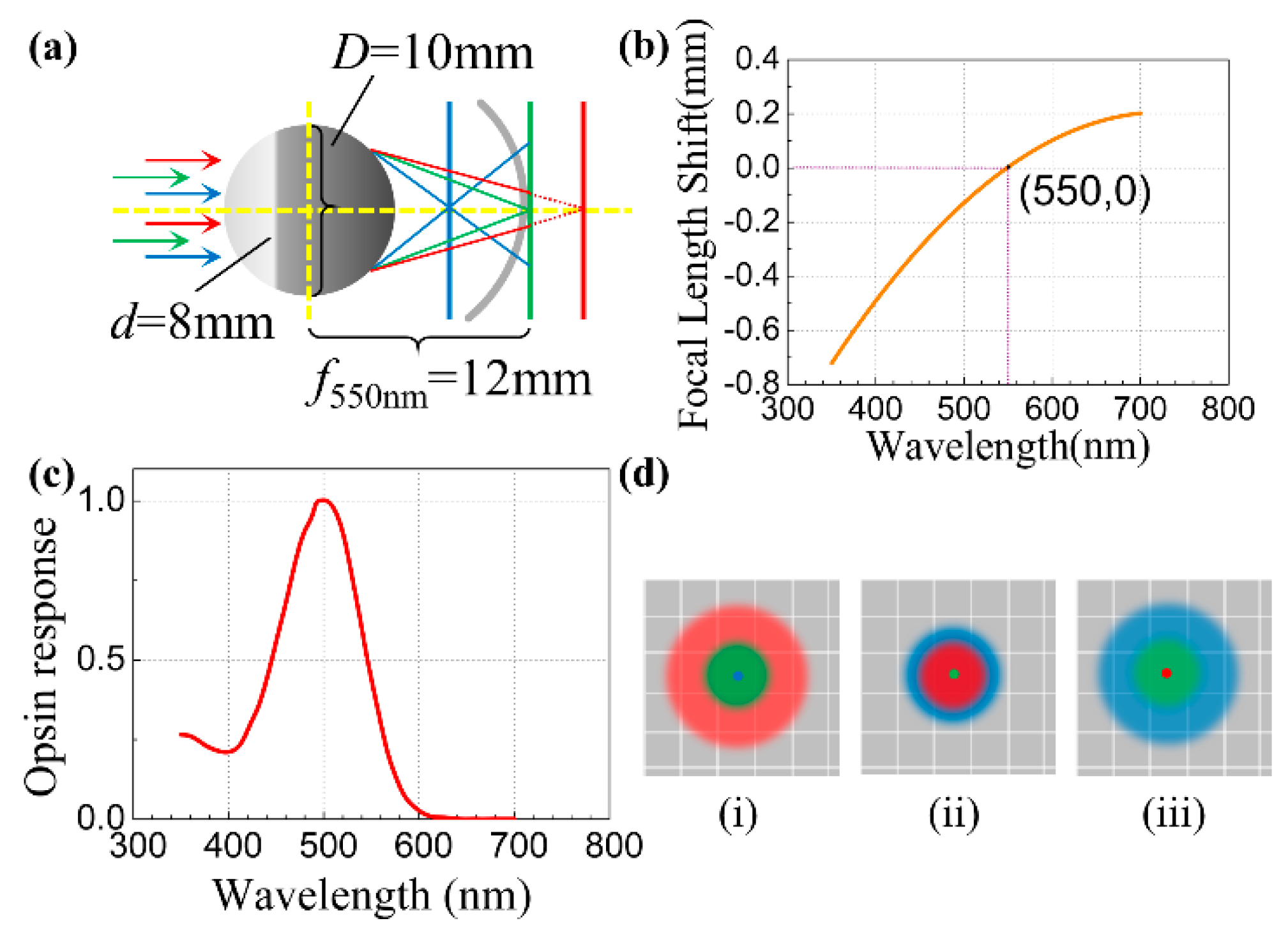
2.1. Eyeball Model
2.2. Chromatically Blurred Images
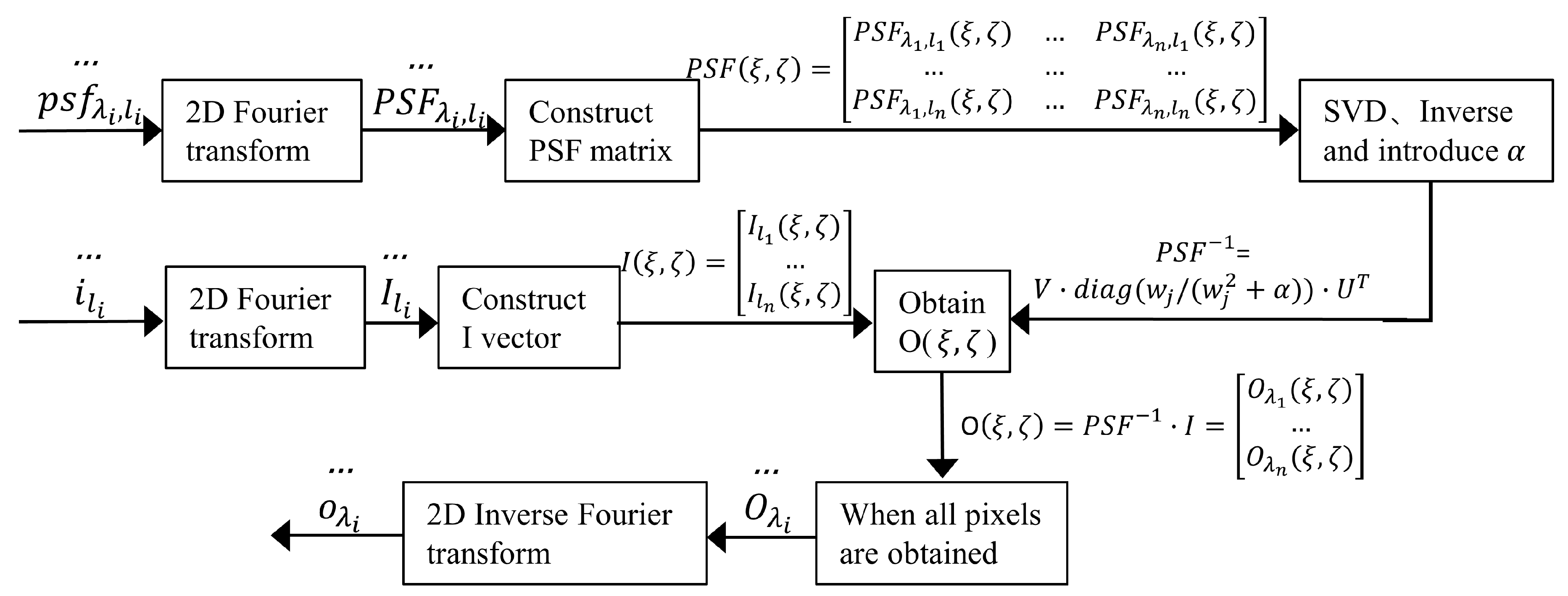
2.3. Deconvolution-Based Image Restoration
- Firstly, perform 2D Fourier transform for all blurred images and PSFs.
- To obtain the values of the restored images at the pixel point (ξ, ζ), we construct the matrix PSF(ξ, ζ) and the vector I(ξ, ζ) based on the PSFs and blurred images in the frequency domain which are obtained in the first step.
- Then, SVD of PSF(ξ, ζ) are carried out, followed by the inverse calculation of the PSF(ξ, ζ) in the frequency domain using the singular values and vectors.
- To avoid the occurrence of zero values in the singular values of the PSFs to affect the image restoration results, we introduce a regularization factor α into the singular values. The regularization factor should be adjusted according to imaging noise by mean square error (MSE) evaluation criterion: the optimal factor is obtained when the MSE is at a minimum. In this study, we set the regularization factor α as 1.0 × 10−7.
- Next, multiply the inverse matrix of PSF(ξ, η) by I(ξ, ζ) to obtain the frequency values of the restored images at the pixel point (ξ, ζ).
- Repeat steps 2–5 until all pixels of the restored images have been computed. Finally, we perform 2D inverse Fourier transform on the frequency restored images to obtain the final spatial restored images.
3. Results and Discussion
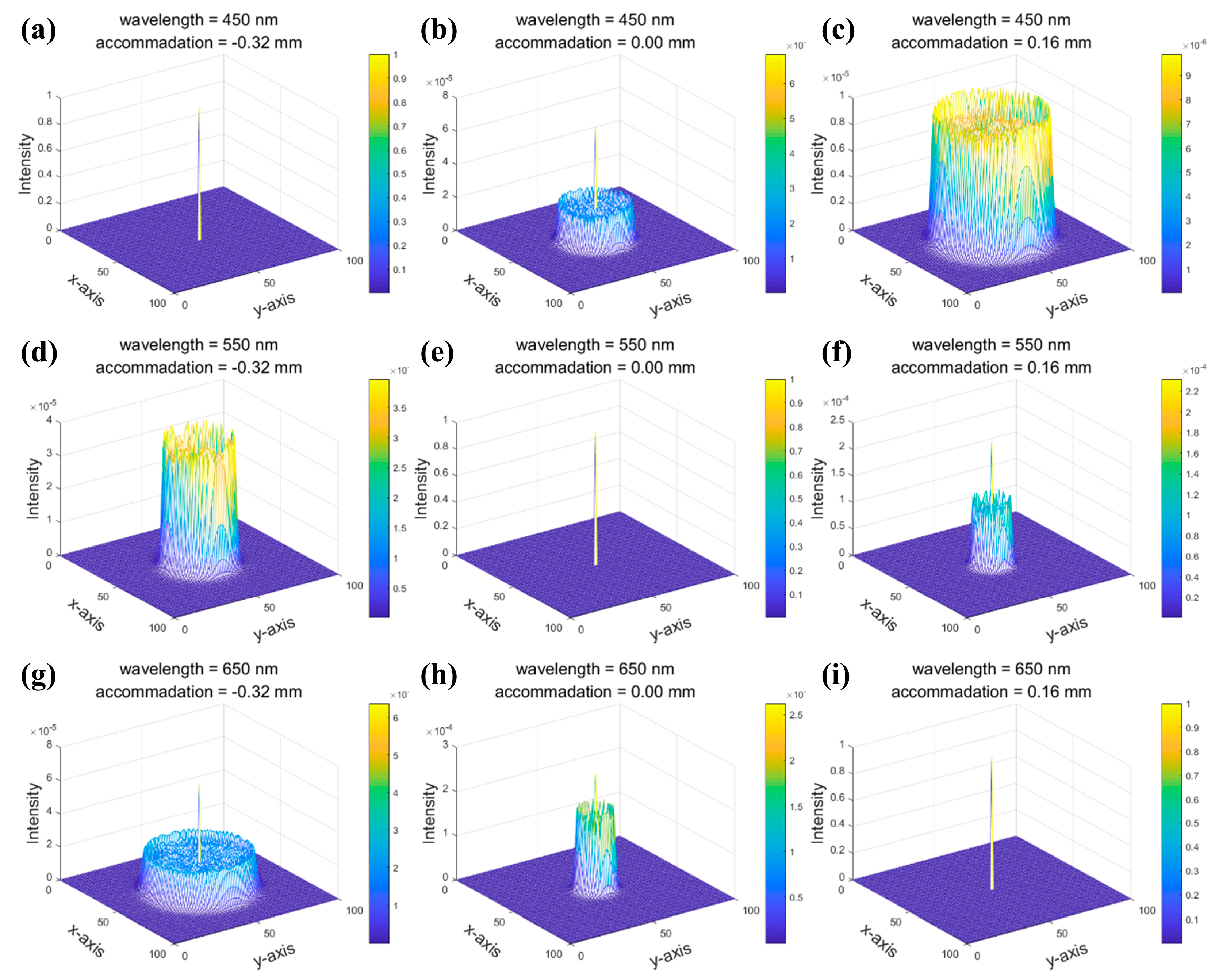
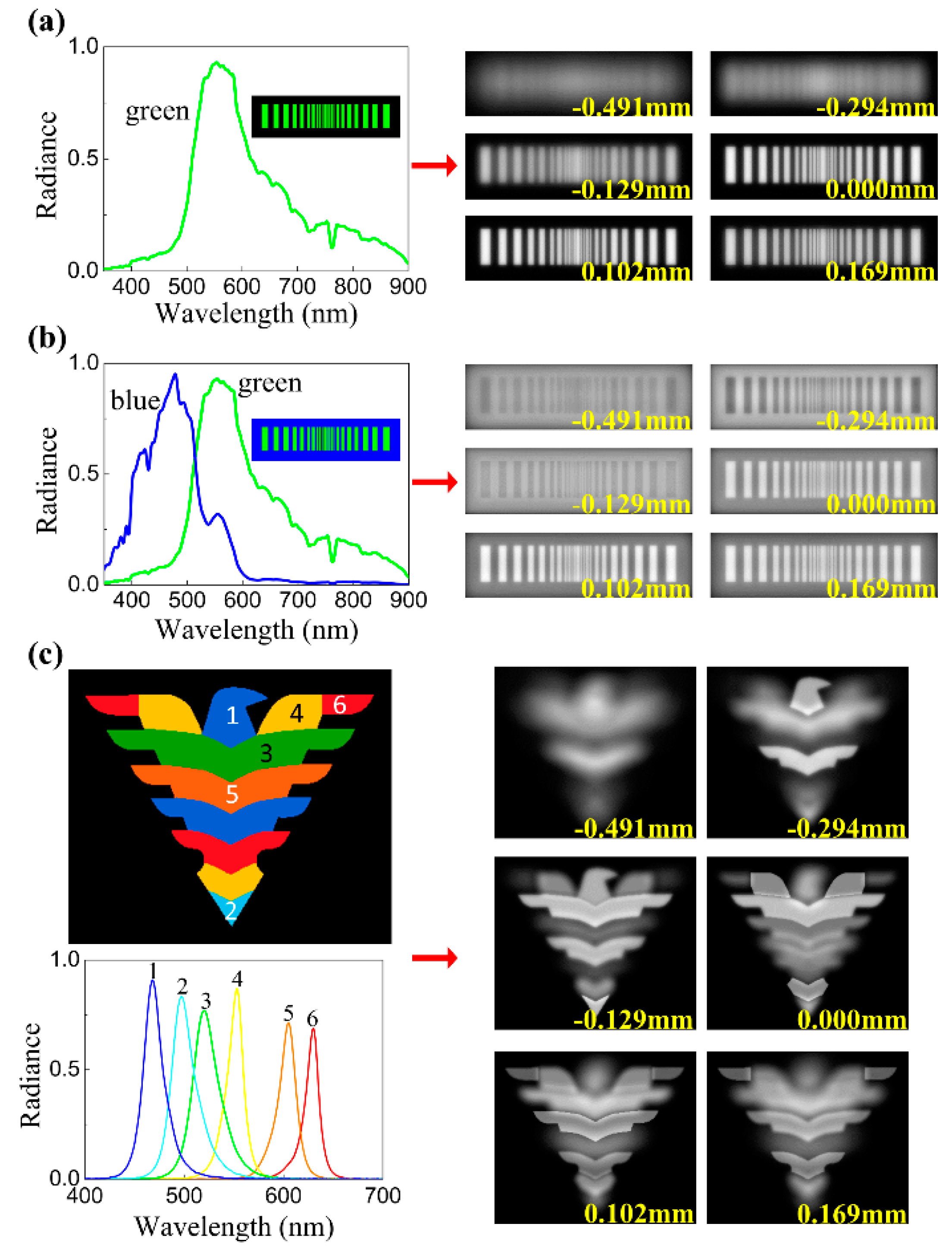
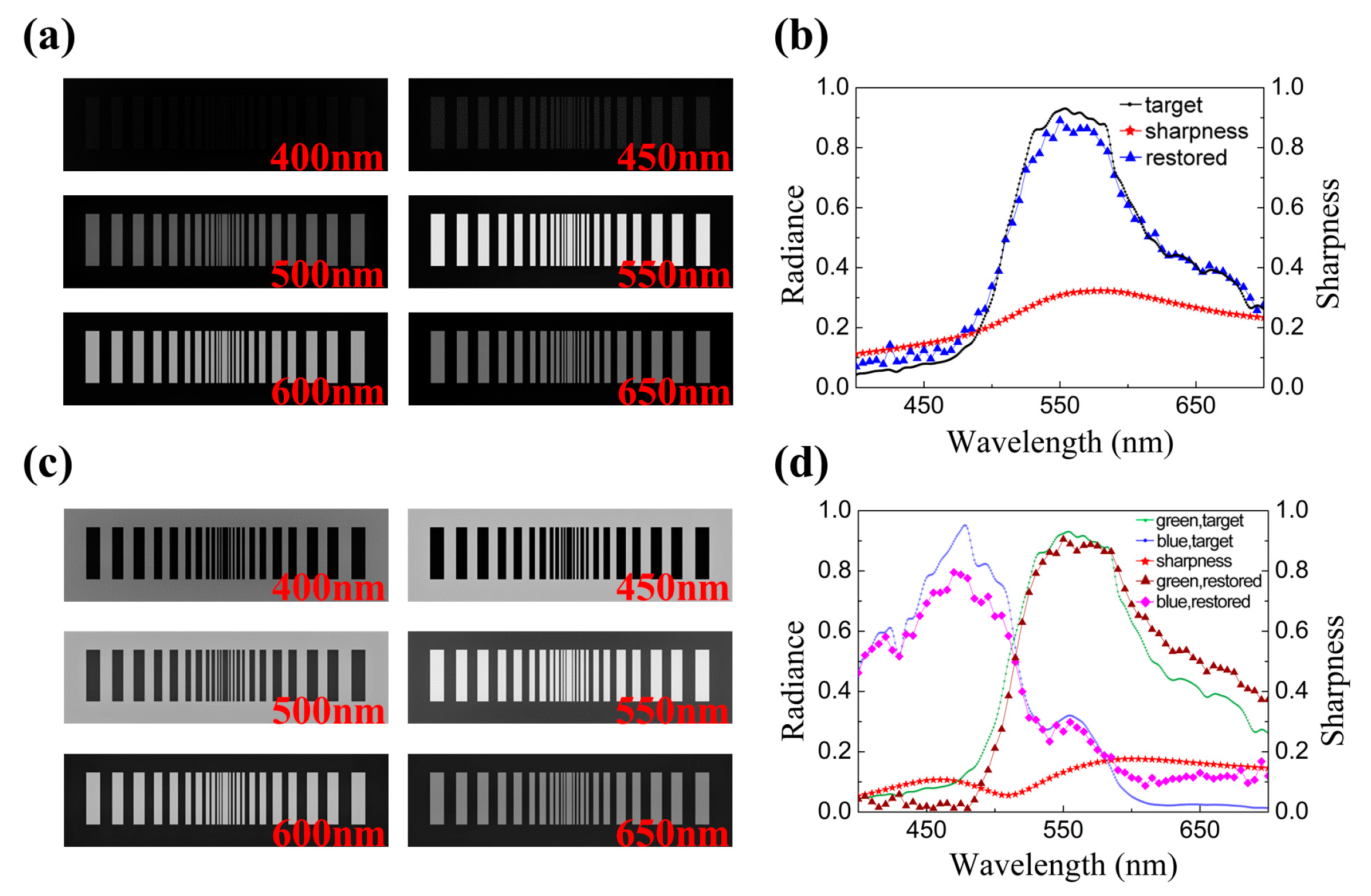
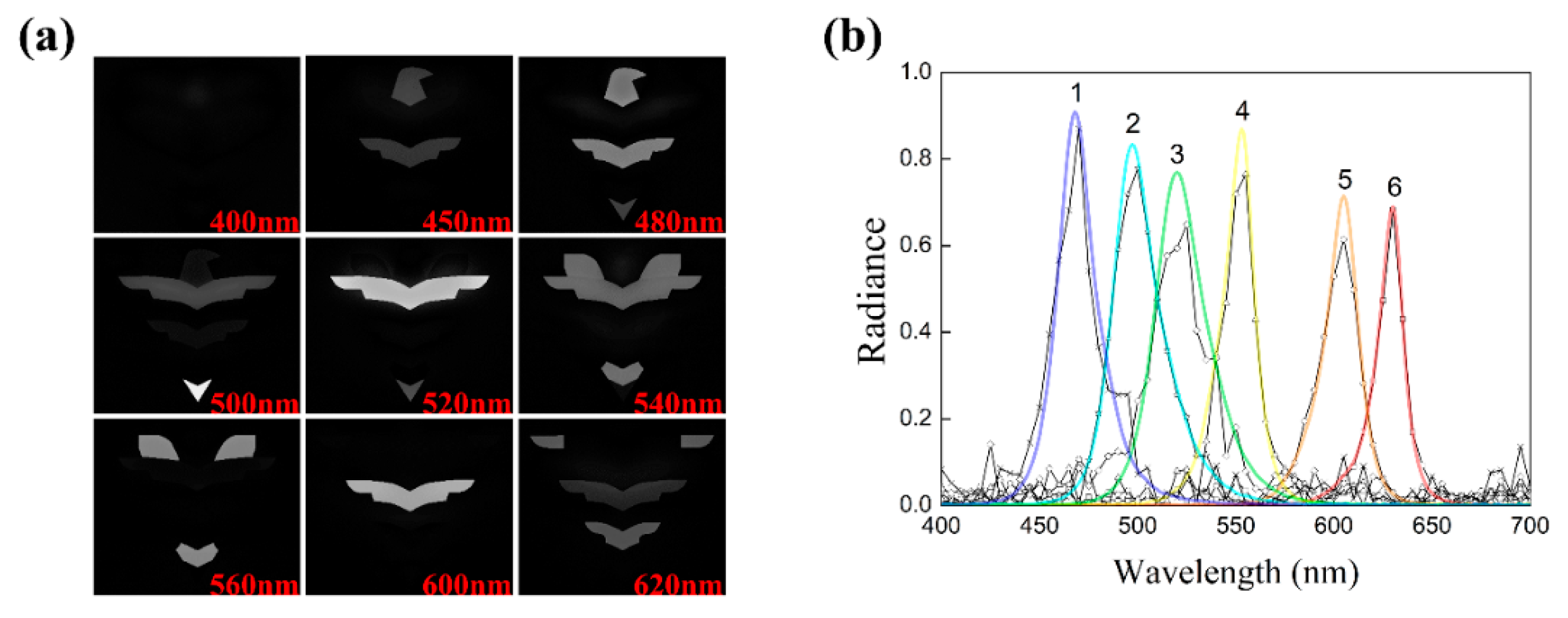
3.1. Spectral Discrimination and Spatial Resolution
3.2. Errors in the Restored Images
3.3. Target Distance
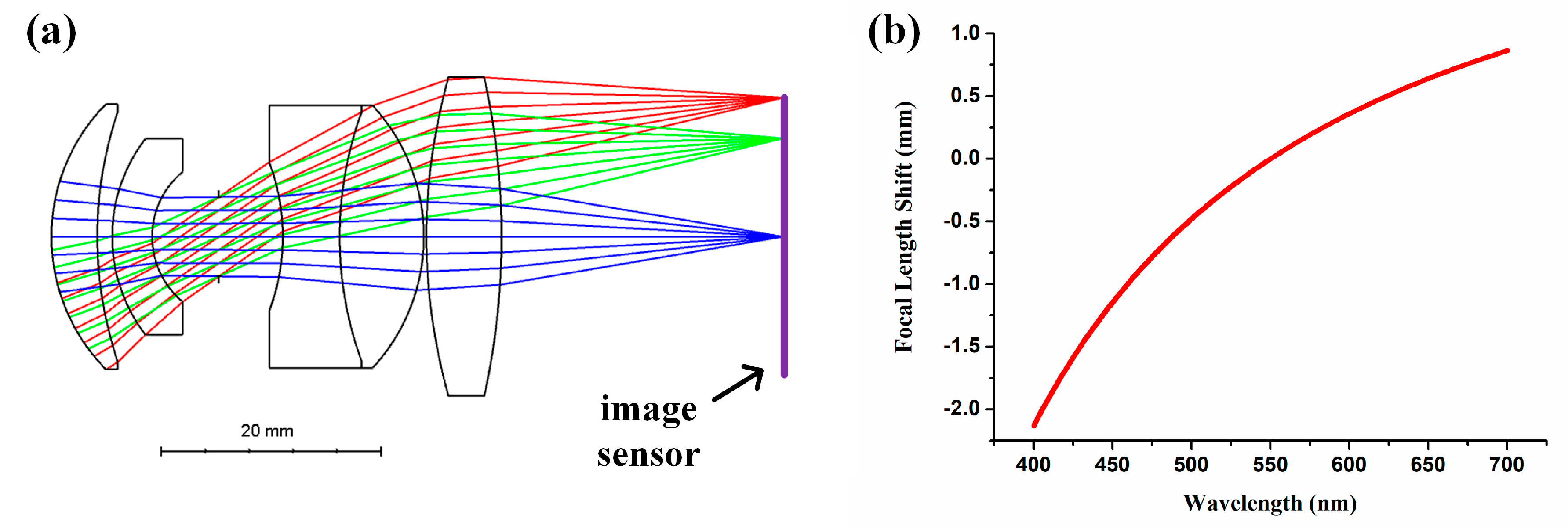
3.4. Chromatic Lens and Imaging System
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kneubuhler, M.; Damm-Reiser, A. Recent Progress and Developments in Imaging Spectroscopy. Remote Sens. 2018, 10, 1497. [Google Scholar] [CrossRef]
- Nakazawa, K.; Mori, K.; Tsuru, T.G.; Ueda, Y.; Awaki, H.; Fukazawa, Y.; Ishida, M.; Matsumoto, H.; Murakami, H.; Okajima, T.; et al. The FORCE mission: Science aim and instrument parameter for broadband X-ray imaging spectroscopy with good angular resolution. In Proceedings of the Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, Austin, TX, USA, 10–15 June 2018. [Google Scholar] [CrossRef]
- Kontar, E.P.; Yu, S.; Kuznetsov, A.A.; Emslie, A.G.; Alcock, B.; Jeffrey, N.L.S.; Melnik, V.N.; Bian, N.H.; Subramanian, P. Imaging spectroscopy of solar radio burst fine structures. Nat. Commun. 2017, 8, 1515. [Google Scholar] [CrossRef] [PubMed]
- Offerhaus, H.L.; Bohndiek, S.E.; Harvey, A.R. Hyperspectral imaging in biomedical applications. J. Opt. 2019, 21, 010202. [Google Scholar] [CrossRef]
- Huang, H.; Shen, Y.; Guo, Y.L.; Yang, P.; Wang, H.Z.; Zhan, S.Y.; Liu, H.B.; Song, H.; He, Y. Characterization of moisture content in dehydrated scallops using spectral images. J. Food Eng. 2017, 205, 47–55. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Stubbs, A.L.; Stubbs, C.W. Spectral discrimination in color blind animals via chromatic aberration and pupil shape. Proc. Natl. Acad. Sci. USA 2016, 113, 8206–8211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brown, P.K.; Brown, P.S. Visual Pigments of the Octopus and Cuttlefish. Nature 1958, 182, 1288–1290. [Google Scholar] [CrossRef] [PubMed]
- Bellingham, J.; Morris, A.G.; Hunt, D.M. The rhodopsin gene of the cuttlefish Sepia officinalis: Sequence and spectral tuning. J. Exp. Biol. 1998, 201, 2299–2306. [Google Scholar] [PubMed]
- Mathger, L.M.; Barbosa, A.; Miner, S.; Hanlon, R.T. Color blindness and contrast perception in cuttlefish (Sepia officinalis) determined by a visual sensorimotor assay. Vis. Res. 2006, 46, 1746–1753. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiao, C.C.; Wickiser, J.K.; Allen, J.J.; Genter, B.; Hanlon, R.T. Hyperspectral imaging of cuttlefish camouflage indicates good color match in the eyes of fish predators. Proc. Natl. Acad. Sci. USA 2011, 108, 9148–9153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buresch, K.C.; Ulmer, K.M.; Akkaynak, D.; Allen, J.J.; Mathger, L.M.; Nakamura, M.; Hanlon, R.T. Cuttlefish adjust body pattern intensity with respect to substrate intensity to aid camouflage, but do not camouflage in extremely low light. J. Exp. Mar. Biol. Ecol. 2015, 462, 121–126. [Google Scholar] [CrossRef]
- Akkaynak, D.; Allen, J.J.; Mathger, L.M.; Chiao, C.C.; Hanlon, R.T. Quantification of cuttlefish (Sepia officinalis) camouflage: A study of color and luminance using in situ spectrometry. J. Comp. Physiol. A 2013, 199, 211–225. [Google Scholar] [CrossRef] [PubMed]
- Jagger, W.S.; Sands, P.J. A wide-angle gradient index optical model of the crystalline lens and eye of the octopus. Vis. Res. 1999, 39, 2841–2852. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.L.; Zhang, X.M.; Kudo, H.; Kaeriyama, M. Development of the Retina in the Cuttlefish Sepia Esculenta. J. Shellfish Res. 2010, 29, 463–470. [Google Scholar] [CrossRef]
- Douglas, R.H.; Williamson, R.; Wagner, H.J. The pupillary response of cephalopods. J. Exp. Biol. 2005, 208, 261–265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chung, W.S. Comparisons of visual capabilities in modern Cephalopods from shallow water to deep sea. PhD Thesis, University of Queensland, Brisbane, Australia, 2014. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 5th ed.; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- McNally, J.G.; Karpova, T.; Cooper, J.; Conchello, J.A. Three-dimensional imaging by deconvolution microscopy. Methods 1999, 19, 373–385. [Google Scholar] [CrossRef] [PubMed]
- Kenig, T.; Kam, Z.; Feuer, A. Blind Image Deconvolution Using Machine Learning for Three-Dimensional Microscopy. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2191–2204. [Google Scholar] [CrossRef] [PubMed]
- Klema, V.C.; Laub, A.J. The Singular Value Decomposition—Its Computation and Some Applications. IEEE Trans. Autom. Control 1980, 25, 164–176. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, S.; Zhou, W.; Ma, X.; Huang, H. Hyperspectral Imaging Bioinspired by Chromatic Blur Vision in Color Blind Animals. Photonics 2019, 6, 91. https://doi.org/10.3390/photonics6030091
Zhan S, Zhou W, Ma X, Huang H. Hyperspectral Imaging Bioinspired by Chromatic Blur Vision in Color Blind Animals. Photonics. 2019; 6(3):91. https://doi.org/10.3390/photonics6030091
Chicago/Turabian StyleZhan, Shuyue, Weiwen Zhou, Xu Ma, and Hui Huang. 2019. "Hyperspectral Imaging Bioinspired by Chromatic Blur Vision in Color Blind Animals" Photonics 6, no. 3: 91. https://doi.org/10.3390/photonics6030091
APA StyleZhan, S., Zhou, W., Ma, X., & Huang, H. (2019). Hyperspectral Imaging Bioinspired by Chromatic Blur Vision in Color Blind Animals. Photonics, 6(3), 91. https://doi.org/10.3390/photonics6030091




