Nonlinear Dynamics of Exclusive Excited-State Emission Quantum Dot Lasers Under Optical Injection
Abstract
1. Introduction
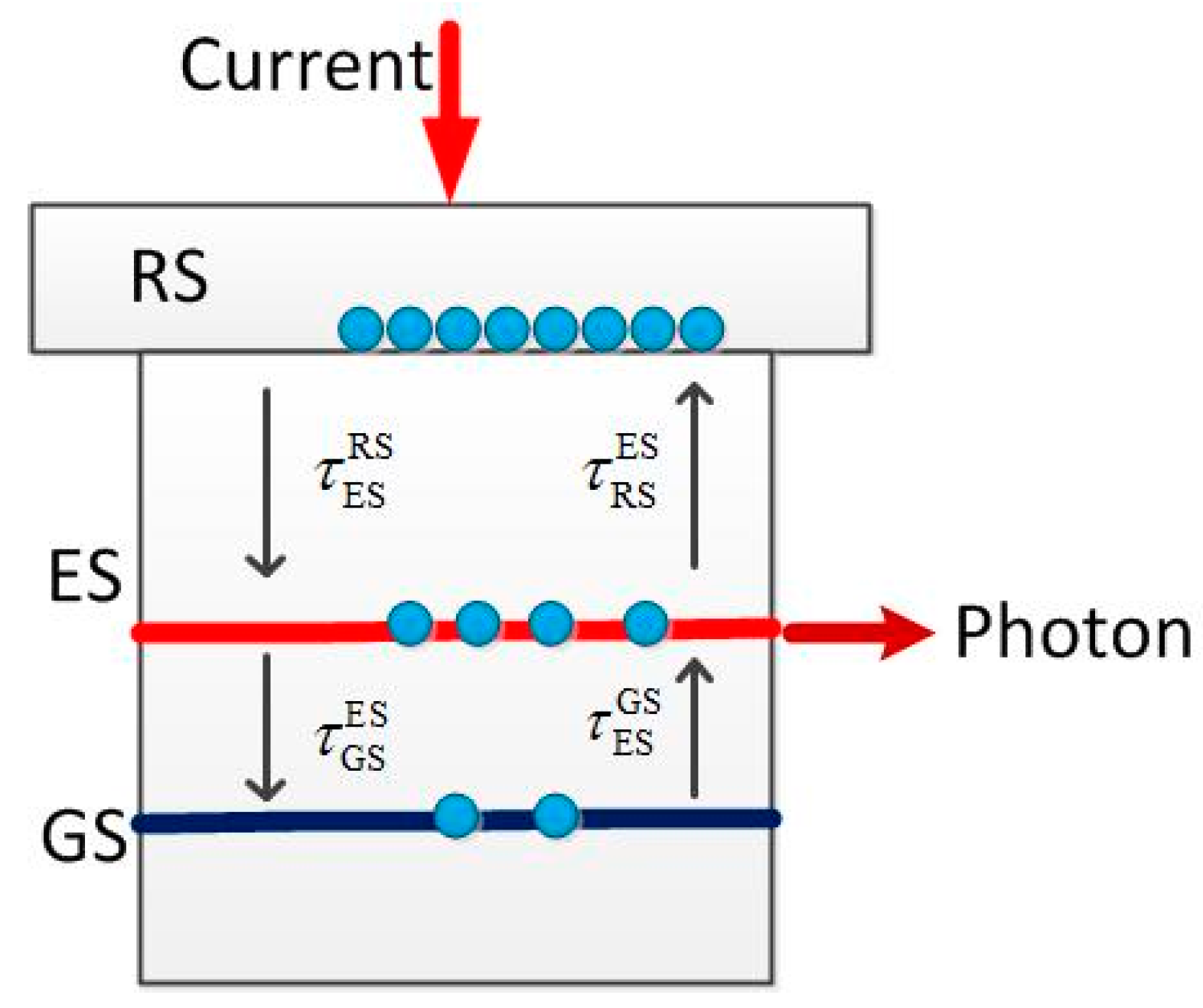
2. Theoretical Model
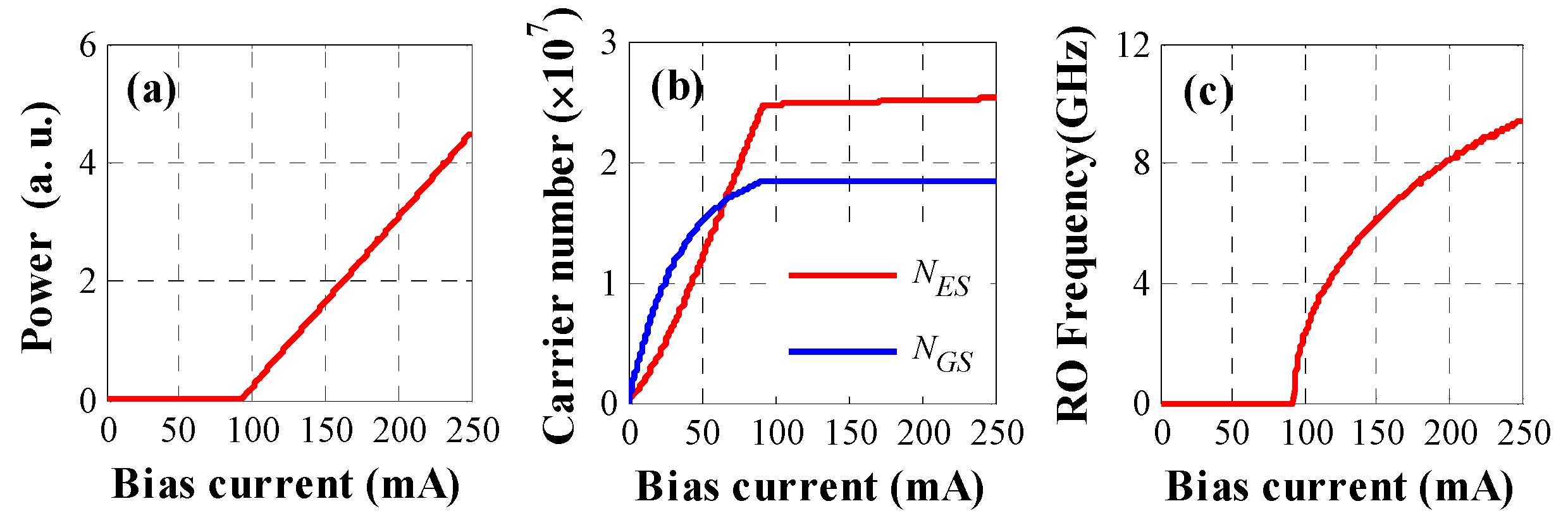
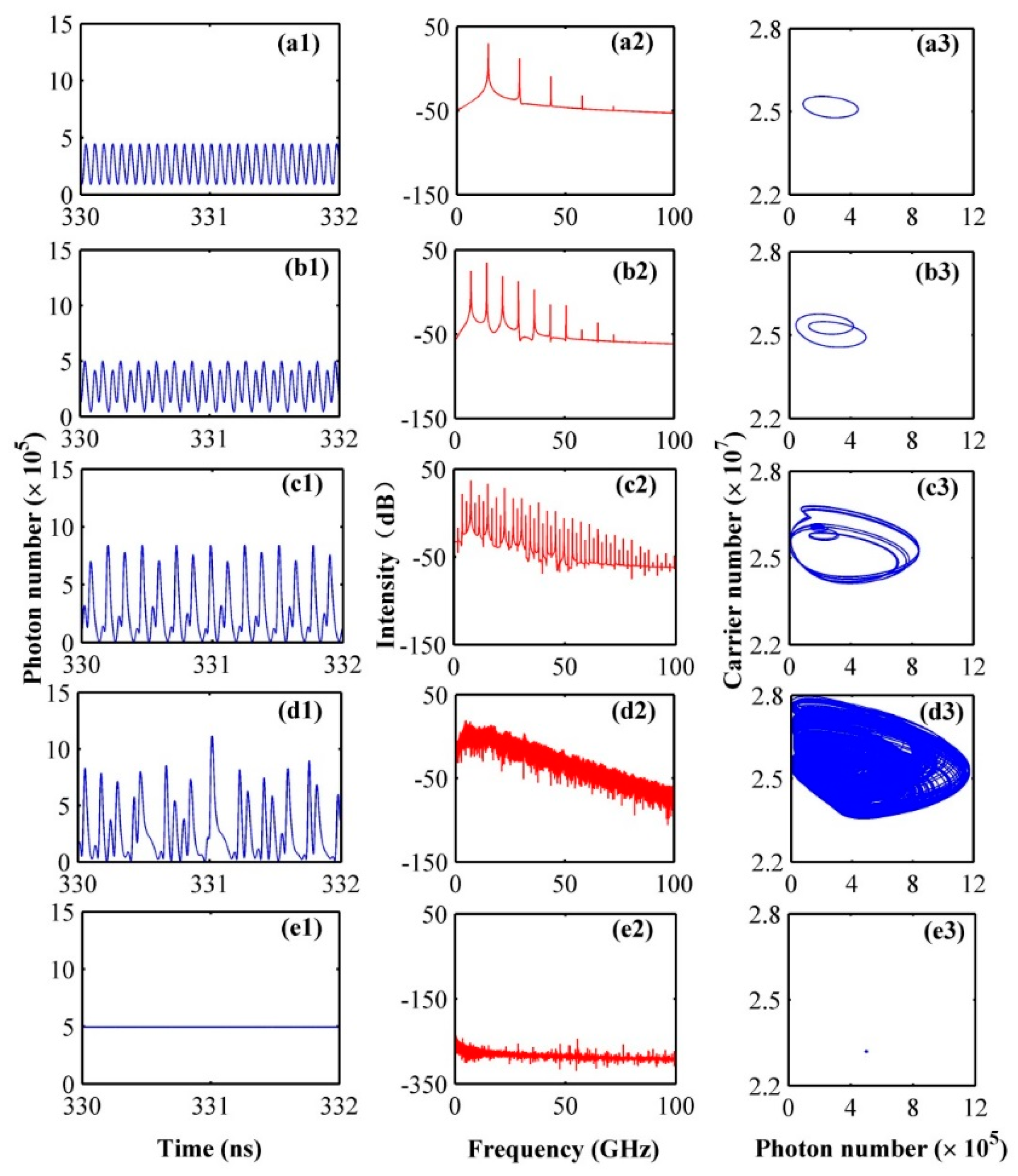
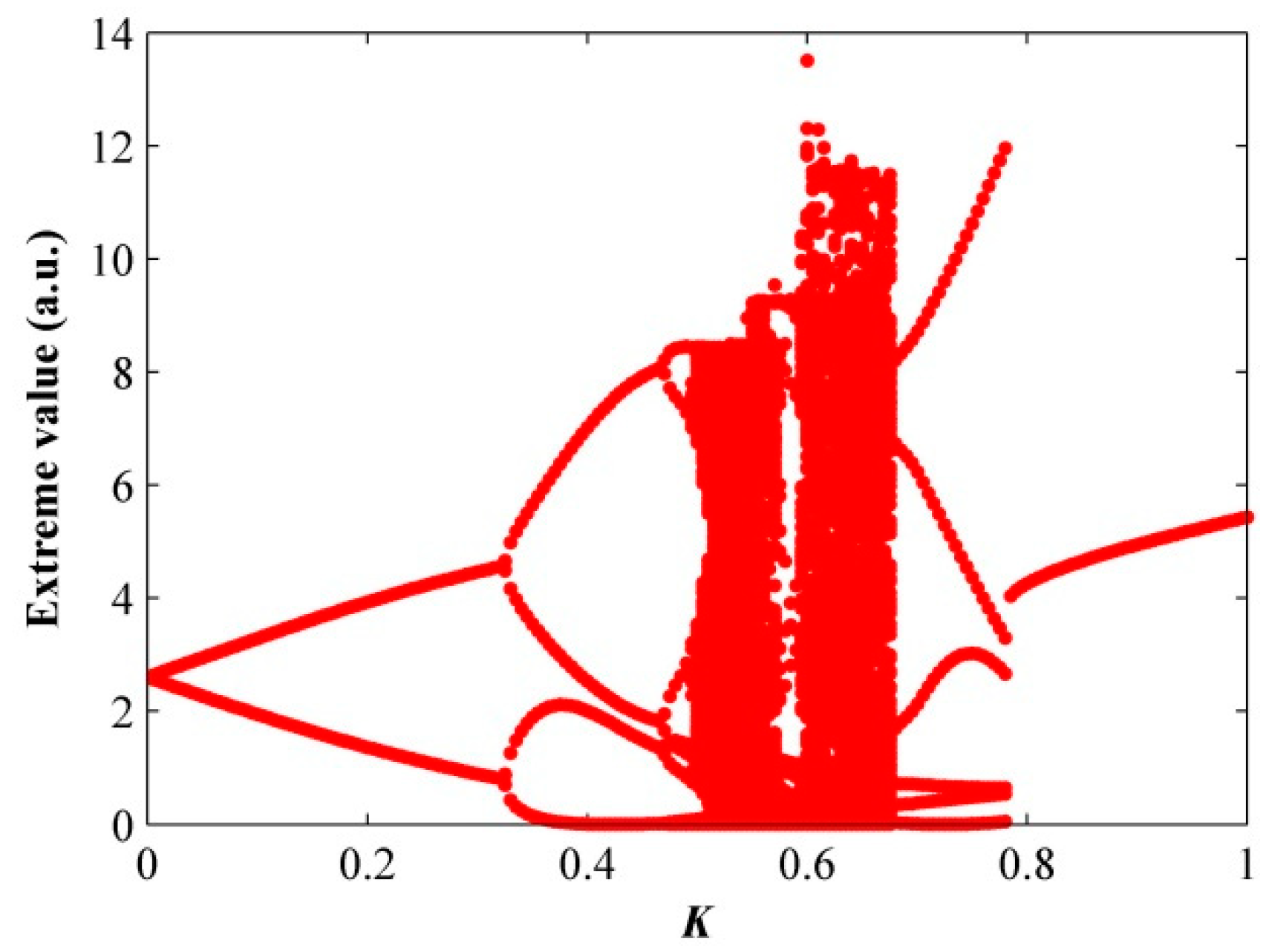
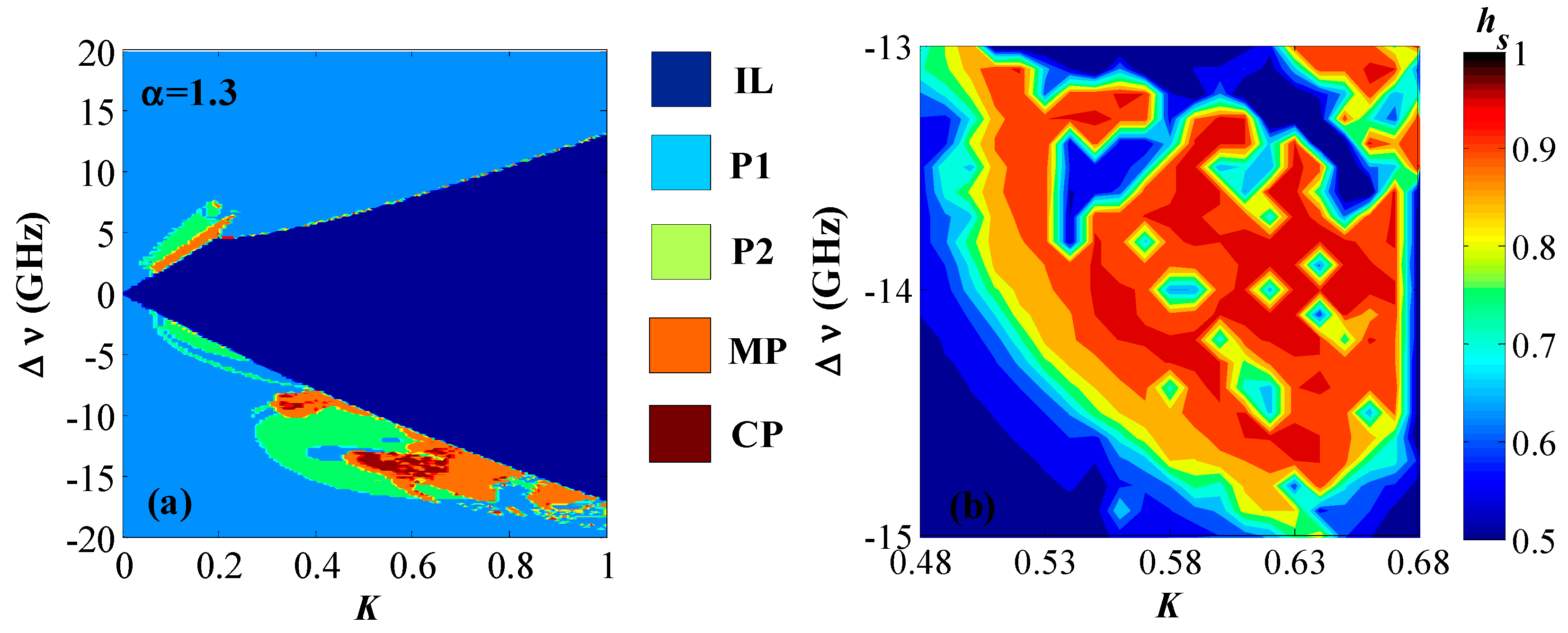
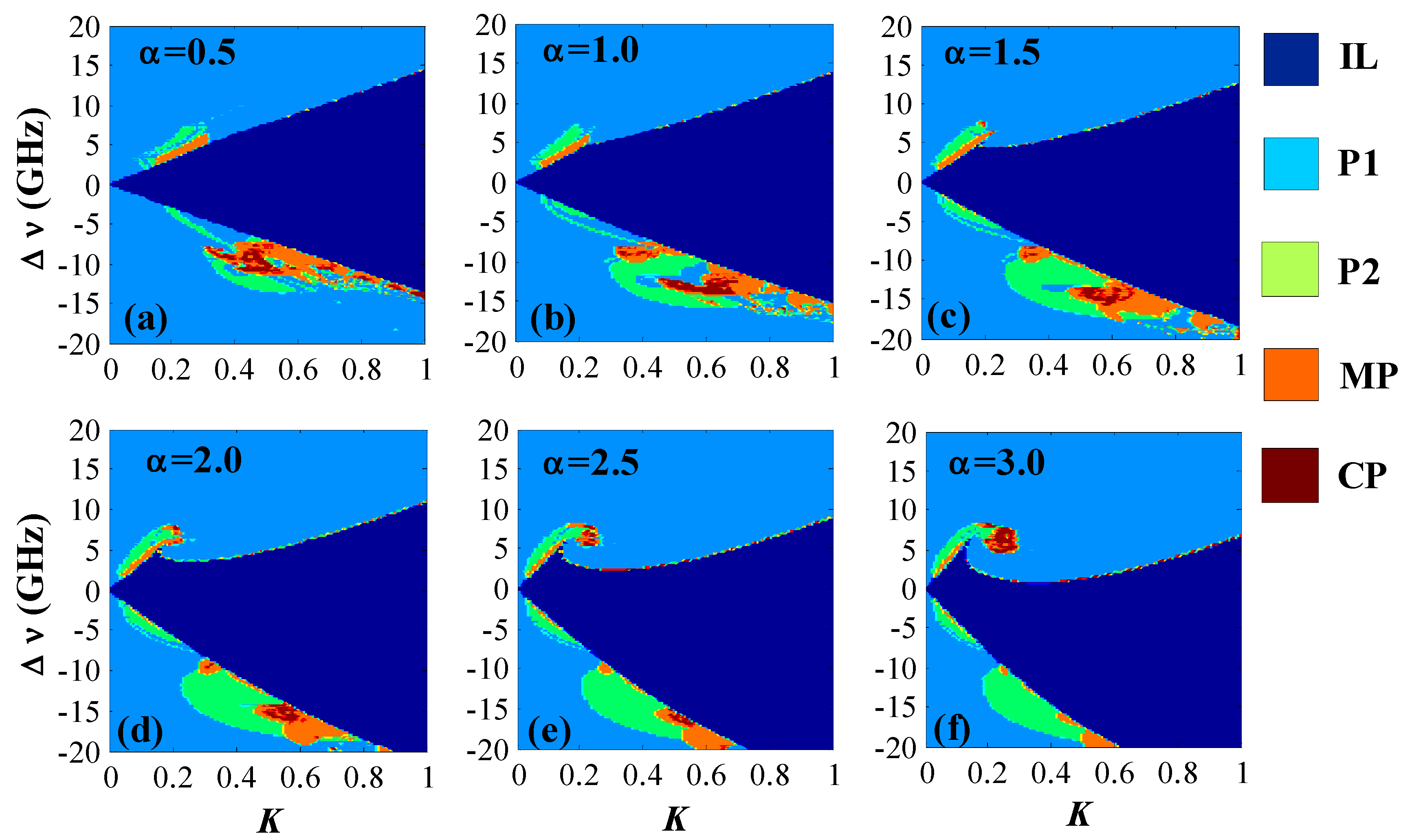
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yan, S.L. Period-control and chaos-anti-control of a semiconductor laser using the twisted fiber. Chin. Phys. B 2016, 25, 090504. [Google Scholar] [CrossRef]
- Chen, J.J.; Duan, Y.N.; Li, L.F.; Zhong, Z.Q. Wideband polarization-resolved chaos with time-delay signature suppression in VCSELs subject to dual chaotic optical injections. IEEE Access 2018, 6, 66807–66815. [Google Scholar] [CrossRef]
- Hohl, A.; Gavrielides, A. Bifurcation cascade in a semiconductor laser subject to optical feedback. Phys. Rev. Lett. 1999, 82, 1148–1151. [Google Scholar] [CrossRef]
- Lin, F.Y.; Liu, J.M. Harmonic frequency locking in a semiconductor laser with delayed negative optoelectronic feedback. Appl. Phys. Lett. 2002, 81, 3128–3130. [Google Scholar] [CrossRef]
- Zhang, M.J.; Niu, Y.N.; Zhao, T.; Zhang, J.Z.; Liu, Y.; Xu, Y.H.; Meng, J.; Wang, Y.C.; Wang, A.B. Chaos generation by a hybrid integrated chaotic semiconductor laser. Chin. Phys. B 2018, 27, 050502. [Google Scholar] [CrossRef]
- Hung, Y.H.; Hwang, S.K. Photonic microwave amplification for radio-over-fiber links using period-one nonlinear dynamics of semiconductor lasers. Opt. Lett. 2013, 38, 3355–3358. [Google Scholar] [CrossRef]
- Hwang, S.K.; Chen, H.F.; Lin, C.Y. All-optical frequency conversion using nonlinear dynamics of semiconductor lasers. Opt. Lett. 2009, 34, 812–814. [Google Scholar] [CrossRef]
- Cui, C.; Fu, X.; Chan, S.C. Double-locked semiconductor laser for radio-over-fiber uplink transmission. Opt. Lett. 2009, 34, 3821–3823. [Google Scholar] [CrossRef]
- Zhong, D.Z.; Luo, W.; Xu, G.L. Controllable all-optical stochastic logic gates and their delay storages based on the cascaded VCSELs with optical-injection. Chin. Phys. B 2016, 25, 094202. [Google Scholar] [CrossRef]
- Cheng, C.H.; Lee, C.W.; Lin, T.W.; Lin, F.Y. Dual-frequency laser Doppler velocimeter for speckle noise reduction and coherence enhancement. Opt. Express 2012, 20, 20255–20265. [Google Scholar] [CrossRef]
- Sciamanna, M.; Shore, K.A. Physics and applications of laser diode chaos. Nat. Photonics 2015, 9, 151–162. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y.C.; Wang, A.B.; Yang, L.Z.; Zhang, M.J.; Zhang, J.Z. Direct generation of all-optical random numbers from optical pulse amplitude chaos. Opt. Express 2012, 20, 4297–4308. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, B.; Chen, G.; Guo, L.; Lu, D.; Zhao, L.; Wang, W. 640-Gbit/s fast physical random number generation using a broadband chaotic semiconductor laser. Sci. Rep. 2017, 7, 45900. [Google Scholar] [CrossRef]
- Liu, A.Y.; Zhang, C.; Norman, J.; Snyder, A.; Lubyshev, D.; Fastenau, J.M.; Liu, A.W.K.; Gossard, A.C.; Bowers, J.E. High performance continuous wave 1.3 μm quantum dot lasers on silicon. Appl. Phys. Lett. 2014, 104, 041104. [Google Scholar] [CrossRef]
- Liu, H.; Wang, T.; Jiang, Q.; Hogg, R.; Tutu, F.; Pozzi, F.; Seeds, A. Long-wavelength InAs/GaAs quantum-dot laser diode monolithically grown on Ge substrate. Nat. Photonics 2011, 5, 416–419. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.; Wu, J.; Jiang, Q.; Tang, M.; Shutts, S.; Elliott, S.N.; Sobiesierski, A.; Seeds, A.J.; Ross, I.; et al. Electrically pumped continuous-wave III-V quantum dot lasers on silicon. Nat. Photonics 2016, 10, 307–312. [Google Scholar] [CrossRef]
- Sellin, R.L.; Ribbat, C.; Grundmann, M.; Ledentsov, N.N.; Bimberg, D. Close-to-ideal device characteristics of high-power InGaAs/GaAs quantum dot lasers. Appl. Phys. Lett. 2001, 78, 1207–1209. [Google Scholar] [CrossRef]
- Capua, A.; Rozenfeld, L.; Mikhelashvili, V.; Eisenstein, G.; Kuntz, M.; Laemmlin, M.; Bimberg, D. Direct correlation between a highly damped modulation response and ultralow relative intensity noise in an InAs/GaAs quantum dot laser. Opt. Express 2007, 15, 5388–5393. [Google Scholar] [CrossRef]
- Newell, T.; Bossert, D.; Stintz, A.; Fuchs, B.; Malloy, K.; Lester, L. Gain and linewidth enhancement factor in InAs quantum-dot laser diodes. IEEE Photon. Technol. Lett. 1999, 11, 1527–1529. [Google Scholar] [CrossRef]
- Ukhanov, A.A.; Stintz, A.; Eliseev, P.G.; Malloy, K.J. Comparison of the carrier induced refractive index, gain, and linewidth enhancement factor in quantum dot and quantum well lasers. Appl. Phys. Lett. 2004, 84, 1058–1060. [Google Scholar] [CrossRef]
- Shchekin, O.B.; Deppe, D.G. 1.3 μm InAs quantum dot laser with T0 = 161 K from 0 to 80 °C. Appl. Phys. Lett. 2002, 80, 3277–3279. [Google Scholar] [CrossRef]
- Markus, A.; Chen, J.X.; Paranthoën, C.; Fiore, A.; Platz, C.; Gauthier-Lafaye, O. Simultaneous two-state lasing in quantum-dot lasers. Appl. Phys. Lett. 2003, 82, 1818–1820. [Google Scholar] [CrossRef]
- Erneux, T.; Viktorov, E.A.; Kelleher, B.; Goulding, D.; Hegarty, S.P.; Huyet, G. Optically injected quantum-dot lasers. Opt. Lett. 2010, 35, 937–939. [Google Scholar] [CrossRef]
- Goulding, D.; Hegarty, S.P.; Rasskazov, O.; Melnik, S.; Hartnett, M.; Greene, G.; McInerney, J.G.; Rachinskii, D.; Huyet, G. Excitability in a quantum dot semiconductor laser with optical injection. Phys. Rev. Lett. 2007, 98, 153903. [Google Scholar] [CrossRef]
- Carroll, O.; O’Driscoll, I.; Hegarty, S.P.; Huyet, G.; Houlihan, J.; Viktorov, E.A.; Mandel, P. Feedback induced instabilities in a quantum dot semiconductor laser. Opt. Express 2006, 14, 10831–10837. [Google Scholar] [CrossRef] [PubMed]
- Viktorov, E.A.; Mandel, P.; O’Driscoll, I.; Carroll, O.; Huyet, G.; Houlihan, J.; Tanguy, Y. Low-frequency fluctuations in two-state quantum dot lasers. Opt. Lett. 2006, 31, 2302–2304. [Google Scholar] [CrossRef]
- Olejniczak, L.; Panajotov, K.; Wieczorek, S.; Thienpont, H.; Sciamanna, M. Intrinsic gain switching in optically injected quantum dot laser lasing simultaneously from the ground and excited state. J. Opt. Soc. Am. B 2010, 27, 2416–2423. [Google Scholar] [CrossRef]
- Viktorov, E.A.; Dubinkin, I.; Fedorov, N.; Erneux, T.; Tykalewicz, B.; Hegarty, S.P.; Huyet, G.; Goulding, D.; Kelleher, B. Injection-induced, tunable, all-optical gating in a two-state quantum dot laser. Opt. Lett. 2016, 41, 3555–3558. [Google Scholar] [CrossRef] [PubMed]
- Tykalewicz, B.; Goulding, D.; Hegarty, S.P.; Huyet, G.; Dubinkin, I.; Fedorov, N.; Erneux, T.; Viktorov, E.A.; Kelleher, B. Optically induced hysteresis in a two-state quantum dot laser. Opt. Lett. 2016, 41, 1034–1037. [Google Scholar] [CrossRef]
- Arsenijević, D.; Schliwa, A.; Schmeckebier, H.; Stubenrauch, M.; Spiegelberg, M.; Bimberg, D.; Mikhelashvili, V.; Eisenstein, G. Comparison of dynamic properties of ground- and excited-state emission in p-doped InAs/GaAs quantum-dot lasers. Appl. Phys. Lett. 2014, 104, 181101. [Google Scholar] [CrossRef]
- Stevens, B.J.; Childs, D.T.D.; Shahid, H.; Hogg, R.A. Direct modulation of excited state quantum dot lasers. Appl. Phys. Lett. 2009, 95, 061101. [Google Scholar] [CrossRef]
- Arsenijević, D.; Bimberg, D. Quantum-dot lasers for 35 Gbit/s pulse-amplitude modulation and 160 Gbit/s differential quadrature phase-shift keying. Proc. SPIE 2016, 9892, 98920S. [Google Scholar]
- Wang, C.; Lingnau, B.; Lüdge, K.; Even, J.; Grillot, F. Enhanced dynamic performance of quantum dot semiconductor lasers operating on the excited state. IEEE J. Quantum Electron. 2014, 50, 723–731. [Google Scholar] [CrossRef]
- Lin, L.C.; Chen, C.Y.; Huang, H.; Arsenijević, D.; Bimberg, D.; Grillot, F.; Lin, F.Y. Comparison of optical feedback dynamics of InAs/GaAs quantum-dot lasers emitting solely on ground or excited states. Opt. Lett. 2018, 43, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Lin, L.C.; Chen, C.Y.; Arsenijević, D.; Bimberg, D.; Lin, F.Y.; Grillot, F. Multimode optical feedback dynamics in InAs/GaAs quantum dot lasers emitting exclusively on ground or excited states: Transition from short- to long-delay regimes. Opt. Express 2018, 26, 1743–1751. [Google Scholar] [CrossRef]
- Yousefvand, H.R.; Faris, Z. Theoretical study of laser-mode competition in quantum-dot semiconductor lasers using a self-consistent electro-opto-thermal model. J. Opt. Soc. Am. B Opt. Phys. 2017, 34, 1580–1586. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.P.; Grillot, F.; Chan, S.C. Contribution of off-resonant states to the phase noise of quantum dot lasers. Opt. Express 2016, 24, 29872–29880. [Google Scholar] [CrossRef]
- Grillot, F.; Wang, C.; Naderi, N.A.; Even, J. Modulation properties of self-injected quantum-dot semiconductor diode lasers. IEEE J. Quantum Electron. 2013, 19, 1900812. [Google Scholar] [CrossRef]
- Ghalib, B.A.; Al-Obaidi, S.J.; Al-Khursan, A.H. Modeling of synchronization in quantum dot semiconductor lasers. Opt. Laser Technol. 2013, 48, 453–460. [Google Scholar] [CrossRef]
- Corless, R.M.; Essex, C.; Nerenberg, M.A.H. Numerical methods can suppress chaos. Phys. Lett. A 1991, 157, 27–36. [Google Scholar] [CrossRef]
- Butusov, D.; Karimov, A.; Tutueva, A.; Kaplun, D.; Nepomuceno, E.G. The effects of Padé numerical integration in simulation of conservative chaotic systems. Entropy 2019, 21, 362. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Toomey, J.P.; Kane, D.M. Mapping the dynamic complexity of a semiconductor laser with optical feedback using permutation entropy. Opt. Express 2014, 22, 1713–1725. [Google Scholar] [CrossRef]
- Osiński, M.; Buus, J. Linewidth broadening factor in semiconductor lasers-an overview. IEEE J. Quantum Electron. 1987, 23, 928. [Google Scholar] [CrossRef]
- AL-Hosiny, N.M. Effect of linewidth enhancement factor on the stability map of optically injected distributed feedback laser. Opt. Rev. 2014, 21, 261–264. [Google Scholar] [CrossRef]
- Heil, T.; Fischer, I.; Elsäßer, W. Influence of amplitude-phase coupling on the dynamics of semiconductor lasers subject to optical feedback. Phys. Rev. A 1999, 60, 634–641. [Google Scholar] [CrossRef]
| Symbol | Parameter | Value |
|---|---|---|
| ERS | RS recombination energy | 0.97 eV |
| EES | ES recombination energy | 0.87 eV |
| EGS | GS recombination energy | 0.82 eV |
| Capture time from RS to ES | 12.6 ps | |
| Relaxation time from ES to GS | 5.8 ps | |
| Escape time from ES to RS | 5.4 ns | |
| Escape time from GS to ES | 20.8 ps | |
| RS spontaneous decay time | 0.5 ns | |
| ES spontaneous decay time | 0.5 ns | |
| GS spontaneous decay time | 1.2 ns | |
| τp | The lifetime of photon | 4.1 ps |
| L | Cavity length | 5 × 10−2 cm |
| aES | Differential gain of ES | 10 × 10−15 cm2 |
| ξ | Gain limiting factor | 2 × 10−16 cm2 |
| Γp | Optical confinement factor | 0.06 |
| NB | Total QD number | 1 × 107 |
| α | Linewidth enhancement factor | 1.3 |
| vg | Group velocity of light | 8.57 × 107 m/s |
| VB | Total volume of QDs | 5 × 10−11 cm3 |
| η | Current pumping efficiency | 0.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.-F.; Wu, Z.-M.; Jayaprasath, E.; Yang, W.-Y.; Hu, C.-X.; Xia, G.-Q. Nonlinear Dynamics of Exclusive Excited-State Emission Quantum Dot Lasers Under Optical Injection. Photonics 2019, 6, 58. https://doi.org/10.3390/photonics6020058
Jiang Z-F, Wu Z-M, Jayaprasath E, Yang W-Y, Hu C-X, Xia G-Q. Nonlinear Dynamics of Exclusive Excited-State Emission Quantum Dot Lasers Under Optical Injection. Photonics. 2019; 6(2):58. https://doi.org/10.3390/photonics6020058
Chicago/Turabian StyleJiang, Zai-Fu, Zheng-Mao Wu, Elumalai Jayaprasath, Wen-Yan Yang, Chun-Xia Hu, and Guang-Qiong Xia. 2019. "Nonlinear Dynamics of Exclusive Excited-State Emission Quantum Dot Lasers Under Optical Injection" Photonics 6, no. 2: 58. https://doi.org/10.3390/photonics6020058
APA StyleJiang, Z.-F., Wu, Z.-M., Jayaprasath, E., Yang, W.-Y., Hu, C.-X., & Xia, G.-Q. (2019). Nonlinear Dynamics of Exclusive Excited-State Emission Quantum Dot Lasers Under Optical Injection. Photonics, 6(2), 58. https://doi.org/10.3390/photonics6020058






