Design Investigation of 4 × 4 Nonblocking Hybrid Plasmonic Electrooptic Switch
Abstract
1. Introduction
- A plasmonic platform is used for the first time to design and simulate a 4 × 4 nonblocking photonic switch.
- Although the design is used based on a 2 × 2 plasmonic switch (reported in Ref. [41]), the paper simulates the performance of the proposed 4 × 4 switch as a single element using a COMSOL environment. Coupling of the input/output interfaces between successive 2 × 2 switches are addressed carefully to achieve low-loss coupling.
- A mathematical framework is developed to assess the performance parameters of the designed switch.
- The capability of using the proposed switch as a routing node is investigated for high bit rate optical communication networks.
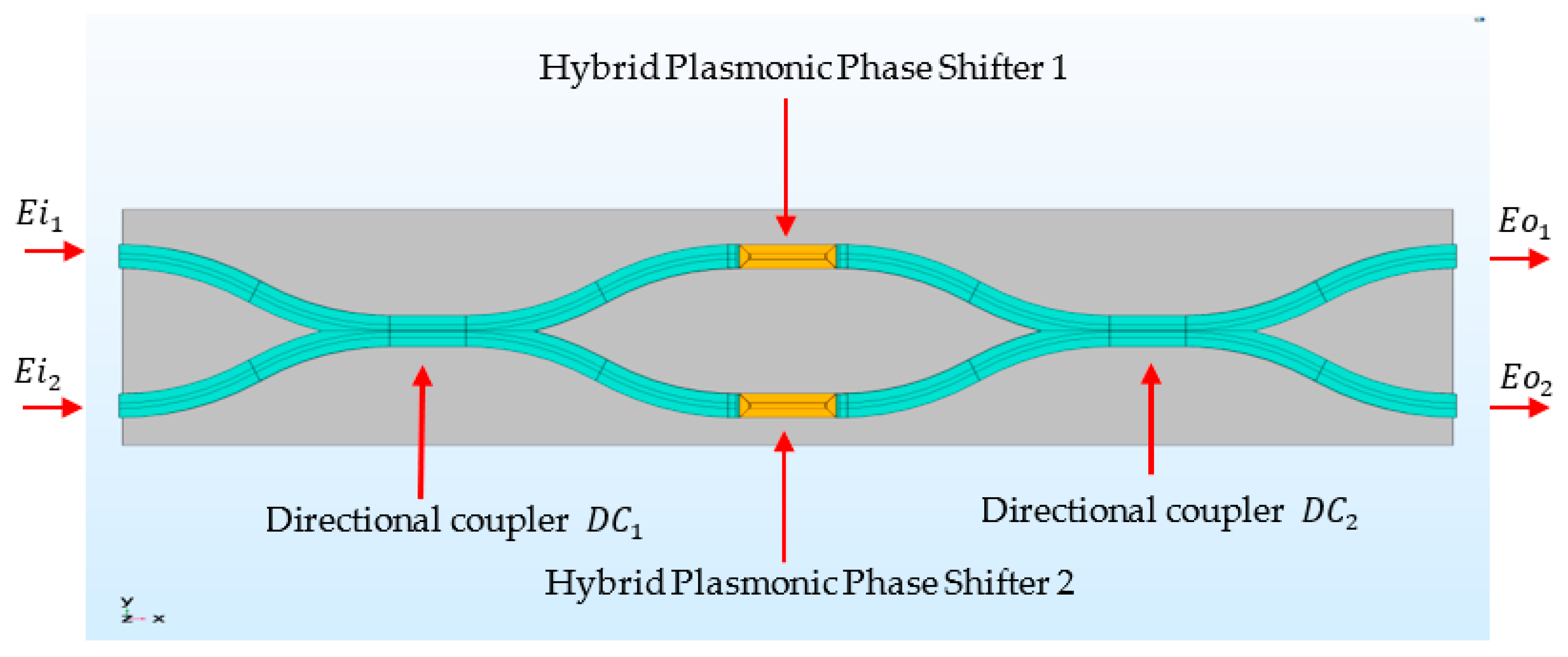
2. 2 × 2 Elementary Switching Cell
2.1. Model and Definitions
- : Transmission coefficient of the input DC
- : Coupling coefficient of the input DC
- : Transmission coefficient of the output DC
- : Coupling coefficient of the output DC
- : Amplitude attenuation coefficient of the upper MZS arm
- : Amplitude attenuation coefficient of the lower MZS arm
- : Length of the upper MZS arm
- : Length of the lower MZS arm
- : Phase shift of the upper MZS arm
- : Phase shift of the lower MZS arm
- (i)
- The attenuation coefficient and the arm phase (i = 1 and 2) are related to the effective complex refractive index associated with the arm-waveguide mode. Let , then:where λ is the operating wavelength. Note that the arm-waveguide loss (dB/µm) is related to (in ) by . Note also that represents the effective complex propagation constant in the arm waveguide.
- (ii)
- The loss of the DC (in dB) is given by when τ = κ. For lossless 3 dB-coupler, .
- i
- Cross state ()
- ii
- Bar state ()
2.2. Hybrid Plasmonic 2 × 2 MZS Implementation
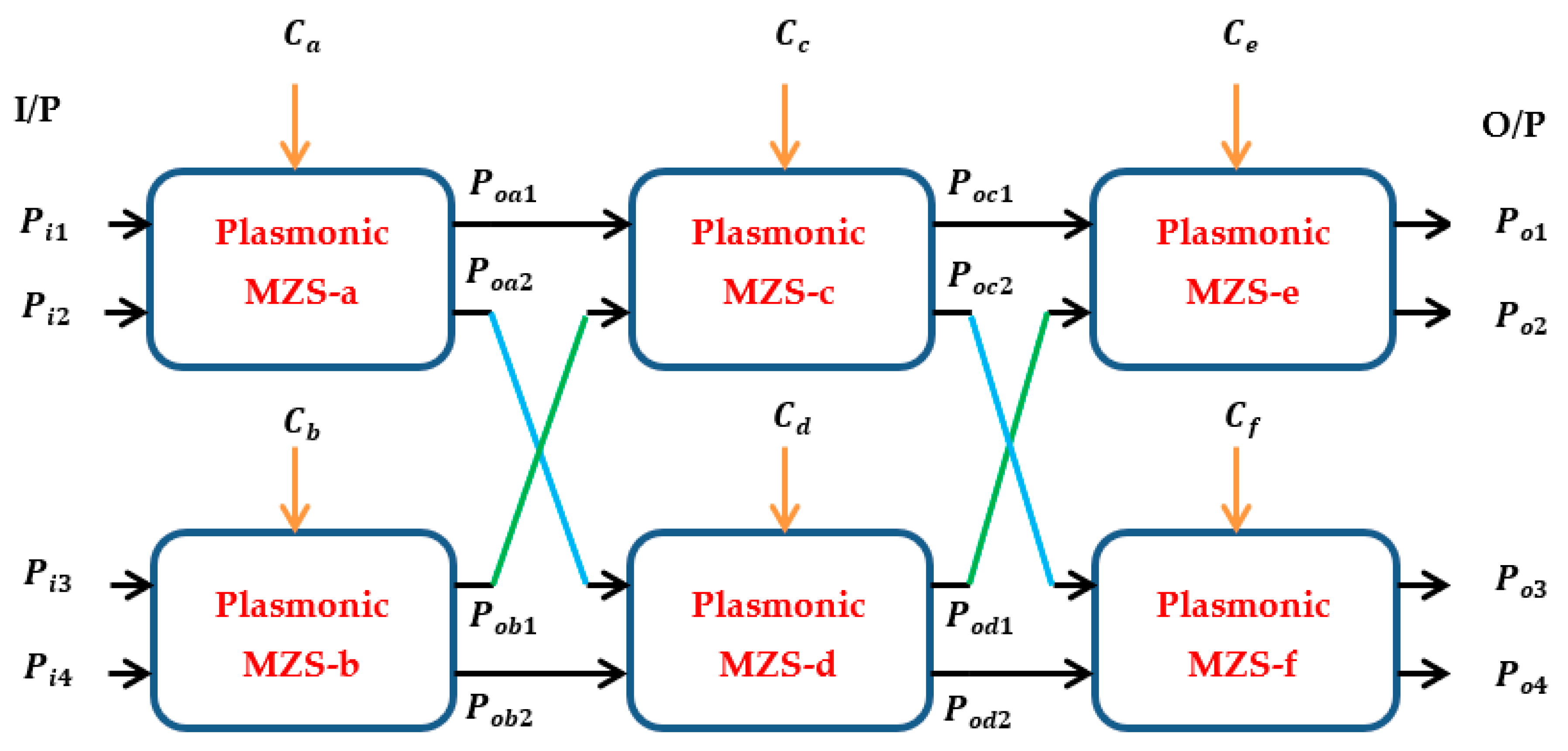
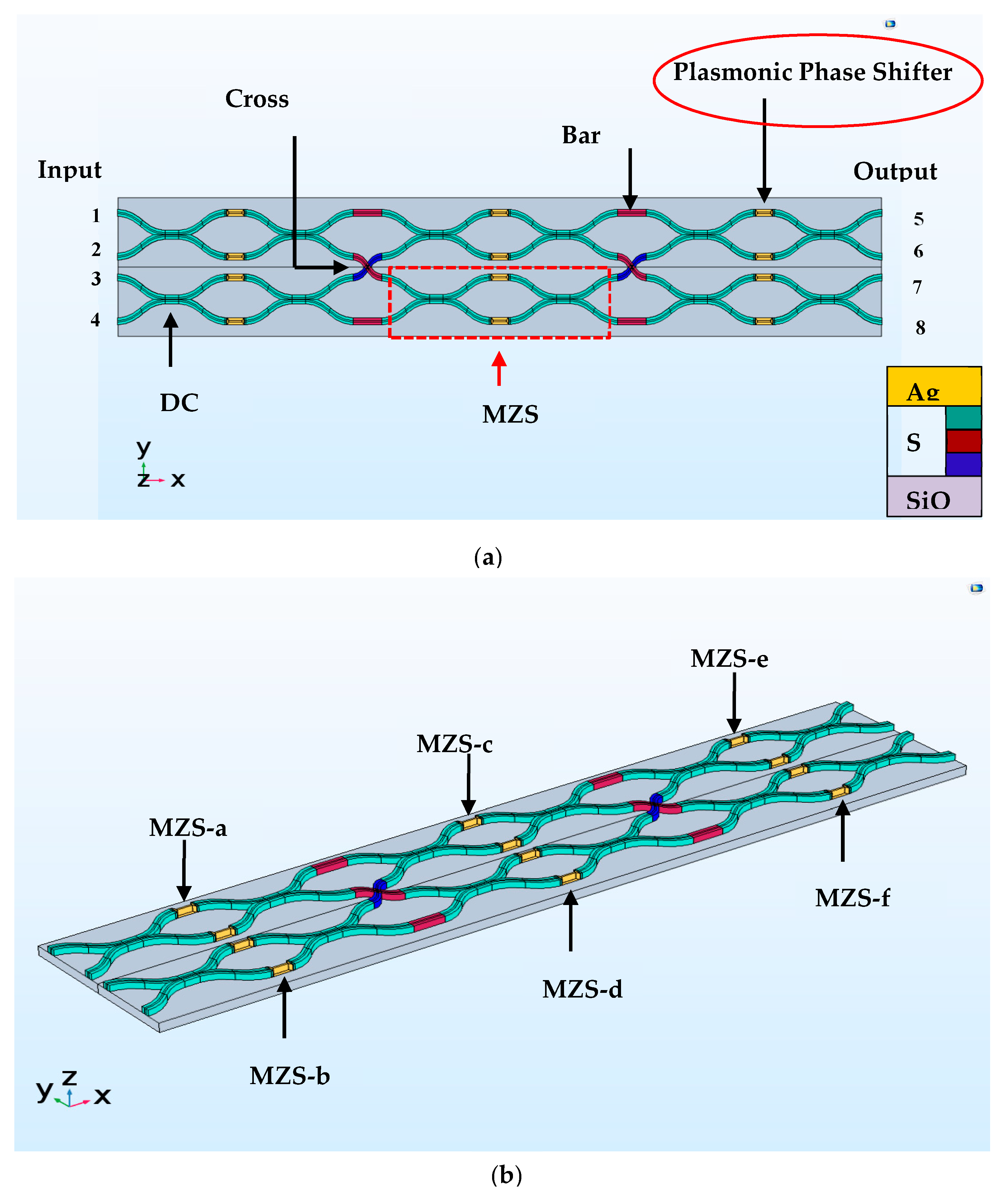
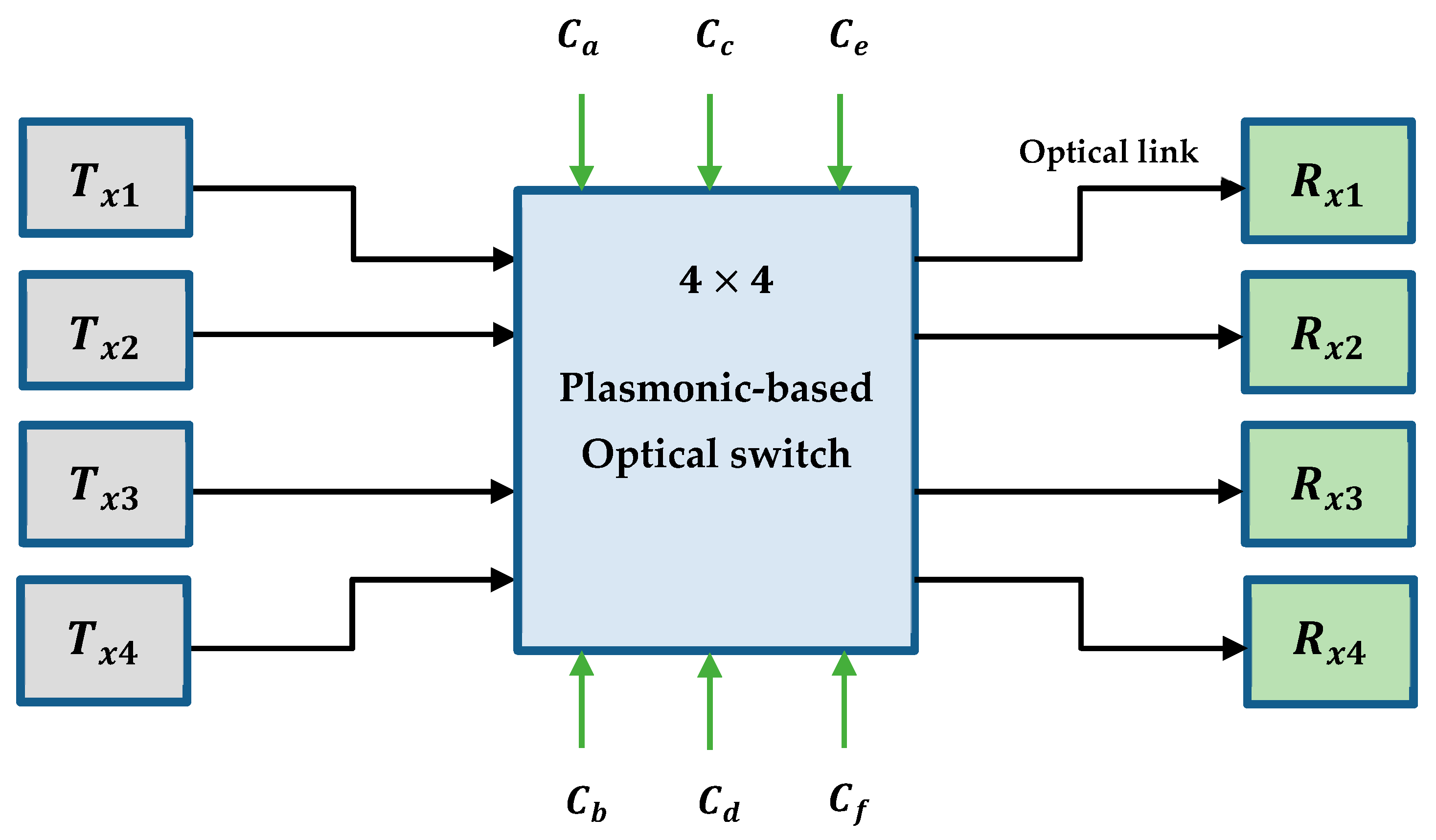
3. Scaling to a 4 × 4 Nonblocking Plasmonic Switch
3.1. Switch Model
3.2. Simulated and Calculated Results
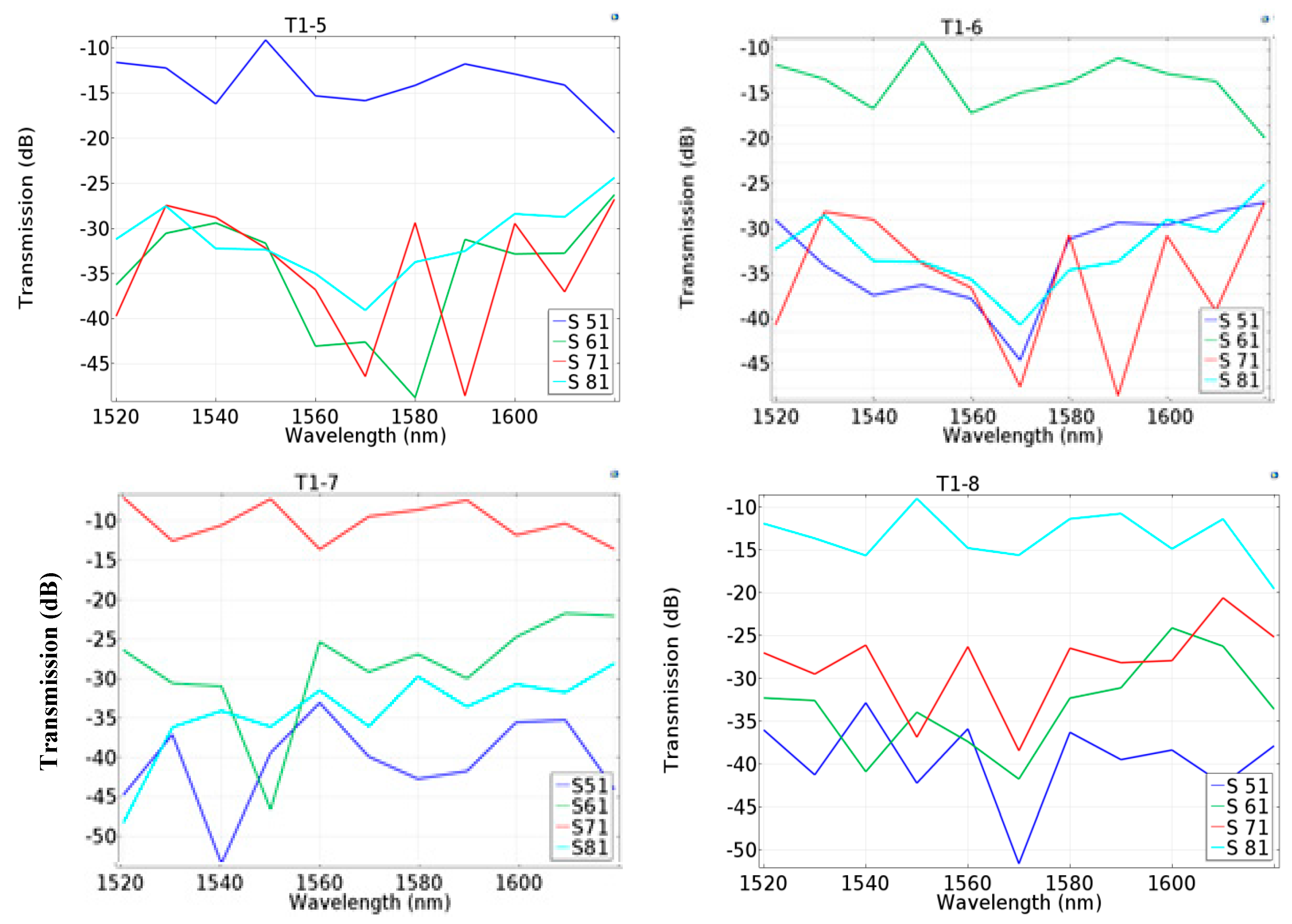
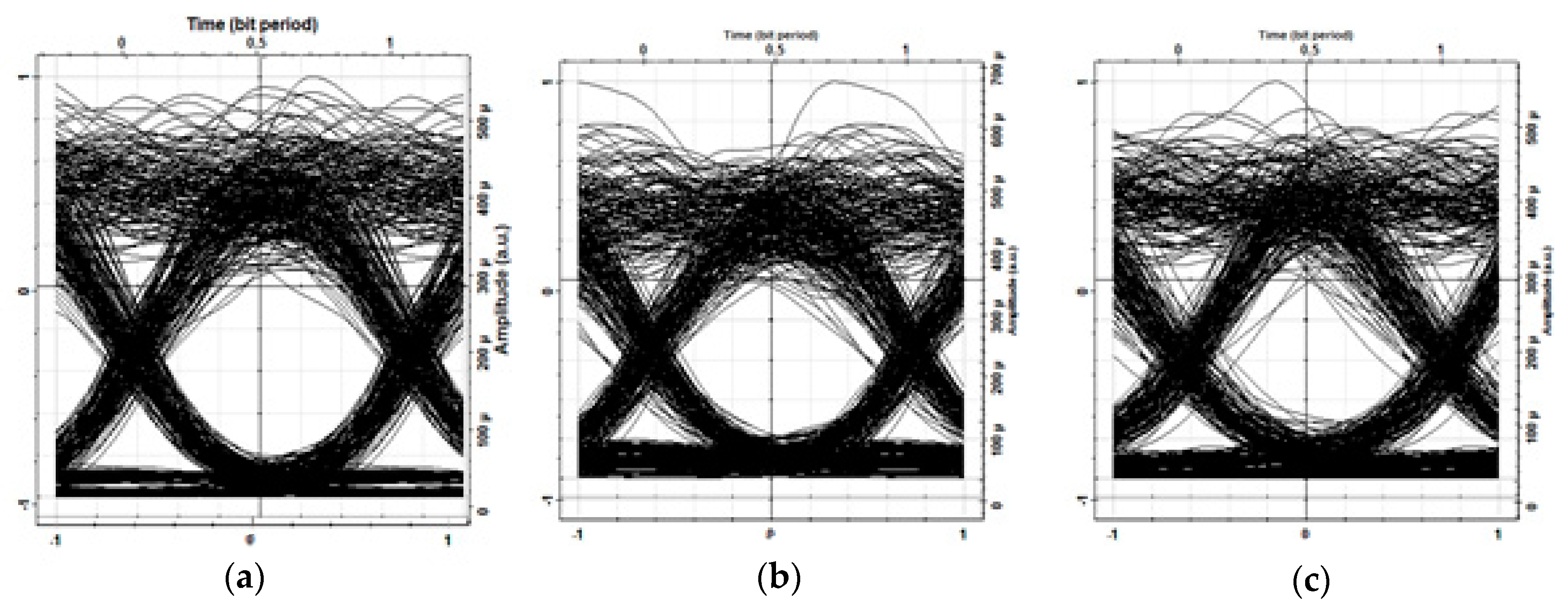
3.2.1. Simulated Results
3.2.2. Calculated Performance Parameters
3.2.3. Performance Comparison with Related Published Works
- (i)
- (ii)
- The proposed switch consumes the lowest power. The other three switches consume about 11, 8, and 7 times the power consumed by the proposed switch, respectively.
- (iii)
- (iv)
- (v)
4. Using the Designed Plasmonic Switch in Optical Networks: Case Study
4.1. Case I: WDM Transmission
- (i)
- The optical bandwidth of the 2 × 2 MZS is assumed to be dominated by the photon transit time across the MZS. Thus, = where c is the speed of the light in vacuum, is the MZS arm length, and is the real part of the effective refractive index of the propagating mode in the MZS arm. The 2 × 2 switch is designed here with = 6 µm and has . These values yield THz. This limited optical bandwidth has been taken into account when the 2 × 2 MZS is designed as a library element in the Optisystem software. A second-order optical Gaussian bandpass filter with 3 THz bandwidth centered at 1550 nm wavelength is inserted at each of the two switch inputs.
- (ii)
- The transmission path between one of the switch inputs and one of its output ports consists of three cascaded 2 × 2 MZS. According to electrical filter theory, cascading in identical filter stages yields a higher-order filter whose bandwidth equals of the single-stage bandwidth. According to this concept, the optical bandwidth of the 4 × 4 switch, equals ≅ 0.5 × 3 = 1.5 THz. Note that the optical bandwidth of the designed 4 × 4 switch is higher than the bandwidth of the 8 × 40 Gbps WDM signal (≅8 × 40 = 320 GHz).
- (iii)
- The 2 × 2 MZS is designed to operate at 1550 nm wavelength, which is almost the center of the 8-channel WDM spectrum. Thus, the maximum frequency deviation DF from the center frequency equals to 320/2 = 160 GHz, which corresponds to the lower (or upper) edge of the WDM spectrum. This frequency deviation, which yields a change in the bar-state phase shift difference, equals Df/ 0.15°, where is the center frequency corresponding to λ = 1550 nm. Therefore = 8.3 × and hence the MZS can be treated to operate with ∆Ø = 180° in the bar state (and 0° in the cross state) over the whole WDM signal spectrum. This will simplify the simulation, since ∆Ø is not modified with each spectrum component and is fixed at or 180° according to the operating state.
- (i)
- The optical switch is able to route the WDM signal from the input to the output without altering its frequency contents. This result is expected since the bandwidth of the WDM signal equals approximately 20% (≅320 GHz/1500 GHz) of the switch optical bandwidth.
- (ii)
- The spectrum level is reduced by 7.7 dB when the signal is routed from first input port to the fourth output port.
- (iii)
- The effect of fiber nonlinear optics is almost negligible, which makes the spectrum at the fiber output match that of the fiber input. This conclusion is confirmed further by noting that the spectrum at the fiber output does not change when the effect of fiber nonlinear optics is turned off in the software.
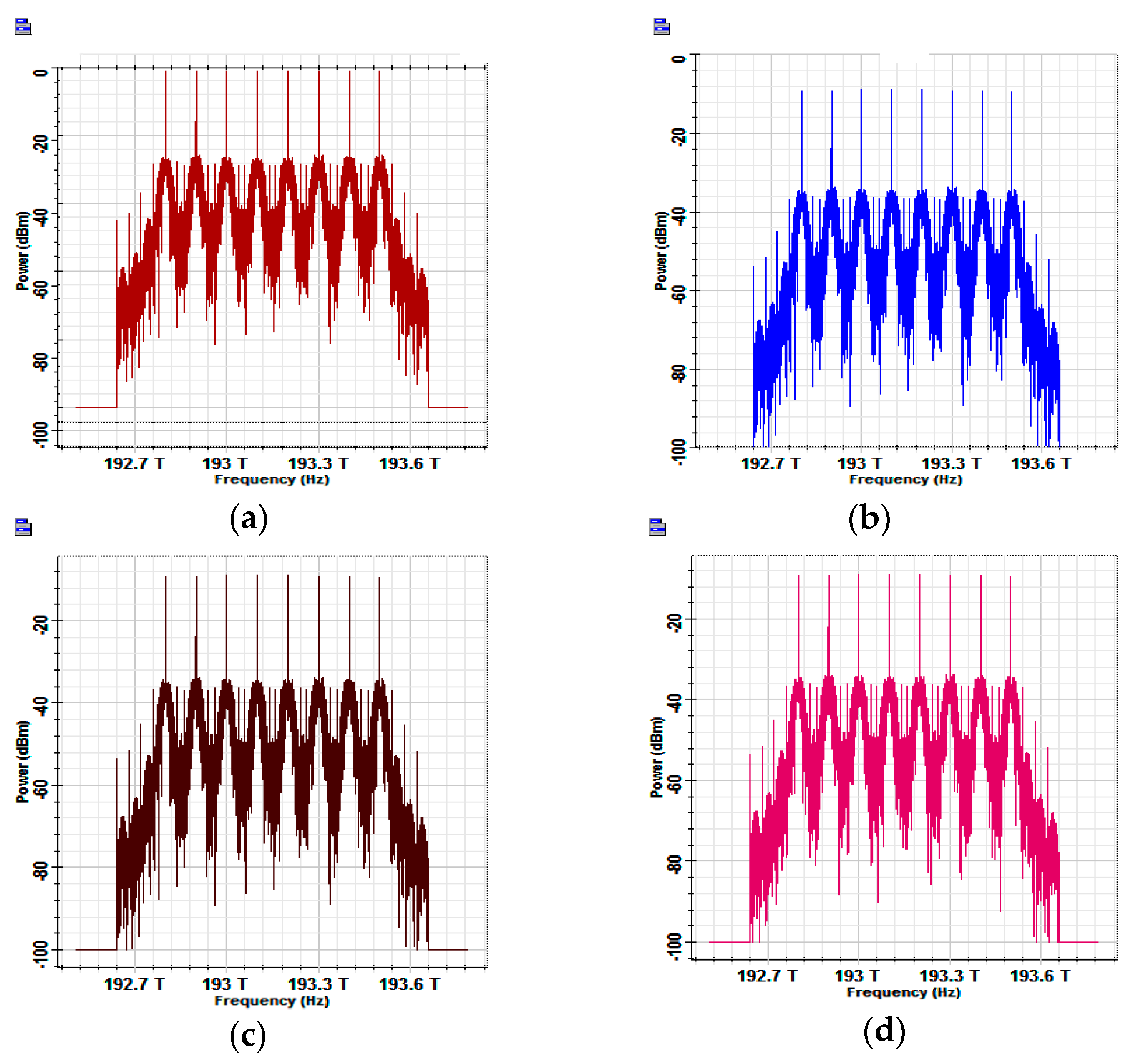
4.2. Case II: Multi-Input Multi-Output Operation
- : 4 × 40 Gbps NRZ (lasers frequencies span from 193.0–193.3 THz).
- : Similar to but with return-to-zero (RZ) signaling.
- : 8 × 40 Gbps NRZ (lasers frequencies span from 192.8–193.5 THz).
- : Similar to but with return-to-zero (RZ) signaling.
- From input 1 to output 3
- From input 2 to output 4
- From input 3 to output 1
- From input 4 to output 2
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, K.; Duan, F.; Yu, Y. Performance-enhanced silicon thermo-optic Mach–Zehnder switch using laterally supported suspended phase arms and efficient electrodes. Opt. Lett. 2019, 44, 951–954. [Google Scholar] [CrossRef]
- Fan, G.; Orobtchouk, R.; Han, B.; Li, Y.; Li, H. 8 × 8 wavelength router of optical network on chip. Opt. Express 2017, 25, 23677–23683. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Hou, W.; Guo, L.; Yang, Q.; Ge, Y.; Liang, H. Low Insertion Loss and Non-Blocking Microring-Based Optical Router for 3D Optical Network-on-Chip. IEEE Photonics J. 2018, 10. [Google Scholar] [CrossRef]
- Annoni, A.; Guglielmi, E.; Carminati, M.; Grillanda, S.; Ciccarella, P.; Ferrari, G.; Sorel, M.; Strain, M.J.; Sampietro, M.; Melloni, A.; et al. Automated Routing and Control of Silicon Photonic Switch Fabrics. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 169–176. [Google Scholar] [CrossRef]
- Chen, C.P.; Zhu, X.; Liu, Y.; Wen, K.; Chik, M.S.; Baehr-Jones, T.; Hochberg, M.; Bergman, K. Programmable Dynamically-Controlled Silicon Photonic Switch Fabric. IEEE J. Lightwave Technol. 2016, 34, 2952–2958. [Google Scholar] [CrossRef]
- Mendez, M.; Okamoto, M.; Ito, Y.; Kita, T. Compact thermo-optic MZI switch in siliconon-insulator using direct carrier injection. Opt. Express 2019, 27, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Rizal, C.S.; Niraula, B. Compact Si-based asymmetric MZI waveguide on SOI as a thermo-optical switch. Opt. Commun. 2017, 410, 947–955. [Google Scholar] [CrossRef]
- Lu, L.; Zhou, L.; Li, Z.; Li, X.; Chen, J. Broadband 4 × 4 Nonblocking Silicon Electrooptic Switches Based on Mach–Zehnder Interferometers. IEEE Photonics J. 2015, 7. [Google Scholar] [CrossRef]
- Lee, B.G.; Rylyakov, A.V.; Green, W.M.; Assefa, S.; Baks, C.W.; Rimolo-Donadio, R.; Kuchta, D.M.; Khater, M.H.; Barwicz, T.; Reinholm, C.; et al. Monolithic Silicon Integration of Scaled Photonic Switch Fabrics, CMOS Logic, and Device Driver Circuits. IEEE J. Lightwave Technol. 2014, 32, 743–751. [Google Scholar] [CrossRef]
- Soref, R. Design of low-energy on-chip electro-optical 1 × M wavelength-selective switches. Photonics Res. 2017, 5, 340–345. [Google Scholar] [CrossRef]
- Dupuis, N.; Lee, B.G. Impact of Topology on the Scalability of Mach–Zehnder-Based Multistage Silicon Photonic Switch Networks. IEEE J. Lightwave Technol. 2018, 36, 763–772. [Google Scholar] [CrossRef]
- Qiao, L.; Tang, W.; Chu, T. 32 × 32 silicon electro-optic switch with built-in monitors and balanced-status units. Sci. Rep. 2017, 7, 42306. [Google Scholar] [CrossRef]
- Jia, H.; Zhou, T.; Zhao, Y.; Xia, Y.; Dai, J.; Zhang, L.; Ding, J.; Fu, X.; Yang, L. Six-port optical switch for cluster-mesh photonic network-on-chip. Nanophotonics 2018, 7, 827–835. [Google Scholar] [CrossRef]
- Soref, R. Tutorial: Integrated-photonic switching structures. Am. Inst. Phys. 2018, 3. [Google Scholar] [CrossRef]
- Lee, B.G.; Dupuis, N. Silicon Photonic Switch Fabrics: Technology and Architecture. IEEE J. Lightwave Technol. 2019, 37, 6–20. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, L.; Li, X.; Hong, Z.; Chen, J. Design and analysis of a phase modulator based on a metal–polymer–silicon hybrid plasmonic waveguide. Appl. Opt. 2011, 50, 3428–3434. [Google Scholar] [CrossRef]
- Tsareva, A.; Tazieva, R.; Hellerc, E.; Chalonyd, M. Polymer electro-optic modulator efficiency enhancement by the high permittivity dielectric strips. Photonics Nanostruct. Fundam. Appl. 2017. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, Y.; Zhang, Y.; Shang, K.; Yoo, S.B. High-Density Wafer-Scale 3-D Silicon-Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24. [Google Scholar] [CrossRef]
- Kish, F.; Lal, V.; Evans, P.; Corzine, S.W.; Ziari, M.; Butrie, T.; Reffle, M.; Tsai, H.; Dentai, A.; Pleumeekers, J.; et al. System-on-Chip Photonic Integrated Circuits. IEEE J. Sel. Top. Quantum Electron. 2018, 24. [Google Scholar] [CrossRef]
- Minkenberg, C.; Farrington, N.; Zilkie, A.; Nelson, D.; Lai, C.P.; Brunina, D.; Byrd, J.; Chowdhuri, B.; Kucharewski, N.; Muth, K.; et al. Reimagining Datacenter Topologies with Integrated Silicon Photonics. J. Opt. Commun. Netw. Opt. Soc. Am. 2018, 10, 126–139. [Google Scholar] [CrossRef]
- Tanaka, S.; Simoyama, T.; Aoki, T.; Mori, T.; Sekiguchi, S.; Jeong, S.; Usuki, T.; Tanaka, Y.; Morito, K. Ultralow-Power (1.59 mW/Gbps), 56-Gbps PAM4 Operation of Si Photonic Transmitter Integrating Segmented PIN Mach–Zehnder Modulator and 28-nm CMOS Driver. IEEE J. Lightwave Technol. 2018, 36, 1275–1280. [Google Scholar] [CrossRef]
- Dabos, G.; Manolis, A.; Papaionnou, S.; Tsiokos, D.; Markey, L.; Weeber, J.-C.; Dereux, A.; Giesecke, A.L.; Porschatis, C.; Chmielak, B.; et al. CMOS plasmonics in WDM data transmission: 200 Gb/s (8 × 25Gb/s) transmission over aluminum plasmonic waveguides. Opt. Express 2018, 26, 12469–12478. [Google Scholar] [CrossRef] [PubMed]
- Heni, W.; Hoessbacher, C.; Haffner, C.; Fedoryshyn, Y.; Baeuerle, B.; Josten, A.; Hillerkuss, D.; Salamin, Y.; Bonjour, R.; Melikyan, A.; et al. High speed plasmonic modulator array enabling dense optical interconnect solutions. Opt. Express 2015, 23, 29746–29757. [Google Scholar] [CrossRef] [PubMed]
- Ozbay, E. Plasmonics: Merging Photonics and Electronics at Nanoscale Dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Tian, Y.; Ye, S.; Chen, L.; Peng, X.; Qu, J. Characteristic Analysis of Low-Threshold Plasmonic Lasers Using Ag Nanoparticles with Various Shapes Using Photochemical Synthesis. IEEE J. Lightwave Technol. 2015, 33, 3215–3223. [Google Scholar] [CrossRef]
- Rahman, M.Z.; Krishna, K.M.; Reddy, K.K.; Babu, M.V.; Mirza, S.S.; Fathima, S.Y. Ultra-Wide-Band Band-Pass Filters Using Plasmonic MIM Waveguide-Based Ring Resonators. IEEE Photonics Technol. Lett. 2018, 30, 1715–1718. [Google Scholar] [CrossRef]
- Dorodnyy, A.; Salamin, Y.; Ma, P.; Plestina, J.V.; Lassaline, N.; Mikulik, D.; Romero-Gomez, P.; Morral, A.F.; Leuthold, J. Plasmonic Photodetectors. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–13. [Google Scholar] [CrossRef]
- Tomadin, A.; Polini, M. Theory of the plasma-wave photoresponse of a gated graphene sheet. Phys. Rev. B 2013, 88, 205426. [Google Scholar] [CrossRef]
- Viti, L.; Coquillat, D.; Politano, A.; Kokh, K.A.; Aliev, Z.S.; Babanly, M.B.; Tereshchenko, O.E.; Knap, W.; Chulkov, E.V.; Vitiello, M.S. Plasma-Wave Terahertz Detection Mediated by Topological Insulators Surface States. Nano Lett. 2016, 16, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Koch, U.; Messner, A.; Hoessbacher, C.; Heni, W.; Josten, A.; Baeuerle, B.; Ayata, M.; Fedoryshyn, Y.; Elder, D.L.; Dalton, L.R.; et al. Ultra-Compact Terabit Plasmonic Modulator Array. IEEE J. Lightwave Technol. 2019, 37, 1484–1491. [Google Scholar] [CrossRef]
- Baeuerle, B.; Heni, W.; Hoessbacher, C.; Fedoryshyn, Y.; Josten, A.; Haffner, C.; Watanabe, T.; Uhl, C.; Hettrich, H.; Elder, D.L.; et al. Reduced Equalization Needs of 100 GHz Bandwidth Plasmonic Modulators. IEEE J. Lightwave Technol. 2019, 37, 2050–2057. [Google Scholar] [CrossRef]
- Wu, H.; Huang, Y.; Shen, P.; Lee, H.; Oketani, R.; Yonemaru, Y.; Yamanaka, M.; Shoji, S.; Lin, K.; Chang, C.; et al. Ultrasmall all-optical plasmonic switch and its application to superresolution imaging. Sci. Rep. 2016. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Datta, A. Modeling of a Vertical Hybrid Plasmonic Switch with VO2 Fin Bragg Grating. IEEE Photonics Technol. Lett. 2018, 30, 997–1000. [Google Scholar] [CrossRef]
- Xiao, J.; Wei, Q.; Yang, D.; Zhang, P.; He, N.; Zhang, G.; Ren, T.; Chen, X. A CMOS-Compatible Hybrid Plasmonic Slot Waveguide with Enhanced Field Confinement. IEEE Electron. Device Lett. 2016, 37, 456–458. [Google Scholar] [CrossRef]
- Huong, N.T.; Chinh, N.V.; Hoang, C.M. Wedge Surface Plasmon Polariton Waveguides Based on Wet-Bulk Micromachining. Photonics 2019, 6, 21. [Google Scholar] [CrossRef]
- Haffner, C.; Heni, W.; Fedoryshyn, Y.; Josten, A.; Baeuerle, B.; Hoessbacher, C.; Salamin, Y.; Koch, U.; Dordevic, N.; Mousel, P.; et al. Plasmonic Organic Hybrid Modulators—Scaling Highest Speed Photonics to the Microscale. Proc. IEEE 2016, 104, 2362–2379. [Google Scholar] [CrossRef]
- Hoessbacher, C.; Josten, A.; Baeuerle, B.; Fedoryshyn, Y.; Hettrich, H.; Salamin, Y.; Heni, W.; Haffner, C.; Kaiser, C.; Schmid, R.; et al. Plasmonic modulator with >170 GHz bandwidth demonstrated at 100 GBd NRZ. Opt. Express 2017, 25, 1762–1768. [Google Scholar] [CrossRef] [PubMed]
- Heni, W.; Haffner, C.; Elder, D.L.; Tillack, A.F.; Fedoryshyn, Y.; Cottier, R.; Salamin, Y.; Hoessbacher, C.; Koch, U.; Cheng, B.; et al. Nonlinearities of organic electro-optic materials in nanoscale slots and implications for the optimum modulator design. Opt. Express 2017, 25, 2627–2653. [Google Scholar] [CrossRef] [PubMed]
- Pitilakis, A.; Kriezis, E.E. Longitudinal 2 × 2 Switching Configurations Based on Thermo-Optically Addressed Dielectric-Loaded Plasmonic Waveguides. IEEE J. Lightwave Technol. 2011, 29, 2636–2646. [Google Scholar] [CrossRef]
- Papaioannou, S.; Giannoulis, G.; Vyrsokinos, K.; Leroy, F.; Zacharatos, F.; Markey, L.; Weeber, J.; Dereux, A.; Bozhevolnyi, S.I.; Prinzen, A.; et al. Ultracompact and Low-Power Plasmonic MZI Switch Using Cyclomer Loading. IEEE Photonics Technol. Lett. 2015, 27, 963–966. [Google Scholar] [CrossRef]
- Jaber, M.S.; Tawfeeq, S.K.; Fyath, R.S. Design Investigation of 2 × 2 Mach-Zehnder Optical Switch Based on a Metal-Polymer-Silicon Hybrid Plasmonic Waveguide. Fiber Integr. Opt. 2019, 38, 21–42. [Google Scholar] [CrossRef]
- Sun, S.; Narayana, V.K.; Sarpkaya, I.; Crandall, J.; Soref, R.A.; Dalir, H.; El-Ghazawi, T.; Sorger, V.J. Hybrid Photonic-Plasmonic Nonblocking Broadband 5 × 5 Router for Optical Networks. IEEE Photonics J. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Papaioannou, S.; Vyrsokinos, K.; Kalavrouziotis, D.; Giannoulis, G.; Apostolopoulos, D.; Avramopoulos, H.; Zacharatos, F.; Hassan, K.; Weeber, J.; Markey, L.; et al. Merging Plasmonics and Silicon Photonics towards Greener and Faster “Network-on-Chip” Solutions for Data Centers and High-Performance Computing Systems. Semant. Sch. 2012. [Google Scholar] [CrossRef]
- Sun, S.; Narayana, V.K.; El-Ghazawi, T.; Sorger, V.J. High Performance Photonic-Plasmonic Optical Router: A Non-blocking WDM Routing Device for Optical Networks. Opt. Soc. Am. 2017. [Google Scholar] [CrossRef]
- Ge, Z.; Zhang, L.; Wang, G.; Zhang, W.; Liu, M.; Li, S.; Wang, L.; Sun, Q.; Ren, W.; Si, J.; et al. On-Chip Router Elements Based on Silicon Hybrid Plasmonic Waveguide. IEEE Photonics Technol. Lett. 2017, 29, 952–955. [Google Scholar] [CrossRef]
- Dupuis, N.; Rylyakov, A.V.; Schow, C.L.; Kuchta, D.M.; Baks, C.W.; Orcutt, J.S.; Gill, D.M.; Green, W.M.; Lee, B.G. Nanosecond-Scale Mach–Zehnder-Based CMOS Photonic Switch Fabrics. IEEE J. Lightwave Technol. 2017, 35, 615–623. [Google Scholar] [CrossRef]
- Dupuis, N.; Lee, B.G.; Rylyakov, A.V.; Kuchta, D.M.; Baks, C.W.; Orcutt, J.S.; Gill, D.M.; Green, W.M.; Schow, C.L. Modeling and Characterization of a Nonblocking 4 × 4 Mach–Zehnder Silicon Photonic Switch Fabric. IEEE J. Lightwave Technol. 2015, 33, 4329–4337. [Google Scholar] [CrossRef]
- Yang, M.; Green, W.M.; Assefa, S.; Van Campenhout, J.; Lee, B.G.; Jahnes, C.V.; Doany, F.E.; Schow, C.L.; Kash, J.A.; Vlasov, Y.A. Non-Blocking 4 × 4 Electro-Optic Silicon Switch for On-Chip Photonic Networks. Opt. Express 2011, 19, 47–54. [Google Scholar] [CrossRef]
- Luan, J.; Fan, M.; Zheng, P.; Yang, H.; Hu, G.; Yun, B.; Cui, Y. Design and Optimization of a Graphene Modulator Based on Hybrid Plasmonic Waveguide with Double Low-Index Slots. Plasmonics 2019, 14, 133–138. [Google Scholar] [CrossRef]
- Optiwave Systems Inc. Available online: https://optiwave (accessed on 8 November 2018).
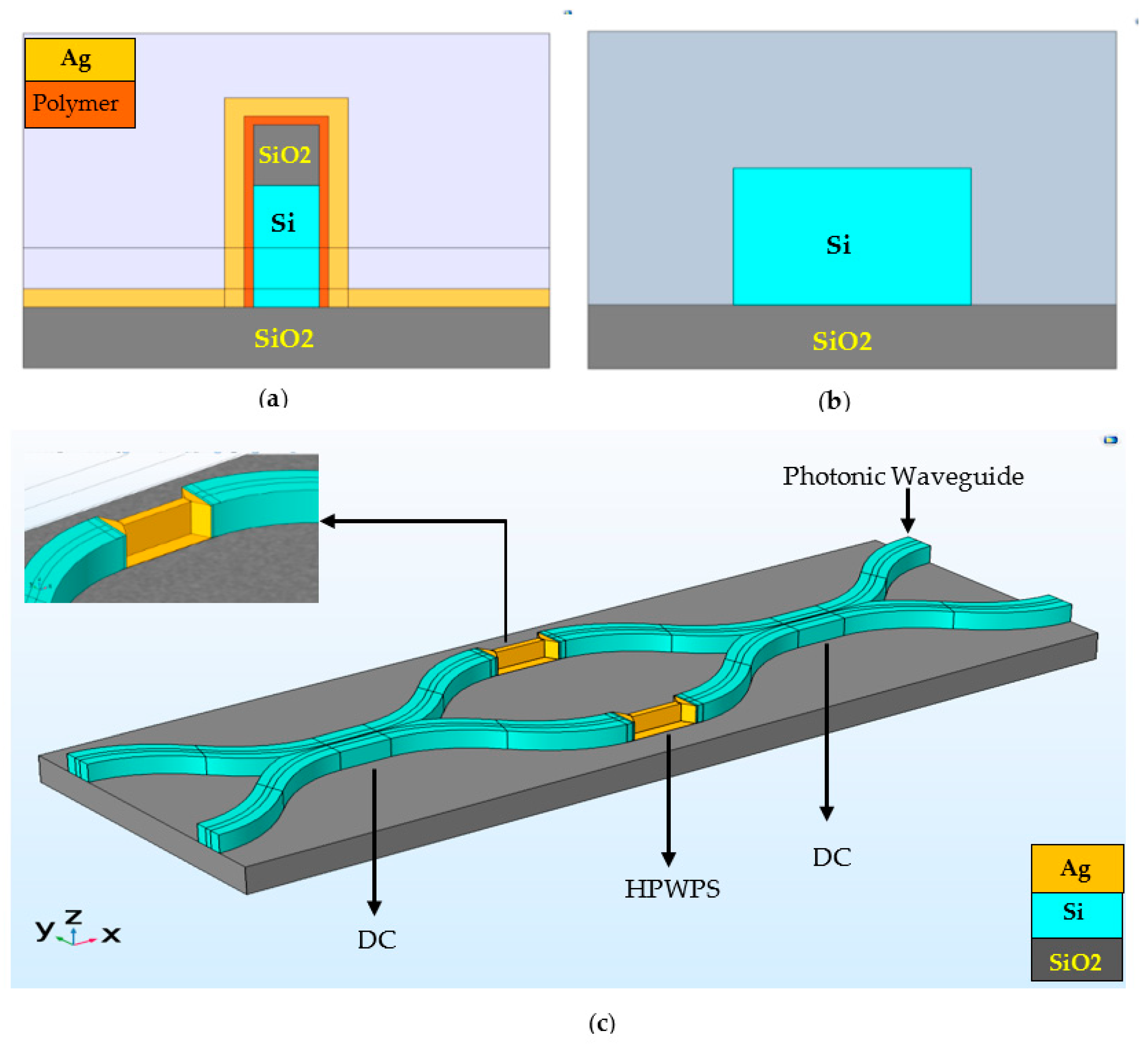


| Material | Refractive Index | Width (nm) | Height (nm) |
|---|---|---|---|
| 3.48 | 200 (Photonic waveguide) | 200 | |
| 100 (Plasmonic waveguide) | |||
| 1.46 | 200 | 100 | |
| 1.81 ( pm/V) | 14 | 14 | |
| 0.1444 + j11.366 | 30 | 30 |
| State No. | Control Logics | Output Power | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | ||||
| 3 | 1 | 0 | 1 | 0 | 0 | 0 | ||||
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | ||||
| 5 | 0 | 0 | 1 | 1 | 0 | 0 | ||||
| 6 | 0 | 0 | 0 | 0 | 1 | 0 | ||||
| 7 | 0 | 0 | 1 | 0 | 1 | 0 | ||||
| 8 | 0 | 0 | 0 | 1 | 1 | 0 | ||||
| 9 | 1 | 0 | 0 | 1 | 1 | 0 | ||||
| 10 | 0 | 0 | 1 | 1 | 1 | 0 | ||||
| 11 | 0 | 0 | 0 | 0 | 0 | 1 | ||||
| 12 | 0 | 0 | 1 | 0 | 0 | 1 | ||||
| 13 | 1 | 0 | 1 | 0 | 0 | 1 | ||||
| 14 | 0 | 0 | 0 | 1 | 0 | 1 | ||||
| 15 | 1 | 0 | 0 | 1 | 0 | 1 | ||||
| 16 | 0 | 1 | 0 | 1 | 0 | 1 | ||||
| 17 | 0 | 0 | 1 | 1 | 0 | 1 | ||||
| 18 | 0 | 0 | 0 | 0 | 1 | 1 | ||||
| 19 | 0 | 0 | 1 | 0 | 1 | 1 | ||||
| 20 | 1 | 0 | 1 | 0 | 1 | 1 | ||||
| 21 | 0 | 1 | 1 | 0 | 1 | 1 | ||||
| 22 | 0 | 0 | 0 | 1 | 1 | 1 | ||||
| 23 | 1 | 0 | 0 | 1 | 1 | 1 | ||||
| 24 | 0 | 0 | 1 | 1 | 1 | 1 | ||||
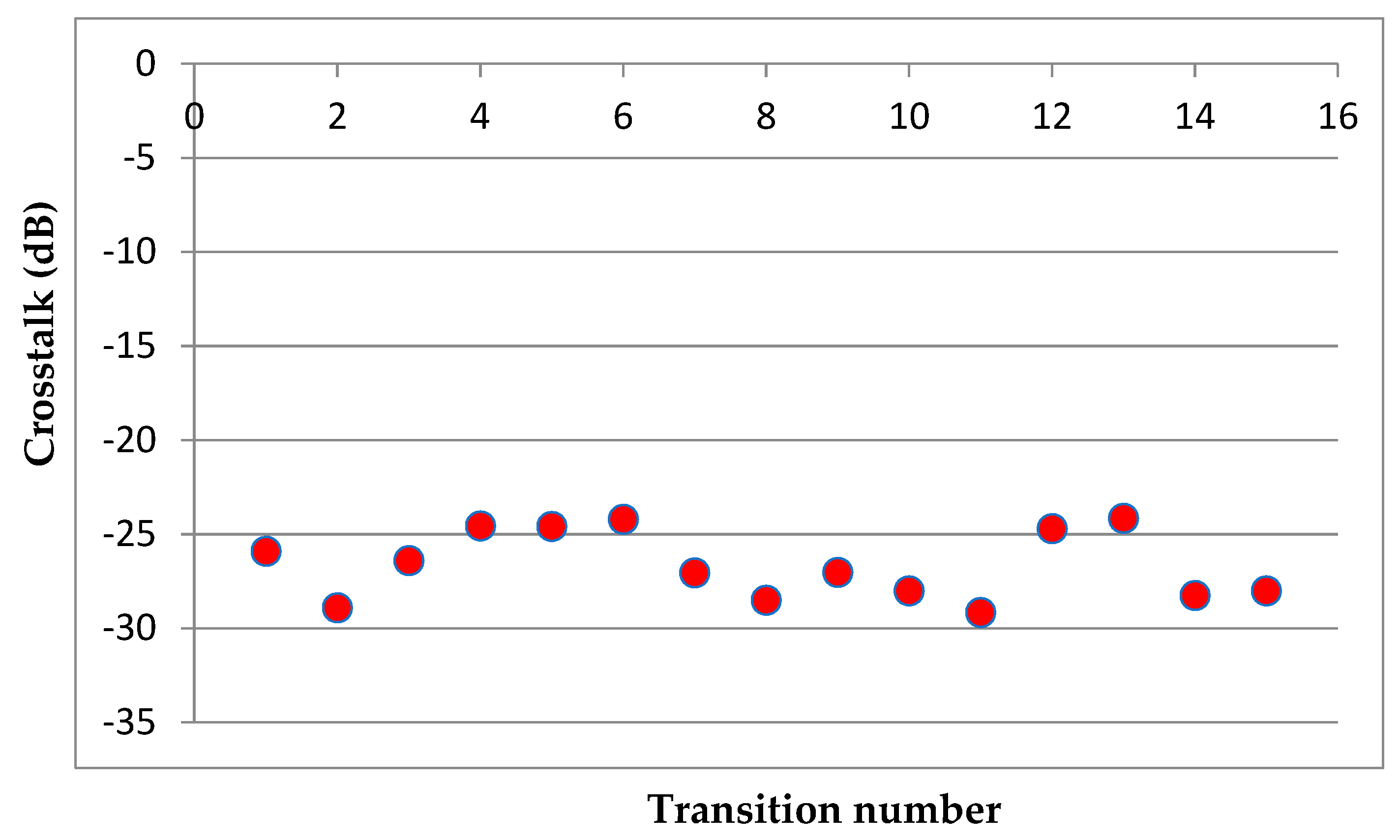
| Transition No. | Input | Required Output Port | Output Power (dBm) | Crosstalk (dB) | |||
|---|---|---|---|---|---|---|---|
| 1 | −7.65 | −32.15 | −33.00 | −34.00 | −24.50 | ||
| 2 | −35.00 | −7.45 | −33.35 | −33.60 | −25.90 | ||
| 3 | −39.00 | −46.50 | −7.40 | −36.30 | −28.90 | ||
| 4 | −42.00 | −33.60 | −37.00 | −7.20 | −26.40 | ||
| 5 | −7.35 | −31.90 | −39.00 | −32.10 | −24.55 | ||
| 6 | −34.20 | −7.20 | −42.00 | −31.80 | −24.60 | ||
| 7 | −41.50 | −34.20 | −7.20 | −31.40 | −24.20 | ||
| 8 | −41.20 | −34.45 | −43.70 | −7.40 | −27.05 | ||
| 9 | −7.40 | −40.00 | −35.90 | −51.20 | −28.50 | ||
| 10 | −38.10 | −7.20 | −34.25 | −52.70 | −27.05 | ||
| 11 | −35.65 | −45.10 | −7.65 | −40.15 | −28.00 | ||
| 12 | −36.55 | −51.50 | −37.70 | −7.40 | −29.15 | ||
| 13 | −7.20 | −32.60 | −32.50 | −31.90 | −24.70 | ||
| 14 | −37.10 | −7.40 | −44.50 | −31.55 | −24.15 | ||
| 15 | −35.65 | −41.55 | −7.40 | −41.18 | −28.25 | ||
| 16 | −36.50 | −41.40 | −35.65 | −7.65 | −28.00 | ||
| 2 × 2 Switch | Cross Loss (dB) | Bar Loss (dB) |
|---|---|---|
| A | 2.30 | 2.50 |
| B | 2.30 | 2.50 |
| C | 2.31 | 2.55 |
| D | 2.31 | 2.55 |
| E | 2.32 | 2.60 |
| F | 2.32 | 2.60 |
| Switch Type | Power Consumption | (V.µm) | Footprint () | Insertion Loss (dB) | Crosstalk (dB) | Phase Shifter Length (µm) |
|---|---|---|---|---|---|---|
| This work (plasmonic + EO) | 3.0 mW/π for 100 Gbps operation | 12 | 550 × 70 | 7.70 | −26.5 | 6 |
| Conventional (EO + thermo-optic) [8] | 33.7 mW/π | − | 3500 × 1400 | 7.70 | −12.0 | 356 |
| Conventional (EO) [47] | 25.0 mW/π | 256.25 | 5000 × 3000 | 3.00 | −25.0 | 250 |
| Conventional (EO) [48] | 20.0 mW/π | 212 | 1600 × 300 | 5.80 | −9.0 | 200 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaber, M.S.; Tawfeeq, S.K.; Fyath, R.S. Design Investigation of 4 × 4 Nonblocking Hybrid Plasmonic Electrooptic Switch. Photonics 2019, 6, 47. https://doi.org/10.3390/photonics6020047
Jaber MS, Tawfeeq SK, Fyath RS. Design Investigation of 4 × 4 Nonblocking Hybrid Plasmonic Electrooptic Switch. Photonics. 2019; 6(2):47. https://doi.org/10.3390/photonics6020047
Chicago/Turabian StyleJaber, Maithem S., Shelan K. Tawfeeq, and Raad S. Fyath. 2019. "Design Investigation of 4 × 4 Nonblocking Hybrid Plasmonic Electrooptic Switch" Photonics 6, no. 2: 47. https://doi.org/10.3390/photonics6020047
APA StyleJaber, M. S., Tawfeeq, S. K., & Fyath, R. S. (2019). Design Investigation of 4 × 4 Nonblocking Hybrid Plasmonic Electrooptic Switch. Photonics, 6(2), 47. https://doi.org/10.3390/photonics6020047




