Abstract
Optical injection locking has been demonstrated as an effective filter for optical communications. These optical filters have advantages over conventional passive filters, as they can be used on active material, allowing them to be monolithically integrated onto an optical circuit. We present an experimental and theoretical study of the optical suppression in injection locked Fabry–Pérot and slotted Fabry–Pérot lasers. We consider both single frequency and optical comb injection. Our model is then used to demonstrate that improving the Q factor of devices increases the suppression obtained when injecting optical combs. We show that increasing the Q factor while fixing the device pump rate relative to threshold causes the locking range of these demultiplexers to asymptotically approach a constant value.
1. Introduction
The demand for higher information transfer rates has led much research into evolving the current infrastructure in place for data transmission. Previous wavelength division multiplexing (WDM) networks were rigid in nature, with fixed channel spacings and bit rates throughout the network. Flexible or elastic optical networks have been proposed as superior, more energy- and bandwidth-efficient alternatives to standard WDM systems, which allow the optical bandwidth and modulation formats used to be dynamically adjusted to meet the requirements of each node in the network [1,2,3,4]. Transmission speeds of greater than 10 Tb/s with spectral efficiencies of 7.7 b/s/Hz have been achieved under laboratory conditions [5], which shows promise that these networks will be able to deliver future transmission speed requirements. These flexible networks have been made realisable due to advances in transmitting and receiving optical super channels, using narrowly-spaced coherent optical combs [5,6,7]. As well as reducing power consumption and the amount of individual components required, optical combs offer advantages such as allowing the WDM channels to be more densely packed and simplifying the digital signal processing [8].
The power consumption and cost of coherent comb sources can be further reduced through photonic integration. Designs using monolithically-integrable injection locked gain switched lasers have previously demonstrated coherent combs on InP, with optical spacings between 4 GHz and 10 GHz [9,10]. The use of these optical combs however requires each comb line to be demultiplexed, in order to enable each frequency to be individually modulated with data. However, standard integrable arrayed waveguide grating technologies suitable for demultiplexing combs with spacings below 10 GHz have yet to be demonstrated on active material and are impractical due to their large size and cost. As a result, new integrated demultiplexers that use optical injection locking to demultiplex were developed [11,12,13,14]. These optical filters operate by injection locking each line in the optical comb to a slave laser, as illustrated in Figure 1a. The injection locked slave laser provides amplification to the targeted carrier in the comb, whereas the other comb lines passing through the slave laser can undergo optical loss. In addition, using optical injection means the demultiplexer can track small frequency drifts without any active control or device tuning, as long as they are within the locking tongue of the slave laser.
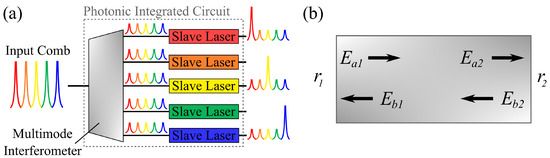
Figure 1.
(a) Illustration of a photonic integrated circuit for demultiplexing optical combs. The comb is first split equally using a multimode interferometer, and then, individual slave lasers are frequency locked to specific lines in the comb. (b) Illustrations of the fields inside a laser cavity, with reflecting mirrors and .
Numerical models for simulating the demultiplexing of these coherent combs have been previously presented in [15,16,17]. In all cases, single-mode rate equation approaches were used to model the suppression of the unlocked comb lines from these demultiplexers, which are not sufficient to describe multimode devices such as Fabry–Pérot (FP) lasers. Optical suppression due to injection of a single wavelength has previously been modelled in many other works, such as in [18], where they used a multimode rate equation approach to model the effect of the bias currents and spontaneous emission coupling factor on the suppression of the unlocked modes in FP lasers. The work in [19] used a similar model to study how detuning and the injected mode relative to the gain centre affect the suppression. Neither of these multimode approaches however investigated optical comb injection.
In this paper, we present a new model for simulating the optical spectra and suppression of comb lines, based on the multimode FP model [20], and the steady state solutions of the rate equation models presented in [21,22]. To our knowledge, the side mode suppression ratio (SMSR) of a slave laser under optical injection from a comb has not previously been studied using a multimode model. Our model is used to simulate the optical spectra of optically-injected FP lasers, slotted FP lasers [23,24], and a demultiplexer, as in [25], and these simulations are shown to be in good agreement with our experimental results. We then use the model to comment on how demultiplexer performance can be improved, by investigating the effect of the Q factor of devices on the SMSR obtainable. We show that improving the Q factor can increase the SMSR of injected optical combs beyond 30 dB and that when a fixed pump rate relative to the threshold is used, the locking ranges of these high Q demultiplexers remain suitable for their application.
2. Description of the Model
The laser model adopted in this work has previously been proven to accurately replicate the characteristics of lasers with multimode and single-mode lasing [20,26,27]. In this section, we will first summarize the model, then describe how the model was altered to include optical injection.
Consider the electric fields within a laser cavity of length L as shown in Figure 1b, and let and represent the electric fields propagating to the right at Boundaries 1 and 2; similarly for and . The fields at the interfaces can be related to one another by:
where is the gain per unit distance of the laser cavity, is the propagation constant, and and are the contribution of the spontaneous emission to the fields as they travel to the left and right. The intensity of the field at the left facet is then given by:
where represents the single-pass gain seen by the fields in the cavity. We assume that the time-averaged contributions of the terms and are zero, and we also assume the magnitude of the spontaneous emission in both directions is equal, so that . Defining and integrating over one period from to give the power from one longitudinal mode in the laser. Hence, the power in each mode of the laser I is given by:
This integral can be evaluated as:
where now the subscript m has been added to indicate that values for the gain, reflection, and spontaneous emission coupling to each mode can differ across the longitudinal modes in the laser. The reflections and for the different laser cavities considered in the following section were calculated using a one-dimensional transmission matrix method [28]. The modal gain dependence is modelled as:
where is the cavity loss, L is the length of the gain section of the laser, is the gain shape of the laser material, and n is the number of free carriers. The gain line shape in the model was chosen to be of the form:
where here, gives the centre gain wavelength and a and are used as fitting parameters to approximate the measured gain. Figure 2 shows the gain compared with the measured gain of the InGaAs semiconductor devices tested, and although the asymmetry of the real device gain is not represented, good qualitative agreement is observed around the peak modal gain.
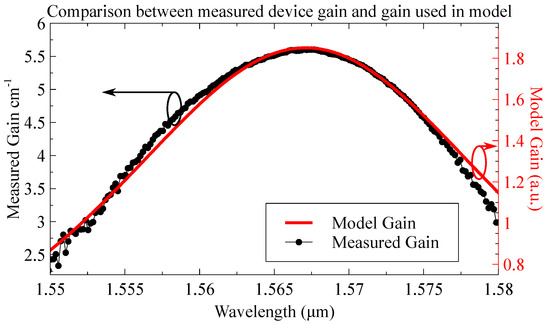
Figure 2.
Comparison between measured device gain (left vertical axis) from a Fabry–Pérot (FP) laser calculated using the Cassidy gain method [29] and the gain implemented in the model (right vertical axis).
The spontaneous emission in the model is defined as in [20], by the term :
where is the spontaneous emission factor and is the photon lifetime. The number of free carriers n is modelled by:
Here, N is the rate of injected carriers, is the carrier lifetime, and takes into account the number of carriers recombining due to stimulated emission in the laser material. The steady state value for the carriers is:
As rate equation models predict the locking range and power in the slave laser under optical injection more accurately [30], the optical injection in the model uses results derived from a rate equation approach. To derive the required results, we start with the standard injection locking rate equations as reported in [21,22]:
Here, and are the rates of cavity gain and cavity losses, is the longitudinal mode spacing, is the linewidth enhancement factor, and is the difference between the natural frequencies of the master and slave laser. In the steady state, Equation (9) gives us a relation between the growth and decay rates inside the laser:
To relate the steady state solution for the amplitude in Equation (11) to the optical power in the FP modes, we note that one can write the power in terms of the saturation power of the gain medium by [21]:
where is the amount by which the unsaturated gain in the laser exceeds the cavity losses. By assuming that the laser growth rate inside the cavity saturates under injection in the form [21],
we can eliminate the unknown saturation power level using Equations (12) and (13) and find:
where the last equality follows from Equation (11). A first-order approximation assuming that is given in [21] as:
Hence, using Equation (15), we can describe how the power in an injection locked mode in the FP model varies with detuning, assuming that our injected optical field strength is small.
From Equation (10), we can also determine the range of frequencies for which the slave laser will be frequency locked. Using Equation (11) in Equation (10), we can determine the locked phase of the slave relative to the master:
The range of frequencies for which the slave laser is locked to the master laser can then also be shown to be [22,31]:
Hence, using the above, the optical power in each mode of the slave laser can be calculated by solving Equations (3) and (8), including the change in optical power as described by Equation (15) when the slave laser is within the locking conditions. In the following section, the optical mode powers were convolved with a Voigt function to create the wideband spectra presented.
As a steady state solution is presumed in Equation (8), the dynamical regions of operation of the slave laser, which arise at different injection strengths and detunings, are omitted by the model. However, it will be shown in the following discussion that under these assumptions, this simple model can still accurately model the behaviour of the SMSR of the slave lasers under injection and can even be used to predict qualitatively the suppression obtainable through injection locking a slave laser to a single injection frequency or to one of the lines of an injected optical comb.
3. Comparison between the Experiment and Model
In the following section, experimental results are presented and compared side by side with the corresponding simulated experiments. The experimental setup used to perform the injection locking experiments is shown in Figure 3. The device under test (DUT) was mounted on a temperature-controlled brass chuck. A tunable laser source (TLS) was used as the master laser. The devices were optically coupled by collecting the light from the uncoated facets using a lensed fibre. To generate the optical combs used in some of the results presented, the components inside the dashed section in Figure 3 were included in the setup. In these cases, an RF signal generator was used to intensity modulate the master laser signal passing through a LiNbO3 Mach–Zehnder modulator (MZM). An erbium-doped fibre amplifier (EDFA) was used to amplify and control the optical power injected into the device. The output from the slave laser was measured on an optical spectrum analyser (OSA). Polarisation controllers (PC) were used before the MZM and the DUT to maintain polarisation throughout the experiments, as both the comb generation and optical injection aspects of the experiment depend strongly on phase [32]. As the coupling efficiency between the lensed fibre and the devices tested was unknown, our calculated results are presented using the ratio of the injection strength to the slave laser power (i.e, ) and assume the coupling efficiency was one in all cases.

Figure 3.
Setup used to measure the intensity plots of the optical injection locking experiments. Dashed lines indicate the additional setup used when injecting optical combs. TLS: tunable laser source, MZM: Mach–Zehnder modulator, RF Gen: RF Generator, Iso: Isolator, PC: polarisation controller, EDFA: erbium–doped fibre amplifier, OSA: optical spectrum analyser, DUT: device under test.
Figure 4 shows a comparison between the measured and the calculated results of a 700 m-long FP laser under optical injection, as the wavelength of the master laser is swept from 1568.95 nm–1569.05 nm in each case. Figure 4a shows the measured spectrum from the FP device, biased at 45 mA (2.5-times the threshold). The mirrors of the device were cleaved facets, each with an estimated reflection of 30%. At 1568.938 nm, the slave laser locked to the master laser and remained frequency locked for 0.031 nm (or 3.87 GHz). While locked, the side modes of the slave laser were suppressed, and the SMSR was larger than 20 dB over a span of 3.6 GHz, with a maximum SMSR of 35.77 dB.
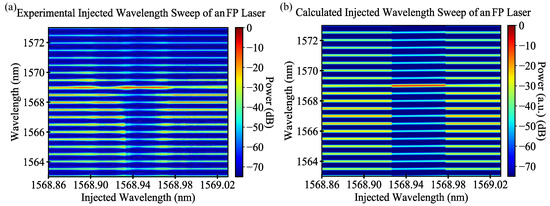
Figure 4.
Experimental and calculated injected wavelength sweeps of a 700-m FP device. In both cases, the slave laser was biased at 2.5-times the threshold. (a) Experimental sweep, for an injected power of dBm and free running slave power of dBm. (b) Calculated sweep, for an injection ratio of .
The simulated results of the same FP sweep are shown in Figure 4b. The optical spectra were calculated by solving Equations (3) and (8), including the change in optical power as described by Equation (15) when the slave laser was within the locking conditions. The parameters used in all the calculations presented are contained in Table 1. The unlocked injected signal was amplified by the single-pass gain of the laser at that wavelength. The output spectrum was then convolved with a Voigt profile to simulate the measured spectra on the OSA, in order to compare the results directly. The refractive index () of the slave laser was used as a fitting parameter to line up the modes of the simulated spectra with the experiment. The simulated slave laser was biased at 2.5-times the threshold, and the injected wavelength sweep matched that in the experimental trace. The optical spectrum of the slave laser underwent sharp transitions at 1568.933 nm and 1568.978 nm, unlike in the experimental case, as the model only calculated the locked steady state solutions. The complicated dynamics at the locking boundaries cannot be replicated using the steady state assumption in the model. The optical suppression seen as the slave laser reached a maximum of 35.1 dB and had an SMSR of over 20 dB over the whole locking range of 3.74 GHz, which are in good agreement with the experiment.

Table 1.
Parametrised values used in the model, unless otherwise stated. The photon lifetime was used to normalise the carrier lifetime , which is typically 2–3 orders of magnitude larger than . We have chosen values for and to match those in similar works [18,28]. Values for , and were obtained through fitting our expression for gain to that which was measured, shown in Figure 2.
Other small discrepancies between the simulated and measured traces are present; in the experimental trace, we see that the apparent thickness of each of the modes grows slightly on the edges of the injection region. This is due to the beating of the slave laser with the injected light, causing nearly degenerate four-wave mixing peaks to appear on all modes of the slave laser [33], at frequencies that could not be resolved on the OSA used. This occurs at very small frequency detunings due to the weak injected power used [34], and its effect is to broaden slightly what is measured on the OSA. Our model cannot reproduce four-wave mixing due to the steady state assumption.
Thermal tuning in the model is shown and compared with the experiment in Figure 5. The experimental trace presented in Figure 5a has been taken from [12]. The slave laser used in this experiment was a two-section, single-mode tunable, slotted Fabry–Pérot (SFP) laser. The slots in these lasers refer to etches made along the ridge of the laser, typically around 1 m wide, which provide optical feedback and increase mode selectivity [23,24]. The temperature of the two-section laser was swept over 2 C, with a constant injected wavelength at 1563.35. At 20.9 C, the slave laser frequency locks for approximately 0.24 C of the temperature sweep. The SMSR from the experiment was >20 dB over a frequency span of 1.29 GHz. The matching simulated result in Figure 5b shows the slave device lock for 0.4 C, with >18 dB SMSR over a frequency span of 0.95 GHz. Thermal tuning was introduced into the model by varying the optical path length of the laser material to match the 0.1 nmC seen in the experiment, as well as allowing the centre of the material gain to red shift with increasing temperature. The SMSR predicted by the model was slightly lower than experiment, likely due to the limitations in using a one-dimensional transmission matrix to describe the slot in the device [35]. The optical power in the mode that undergoes the frequency locking has a strong impact on the amplification the injected signal sees when locked, and the mismatch in the power of that mode could be the cause of the different SMSRs predicted.
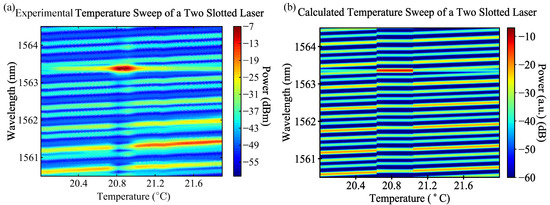
Figure 5.
Experimental and calculated temperature sweeps of an optically-injected 600 m-long two-section slotted FP device, with a single etched slot in the centre of the device separating the sections. In each case, the slave laser was under optical injection at a wavelength of 1563.36 nm. (a) Experimental sweep from [12]. (b) Calculated sweep for an injection ratio of .
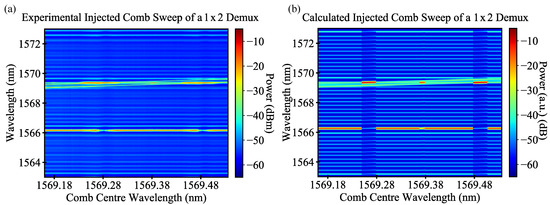
As a final example, results from a demultiplexer as shown in Figure 6a were simulated. A two-line optical comb, as shown in Figure 6b, was injected. Each line of the two-line optical comb locked to the two side modes of the SFP laser, with the centre of the comb (8 dB lower) also interacting with the slave laser’s side mode as it tuned.
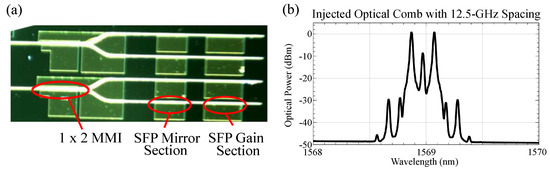
Figure 6.
(a) Comb demultiplexer, featuring a multimode interferometer (MMI) and two SFP lasers [25]. (b) Optical comb injected into the demultiplexer. This two line comb was generated by biasing the MZM at the point where the carrier is suppressed, giving two strong lines.
In the experimental trace in Figure 7a, maximum SMSRs of 18.4 dB and 20.6 dB were achieved as the two strongest comb lines locked to the side mode of the slave laser. The slave laser in the demultiplexer remained locked for spans of 2 GHz and 2.5 GHz, respectively. The straight through line (8 dB lower than the two comb lines) is amplified slightly as it passes over the side mode; however, it does not stably lock to the side mode. In the simulated trace in Figure 7b, the results obtained are quite similar. The SMSRs were obtained as the comb locked to the side mode, 22.1 dB and 22.9 dB, and the slave laser was locked over 3.2 GHz in each case. The model did predict that the centre line of the comb locked to the side mode; however, at 8 dB less peak power, the injected power was not sufficient to suppress the main lasing mode. The locking ranges in the simulated case were larger than in the experiment again, as bi-stable and dynamical locking regions are included in Equation (18), but the suppression seen in the model closely resembled what was measured. As the SMSRs obtained when demultiplexing these optical combs do not meet the 30-dB figure required for most telecommunications applications, the following section investigates how the SMSRs of devices can be improved.
4. The Effect of the Cavity Quality Factor on Optical Comb Demultiplexing
We now wish to use our model to identify the parameters of the slave laser, which can be optimised in order to increase the slave laser’s demultiplexing ability. In the case of passive resonators, the quality factor (or Q factor) is related to the frequency selectivity of the resonator, with higher Q cavities acting as better frequency filters than those with low Q. As a result, we start by investigating how the Q factor of the laser cavity affects the SMSR of the injected optical comb. In the following, we vary the Q of an FP laser by varying the reflection of the facets and measuring the Q of the equivalent lossless cavity, given by:
Figure 8a compares the SMSR achieved as the Q of the laser cavity is improved, when injecting a three-line 12.5-GHz optical comb into an FP laser for high and low injection ratios. The slave laser was biased at three-times the threshold for each Q value used, to avoid influencing the results by increasing the pumping of the slave. As the power of the free running slave laser was not constant as the Q factor of devices was increased and a fixed injection strength was used throughout, hence the injection ratios are given for the lowest Q factor in each plot in Figure 8. Figure 8a shows that for the lower injection ratio, the SMSR increases with the improved cavity quality factor up until , with a similar behaviour for the slightly higher ratio. As Q increased past this point, the other longitudinal modes in the laser cavity became less suppressed due to the optical injection, and as a result, eventually, the unlocked FP modes became stronger than the unlocked comb lines passing through the cavity. As shown in the red dashed line in Figure 8a, stronger injected optical powers suppressed the unlocked FP modes up to a higher Q value. For a qualitative comparison, the SMSR obtainable from a passive FP cavity with equivalent Q is also plotted in Figure 8a, in a blue dotted line. Notably, the increase in SMSR seen by the injection locked FP laser sees a similar growth rate as the passive case.
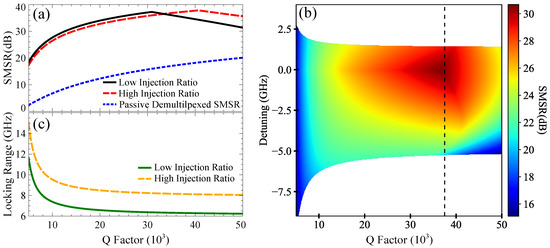
Figure 8.
Calculated results from optical comb injection simulations, of a 700-m FP laser. (a) Plot showing how the SMSR of the output spectrum varies as the Q of the laser cavity increases, for two different injection ratios, assuming zero detuning and biased at 3.0-times the threshold. The higher injection ratio was initialised at and the corresponding lower injection ratio at . For qualitative comparison, the side mode suppression ratio (SMSR) from a passive cavity with equivalent Q is also plotted. (b) Intensity plot of how SMSR varies versus detuning and the Q factor, for an injection ratio of , at a current of 2.5-times the threshold. The white regions indicate where the slave laser was unlocked. (c) Plot of the locking range of the FP laser versus Q, for the same injection ratios and parameters as in (a).
The SMSR obtainable also varied with the detuning between the slave laser and the injected optical comb. Figure 8b shows a colour map of how the SMSR varied as the detuning and Q factor were varied. The importance of the detuning between the slave and master is highlighted, and as the Q factor of the laser increased, the gradient in the SMSR over the detuning increased notably. At (marked with the vertical dotted line), we see that the SMSR varied by a maximum of 10 dB as the detuning was varied. As a result, even though the slave laser can account for some frequency drift in either the injected comb or its lasing frequency, we have shown that drift can still strongly impact the output SMSR.
An investigation into the behaviour of the locking range of the laser as its quality factor is improved is presented in Figure 8c, for the two injection ratios used in Figure 8a. From the comparisons of the model with the experiment in Section 3, we expect the locking range of real devices to be slightly smaller than what is predicted here. However, the trend shown in Figure 8c is encouraging, as for higher Q, the locking range tends to a constant value.
We can conclude that higher Q cavities increase the SMSR obtainable. We have found that improving the Q of laser cavities increased the SMSR at a rate comparable to a passive demultiplexer. At higher Q values, the unlocked modes in the FP laser required a higher injected power to be suppressed, and as a result, the side modes became stronger than the unlocked comb lines. The locking range of the slave laser varied slowly in high Q cavities; however, the effect of detuning the slave laser relative to the injected comb increased in sensitivity as Q increased.
5. Conclusions
In the above, a numerical model for simulating the mode suppression in weakly-optically-injected semiconductors was presented. The model was compared with experimental optical injection wavelength sweeps, and although the simulations omitted dynamical regions of operation, good agreement was observed for both single-mode and multimode devices. Experimental and theoretical results for the SMSR obtainable when injecting an optical comb were also presented, and the effect of the Q factor of the slave laser on the demultiplexed comb output was investigated theoretically. It was found that increasing the Q factor of the device does increase the output SMSR and that for a fixed pump rate relative to the threshold, the locking range of the devices tends asymptotically to a fixed value with increasing Q.
Author Contributions
K.S. was responsible for the implementation of the model and writing of the paper. M.S. performed the optical comb injection experiments. W.C. performed the single frequency optical injection experiments. A.H.P. measured the gain spectra used in the model. M.D. fabricated the test devices and analysed the results. F.H.P. was responsible for the funding acquisition, conceptualization of the project, and reviewing/editing of the manuscript.
Funding
This research was funded by Science Foundation Ireland under Grant Number SFI 13/IA/1960.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Christodoulopoulos, K.; Tomkos, I.; Varvarigos, E.A. Elastic Bandwidth Allocation in Flexible OFDM-Based Optical Networks. J. Lightwave Technol. 2011, 29, 1354–1366. [Google Scholar] [CrossRef]
- Tomkos, I.; Azodolmolky, S.; Sole-Pareta, J.; Careglio, D.; Palkopoulou, E. A tutorial on the flexible optical networking paradigm: State of the art, trends, and research challenges. Proc. IEEE 2014, 102, 1317–1337. [Google Scholar] [CrossRef]
- Jinno, M.; Takara, H.; Kozicki, B.; Tsukishima, Y.; Sone, Y.; Matsuoka, S. Spectrum-efficient and scalable elastic optical path network: Architecture, benefits, and enabling technologies. IEEE Commun. Mag. 2009, 47, 66–73. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Y.; Yu, X.; Zhang, J.; Song, M.; Ji, Y.; Mukherjee, B. Energy-Efficient Traffic Grooming in Sliceable-Transponder-Equipped IP-Over-Elastic Optical Networks [Invited]. J. Opt. Commun. Netw. 2015, 7, A142. [Google Scholar] [CrossRef]
- Mazur, M.; Lorences-Riesgo, A.; Schroder, J.; Andrekson, P.A.; Karlsson, M. 10 Tb/s PM-64QAM Self-Homodyne Comb-Based Superchannel Transmission With 4% Shared Pilot Tone Overhead. J. Lightwave Technol. 2018, 36, 3176–3184. [Google Scholar] [CrossRef]
- Puttnam, B.J.; Luis, R.S.; Klaus, W.; Sakaguchi, J.; Delgado Mendinueta, J.M.; Awaji, Y.; Wada, N.; Tamura, Y.; Hayashi, T.; Hirano, M.; et al. 2.15 Pb/s transmission using a 22 core homogeneous single-mode multi-core fibre and wideband optical comb. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Pascual, M.D.G.; Zhou, R.; Smyth, F.; Anandarajah, P.M.; Barry, L.P. Software reconfigurable highly flexible gain switched optical frequency comb source. Opt. Express 2015, 23, 23225. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, L.; Karlsson, M.; Lorences-Riesgo, A.; Mazur, M.; Torres-Company, V.; Schröder, J.; Andrekson, P. Frequency Comb-Based WDM Transmission Systems Enabling Joint Signal Processing. Appl. Sci. 2018, 8, 718. [Google Scholar] [CrossRef]
- Alexander, J.K.; Morrissey, P.E.; Yang, H.; Yang, M.; Marraccini, P.J.; Corbett, B.; Peters, F.H. Monolithically integrated low linewidth comb source using gain switched slotted Fabry-Perot lasers. Opt. Express 2016, 24, 7960. [Google Scholar] [CrossRef] [PubMed]
- Pascual, M.D.G.; Vujicic, V.; Braddell, J.; Smyth, F.; Anandarajah, P.; Barry, L. Photonic Integrated Gain Switched Optical Frequency Comb for Spectrally Efficient Optical Transmission Systems. IEEE Photonics J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Peters, F.H.; Ellis, A.D. Integrated Optical Comb Source System and Method. U.S. Patent US8,488,640B2, 16 July 2013. [Google Scholar]
- Cotter, W.; Goulding, D.; Roycroft, B.; O’Callaghan, J.; Corbett, B.; Peters, F.H. Investigation of active filter using injection-locked slotted Fabry–Perot semiconductor laser. Appl. Opt. 2012, 51, 7357. [Google Scholar] [CrossRef]
- Gutierrez, M.D.; Braddell, J.; Smyth, F.; Barry, L.P. Monolithically integrated 1x4 comb de-multiplexer based on injection locking. In Proceedings of the European Conference Integrated Optics, Warsaw, Poland, 18–20 May 2016; pp. 1–2. [Google Scholar]
- Zhou, R.; Gutierrez Pascual, M.D.; Anandarajah, P.M.; Shao, T.; Smyth, F.; Barry, L.P. Flexible wavelength de-multiplexer for elastic optical networking. Opt. Lett. 2016, 41, 2241. [Google Scholar] [CrossRef] [PubMed]
- Duill, S.P.Ó.; Anandarajah, P.M.; Smyth, F.; Barry, L.P. Injection-locking criteria for simultaneously locking single-mode lasers to optical frequency combs from gain-switched lasers. Int. Soc. Opt. Photonics 2017, 10098, 100980H. [Google Scholar] [CrossRef]
- Shortiss, K.J.; Shayesteh, M.; Peters, F.H. Modelling the effect of slave laser gain and frequency comb spacing on the selective amplification of injection locked semiconductor lasers. Opt. Quantum Electron. 2018, 50, 49. [Google Scholar] [CrossRef]
- Wu, D.S.; Richardson, D.J.; Slavík, R. Selective amplification of frequency comb modes via optical injection locking of a semiconductor laser: Influence of adjacent unlocked comb modes. Proc. SPIE 2013, 8781, 87810J. [Google Scholar] [CrossRef]
- Krstić, M.; Gvozdić, D. Side-Mode-Suppression-Ratio of Injection-Locked Fabry-Perot Lasers. Acta Phys. Polonica A 2009, 116, 664–667. [Google Scholar] [CrossRef]
- Zhang, D.; Nakarmi, B.; Zhang, X. Analysis of wavelength detuning, injected power, and injected mode effect on Fabry-Perot laser diode. Int. Soc. Opt. Photonics 2014, 9270, 92700F. [Google Scholar] [CrossRef]
- Cassidy, D.T. Comparison of rate-equation and Fabry-Perot approaches to modeling a diode laser. Appl. Opt. 1983, 22, 3321. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Sausalito, CA, USA, 1986; p. 1283. [Google Scholar]
- Mogensen, F.; Olesen, H.; Jacobsen, G. Locking conditions and stability properties for a semiconductor laser with external light injection. IEEE J. Quantum Electron. 1985, 21, 784–793. [Google Scholar] [CrossRef]
- Corbett, B.; McDonald, D. Single longitudinal mode ridge waveguide 1.3 μm Fabry-Perot laser by modal perturbation. Electron. Lett. 1995, 31, 2181–2182. [Google Scholar] [CrossRef]
- Lu, Q.; Guo, W.-H.; Byrne, D.; Donegan, J.F. Design of Slotted Single-Mode Lasers Suitable for Photonic Integration. IEEE Photonics Technol. Lett. 2010, 22, 787–789. [Google Scholar] [CrossRef]
- Cotter, W.E. Photonic Integrated Circuit for the Manipulation of Coherent Optical Combs. Ph.D. Thesis, University College Cork, Cork, Ireland, 2014. [Google Scholar]
- Gordon, E.I. Optical Maser Oscillators and Noise. Bell Syst. Tech. J. 1964, 43, 507. [Google Scholar] [CrossRef]
- Peters, F.H.; Cassidy, D.T. Model of the spectral output of gain-guided and index-guided semiconductor diode lasers. J. Opt. Soc. Am. B 1991, 8, 99. [Google Scholar] [CrossRef]
- Coldren, L.A.; Corzine, S.W.; Mashanovitch, M. Diode Lasers and Photonic Integrated Circuits; Wiley: Hoboken, NJ, USA, 2012; p. 709. [Google Scholar]
- Cassidy, D.T. Technique for measurement of the gain spectra of semiconductor diode lasers. J. Appl. Phys. 1984, 56, 3096–3099. [Google Scholar] [CrossRef]
- Ibrahim, M.M.; Ibrahim, M. A comparison between rate-equation and Fabry-Perot amplifier models of injection locked laser diodes. Opt. Laser Technol. 1996, 28, 39–42. [Google Scholar] [CrossRef]
- Petitbon, I.; Gallion, P.; Debarge, G.; Chabran, C. Locking bandwidth and relaxation oscillations of an injection-locked semiconductor laser. IEEE J. Quantum Electron. 1988, 24, 148–154. [Google Scholar] [CrossRef]
- Hurtado, A.; Henning, I.; Adams, M. Polarisation effects on injection locking bandwidth of 1550 nm VCSEL. Electron. Lett. 2009, 45, 886. [Google Scholar] [CrossRef]
- Jiang, S.; Dagenais, M. Nearly degenerate four-wave mixing in Fabry–Perot semiconductor lasers. Opt. Lett. 1993, 18, 1337. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.W.; Won, Y.H. Nearly Degenerate Four-Wave Mixing in Single-Mode Fabry–Pérot Laser Diode Subject to Single Beam Optical Injection. IEEE Photonics J. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Lu, Q.Y.; Guo, W.H.; Phelan, R.; Byrne, D.; Donegan, J.F.; Lambkin, P.; Corbett, B. Analysis of Slot Characteristics in Slotted Single-Mode Semiconductor Lasers Using the 2-D Scattering Matrix Method. IEEE Photonics Technol. Lett. 2006, 18, 2605–2607. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).