Holographic Fabrication and Optical Property of Graded Photonic Super-Crystals with a Rectangular Unit Super-Cell
Abstract
1. Introduction
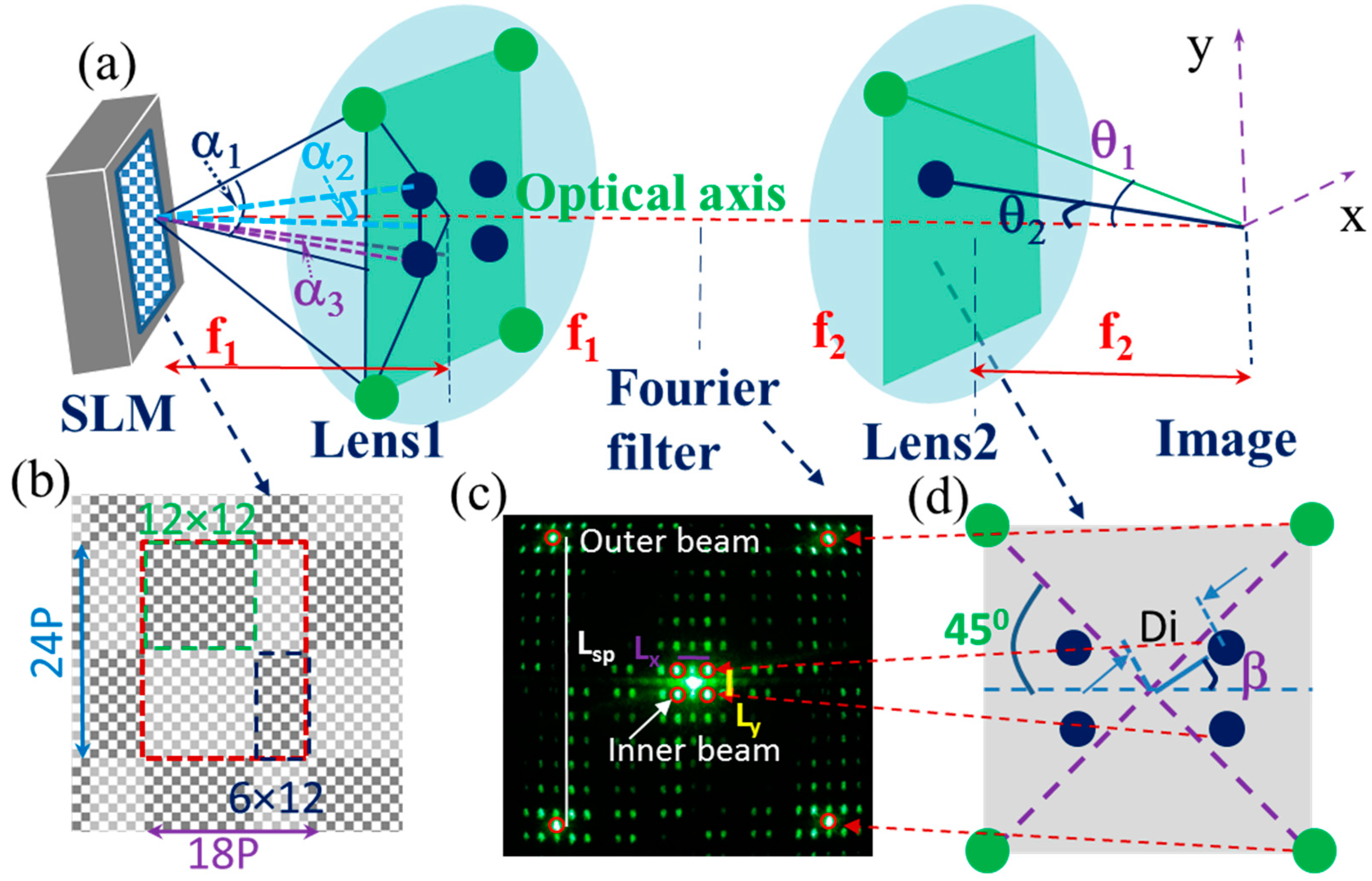
2. Description of Experimental Methods and Formation of Graded Photonic Super-crystal
3. Results
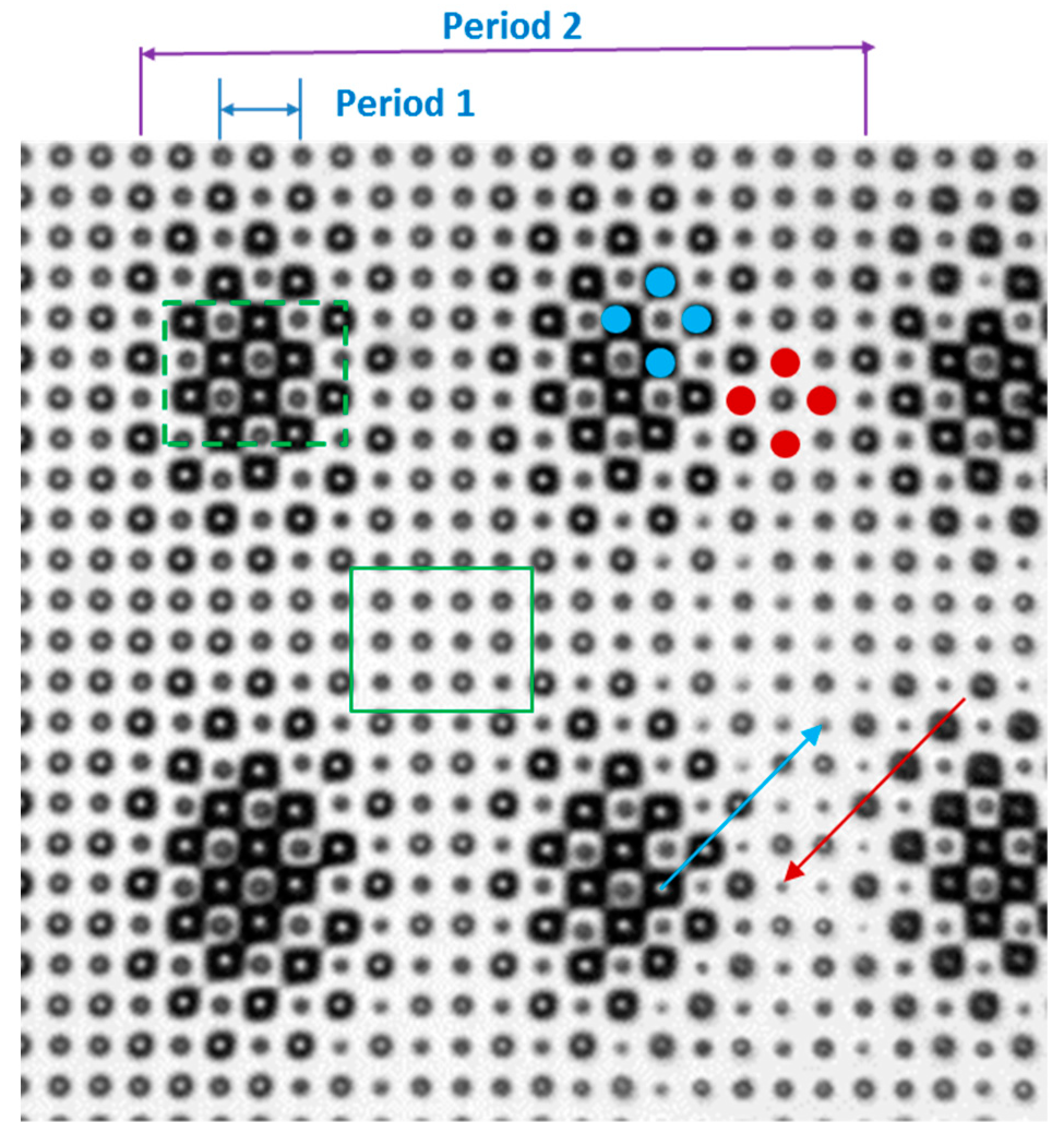
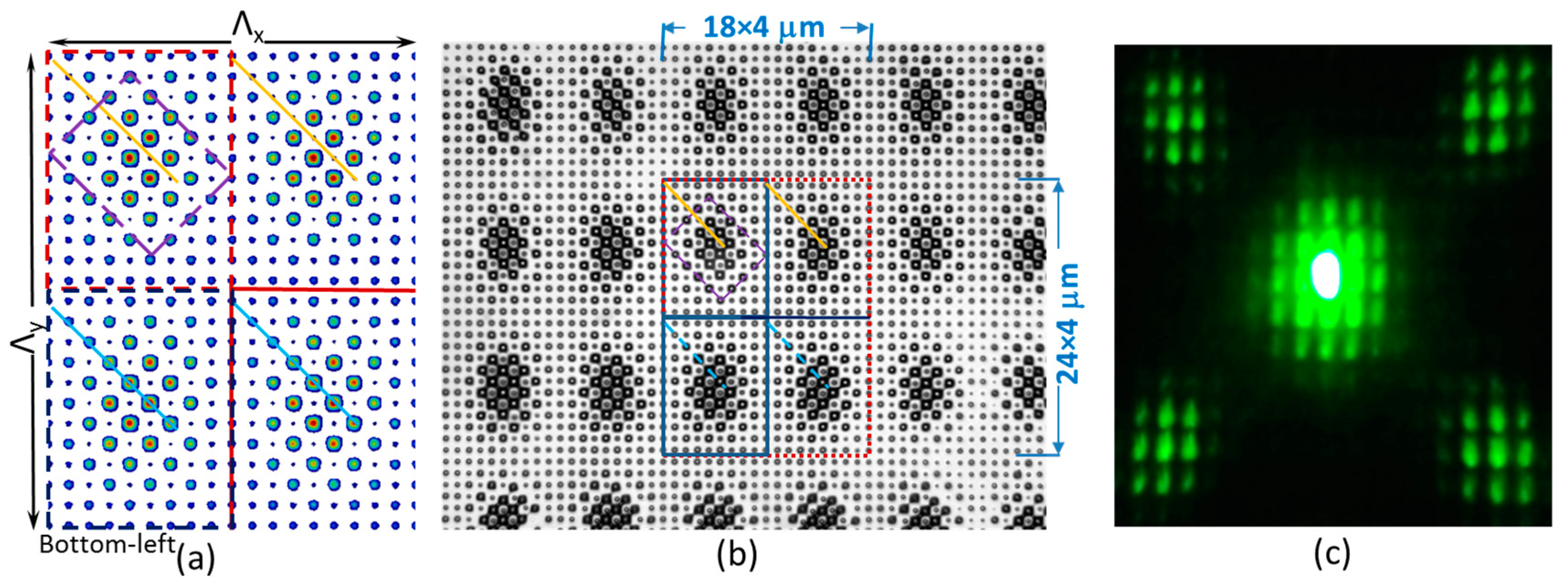
3.1. Holographic Fabrication Results
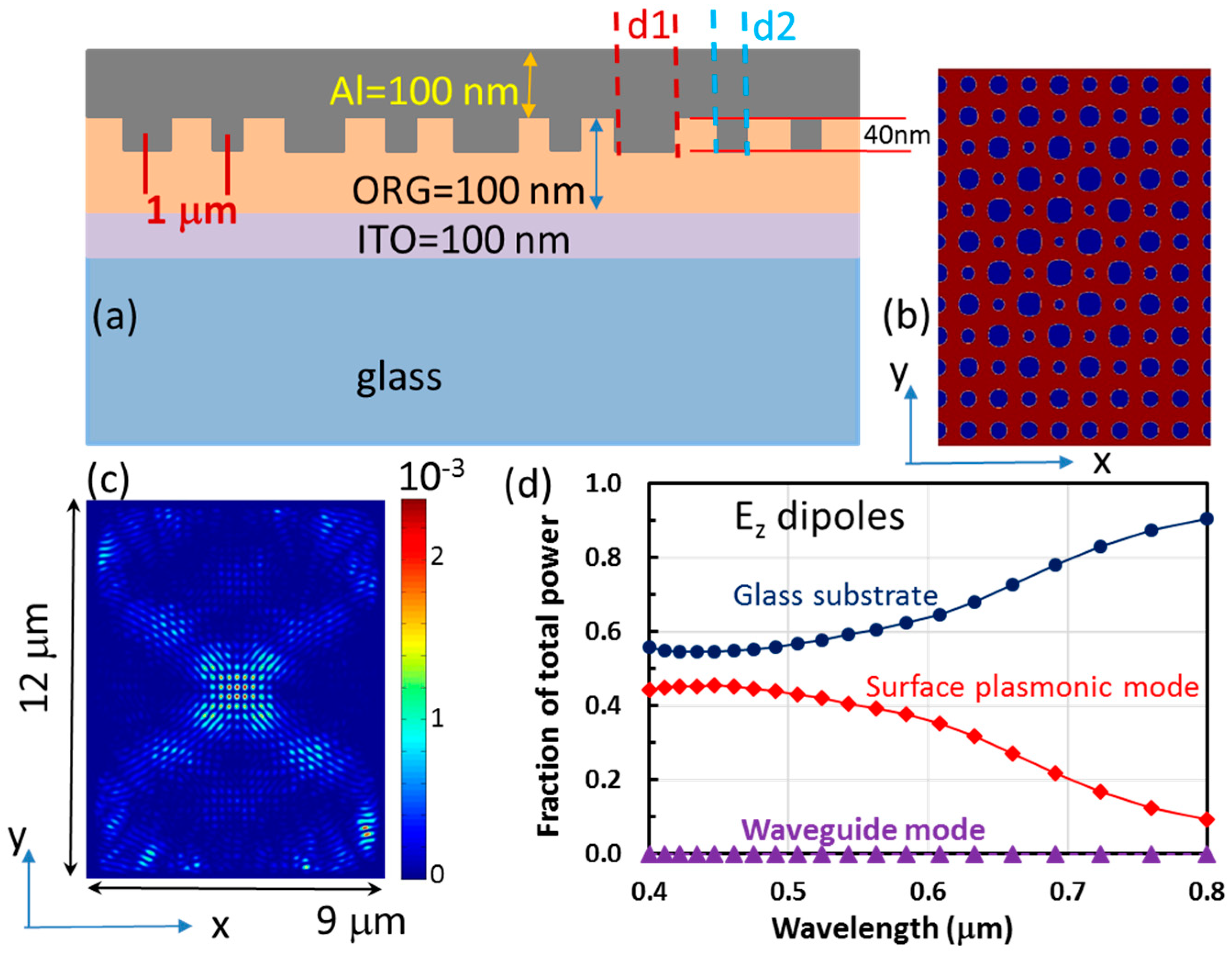
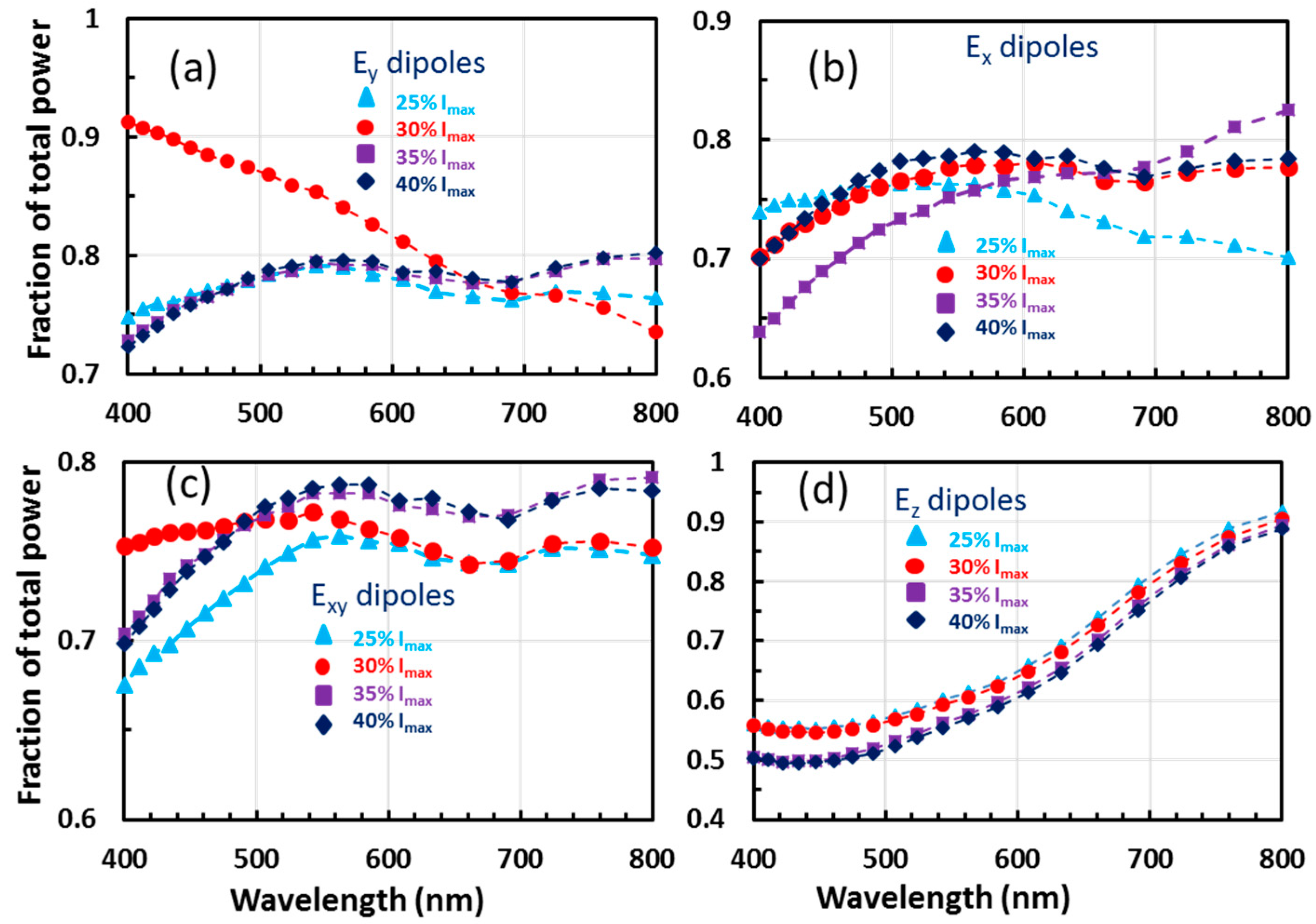
3.2. Simulation of Light Extraction Efficiency
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tandaechanurat, A.; Ishida, S.; Guimard, D.; Nomura, M.; Iwamoto, S.; Arakawa, Y. Lasing oscillation in a three-dimensional photonic crystal nanocavity with a complete bandgap. Nat. Photonics 2011, 5, 91–94. [Google Scholar] [CrossRef]
- Ergin, T.; Stenger, N.; Brenner, P.; Pendry, J.B.; Wegener, M. Three-dimensional invisibility cloak at optical wavelengths. Science 2010, 328, 337–339. [Google Scholar] [CrossRef] [PubMed]
- Qi, M.; Lidorikis, E.; Rakich, P.T.; Johnson, S.G.; Joannopoulos, J.D.; Ippen, E.P.; Smith, H.I. A three-dimensional optical photonic crystal with designed point defects. Nature 2004, 429, 538–542. [Google Scholar] [CrossRef] [PubMed]
- Joannopoulos, J.D.; Villeneuve, P.R.; Fan, S.H. Photonic crystals: Putting a new twist on light. Nature 1997, 386, 143–149. [Google Scholar] [CrossRef]
- Rinnerbauer, V.; Shen, Y.; Joannopoulos, J.D.; Soljačić, M.; Schäffler, F.; Celanovic, I. Superlattice photonic crystal as broadband solar absorber for high temperature operation. Opt. Express 2014, 22, A1895–A1906. [Google Scholar] [CrossRef] [PubMed]
- Rinnerbauer, V.; Lausecker, E.; Schäffler, F.; Reininger, P.; Strasser, G.; Geil, R.D.; Joannopoulos, J.D.; Soljačić, M.; Celanovic, I. Nanoimprinted superlattice metallic photonic crystal as ultraselective solar absorber. Optica 2015, 2, 743–746. [Google Scholar] [CrossRef]
- Lowell, D.; Lutkenhaus, J.; George, D.; Philipose, U.; Chen, B.; Lin, Y. Simultaneous direct holographic fabrication of photonic cavity and graded photonic lattice with dual periodicity, dual basis, and dual symmetry. Opt. Express 2017, 25, 14444–14452. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.; Lowell, D.; Lin, Y. High light extraction efficiency in organic light-emitting diodes by patterning the cathode in graded superlattice with dual periodicity and dual basis. J. Appl. Phys. 2017, 121, 233104. [Google Scholar] [CrossRef]
- Hassan, S.; Lowell, D.; Adewole, M.; George, D.; Zhang, H.; Lin, Y. Extraordinary light trapping enhancement in silicon solar cell patterned with graded photonic super-crystals. Photonics 2017, 4, 50. [Google Scholar] [CrossRef]
- Lowell, D.; Hassan, S.; Adewole, M.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-crystals using an integrated spatial light modulator and reflective optical element laser projection system. Appl. Opt. 2017, 56, 9888–9891. [Google Scholar] [CrossRef]
- Lowell, D.; Hassan, S.; Sale, O.; Adewole, M.; Hurley, N.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-quasi-crystal with multiple level gradients. Appl. Opt. 2018, 57, 6598–6604. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.; Sharp, D.N.; Harrison, M.T.; Denning, R.G.; Turberfield, A.J. Fabrication of photonic crystals for the visible spectrum by holographic lithography. Nature 2000, 404, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Herman, P.R.; Darmawikarta, J. Design and holographic fabrication of tetragonal and cubic photonic crystals with phase mask: Toward the mass-production of three-dimensional photonic crystals. Appl. Phys. Lett. 2005, 86, 071117. [Google Scholar] [CrossRef]
- Chanda, D.; Abolghasemi, L.E.; Haque, M.; Ng, M.L.; Herman, P.R. Multi-level diffractive optics for single laser exposure fabrication of telecom-band diamond-like 3-dimensional photonic crystals. Opt. Express 2008, 16, 15402–15414. [Google Scholar] [CrossRef] [PubMed]
- Ohlinger, K.; Zhang, H.; Lin, Y.; Xu, D.; Chen, K.P. A tunable three layer phase mask for single laser exposure 3D photonic crystal generations: Bandgap simulation and holographic fabrication. Opt. Mater. Express 2008, 1, 1034–1039. [Google Scholar] [CrossRef]
- Chan, T.Y.M.; Toader, O.; John, S. Photonic band-gap formation by optical-phase-mask lithography. Phys. Rev. E 2006, 73, 046610. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Chen, K.P.; Harb, A.; Rodriguez, D.; Lozano, K.; Lin, Y. Phase tunable holographic fabrication for three-dimensional photonic crystal templates by using a single optical element. Appl. Phys. Lett. 2009, 94, 231116. [Google Scholar] [CrossRef]
- George, D.; Lutkenhaus, J.; Lowell, D.; Moazzezi, M.; Adewole, M.; Philipose, U.; Zhang, H.; Poole, Z.L.; Chen, K.P.; Lin, Y. Holographic fabrication of 3D photonic crystals through interference of multi-beams with 4 + 1, 5 + 1 and 6 + 1 configurations. Opt. Express 2014, 22, 22421–22431. [Google Scholar] [CrossRef] [PubMed]
- Lutkenhaus, J.; Farro, F.; George, D.; Ohlinger, K.; Zhang, H.; Poole, Z.; Chen, K.P.; Lin, Y. Holographic fabrication of 3D photonic crystals using silicon based reflective optics element. Opt. Mater. Express 2012, 2, 1236–1241. [Google Scholar] [CrossRef]
- Xavier, J.; Boguslawski, M.; Rose, P.; Joseph, J.; Denz, C. Reconfigurable optically induced quasicrystallographic three-dimensional complex nonlinear photonic lattice structures. Adv. Mater. 2010, 22, 356–360. [Google Scholar] [CrossRef] [PubMed]
- Arrizón, V.; Sánchez-de-la-Llave, D.; Méndez, G.; Ruiz, U. Efficient generation of periodic and quasi-periodic non-diffractive optical fields with phase holograms. Opt. Express 2011, 34, 10553–10562. [Google Scholar] [CrossRef] [PubMed]
- Boguslawski, M.; Rose, P.; Denz, C. Increasing the structural variety of discrete nondiffracting wave fields. Phys. Rev. A 2011, 84, 013832. [Google Scholar] [CrossRef]
- Behera, S.; Joseph, J. Single-step optical realization of bio-inspired dual-periodic motheye and gradient-index-array photonic structures. Opt. Lett. 2016, 41, 3579–3582. [Google Scholar] [CrossRef] [PubMed]
- Lutkenhaus, J.; George, D.; Moazzezi, M.; Philipose, U.; Lin, Y. Digitally tunable holographic lithography using a spatial light modulator as a programmable phase mask. Opt. Express 2013, 21, 26227–26235. [Google Scholar] [CrossRef] [PubMed]
- Lutkenhaus, J.; George, D.; Arigong, B.; Zhang, H.; Philipose, U.; Lin, Y. Holographic fabrication of functionally graded photonic lattices through spatially specified phase patterns. Appl. Opt. 2014, 53, 2548–2555. [Google Scholar] [CrossRef] [PubMed]
- Ohlinger, K.; Lutkenhaus, J.; Arigong, B.; Zhang, H.; Lin, Y. Spatially addressable design of gradient index structures through spatial light modulator based holographic lithography. J. Appl. Phys. 2013, 114, 213102. [Google Scholar] [CrossRef]
- Lutkenhaus, J.; Lowell, D.; George, G.; Zhang, H.; Lin, Y. Holographic Fabrication of Designed Functional Defect Lines in Photonic Crystal Lattice Using a Spatial Light Modulator. Micromachines 2016, 7, 59. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Oskooi, A. Texturing the cathode of white organic light-emitting diodes with a lattice of nanoscale scatterers for enhanced light out-coupling. Appl. Phys. Lett. 2015, 106, 041111. [Google Scholar] [CrossRef]
- Grell, M.; Bradley, D.D.C. Polarized luminescence from oriented molecular materials. Adv. Mater. 1999, 11, 895–905. [Google Scholar] [CrossRef]
- Shi, J.; Pollard, M.E.; Angeles, C.A.; Chen, R.; Gates, J.C.; Charlton, M.D.B. Photonic crystal and quasi-crystals providing simultaneous light coupling and beam splitting within a low refractive-index slab waveguide. Sci. Rep. 2017, 7, 1812. [Google Scholar] [CrossRef] [PubMed]
- Adewole, M.; Lowell, D.; Hassan, S.; George, D.; Zhang, H.; Cui, J.; Lin, Y. Broadband plasmonic total light absorption in an Al-doped ZnO/spacer/silver stack patterned with graded photonic super-crystal. Res. J. Opt. Photonics 2017, 1, 1. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, S.; Sale, O.; Lowell, D.; Hurley, N.; Lin, Y. Holographic Fabrication and Optical Property of Graded Photonic Super-Crystals with a Rectangular Unit Super-Cell. Photonics 2018, 5, 34. https://doi.org/10.3390/photonics5040034
Hassan S, Sale O, Lowell D, Hurley N, Lin Y. Holographic Fabrication and Optical Property of Graded Photonic Super-Crystals with a Rectangular Unit Super-Cell. Photonics. 2018; 5(4):34. https://doi.org/10.3390/photonics5040034
Chicago/Turabian StyleHassan, Safaa, Oliver Sale, David Lowell, Noah Hurley, and Yuankun Lin. 2018. "Holographic Fabrication and Optical Property of Graded Photonic Super-Crystals with a Rectangular Unit Super-Cell" Photonics 5, no. 4: 34. https://doi.org/10.3390/photonics5040034
APA StyleHassan, S., Sale, O., Lowell, D., Hurley, N., & Lin, Y. (2018). Holographic Fabrication and Optical Property of Graded Photonic Super-Crystals with a Rectangular Unit Super-Cell. Photonics, 5(4), 34. https://doi.org/10.3390/photonics5040034





