Highly-Efficient Longitudinal Second-Harmonic Generation from Doubly-Resonant AlGaAs Nanoantennas
Abstract
1. Introduction
2. Results and Discussion
2.1. Theoretical Model and Numerical Simulations
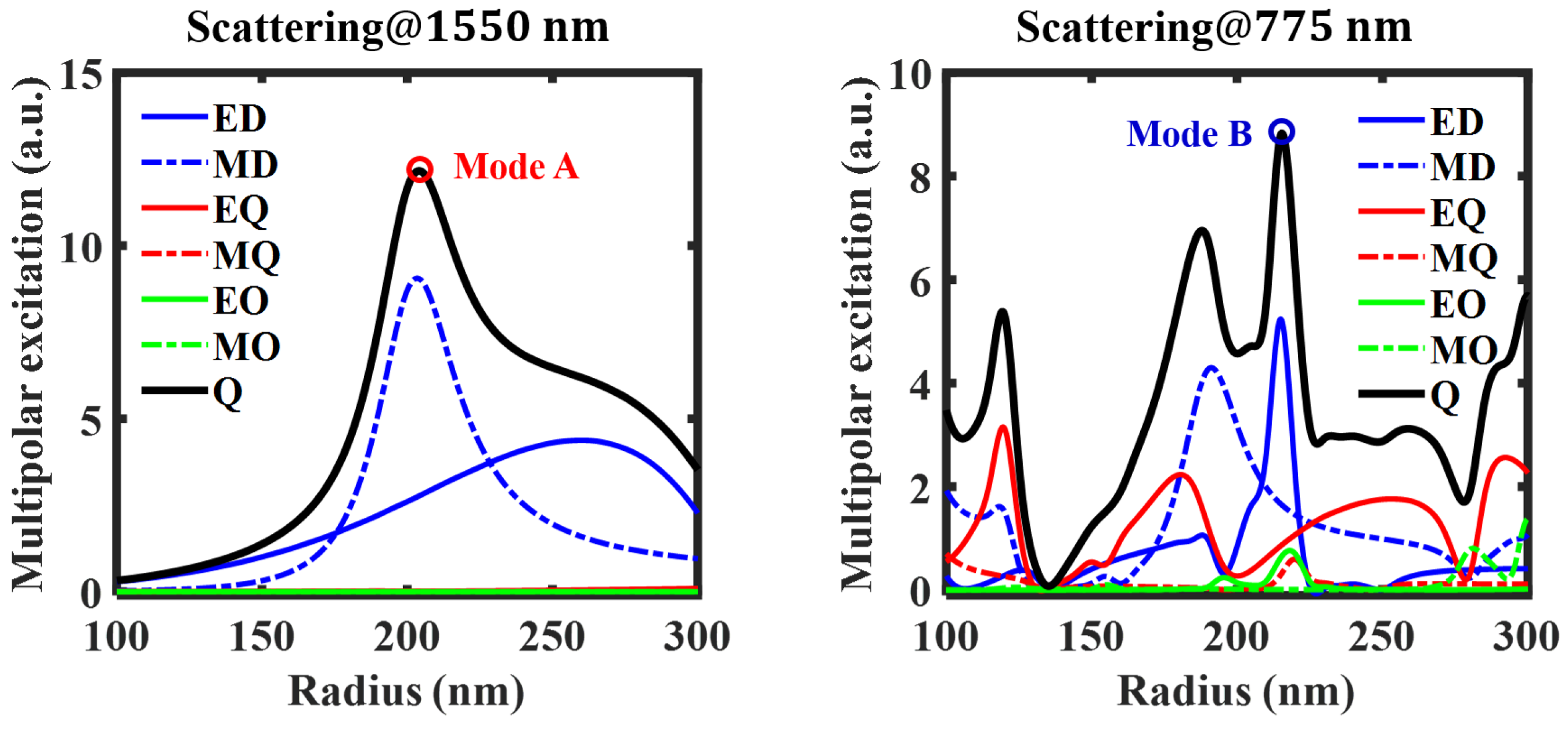
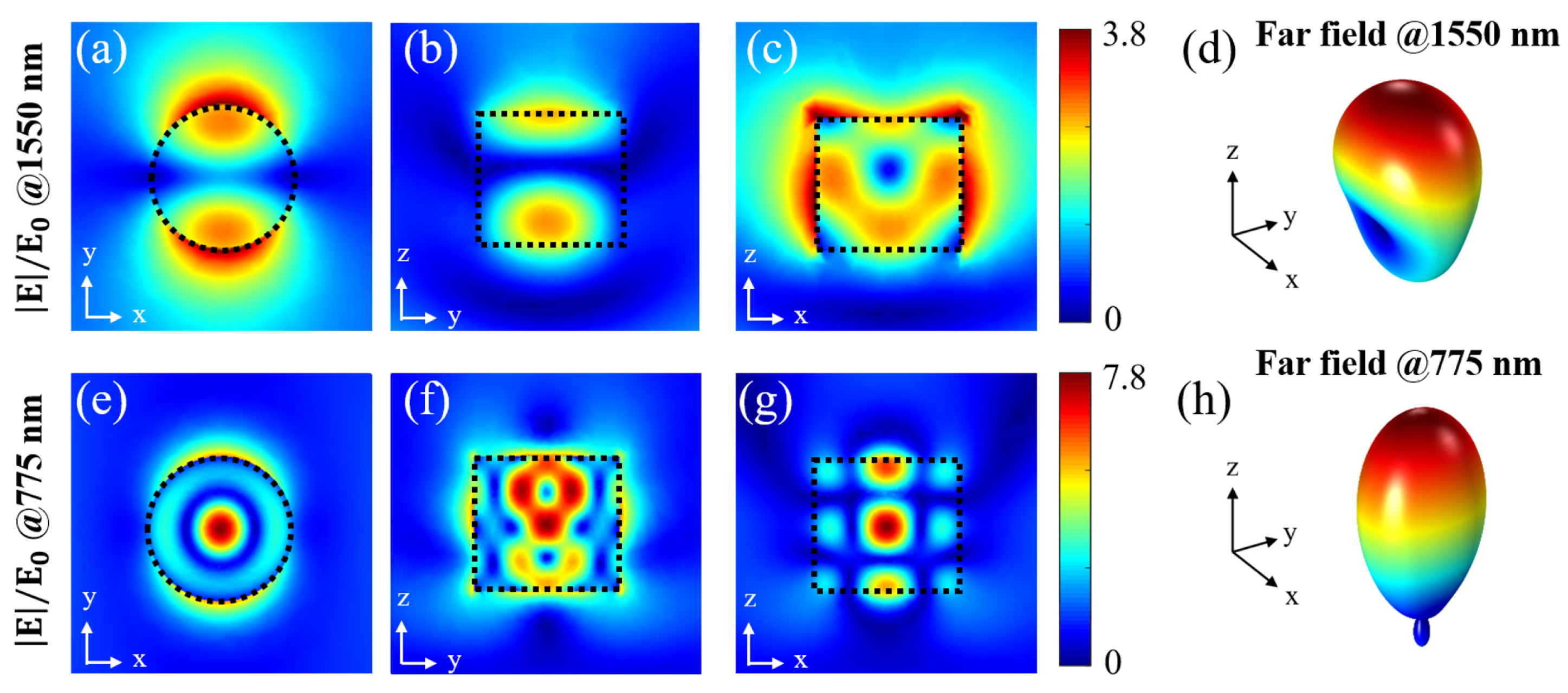
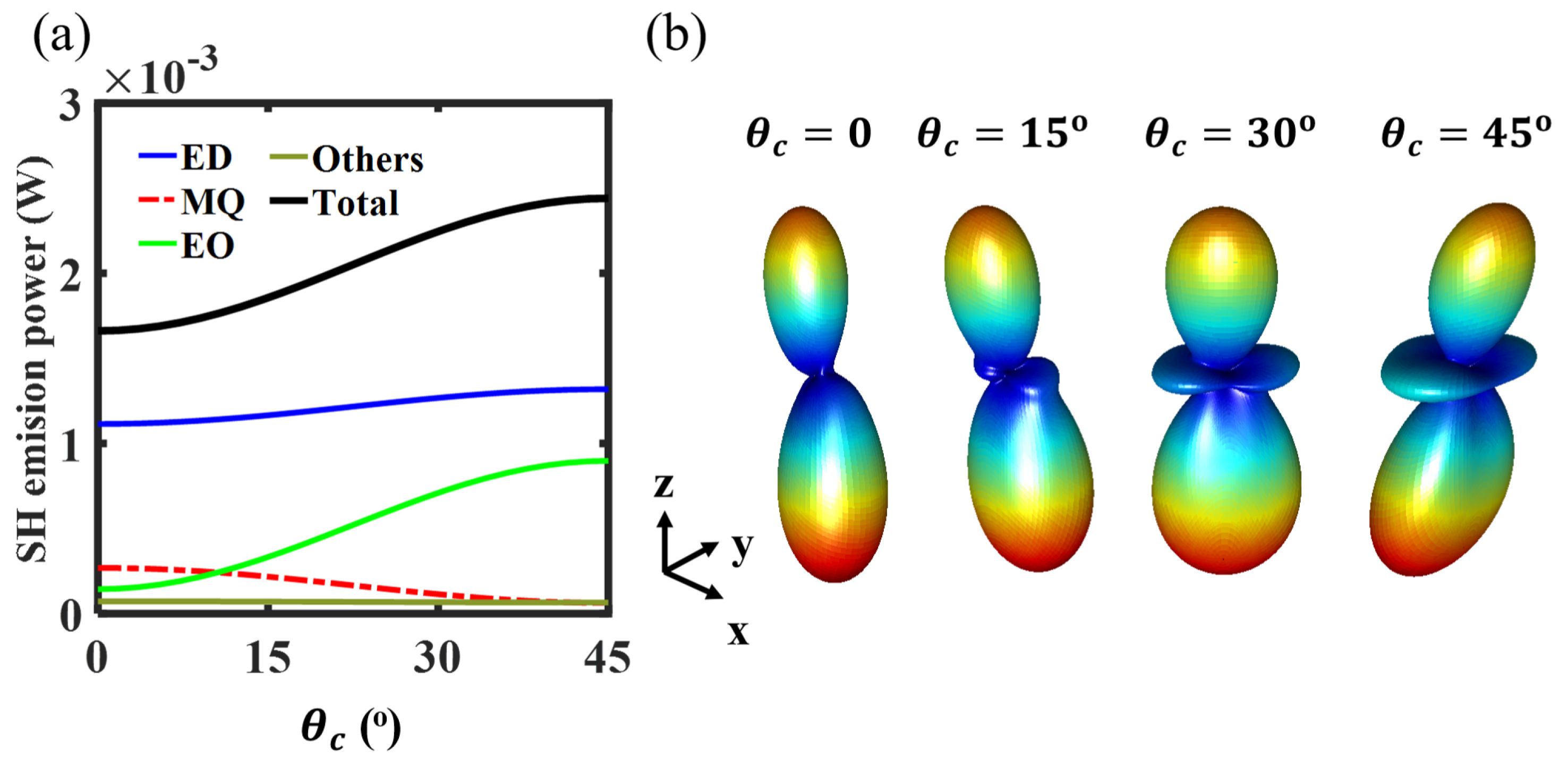
2.2. Linear and Nonlinear Responses from a Single AlGaAs Nanodisc
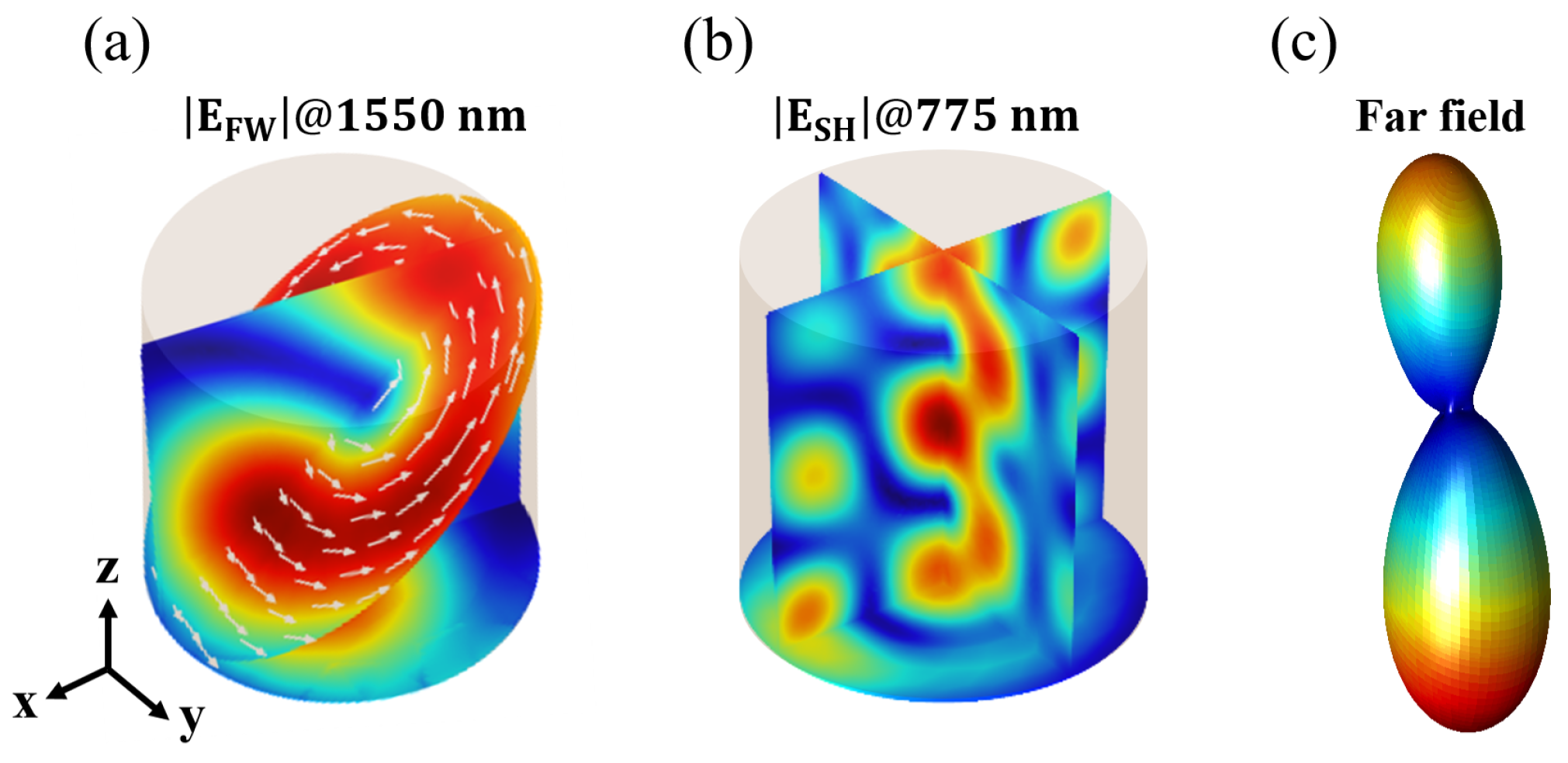
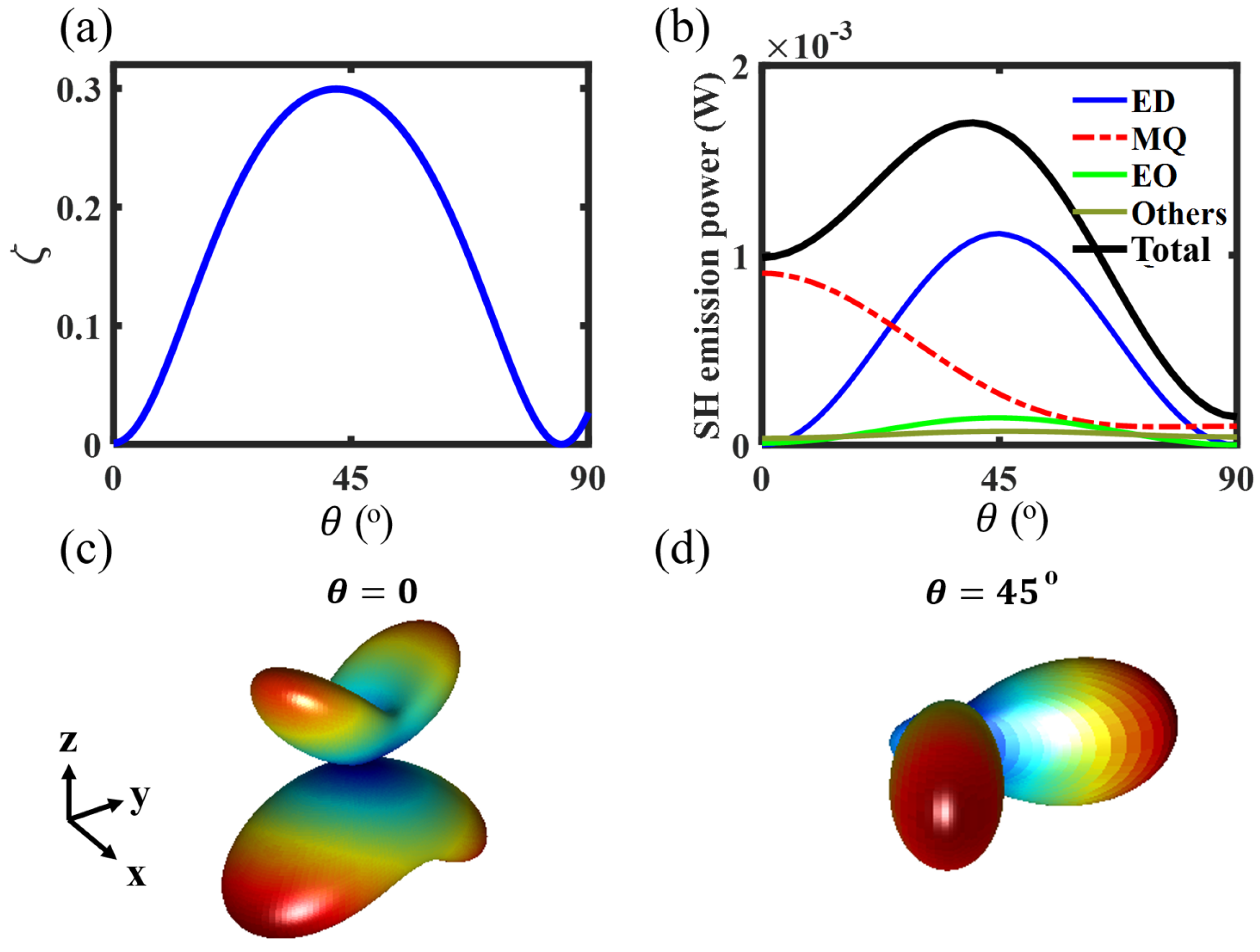
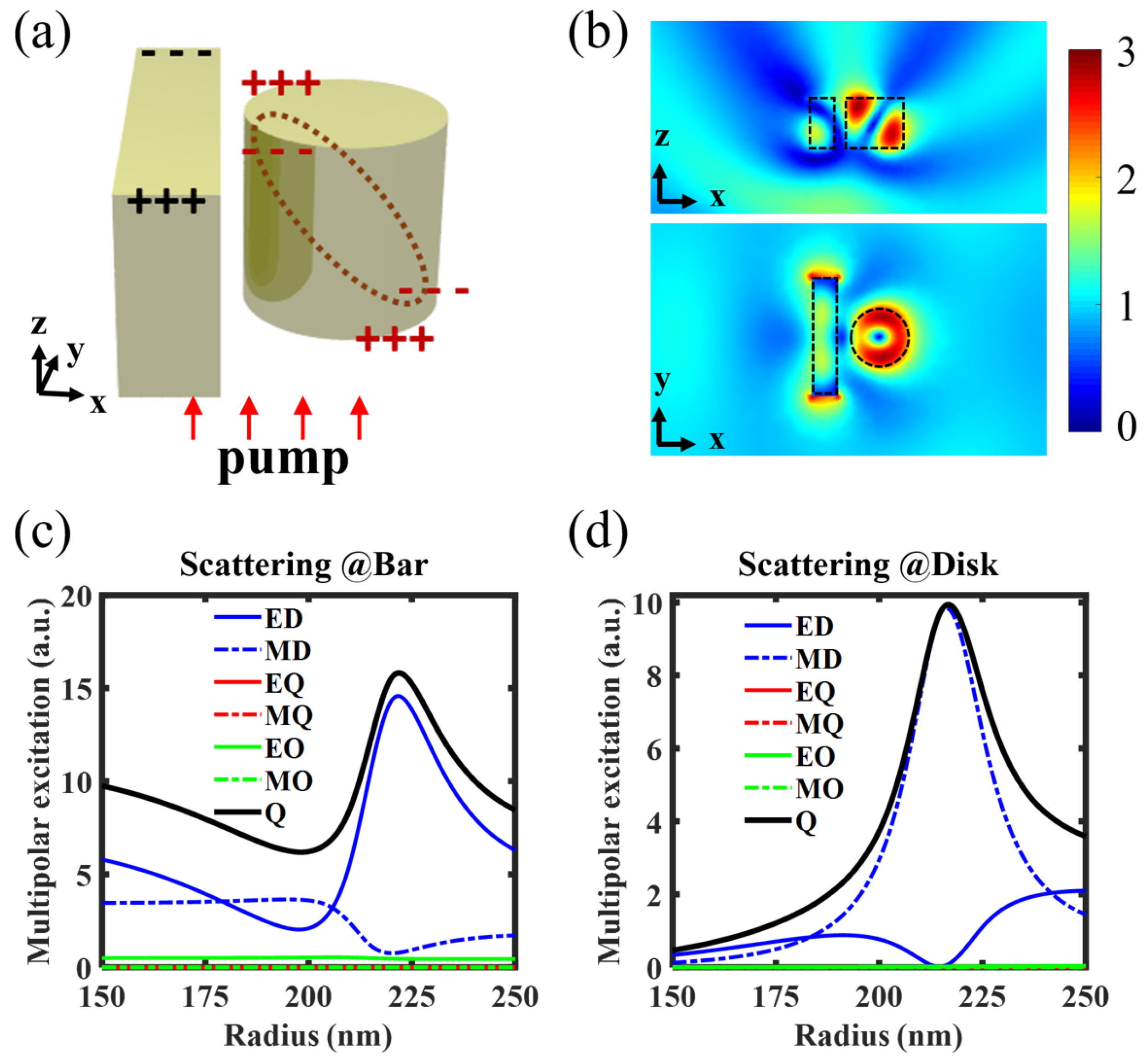
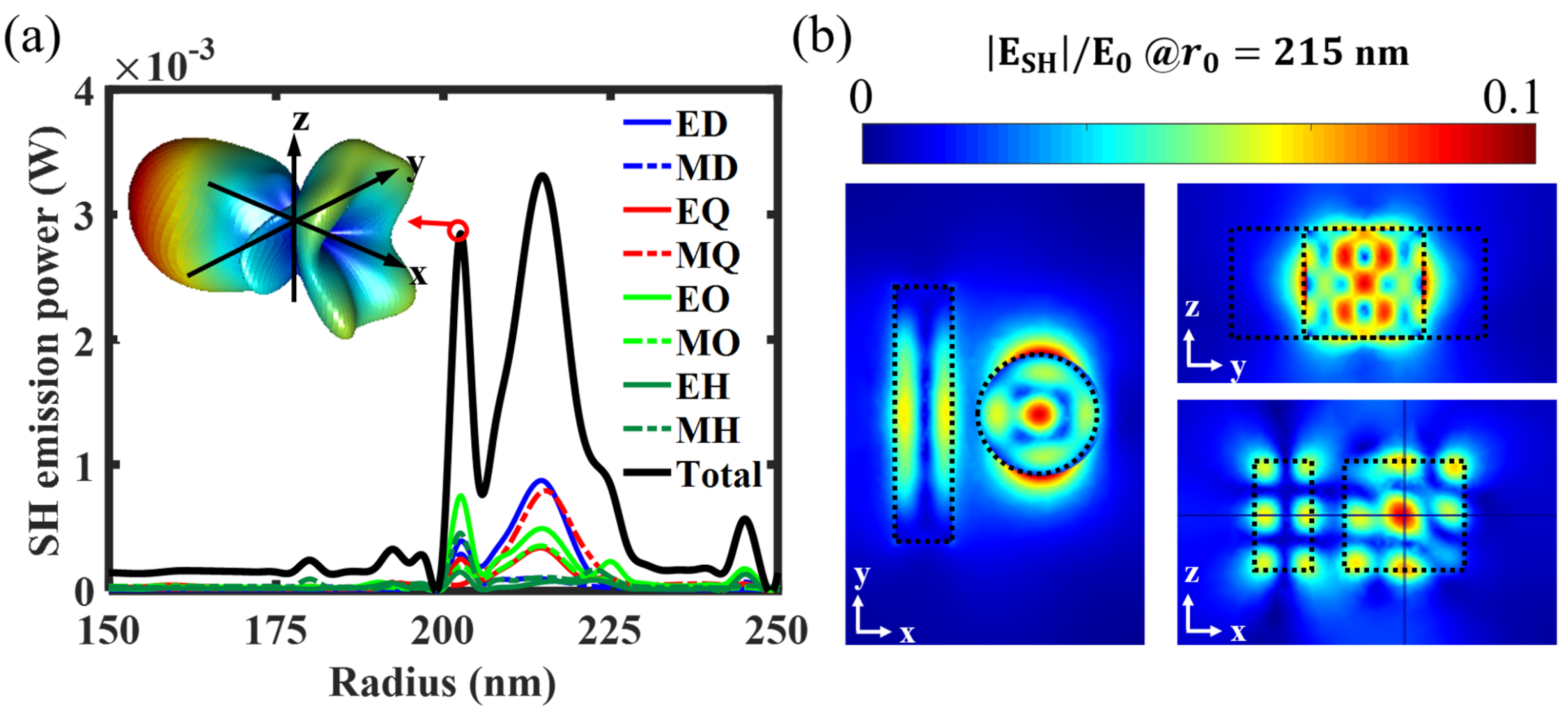
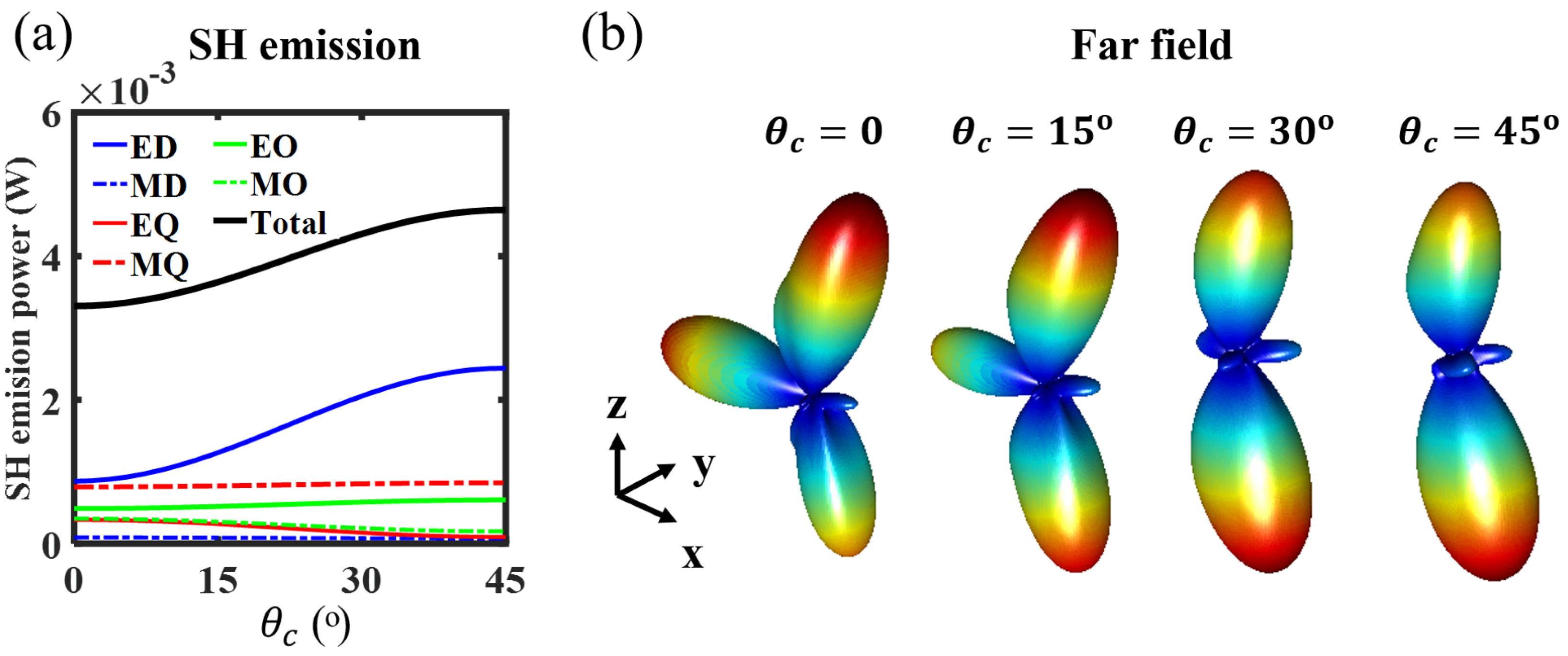
2.3. Longitudinal SHG through a Doubly-Resonant Asymmetric AlGaAs Nanoantenna
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Solntsev, A.; Carletti, L.; Xu, L.; Poddubny, A.; De Angelis, C.; Leo, G.; Kivshar, Y.; Neshev, D.N.; Sukhorukov, A.A. Quantum-classical correspondence for photon-pair generation in nonlinear dielectric nano-resonators. In Nonlinear Photonics; Optical Society of America: Washington, DC, USA, 2016; p. NT3A–4. [Google Scholar]
- van Sark, W.G.; de Wild, J.; Rath, J.K.; Meijerink, A.; Schropp, R.E. Upconversion in solar cells. Nanoscale Res. Lett. 2013, 8, 81. [Google Scholar] [CrossRef] [PubMed]
- Bautista, G.; Kauranen, M. Vector-field nonlinear microscopy of nanostructures. ACS Photonics 2016, 3, 1351–1370. [Google Scholar] [CrossRef]
- DaCosta, M.V.; Doughan, S.; Han, Y.; Krull, U.J. Lanthanide upconversion nanoparticles and applications in bioassays and bioimaging: A review. Anal. Chim. Acta 2014, 832, 1–33. [Google Scholar] [CrossRef] [PubMed]
- Klimov, V. Nanoplasmonics: Fundamentals and Applications; Pan Stanford: Singapore, 2012. [Google Scholar]
- Lippitz, M.; van Dijk, M.A.; Orrit, M. Third-harmonic generation from single gold nanoparticles. Nano Lett. 2005, 5, 799–802. [Google Scholar] [CrossRef] [PubMed]
- Aouani, H.; Rahmani, M.; Navarro-Cía, M.; Maier, S.A. Third-harmonic-upconversion enhancement from a single semiconductor nanoparticle coupled to a plasmonic antenna. Nat. Nanotechnol. 2014, 9, 290–294. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Jin, J.; Kim, Y.J.; Park, I.Y.; Kim, Y.; Kim, S.W. High-harmonic generation by resonant plasmon field enhancement. Nature 2008, 453, 757–760. [Google Scholar] [CrossRef] [PubMed]
- Hanke, T.; Cesar, J.; Knittel, V.; Trügler, A.; Hohenester, U.; Leitenstorfer, A.; Bratschitsch, R. Tailoring spatiotemporal light confinement in single plasmonic nanoantennas. Nano Lett. 2012, 12, 992–996. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Utikal, T.; Giessen, H.; Lippitz, M. Quantitative modeling of the third harmonic emission spectrum of plasmonic nanoantennas. Nano Lett. 2012, 12, 3778–3782. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, M.; Xu, L.; Miroshnichenko, A.E.; Komar, A.; Camacho-Morales, R.; Chen, H.; Zárate, Y.; Kruk, S.; Zhang, G.; Neshev, D.N.; et al. Reversible Thermal Tuning of All-Dielectric Metasurfaces. Adv. Funct. Mater. 2017, 27, 1700580. [Google Scholar] [CrossRef]
- Nemati, A.; Wang, Q.; Hong, M.; Teng, J. Tunable and reconfigurable metasurfaces and metadevices. Opto-Electron. Adv. 2018, 1, 18000901–18000925. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, D.; Kivshar, Y.S. Multipolar nonlinear nanophotonics. Optica 2016, 3, 1241–1255. [Google Scholar] [CrossRef]
- Liu, S.; Keeler, G.A.; Reno, J.L.; Sinclair, M.B.; Brener, I. III–V semiconductor nanoresonators—A new strategy for passive, active, and nonlinear all-dielectric metamaterials. Adv. Opt. Mater. 2016, 4, 1457–1462. [Google Scholar] [CrossRef]
- Baranov, D.G.; Zuev, D.A.; Lepeshov, S.I.; Kotov, O.V.; Krasnok, A.E.; Evlyukhin, A.B.; Chichkov, B.N. All-dielectric nanophotonics: The quest for better materials and fabrication techniques. Optica 2017, 4, 814–825. [Google Scholar] [CrossRef]
- Cao, Y.; Xie, F.; Zhang, P.; Li, X. Dual-beam super-resolution direct laser writing nanofabrication technology. Opto-Electron. Eng. 2017, 44, 1133–1145. [Google Scholar]
- Shcherbakov, M.R.; Neshev, D.N.; Hopkins, B.; Shorokhov, A.S.; Staude, I.; Melik-Gaykazyan, E.V.; Decker, M.; Ezhov, A.A.; Miroshnichenko, A.E.; Brener, I.; et al. Enhanced Third-Harmonic Generation in Silicon Nanoparticles Driven by Magnetic Response. Nano Lett. 2014, 14, 6488–6492. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wang, W.; Boulesbaa, A.; Kravchenko, I.I.; Briggs, D.P.; Puretzky, A.; Geohegan, D.; Valentine, J. Nonlinear Fano-resonant dielectric metasurfaces. Nano Lett. 2015, 15, 7388–7393. [Google Scholar] [CrossRef] [PubMed]
- Shorokhov, A.S.; Melik-Gaykazyan, E.V.; Smirnova, D.A.; Hopkins, B.; Chong, K.E.; Choi, D.Y.; Shcherbakov, M.R.; Miroshnichenko, A.E.; Neshev, D.N.; Fedyanin, A.A.; et al. Multifold Enhancement of Third-Harmonic Generation in Dielectric Nanoparticles Driven by Magnetic Fano Resonances. Nano Lett. 2016, 16, 4857–4861. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Rahmani, M.; Li, K.F.; Miroshnichenko, A.; Zentgraf, T.; Li, G.; Neshev, D.; Zhang, S. Third Harmonic Generation Enhanced by Multipolar Interference in Complementary Silicon Metasurfaces. ACS Photonics 2018, 5, 1671–1675. [Google Scholar] [CrossRef]
- Grinblat, G.; Li, Y.; Nielsen, M.P.; Oulton, R.F.; Maier, S.A. Enhanced third harmonic generation in single germanium nanodiscs excited at the anapole mode. Nano Lett. 2016, 16, 4635–4640. [Google Scholar] [CrossRef] [PubMed]
- Shibanuma, T.; Grinblat, G.; Albella, P.; Maier, S.A. Efficient Third Harmonic Generation from Metal—Dielectric Hybrid Nanoantennas. Nano Lett. 2017, 17, 2647–2651. [Google Scholar] [CrossRef] [PubMed]
- Vabishchevich, P.P.; Liu, S.; Sinclair, M.B.; Keeler, G.A.; Peake, G.M.; Brener, I. Enhanced second-harmonic generation using broken symmetry III–V semiconductor fano metasurfaces. ACS Photonics 2018, 5, 1685–1690. [Google Scholar] [CrossRef]
- Xu, L.; Rahmani, M.; Zangeneh Kamali, K.; Lamprianidis, A.; Ghirardini, L.; Sautter, J.; Camacho-Morales, R.; Chen, H.; Parry, M.; Staude, I.; et al. Boosting third-harmonic generation by a mirror-enhanced anapole resonator. Light Sci. Appl. 2018, 7, 44. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press: New York, NY, USA, 2008. [Google Scholar]
- Shcherbakov, M.R.; Liu, S.; Zubyuk, V.V.; Vaskin, A.; Vabishchevich, P.P.; Keeler, G.; Pertsch, T.; Dolgova, T.V.; Staude, I.; Brener, I.; et al. Ultrafast all-optical tuning of direct-gap semiconductor metasurfaces. Nat. Commun. 2017, 8, 17. [Google Scholar] [CrossRef] [PubMed]
- Carletti, L.; Locatelli, A.; Stepanenko, O.; Leo, G.; De Angelis, C. Enhanced second-harmonic generation from magnetic resonance in AlGaAs nanoantennas. Opt. Express 2015, 23, 26544–26550. [Google Scholar] [CrossRef] [PubMed]
- Gili, V.; Carletti, L.; Locatelli, A.; Rocco, D.; Finazzi, M.; Ghirardini, L.; Favero, I.; Gomez, C.; Lemaître, A.; Celebrano, M.; et al. Monolithic AlGaAs second-harmonic nanoantennas. Opt. Express 2016, 24, 15965–15971. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Sinclair, M.B.; Saravi, S.; Keeler, G.A.; Yang, Y.; Reno, J.; Peake, G.M.; Setzpfandt, F.; Staude, I.; Pertsch, T.; et al. Resonantly enhanced second-harmonic generation using III–V semiconductor all-dielectric metasurfaces. Nano Lett. 2016, 16, 5426–5432. [Google Scholar] [CrossRef] [PubMed]
- Camacho-Morales, R.; Rahmani, M.; Kruk, S.; Wang, L.; Xu, L.; Smirnova, D.A.; Solntsev, A.S.; Miroshnichenko, A.; Tan, H.H.; Karouta, F.; et al. Nonlinear generation of vector beams from AlGaAs nanoantennas. Nano Lett. 2016, 16, 7191–7197. [Google Scholar] [CrossRef] [PubMed]
- Carletti, L.; Locatelli, A.; Neshev, D.; De Angelis, C. Shaping the Radiation Pattern of Second-Harmonic Generation from AlGaAs Dielectric Nanoantennas. ACS Photonics 2016, 3, 1500–1507. [Google Scholar] [CrossRef]
- Ghirardini, L.; Carletti, L.; Gili, V.; Pellegrini, G.; Duò, L.; Finazzi, M.; Rocco, D.; Locatelli, A.; De Angelis, C.; Favero, I.; et al. Polarization properties of second-harmonic generation in AlGaAs optical nanoantennas. Opt. Lett. 2017, 42, 559–562. [Google Scholar] [CrossRef] [PubMed]
- Timofeeva, M.; Lang, L.; Timpu, F.; Renaut, C.; Bouravleuv, A.; Shtrom, I.V.; Cirlin, G.; Grange, R. Anapoles in Free-Standing III-V Nanodiscs Enhancing Second-Harmonic Generation. Nano Lett. 2018, 18, 3695–3702. [Google Scholar] [CrossRef] [PubMed]
- Shoji, I.; Kondo, T.; Kitamoto, A.; Shirane, M.; Ito, R. Absolute scale of second-order nonlinear-optical coefficients. JOSA B 1997, 14, 2268–2294. [Google Scholar] [CrossRef]
- Ohashi, M.; Kondo, T.; Ito, R.; Fukatsu, S.; Shiraki, Y.; Kumata, K.; Kano, S. Determination of quadratic nonlinear optical coefficient of AlxGa1-x As system by the method of reflected second harmonics. J. Appl. Phys. 1993, 74, 596–601. [Google Scholar] [CrossRef]
- Melik-Gaykazyan, E.V.; Kruk, S.S.; Camacho-Morales, R.; Xu, L.; Rahmani, M.; Zangeneh Kamali, K.; Lamprianidis, A.; Miroshnichenko, A.E.; Fedyanin, A.A.; Neshev, D.N.; et al. Selective third-harmonic generation by structured light in Mie-resonant nanoparticles. ACS Photonics 2017, 5, 728–733. [Google Scholar] [CrossRef]
- Carletti, L.; Koshelev, K.; De Angelis, C.; Kivshar, Y. Giant nonlinear response at the nanoscale driven by bound states in the continuum. arXiv, 2018; arXiv:1804.02947. [Google Scholar] [CrossRef] [PubMed]
- Camacho-Morales, R.; Bautista, G.; Zang, X.; Xu, L.; Turquet, L.; Miroshnichenko, A.; Lamprianidis, A.; Rahmani, M.; Neshev, D.N.; Kauranen, M. Resonant harmonic generation in AlGaAs nanoantennas using cylindrical vector beams. In Proceedings of the CLEO: QELS_Fundamental Science, Optical Society of America, San Jose, CA, USA, 13–18 May 2018; p. FF1E–6. [Google Scholar]
- Yang, Y.; Miroshnichenko, A.E.; Kostinski, S.V.; Odit, M.; Kapitanova, P.; Qiu, M.; Kivshar, Y.S. Multimode directionality in all-dielectric metasurfaces. Phys. Rev. B 2017, 95, 165426. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Rahmani, M.; Smirnova, D.; Zangeneh Kamali, K.; Zhang, G.; Neshev, D.; Miroshnichenko, A.E. Highly-Efficient Longitudinal Second-Harmonic Generation from Doubly-Resonant AlGaAs Nanoantennas. Photonics 2018, 5, 29. https://doi.org/10.3390/photonics5030029
Xu L, Rahmani M, Smirnova D, Zangeneh Kamali K, Zhang G, Neshev D, Miroshnichenko AE. Highly-Efficient Longitudinal Second-Harmonic Generation from Doubly-Resonant AlGaAs Nanoantennas. Photonics. 2018; 5(3):29. https://doi.org/10.3390/photonics5030029
Chicago/Turabian StyleXu, Lei, Mohsen Rahmani, Daria Smirnova, Khosro Zangeneh Kamali, Guoquan Zhang, Dragomir Neshev, and Andrey E. Miroshnichenko. 2018. "Highly-Efficient Longitudinal Second-Harmonic Generation from Doubly-Resonant AlGaAs Nanoantennas" Photonics 5, no. 3: 29. https://doi.org/10.3390/photonics5030029
APA StyleXu, L., Rahmani, M., Smirnova, D., Zangeneh Kamali, K., Zhang, G., Neshev, D., & Miroshnichenko, A. E. (2018). Highly-Efficient Longitudinal Second-Harmonic Generation from Doubly-Resonant AlGaAs Nanoantennas. Photonics, 5(3), 29. https://doi.org/10.3390/photonics5030029






