Determining Vortex-Beam Superpositions by Shear Interferometry
Abstract
1. Introduction
2. Theory
2.1. Modal Superpositions
- When , the modal pattern is quite predictable and shows the following features:
- -
- The center of the pattern has an optical vortex of charge . This is what is theoretically predicted. In practice, a multiply-charged point is very susceptible to perturbations, and so, the center of the pattern may consist of singly-charged vortices of sign in close proximity.
- -
- The center is surrounded by vortices arranged symmetrically [28] and located at a radial distance that satisfies:For the case of pure Laguerre–Gauss modes, we know the analytical expressions of , and so, we can deduce :The angular position of the vortices depends on the relative phase between the two modes [28]:where is an odd integer.
For example, when and , the composite mode for consists of a central vortex of charge surrounded by three vortices of charge located at a radius . - When and , the pattern contains a central vortex of charge . At , there is no central vortex, and the composite mode has radial lines (nodes) of shear phase, evenly separated. The relative weights of the modes produce subtle variations in intensity, which yields greater uncertainty in the determination. The method presented in this article is much more effective for the first case.
2.2. Shear Interference Pattern
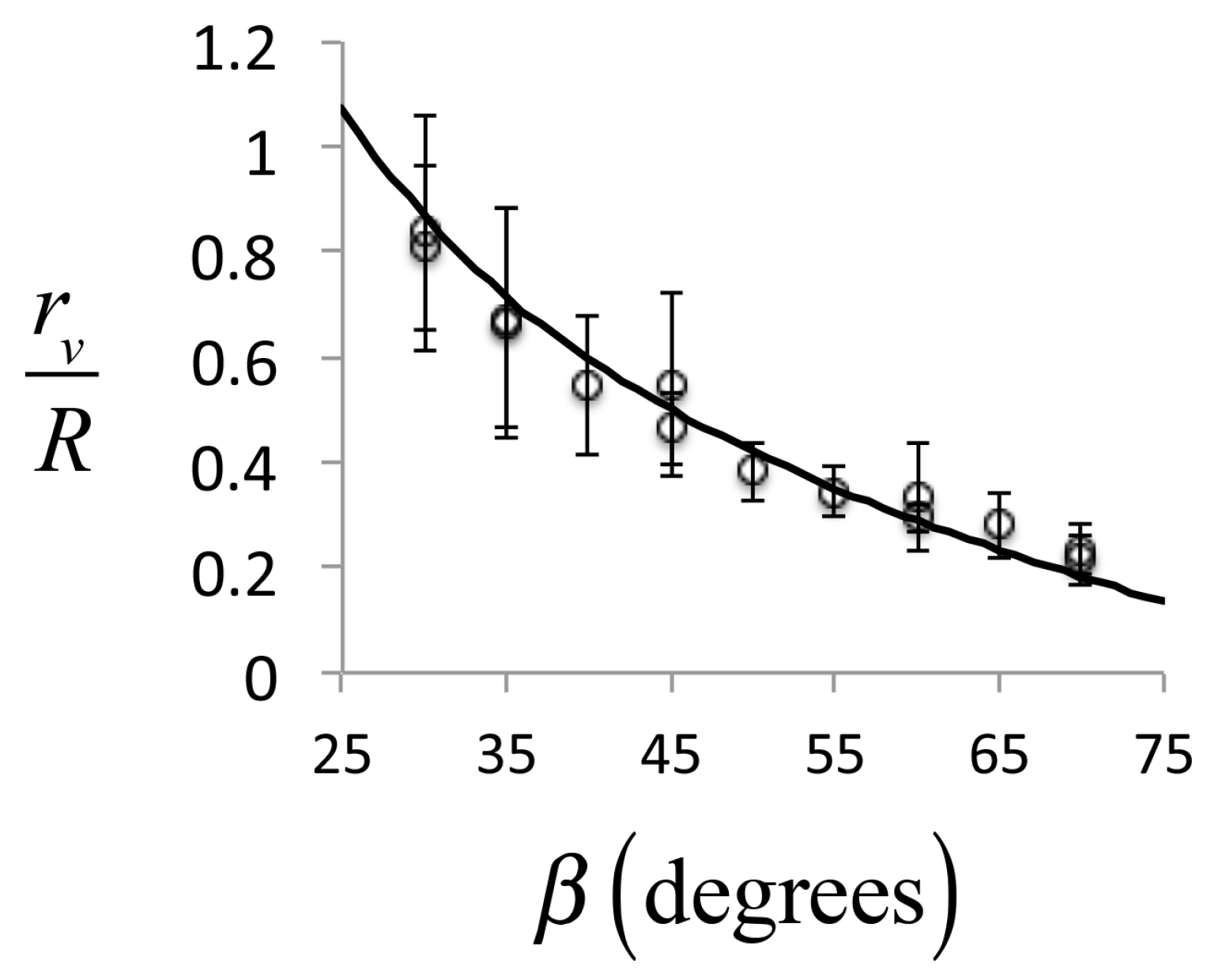
- The pattern consists of conjoined forks formed by the interference of the vortex beam with a displaced and tilted copy of it. If the shear interferometer is air spaced, the centers of the vortices are displaced by:where is the incident angle and t is the average separation between the reflecting surfaces. This relation is modified if the fringes are not parallel to the displacement of the two modes.
- The overall phase of the pattern is determined by the optical path-length difference and the reflection phases, which for our case is given by:where is the wavelength of the light.
- The fringe density of the pattern is given by:where:is the angle that the back reflection makes with the horizontal. We use the convention when the beam coming from the back reflection is tilted downward and assuming that the front reflection is in the horizontal plane. is the wedge angle between the two reflecting surfaces.
3. Results
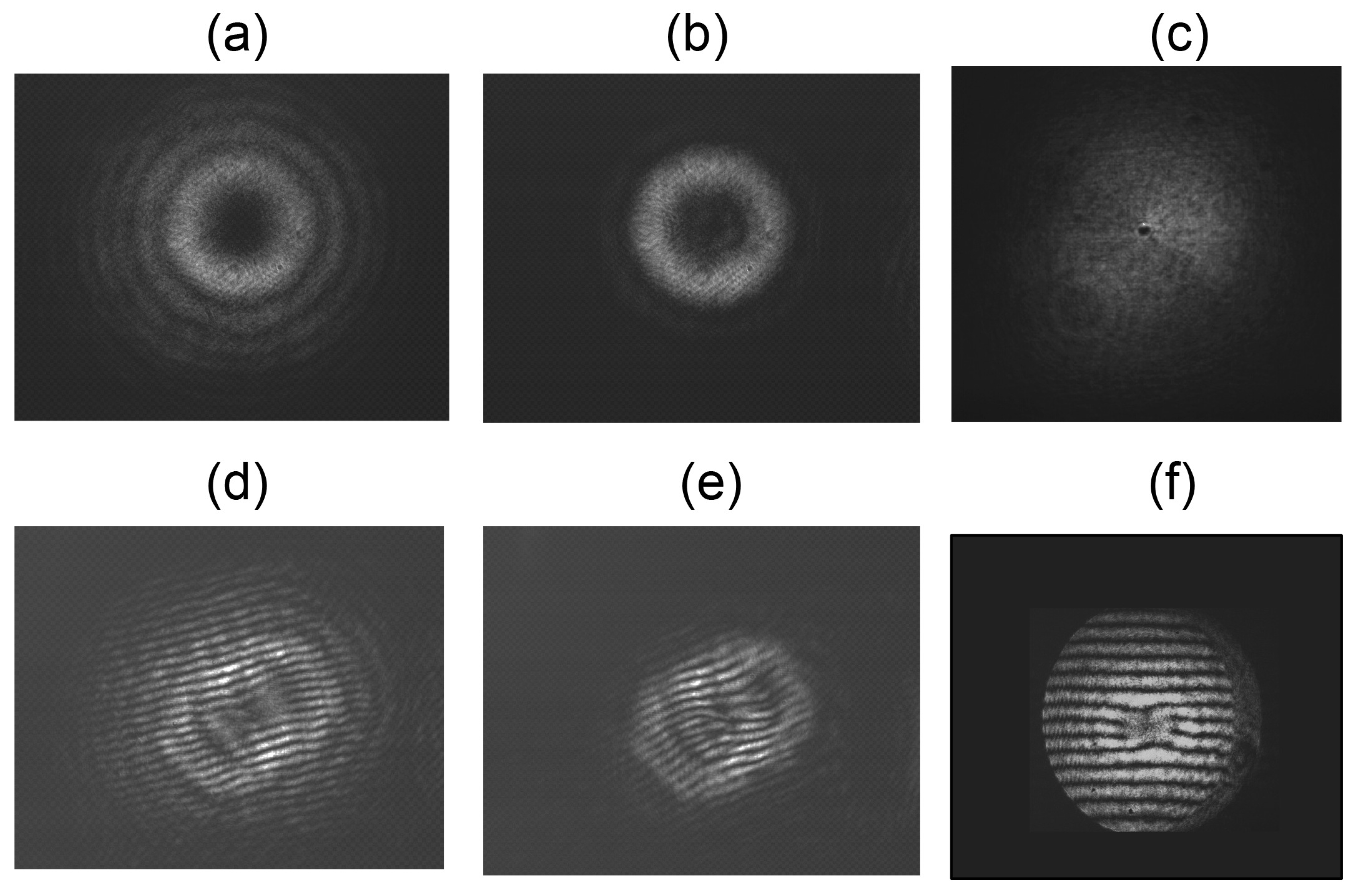
3.1. Mode Comparison
3.2. Determining the Topological Charge of the Component Beams
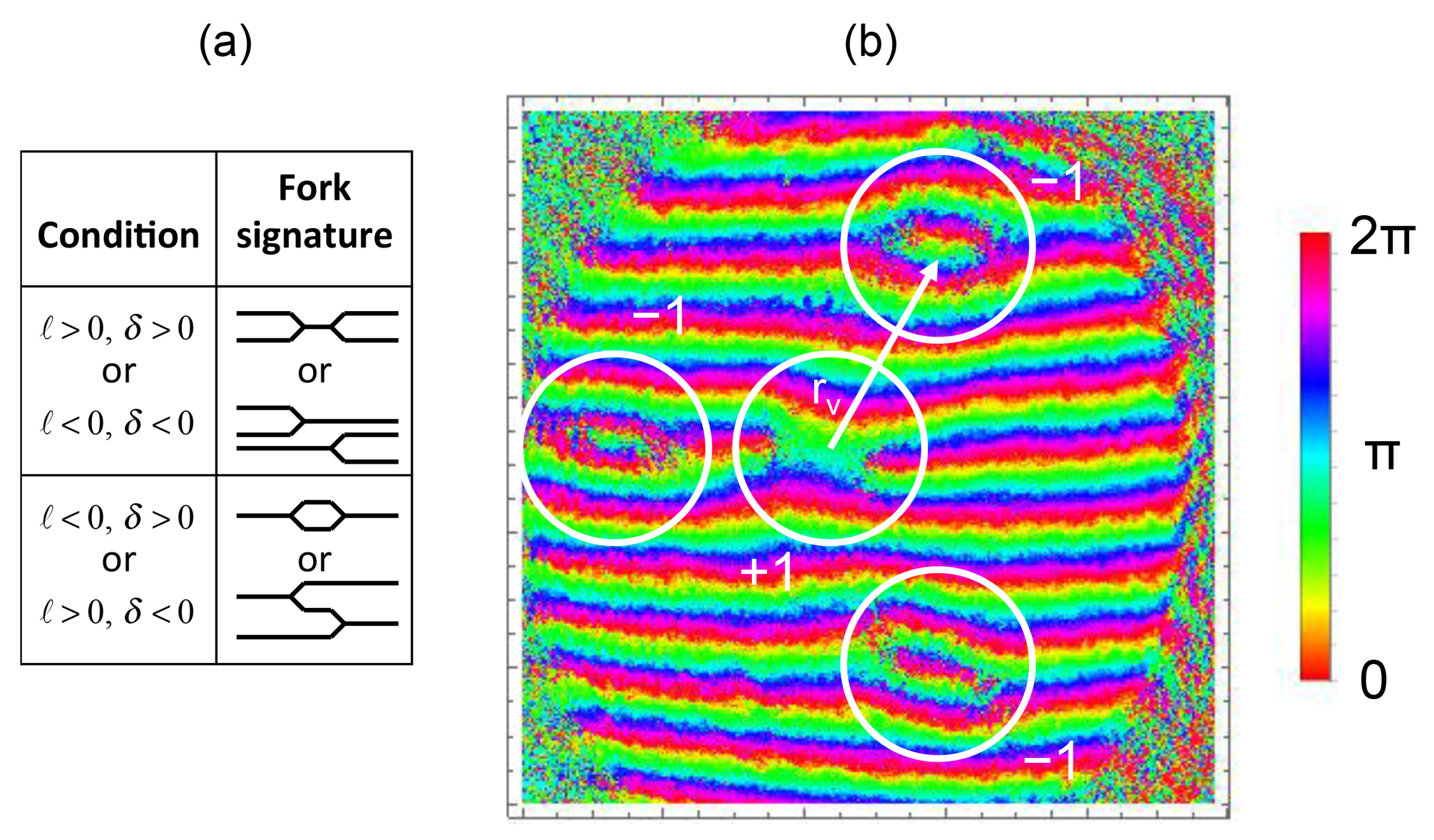
- We first examine the fork pattern in the center of the mode. From it, we extract the magnitude and sign of the mode with smaller topological charge (recall that we assume ). No vortices means . In the case of Figure 2b, we see the conjoined-fork pattern of a vortex, revealing that . In the table in Figure 2a, we give the correspondence between the sign of the topological charge of the vortex and its forked signature in the shear pattern.
- We count the number of peripheral vortices N (in Figure 2b, we see that ). The type of conjoined forks specifies their sign. If the sign of peripheral vortices is the same as the one at the center, then:If the sign is different than the center vortex, then:In our example of Figure 2b, because the sign of the peripheral vortices is different from the one of the central vortex, we conclude that .
- The angular orientation of the vortices reveals the relative phase between the modes per Equation (5). In our example, .
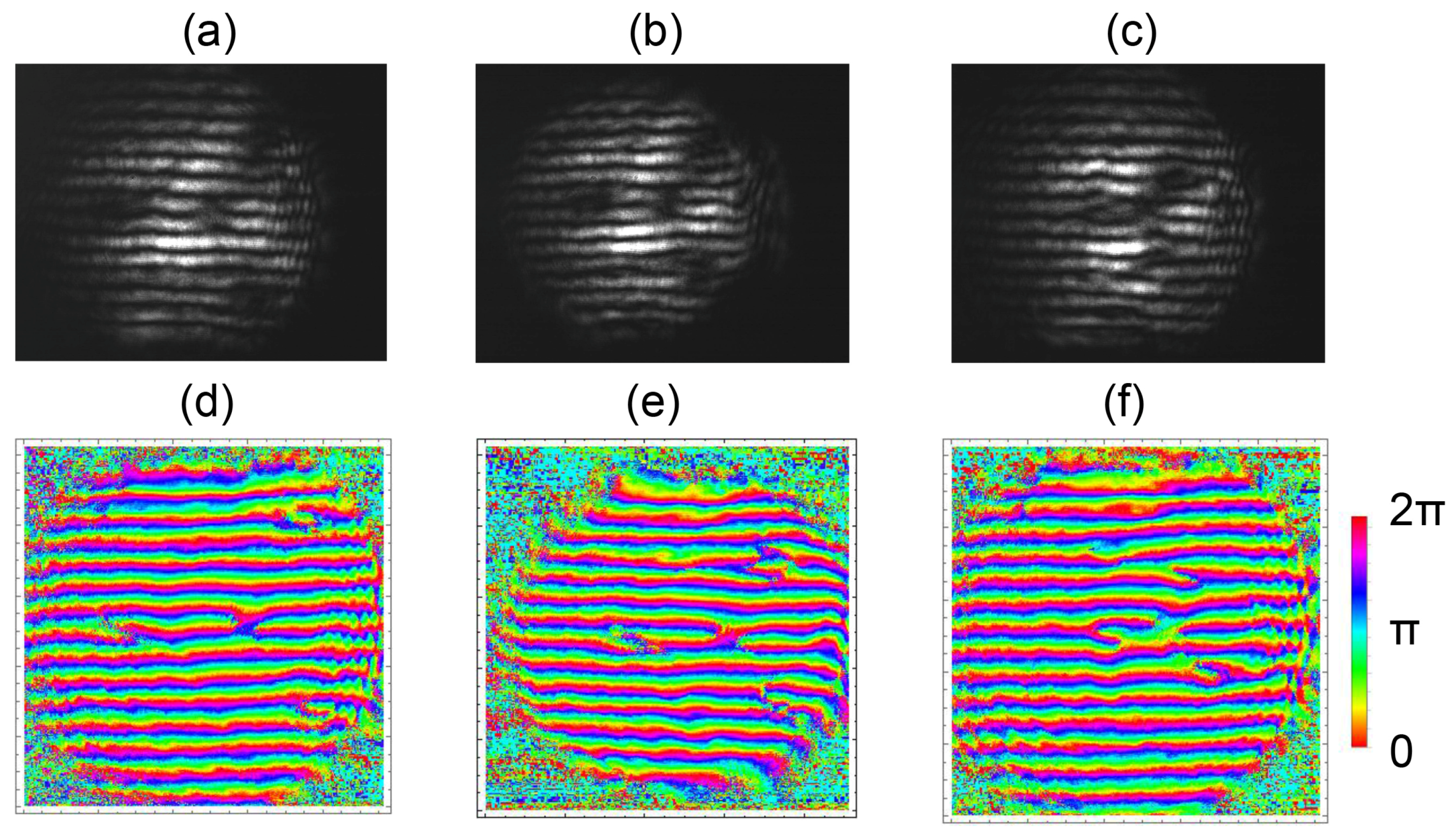
3.3. Determining the Relative Amplitude of the Component Beams
4. Discussion
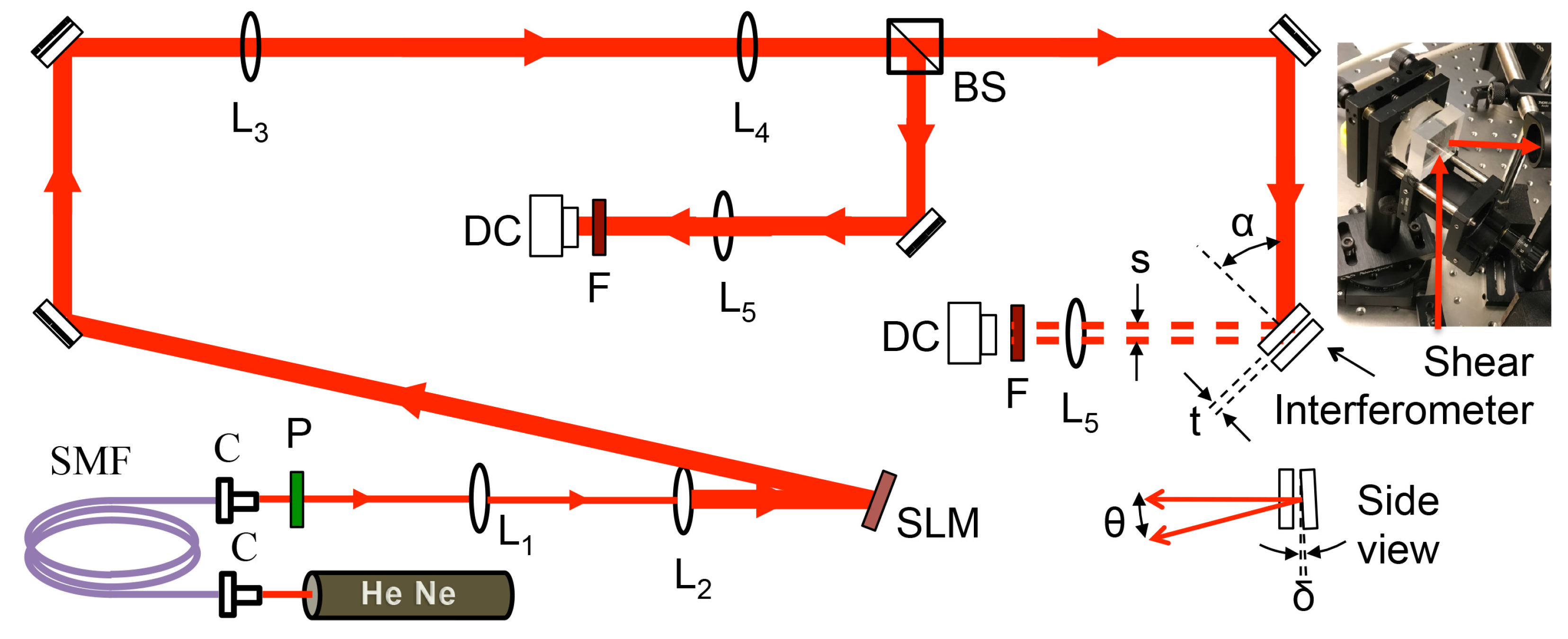
5. Apparatus and Methods
5.1. Shear Interferometer
5.2. Shear-Pattern Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Gibson, G.; Courtial, J.; Padgett, M.; Vasnetsov, M.; Pas’ko, V.P.; Barnett, S.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 340, 488–496. [Google Scholar] [CrossRef]
- Mair, A.; Vaziri, A.; Weihs, G.; Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 2001, 412, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Molina-Terriza, G.; Torres, J.; Torner, L. Twisted photons. Nat. Phys. 2008, 3, 305–310. [Google Scholar] [CrossRef]
- Rodenburg, B.; Lavery, M.; Malik, M.; O’Sullivan, M.; Mirhosseini, M.; Robertson, D.; Padgett, M.; Boyd, R. Influence of atmospheric turbulence on states of light carrying orbital angular momentum. Opt. Lett. 2012, 37, 3735–3737. [Google Scholar] [CrossRef] [PubMed]
- Malik, M.; O’Sullivan, M.; Rodenburg, B.; Mirhosseini, M.; Leach, J.; Lavery, M.P.J.; Padgett, M.; Boyd, R. Influence of atmospheric turbulence on optical communications using orbital angular momentum for encoding. Opt. Express 2012, 20, 13195–13200. [Google Scholar] [CrossRef] [PubMed]
- D’Ambrosio, V.; Nagali, E.; Walborn, S.; Aolita, A.; Slussarenko, S.; Marrucci, L.; Sciarrino, F. Complete experimental toolbox for alignment-free quantum communication. Nat. Commun. 2012, 3, 961. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Wang, Z.; Xie, G.; Li, L.; Willner, A.; Cao, Y.; Zhao, Z.; Yan, Y.; Ahmed, N.; Ashrafi, N.; et al. Atmospheric turbulence mitigation in an OAM-based MIMO free-space optical link using spatial diversity combined with MIMO equalization. Opt. Lett. 2016, 41, 2406–2409. [Google Scholar] [CrossRef] [PubMed]
- Krenn, M.; Handsteiner, J.; Fink, M.; Fickler, R.; Ursin, R.; Malik, M.; Zeilinger, A. Twisted light transmission over 143 km. Proc. Natl. Acad. Sci. USA 2016, 113, 13648–13653. [Google Scholar] [CrossRef] [PubMed]
- Krenn, M.; Fickler, R.; Fink, M.; Handsteiner, J.; Malik, M.; Scheidl, T.; Ursin, R.; Zeilinger, A. Communication with spatially modulated light through turbulent air across Vienna. New J. Phys. 2014, 16, 113028. [Google Scholar] [CrossRef]
- Molina-Terriza, G.; Torres, J.; Torner, L. Management of the angular momentum of light: Preparation of photons in multidimensional vector states of angular momentum. Phys. Rev. Lett. 2002, 88, 013601. [Google Scholar] [CrossRef] [PubMed]
- Barreiro, J.; Langford, N.; Peters, N.; Kwiat, P. Generation of hyperentangled photon pairs. Phys. Rev. Lett. 2005, 95, 260501. [Google Scholar] [CrossRef] [PubMed]
- Heckenberg, N.; McDuff, R.; Smith, C.; Rubinsztein-Dunlop, H.; Wegener, M. Laser beams with phase singularities. Opt. Quanum Electron. 1992, 24, 355–361. [Google Scholar] [CrossRef]
- Leach, J.; Padgett, M.J.; Barnett, S.M.; Franke-Arnold, S.; Courtial, J. Measuring the orbital angular momentum of a single photon. Phys. Rev. Lett. 2002, 88, 257901. [Google Scholar] [CrossRef] [PubMed]
- Sztul, H.I.; Alfano, R.R. Double-slit interference with Laguerre–Gaussian beams. Opt. Lett. 2006, 31, 999–1001. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, Q.; Jesus-Silva, A.; Fonseca, E.; Hickmann, J. Fraunhofer diffraction of light with orbital angular momentum by a slit. Opt. Lett. 2011, 36, 3106–3108. [Google Scholar] [CrossRef] [PubMed]
- Hickmann, J.; Fonseca, E.; Soares, W.; Chavez-Cerda, S. Unveiling a truncated optical lattice associated with a triangular aperture using light’s orbital angular momentum. Phys. Rev. Lett. 2010, 105, 053904. [Google Scholar] [CrossRef] [PubMed]
- Beijersbergen, M.W.; Allen, L.; van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Berkhout, G.C.; Lavery, M.P.; Courtial, J.; Beijersbergen, M.W.; Padgett, M.J. Efficient sorting of orbital angular momentum states of light. Phys. Rev. Lett. 2010, 105, 153601. [Google Scholar] [CrossRef] [PubMed]
- Schulze, C.; Dudley, A.; Flamm, D.; Duparré, M.; Forbes, A. Measurement of the orbital angular momentum density of light by modal decomposition. New J. Phys. 2013, 15, 073025. [Google Scholar] [CrossRef]
- Khajavi, B.; Galvez, E. Determining topological charge of an optical beam using a wedged optical flat. Opt. Lett. 2017, 42, 1516–1519. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.G.; Wang, K.; Lee, Y.H.; Wang, D.; Li, P.P.; Gou, F.; Li, Y.; Tu, C.; Wu, S.T.; Wang, H.T. Measurement of the topological charge of vortex vector optical fields with a space-variant half-wave plate. Opt. Lett. 2018, 43, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Jack, B.; Leach, J.; Ritsch, H.; Barnett, S.; Padgett, M.; Franke-Arnold, S. Precise quantum tomography of photon pairs with entangled orbital angular momentum. New J. Phys. 2009, 11, 103024. [Google Scholar] [CrossRef]
- O’Sullivan, M.; Mirhosseini, M.; Malik, M.; Boyd, R. Near-perfect sorting of orbital angular momentum and angular position states of light. Opt. Express 2012, 20, 24444. [Google Scholar] [CrossRef] [PubMed]
- Ghai, D.P.; Senthilkumaran, P.; Sirohi, R. Shearograms of an optical phase singularity. Opt. Commun. 2008, 281, 1315–1322. [Google Scholar] [CrossRef]
- Baumann, S.; Kalb, D.; MacMillan, L.; Galvez, E. Propagation dynamics of optical vortices due to Gouy phase. Opt. Express 2009, 17, 9818–9827. [Google Scholar] [CrossRef] [PubMed]
- Khajavi, B.; Galvez, E. Determination of the topological charge of complex light beams by shearing interference from a wedged optical flat. Proc. SPIE 2018, 10549, 105490M. [Google Scholar]
- Riley, M.E.; Gusinow, M.A. Laser beam divergence utilizing a lateral shearing interferometer. Appl. Opt. 1977, 16, 2753–2756. [Google Scholar] [CrossRef] [PubMed]
- Bazhenov, V.; Vatnetsov, M.; Soskin, M. Laser beams with screw dislocations in their wavefronts. JETP Lett. 1990, 52, 1037–1039. [Google Scholar]
- Beijersbergen, M.; Coerwinkel, R.; Kristensen, M.; Woerdman, J. Helical-wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Curtis, J.; Grier, D. Structure of optical vortices. Phys. Rev. Lett. 2003, 90, 133901. [Google Scholar] [CrossRef] [PubMed]
- Leach, J.; Yao, E.; Padgett, M. Observation of the vortex structure of a non-integer vortex beam. New J. Phys. 2004, 6, 71. [Google Scholar] [CrossRef]
- Karimi, E.; Zito, G.; Piccirillo, B.; Marrucci, L.; Santamato, E. Hypergeometric-Gaussian modes. Opt. Lett. 2007, 32, 3053–3055. [Google Scholar] [CrossRef] [PubMed]
- Berry, M. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259–268. [Google Scholar] [CrossRef]
- Basistiy, I.; Pas’ko, V.; Slyusar, V.; Soskin, M.; Vasnetsov, M. Synthesis and analysis of optical vortices with fractional topological charges. J. Opt. A Pure Appl. Opt. 2004, 6, S166–S169. [Google Scholar] [CrossRef]
- Bekshaev, A.; Karamoch, A. Spatial characteristics of vortex light beams produced by diffraction gratings with embedded phase singularity. Opt. Commun. 2008, 281, 1366–1374. [Google Scholar] [CrossRef]
- Sephton, B.; Dudley, A.; Forbes, A. Revealing the radial modes in vortex beams. Appl. Opt. 2016, 55, 7830–7835. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khajavi, B.; Ureta, J.R.G.; Galvez, E.J. Determining Vortex-Beam Superpositions by Shear Interferometry. Photonics 2018, 5, 16. https://doi.org/10.3390/photonics5030016
Khajavi B, Ureta JRG, Galvez EJ. Determining Vortex-Beam Superpositions by Shear Interferometry. Photonics. 2018; 5(3):16. https://doi.org/10.3390/photonics5030016
Chicago/Turabian StyleKhajavi, Behzad, Junior R. Gonzales Ureta, and Enrique J. Galvez. 2018. "Determining Vortex-Beam Superpositions by Shear Interferometry" Photonics 5, no. 3: 16. https://doi.org/10.3390/photonics5030016
APA StyleKhajavi, B., Ureta, J. R. G., & Galvez, E. J. (2018). Determining Vortex-Beam Superpositions by Shear Interferometry. Photonics, 5(3), 16. https://doi.org/10.3390/photonics5030016




