Shaping Light in Backward-Wave Nonlinear Hyperbolic Metamaterials
Abstract
1. Introduction
2. Hyperbolic Metamaterials Which Provide Phase Matching of Coupled Guided Contra-Propagating Electromagnetic Waves [16,17,18,19,20,21]
3. Backward-Wave Second Harmonic Generation [2,7,9,19,20,32]
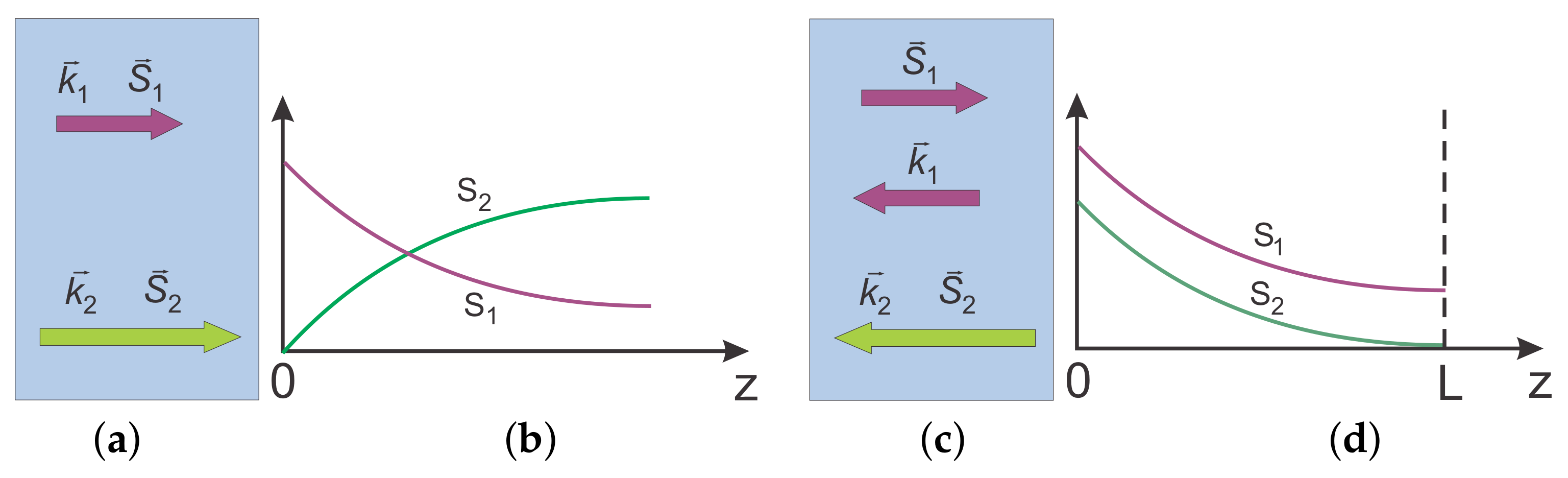
3.1. Continuous Wave Phase-Matched SHG in a Loss-Free Medium: Forward and Backward Waves
3.1.1. SHG in Ordinary NLO Medium
3.1.2. SHG: Backward Fundamental and Forward SH Waves
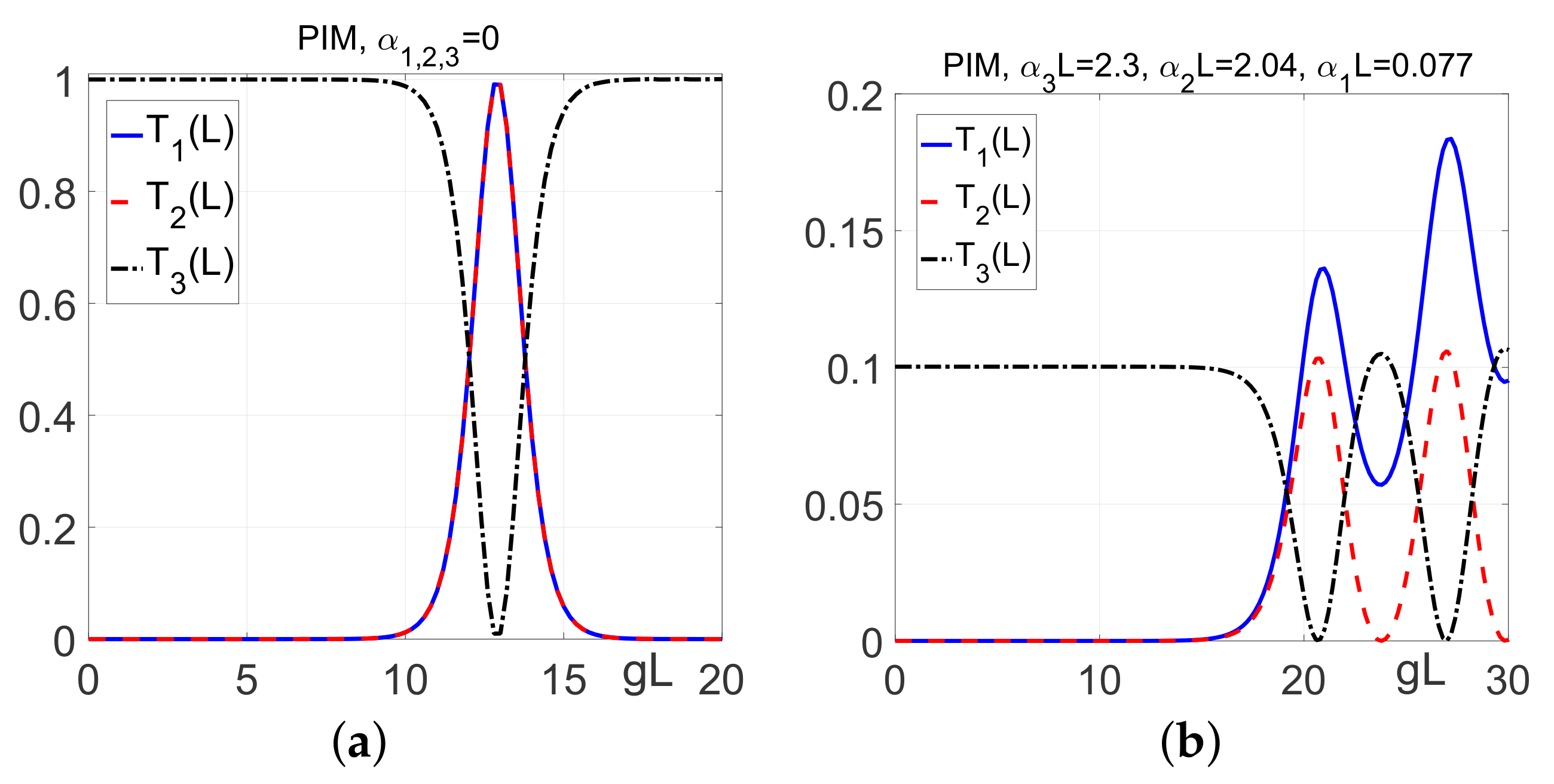
3.1.3. Comparison of SHG for the Cases of Co-Propagating and Contra-Propagating Phase-Matched Waves
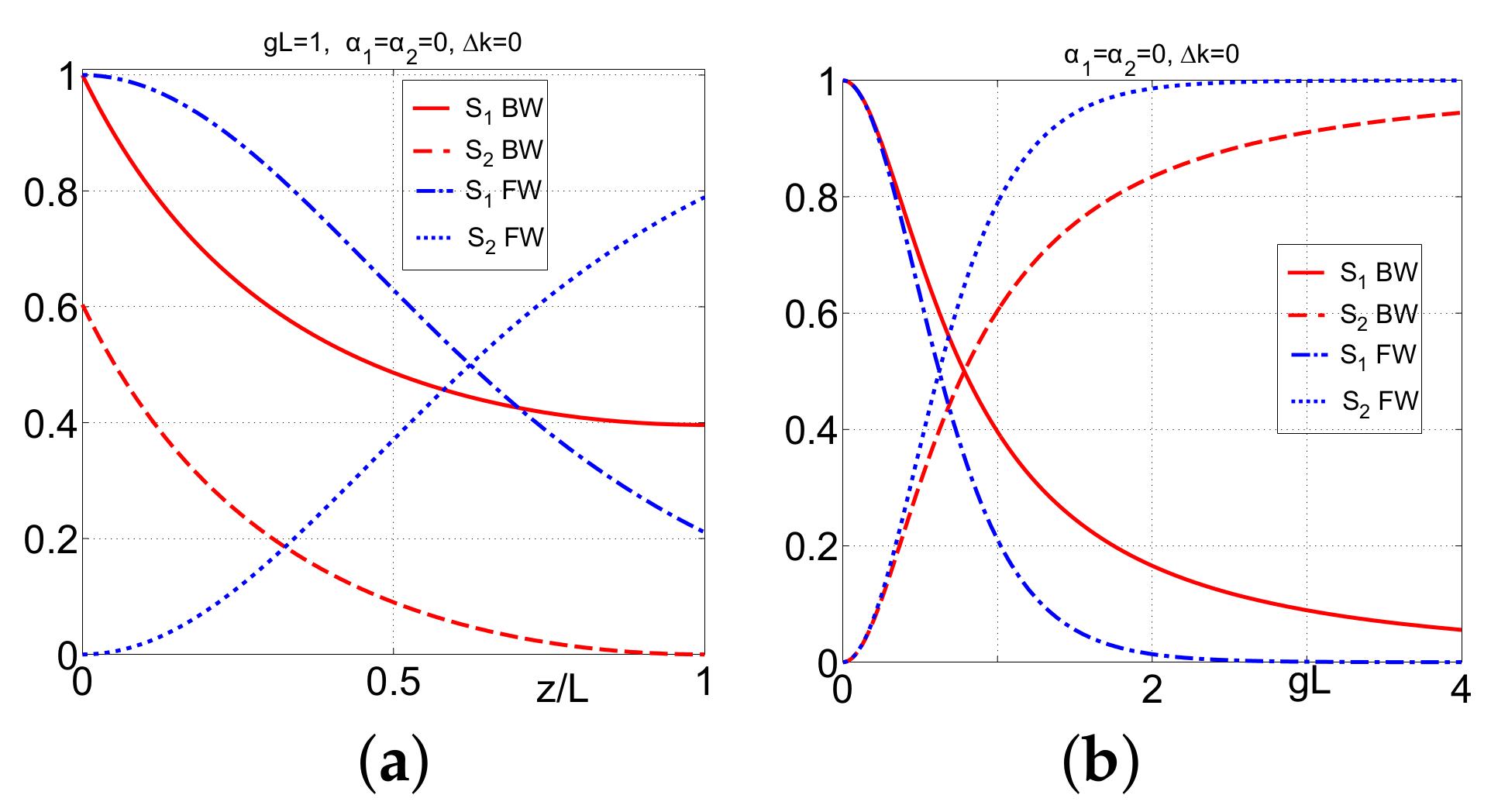
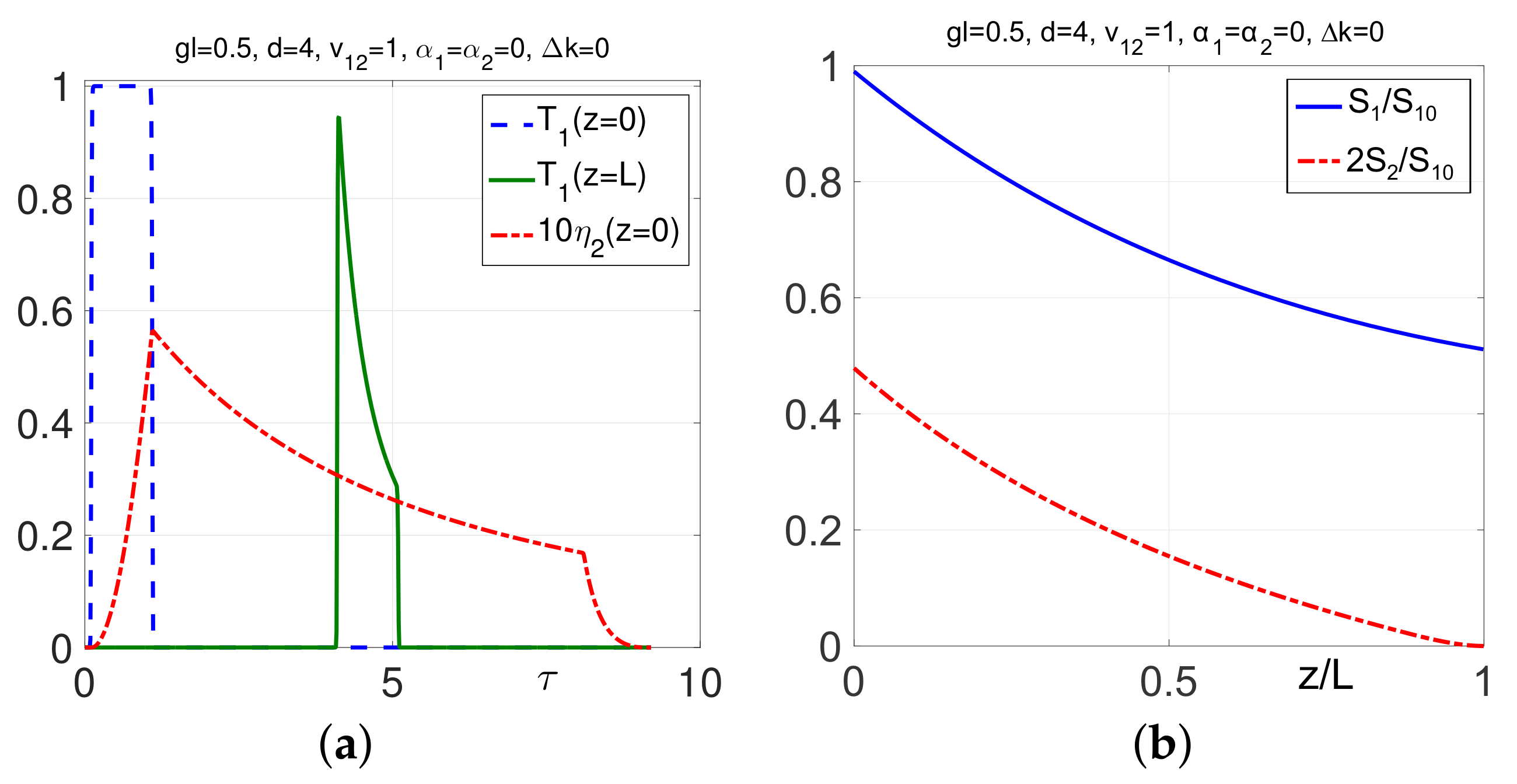
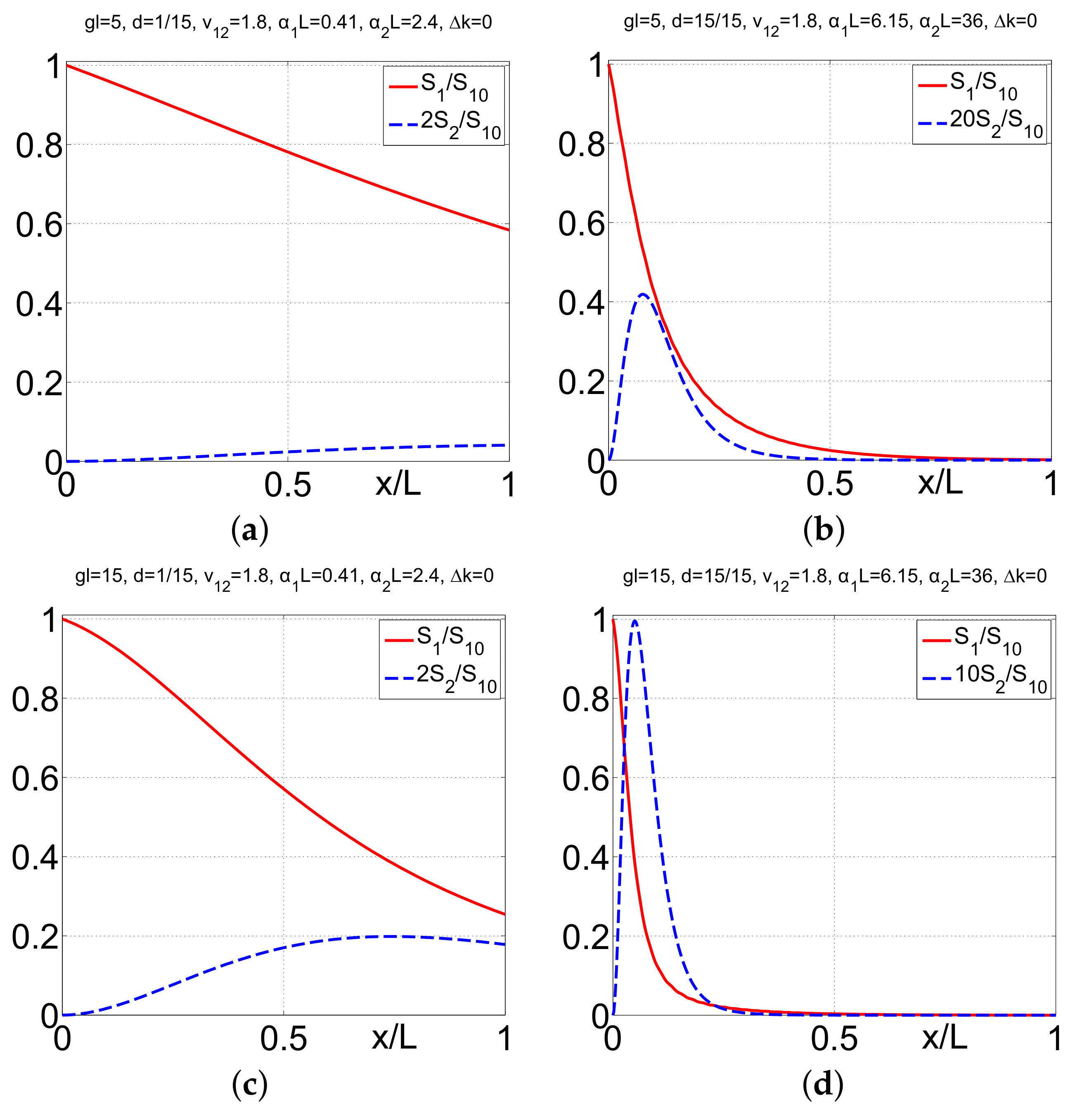
3.2. Pulsed Regime
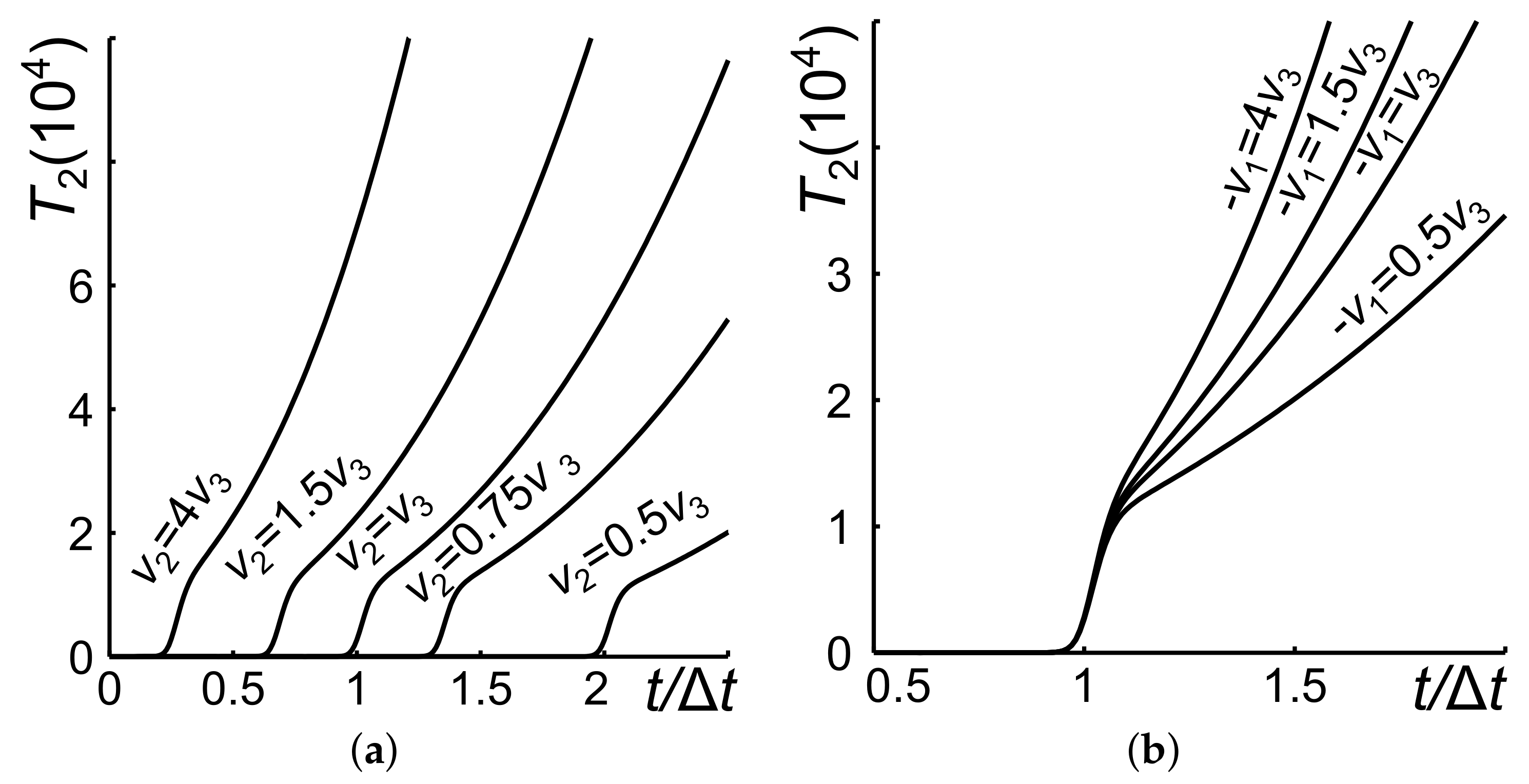
3.3. Comparison of FW and BW SHG in Short-Pulse Regimes
3.4. Backward-Wave Second Harmonic Generation in the Carbon Nanoforest [16,19,20]
4. Backward-Wave Three Wave Mixing: Parametric Amplification, Nonlinear Frequency-Shifting Reflectivity, Transients and Pulse Shaping [2,3,4,21,34,35]
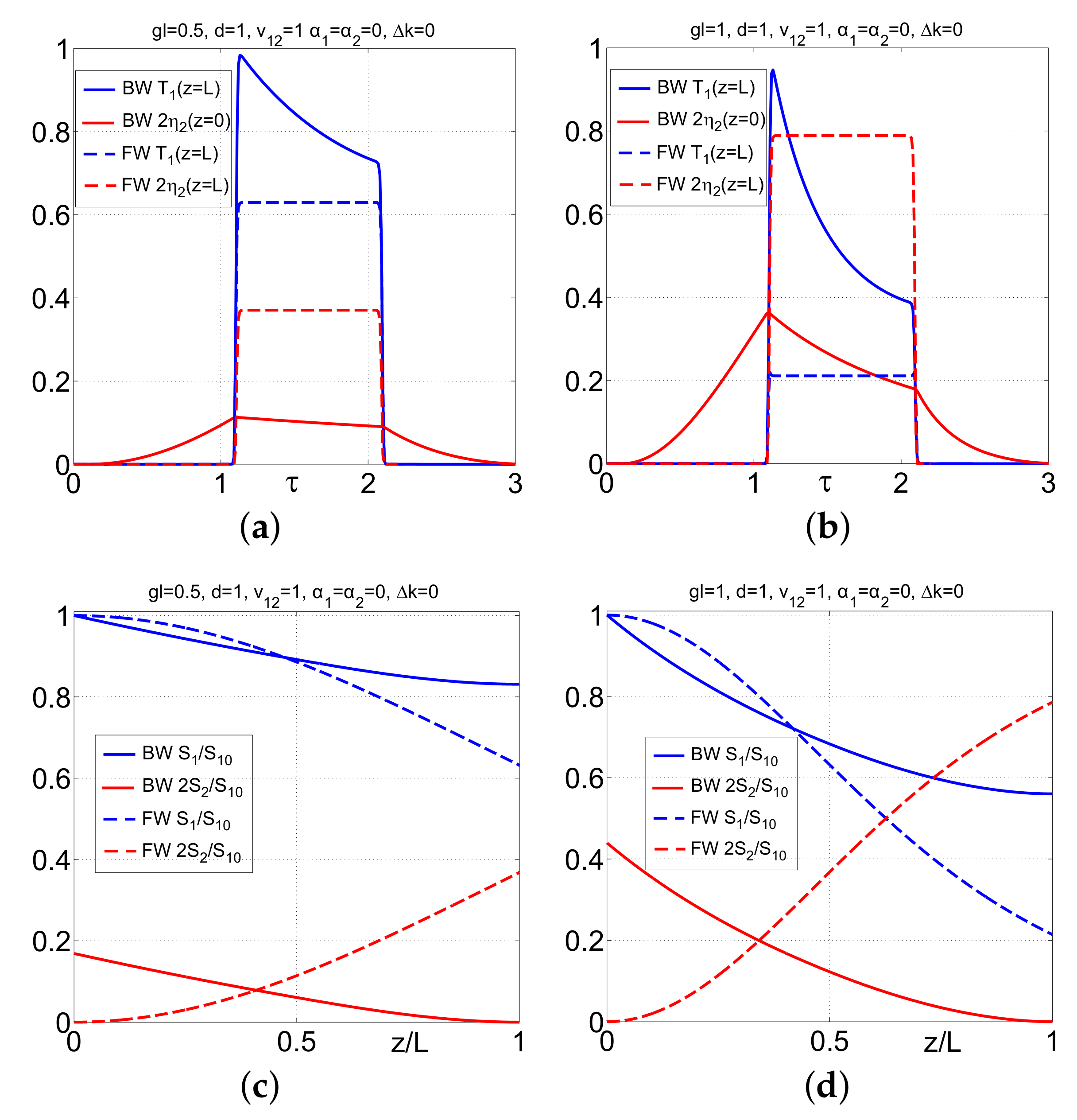
4.1. Three-Wave Mixing of Continuous Electromagnetic Waves: Approximation of Neglected Depletion of Pump Wave
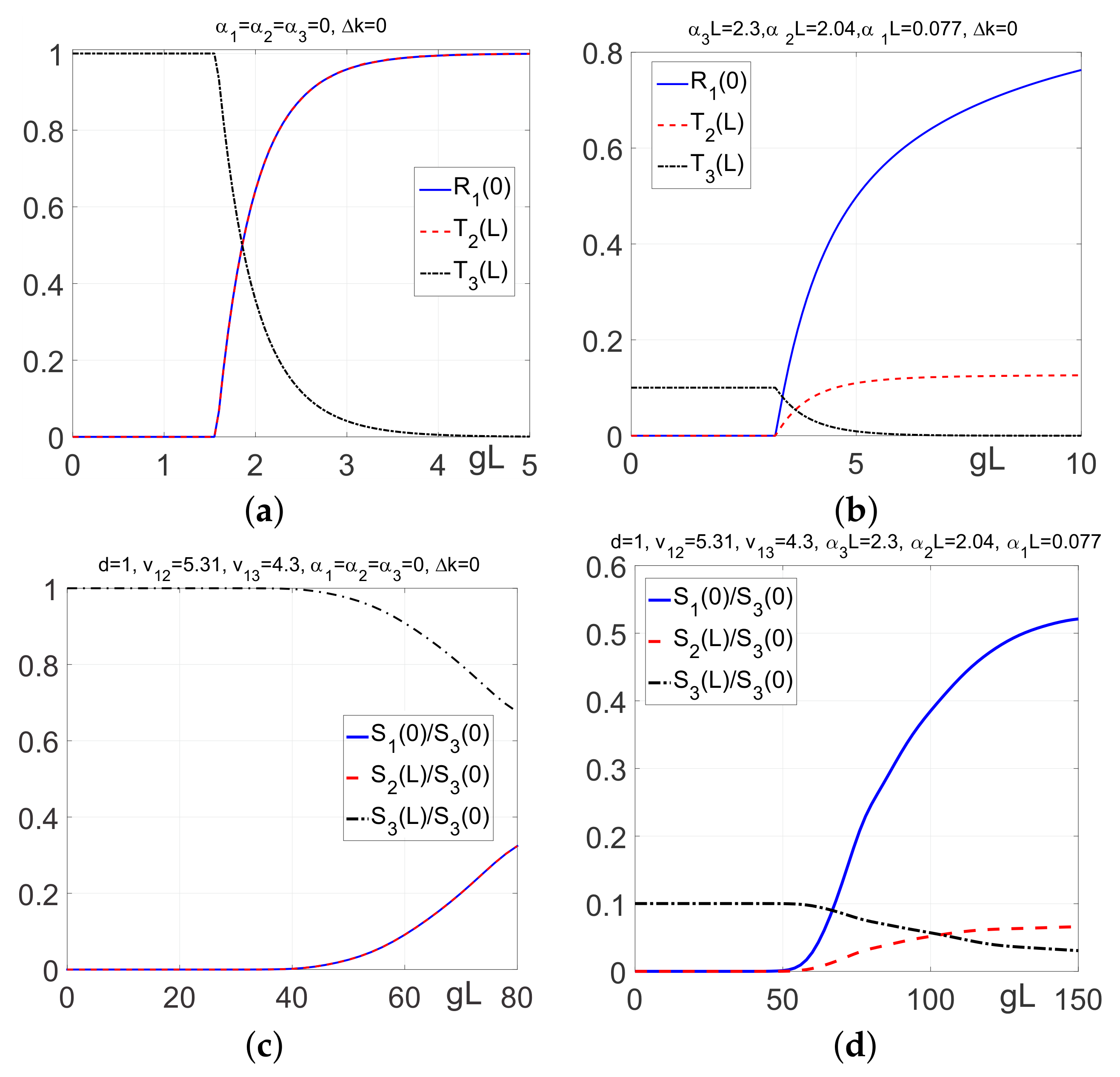
4.1.1. Tailored Transparency, Parametric Amplification and Compensating Optical Losses
4.1.2. Tailored Reflectivity and Nonlinear Optical Metamirror
4.2. Three Alternative Coupling Schemes—Three Sensing Options
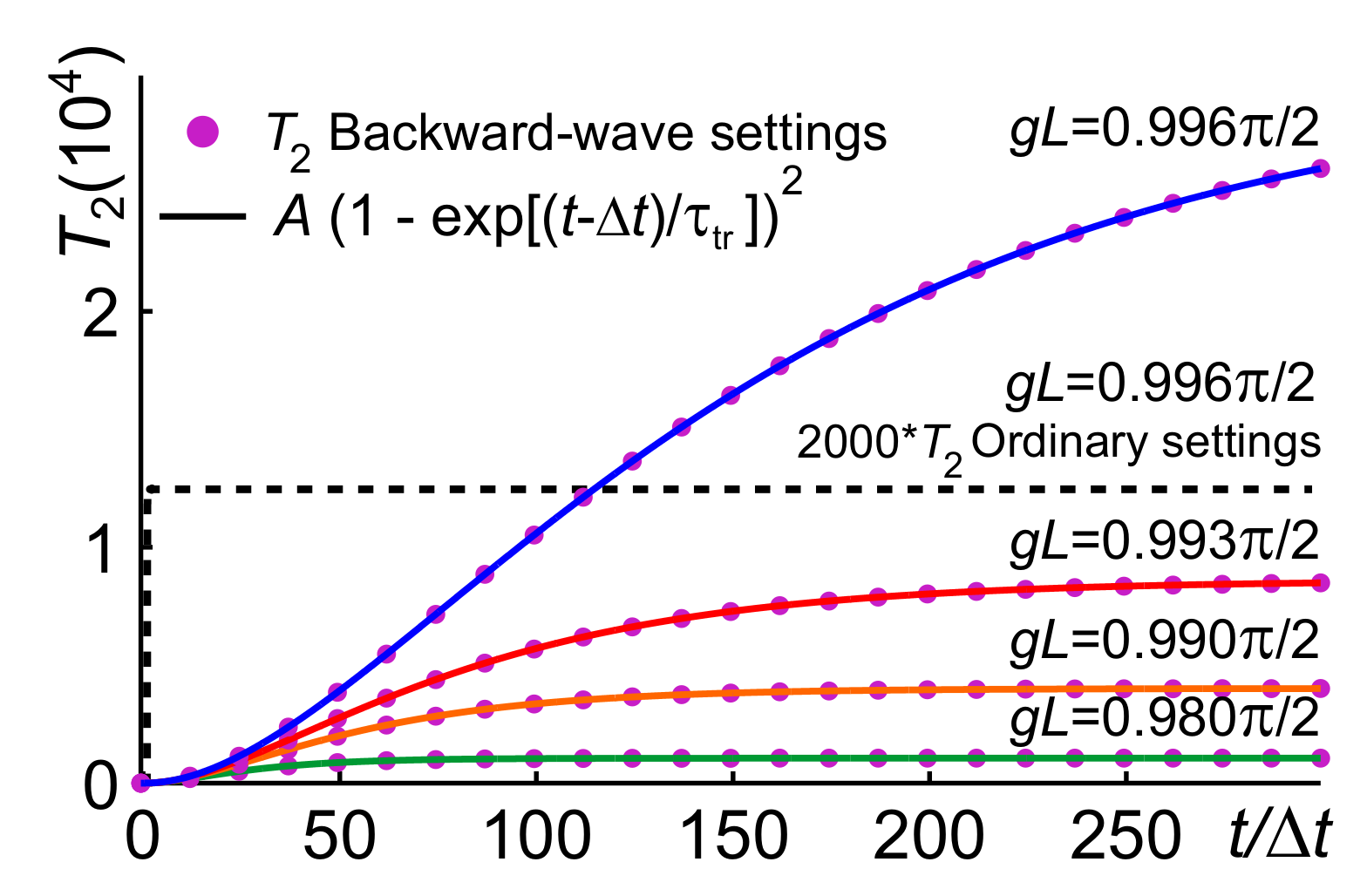
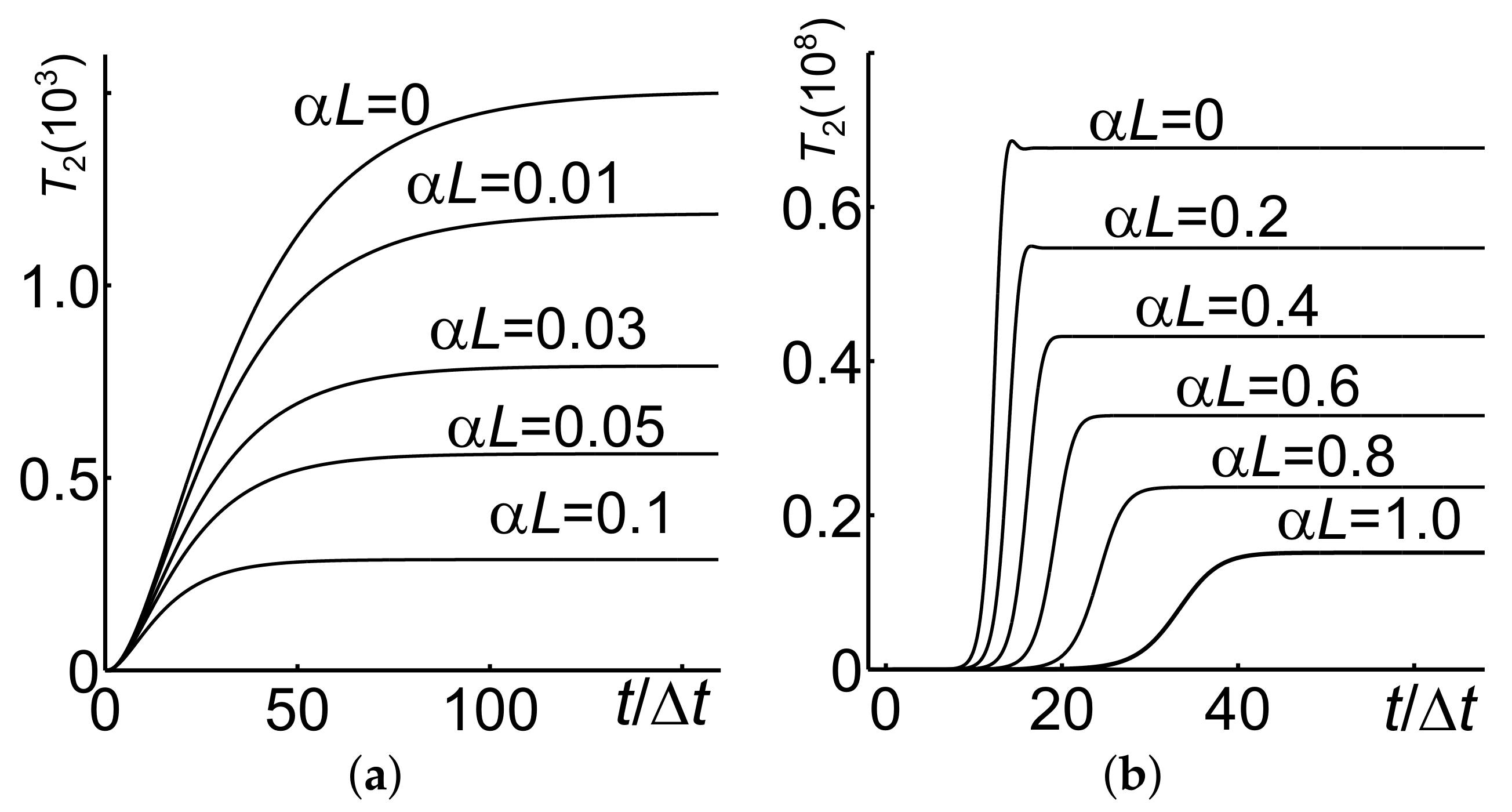
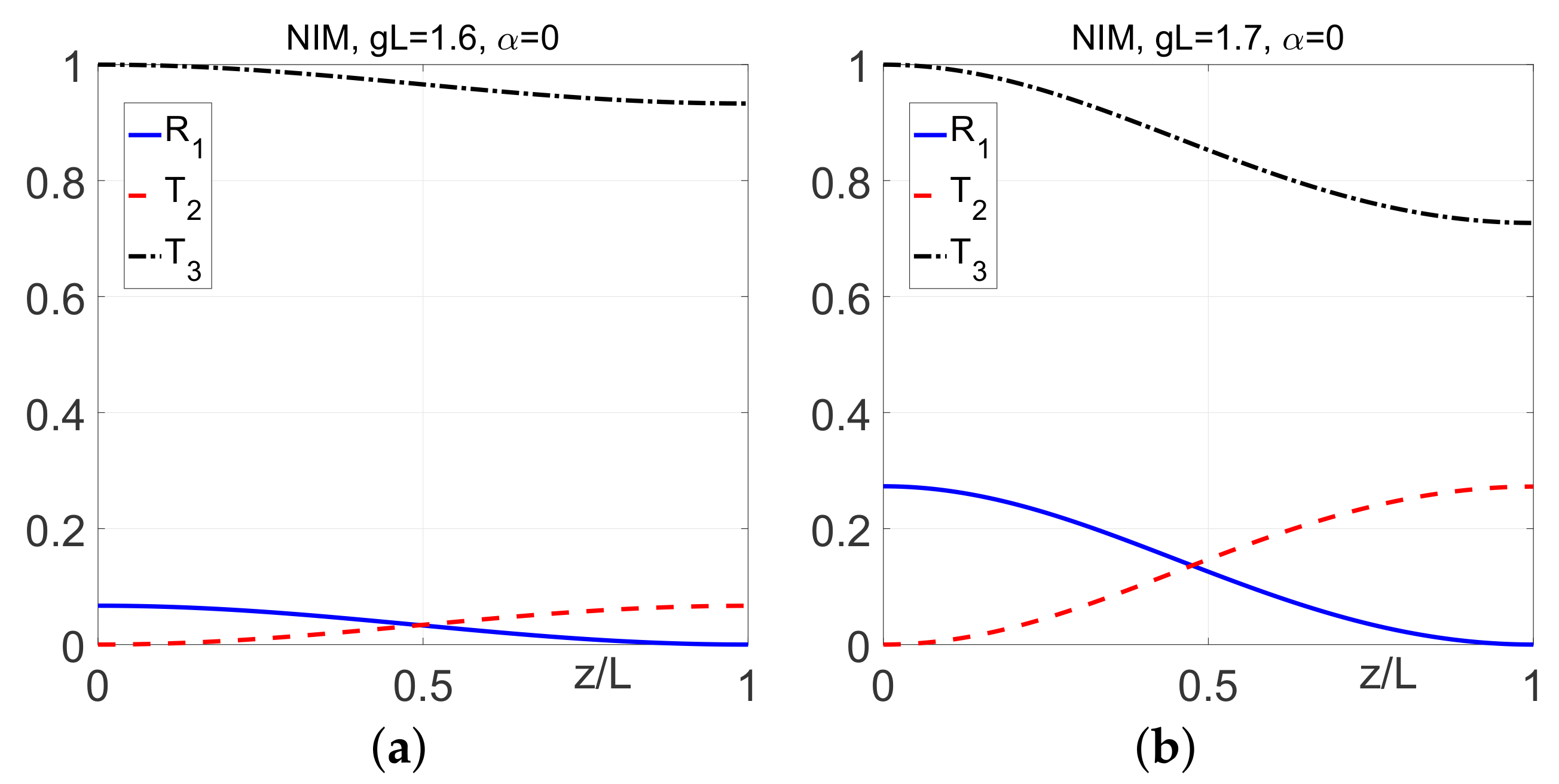
4.3. Parametric Amplification and Nonlinear Reflectivity in the Vicinity of the Critical Pump Intensity: Extraordinary Transients
4.4. Parametric Amplification and Frequency-Shifting Nonlinear Reflectivity in the Carbon Nanoforest [21]
5. Conclusions
Acknowledgments
Conflicts of Interest
Abbreviations
| BW | Backward wave |
| FW | Forward wave |
| MM | Metamaterial |
| FH | First harmonic (fundamental wave) |
| SH | Second harmonic |
| SHG | Second harmonic generation |
| BWSH | Backward wave second harmonic generation |
| TWM | Three-wave mixing |
| BWTWM | Backward-wave three-wave mixing |
| OPA | Optical parametric amplification |
| CW | Continuous wave |
References
- Cai, W.; Shalaev, V. Optical Metamaterials: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Popov, A.K.; Shalaev, V.M. Negative-index metamaterials: Second-harmonic generation, Manley Rowe relations and parametric amplification. Appl. Phys. B 2006, 84, 131–137. [Google Scholar] [CrossRef]
- Popov, A.K.; Shalaev, V.M. Compensating losses in negative-index metamaterials by optical parametric amplification. Opt. Lett. 2006, 31, 2169–2171. [Google Scholar] [CrossRef] [PubMed]
- Slabko, V.V.; Popov, A.K.; Tkachenko, V.A.; Myslivets, S.A. Three-wave mixing of ordinary and backward electromagnetic waves: Extraordinary transients in the nonlinear reflectivity and parametric amplification. Opt. Lett. 2016, 41, 3976–3979. [Google Scholar] [CrossRef] [PubMed]
- Popov, A.K.; Myslivets, S.A.; George, T.F.; Shalaev, V.M. Four-wave mixing, quantum control, and compensating losses in doped negative-index photonic metamaterials. Opt. Lett. 2007, 32, 3044–3046. [Google Scholar] [CrossRef] [PubMed]
- Popov, A.K.; George, T.F. Computational studies of tailored negative-index metamaterials and microdevices. In Computational Studies of New Materials II: From Ultrafast Processes and Nanostructures to Optoelectronics, Energy Storage and Nanomedicine; George, T.F., Jelski, D., Letfullin, R.R., Zhang, G., Eds.; World Scientific: Singapore, 2011; pp. 331–378. [Google Scholar]
- Popov, A.K.; Slabko, V.V.; Shalaev, V.M. Second harmonic generation in left-handed metamaterials. Laser Phys. Lett. 2006, 3, 293–296. [Google Scholar] [CrossRef]
- Kudyshev, Z.; Gabitov, I.; Maimistov, A. Effect of phase mismatch on second-harmonic generation in negative-index materials. Phys. Rev. A 2013, 87, 063840. [Google Scholar] [CrossRef]
- Popov, A.K.; Myslivets, S.A. Second harmonic generation and pulse shaping in positively and negatively spatially dispersive nanowaveguides: Comparative analysis. Opt. Quantum Electron. 2016, 48, 143. [Google Scholar] [CrossRef]
- Ding, Y.J.; Khurgin, J.B. Second-harmonic generation based on quasi-phase matching: A novel configuration. Opt. Lett. 1996, 21, 1445–1447. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.J.; Khurgin, J.B. Backward optical parametric oscillators and amplifiers. IEEE J. Quantum Electron. 1996, 32, 1574–1582. [Google Scholar] [CrossRef]
- Khurgin, J.B. Optical parametric oscillator: Mirrorless magic. Nat. Photonics 2007, 1, 446–447. [Google Scholar] [CrossRef]
- Canalias, C.; Pasiskevicius, V. Mirrorless optical parametric oscillator. Nat. Photonics 2007, 1, 459–462. [Google Scholar] [CrossRef]
- Minor, C.E.; Cudney, R.S. Mirrorless optical parametric oscillation in bulk PPLN and PPLT: A feasibility study. Appl. Phys. B 2017, 123, 38. [Google Scholar] [CrossRef]
- Jang, H.; Viotti, A.L.; Strömqvist, G.; Zukauskas, A.; Canalias, C.; Pasiskevicius, V. Counter-propagating parametric interaction with phonon-polaritons in periodically poled KTiOPO4. Opt. Express 2017, 25, 2677–2686. [Google Scholar] [CrossRef] [PubMed]
- Popov, A.K.; Shalaev, M.I.; Myslivets, S.A.; Slabko, V.V.; Nefedov, I.S. Enhancing coherent nonlinear-optical processes in nonmagnetic backward-wave materials. Appl. Phys. A 2012, 109, 835–840. [Google Scholar] [CrossRef]
- Popov, A.K.; Shalaev, M.I.; Slabko, V.V.; Myslivets, S.A.; Nefedov, I.S. Nonlinear backward-wave photonic metamaterials. Adv. Sci. Technol. 2013, 77, 246–252. [Google Scholar] [CrossRef]
- Popov, A.K.; Slabko, V.V.; Shalaev, M.I.; Nefedov, I.S.; Myslivets, S.A. Nonlinear optics with backward waves: Extraordinary features, materials and applications. Solid State Phenom. 2014, 213, 222–225. [Google Scholar] [CrossRef]
- Popov, A.K.; Nefedov, I.S.; Myslivets, S.A. Phase matched backward-wave second harmonic generation in a hyperbolic carbon nanoforest. arXiv, 2016; arXiv:1602.02497. [Google Scholar]
- Popov, A.K.; Nefedov, I.S.; Myslivets, S.A. Hyperbolic carbon nanoforest for phase matching of ordinary and backward electromagnetic waves: Second harmonic generation. ACS Photonics 2017, 4, 1240–1244. [Google Scholar] [CrossRef]
- Popov, A.K.; Myslivets, S.A. Generation, amplification, frequency conversion, and reversal of propagation of THz photons in nonlinear hyperbolic metamaterial. Opt. Lett. 2017, 42, 4151–4154. [Google Scholar] [CrossRef] [PubMed]
- Agranovich, V.M.; Gartstein, Y.N. Spatial dispersion and negative refraction of light. Phys. Usp. 2006, 49, 1029–1044. [Google Scholar] [CrossRef]
- Agranovich, V.M.; Gartstein, Y.N. Spatial Dispersion, Polaritons, and Negative Refraction. In Physics of Negative Refraction and Negative Index Materials; Krowne, C.M., Zhang, Y., Eds.; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 98, pp. 95–132. [Google Scholar]
- Agranovich, V.M.; Shen, Y.R.; Baughman, R.H.; Zakhidov, A.A. Linear and nonlinear wave propagation in negative refraction metamaterials. Phys. Rev. B 2004, 69, 165112. [Google Scholar] [CrossRef]
- Lindell, I.V.; Tretyakov, S.A.; Nikoskinen, K.I.; Ilvonen, S. BW media—Media with negative parameters, capable of supporting backward waves. Microw. Opt. Technol. Lett. 2001, 31, 129–133. [Google Scholar] [CrossRef]
- Nefedov, I.S. Electromagnetic waves propagating in a periodic array of parallel metallic carbon nanotubes. Phys. Rev. B 2010, 82, 155423. [Google Scholar] [CrossRef]
- Nefedov, I.; Tretyakov, S. Effective medium model for two-dimensional periodic arrays of carbon nanotubes. Photonics Nanostruct. Fundam. Appl. 2011, 9, 374–380. [Google Scholar] [CrossRef]
- Nefedov, I.; Tretyakov, S. Ultrabroadband electromagnetically indefinite medium formed by aligned carbon nanotubes. Phys. Rev. B 2011, 84, 113410. [Google Scholar] [CrossRef]
- Argyropoulos, C.; Estakhri, N.M.; Monticone, F.; Alú, A. Negative refraction, gain and nonlinear effects in hyperbolic metamaterials. Opt. Express 2013, 21, 15037–15047. [Google Scholar] [CrossRef] [PubMed]
- Lapine, M.; Shadrivov, I.V.; Kivshar, Y.S. Colloquium. Nonlinear metamaterials. Rev. Mod. Phys. 2014, 86, 1093–1123. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Popov, A.K.; Myslivets, S.A. Nonlinear-optical frequency-doubling metareflector: pulsed regime. Appl. Phys. A 2016, 122, 39. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Popov, A.K. Frequency-tunable nonlinear-optical negative-index metamirror for sensing applications. Proc. SPIE 2011, 8034, 80340L. [Google Scholar] [CrossRef]
- Popov, A.K. Nonlinear Optics with Backward Waves. In Nonlinear, Tunable and Active Metamaterials; Shadrivov, I.V., Lapine, M., Kivshar, Y.S., Eds.; Springer Series in Materials Science; Preface by J. Pendry; Springer International Publishing: Cham, Switzerland, 2014; Volume 200, pp. 193–215. ISBN 3319083856, 9783319083858. [Google Scholar]
- Harris, S.E. Proposed backward wave oscillation in the infrared. Appl. Phys. Lett. 1966, 9, 114–116. [Google Scholar] [CrossRef]
- Yariv, A. Introduction to Optical Electronics, 2nd ed.; Holt, Rinehart & Winston: New York, NY, USA, 1976. [Google Scholar]
- Volyak, K.I.; Gorshkov, A.S. Investigation of backward-wave parametric generator. Radiotech. Electron. 1973, 18, 2075–2082. (In Russian) [Google Scholar]
- Popov, A.K.; Myslivets, S.A. Nonlinear-optical metamirror. Appl. Phys. A 2011, 103, 725–729. [Google Scholar] [CrossRef]
- Popov, A.K.; Myslivets, S.A. Remote sensing with nonlinear negative-index metamaterials. Proc. SPIE 2014, 9157, 91573B. [Google Scholar]
- Popov, A.; Myslivets, S.; Shalaev, V. Resonant nonlinear optics of backward waves in negative-index metamaterials. Appl. Phys. B 2009, 96, 315–323. [Google Scholar] [CrossRef][Green Version]
- Guler, U.; Boltasseva, A.; Shalaev, V.M. Refractory plasmonics. Science 2014, 344, 263–264. [Google Scholar] [CrossRef] [PubMed]
- Guler, U.; Zemlyanov, D.; Kim, J.; Wang, Z.; Chandrasekar, R.; Meng, X.; Stach, E.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Plasmonics: Plasmonic titanium nitride nanostructures via nitridation of nanopatterned titanium Dioxide. Adv. Opt. Mater. 2017, 5, 1600717. [Google Scholar] [CrossRef]
- Ferrera, M.; Kinsey, N.; Shaltout, A.; DeVault, C.; Shalaev, V.; Boltasseva, A. Dynamic nanophotonics. J. Opt. Soc. Am. B 2017, 34, 95–103. [Google Scholar] [CrossRef]
- Lan, S.; Kang, L.; Schoen, D.T.; Rodrigues, S.P.; Cui, Y.; Brongersma, M.L.; Cai, W. Backward phase-matching for nonlinear optical generation in negative-index materials. Nat. Mater. 2015, 14, 807–811. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zheng, Z.; Cheng, J.; Sun, G.; Qiao, G. Highly efficient second harmonic generation in hyperbolic metamaterial slot waveguides with large phase matching tolerance. Opt. Express 2015, 23, 6370–6378. [Google Scholar] [CrossRef] [PubMed][Green Version]


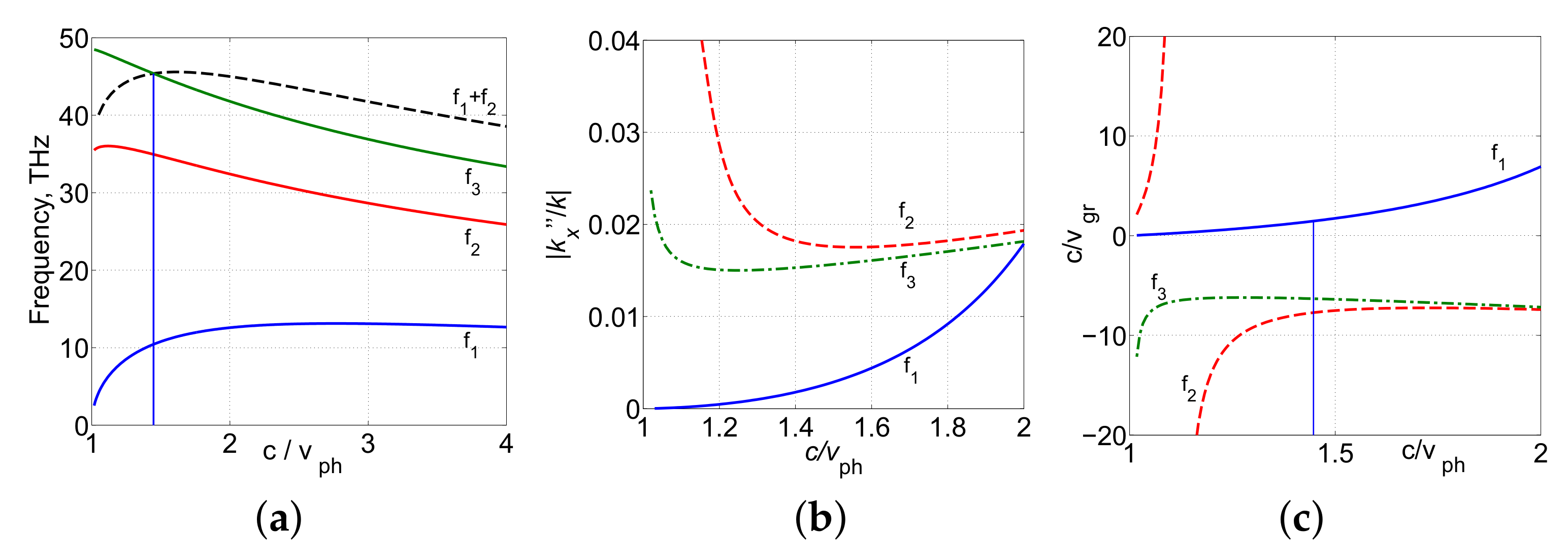






| Mode | f, THz | k, m | , m | , m | , m | , m | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 10.43 | 2.186 | 2.26 | 0.988 | 2331 | 28.74 | 19.86 | |
| 2 | 34.95 | 7.325 | 17.8 | 2.61 | 88.2 | 8.58 | 5.93 | |
| 3 | 45.38 | 9.511 | 15.46 | 2.94 | 78.3 | 6.61 | 4.57 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, A.K.; Myslivets, S.A.; Slabko, V.V.; Tkachenko, V.A.; George, T.F. Shaping Light in Backward-Wave Nonlinear Hyperbolic Metamaterials. Photonics 2018, 5, 8. https://doi.org/10.3390/photonics5020008
Popov AK, Myslivets SA, Slabko VV, Tkachenko VA, George TF. Shaping Light in Backward-Wave Nonlinear Hyperbolic Metamaterials. Photonics. 2018; 5(2):8. https://doi.org/10.3390/photonics5020008
Chicago/Turabian StylePopov, Alexander K., Sergey A. Myslivets, Vitaly V. Slabko, Victor A. Tkachenko, and Thomas F. George. 2018. "Shaping Light in Backward-Wave Nonlinear Hyperbolic Metamaterials" Photonics 5, no. 2: 8. https://doi.org/10.3390/photonics5020008
APA StylePopov, A. K., Myslivets, S. A., Slabko, V. V., Tkachenko, V. A., & George, T. F. (2018). Shaping Light in Backward-Wave Nonlinear Hyperbolic Metamaterials. Photonics, 5(2), 8. https://doi.org/10.3390/photonics5020008






