Two Types of Localized States in a Photonic Crystal Bounded by an Epsilon near Zero Nanocomposite
Abstract
1. Introduction
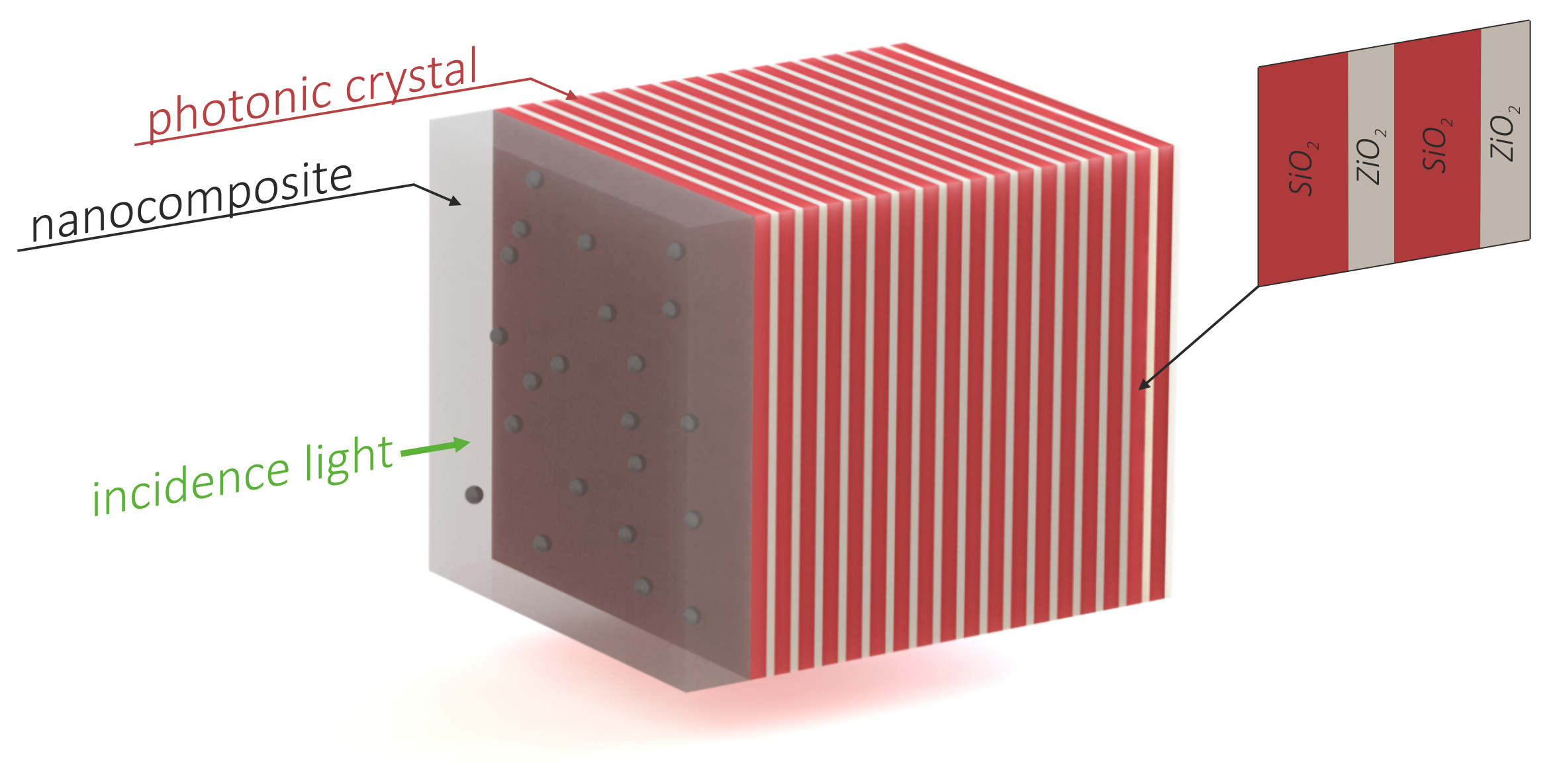
2. Model Description and Determining the Transmittance
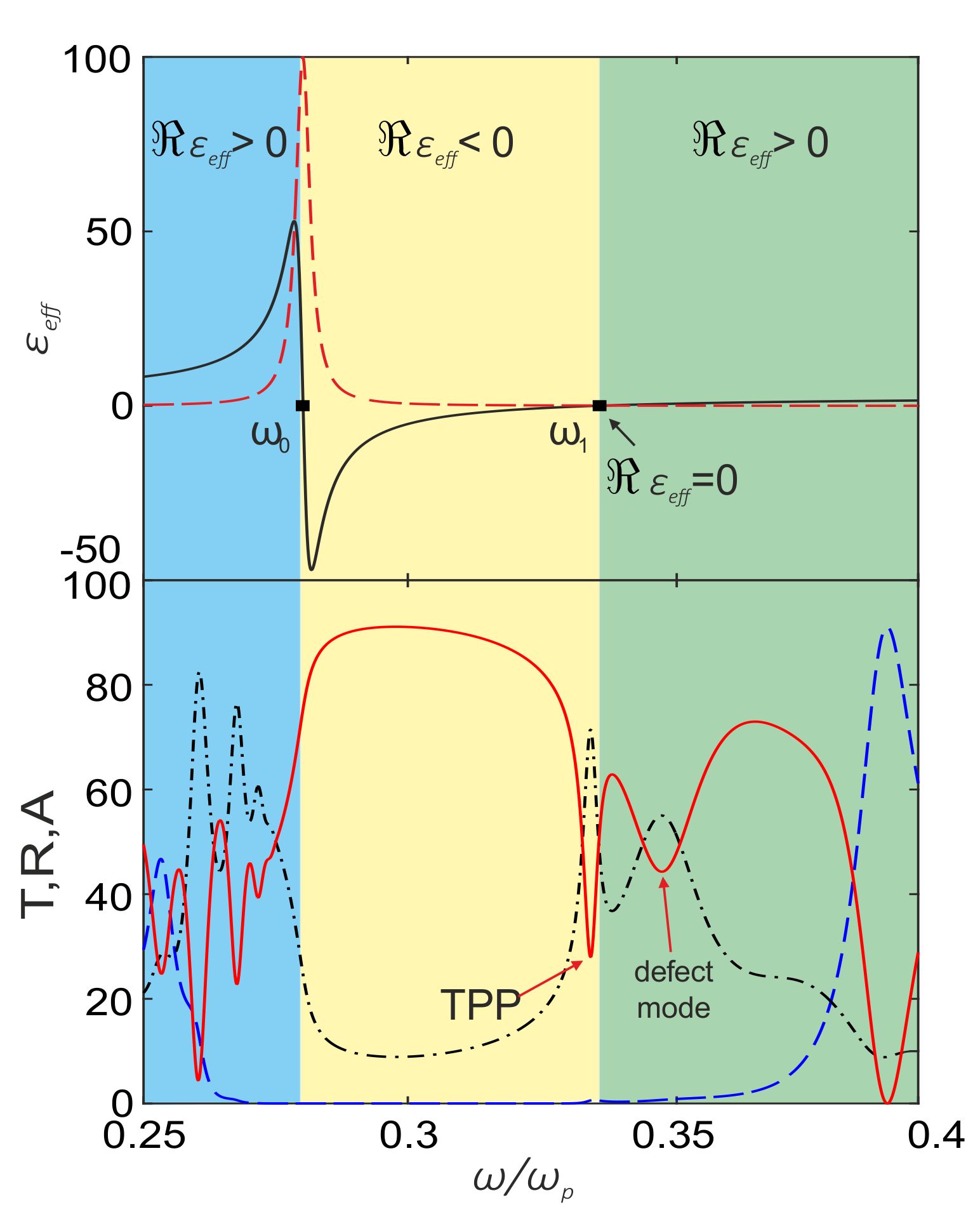
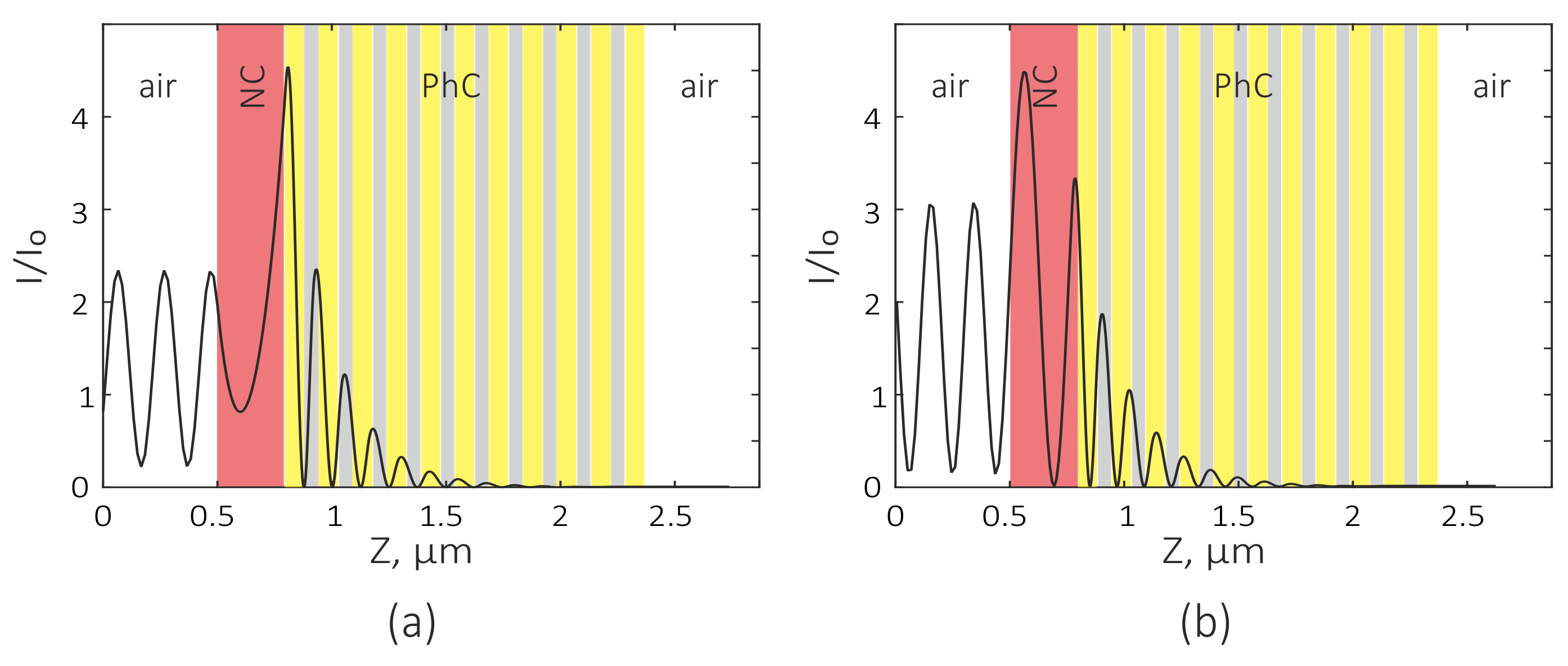
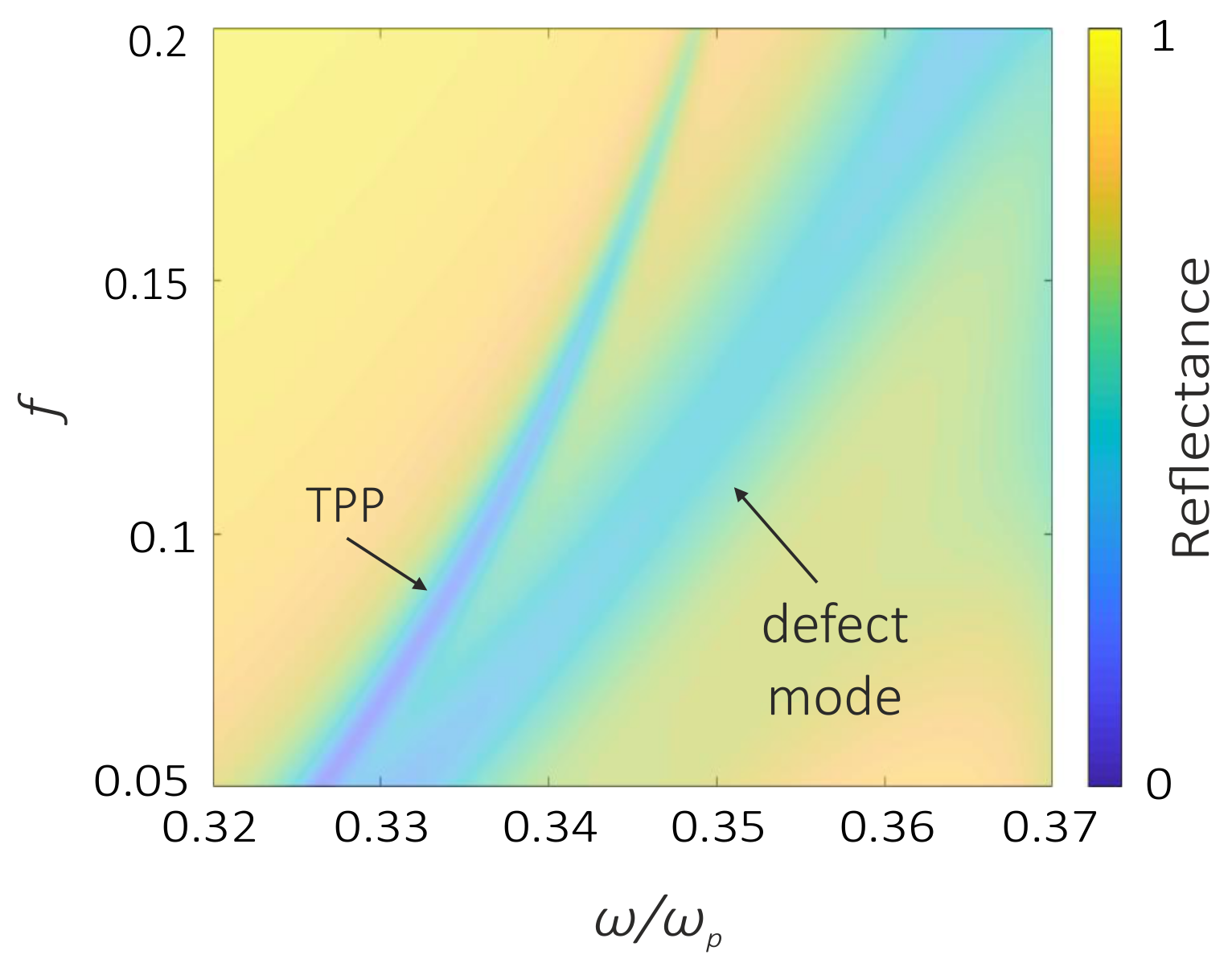
3. Results and Discussion
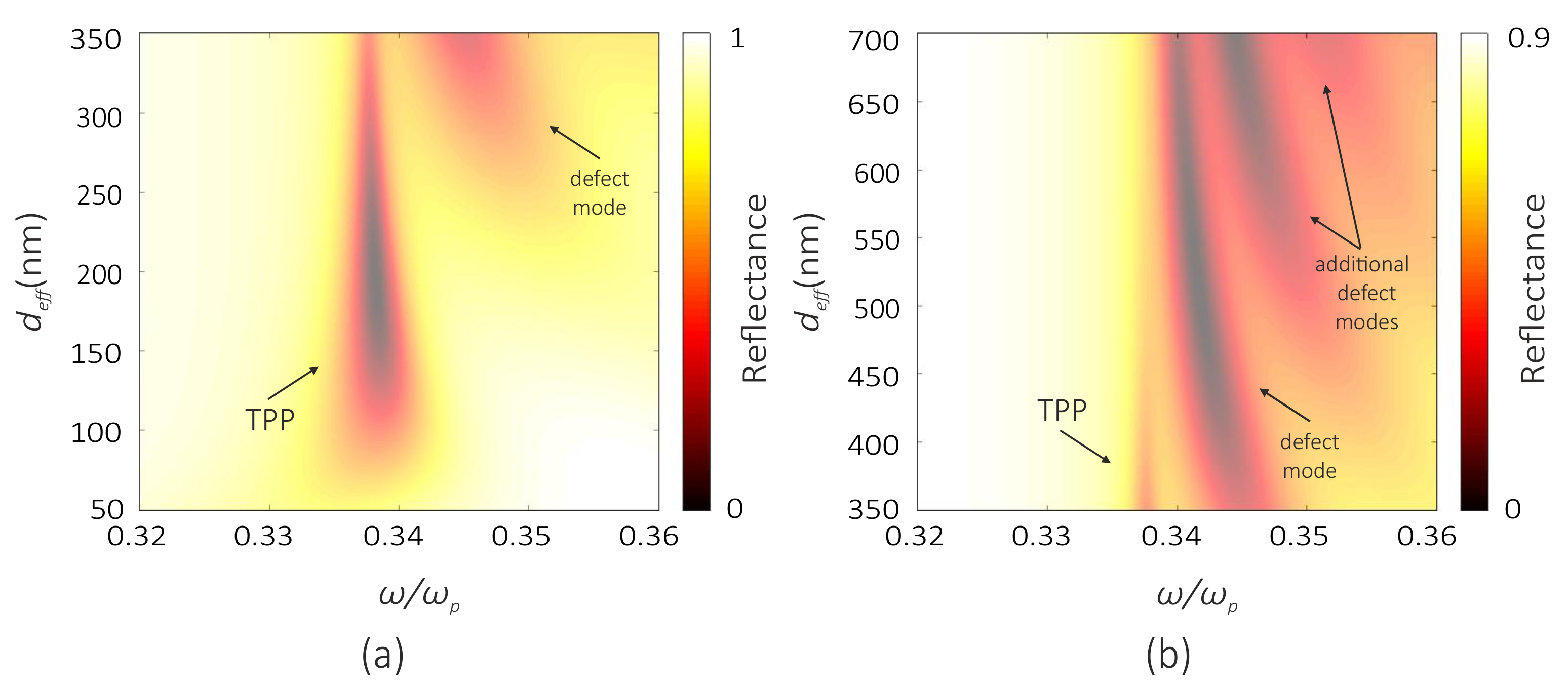
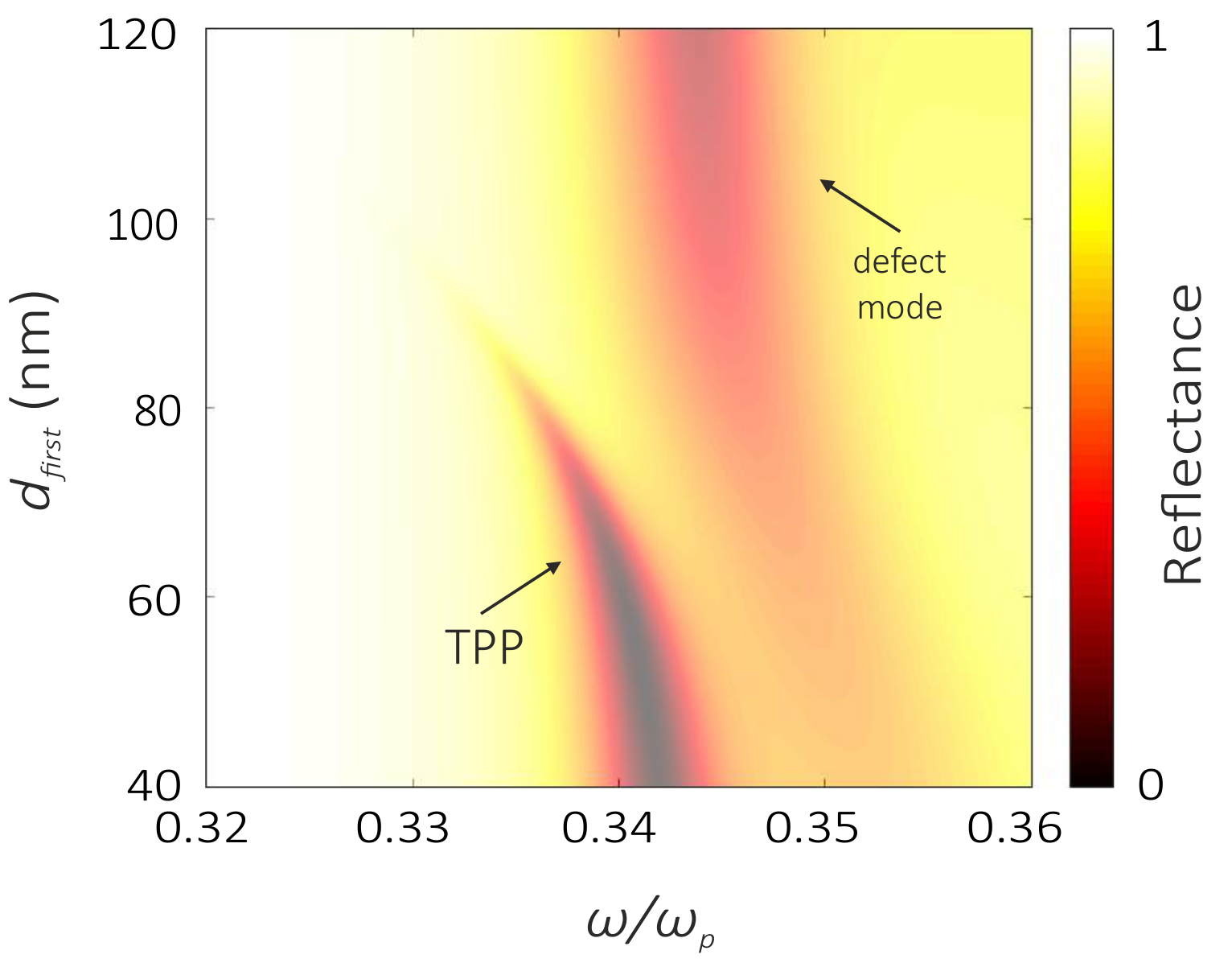
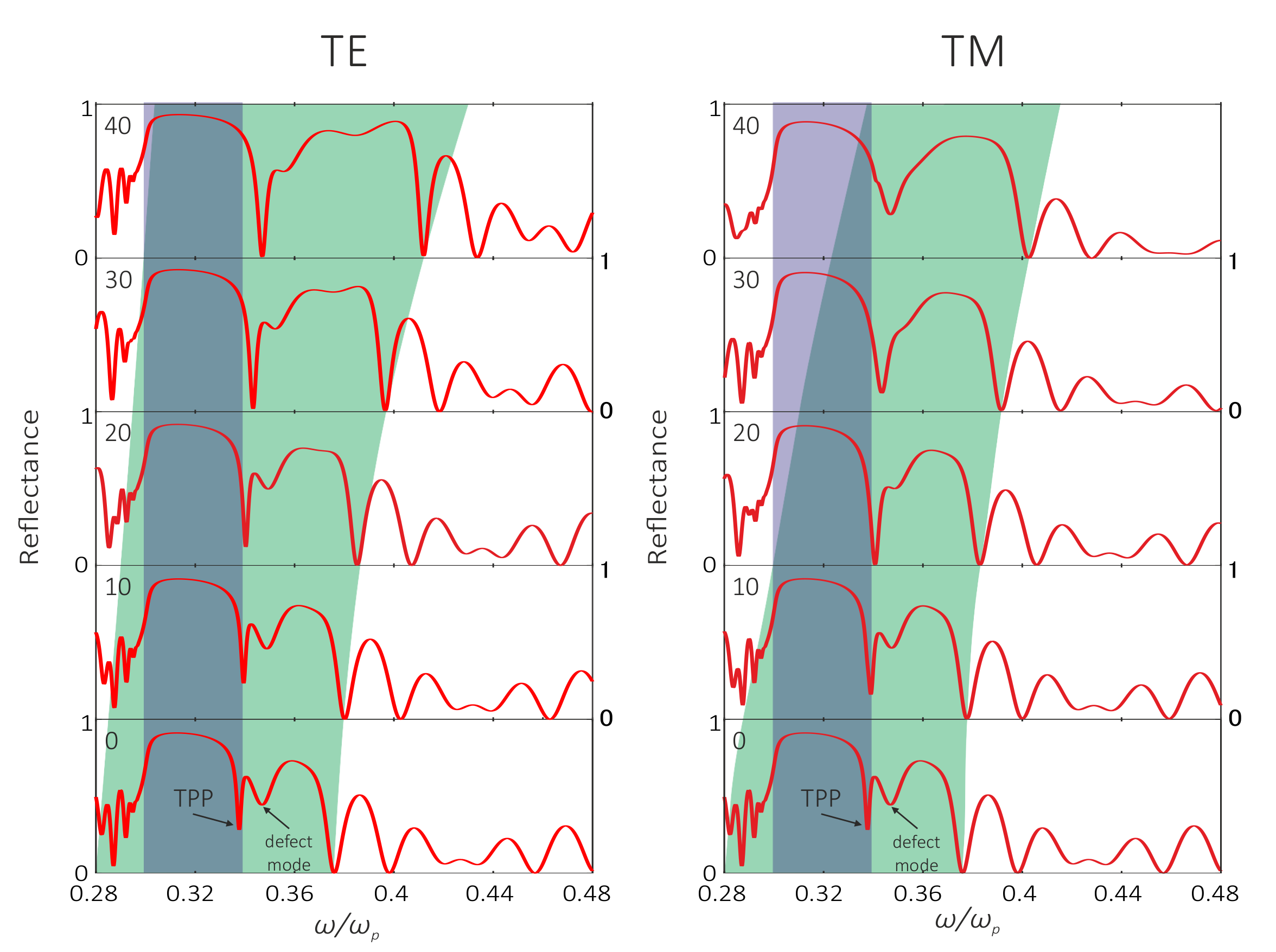
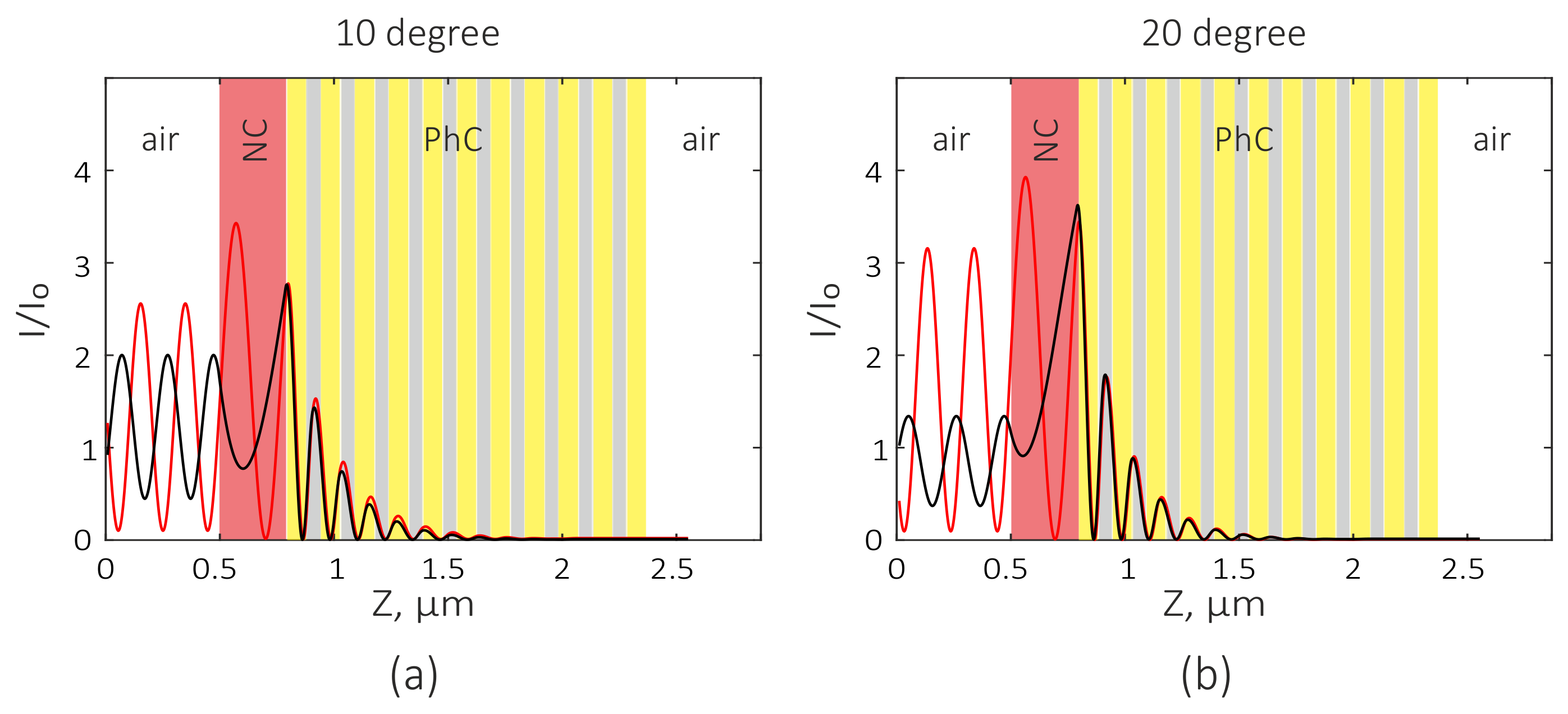
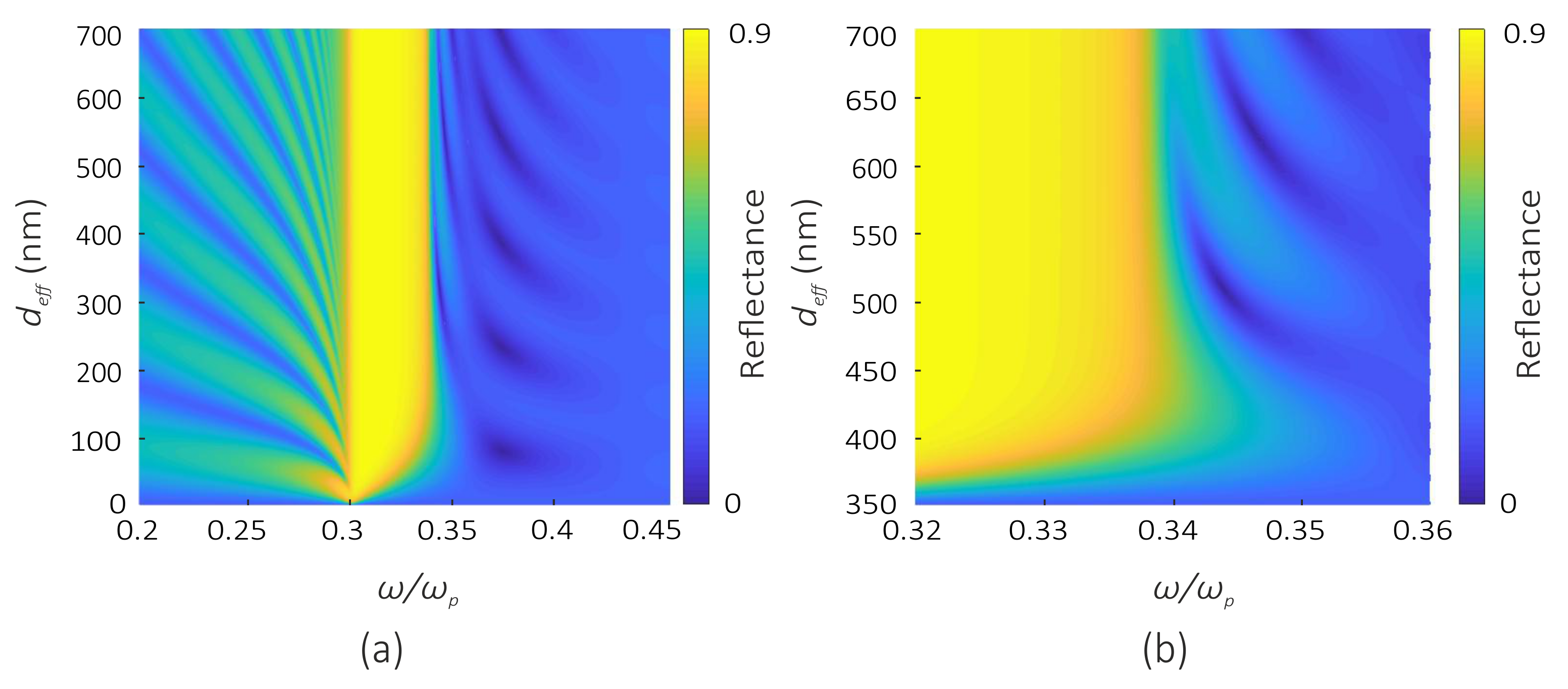
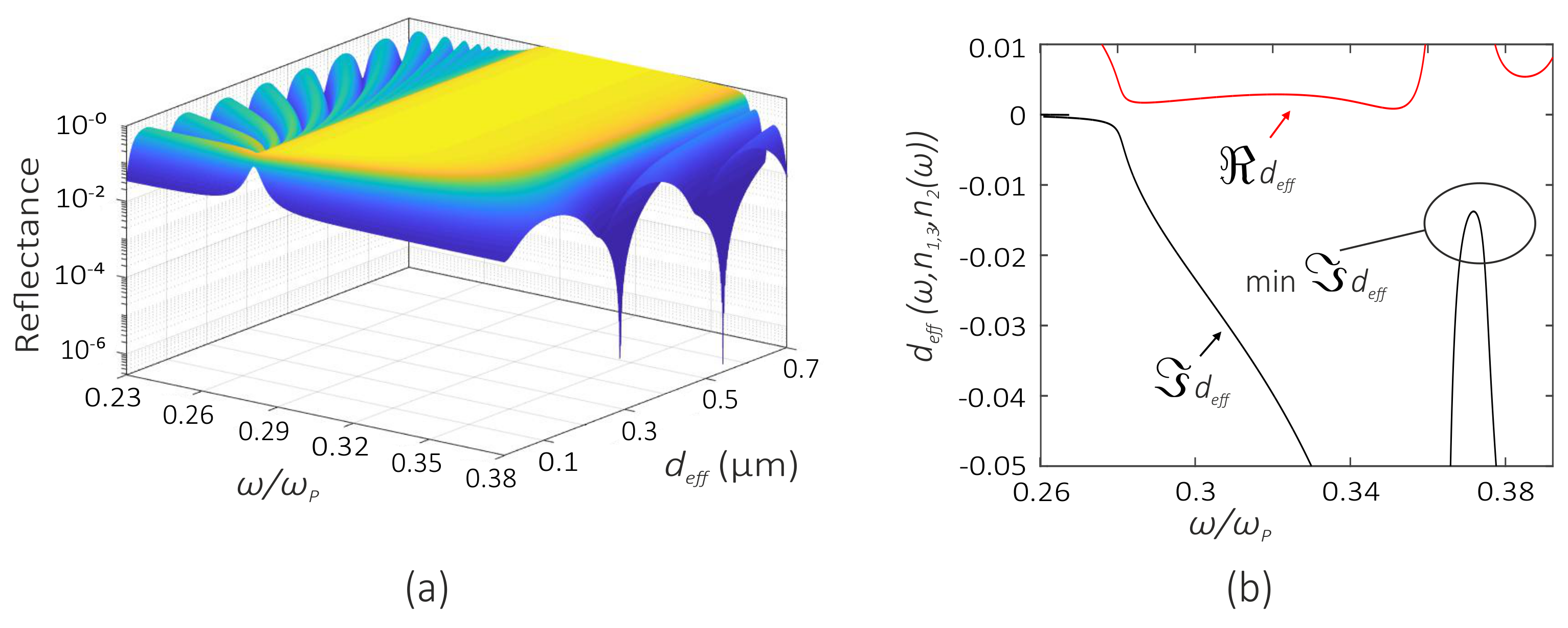
3.1. Fresnel Reflection from a Nanocomposite Film
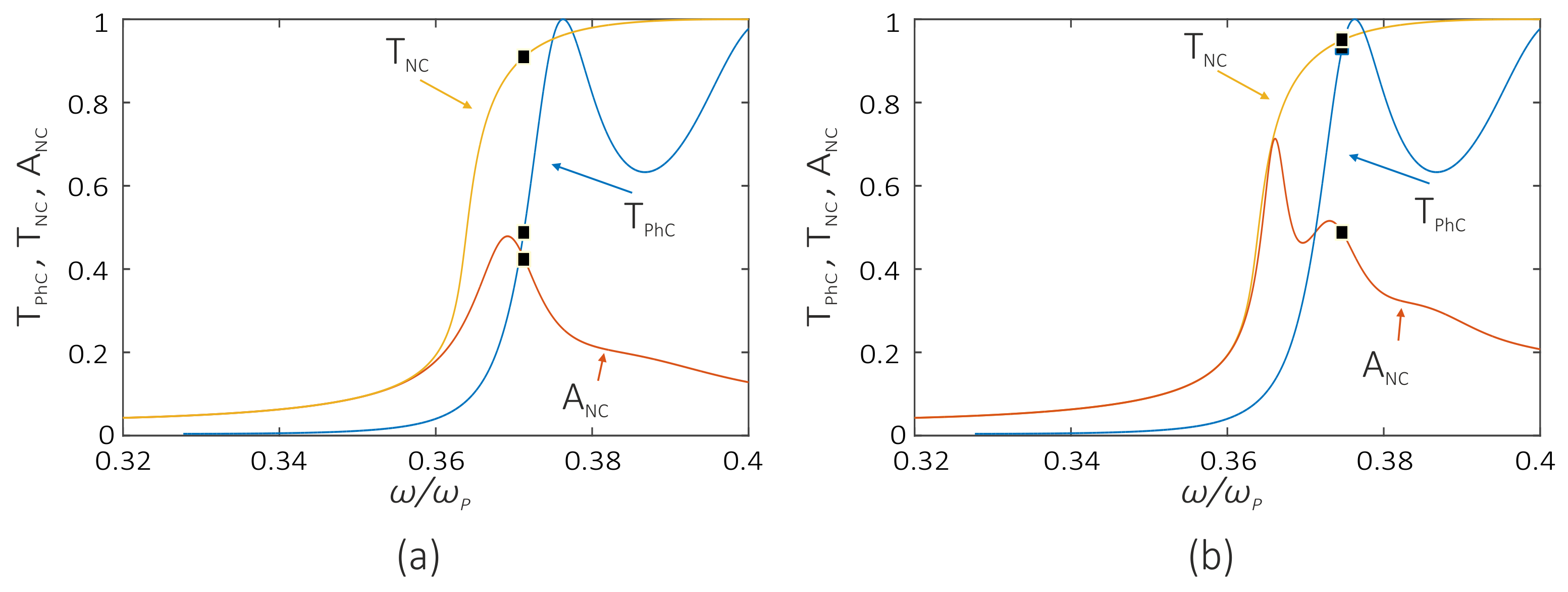
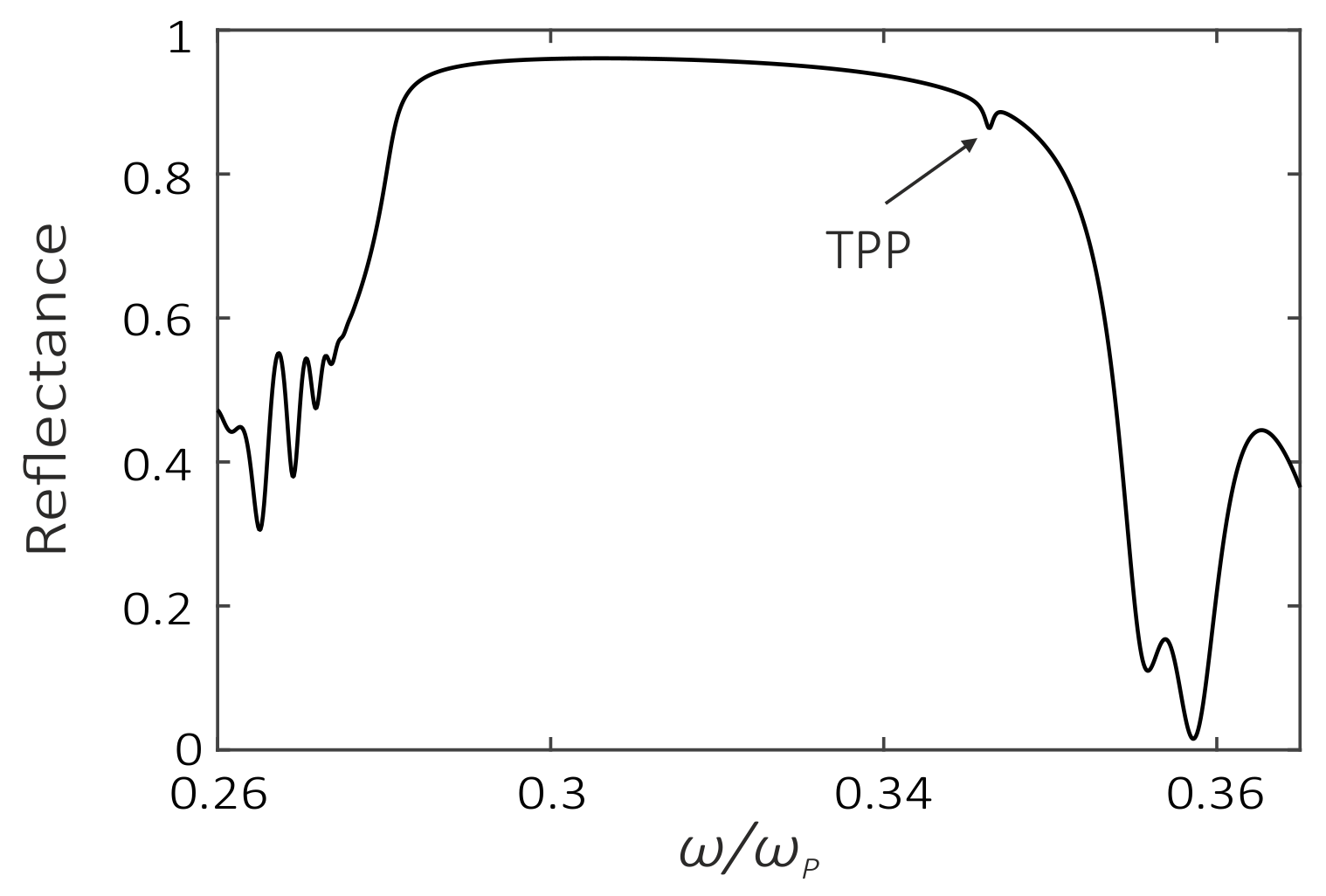
3.2. Coupled Mode Theory
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tamm, I.E. On the possible bound states of electrons on a crystal surface. Phys. Z. Sowjetunion 1932, 1, 733–735. [Google Scholar]
- Kaliteevski, M.A.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef]
- Goto, T.; Dorofeenko, A.V.; Merzlikin, A.M.; Baryshev, A.V.; Vinogradov, A.P.; Inoue, M.; Lisyansky, A.A.; Granovsky, A.B. Optical tamm states in one-dimensional magnetophotonic structures. Phys. Rev. Lett. 2008, 101, 14–16. [Google Scholar] [CrossRef] [PubMed]
- Sasin, M.E.; Seisyan, R.P.; Kaliteevski, M.A.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Egorov, A.Y.; Vasil’ev, A.P.; Mikhrin, V.S.; Kavokin, A.V. Tamm plasmon polaritons: Slow and spatially compact light. Appl. Phys. Lett. 2008, 92, 251112. [Google Scholar] [CrossRef]
- Sasin, M.E.; Seisyan, R.P.; Kaliteevski, M.A.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Iorsh, I.V.; Shelykh, I.A.; Egorov, A.Y.; Vasil’ev, A.P.; et al. Tamm plasmon-polaritons: First experimental observation. Superlatt. Microstruc. 2010, 47, 44–49. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Bikbaev, R.G.; Timofeev, I. Optical Tamm states at the interface between a photonic crystal and a nanocomposite with resonance dispersion. J. Exp. Theor. Phys. 2013, 117, 988–998. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Bikbaev, R.G.; Timofeev, I. The optical Tamm states at the edges of a photonic crystal bounded by one or two layers of a strongly anisotropic nanocomposite. Opt. Commun. 2017, 395, 275–281. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Pankin, P.S.; Timofeev, I. The optical Tamm states at the interface between a photonic crystal and a nanocomposite containing core–shell particles. J. Opt. 2016, 18, 065106. [Google Scholar] [CrossRef][Green Version]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I. The optical Tamm states at the interface between a photonic crystal and nanoporous silver. J. Opt. 2017, 19, 015104. [Google Scholar] [CrossRef]
- Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I. Optical Tamm states at the interface between a photonic crystal and a gyroid layer. J. Opt. Soc. Am. B 2017, 34, 2198–2202. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, X.; Wang, L.; Lu, H.; Wang, G. Multiple responses of TPP-assisted near-perfect absorption in metal/Fibonacci quasiperiodic photonic crystal. Opt. Express 2011, 19, 9759–9769. [Google Scholar] [CrossRef] [PubMed]
- Gong, Y.; Liu, X.; Lu, H.; Wang, L.; Wang, G. Perfect absorber supported by optical Tamm states in plasmonic waveguide. Opt. Express 2011, 19, 18393–18398. [Google Scholar] [CrossRef] [PubMed]
- Fang, M.; Shi, F.; Chen, Y. Unidirectional All-Optical Absorption Switch Based on Optical Tamm State in Nonlinear Plasmonic Waveguide. Plasmonics 2016, 11, 197–203. [Google Scholar] [CrossRef]
- Xue, C.H.; Wu, F.; Jiang, H.T.; Li, Y.; Zhang, Y.W.; Chen, H. Wide-angle Spectrally Selective Perfect Absorber by Utilizing Dispersionless Tamm Plasmon Polaritons. Sci. Rep. 2016, 6, 39418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Yu, S. Bistable switching using an optical Tamm cavity with a Kerr medium. Opt. Commun. 2010, 283, 2622–2626. [Google Scholar] [CrossRef]
- Zhang, X.L.; Song, J.F.; Li, X.B.; Feng, J.; Sun, H.B. Optical Tamm states enhanced broad-band absorption of organic solar cells. Appl. Phys. Lett. 2012, 101, 243901. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Ishii, S.; Yokoyama, T.; Dao, T.D.; Sun, M.G.; Nagao, T.; Chen, K.P. Tamm plasmon selective thermal emitters. Opt. Lett. 2016, 41, 4453–4456. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.Y.; Ishii, S.; Yokoyama, T.; Dao, T.D.; Sun, M.G.; Pankin, P.S.; Timofeev, I.; Nagao, T.; Chen, K.P. Narrowband Wavelength Selective Thermal Emitters by Confined Tamm Plasmon Polaritons. ACS Photonics 2017, 4, 2212–2219. [Google Scholar] [CrossRef]
- Huang, S.G.; Chen, K.P.; Jeng, S.C. Phase sensitive sensor on Tamm plasmon devices. Opt. Mater. Express 2017, 7, 1267–1273. [Google Scholar] [CrossRef]
- Auguié, B.; Fuertes, M.C.; Angelomé, P.C.; Abdala, N.L.; Soler Illia, G.J.A.A.; Fainstein, A. Tamm Plasmon Resonance in Mesoporous Multilayers: Toward a Sensing Application. ACS Photonics 2014, 1, 775–780. [Google Scholar] [CrossRef]
- Kumar, S.; Shukla, M.K.; Maji, P.S.; Das, R. Self-referenced refractive index sensing with hybrid-Tamm-plasmon-polariton modes in sub-wavelength analyte layers. J. Phys. D Appl. Phys. 2017, 50, 375106. [Google Scholar] [CrossRef]
- Gubaydullin, A.R.; Symonds, C.; Bellessa, J.; Ivanov, K.A.; Kolykhalova, E.D.; Sasin, M.E.; Lemaitre, A.; Senellart, P.; Pozina, G.; Kaliteevski, M.A. Enhancement of spontaneous emission in Tamm plasmon structures. Sci. Rep. 2017, 7, 9014. [Google Scholar] [CrossRef] [PubMed]
- Vinogradov, A.P.; Dorofeenko, A.V.; Erokhin, S.G.; Inoue, M.; Lisyansky, A.A.; Merzlikin, A.M.; Granovsky, A.B. Surface state peculiarities in one-dimensional photonic crystal interfaces. Phys. Rev. B 2006, 74, 045128. [Google Scholar] [CrossRef]
- Xue, C.H.; Jiang, H.T.; Lu, H.; Du, G.Q.; Chen, H. Efficient third-harmonic generation based on Tamm plasmon polaritons. Opt. Lett. 2013, 38, 959–961. [Google Scholar] [CrossRef] [PubMed]
- Afinogenov, B.I.; Bessonov, V.O.; Fedyanin, A.A. Second-harmonic generation enhancement in the presence of Tamm plasmon-polaritons. Opt. Lett. 2014, 39, 6895–6898. [Google Scholar] [CrossRef] [PubMed]
- Treshin, I.V.; Klimov, V.V.; Melentiev, P.N.; Balykin, V.I. Optical Tamm state and extraordinary light transmission through a nanoaperture. Phys. Rev. A 2013, 88, 023832. [Google Scholar] [CrossRef]
- Symonds, C.; Lheureux, G.; Hugonin, J.P.; Greffet, J.J.; Laverdant, J.; Brucoli, G.; Lemaitre, A.; Senellart, P.; Bellessa, J. Confined Tamm Plasmon Lasers. Nano Lett. 2013, 13, 3179–3184. [Google Scholar] [CrossRef] [PubMed]
- Symonds, C.; Lemaître, A.; Senellart, P.; Jomaa, M.H.; Aberra Guebrou, S.; Homeyer, E.; Brucoli, G.; Bellessa, J. Lasing in a hybrid GaAs/silver Tamm structure. Appl. Phys. Lett. 2012, 100, 121122. [Google Scholar] [CrossRef]
- Dyer, G.C.; Aizin, G.R.; Allen, S.J.; Grine, A.D.; Bethke, D.; Reno, J.L.; Shaner, E.A. Induced transparency by coupling of Tamm and defect states in tunable terahertz plasmonic crystals. Nat. Photonics 2013, 7, 925–930. [Google Scholar] [CrossRef]
- Gazzano, O.; Michaelis de Vasconcellos, S.; Gauthron, K.; Symonds, C.; Voisin, P.; Bellessa, J.; Lemaître, A.; Senellart, P. Single photon source using confined Tamm plasmon modes. Appl. Phys. Lett. 2012, 100, 232111. [Google Scholar] [CrossRef]
- Gessler, J.; Baumann, V.; Emmerling, M.; Amthor, M.; Winkler, K.; Höfling, S.; Schneider, C.; Kamp, M. Electro optical tuning of Tamm-plasmon exciton-polaritons. Appl. Phys. Lett. 2014, 105, 181107. [Google Scholar] [CrossRef]
- Timofeev, I.V.; Arkhipkin, V.G.; Vetrov, S.Y.; Zyryanov, V.Y.; Lee, W. Enhanced light absorption with a cholesteric liquid crystal layer. Opt. Mater. Express 2013, 3, 496–501. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Pyatnov, M.V.; Timofeev, I. Surface modes in “photonic cholesteric liquid crystal–phase plate–metal” structure. Opt. Lett. 2014, 39, 2743–2746. [Google Scholar] [CrossRef] [PubMed]
- Timofeev, I.; Vetrov, S.Y. Chiral optical Tamm states at the boundary of the medium with helical symmetry of the dielectric tensor. JETP Lett. 2016, 104, 380–383. [Google Scholar] [CrossRef]
- Rudakova, N.V.; Timofeev, I.; Pankin, P.S.; Vetrov, S.Y. Polarization-preserving anisotropic mirror on the basis of metal–dielectric nanocomposite. Bull. Russ. Acad. Sci. Phys. 2017, 81, 5–9. [Google Scholar] [CrossRef]
- Alù, A.; Silveirinha, M.G.; Salandrino, A.; Engheta, N. Epsilon-near-zero metamaterials and electromagnetic sources: Tailoring the radiation phase pattern. Phys. Rev. B 2007, 75, 155410. [Google Scholar] [CrossRef]
- Inampudi, S.; Adams, D.C.; Ribaudo, T.; Slocum, D.; Vangala, S.; Goodhue, W.D.; Wasserman, D.; Podolskiy, V.A. Epsilon-near-zero enhanced light transmission through a subwavelength slit. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Ciattoni, A.; Rizza, C.; Marini, A.; Di Falco, A.; Faccio, D.; Scalora, M. Enhanced nonlinear effects in pulse propagation through epsilon-near-zero media. Laser Photonics Rev. 2016, 10, 517–525. [Google Scholar] [CrossRef]
- Kaipurath, R.P.M.; Pietrzyk, M.; Caspani, L.; Roger, T.; Clerici, M.; Rizza, C.; Ciattoni, A.; Di Falco, A.; Faccio, D. Optically induced metal-to-dielectric transition in Epsilon-Near-Zero metamaterials. Sci. Rep. 2016, 6, 27700. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Kang, J.H.; Liu, X.; Brongersma, M.L. Electrically Tunable Epsilon-Near-Zero (ENZ) Metafilm Absorbers. Sci. Rep. 2015, 5, 15754. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Roberts, C.M.; Zhong, Y.; Podolskiy, V.A.; Wasserman, D. Epsilon-Near-Zero Photonics Wires. ACS Photonics 2016, 3, 1045–1052. [Google Scholar] [CrossRef]
- Davoyan, A.; Mahmoud, A.; Engheta, N. Optical isolation with epsilon-near-zero metamaterials. Opt. Express 2013, 21, 3279–3286. [Google Scholar] [CrossRef] [PubMed]
- Luk, T.S.; De Ceglia, D.; Liu, S.; Keeler, G.A.; Prasankumar, R.P.; Vincenti, M.A.; Scalora, M.; Sinclair, M.B.; Campione, S. Enhanced third harmonic generation from the epsilon-near-zero modes of ultrathin films. Appl. Phys. Lett. 2015, 106. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Bikbaev, R.G.; Rudakova, N.V.; Chen, K.P.; Timofeev, I. Optical Tamm states at the interface between a photonic crystal and an epsilon-near-zero nanocomposite. J. Opt. 2017, 19, 085103. [Google Scholar] [CrossRef]
- Oraevsky, A.N.; Protsenko, I.E. Optical properties of heterogeneous media. Quantum Electron. 2001, 31, 252–256. [Google Scholar] [CrossRef]
- Sihvola, A.H. Electromagnetic Mixing Formulas and Applications; Book Review; The Institution of Engineering and Technology: Stevenage, UK, 1999; 296p. [Google Scholar]
- Vetrov, S.Y.; Avdeeva, A.Y.; Bikbaev, R.G.; Timofeev, I. Traveling of light through a 1D photonic crystal containing a defect layer with resonant dispersion. Opt. Spectrosc. 2012, 113, 517–521. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C. Colours in metal glasses, in metallic films, and in metallic solutions. II. Philos. R. Soc. Lond. 1906, 205, 237–288. [Google Scholar] [CrossRef]
- Markel, V.A. Introduction to the Maxwell Garnett approximation: Tutorial. J. Opt. Soc. Am. A 2016, 33, 1244–1256. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P. Electromagnetic propagation in birefringent layered media. J. Opt. Soc. Am. 1979, 69, 742–756. [Google Scholar] [CrossRef]
- Brückner, R.; Sudzius, M.; Hintschich, S.I.; Fröb, H.; Lyssenko, V.G.; Leo, K. Hybrid optical Tamm states in a planar dielectric microcavity. Phys. Rev. B 2011, 83, 033405. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008; p. 304. [Google Scholar]
| Method | Reflectance |
|---|---|
| Transfer martix | 0.9694 |
| CMT | 0.9693 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bikbaev, R.G.; Vetrov, S.Y.; Timofeev, I.V. Two Types of Localized States in a Photonic Crystal Bounded by an Epsilon near Zero Nanocomposite. Photonics 2018, 5, 22. https://doi.org/10.3390/photonics5030022
Bikbaev RG, Vetrov SY, Timofeev IV. Two Types of Localized States in a Photonic Crystal Bounded by an Epsilon near Zero Nanocomposite. Photonics. 2018; 5(3):22. https://doi.org/10.3390/photonics5030022
Chicago/Turabian StyleBikbaev, Rashid G., Stepan Ya. Vetrov, and Ivan V. Timofeev. 2018. "Two Types of Localized States in a Photonic Crystal Bounded by an Epsilon near Zero Nanocomposite" Photonics 5, no. 3: 22. https://doi.org/10.3390/photonics5030022
APA StyleBikbaev, R. G., Vetrov, S. Y., & Timofeev, I. V. (2018). Two Types of Localized States in a Photonic Crystal Bounded by an Epsilon near Zero Nanocomposite. Photonics, 5(3), 22. https://doi.org/10.3390/photonics5030022







