Light–Matter Interaction of Single Quantum Emitters with Dielectric Nanostructures
Abstract
1. Introduction
2. Platforms for Realization of Single Quantum Emitters
2.1. Single Quantum Dots
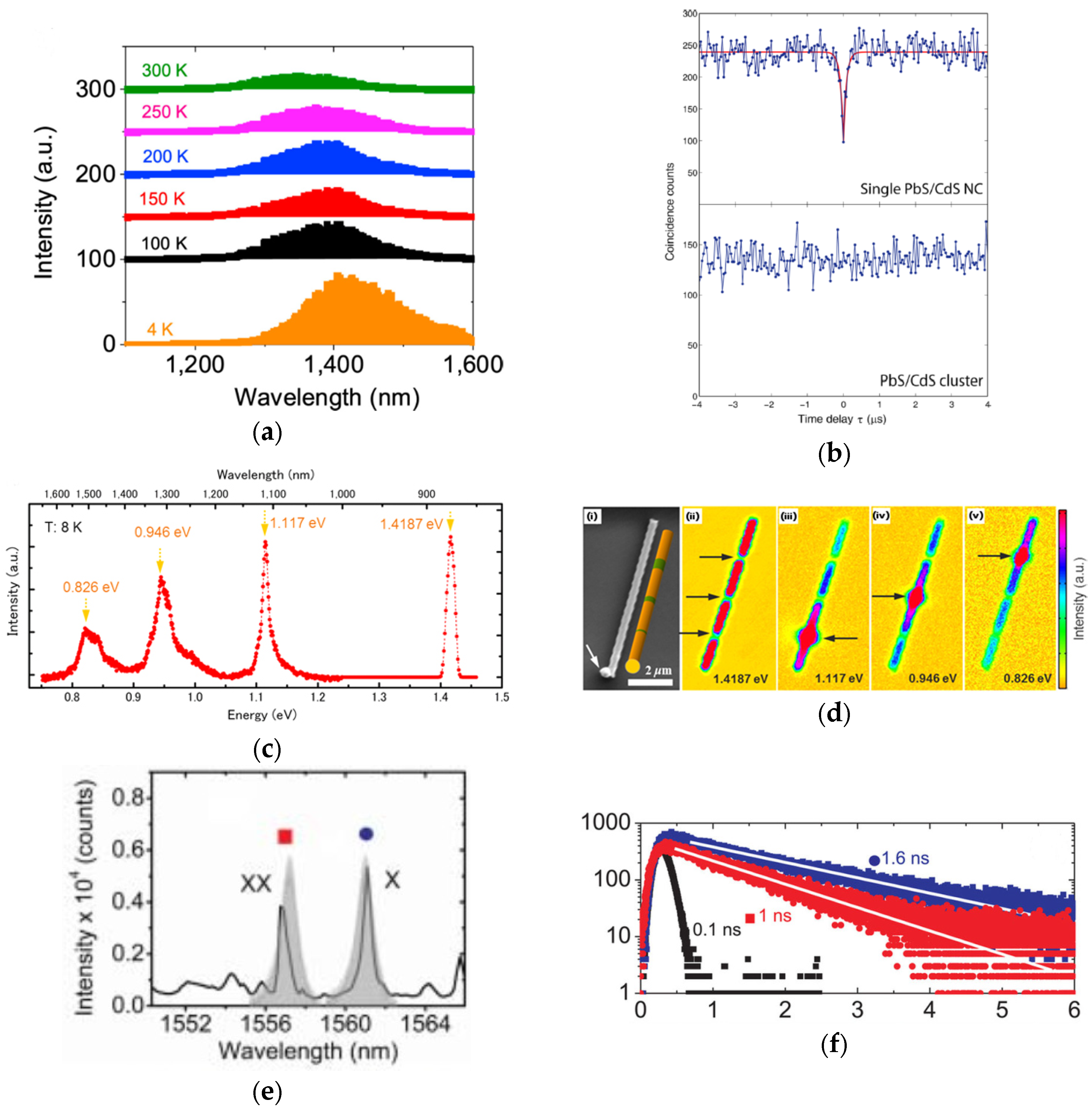
2.2. Fluorescent Point Defects in Bulk and Single Nanocrystal
2.3. Defects in Two-Dimensional Material
3. Controlling Spontaneous Emission Rate through Local Density of Photonic States of Nanostructures
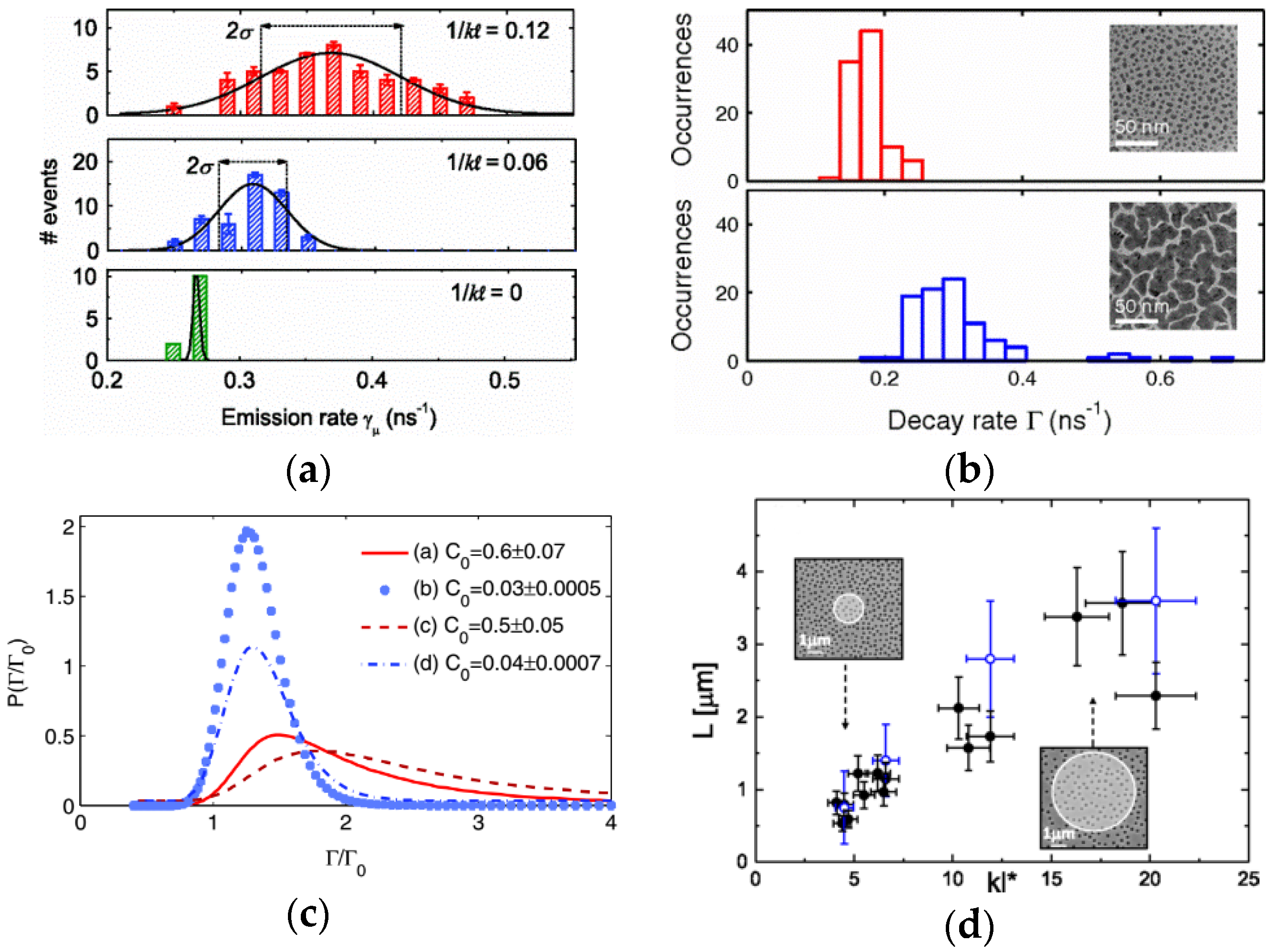
3.1. Random Photonic Materials
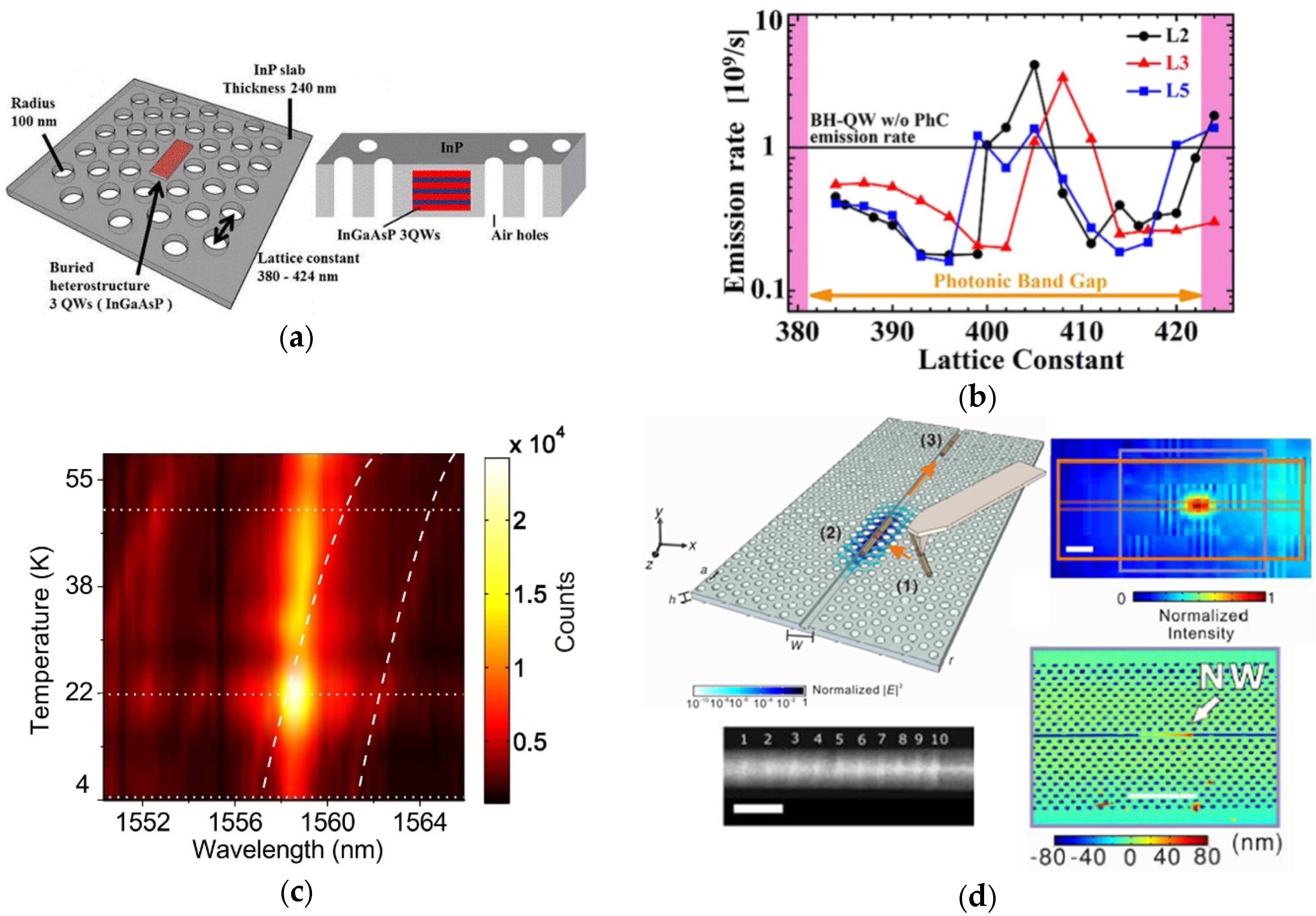
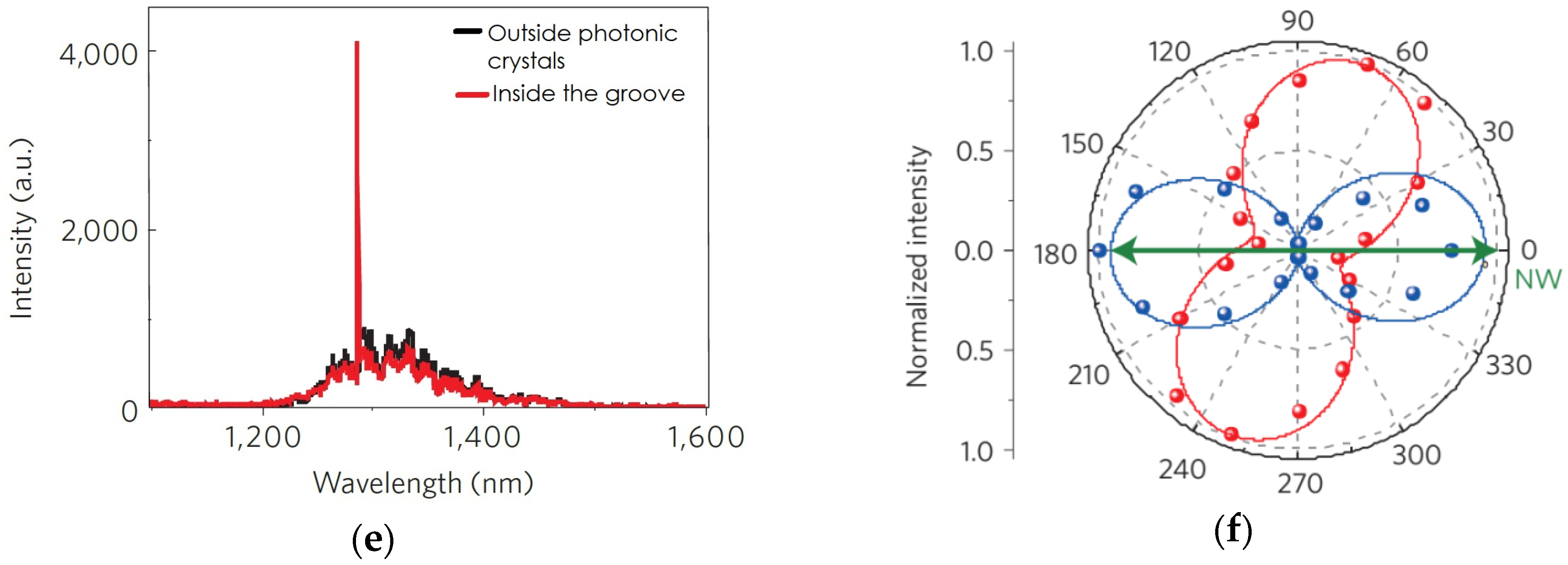
3.2. Photonic Crystal (PhC) Cavity
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Hu, J.-Y.; Yu, B.; Jing, M.-Y.; Xiao, L.-T.; Jia, S.-T.; Qin, G.-Q.; Long, G.-L. Experimental quantum secure direct communication with single photons. Light Sci. Appl. 2016, 5, e16144. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Bertocchi, G.; Alibart, O.; Ostrowsky, D.B.; Tanzilli, S.; Baldi, P. Single-photon Sagnac interferometer. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 1011–1016. [Google Scholar] [CrossRef]
- Aharonovich, I.; Englund, D.; Toth, M. Solid-state single-photon emitters. Nat. Photonics 2016, 10, 631–641. [Google Scholar] [CrossRef]
- Iwamoto, S.; Tatebayashi, J.; Fukuda, T.; Nakaoka, T.; Ishida, S.; Arakawa, Y. Observation of 1.55 μm light emission from InAs quantum dots in photonic crystal microcavity. Jpn. J. Appl. Phys. 2005, 44, 2579–2583. [Google Scholar] [CrossRef]
- Takemoto, K.; Takatsu, M.; Hirose, S.; Yokoyama, N.; Sakuma, Y.; Usuki, T.; Miyazawa, T.; Arakawa, Y. An optical horn structure for single-photon source using quantum dots at telecommunication wavelength. J. Appl. Phys. 2007, 101, 081720. [Google Scholar] [CrossRef]
- Takemoto, K.; Nambu, Y.; Miyazawa, T.; Wakui, K.; Hirose, S.; Usuki, T.; Takatsu, M.; Yoshino, K.; Tomita, A.; Yorozu, S.; et al. Transmission experiment of quantum keys over 50 km using high-performance quantum-dot single-photon source at 1.5 μm wavelength. Appl. Phys. Exp. 2010, 3, 092802. [Google Scholar] [CrossRef]
- Chauvin, N.; Zinoni, C.; Francardi, M.; Gerardino, A.; Balet, L.; Alloing, B.; Li, L.H.; Fiore, A. Controlling the charge environment of single quantum dots in a photonic-crystal cavity. Phys. Rev. B 2009, 80, 241306. [Google Scholar] [CrossRef]
- Dalacu, D.; Mnaymneh, K.; Sazonova, V.; Poole, P.J.; Aers, G.C.; Lapointe, J.; Cheriton, R.; Thorpe, A.J.S.; Williams, R. Deterministic emitter-cavity coupling using a single-site controlled quantum dot. Phys. Rev. B 2010, 82, 033301. [Google Scholar] [CrossRef]
- Rakher, M.T.; Ma, L.; Slattery, O.; Tang, X.; Srinivasan, K. Quantum transduction of telecommunications-band single photons from a quantum dot by frequency upconversion. Nat. Photonics 2010, 4, 786–791. [Google Scholar] [CrossRef]
- Lohrmann, A.; Iwamoto, N.; Bodrog, Z.; Castelletto, S.; Ohshima, T.; Karle, T.J.; Gali, A.; Prawer, S.; McCallum, J.C.; Johnson, B.C. Single-photon emitter diode in silicon carbide. Nat. Commun. 2015, 6, 7783. [Google Scholar] [CrossRef] [PubMed]
- Rarity, J.G.; Tapster, P.R.; Gorman, P.M. Secure free-space key exchange to 1.9 km and beyond. J. Mod. Opt. 2001, 48, 1887–1901. [Google Scholar] [CrossRef]
- Hadfield, R.H. Single-photon detectors for optical quantum information applications. Nat. Photonics 2009, 3, 696–705. [Google Scholar] [CrossRef]
- Ates, S.; Agha, I.; Gulinatti, A.; Rech, I.; Badolato, A.; Srinivasan, K. Improving the performance of bright quantum dot single photon sources using temporal filtering via amplitude modulation. Sci. Rep. 2013, 3, 1397. [Google Scholar] [CrossRef] [PubMed]
- Lounis, B.; Orrit, M. Single-photon sources. Rep. Prog. Phys. 2005, 68, 1129–1179. [Google Scholar] [CrossRef]
- Somachi, N.; Giesz, V.; Santis, L.D.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Birowosuto, M.B.; Takiguchi, M.; Olivier, A.; Tobing, L.Y.; Kuramochi, E.; Yokoo, A.; Hong, W.; Notomi, M. Temperature-dependent spontaneous emission of PbS quantum dots inside photonic nanostructures at telecommunication wavelength. Opt. Commun. 2017, 383, 555–560. [Google Scholar] [CrossRef]
- Correa, R.E.; Dauler, E.A.; Nair, G.; Pan, S.H.; Rosenberg, D.; Kerman, A.J.; Molnar, R.J.; Hu, X.; Marsili, F.; Anant, V.; et al. Single Photon Counting from Individual Nanocrystals in the Infrared. Nano Lett. 2012, 12, 2953–2958. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.-S.; Guo, S.; Marakov, N.S.; Klimov, V.I. Room Temperature Single-Photon Emission from Individual Perovskite Quantum Dots. ACS Nano 2015, 9, 10386–10393. [Google Scholar] [CrossRef] [PubMed]
- Bleuse, J.; Claudon, J.; Creasey, M.; Malik, N.S.; Gérard, J.-M. Inhibition, Enhancement, and Control of Spontaneous Emission in Photonic Nanowires. Phys. Rev. Lett. 2011, 106, 103601. [Google Scholar] [CrossRef] [PubMed]
- Birowosuto, M.D.; Zhang, G.; Yokoo, A.; Takiguchi, M.; Notomi, M. Spontaneous emission inhibition of telecom-band quantum disks inside single nanowire on different substrates. Opt. Express 2014, 22, 11713–11726. [Google Scholar] [CrossRef] [PubMed]
- Birowosuto, M.D.; Sumikura, H.; Matsuo, S.; Taniyama, H.; van Veldhoven, P.J.; Nötzel, R.; Notomi, M. Fast-Purcell-enhanced single photon source in 1550-nm telecom band from a resonant quantum dot-cavity coupling. Sci. Rep. 2012, 2, 231. [Google Scholar] [CrossRef] [PubMed]
- Cade, N.I.; Gotoh, H.; Kamada, H.; Nakano, H.; Anantathanasarn, S.; Nötzel, R. Optical characteristics of single InAs/InAsP/InP(100) quantum dots emitting at 1.55 nm. Appl. Phys. Lett. 2006, 89, 181113. [Google Scholar] [CrossRef]
- Dusanowski, Ł.; Syperek, M.; Rudno-Rudziński, W.; Mrowiński, P.; Sȩk, G.; Misiewicz, J.; Somers, A.; Reithmaier, J.P.; Höfling, S.; Forchel, A. Exciton and biexciton dynamics in single self-assembled InAs/InGaAlAs/InP quantum dash emitting near 1.55 μm. Appl. Phys. Lett. 2013, 103, 253113. [Google Scholar] [CrossRef]
- Miyazawa, T.; Nakaoka, T.; Usuki, T.; Arakawa, Y.; Takemoto, K.; Hirose, S.; Okumura, S.; Takatsu, M.; Yokoyama, N. Exciton dynamics in current-injected single quantum dot at 1.55 mm. Appl. Phys. Lett. 2008, 92, 161104. [Google Scholar] [CrossRef]
- Dorenbos, S.N.; Sasakura, H.; van Kouwen, M.P.; Akopian, N.; Adachi, S.; Namekata, N.; Jo, M.; Motohisa, J.; Kobayashi, Y.; Tomioka, K.; et al. Position controlled nanowires for infrared single photon emission. Appl. Phys. Lett. 2010, 97, 171106. [Google Scholar] [CrossRef]
- Thoma, A.; Schnauber, P.; Gschrey, M.; Seifried, M.; Wolters, J.; Schulze, J.H.; Strittmatter, A.; Rodt, S.; Carmele, A.; Knorr, A.; et al. Exploring dephasing of a solid-state quantum emitter via time- and temperature-dependent hong-ou-mandel experiments. Phys. Rev. Lett. 2016, 116, 033601. [Google Scholar] [CrossRef] [PubMed]
- Aharonovich, I.; Neu, E. Diamond Nanophotonics. Adv. Opt. Mater. 2014, 2, 911–928. [Google Scholar] [CrossRef]
- Acosta, V.M.; Santori, C.; Faraon, A.; Juang, Z.; Fu, K.-M.C.; Stacey, A.; Simpson, D.A.; Ganesan, K.; Tomljenovic-Hanic, S.; Greentree, A.D.; et al. Dynamic stabilization of the optical resonances of single nitrogen-vacancy centers in diamond. Phys. Rev. Lett. 2012, 108, 206401. [Google Scholar] [CrossRef] [PubMed]
- Wolters, J.; Sadzak, N.; Schell, A.W.; Schröder, T.; Benson, O. Measurement of the ultrafast spectral diffusion of the optical transition of nitrogen vacancy centers in nano-size diamond using correlation interferometry. Phys. Rev. Lett. 2013, 110, 027401. [Google Scholar] [CrossRef] [PubMed]
- Wolters, J. Integrated Quantum Hybrid Systems, 1st ed.; Pan Stanford: New York, NY, USA, 2015. [Google Scholar]
- Sipahigil, A.; Jahnke, K.D.; Rogers, L.J.; Teraji, T.; Isoya, J.; Zibrov, A.S.; Jelezko, F.; Lukin, M.D. Indistinguishable photons from separated silicon-vacancy centers in diamond. Phys. Rev. Lett. 2014, 113, 113602. [Google Scholar] [CrossRef] [PubMed]
- Castelletto, S.; Johnson, B.C.; Ivády, V.; Umeda, T.; Gali, A.; Ohshima, T. A silicon carbide room-temperature single-photon source. Nat. Mater. 2013, 13, 151–156. [Google Scholar] [CrossRef] [PubMed]
- Morfa, A.J.; Gibson, B.C.; Karg, M.; Karle, T.J.; Greentree, A.D.; Mulvaney, P.; Tomljenovic-Hanic, S. Single-photon emission and quantum characterization of zinc oxide defects. Nano Lett. 2012, 12, 949–954. [Google Scholar] [CrossRef] [PubMed]
- Neitzke, O.; Morfa, A.; Wolters, J.; Schell, A.W.; Kewes, G.; Benson, O. Investigation of line width narrowing and spectral jumps of single stable defect centers in ZnO at cryogenic temperature. Nano Lett. 2015, 15, 3024–3029. [Google Scholar] [CrossRef] [PubMed]
- Kolesov, R.; Xia, K.; Reuter, R.; Stöhr, R.; Zappe, A.; Meijer, J.; Hemmer, P.R.; Wrachtrup, J. Optical detection of a single rare-earth ion in a crystal. Nat. Commun. 2012, 3, 1029. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, C.; Kinnischtzke, L.; Goodfellow, K.M.; Beams, R.; Vamivakas, A.N. Voltage-controlled quantum light from an atomically thin semiconductor. Nat. Nanotechnol. 2015, 10, 507–511. [Google Scholar] [CrossRef] [PubMed]
- He, Y.-M.; Clark, G.; Schaibley, J.R.; He, Y.; Chen, M.-C.; Wei, Y.-J.; Ding, X.; Zhang, Q.; Yao, W.; Xu, X.; et al. Single quantum emitters in monolayer semiconductors. Nat. Nanotechnol. 2015, 10, 497–502. [Google Scholar] [CrossRef] [PubMed]
- Koperski, M.; Nogajewski, K.; Arora, A.; Cherkez, V.; Mallet, P.; Veuillen, J.-Y.; Marcus, J.; Kossacki, P.; Potemski, M. Single photon emitters in exfoliated WSe2 structures. Nat. Nanotechnol. 2015, 10, 503–506. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Sidler, M.; Allain, A.V.; Lembke, D.S.; Kis, A.; Imamoğlu, A. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 2015, 10, 491–496. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.T.; Bray, K.; Ford, M.J.; Toth, M.; Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 2016, 11, 37–41. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.T.; Elbadawi, C.; Totonjian, D.; Lobo, C.J.; Grosso, G.; Moon, H.; Englund, D.R.; Ford, M.J.; Aharonovich, I.; Toth, M. Robust Multicolor Single Photon Emission from Point Defects in Hexagonal Boron Nitride. ACS Nano 2016, 10, 7331–7338. [Google Scholar] [CrossRef] [PubMed]
- Hou, S.; Birowosuto, M.D.; Umar, S.; Anicet, M.A.; Tay, R.Y.; Coquet, P.; Tay, B.K.; Wang, H.; Teo, H.T. Localized emission from laser-irradiated defects in two-dimensional hexagonal boron nitride. 2D Mater. 2018, 5, 015010. [Google Scholar] [CrossRef]
- Sontheimer, B.; Braun, M.; Nikolay, N.; Sadzak, N.; Aharonovich, I.; Benson, O. Photodynamics of quantum emitters in hexagonal boron nitride revealed by low-temperature spectroscopy. Phys. Rev. B 2017, 96, 121202. [Google Scholar] [CrossRef]
- Palacios-Berraquero, C.; Barbone, M.; Kara, D.M.; Chen, X.; Goykhman, I.; Yoon, D.; Ott, A.K.; Beitner, J.; Watanabe, K.; Taniguchi, T.; et al. Atomically thin quantum light-emitting diodes. Nat. Commun. 2016, 7, 12978. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, S.; Shalaginov, M.Y.; Lagutchev, A.; Chiang, C.-C.; Shah, D.; Baburin, A.S.; Ryzhikov, I.A.; Rodionov, I.A.; Boltasseva, A.; Shalaev, V.M. Ultrabright room-temperature single-photon emission from nanodiamond nitrogen-vacancy centers with sub-nanosecond excited-state lifetime. arXiv 2017, arXiv:1711.09481. [Google Scholar]
- Hoang, T.B.; Gleb, M.; Akselrod, G.M.; Mikkelsen, M.H. Ultrafast Room-Temperature Single Photon Emission from Quantum Dots Coupled to Plasmonic Nanocavities. Nano Lett. 2016, 16, 270–275. [Google Scholar] [CrossRef] [PubMed]
- Babinec, T.M.; Hausmann, B.J.M.; Khan, M.; Zhang, Y.; Maze, J.R.; Hemmer, P.R.; Lončar, M. A diamond nanowire single-photon source. Nat. Nanotechnol. 2010, 5, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Toninelli, C.; Early, K.; Bremi, J.; Renn, A.; Götzinger, S.; Sandoghdar, V. Near-infrared single-photons from aligned molecules in ultrathin crystalline films at room temperature. Opt. Express 2010, 18, 6577–6582. [Google Scholar] [CrossRef] [PubMed]
- Kewes, G.; Schoengen, M.; Neitzke, O.; Lombardi, P.; Schönfeld, R.-S.; Mazzamuto, G.; Schell, A.W.; Probst, J.; Wolters, J.; Löchel, B.; et al. A realistic fabrication and design concept for quantum gates based on single emitters integrated in plasmonic-dielectric waveguide structures. Sci. Rep. 2016, 6, 28877. [Google Scholar] [CrossRef] [PubMed]
- Birowosuto, M.D.; Yokoo, A.; Zhang, G.; Tateno, K.; Kuramochi, E.; Takiguchi, M.; Notomi, M. Movable high-Q nanoresonators realized by semiconductor nanowires on a Si photonic crystal platform. Nat. Mater. 2014, 13, 279–285. [Google Scholar] [CrossRef] [PubMed]
- Lodahl, P.; van Driel, A.F.; Nikolaev, I.S.; Irman, A.; Overgaag, K.; Vanmaekelbergh, D.; Vos, W.L. Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals. Nature 2004, 430, 654–657. [Google Scholar] [CrossRef] [PubMed]
- Sapienza, L.; Thyrrestrup, H.; Stobbe, S.; Gracia, P.D.; Smolka, S.; Lodahl, P. Cavity Quantum Electrodynamics with Anderson-Localized Modes. Science 2010, 327, 1352–1355. [Google Scholar] [CrossRef] [PubMed]
- Vynck, K.; Burresi, M.; Riboli, F.; Wiersma, D.S. Photon management in two-dimensional disordered media. Nat. Mater. 2012, 11, 1017–1022. [Google Scholar] [CrossRef] [PubMed]
- Topolancik, J.; Ilic, B.; Vollmer, F. Experimental Observation of Strong Photon Localization in Disordered Photonic Crystal Waveguides. Phys. Rev. Lett. 2007, 99, 253901. [Google Scholar] [CrossRef] [PubMed]
- Taminiau, T.H.; Stefani, F.D.; Segerink, F.B.; van Hulst, N.F. Optical antennas direct single-molecule emission. Nat. Photonics 2008, 2, 234–237. [Google Scholar] [CrossRef]
- Russell, K.J.; Liu, T.-L.; Cui, S.; Hu, E.L. Large spontaneous emission enhancement in plasmonic nanocavities. Nat. Photonics 2012, 6, 459–462. [Google Scholar] [CrossRef]
- Hoang, T.B.; Akselrod, G.M.; Argyropoulos, C.; Huang, J.; Smith, D.R.; Mikkelsen, M.H. Ultrafast spontaneous emission source using plasmonic nanoantennas. Nat. Commun. 2015, 6, 7788. [Google Scholar] [CrossRef] [PubMed]
- Saleem, U.; Permatasari, F.A.; Iskandar, F.; Ogi, T.; Okuyama, K.; Darma, Y.; Zhao, M.; Loh, K.P.; Rusydi, A.; Coquet, P.; et al. Surface Plasmon Enhanced Nitrogen-Doped Graphene Quantum Dot Emission by Single Bismuth Telluride Nanoplates. Adv. Opt. Mater. 2017, 5, 1700176. [Google Scholar] [CrossRef]
- Sprik, R.; van Tiggelen, B.A.; Lagendijk, A. Optical emission in periodic dielectrics. Europhys. Lett. 1996, 35, 265–270. [Google Scholar] [CrossRef]
- Mirlin, A.D. Statistics of energy levels and eigenfunctions in disordered systems. Phys. Rep. 2000, 326, 259–382. [Google Scholar] [CrossRef]
- Van Tiggelen, B.A.; Skipetrov, S.E. Fluctuations of local density of states and C0 speckle correlations are equal. Phys. Rev. E 2006, 73, 045601. [Google Scholar] [CrossRef] [PubMed]
- Birowosuto, M.D.; Skipetrov, S.E.; Vos, W.L.; Mosk, A.P. Observation of Spatial Fluctuations of the Local Density of States in Random Photonic Media. Phys. Rev. Lett. 2010, 105, 013904. [Google Scholar] [CrossRef] [PubMed]
- Krachmalnicoff, V.; Castanié, E.; Wilde, Y.D.; Carminati, R. Fluctuations of the Local Density of States Probe Localized Surface Plasmons on Disordered Metal Films. Phys. Rev. Lett. 2010, 105, 183901. [Google Scholar] [CrossRef] [PubMed]
- Sapienza, R.; Bondareff, P.; Pierrat, R.; Habert, B.; Carminati, R.; van Hulst, N.F. Long-Tail Statistics of the Purcell Factor in Disordered Media Driven by Near-Field Interactions. Phys. Rev. Lett. 2011, 106, 163902. [Google Scholar] [CrossRef] [PubMed]
- Riboli, F.; Uccheddu, F.; Monaco, G.; Caselli, N.; Intonti, F.; Gurioli, M.; Skipetrov, S.E. Tailoring correlations of the local density of states in disordered photonic materials. Phys. Rev. Lett. 2017, 119, 043902. [Google Scholar] [CrossRef] [PubMed]
- Bykov, V.P. Spontaneous Emission in a Periodic Structure. Sov. Phys. JETP 1972, 35, 269–273. [Google Scholar]
- Ohtaka, K. Energy band of photons and low-energy photon diffraction. Phys. Rev. B 1979, 19, 5057–5067. [Google Scholar] [CrossRef]
- Russell, P.S.J. Novel thick-grating beam-squeezing device in Ta2O5 corrugated planar waveguide. J. Electron. Lett. 1984, 20, 72–73. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong Localization of Photons in Certain Disordered Dielectric Superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Englund, D.; Fattal, D.; Solomon, G.; Zhang, B.; Nakaoka, T.; Arakawa, Y.; Yamamoto, Y.; Vučković, J. Controlling the Spontaneous Emission Rate of Single Quantum Dots in a Two-Dimensional Photonic Crystal. Phys. Rev. Lett. 2005, 95, 013904. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, S.; Imada, M.; Yoshimoto, S.; Okano, M.; Noda, S. Control of light emission by 3D photonic crystals. Science 2004, 305, 227–229. [Google Scholar] [CrossRef] [PubMed]
- Takiguchi, M.; Sumikura, H.; Birowosuto, M.D.; Kuramochi, E.; Sato, T.; Takeda, K.; Matsuo, S.; Notomi, M. Enhanced and suppressed spontaneous emission from a buried heterostructure photonic crystal cavity. Appl. Phys. Lett. 2013, 103, 091113. [Google Scholar] [CrossRef]
- Ee, Y.-K.; Kumnorkaew, P.; Arif, R.A.; Tong, H.; Zhao, H.; Gilchrist, J.F.; Tansu, N. Optimization of Light Extraction Efficiency of III-Nitride LEDs with Self-Assembled Colloidal-Based Microlenses. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1218–1225. [Google Scholar] [CrossRef]
- Ee, Y.K.; Kummorkaew, P.; Arif, R.A.; Tong, H.; Gilchrist, J.F.; Tansu, N. Light extraction efficiency enhancement of InGaN quantum wells light-emitting diodes with polydimethylsiloxane concave microstructures. Opt. Express 2009, 17, 13747–13757. [Google Scholar] [CrossRef] [PubMed]
- Li, X.H.; Song, R.; Ee, Y.-K.; Kumnorkaew, P.; Gilchrist, J.F.; Tansu, N. Light Extraction Efficiency and Radiation Patterns of III-Nitride Light-Emitting Diodes With Colloidal Microlens Arrays with Various Aspect Ratios. IEEE Photon. J. 2011, 3, 489–499. [Google Scholar] [CrossRef]
- Takiguchi, M.; Taniyama, H.; Sumikura, H.; Birowosuto, M.D.; Kuramochi, E.; Shinya, A.; Sato, T.; Takeda, K.; Matsuo, S.; Notomi, M. Systematic study of thresholdless oscillation in high-β buried multiple-quantum-well photonic crystal nanocavity lasers. Opt. Express 2016, 24, 3441–3450. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wang, H.; Meng, Q.; Gao, B.; Ang, K.S. Modal Gain and Photoluminescence Investigation of Two-State Lasing in GaAs-Based 1.3 µm InAs/InGaAs Quantum Dot Lasers. Appl. Phys. Exp. 2013, 6, 102702. [Google Scholar] [CrossRef]
- Liu, C.; Wang, H.; Meng, Q. Characterization and Analysis of 1.3-μm InAs/InGaAs Self-Assembled Quantum Dot Lasers. IEEE Trans. Nanotechnol. 2014, 13, 446–451. [Google Scholar] [CrossRef]
- Diguna, L.J.; Murakami, M.; Sato, A.; Kumagai, Y.; Ishihara, T.; Kobayashi, N.; Shen, Q.; Toyoda, T. Photoacoustic and Photoelectrochemical Characterization of Inverse Opal TiO2 Sensitized with CdSe Quantum Dots. Jpn. J. Appl. Phys. 2006, 45, 5563–5568. [Google Scholar] [CrossRef]
- Diguna, L.J.; Shen, Q.; Sato, A.; Katayama, K.; Sawada, T.; Toyoda, T. Optical absorption and ultrafast carrier dynamics characterization of CdSe quantum dots deposited on different morphologies of nanostructured TiO2 films. Mater. Sci. Eng. C 2007, 27, 1514–1520. [Google Scholar] [CrossRef]
- Diguna, L.J.; Shen, Q.; Kobayashi, J.; Toyoda, T. High efficiency of CdSe quantum-dot-sensitized TiO2 inverse opal solar cells. Appl. Phys. Lett. 2007, 91, 023116. [Google Scholar] [CrossRef]
- Diguna, L.J.; Darma, Y.; Birowosuto, M.D. The coupling of single-photon exciton-biexciton quantum dot and cavity. J. Nonlinear Opt. Phys. Mat. 2017, 26, 1750029. [Google Scholar] [CrossRef]
- Wolters, J.; Kabuss, J.; Knorr, A.; Benson, O. Deterministic and robust entanglement of nitrogen-vacancy centers using low-Q photonic-crystal cavities. Phys. Rev. A 2014, 89, 060303. [Google Scholar] [CrossRef]
- Yang, W.L.; Yin, Z.Q.; Xu, Z.Y.; Feng, M.; Oh, C.H. Quantum dynamics and quantum state transfer between separated nitrogen-vacancy centers embedded in photonic crystal cavities. Phys. Rev. A 2011, 84, 043849. [Google Scholar] [CrossRef]
- Kreinberg, S.; Chow, W.W.; Wolters, J.; Schneider, C.; Gies, C.; Jahnke, F.; Höfling, S.; Kamp, M.; Reitzenstein, S. Emission from quantum-dot high-β microcavities: Transition from spontaneous emission to lasing and the effects of superradiant emitter coupling. Light Sci. Appl. 2017, 6, e17030. [Google Scholar] [CrossRef]
- Gies, C.; Gericke, F.; Gartner, P.; Holzinger, S.; Hopfmann, C.; Heindel, T.; Wolters, J.; Schneider, C.; Florian, M.; Jahnke, F.; et al. Strong light-matter coupling in the presence of lasing. Phys. Rev. A 2017, 96, 023806. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diguna, L.J.; Tjahjana, L.; Darma, Y.; Zeng, S.; Wang, H.; Birowosuto, M.D. Light–Matter Interaction of Single Quantum Emitters with Dielectric Nanostructures. Photonics 2018, 5, 14. https://doi.org/10.3390/photonics5020014
Diguna LJ, Tjahjana L, Darma Y, Zeng S, Wang H, Birowosuto MD. Light–Matter Interaction of Single Quantum Emitters with Dielectric Nanostructures. Photonics. 2018; 5(2):14. https://doi.org/10.3390/photonics5020014
Chicago/Turabian StyleDiguna, Lina Jaya, Liliana Tjahjana, Yudi Darma, Shuwen Zeng, Hong Wang, and Muhammad Danang Birowosuto. 2018. "Light–Matter Interaction of Single Quantum Emitters with Dielectric Nanostructures" Photonics 5, no. 2: 14. https://doi.org/10.3390/photonics5020014
APA StyleDiguna, L. J., Tjahjana, L., Darma, Y., Zeng, S., Wang, H., & Birowosuto, M. D. (2018). Light–Matter Interaction of Single Quantum Emitters with Dielectric Nanostructures. Photonics, 5(2), 14. https://doi.org/10.3390/photonics5020014






