High Harmonics with Controllable Polarization by a Burst of Linearly-Polarized Driver Pulses
Abstract
:1. Introduction
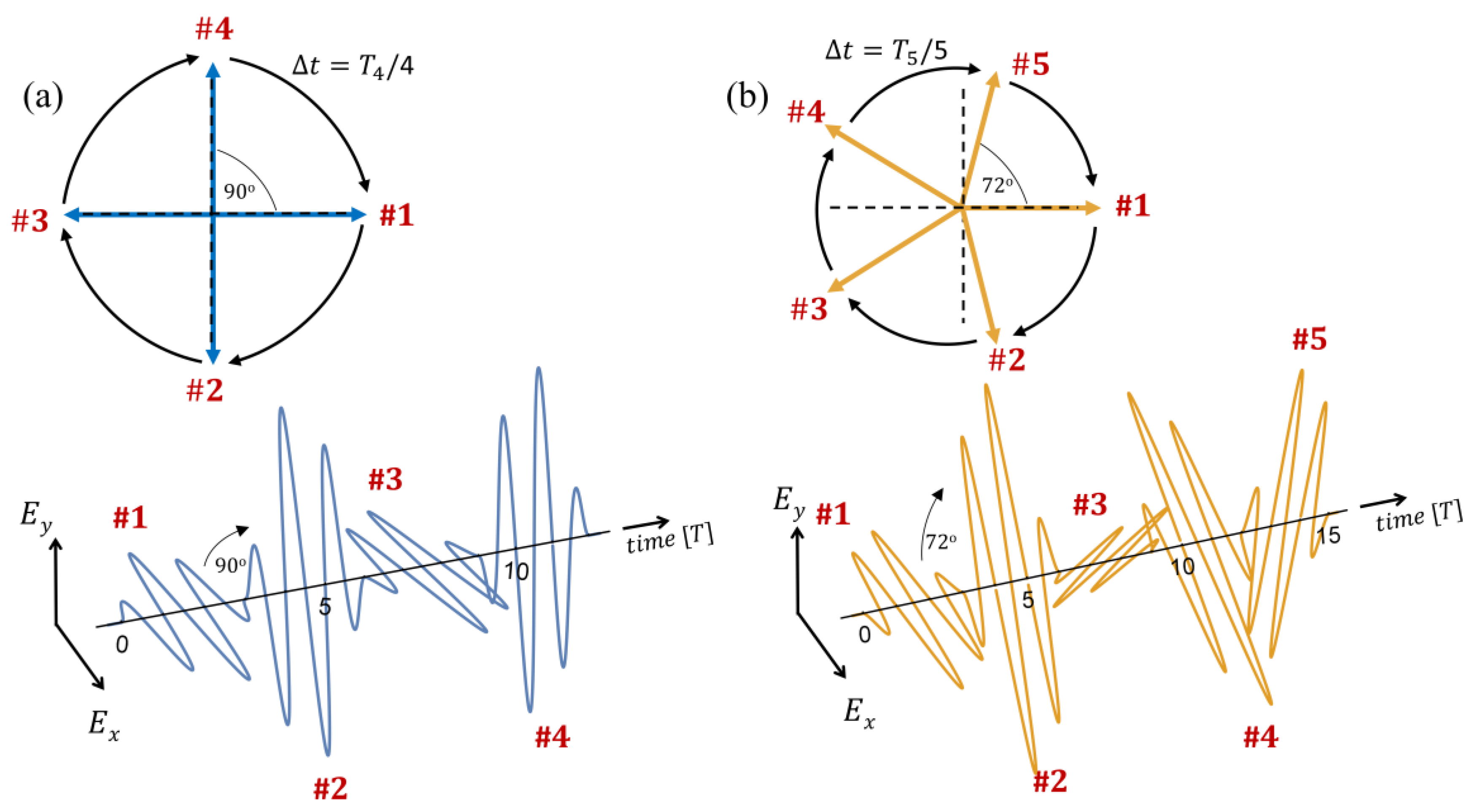
2. High Harmonic Generation Scheme
3. Analytical Model
3.1. Circular Harmonics
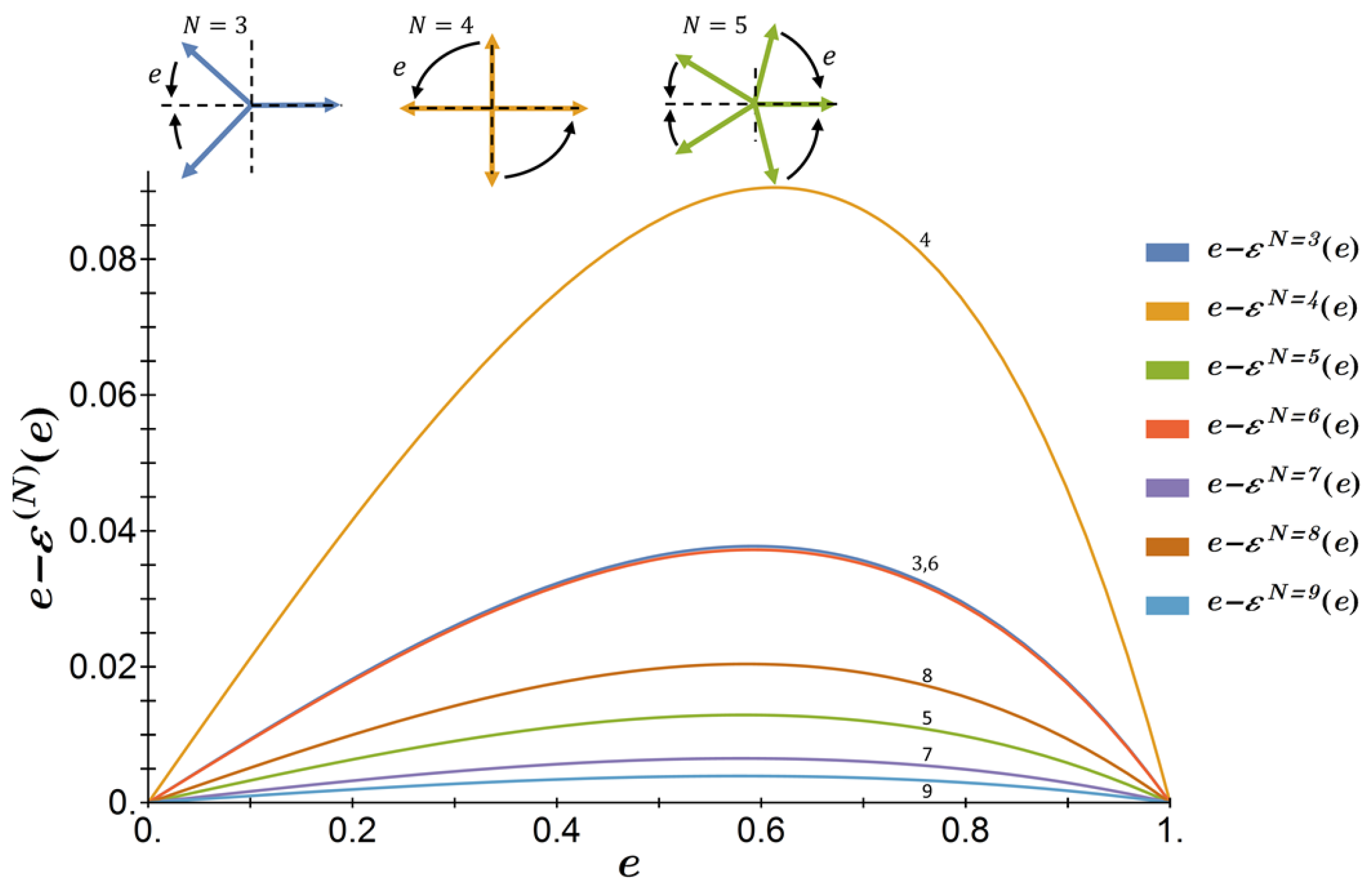
3.2. Polarization Control
3.3. Photonic Conservation Laws
4. Quantum Simulations
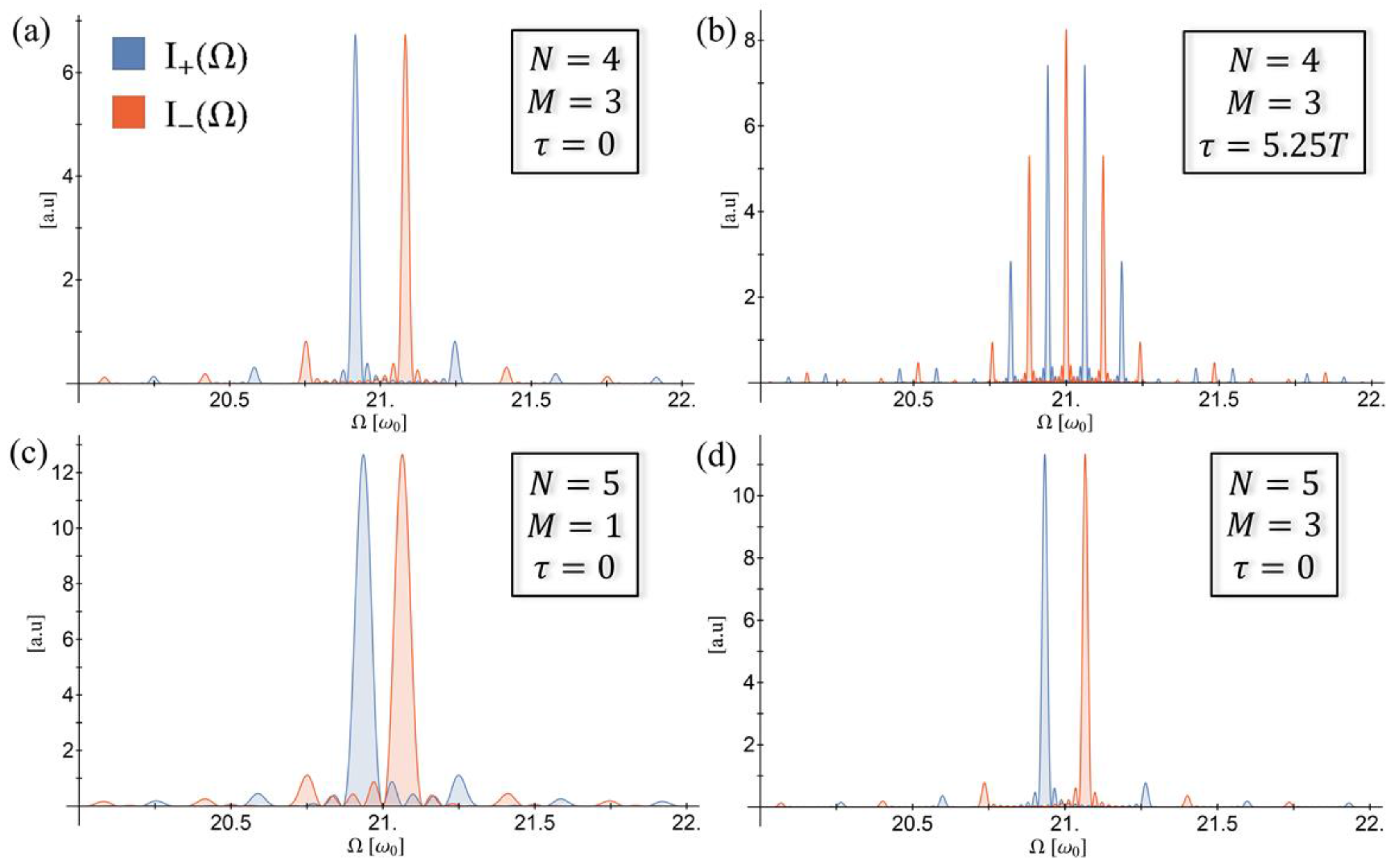
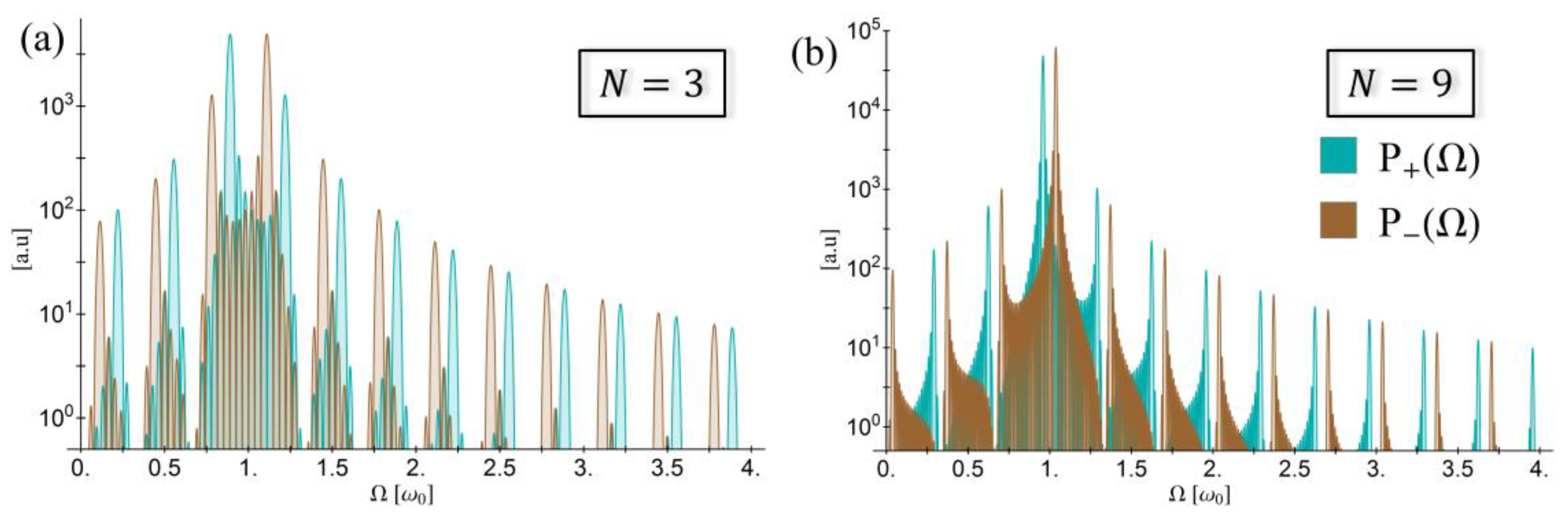
4.1. Numerical Model
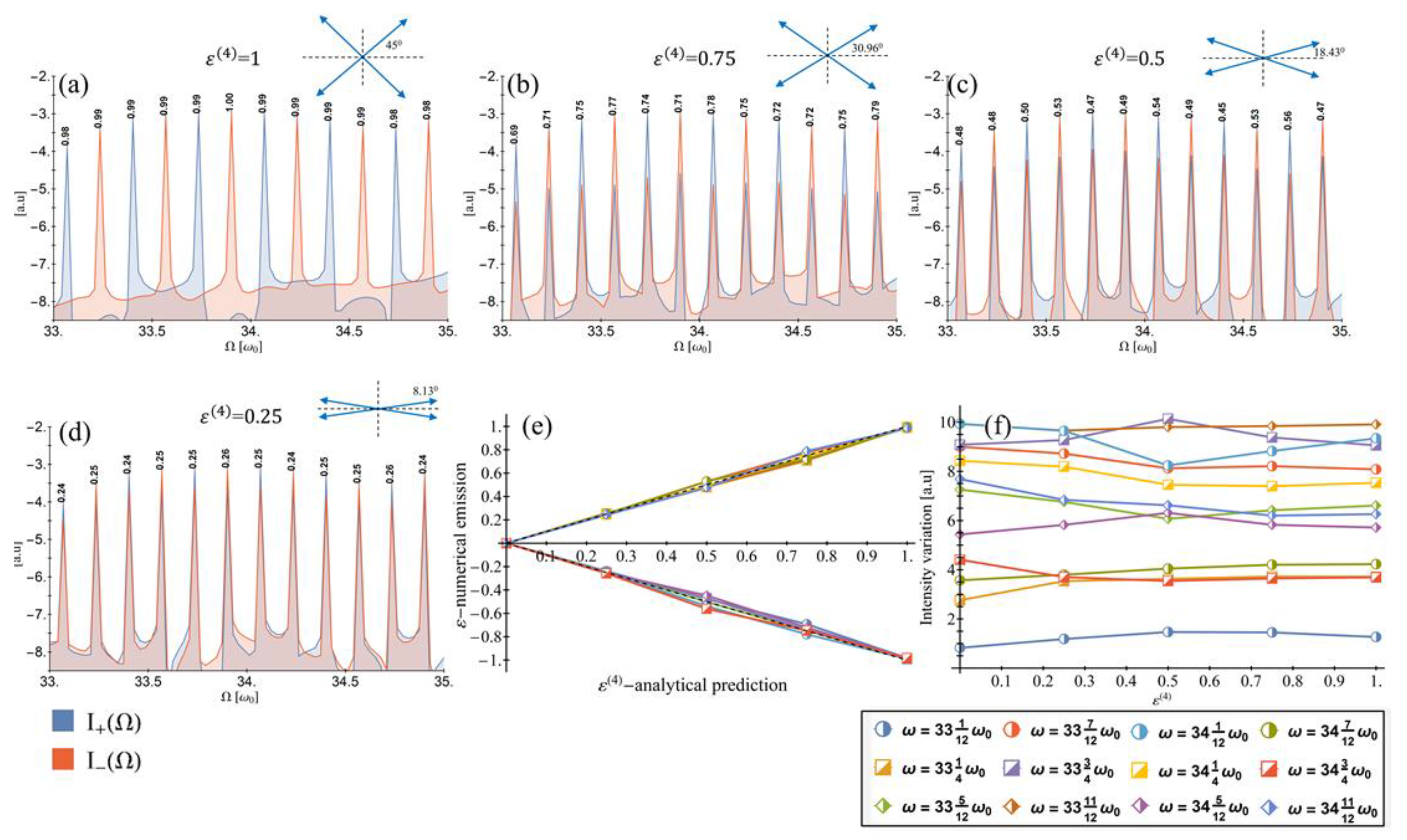
4.2. Numerical Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ferray, M.; L’Huillier, A.; Li, X.F.; Lompre, L.A.; Mainfray, G.; Manus, C. Multiple-harmonic conversion of 1064 nm radiation in rare gases. J. Phys. B At. Mol. Opt. Phys. 1988, 21, L31–L35. [Google Scholar] [CrossRef]
- Li, X.F.; L’Huillier, A.; Ferray, M.; Lompré, L.A.; Mainfray, G. Multiple-harmonic generation in rare gases at high laser intensity. Phys. Rev. A 1989, 39, 5751–5761. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Ben-Tal, N.; Moiseyev, N.; Beswick, A. The effect of Hamiltonian symmetry on generation of odd and even harmonics. J. Phys. B At. Mol. Opt. Phys. 1993, 26, 3017–3024. [Google Scholar] [CrossRef]
- Alon, O.E.; Averbukh, V.; Moiseyev, N. Selection Rules for the High Harmonic Generation Spectra. Phys. Rev. Lett. 1998, 80, 3743–3746. [Google Scholar] [CrossRef]
- Antoine, P.; Carré, B.; L’Huillier, A.; Lewenstein, M. Polarization of high-order harmonics. Phys. Rev. A 1997, 55, 1314–1324. [Google Scholar] [CrossRef]
- Weihe, F.A.; Dutta, S.K.; Korn, G.; Du, D.; Bucksbaum, P.H.; Shkolnikov, P.L. Polarization of high-intensity high-harmonic generation. Phys. Rev. A 1995, 51, R3433–R3436. [Google Scholar] [CrossRef] [PubMed]
- Strelkov, V.V.; Gonoskov, A.A.; Gonoskov, I.A.; Ryabikin, M.Y. Origin for ellipticity of high-order harmonics generated in atomic gases and the sublaser-cycle evolution of harmonic polarization. Phys. Rev. Lett. 2011, 107, 043902. [Google Scholar] [CrossRef] [PubMed]
- Kanai, T.; Minemoto, S.; Sakai, H. Ellipticity dependence of high-order harmonic generation from aligned molecules. Phys. Rev. Lett. 2007, 98, 053002. [Google Scholar] [CrossRef] [PubMed]
- Möller, M.; Cheng, Y.; Khan, S.D.; Zhao, B.; Zhao, K.; Chini, M.; Paulus, G.G.; Chang, Z. Dependence of high-order-harmonic-generation yield on driving-laser ellipticity. Phys. Rev. A 2012, 86, 011401. [Google Scholar] [CrossRef]
- Long, S.; Becker, W.; McIver, J.K. Model calculations of polarization-dependent two-color high-harmonic generation. Phys. Rev. A 1995, 52, 2262–2278. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.-M.; Chu, S.-I. Generation of circularly polarized multiple high-order harmonic emission from two-color crossed laser beams. Phys. Rev. A 1998, 58, R2656. [Google Scholar] [CrossRef]
- Xie, X.; Scrinzi, A.; Wickenhauser, M.; Baltuška, A.; Barth, I.; Kitzler, M. Internal momentum state mapping using high harmonic radiation. Phys. Rev. Lett. 2008, 101, 033901. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.-J.; Bandrauk, A.D. Generation of circularly polarized attosecond pulses by intense ultrashort laser pulses from extended asymmetric molecular ions. Phys. Rev. A 2011, 84, 023410. [Google Scholar] [CrossRef]
- Liu, L.Z.; O’Keeffe, K.; Hooker, S.M. Optical rotation quasi-phase-matching for circularly polarized high harmonic generation. Opt. Lett. 2012, 37, 2415–2417. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Nisoli, M. Control of the polarization of isolated attosecond pulses in atoms with nonvanishing angular quantum number. Phys. Rev. A 2012, 85, 013418. [Google Scholar] [CrossRef]
- Yuan, K.-J.; Bandrauk, A.D. Circularly polarized attosecond pulses from molecular high-order harmonic generation by ultrashort intense bichromatic circularly and linearly polarized laser pulses. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 074001. [Google Scholar] [CrossRef]
- Yuan, K.J.; Bandrauk, A.D. Single circularly polarized attosecond pulse generation by intense few cycle elliptically polarized laser pulses and terahertz fields from molecular media. Phys. Rev. Lett. 2013, 110, 023003. [Google Scholar] [CrossRef] [PubMed]
- Fleischer, A.; Sidorenko, P.; Cohen, O. Generation of high-order harmonics with controllable elliptical polarization. Opt. Lett. 2013, 38, 223–225. [Google Scholar] [CrossRef] [PubMed]
- Medišauskas, L.; Wragg, J.; Van Der Hart, H.; Ivanov, M.Y. Generating Isolated Elliptically Polarized Attosecond Pulses Using Bichromatic Counterrotating Circularly Polarized Laser Fields. Phys. Rev. Lett. 2015, 115, 153001. [Google Scholar] [CrossRef] [PubMed]
- Reich, D.M.; Madsen, L.B. A Rotating-Frame Perspective on High-Harmonic Generation of Circularly Polarized Light. Phys. Rev. A 2016, 93, 043411. [Google Scholar] [CrossRef]
- Zhou, X.; Lock, R.; Wagner, N.; Li, W.; Kapteyn, H.C.; Murnane, M.M. Elliptically polarized high-order harmonic emission from molecules in linearly polarized laser fields. Phys. Rev. Lett. 2009, 102, 073902. [Google Scholar] [CrossRef] [PubMed]
- Mairesse, Y.; Higuet, J.; Dudovich, N.; Shafir, D.; Fabre, B.; Mével, E.; Constant, E.; Patchkovskii, S.; Walters, Z.; Ivanov, M.Y.; et al. High harmonic spectroscopy of multichannel dynamics in strong-field ionization. Phys. Rev. Lett. 2010, 104, 213601. [Google Scholar] [CrossRef] [PubMed]
- Vodungbo, B.; Barszczak Sardinha, A.; Gautier, J.; Lambert, G.; Valentin, C.; Lozano, M.; Iaquaniello, G.; Delmotte, F.; Sebban, S.; Lüning, J.; et al. Polarization control of high order harmonics in the EUV photon energy range. Opt. Express 2011, 19, 4346–4356. [Google Scholar] [CrossRef] [PubMed]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photonics 2014, 8, 543–549. [Google Scholar] [CrossRef]
- Kfir, O.; Grychtol, P.; Turgut, E.; Knut, R.; Zusin, D.; Popmintchev, D.; Popmintchev, T.; Nembach, H.; Shaw, J.M.; Fleischer, A.; et al. Generation of bright phase-matched circularly-polarized extreme ultraviolet high harmonics. Nat. Photonics 2014, 9, 99–105. [Google Scholar] [CrossRef]
- Ferré, A.; Handschin, C.; Dumergue, M.; Burgy, F.; Comby, A.; Descamps, D.; Fabre, B.; Garcia, G.A.; Géneaux, R.; Merceron, L.; et al. A table-top ultrashort light source in the extreme ultraviolet for circular dichroism experiments. Nat. Photonics 2014, 9, 93–98. [Google Scholar] [CrossRef]
- Lambert, G.; Vodungbo, B.; Gautier, J.; Mahieu, B.; Malka, V.; Sebban, S.; Zeitoun, P.; Luning, J.; Perron, J.; Andreev, A.; et al. Towards enabling femtosecond helicity-dependent spectroscopy with high-harmonic sources. Nat. Commun. 2015, 6, 6167. [Google Scholar] [CrossRef] [PubMed]
- Hickstein, D.D.; Dollar, F.J.; Grychtol, P.; Ellis, J.L.; Knut, R.; Hernández-García, C.; Zusin, D.; Gentry, C.; Shaw, J.M.; Fan, T.; et al. Non-collinear generation of angularly isolated circularly polarized high harmonics. Nat. Photonics 2015, 9, 743–750. [Google Scholar] [CrossRef]
- Fan, T.; Grychtol, P.; Knut, R.; Hernández-García, C.; Hickstein, D.D.; Zusin, D.; Gentry, C.; Dollar, F.J.; Mancuso, C.A.; Hogle, C.W.; et al. Bright circularly polarized soft X-ray high harmonics for X-ray magnetic circular dichroism. Proc. Natl. Acad. Sci. USA 2015, 112, 14206–14211. [Google Scholar] [CrossRef] [PubMed]
- Kfir, O.; Grychtol, P.; Turgut, E.; Knut, R.; Zusin, D.; Fleischer, A.; Bordo, E.; Fan, T.; Popmintchev, D.; Popmintchev, T.; et al. Helicity-selective phase-matching and quasi-phase matching of circularly polarized high-order harmonics: Towards chiral attosecond pulses. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 123501. [Google Scholar] [CrossRef]
- Chen, C.; Tao, Z.; Hernández-García, C.; Matyba, P.; Carr, A.; Knut, R.; Kfir, O.; Zusin, D.; Gentry, C.; Grychtol, P.; et al. Tomographic reconstruction of circularly polarized high-harmonic fields: 3D attosecond metrology. Sci. Adv. 2016, 2, e1501333. [Google Scholar] [CrossRef] [PubMed]
- Baykusheva, D.; Ahsan, M.S.; Lin, N.; Wörner, H.J. Bicircular High-Harmonic Spectroscopy Reveals Dynamical Symmetries of Atoms and Molecules. Phys. Rev. Lett. 2016, 116, 123001. [Google Scholar] [CrossRef] [PubMed]
- Kfir, O.; Bordo, E.; Ilan Haham, G.; Lahav, O.; Fleischer, A.; Cohen, O. In-line production of a bi-circular field for generation of helically polarized high-order harmonics. Appl. Phys. Lett. 2016, 108, 211106. [Google Scholar] [CrossRef]
- Tompkins, H.; Irene, E.A. Handbook of Ellipsometry; William Andrew: Norwich, NY, USA, 2005. [Google Scholar]
- Brimhall, N.; Herrick, N.; Allred, D.D.; Turley, R.S.; Ware, M.; Peatross, J. Characterization of optical constants for uranium from 10 to 47 nm. Appl. Opt. 2010, 49, 1581–1585. [Google Scholar] [CrossRef] [PubMed]
- Neufeld, O.; Bordo, E.; Fleischer, A.; Cohen, O. High harmonic generation with fully tunable polarization by train of linearly-polarized pulses. New J. Phys. 2017, 19, 023051. [Google Scholar] [CrossRef]
- Milošević, D.B. Circularly polarized high harmonics generated by a bicircular field from inert atomic gases in the p state: A tool for exploring chirality-sensitive processes. Phys. Rev. A 2015, 92, 43827. [Google Scholar] [CrossRef]
- Barth, I.; Lein, M. Numerical verification of the theory of nonadiabatic tunnel ionization in strong circularly polarized laser fields. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 204016. [Google Scholar] [CrossRef]
- Fleck, J.A.; Morris, J.R.; Feit, M.D. Time-dependent propagation of high energy laser beams through the atmosphere. Appl. Phys. 1976, 10, 129–160. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck, J.A.; Steiger, A. Solution of the Schrödinger equation by a spectral method. J. Comput. Phys. 1982, 47, 412–433. [Google Scholar] [CrossRef]
- Burnett, K.; Reed, V.C.; Cooper, J.; Knight, P.L. Calculation of the background emitted during high-harmonic generation. Phys. Rev. A 1992, 45, 3347–3349. [Google Scholar] [CrossRef] [PubMed]
- Dejan, B. Milošević Generation of elliptically polarized attosecond pulse trains. Opt. Lett. 2015, 40, 2381–2384. [Google Scholar]
- Radu, I.; Vahaplar, K.; Stamm, C.; Kachel, T.; Pontius, N.; Durr, H.A.; Ostler, T.A.; Barker, J.; Evans, R.F.L.; Chantrell, R.W.; et al. Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 2011, 472, 205–208. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neufeld, O.; Bordo, E.; Fleischer, A.; Cohen, O. High Harmonics with Controllable Polarization by a Burst of Linearly-Polarized Driver Pulses. Photonics 2017, 4, 31. https://doi.org/10.3390/photonics4020031
Neufeld O, Bordo E, Fleischer A, Cohen O. High Harmonics with Controllable Polarization by a Burst of Linearly-Polarized Driver Pulses. Photonics. 2017; 4(2):31. https://doi.org/10.3390/photonics4020031
Chicago/Turabian StyleNeufeld, Ofer, Eliyahu Bordo, Avner Fleischer, and Oren Cohen. 2017. "High Harmonics with Controllable Polarization by a Burst of Linearly-Polarized Driver Pulses" Photonics 4, no. 2: 31. https://doi.org/10.3390/photonics4020031
APA StyleNeufeld, O., Bordo, E., Fleischer, A., & Cohen, O. (2017). High Harmonics with Controllable Polarization by a Burst of Linearly-Polarized Driver Pulses. Photonics, 4(2), 31. https://doi.org/10.3390/photonics4020031



