High-Resolution Arrayed-Waveguide-Gratings in Astronomy: Design and Fabrication Challenges
Abstract
:1. Introduction
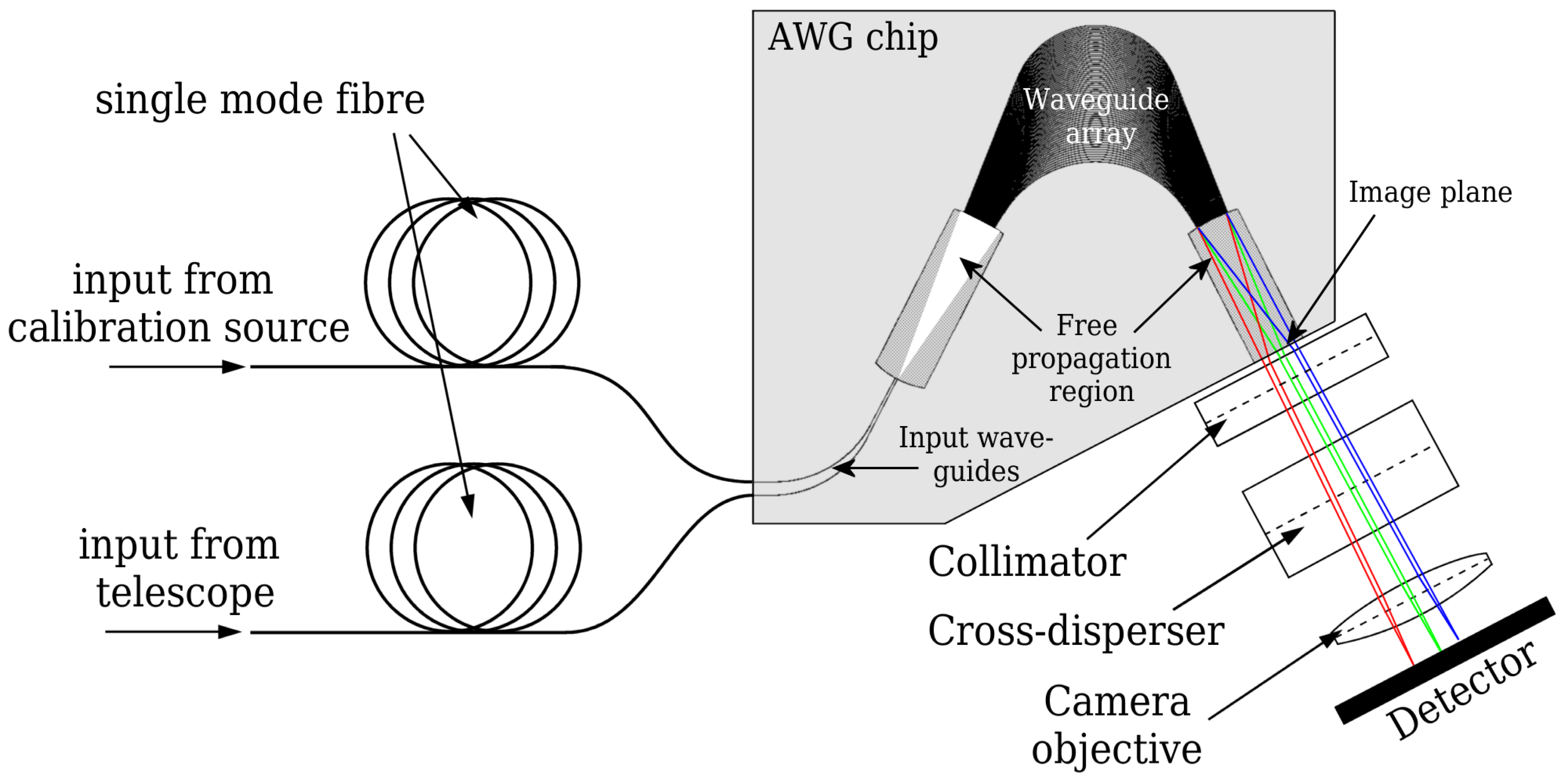
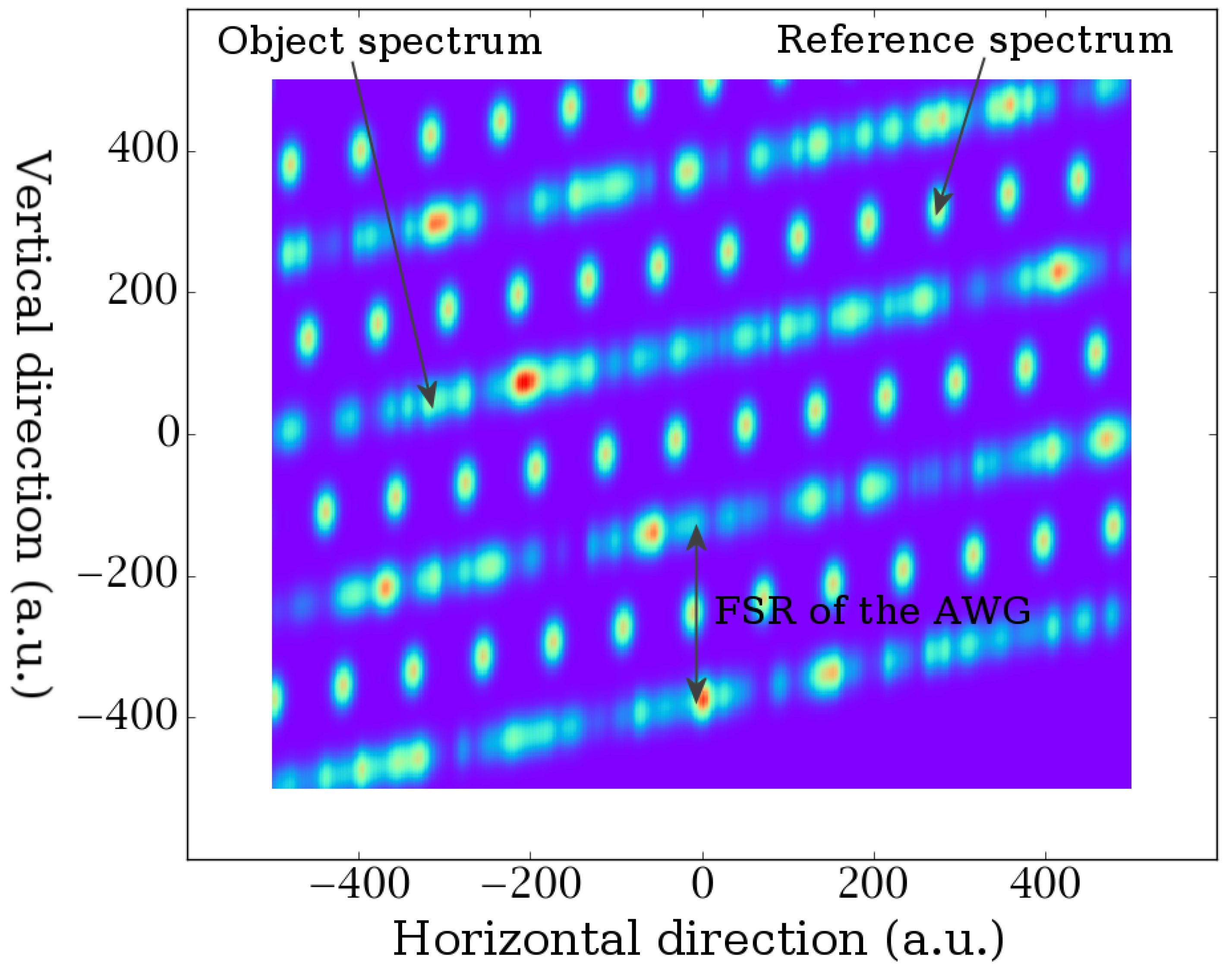
2. Principle of the AWG-Based IPS
3. Features of the AWG Design
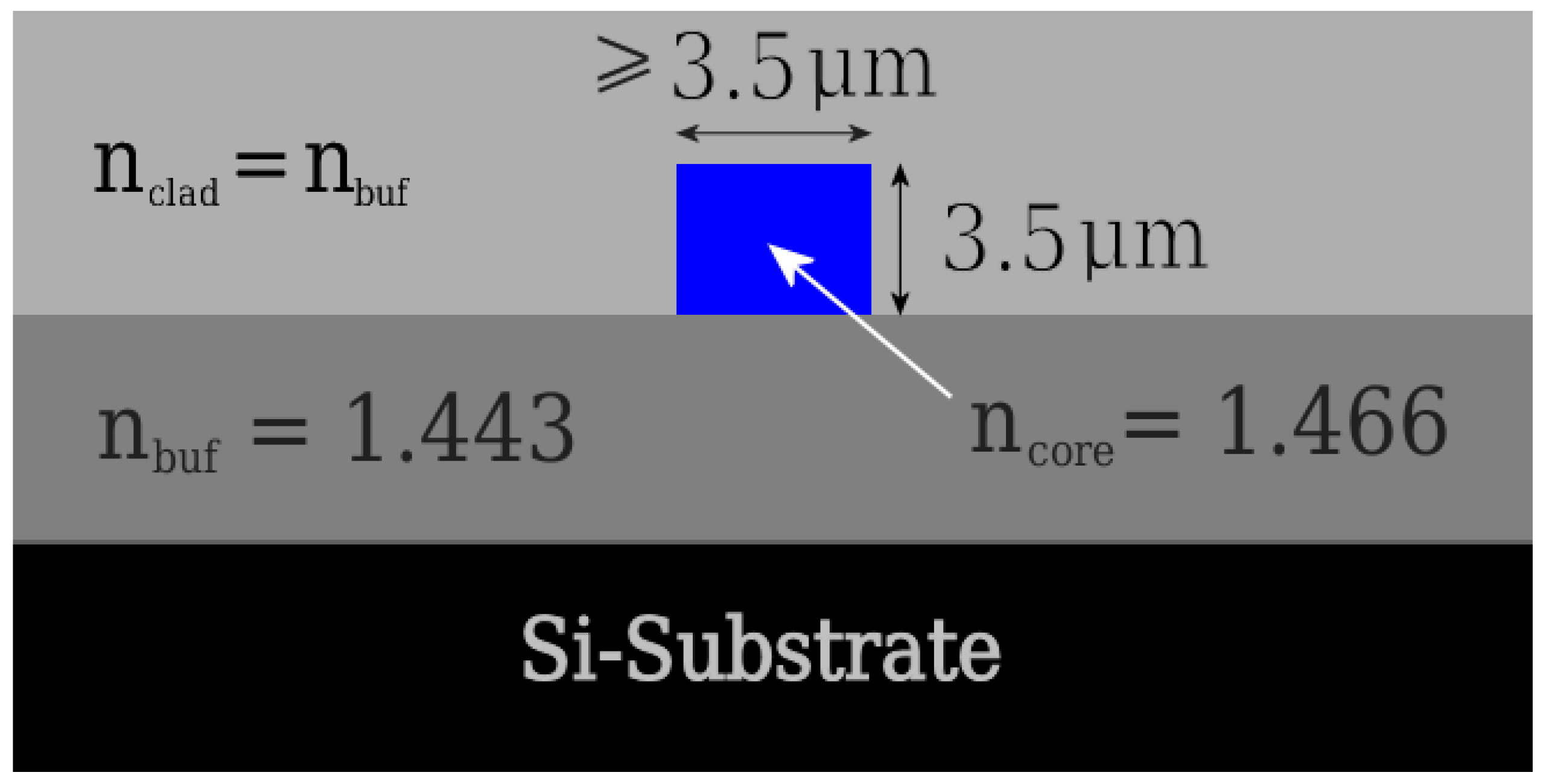
3.1. Target Application and Material Platform
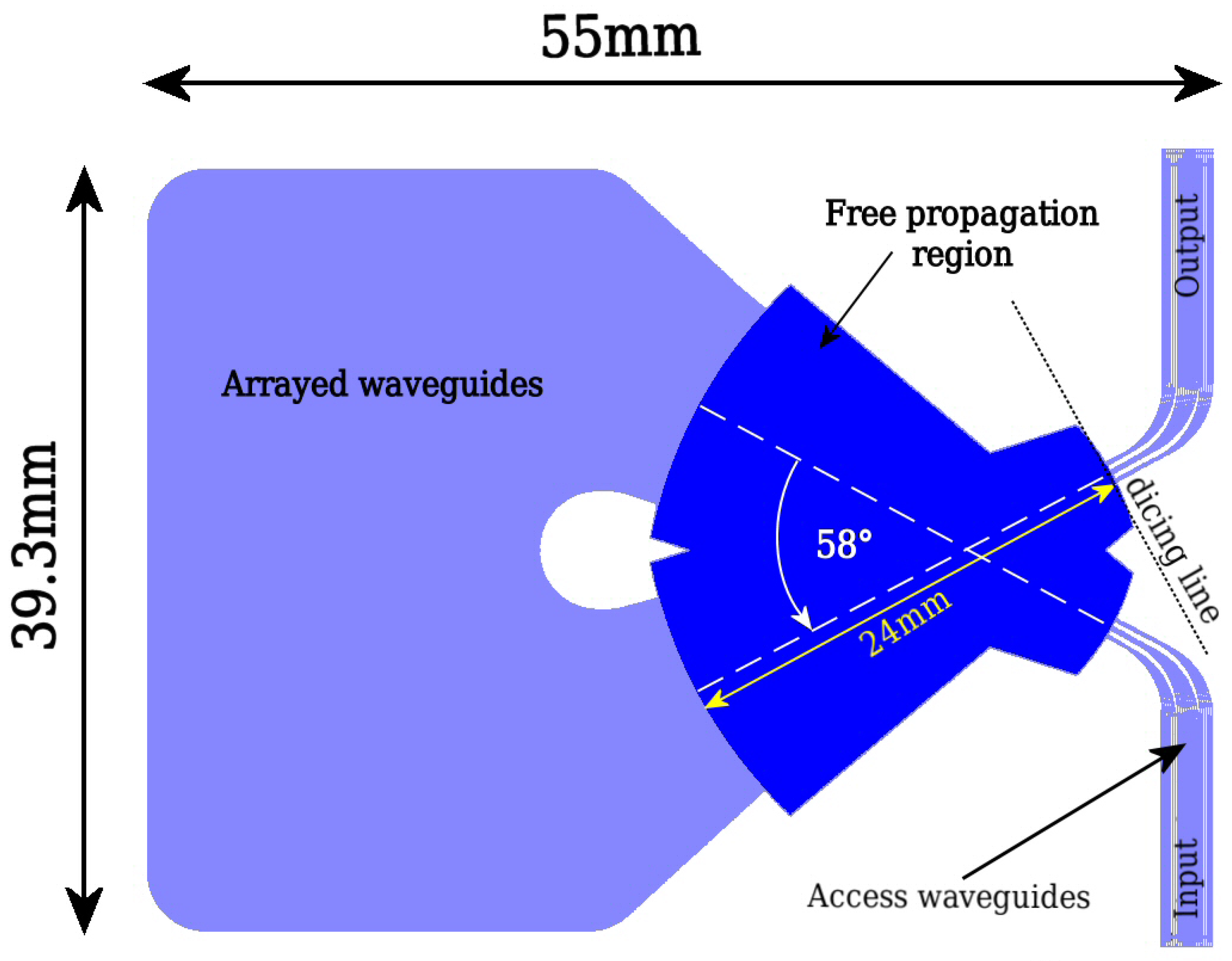
3.2. General Structure of the AWG
3.3. Customized Input Waveguide Interface
3.4. Loss Reduction by Modification of the FPR-Array Interface
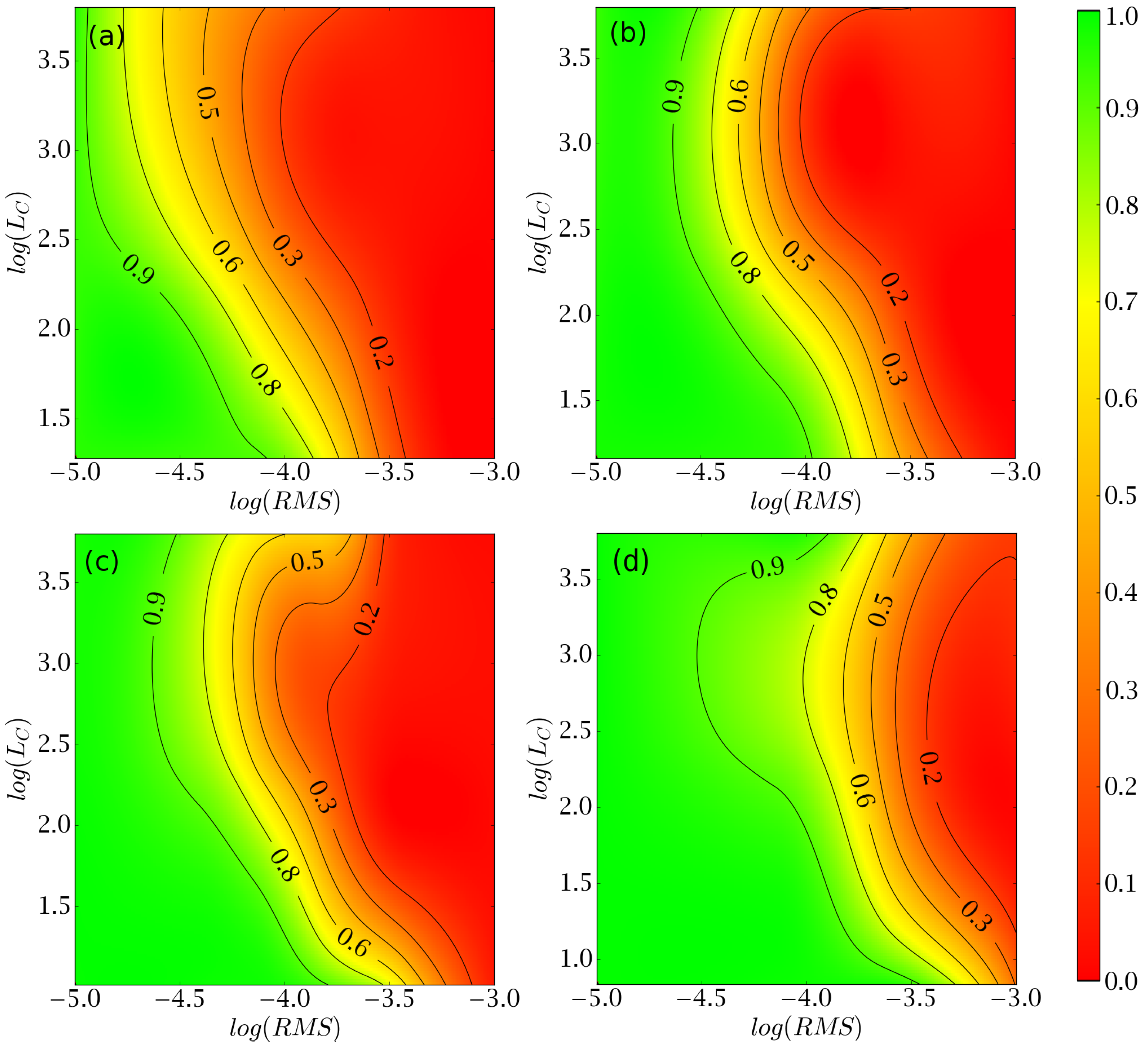
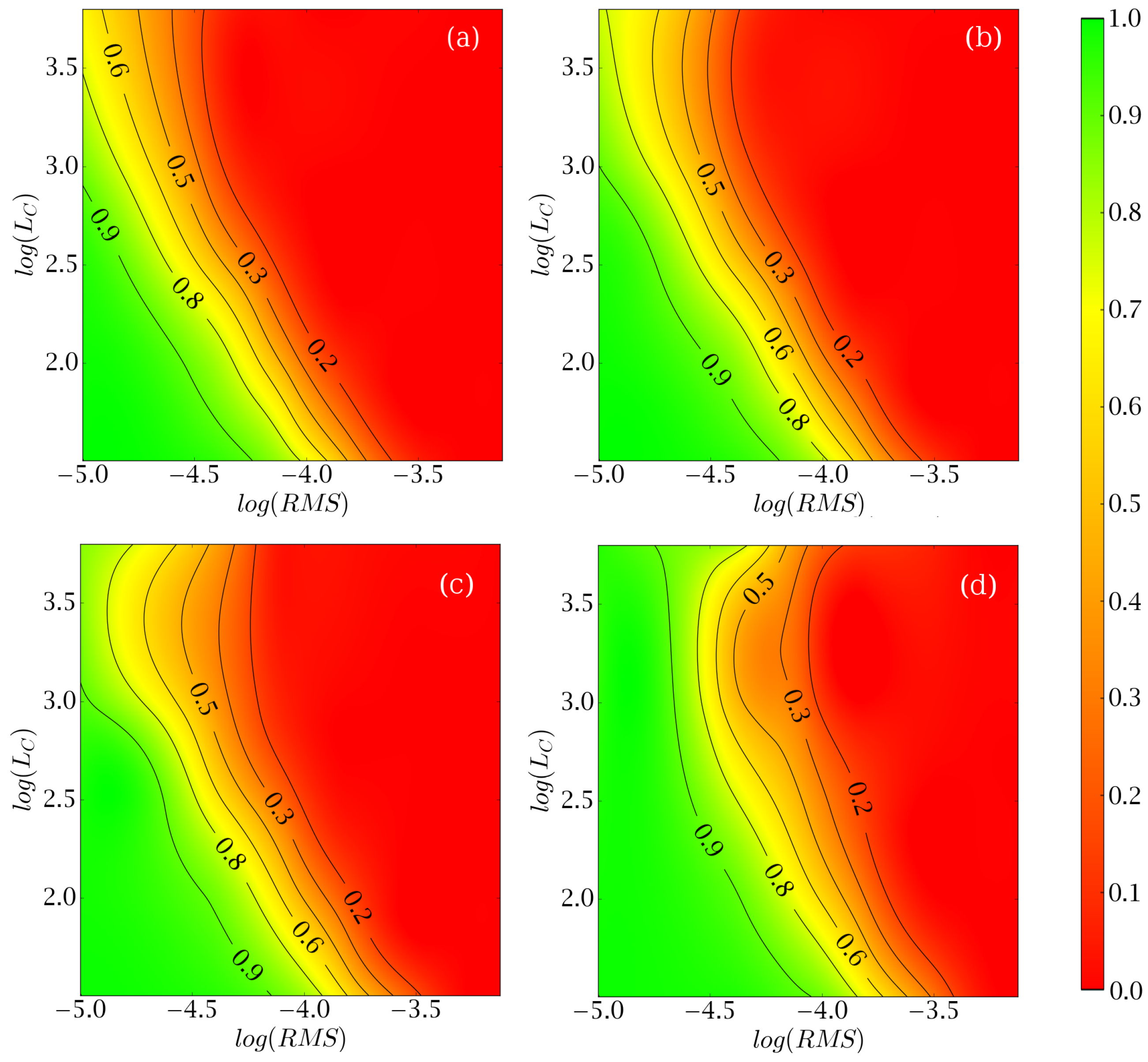
4. Fabrication-Tolerance Investigation
4.1. Effects of Random Perturbations of the Refractive Index Distribution in the FPR
4.2. Effects of Random Effective RI Variations in the Waveguide Array Region
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Smit, M.K. New focusing and dispersive planar component based on an optical phased array. Electron. Lett. 1988, 24, 385–386. [Google Scholar] [CrossRef]
- Takahashi, H.; Suzuki, S.; Kato, K.; Nishi, L. Arrayed-waveguide grating for wavelength division multi/demultiplexer with nanometer resolution. Electron. Lett. 1990, 26, 87–88. [Google Scholar] [CrossRef]
- Dragone, C. An N×N optical multiplexer using a planar arrangement of two star couplers. IEEE Photonics Technol. Lett. 1991, 3, 812–815. [Google Scholar] [CrossRef]
- Ismail, N.; Choo-Smith, L.P.; Wörhoff, K.; Driessen, A.; Baclig, A.C.; Caspers, P.J.; Puppels, G.J.; de Ridder, R.M.; Pollnau, M. Raman spectroscopy with an integrated arrayed-waveguide grating. Opt. Lett. 2011, 36, 4629–4631. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Liu, X. Fiber Bragg grating sensors interrogation system using arrayed waveguide gratings demultiplexer. In Proceedings of the 2009 Asia Communications and Photonics Conference and Exhibition (ACP), Shanghai, China, 2–6 November 2009. [Google Scholar]
- Yebo, N.A. On-Chip Arrayed Waveguide Grating Interrogated Silicon-on-Insulator Microring Resonator-Based Gas Sensor. IEEE Photonics Technol. Lett. 2011, 23, 1505–1507. [Google Scholar] [CrossRef]
- Bland-Hawthorn, J.; Horton, A. Instruments without optics: an integrated photonic spectrograph. Proc. SPIE 2006, 21. [Google Scholar] [CrossRef]
- Jovanovic, N.; Schwab, C.; Cvetojevic, N.; Guyon, O.; Martinache, F. Enhancing Stellar Spectroscopy with Extreme Adaptive Optics and Photonics. Publ. Astron. Soc. Pac. 2016, 128, 970. [Google Scholar] [CrossRef]
- Harris, R.J.; Allington-Smith, J.R. Applications of Integrated Photonic Spectrographs in astronomy. Mon. Not. R. Astron. Soc. 2013, 428, 3139–3150. [Google Scholar] [CrossRef]
- Cvetojevic, N.; Lawrence, J.S.; Ellis, S.C.; Bland-Hawthorn, J.; Haynes, R.; Horton, A. Characterization and on-sky demonstration of an integrated photonic spectrograph for astronomy. Opt. Express 2009, 17, 18643–18650. [Google Scholar] [CrossRef] [PubMed]
- Cvetojevic, N.; Jovanovic, N.; Betters, C.; Lawrence, J.S.; Ellis, S.C.; Robertson, G.; Bland-Hawthorn, J. First starlight spectrum captured using an integrated photonic micro-spectrograph. Astron. Astrophys. 2012, 544. [Google Scholar] [CrossRef]
- Imran Akca, B.; Sengo, G.; Pollnau, M.; Driessen, A.; Wörhoff, K.; de Ridder, R.M. Flat-focal-field integrated spectrometer using a field-flattening lens. Opt. Lett. 2012, 37, 4281–4283. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Wong, W.H.; Pun, E.Y.B.; Yan, Y.; Wang, D.; Yi, D.; Jin, G. Design of flat-field arrayed waveguide grating with three stigmatic points. Opt. Quantum Electron. 2003, 35, 783–790. [Google Scholar] [CrossRef]
- Kaltenegger, L.; Traub, W.A. Transits of Earth-Like Planets. Astrophys. J. 2009, 698, 519–527. [Google Scholar] [CrossRef]
- Corning Inc. Product Information PI1036; Corning Inc.: Corning, NY, USA, 2002. [Google Scholar]
- Wörhoff, K.; Heideman, R.G.; Leinse, A.; Hoekman, M. TriPleX: A versatile dielectric photonic platform. Adv. Opt. Technol. 2015, 4, 189–207. [Google Scholar] [CrossRef]
- Bauters, J.; Heck, M.; John, D.; Tien, M.; Li, W.; Barton, J.; Blumenthal, D.; Bowers, J.; Leinse, A.; Heideman, R. Ultra-low-loss Single-mode Silicon Nitride Waveguides with 0.7 dB/m Propagation Loss. In Proceedings of the 37th European Conference and Exposition on Optical Communications, OSA Technical Digest (CD) (Optical Society of America, 2011), Geneva, Switzerland, 18–22 September 2011. [Google Scholar]
- Adar, R.; Serbin, M.R.; Mizrahi, V. Less than 1 dB per meter propagation loss of silica waveguides measured using a ring resonator. J. Lightwave Technol. 2002, 12, 1369–1372. [Google Scholar] [CrossRef]
- Beelen, G.B.L.; Bulthuis, H.F. Folded AWG Architecture. U.S. Patent 7,382,953, 3 June 2008. [Google Scholar]
- Okamoto, K.; Ishii, M.; Hibino, Y.; Ohmori, Y. Fabrication of variable bandwidth filters using arrayed-waveguide gratings. Electron. Lett. 1995, 31, 1592–1593. [Google Scholar] [CrossRef]
- Okamoto, K. Fundamentals of Optical Waveguides, 2nd ed.; Academic Press: Burlington, VT, USA, 2005. [Google Scholar]
- Jaglarz, J. Description of Topography of Surfaces and Thin Films with the use Fourier Transformation, Obtained from Non-Standard Optical Measurements. In Fourier Transforms—New Analytical Approaches and FTIR Strategies; Nikolic, G., Ed.; INTECH: Rijeka, Croatia, 2011. [Google Scholar]
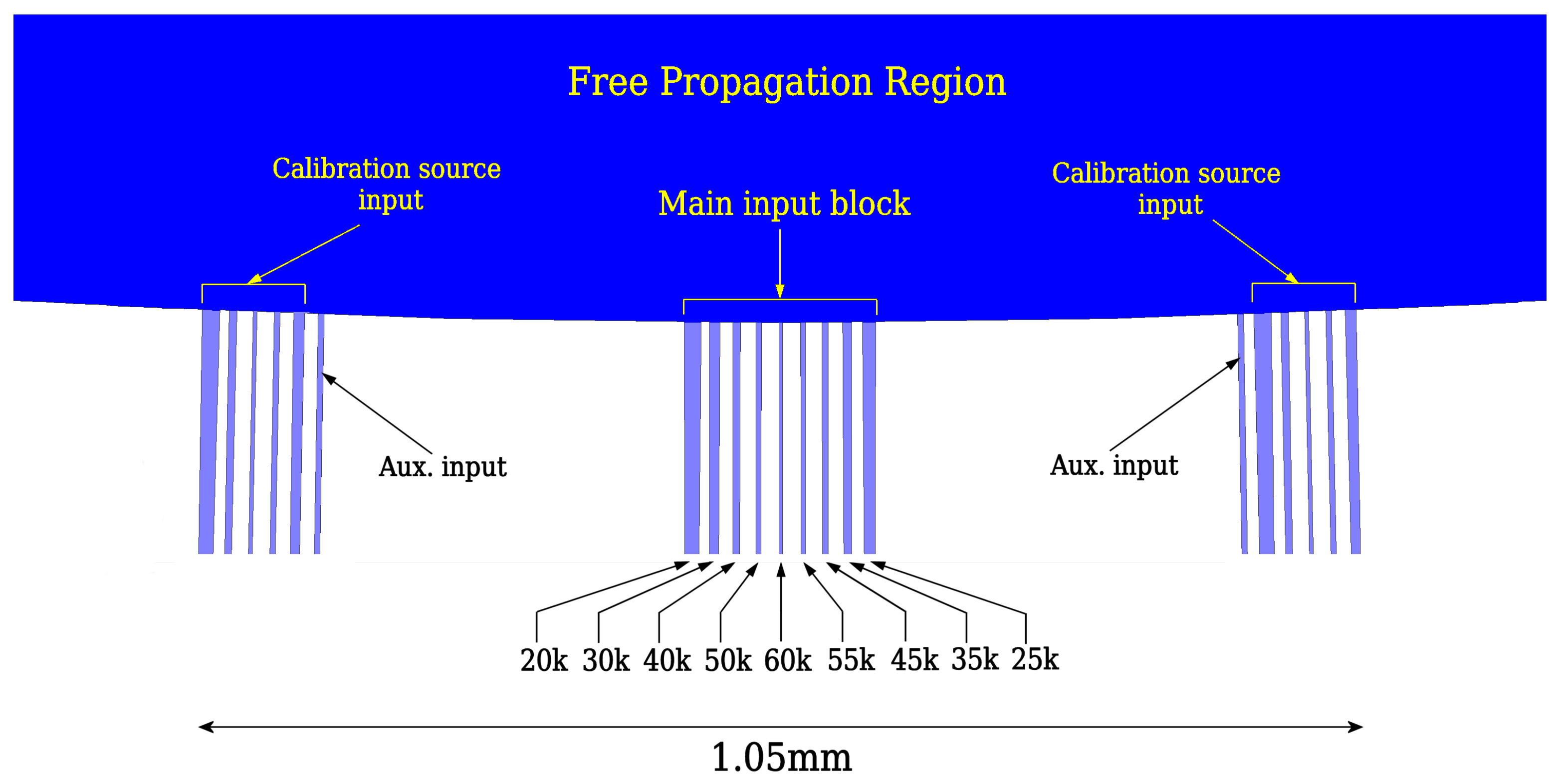
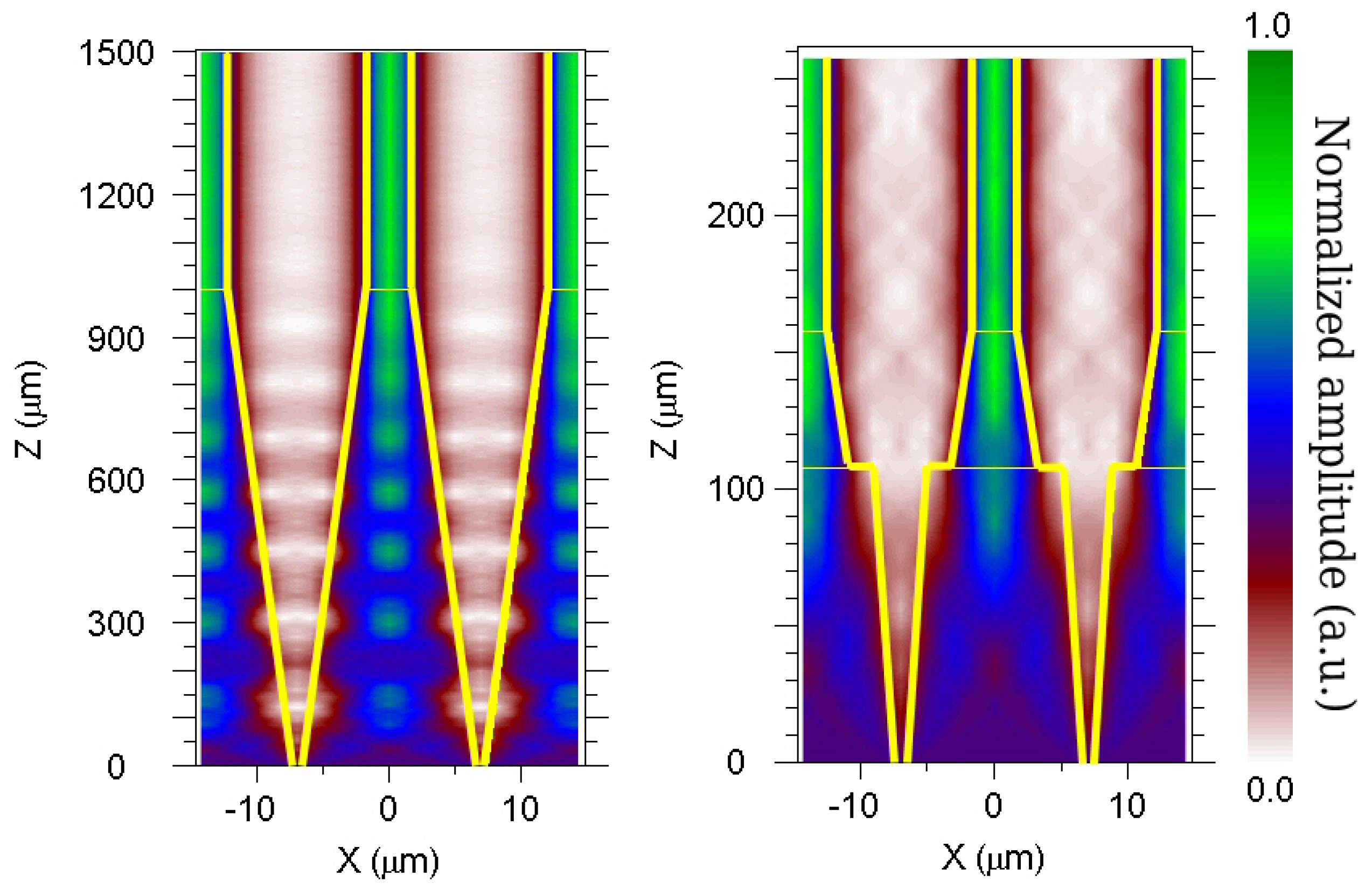
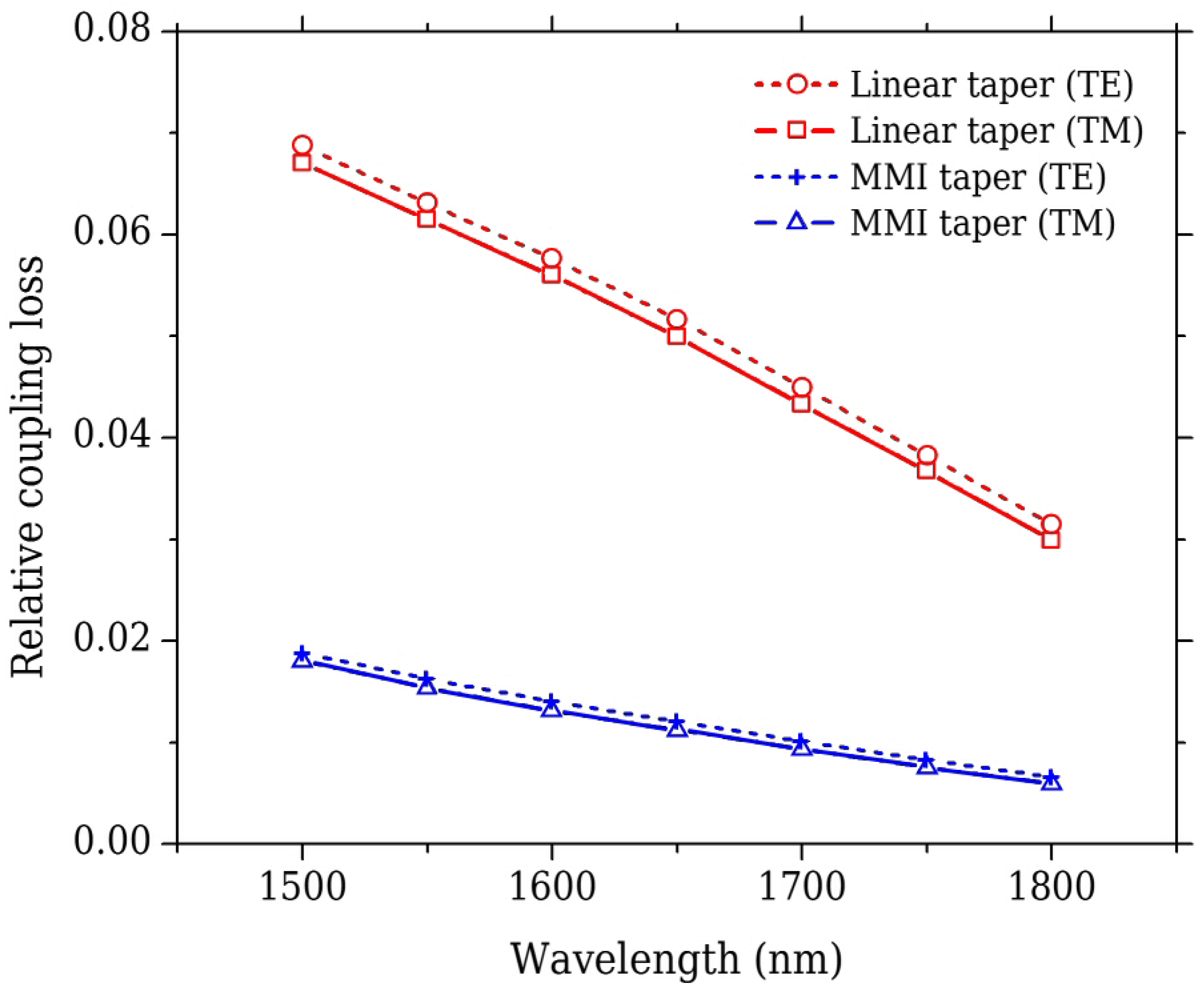
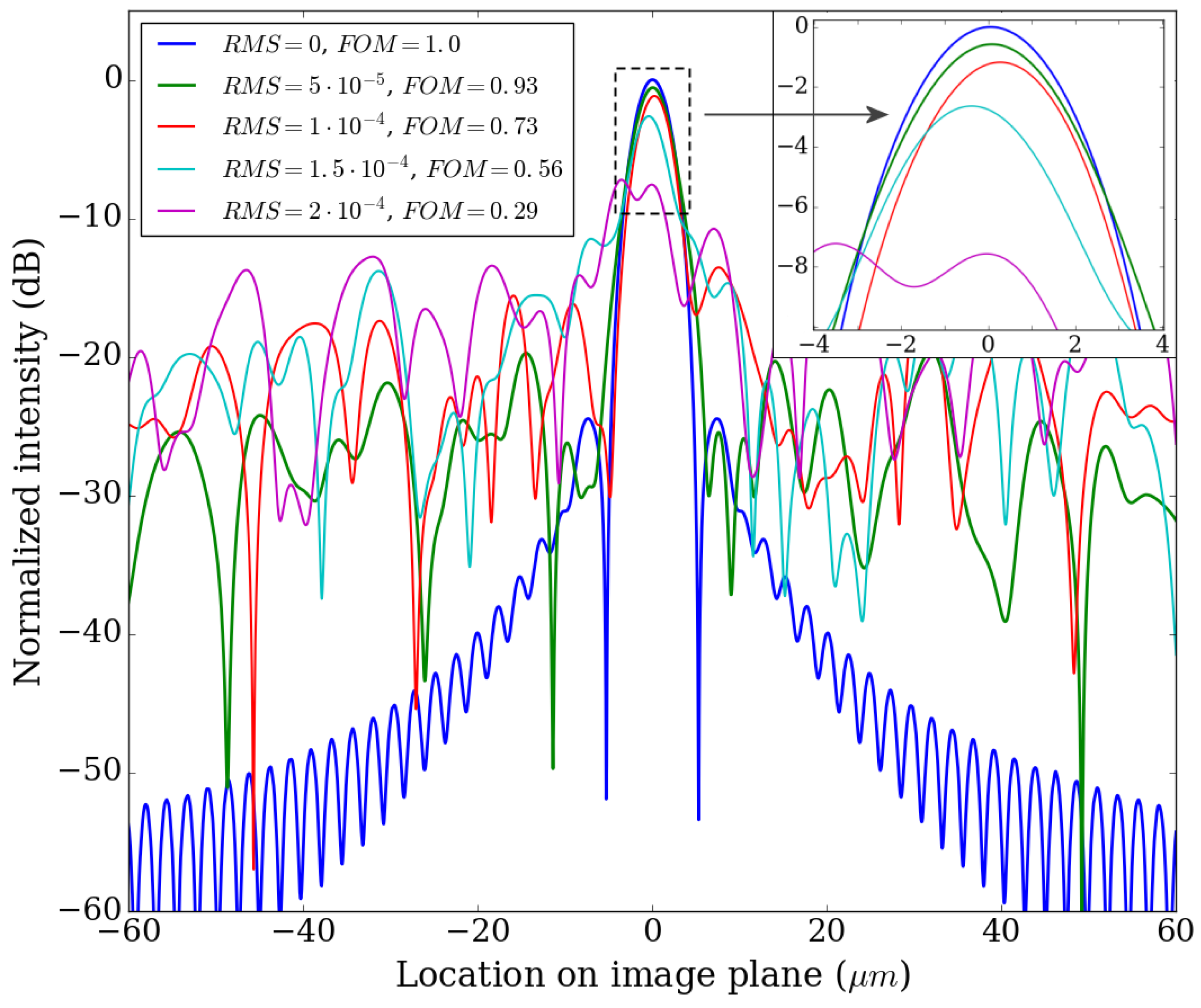
| λ/Δλ | 20 k | 25 k | 30 k | 35 k | 40 k | 45 k | 50 k | 55 k | 60 k |
|---|---|---|---|---|---|---|---|---|---|
| Width (μm) | 16.03 | 12.42 | 10.02 | 8.30 | 7.01 | 6.01 | 5.20 | 4.55 | 3.5 |
| Location (μm) | −80 | 80 | −60 | 60 | −40 | 40 | −20 | 20 | 0 |
| R | 60 k | 45 k | 30 k | 15 k | |
|---|---|---|---|---|---|
| Lc | |||||
| 100 m | |||||
| 500 m | |||||
| 1000 m | |||||
| 3000 m | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stoll, A.; Zhang, Z.; Haynes, R.; Roth, M. High-Resolution Arrayed-Waveguide-Gratings in Astronomy: Design and Fabrication Challenges. Photonics 2017, 4, 30. https://doi.org/10.3390/photonics4020030
Stoll A, Zhang Z, Haynes R, Roth M. High-Resolution Arrayed-Waveguide-Gratings in Astronomy: Design and Fabrication Challenges. Photonics. 2017; 4(2):30. https://doi.org/10.3390/photonics4020030
Chicago/Turabian StyleStoll, Andreas, Ziyang Zhang, Roger Haynes, and Martin Roth. 2017. "High-Resolution Arrayed-Waveguide-Gratings in Astronomy: Design and Fabrication Challenges" Photonics 4, no. 2: 30. https://doi.org/10.3390/photonics4020030
APA StyleStoll, A., Zhang, Z., Haynes, R., & Roth, M. (2017). High-Resolution Arrayed-Waveguide-Gratings in Astronomy: Design and Fabrication Challenges. Photonics, 4(2), 30. https://doi.org/10.3390/photonics4020030





