Abstract
Vortex light beams are structures of the electromagnetic field with a spiral phase ramp around a point-phase singularity. These vortices have many applications in the optical regime, ranging from optical trapping and quantum information to spectroscopy and microscopy. The extension of vortices into the extreme-ultraviolet (XUV)/X-ray regime constitutes a significant step forward to bring those applications to the nanometer or even atomic scale. The recent development of a new generation of X-ray sources, and the refinement of other techniques, such as harmonic generation, have boosted the interest of producing vortex beams at short wavelengths. In this manuscript, we review the recent studies in the subject, and we collect the major prospects of this emerging field. We also focus on the unique and promising applications of ultrashort XUV/X-ray vortex pulses.
1. Introduction
The mechanical properties of light have been known, or at least suspected, since Kepler conjectured the Sun’s radiation pressure to explain the tails of comets. With the development of Maxwell’s unified theory of electric, magnetic and optical phenomena, a quantitative description of such effects became possible. Just as it occurs with matter, electromagnetic radiation was shown to carry energy as well as linear and angular momenta. It was therefore expected that, under suitable conditions, the momentum exchange should be observable during the interaction of radiation and matter.
In 1909, Poynting demonstrated the connection of the angular momentum of light to its polarization [1]. It is actually well known that each photon of a collimated circularly polarized beam carries of angular momentum, which is called spin angular momentum (SAM). Eight decades later, in 1992, Allen and coworkers [2] demonstrated a way to generate laser beams having a orbital angular momentum (OAM) imprinting helical phase fronts with azimuthal dependence . In such beams, each photon carries OAM, in addition to SAM, along the propagation direction. While this transverse spatial mode of light is related to OAM, the polarization is related to SAM. Different experimental observations have demonstrated that both angular momenta, OAM and SAM, can be transferred to macroscopic objects [2,3], paving the way to new opto-mechanical devices, at least for visible and long wavelength light.
OAM beams have opened a wide range of applications in the optical regime. The transversal structure allows for spatial optical trapping of microscopic objects, with interesting applications on micromachine and biotechnology, and phase-contrast microscopy [4,5]. On the other hand, the exchange of momentum—the possibility to transfer OAM from light to atoms, molecules, or an ensemble of atoms—arose interesting applications in quantum optics, quantum communication and information [6]. Since 1992, we have witnessed an extraordinary progress in different and multidisciplinary fields using optical vortices.
In recent years the production of XUV/X-ray vortices has been boosted by the interest to extend microscopy and spectroscopy applications down to the atomic and nanometric scale. Short wavelengths drastically reduce the diffraction limit, but also make it possible to generate ultrashort pulses in the femtosecond (10 s) and attosecond (10 s) regimes, opening the door to “real time” observation at the natural time scales of electron and nuclei motion.
Nowadays there are two main methods to produce ultrashort XUV/X-ray pulses: using laser-based or accelerator-based sources. In this manuscript we review the recent studies in the emerging field of short wavelength vortex production and we summarize some of the most promising applications that resort to ultrashort XUV/X-ray vortex pulses.
2. Generation of XUV Vortices with Laser-Based Sources
Since 1985, with the development of the chirped pulse amplification (CPA) technique [7], we have seen an extraordinary progress in the production of high-power ultrashort lasers. Intense infrared (IR) ultrashort pulses of femtosecond duration, from single-cycle to several dozens of femtoseconds or above, are produced using typically a broadband gain material such as Ti:Sapphire. These ultrashort lasers have opened new possibilities to use the light-matter interaction for a large number of applications in different fields of chemistry, biology, medicine, materials science and physics.
There are two main schemes to generate XUV/X-ray light using intense lasers: a gas-phase atomic target interacting with a moderately-intense (10–10 W/cm) laser pulse, the so-called high-order harmonic generation (HHG), and a plasma interacting with an intense (>10 W/cm) laser pulse. In the following, we collect the recent theoretical proposals to generate vortex XUV/X-ray pulses using these schemes. At the end of this section we also revise some recent proposals to generate vortices in the XUV/X-ray regime based on a Compton backscattering scheme, where an intense laser pulse interacts with a relativistic electron beam, moving in the direction opposite to the laser pulse.
2.1. High Harmonic Vortex Generation
Although X-ray optics can be used to imprint angular momentum onto XUV and X-ray light, in practice such optics are challenging to fabricate and have poor throughput and limited bandwidth. A novel and appealing option is the direct generation of XUV/soft X-ray beams carrying OAM through HHG. The basic mechanism underlying HHG is based on nonlinear optics, and opens a rich scenario where the production of laser-driven coherent XUV/soft X-rays can be precisely controlled.
The nonlinear process of HHG is induced during the interaction of intense lasers with atoms, molecules, and clusters [8,9]. In contrast to perturbative harmonic generation, HHG is a non-perturbative process, as the strong field involved in HHG is comparable to the binding Coulomb field in an atom or molecule. It can be understood with a simple semiclassical picture [10,11]: the electron in a valence shell is promoted into the continuum via tunnel ionization. The electron is driven far from the parent system and driven back by the oscillating electromagnetic laser field, acquiring kinetic energy from it. This continuum electron may rescatter with the parent system and induce the emission of a high-energy photon whose frequency extends into the XUV and even the soft X-ray region. The common scenario in actual laboratories consists of focusing an intense IR femtosecond laser pulse into a gas target. The target, usually atomic, is commonly found in experiments as a gas jet, a gas cell, or a gas-filled capillary. The high nonlinear interaction between the IR field and each atom results in the emission of high-order harmonics of the central frequency of the fundamental IR field. Notably, radiation emitted by the atoms is coherent. Hence, the harmonic signal reaching the detector is strongly affected by the phase-matching between the driving IR field and the high-order harmonics as they propagate through the target medium [12]. Thus, HHG radiation results from the interplay between the microscopic single-atom emission and the macroscopic superposition of the emitted radiation from all atoms in the target. Harmonic energies up to the soft X-ray regime have been demonstrated using mid-infrared [13,14] and vacuum ultraviolet [15] driving lasers. Interestingly, high-order harmonics are emitted in the form of extremely short laser pulses, in particular with pulse duration in the attosecond and femtosecond regimes [8,9].
A remarkable aspect of HHG is its fully coherent nature, mapping characteristics of the driver to the high-frequency harmonics. This property makes it possible to control the angular momentum features of the HHG radiation through the nonlinear interaction of the driving field with the target medium. The production of XUV vortices is achieved when the driving IR beam is also a vortex, as depicted in Figure 1. The different emitters in the target perceive a different phase due to the helical phase structure of the driving beam. The local phase is imprinted to the harmonics, resulting also in vortex structures after the coherent superposition of the emission from the different points in the target. Harmonic vortices with different OAM modes have been obtained tailored by the driving beam, as we show in the following sections.
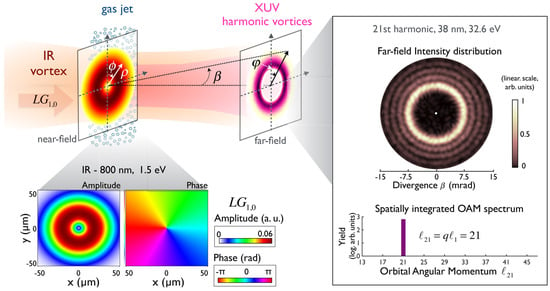
Figure 1.
Left panel: scheme of the OAM-HHG scenario when driven by a single-OAM mode (ℓ = 1). The IR driving beam (with transverse coordinates and in the near field) is focused into a gas jet, where high-order harmonics are emitted. The XUV harmonic beams are detected in the far field, where they are represented by the divergence and azimuth coordinates. The bottom insets show the IR amplitude and phase of the LG driving field. Right panel: Intensity profile and OAM spectrum of the 21st emitted harmonic. Numerical results were calculated with the 3D quantum SFA model.
2.1.1. First Experiments and Theory
The first experiment by Zürch and coworkers in 2012 demonstrated the production of a low-order OAM vortex via HHG—in particular the 23rd harmonic of a 800 nm beam (around 34 eV)—[16,17]. This finding was surprising in the view of the present understanding of HHG, in which the phase of the harmonics scales roughly with the harmonic order [12]. Zürch and coworkers attribute the appearance of only low-charged vortices to parametric instabilities in the nonlinear propagation of the fundamental field.
In 2013, a theoretical approach, which considered both the generation of HHG by a single atom and the macroscopic superposition, predicted the production of high-OAM order vortices via HHG [18]. In particular, if the non-linear propagation of the driver is negligible—as in standard low density HHG experiments—each harmonic is generated with a topological charge of qℓ (q being the harmonic order and ℓ the topological charge of the driving field), see Figure 1. Shortly afterwards, this finding was experimentally proven by Gariepy et al. in Ref. [19] by measuring the transverse phase by an interferometric technique. Very recently, different approaches that make use of specific driving laser configurations have been proposed to control and tune the OAM content of the harmonic vortices [20,21,22,23], as we will describe below.
Two theoretical approaches were described in Refs. [18,24] in order to describe the nonlinear process of HHG with a vortex-structure driving beam. The first method includes a complete quantum description both at the microscopic (quantum single-atom) and 3D macroscopic (phase-matching) levels [25]. The calculation of the single-atom HHG is based on the Strong-Field Approximation (SFA) [26,27,28,29]. An extension of the standard SFA, referred as SFA+ [30,31], can also be used to correct dynamical Stark-shift effects on the ground state, relevant for driving fields with IR and mid-IR wavelengths. The effect of propagation is computed using the electromagnetic field propagator in which the target, gas jet for example, is discretized into a set of j elementary radiating volumes (typically ) [25]. Propagation effects in the fundamental field such as the dispersion due to the plasma and neutral atoms, and the group velocity walk-off during the harmonic generation process are taken into account [32]. The second method to compute HHG vortex generation is based on assuming the target as a 2D thin slab perpendicular to the propagation axis of the fundamental beam. The thin slab model (TSM) is suited for studying pure transverse phase matching and neglects other effects that are induced from the longitudinal phase matching. In the TSM, a nonlinear model is used to describe the local HHG [33] at every point in the thin slab. The harmonics detected in the far field are computed using the Fraunhofer diffraction formula. Despite its simplified approach, the TSM provides a very useful insight of the transverse phase matching effects for a vortex driving field, where it has shown excellent agreement with the 3D SFA calculations including propagation [21,24]. A review of both theoretical approaches can be found in Ref. [34].
High-order harmonics are emitted with an intrinsic phase proportional to the intensity. This phase reflects the quantum nature of HHG, where the harmonics are generated by electrons following semiclassical recollision paths [29,35]. Each cycle, two of these trajectories (long and short) contribute to the radiation of a particular harmonic, with a phase proportional to their mechanical action [12]. Therefore, any intensity variation is translated to the harmonic phase, as the trajectories leading to HHG are modified. In particular, the transverse intensity profile of the driving beam can lead to phase cancellations and to transverse phase matching effects [36]. This is specially important for the case of a vortex driver, where the singularity at the center creates a transverse annular intensity profile. The transverse phase matching leads to a different divergence angle of the harmonics generated by long and short trajectories [24]. It is possible, therefore, to select the radiation emitted from short and/or long paths and, consequently, to control the positive or negative temporal chirp of the associated attosecond pulses.
2.1.2. XUV Attosecond Helical Pulses
One of the most powerful spectroscopic tools provided by HHG is the generation XUV pulses of sub-femtosecond duration [8,9,37,38]. An attosecond pulse train (1 as s) is obtained by the selection of the higher frequency part of the harmonic spectrum that conform the plateau region [39]. There are two main ideal conditions that should be satisfied for the synthesis of attosecond pulses: the harmonic intensities should be similar and the harmonics should be phase-locked with a constant relative phase (phase locking). Those conditions are well approximated in a typical HHG scheme, and also when the driving field carries a nonzero OAM. In this later case, the similar divergence of the emitted harmonics allows the spatial superposition needed to synthesize attosecond pulses [18]. It has been shown that attosecond pulses as short as ∼200 as are possible to be generated with a vortex structure [40], the so-called attosecond helical beams. The structure and properties of helical beams are explored in Ref. [41] in terms of superposition of different OAM modes. Phase-matching control of the temporal and spatial properties of attosecond helical beams is explored in Refs. [24,42].
A recent experiment demonstrated the synthesis and characterization of XUV attosecond helical pulses [40]. In this experiment, the attosecond vortex pulse ionizes the gas target (Neon and Argon), producing electron wavepackets with helical shape. By using a well-known technique to characterize XUV attosecond pulses, called RABBIT [43] (reconstruction of attosecond beating by interference of two-photon transitions), in which synchronized XUV harmonics and IR beams ionize a target gas, the attosecond vortex pulse can be characterized. This experiment established the ground for characterizing ultrashort vortex pulses as well as opening the door for manipulating and generating helical electron bursts.
2.1.3. OAM Mode Mixing
First theoretical approaches of OAM HHG show a linear scaling law of the vortex charge with the harmonic order [18], i.e., each harmonic was generated with a topological charge of qℓ (q being the harmonic order and ℓ the topological charge of the driving field). However, the nonperturbative character of HHG modifies this law when the driving field is composed by a superposition of different OAM modes. A recent theoretical study analyzes the complexity of the twisted XUV beams generated by a driving field with non-pure OAM modes [21]. The non-pure OAM driving field presents a spatial intensity distribution in the transverse plane perpendicular to the propagation direction, with no cylindrical symmetry. As the accumulated intrinsic phase of the HHG process is intensity dependent, the coherent radiation emitted from all atoms in the gas target acquires an additional angular phase. This situation is analogous to applying a phase diffraction grating, which is dependent of the intensity distribution of the driving field, along the azimuthal coordinate, which explains the appearance of new OAM modes in the harmonic field.
In order to get a closer insight into the underlying mechanism, we consider a driving field composed of two OAM modes with the same weight: = 1 and = 2, as depicted in Figure 2. If we consider the HHG process as perturbative, the OAM buildup of the q-th order harmonic is composed of different absorption channels (q −n, n), n ranging from 0 to q, associated with the two modes of the driving field. Each channel (q −n, n) has a weight proportional to the binomial probability distribution associated with the photon number combinations of absorbing q −n photons from the mode and n photons from the mode. As a consequence, the linear OAM buildup law ( = qℓ) is expressed in the perturbative regime with two driving fields as = (q −n) + n . However, in the nonperturbative regime of HHG, the OAM build up law is expressed as = (q −n) + n + , where the new term depending on the index m represents the azimuthal diffraction order induced by the nonperturbative intrinsic phase modulation, whose upper bound is proportional to the maximum driving field intensity and depends on the short and long quantum paths [21]. By comparing the right panel of Figure 1 and Figure 2, we observe that the OAM spectrum of the emitted harmonics drastically deviates from the linear OAM law scaling in the case of a driving field with a OAM-mode superposition.
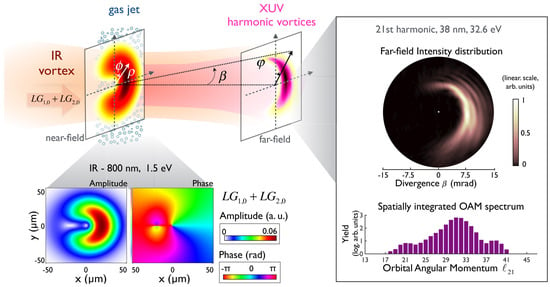
Figure 2.
Left panel: scheme of the OAM-HHG scenario when driven by a combination of = 1 and = 2 modes. The IR driving beam (with transverse coordinates and in the near field) is focused into a gas jet, where high-order harmonics are emitted. The XUV harmonic beams are detected in the far field, where they are represented by the divergence and azimuth coordinates. The bottom insets show the IR amplitude and phase of the OAM-superposition driving field. Right panel: Intensity profile and OAM spectrum of the 21st emitted harmonic. Numerical results calculated with the 3D quantum SFA model.
Note that the linear scaling law found in previous works corresponds to the collapse of this scenario for the particular case of pure (single-mode) OAM driving fields. This theoretical work shows the sensitivity of the nonperturbative aspects of strong-field interactions, which can be exploited to develop diagnostic tools for spatial intensity distributions and to tailor the OAM modes in the emitted harmonics in the XUV/X-ray regime.
2.1.4. OAM Two-Color Mixing
A promising possibility to control the topological charge in the XUV/X-ray spectral region using HHG is to employ two separate driving beams that interact in the generation medium. The two beams can have different wavelengths and can carry a different topological charge. The approach used here is similar to studies aiming to control the polarization in HHG [44,45]. A theoretical scheme was proposed in Ref. [19] in order to control the topological charge of the emitted harmonics by resorting to a non-collinear wave-mixing scheme with two-color laser beams. Recently, this scheme has been experimentally demonstrated [22]. In the experiment, one driving pulse at 800 nm carries zero OAM (Gaussian beam) and the other driving pulse at 400 nm carries a nonzero OAM (LG beam), generating high harmonics with controlled topological charge. The method allows the generation of harmonics with a low topological charge, independently of the harmonic order. This two-color experiment has been performed in a non-collinear as well as in a collinear geometry. In the non-collinear geometry, the generated harmonic beams carrying various OAM are distributed spatially with an angle related to their topological charge, while there are spatially overlapped in the collinear geometry. Notice that the same experiment has been also performed with two beams of the same wavelength [23]. These beam-mixing configurations make HHG a feasible tool to produce femtosecond XUV/X-ray pulses carrying a controllable amount of OAM. The approach can be extended to any combination of generating beams with various spatial properties and paves the route towards complete control of the spatial properties of HHG light [46].
2.2. Plasma-Based Vortex Generation
Developing ultra-intense lasers is essential to excite and to probe matter in high energy density science. One of the key challenges for generating these extreme beams resides in the breakdown thresholds of standard optical elements, which limit the energy densities that can achieved by conventional means. Instead, because it is intrinsically broken, the plasma can behave as a nonlinear optical medium capable of withstanding extremely intense electromagnetic fields, without changing its nonlinear optical properties [47].
While being exploited towards advanced acceleration concepts [48], the recent advances are pushing the technological limits of plasma sources. Stable plasma sources, with density fluctuations below the sub-percent level, and characterised by pre-designed density profiles, are now possible [49]. With these advances, the plasma can be regarded as an optical element for ultra-intense light.
The nonlinear optical properties of the plasma are mostly determined by the motion of background plasma electrons. Their motion is not bound to physical boundaries, and can be shaped nearly arbitrarily, provided that it is subject to appropriately tailored electric and magnetic fields. Hence, in addition to supporting very high intensities without breaking, the plasma can be seen as a flexible optical element, whose properties can be nearly arbitrarily shaped. Ultra-intense vortex laser pulses carrying OAM provide an additional degree of freedom to control the motion of plasma electrons at ultra-high intensities. These vortex beams are then attractive to manipulate the nonlinear optics of plasmas, and to be, in turn, manipulated by the plasmonic structures themselves.
Despite these exciting prospects, the nonlinear optics of plasmas appearing when OAM is present is yet to be assessed at ultra-high intensities. This has motivated several experimental, theoretical and numerical advances that take advantage of the nonlinear optical properties of plasmas [50,51,52,53,54,55,56,57,58,59,60,61]. The generation and amplification of vortex beams and its harmonics has been a key component of research related to these recent, but truly exciting, developments.
2.2.1. Generation and Amplification of Ultra-Intense Vortex Beams
An attractive path to create ultra-intense vortex laser pulses leverages on Raman amplification [50], relying on stimulated Raman backscattering [62,63,64]. Just as in parametric amplification using a nonlinear crystal, Raman amplification relies on a three wave process to transfer the energy of a long pump laser pulse, with frequency and wavenumber , to a counter propagating seed laser pulse, with , through the generation of a plasma wave during the interaction, with . The plasma wave plays the role of an idler wave in parametric amplification.
Stimulated Raman backscattering occurs when the frequency and wavenumber of the intervening lasers satisfy the matching conditions that ensure photon energy and momentum conservation. In the absence of OAM, seed pulse amplification then occurs when . In addition, the corresponding matching condition for the wavenumber is . The matching conditions for and k need to be supplemented by an additional condition in the presence of twisted light. This additional matching condition, which expresses conservation of OAM, leads to the generation of a plasma wave with OAM. Similarly to the wavenumber matching condition, the OAM level of the plasma wave is given , where are the orbital angular momentum levels of the plasma wave , pump , and seed . Generation (and amplification) of new OAM modes can also occur in Raman amplification when the pump beam has field components in two orthogonal polarisations, with OAM and in each polarisation [50,65]. Hence, if the seed is initially polarised only along one of them, with , a new mode, with appears to ensure momentum conservation.
Because plasma electrons can usually adjust to the beating structure of the lasers, the plasma wave can always absorb the momentum mismatch (both the linear momentum, associated with the axial laser wavenumber, and the OAM) between seed and pump lasers. Thus, the amplification of a twisted laser pulse is possible even when the pump laser contains no OAM. This property is very attractive because the amplification of twisted light and non-twisted light can then be achieved using identical experimental setups.
2.2.2. High Orbital Angular Momentum Harmonics in Plasmas
Because of energy conservation, the nth harmonic of a laser with frequency and orbital angular momentum ℓ is characterised by frequency and orbital angular momentum . Apart from an exceptional experimental result where this has not been observed [16], conservation of energy and angular momentum is usually expected to occur, and has been demonstrated experimentally [19,66]. These fundamental conservation laws appear to suggest that the OAM is always coupled to the high frequency harmonics. In strong contrast with these observations, Raman amplification can be used to generate high OAM harmonics while keeping the laser frequency unchanged, thereby manipulating the OAM as an independent degree of freedom. As a result, it may open the way to produce ultra-short vortex beams over the entire frequency spectrum and OAM range if combined with some other high harmonic generation mechanism [51].
The generation of OAM harmonics in Raman amplification can be achieved by considering a pump beam consisting of a superposition of modes with different OAM modes, as shown in Figure 3a. The high OAM harmonics obey a simple algebraic rule, where the OAM of the nth harmonic is given by , where n is an integer that refers to the harmonic order and is the difference between the OAM levels in the pump. All harmonics then appear when , even harmonics are created when both and are even, and odd when is even and is odd.
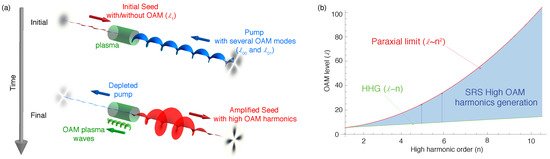
Figure 3.
(a) scheme of the OAM-HHG scenario based on Raman amplification; (b) Potential OAM range and harmonics spectrum that can be achieved when manipulating the laser OAM and frequency independently.
The high OAM harmonics are created through an angular momentum cascade, where the energy flows from lower OAM components to neighbouring modes with higher OAM. An initial seed with and pump with and , create a plasma wave that is a combination of two OAM modes, with and . The pump mode beats with the plasma wave produces a sideband component in the seed pulse with (). The other pump mode with beats with the remaining plasma wave OAM component, with , creating a seed sideband component with . Each of these seed sidebands will continue to beat with the pump, adding new OAM harmonics. The high harmonics will be generated at least up to the order allowed by the paraxial approximation, valid as long as the azimutal laser wavenumber (associated with the OAM) is smaller than the longitudinal laser wavenumber (red line in Figure 3b). If combined with conventional high harmonics generation, where the frequency and the OAM harmonics are upshifted by the same factor (red line in Figure 3b), the scheme may enable the generation of light over the full OAM-frequency spectrum (shaded blue in Figure 3b).
The generation of the OAM harmonics usually requires orbital angular momentum to be initially present. This requirement can be relaxed if circularly polarised lasers are used instead. According to theoretical and numerical calculations, the plasma can be used to convert SAM into OAM in second harmonic generation of circularly polarised photons [52]. Being an illustration of energy and angular momentum conservation, this process is also a demonstration of the spin to orbital angular momentum conversion. The process occurs when a circularly polarised photon, with wavenumber and spin angular momentum , interacts with a plasmon, with wavenumber and with no angular momentum. The plasmon can be initially produced by any high order process. During the interaction, a virtual plasmon appears with a frequency close to the optical frequency, with a wavenumber , and with an angular momentum associated with the initial photon spin. Because of energy and momentum conservation, the interaction between the virtual plasmon with another spin polarised photon produces a second harmonic photon with wavenumber and angular momentum . Because s cannot be larger than the unity, the upshifted photon OAM is finite and given by .
High vortex harmonic generation can also occur as an intense laser pulse propagates in an underdense plasma. This configuration was investigated theoretically and with numerical simulations. The mechanism for the generation of the high vortex harmonics depends on the laser polarisation. In linear polarisation, the high harmonics appear as a result of a cascade involving four-wave mixing. In circular polarisation, a three-wave mixing cascade is involved [53].
High harmonic generation using vortex beams has also been investigated theoretically, numerically and experimentally, in a configuration where an ultra-intense twisted laser pulse interacts with a plasma mirror, a solid density target where . The high harmonic generation model that is usually employed at laser intensities above is the relativistic oscillating mirror (ROM) [54]. At these intensities, the quiver motion of the electrons at the target surface is relativistic. As electrons execute periodic oscillations in the laser fields, they also emit radiation at very high harmonics, which can reach the XUV for IR lasers with central wavelength m. In the presence of twisted light, the oscillations at the target surface have an azimutal phase dependence, forming a vortex oscillating mirror (VOM) [55]. The reflected light electric (or magnetic) field, given by , can be decomposed in a Fourier series as , where is the peak normalised laser vector potential, related to the laser intensity through m and is a parameter related to the amplitude of the electron oscillations. The highest harmonic order is set by the plasma frequency, , of the solid density. Thus, efficient generation of photons with occurs. In addition, and just as in the ROM, only the odd harmonics appear.
The coherent wake emission (CWE) is a distinct mechanism for high harmonics generation, which operates at intensities well below the relativistic regime, for [56]. In the CWE, the high harmonics are generated by the periodic motion of electron bunches which are generated near the critical density. These electron bunches oscillate across the overdense plasma region, emitting a train of attosecond pulses that can be decomposed in high frequency harmonics that can extend up to the extreme ultraviolet.
The CWE of vortex light has been demonstrated experimentally, employing the 100 TW-class Ti:sapphire laser facility at CEA-IRAMIS, delivering laser pulses [57]. The optical vortex of the main laser pulse, used to drive the high harmonics, was created experimentally by introducing a spiral phase plate in the collimated laser pulse. After the spiral phase plate, the laser acquired an OAM level . The OAM corresponding to each frequency harmonic was retrieved with the aid of the interference pattern between the interacting high power beam and a reference Gaussian laser pulse. The reconstructed phase profile corresponding to each harmonic provided a clear demonstration that the upshifted frequency photons with frequency were also characterised by an OAM .
2.2.3. Plasma Holograms and Phase Plates for Ultra-Intense Lasers
The use of transient plasma gratings [58] to manipulate light at ultra-high intensities has attracted considerable experimental attention as it can be used to generate high power vortex laser beams, and their harmonics, at ultra-high intensities. Instead of being formed in an underdense plasma, as in Raman scattering, a transient plasma grating can be formed at the surface of a solid target. The use of this concept to generate intense vortex light has been recently demonstrated experimentally [59].
The starting point to understand how a transient plasma grating can form is the observation that the plasma expansion velocity at the surface of a solid target can be controlled by the local laser fluence. Consider, for instance, the interference pattern of two laser pulses colliding at an angle, characterised by a sinusoidal fluence variation. Focusing these lasers at the surface of a solid target will lead to the generation of a sinusoidally varying density profile, a transient plasma grating. Because the plasma is not bound to physical boundaries, the electron expansion can assume the shape of complex interference patterns. Using a spiral phase plate to create a vortex beam from one of the two interfering lasers, the object beam, leads to a complex interference pattern that results in a forked plasma grating. This profile can be imprinted at the surface of the solid target, forming the plasma hologram. The information stored in the transient grating can be recovered by reflecting an ultra-intense laser pulse onto its surface. This procedure allows to create very high energy replicas of the object beam in the diffracted orders. At intensities above the response of the transient plasma grating becomes strongly nonlinear, leading to the generation of high harmonics.
A complementary theoretical proposal for the generation of ultra-intense vortex beams consists of using a solid density plasma target with a azimuthally varying thickness. Numerical simulations demonstrated that an intense Gaussian beam without orbital angular momentum interacting with this plasma-based spiral phase-plate could be used to generate OAM beams.
2.3. Compton-Based Vortex Generation
Thomson or inverse Compton backscattering light source is able to generate photons in a wide energy range from the x to the gamma ray. Based on the working principle of this source, a scheme has been proposed to produce OAM beams. This scheme consists of sending a relativistic high-brightness electron beam in opposite direction to a laser beam carrying a well-defined OAM; the transfer of OAM to the emitted radiation has been studied theoretically [67,68].
3. Generation of XUV Vortices with Accelerator-Based Sources
Accelerator based light sources such as synchrotrons and free-electron lasers (FELs) are commonly used to generate coherent radiation in the XUV/X-ray spectral domain. In these two sources, light is produced by relativistic electrons wiggling inside a periodic and static magnetic field of an undulator (For Synchrotrons, Incoherent Light Is Also Generated from Bending Magnets). While synchrotrons are typically used for chemical and structural characterization at the picosecond time scale, modern FELs delivering ultra-short, high peak brightness light pulses are capable of probing structural and chemical properties of matter with a femtosecond temporal and nanometer spatial resolution.
During first experiments with accelerator-based sources, optical elements such as spiral phase plates were placed directly into the XUV/X-ray light beams to generate OAM [69,70]. However, this approach may not be a good option for high-intensity X-ray pulses, mainly due to the difficulties to fabricate high-quality optics, the lack of wavelength tunability, and the damage threshold at high intensities. Therefore, in-situ techniques such as, e.g., generation of OAM from helical undulators are being explored. Latest approaches take advantage of seeded FELs where the vortex structure can be directly imprinted onto the relativistic electron beam.
3.1. Undulator Based OAM Radiation
The transverse radiation profile from a planar undulator at the fundamental wavelength of emission is limited to a Gaussian-like mode with no azimuthal phase variation. On the other hand, an undulator also emits higher harmonics whose transverse profile depends on the undulator geometry. E.g., in a helical undulator, generating circularly polarized light, the harmonics are characterized by a vortex structure of the transverse mode and carry an OAM of (with the topological charge ), where h is the harmonic order. The theory was developed by Sasaski and McNulty [71] and experiments demonstrating this approach were performed in 2013 with a synchrotron light source [72] and 2014 with a FEL [73]. Despite the experimental simplicity, the approach suffers from low efficiency (few percent) of the undulator harmonic emission compared to the fundamental.
3.2. High-Intensity X-ray Pulses: FELs
The natural approach to generate vortex beams in a FEL is to use a seeding scheme. In a seeded FEL, an external laser imprints a periodic energy modulation at the seed wavelength onto a relativistic electron beam traveling inside the first undulator (called the modulator). This energy modulation is converted into a spatial current density modulation (bunching), after the electron beam goes through a dispersive section. The bunched beam emits coherent XUV or X-ray radiation as it travels along subsequent undulators (called radiators). In a seeded FEL, the generated pulse inherits the properties of the seed laser, in particular the high longitudinal and transversal coherence [74].
The first proposition for generation of OAM in a seeded FEL derives from the previous approach by Sasaski and McNulty. A Gaussian seed is superimposed on the electron beam in a helical undulator [75]. The resonant wavelength (equal to the seed wavelength) is set to the second harmonic resonance of the undulator instead of the fundamental (as for the standard seeded FEL). This interaction directly imposes a helical spatial structure onto the electron beam. Such a helicaly bunched beam generates an optical vortex as the beam goes through the radiator. In this case, OAM beams with a topological charge are produced at the fundamental frequency of the seed. The method therefore requires a coherent XUV or X-ray input signal.
Two other theoretical propositions exploit the harmonic seeding scheme where the emission and amplification of X-ray radiation occur at a high harmonic n of the seed. This is the working principle of High Gain Harmonic Generation (HGHG) FELs which allow generation of XUV to X-ray light starting from a visible or UV laser [74,76] (see top panel Figure 4). The simplest way to produce helical bunching would be to seed the FEL directly with an OAM beam, by putting a spiral phase mask into the path of the visible seed laser. However, this approach fails for HGHG FELs, because the frequency up-conversion produces a high order optical vortex (with , where is the topological charge of the seed). Such high order optical modes cannot be sustained during amplification in the radiator due to strong diffraction and low coupling with the electron beam. To overcome this issue, the corkscrew-like distribution is imprinted on the electron beam at the final emission wavelength, such that the topological charge does not depend on the harmonic number and is equal to unity (). The first idea is based on frequency mixing between two seed lasers in an Echo-Enabled Harmonic Generation configuration [77]. The second approach uses a particular shaping of the transverse profile of the seed laser in a HGHG FEL [78] (see bottom panels Figure 4). These seeding methods represent the most promising way to generate powerful OAM radiation. However, no experimental demonstration has been carried out so far in the short wavelength range.
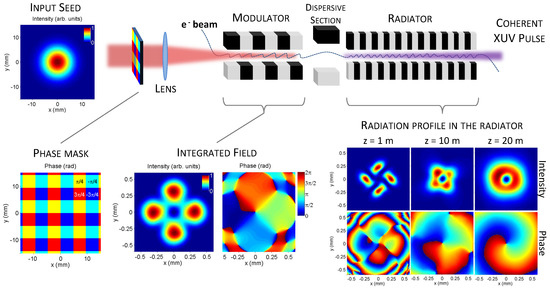
Figure 4.
Top panel: Seeded FEL working in the HGHG configuration (excluding the phase mask). Bottom panels: OAM generation based on the transverse shaping of an initially Gaussian seed laser. The phase mask is used to modulate the transverse intensity and phase distributions of the seed that interacts with the electron beam along the modulator. The four-quadrant staircase-like phase dependence of the seed is then transferred to the electron beam. In the radiator, the electron beam generates XUV radiation that evolves into an OAM mode after amplification in a, e.g., 20-m-long radiator.
4. Perspectives and Applications
Novel sources capable of generating vortices at short wavelengths not only offer the possibility of extending previous applications of optical vortices in the XUV/X-ray regime, but also of exploring and developing applications with no precedence. For example, absorption and photoionization of atoms, molecules, and nanostructures with vortex beams offer a richer light-matter interaction beyond the customary plane-wave selection rules [79,80,81,82,83,84,85,86,87,88,89]. Those open new prospects for spectroscopy in the XUV and X-ray regime, such as exciting forbidden-electric-dipole transitions in quantum dots [90], discerning the magnetic sublevels in atoms and clusters [91], inducing charge current loops in fullerenes controlled by the topological charge of the vortex [92], novel dichroism absorption spectroscopy beyond circularly polarized light [93,94,95], and for the production of unconventional skyrmionic defects [96], which are very promising to produce magnetic memory devices at the nanometer scale [97]. The ionization of atoms with attosecond vortex pulses can also have further applications to tailor and manipulate the ionized electron wavepackets, imprinting an helical phase [40]. Those helical electron bursts can be used for spectroscopy and microscopy applications in condensed matter systems [98,99]. Here we should also note another type of helical electron bursts produced by two circularly polarized pulses instead of pulses carrying OAM [100,101]. Other schemes have been proposed for X-ray spectroscopy based on scattering rather than absorption. A resonant inelastic spontaneous scattering has been theoretically studied for molecular vibrational spectroscopy [102]. Also, the possibility to explore the dynamics of magnetic vortices have been proposed with resonant OAM X-ray scattering [103]. X-ray vortices can also find applications in which spatial coherence is required, such as coherent phase-contrast imaging or ptychography [104,105]. Also in the excitation of nuclear transitions that requiere large amount of angular momentum [106].
Optical vortices in the XUV/X-ray regime can also be generated in the form of attosecond and femtosecond pulses. This ultrashort pulse duration allows the study of very fast dynamics with time-resolved schemes combined with the unique properties of vortex pulses. This is definitely a new landscape ideal to be explored with the new generation of ultrashort vortex pulses.
Although SAM and OAM stand for different properties of light, they are not independent, and light beams are known to exchange SAM and OAM at the nanoscale [107,108,109,110]. A recent work has proven that fractional OAM harmonics can be generated through HHG in an scheme where OAM and SAM are conserved separately [111]. On the other hand, vector beams, i.e., beams with varying spatial polarization [112], are nowadays produced in the XUV regime [113] and they could be used to trigger SAM-OAM interaction in harmonic generation schemes. Whether OAM and SAM are exchanged in the HHG process remains unobserved.
Acknowledgments
A.P. acknowledges support from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 702565. C.H.-G. acknowledges support from the Marie Curie International Outgoing Fellowship within the EU Seventh Framework Programme for Research and Technological Development (2007-2013), under REA grant Agreement No 328334. We acknowledge support and from Junta de Castilla y León (Project SA046U16) and MINECO (FIS2013-44174-P, FIS2015-71933-REDT, FIS2016-75652-P).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Poynting, J.H. The Wave Motion of a Revolving Shaft, and a Suggestion as to the Angular Momentum in a Beam of Circularly Polarised Light. Proc. R. Soc. Lond. A 1909, 82, 560. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Beth, B. Mechanical Detection and Measurement of the Angular Momentum of Light. Phys. Rev. 1936, 50, 115. [Google Scholar] [CrossRef]
- Allen, L.; Barnett, S.M.; Padgett, M.J. (Eds.) Optical Angular Momentum; Institute of Physics Publishing: Bristol, UK, 2003. [Google Scholar]
- Andrews, D.L.; Babiker, M. (Eds.) The Angular Momentum of Light; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Torres, J.P.; Torner, L. (Eds.) Twisted Photons; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219. [Google Scholar] [CrossRef]
- Agostini, P.; DiMauro, L.F. The physics of attosecond light pulses. Rep. Prog. Phys. 2004, 67, 813–855. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Schafer, K.J.; Yang, B.; DiMauro, L.F.; Kulander, K.C. Above threshold ionization beyond the high harmonic cutoff. Phys. Rev. Lett. 1993, 70, 1599–1602. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Gaarde, M.B.; Tate, J.L.; Schafer, K.J. Macroscopic aspects of attosecond pulse generation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 132001. [Google Scholar] [CrossRef]
- Popmintchev, T.; Chen, M.-C.; Popmintchev, D.; Arpin, P.; Brown, S.; Alisauskas, S.; Andriukaitas, G.; Balciunas, T.; Mücke, O.; Pugzlys, A.; et al. Bright coherent ultrahigh harmonics in the keV X-ray regime from mid-infrared femtosecond lasers. Science 2012, 336, 1287. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.; Teichmann, S.M.; Cousin, S.L.; Biegert, J. Spatiotemporal isolation of attosecond soft X-ray pulses in the water window. Nat. Commun. 2015, 6, 6611. [Google Scholar] [CrossRef] [PubMed]
- Popmintchev, D.; Hernández-García, C.; Dollar, F.; Mancuso, C.; Pérez-Hernández, J.A.; Chen, M.-C.; Hankla, A.; Gao, X.; Shim, B.; Gaeta, A.L.; et al. Ultraviolet surprise: Efficient soft X-ray high-harmonic generation in multiply ionized plasmas. Science 2015, 350, 1225. [Google Scholar] [CrossRef] [PubMed]
- Zürch, M.; Kern, C.; Hansinger, P.; Dreischuh, A.; Spielmann, C. Strong-field physics with singular light beams. Nat. Phys. 2012, 8, 743–746. [Google Scholar] [CrossRef]
- Patchkovskii, S.; Spanner, M. Nonlinear optics: high harmonics with a twist. Nat. Phys. 2012, 8, 707–708. [Google Scholar] [CrossRef]
- Hernández-García, C.; Picón, A.; San Román, J.; Plaja, L. Attosecond Extreme Ultraviolet Vortices from High-Order Harmonic Generation. Phys. Rev. Lett. 2013, 111, 083602. [Google Scholar] [CrossRef] [PubMed]
- Gariepy, G.; Leach, J.; Kim, K.T.; Hammond, T.J.; Frumker, E.; Boyd, R.W.; Corkum, P.B. Creating High-Harmonic Beams with Controlled Orbital Angular Momentum. Phys. Rev. Lett. 2014, 113, 153901. [Google Scholar] [CrossRef] [PubMed]
- Hernández-García, C. A twist in coherent X-rays. Nat. Phys. 2017, 13, 327. [Google Scholar] [CrossRef]
- Rego, L.; San Román, J.; Picón, A.; Plaja, L.; Hernández-García, C. Non-perturbative twist in the generation of extreme ultraviolet vortices. Phys. Rev. Lett. 2016, 117, 163202. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, D.; Ribic, P.R.; Adhikary, G.; Camper, A.; Chappuis, C.; Cucini, R.; DiMauro, L.F.; Dovillaire, G.; Frassetto, F.; Géneaux, R.; et al. Tunable orbital angular momentum in high-harmonic generation. Nat. Commun. 2017, 8, 14971. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.; Zhang, C.; Bouchard, F.; Li, Z.; Brown, G.G.; Ko, D.H.; Hammond, T.J.; Arissian, L.; Boyd, R.W.; Karimi, E.; et al. Controlling the orbital angular momentum of high harmonic vortices. Nat. Commun. 2017, 8, 14970. [Google Scholar] [CrossRef] [PubMed]
- Hernández-García, C.; San Román, J.; Plaja, L.; Picón, A. Quantum-path signatures in attosecond helical beams driven by optical vortices. New J. Phys. 2015, 17, 093029. [Google Scholar] [CrossRef]
- Hernández-García, C.; Pérez-Hernández, J.A.; Ramos, J.; Jarque, E.C.; Roso, L.; Plaja, L. High order harmonic propagation in gases within the Discrete Dipole Approximation. Phys. Rev. A 2010, 82, 033432. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the Field of a Strong Electromagnetic Wave. Zh. Eksp. Teor. Fiz. 1964, 47, 1945. [Google Scholar]
- Faisal, F.H.M. Multiple absorption of laser photons by atoms. J. Phys. B 1973, 6, L89. [Google Scholar] [CrossRef]
- Reiss, H.R. Effect of an intense electromagnetic field on a weakly bound system. Phys. Rev. A 1980, 22, 1786. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low frequency laser fields. Phys. Rev. A 1994, 49, 2117. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Hernández, J.A.; Roso, L.; Plaja, L. Harmonic generation beyond the Strong-Field Approximation: the physics behind the short-wave-infrared scaling laws. Opt. Express 2009, 17, 9891. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Hernández, J.A.; Hernández-García, C.; Ramos, J.; Plaja, L.; Roso, L. Book Chapter: Progress in Ultrafast Intense Laser Science VII; Springer: Berlin/Heidelberg, Germany, 2011; pp. 145–162. [Google Scholar]
- Hernández-García, C.; Popmintchev, T.; Murnane, M.M.; Kapteyn, H.C.; Plaja, L.; Becker, A.; Jaron-Becker, A. Group velocity matching in high-order harmonic generation driven by mid-infrared lasers. New J. Phys. 2016, 18, 073031. [Google Scholar] [CrossRef]
- L’Huillier, A.; Balcou, P.; Candel, S.; Schafer, K.J.; Kulander, K.C. Calculations of high-order harmonic-generation processes in xenon at 1064 nm. Phys. Rev. A 1992, 46, 2778. [Google Scholar] [CrossRef] [PubMed]
- Rego, L.; San Román, J.; Plaja, L.; Picón, A.; Hernández-García, C. Ultrashort extreme-ultraviolet vortices. In Vortex Dynamics; Perez-De-Tejada, H., Ed.; InTech: Rijeka, Croatia, 2017. [Google Scholar]
- Bellini, M.; Lynga, C.; Tozzi, A.; Gaarde, M.B.; Hänsch, T.W.; L’Huillier, A.; Wahlström, C.-G. Temporal Coherence of Ultrashort High-Order Harmonic Pulses. Phys. Rev. Lett. 1998, 81, 297. [Google Scholar] [CrossRef]
- Hernández-García, C.; Sola, I.J.; Plaja, L. Signature of the transversal coherence length in high-order harmonic generation. Phys. Rev. A 2013, 88, 043848. [Google Scholar] [CrossRef]
- Lompré, L.; L’Huillier, A.; Ferray, M.; Monot, P.; Mainfray, G.; Manus, C. High-order harmonic generation in xenon: intensity and propagation effects. J. Opt. Soc. Am. B 1990, 7, 754–761. [Google Scholar] [CrossRef]
- Farkas, G.; Toth, C. Proposal for attosecond light pulse generation using laser induced multiple-harmonic conversion processes in rare gases. Phys. Lett. A 1992, 168, 447. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a train of attosecond pulses from high harmonic generation. Science 2001, 292, 1689. [Google Scholar] [CrossRef] [PubMed]
- Géneaux, R.; Camper, A.; Auguste, T.; Gobert, O.; Caillat, J.; Taïeb, R.; Ruchon, T. Synthesis and characterization of attosecond light vortices in the extreme ultraviolet. Nat. Commun. 2016, 7, 12583. [Google Scholar] [CrossRef] [PubMed]
- Pariente, G.; Quéré, F. Spatio-temporal light springs: extended encoding of orbital angular momentum in ultrashort pulses. Opt. Lett. 2015, 40, 2037. [Google Scholar] [CrossRef] [PubMed]
- Hernández-García, C.; Rego, L.; San Román, J.; Picón, A.; Plaja, L. Attosecond twisted beams from high-order harmonic generation driven by optical vortices. High Power Laser Sci. Eng. 2017, 5, e3. [Google Scholar] [CrossRef]
- Mairesse, Y.; de Bohan, A.; Frasinski, L.J.; Merdji, H.; Dinu, L.C.; Monchicourt, P.; Breger, P.; Kovacev, M.; Taieb, R.; Carré, B.; et al. Attosecond Synchronization of High-Harmonic Soft X-rays. Science 2003, 302, 1540. [Google Scholar] [CrossRef] [PubMed]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photonics 2014, 8, 543. [Google Scholar] [CrossRef]
- Lambert, G.; Vodungbo, B.; Gautier, J.; Mahieu, B.; Malka, V.; Sebban, S.; Zeitoun, P.; Luning, J.; Perron, J.; Andreev, A.; et al. Towards enabling femtosecond helicity-dependent spectroscopy with high-harmonic sources. Nat. Commun. 2015, 6, 6167. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Brown, G.; Ko, D.H.; Kong, F.; Arissian, L.; Corkum, P.B. Perturbative High Harmonic Wave Front Control. Phys. Rev. Lett. 2017, 118, 033905. [Google Scholar] [CrossRef] [PubMed]
- Vieira, J.; Mendonça, J.T. Nonlinear Laser Driven Donut Wakefields for Positron and Electron Acceleration. Phys. Rev. Lett. 2014, 112, 215001. [Google Scholar] [CrossRef]
- Tajima, T.; Dawson, J.M. Laser electron accelerator. Phys. Rev. Lett. 1979, 43, 267. [Google Scholar] [CrossRef]
- Oz, E.; Muggli, P. An accurate Rb density measurement method for a plasma wakefield accelerator experiment using a novel Rb reservoir. Nucl. Instrum. Methods Phys. Res. A 2016, 829, 321–325. [Google Scholar] [CrossRef]
- Vieira, J.; Trines, R.M.G.M.; Alves, E.P.; Fonseca, R.A.; Mendonça, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. Amplification and generation of ultra-intense twisted laser pulses via stimulated Raman scattering. Nat. Commun. 2016, 7, 10371. [Google Scholar] [CrossRef] [PubMed]
- Vieira, J.; Trines, R.M.G.M.; Alves, E.P.; Fonseca, R.A.; Mendonça, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. High orbital angular momentum harmonic generation. Phys. Rev. Lett. 2016, 117, 265001. [Google Scholar] [CrossRef] [PubMed]
- Gordon, D.F.; Hafizi, B.; Ting, A. Nonlinear conversion of photon spin to photon orbital angular momentum. Opt. Lett. 2009, 34, 3280. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, J.T.; Vieira, J. High harmonic generation in underdense plasmas by intense laser pulses with orbital angular momentum. Phys. Plasmas 2015, 22, 123106. [Google Scholar] [CrossRef]
- Bulanov, S.V.; Naumova, N.M.; Pegoraro, F. Interaction of an ultrashort, relativistically strong laser pulse with an overdense plasma. Phys. Plasmas 1994, 1, 745. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, B.; Shi, Y.; Wang, X.; Zhang, L.; Wang, W.; Xu, J.; Yi, L.; Xu, Z. Generation of Intense High-Order Vortex Harmonics. Phys. Rev. Lett. 2015, 114, 173901. [Google Scholar] [CrossRef] [PubMed]
- Quéré, F.; Thaury, C.; Monot, P.; Dobosz, S.; Martin, P.; Geindre, J.-P.; Audebert, P. Coherent Wake Emission of High-Order Harmonics from Overdense Plasmas. Phys. Rev. Lett. 2006, 96, 125004. [Google Scholar] [CrossRef] [PubMed]
- Denoeud, A.; Chopineau, L.; Leblanc, A.; Quéré, F. Interaction of Ultraintense Laser Vortices with Plasma Mirrors. Phys. Rev. Lett. 2017, 118, 033902. [Google Scholar] [CrossRef] [PubMed]
- Monchocé, S.; Kahaly, S.; Leblanc, A.; Videau, L.; Combis, P.; Réau, F.; Garzella, D.; Oliveira, P.D.; Martin, P.; Quéré, F. Optically controlled solid-density transient plasma gratings. Phys. Rev. Lett. 2014, 112, 145008. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, A.; Denoeud, A.; Chopineau, L.; Mennerat, G.; Martin, P.; Quéré, F. Plasma holograms for ultrahigh-intensity optics. Nat. Phys. 2017. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, B.; Zhang, L.; Zhang, X.; Wang, W.; Xu, Z. Light Fan Driven by a Relativistic Laser Pulse. Phys. Rev. Lett. 2014, 112, 235001. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Shen, B.; Shi, Y.; Zhang, L.; Ji, L.; Wang, X.; Xu, Z.; Tajima, T. Intense harmonics generation with customized photon frequency and optical vortex. New J. Phys. 2016, 18, 083046. [Google Scholar] [CrossRef]
- Forslund, D.W.; Kindel, J.M.; Lindman, E.L. Theory of stimulated scattering processes in laser-irradiated plasmas. Phys. Fluis 1975, 18, 1002. [Google Scholar] [CrossRef]
- Shvets, G.; Fisch, N.J.; Pukhov, A.; Meyer-ter-Vehn, J. Superradiant Amplification of an Ultrashort Laser Pulse in a Plasma by a Counterpropagating Pump. Phys. Rev. Lett. 1998, 81, 4879. [Google Scholar] [CrossRef]
- Trines, R.M.G.M.; Fiúza, F.; Bingham, R.; Fonseca, R.A.; Silva, L.O.; Cairns, R.A.; Norreys, P.A. Simulations of efficient Raman amplification into the multipetawatt regime. Nat. Phys. 2011, 7, 87. [Google Scholar] [CrossRef]
- Mendonça, J.T.; Thidé, B.; Then, H. Stimulated Raman and Brillouin Backscattering of Collimated Beams Carrying Orbital Angular Momentum. Phys. Rev. Lett. 2009, 102, 185005. [Google Scholar] [CrossRef] [PubMed]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.J. Second-harmonic generation and the conservation of orbital angular momentum with high-order Laguerre-Gaussian modes. Phys. Rev. A 1997, 56, 4193. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Serbo, V.G. Generation of High-Energy Photons with Large Orbital Angular Momentum by Compton Backscattering. Phys. Rev. Lett. 2011, 106, 013001. [Google Scholar] [CrossRef] [PubMed]
- Petrillo, V.; Dattoli, G.; Drebot, I.; Nguyen, F. Compton Scattered X-Gamma Rays with Orbital Momentum. Phys. Rev. Lett. 2016, 117, 123903. [Google Scholar] [CrossRef] [PubMed]
- Terhalle, B.; Langner, A.; Päivänranta, B.; Guzenko, V.A.; David, C.; Ekinci, Y. Generation of extreme ultraviolet vortex beams using computer generated holograms. Opt. Lett. 2011, 36, 4143. [Google Scholar] [CrossRef] [PubMed]
- Peele, A.G.; McMahon, P.J.; Paterson, D.; Tran, C.Q.; Mancuso, A.P.; Nugent, K.A.; Hayes, J.P.; Harvey, E.; Lai, B.; McNulty, I. Observation of an X-ray vortex. Opt. Lett. 2002, 27, 1752. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, S.; McNulty, I. Proposal for Generating Brilliant X-ray Beams Carrying Orbital Angular Momentum. Phys. Rev. Lett. 2008, 100, 124801. [Google Scholar] [CrossRef] [PubMed]
- Bahrdt, J.; Holldack, K.; Kuske, P.; Müller, R.; Scheer, M.; Schmid, P. First Observation of Photons Carrying Orbital Angular Momentum in Undulator Radiation. Phys. Rev. Lett. 2013, 111, 034801. [Google Scholar] [CrossRef] [PubMed]
- Hemsing, E.; Dunning, M.; Hast, C.; Raubenheimer, T.; Xiang, D. First Characterization of Coherent Optical Vortices from Harmonic Undulator Radiation. Phys. Rev. Lett. 2014, 113, 134803. [Google Scholar] [CrossRef] [PubMed]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 2012, 6, 669. [Google Scholar] [CrossRef]
- Hemsing, E.; Knyazik, A.; Dunning, M.; Xiang, D.; Marinelli, A.; Hast, C.; Rosenzweig, J.B. Coherent optical vortices from relativistic electron beams. Nat. Phys. 2013, 9, 549. [Google Scholar] [CrossRef]
- Allaria, E.; Castronovo, D.; Cinquegrana, P.; Craievich, P.; Dal Forno, M.; Danailov, M.B.; D’Auria, G.; Demidovich, A.; De Ninno, G.; Di Mitri, S.; et al. Two-stage seeded soft-X-ray free-electron laser. Nat. Photonics 2013, 7, 913. [Google Scholar] [CrossRef]
- Hemsing, E.; Marinelli, A. Echo-Enabled X-ray Vortex Generation. Phys. Rev. Lett. 2012, 109, 224801. [Google Scholar] [CrossRef] [PubMed]
- Ribic, P.R.; Gauthier, D.; de Ninno, G. Generation of Coherent Extreme-Ultraviolet Radiation Carrying Orbital Angular Momentum. Phys. Rev. Lett. 2014, 112, 203602. [Google Scholar] [CrossRef]
- Picón, A.; Mompart, J.; de Aldana, J.R.V.; Plaja, L.; Calvo, G.F.; Roso, L. Photoionization with orbital angular momentum beams. Opt. Express 2010, 18, 3660. [Google Scholar] [CrossRef] [PubMed]
- Picón, A.; Benseny, A.; Mompart, J.; de Aldana, J.R.V.; Plaja, L.; Calvo, G.F.; Roso, L. Transferring orbital and spin angular momenta of light to atoms. New J. Phys. 2010, 12, 083053. [Google Scholar] [CrossRef]
- Jauregui, R. Rotational effects of twisted light on atoms beyond the paraxial approximation. Phys. Rev. A 2004, 70, 033415. [Google Scholar] [CrossRef]
- Babiker, M.; Power, W.L.; Allen, L. Light-induced Torque on Moving Atoms. Phys. Rev. Lett. 1994, 73, 1239. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.A.; Seipt, D.; Beerwerth, R.; Ornigotti, M.; Szameit, A.; Fritzsche, S.; Surzhykov, A. Photoionization of neutral atoms by X waves carrying orbital angular momentum. Phys. Rev. A 2016, 94, 041402. [Google Scholar] [CrossRef]
- Peshkov, A.A.; Serbo, V.G.; Fritzsche, S.; Surzhykov, A. Absorption of twisted light by a mesoscopic atomic target. Phys. Scr. 2016, 91, 064001. [Google Scholar] [CrossRef]
- Alexandrescu, A.; Cojoc, D.; DiFabrizio, E.I. Mechanism of Angular Momentum Exchange between Molecules and Laguerre-Gaussian Beams. Phys. Rev. Lett. 2006, 96, 243001. [Google Scholar] [CrossRef] [PubMed]
- Babiker, M.; Bennett, C.R.; Andrews, D.L.; Romero, L.D. Orbital Angular Momentum Exchange in the Interaction of Twisted Light with Molecules. Phys. Rev. Lett. 2002, 89, 143601. [Google Scholar] [CrossRef] [PubMed]
- Toyoda, K.; Takahashi, F.; Takizawa, S.; Tokizane, Y.; Miyamoto, K.; Morita, R.; Omatsu, T. Transfer of Light Helicity to Nanostructures. Phys. Rev. Lett. 2013, 110, 143603. [Google Scholar] [CrossRef] [PubMed]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef] [PubMed]
- Giammanco, F.; Perona, A.; Marsili, P.; Conti, F.; Fidecaro, F.; Gozzini, S.; Lucchesini, A. Influence of the photon orbital angular momentum on electric dipole transitions: negative experimental evidence. Opt. Lett. 2017, 42, 219. [Google Scholar] [CrossRef] [PubMed]
- Quinteiro, G.F.; Tamborenea, P.I. Electronic transitions in disk-shaped quantum dots induced by twisted light. Phys. Rev. B 2009, 79, 155450. [Google Scholar] [CrossRef]
- Wätzel, J.; Berakdar, J. Discerning on a sub-optical-wavelength the attosecond time delays in electron emission from magnetic sublevels by optical vortices. Phys. Rev. A 2016, 94, 033414. [Google Scholar] [CrossRef]
- Wätzel, J.; Pavlyukh, Y.; Schäffer, A.; Berakdar, J. Optical vortex driven charge current loop and optomagnetism in fullerenes. Carbon 2016, 99, 439. [Google Scholar] [CrossRef]
- Van Veenendaal, M.; McNulty, I. Prediction of strong dichroism induced by x rays carrying orbital momentum. Phys. Rev. Lett. 2007, 98, 157401. [Google Scholar] [CrossRef] [PubMed]
- Zambrana-Puyalto, X.; Vidal, X.; Molina-Terriza, G. Angular momentum-induced circular dichroism in non-chiral nanostructures. Nat. Commun. 2014, 5, 4922. [Google Scholar] [CrossRef] [PubMed]
- Seipt, D.; Müller, R.A.; Surzhykov, A.; Fritzsche, S. Two-color above-threshold ionization of atoms and ions in XUV Bessel beams and intense laser light. Phys. Rev. A 2016, 94, 053420. [Google Scholar] [CrossRef]
- Fujita, H.; Sato, M. Ultrafast generation of skyrmionic defects with vortex beams: Printing laser profiles on magnets. Phys. Rev. B 2017, 95, 054421. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198. [Google Scholar] [CrossRef] [PubMed]
- Grillo, V.; Gazzadi, G.C.; Karimi, E.; Mafakheri, E.; Boyd, R.W.; Frabboni, S. Highly efficient electron vortex beams generated by nanofabricated phase holograms. Appl. Phys. Lett. 2014, 104, 043109. [Google Scholar] [CrossRef]
- Asenjo-Garcia, A.; de Abajo, F.J.G. Dichroism in the interaction between vortex electron beams, plasmons, and molecules. Phys. Rev. Lett. 2014, 113, 066102. [Google Scholar] [CrossRef] [PubMed]
- Djiokap, J.M.N.; Hu, S.X.; Madsen, L.B.; Manakov, N.L.; Meremianin, A.V.; Starace, A.F. Electron vortices in photoionization by circularly polarized attosecond pulses. Phys. Rev. Lett. 2015, 115, 113004. [Google Scholar] [CrossRef] [PubMed]
- Pengel, D.; Kerbstadt, S.; Johannmeyer, D.; Englert, L.; Bayer, T.; Wollenhaupt, M. Electron Vortices in Femtosecond Multiphoton Ionization. Phys. Rev. Lett. 2017, 118, 053003. [Google Scholar] [CrossRef] [PubMed]
- Rury, A.S. Examining resonant inelastic spontaneous scattering of classical Laguerre-Gauss beams from molecules. Phys. Rev. A 2013, 87, 043408. [Google Scholar] [CrossRef]
- Van Veenendaal, M. Interaction between X-ray and magnetic vortices. Phys. Rev. B 2015, 92, 245116. [Google Scholar] [CrossRef]
- Paganin, D. Coherent X-ray Optics; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Nugent, K.A. Coherent methods in the X-ray sciences. Adv. Phys. 2010, 59, 1. [Google Scholar] [CrossRef]
- Zadernovsky, A.A. Excitation of Nuclei by Photon Beams Carrying Orbital Angular Momentum. Laser Phys. 2006, 16, 571. [Google Scholar] [CrossRef]
- Calvo, G.F.; Picón, A. Spin-induced angular momentum switching. Opt. Lett. 2007, 32, 838. [Google Scholar] [CrossRef] [PubMed]
- Picón, A.; Benseny, A.; Mompart, J.; Calvo, G.F. Spin and orbital angular momentum propagation in anisotropic media: theory. J. Opt. 2011, 13, 064019. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Nori, F.; Zayats, A.V. Spin-orbit interactions of light. Nat. Photonics 2015, 9, 796–803. [Google Scholar] [CrossRef]
- Cardano, F.; Marrucci, L. Spin-orbit photonics. Nat. Photonics 2015, 9, 776–778. [Google Scholar] [CrossRef]
- Turpin, A.; Rego, L.; Picón, A.; San Román, J.; Hernández-García, C. Extreme Ultraviolet Fractional Orbital Angular Momentum Beams from High Harmonic Generation. Sci. Rep. 2017, 7, 43888. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Q. Cylindrical vector beams: from mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Hernández-García, C.; Turpin, A.; San Román, J.; Picón, A.; Drevinskas, R.; Cerkauskaite, A.; Kazansky, P.G.; Durfee, C.G.; Sola, I.J. Extreme ultraviolet vector beams driven by infrared lasers. Optica 2017. submitted. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).