Differential Service in a Bidirectional Radio-over-Fiber System over a Spectral-Amplitude-Coding OCDMA Network
Abstract
:1. Introduction
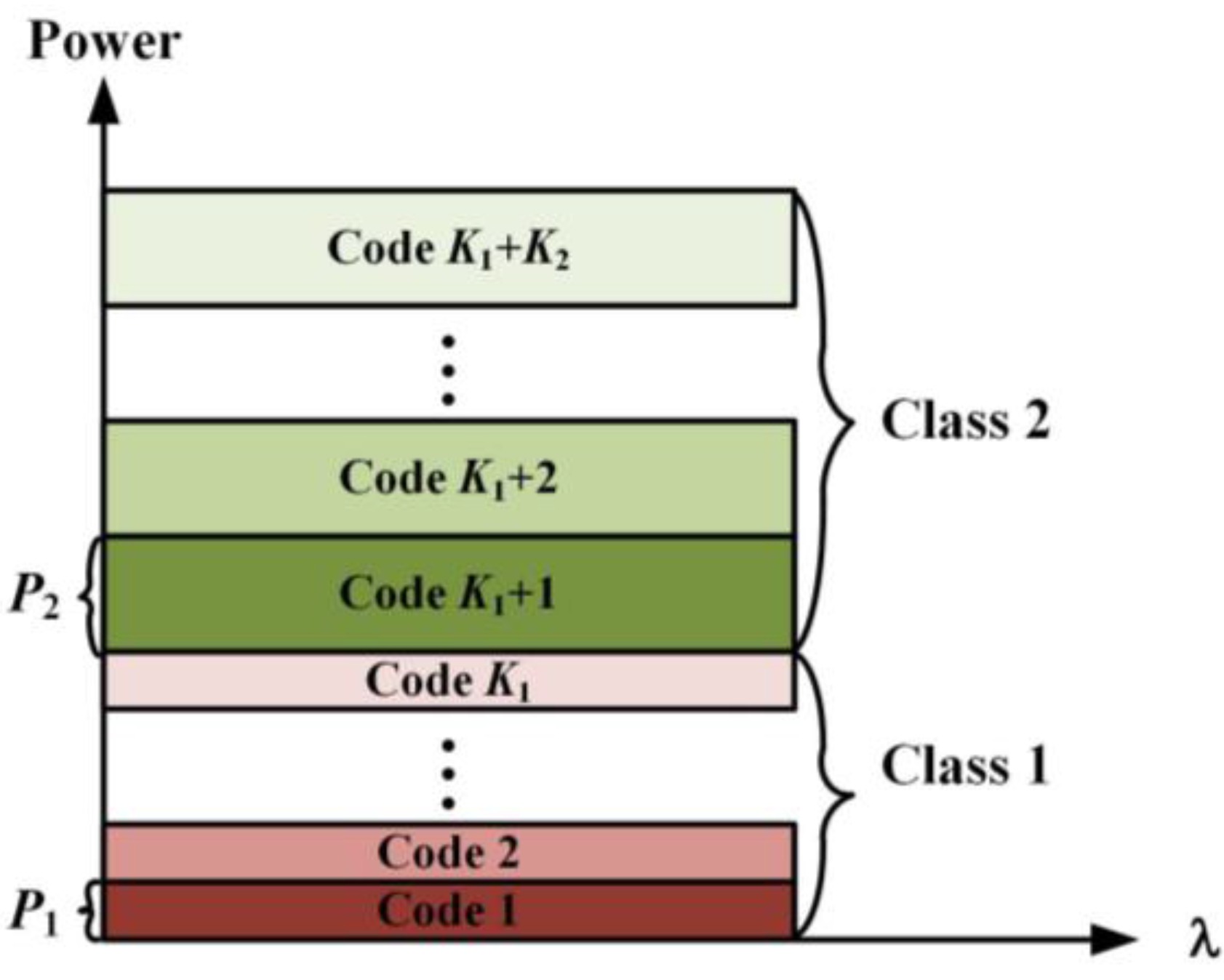
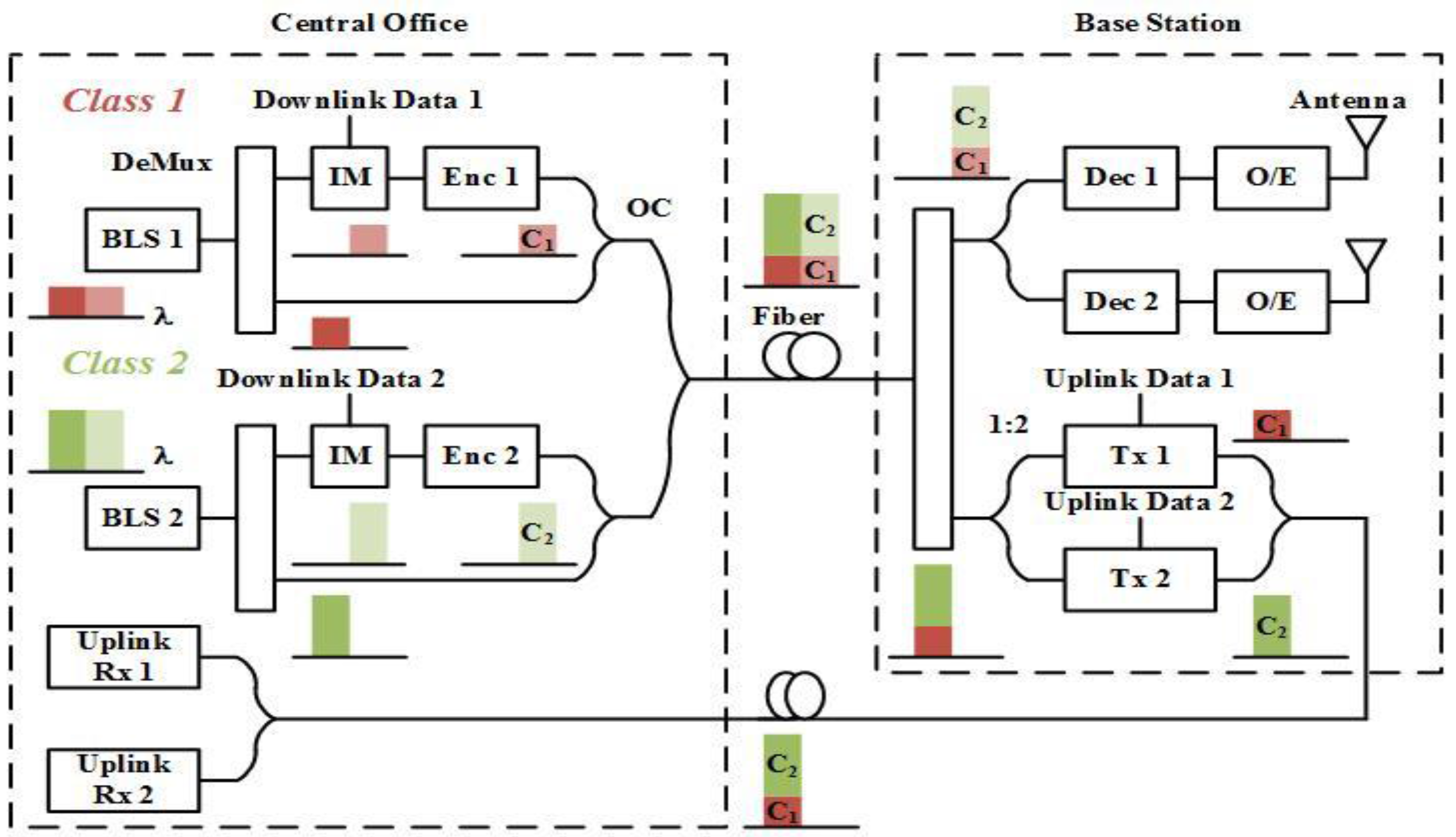
2. The Proposed Bi-Directional RoF System with Power Control Scheme
3. System Performance Analysis
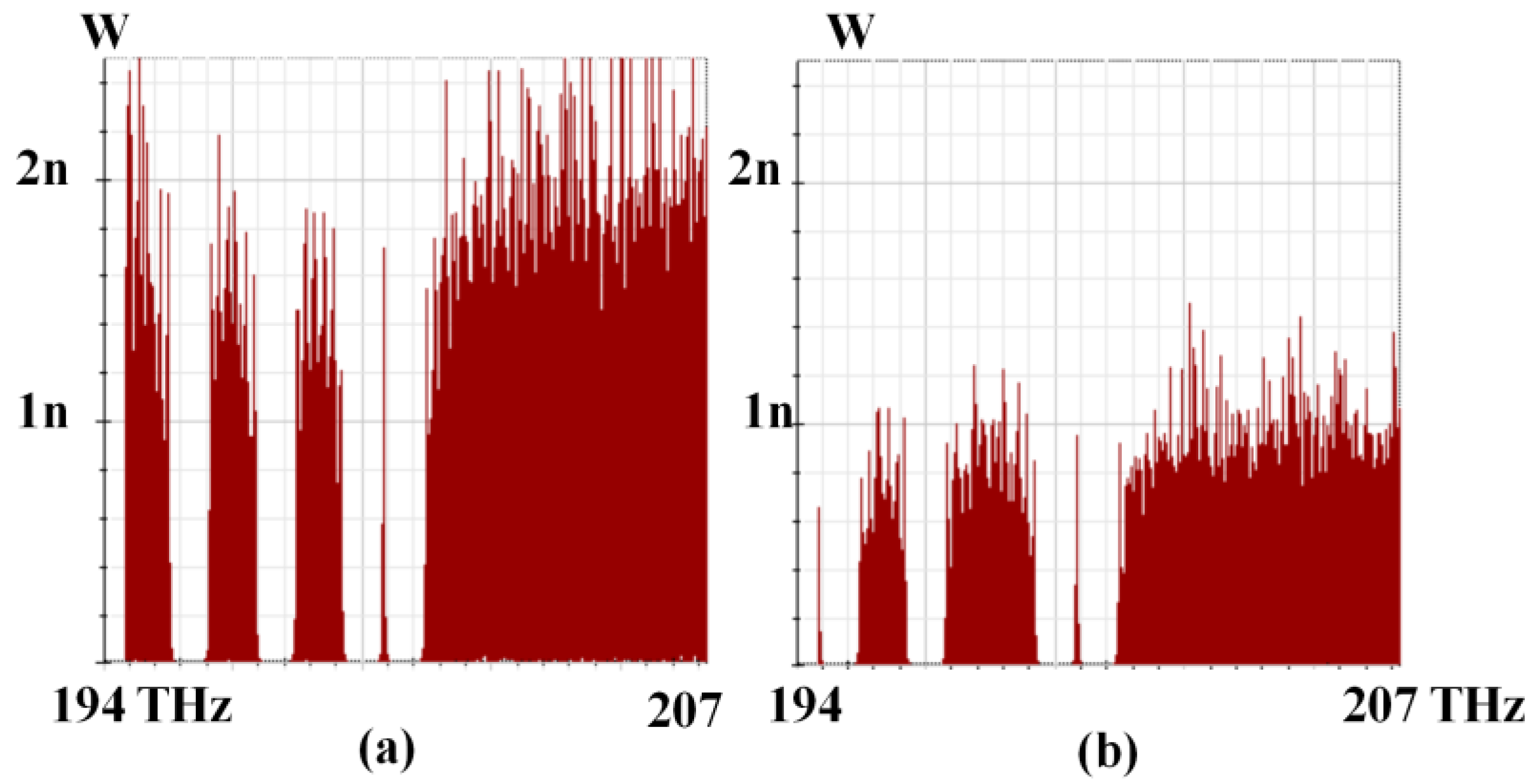
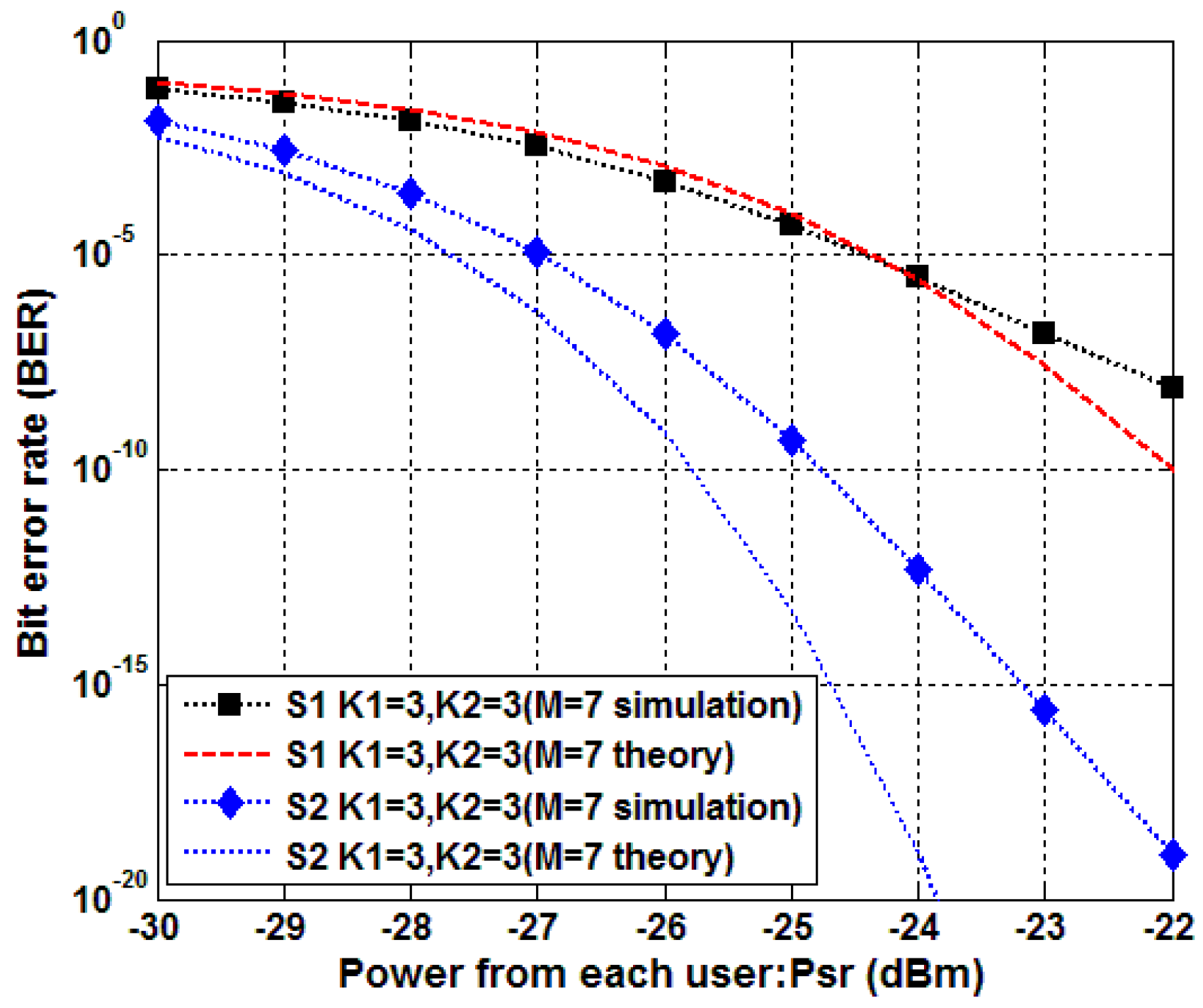
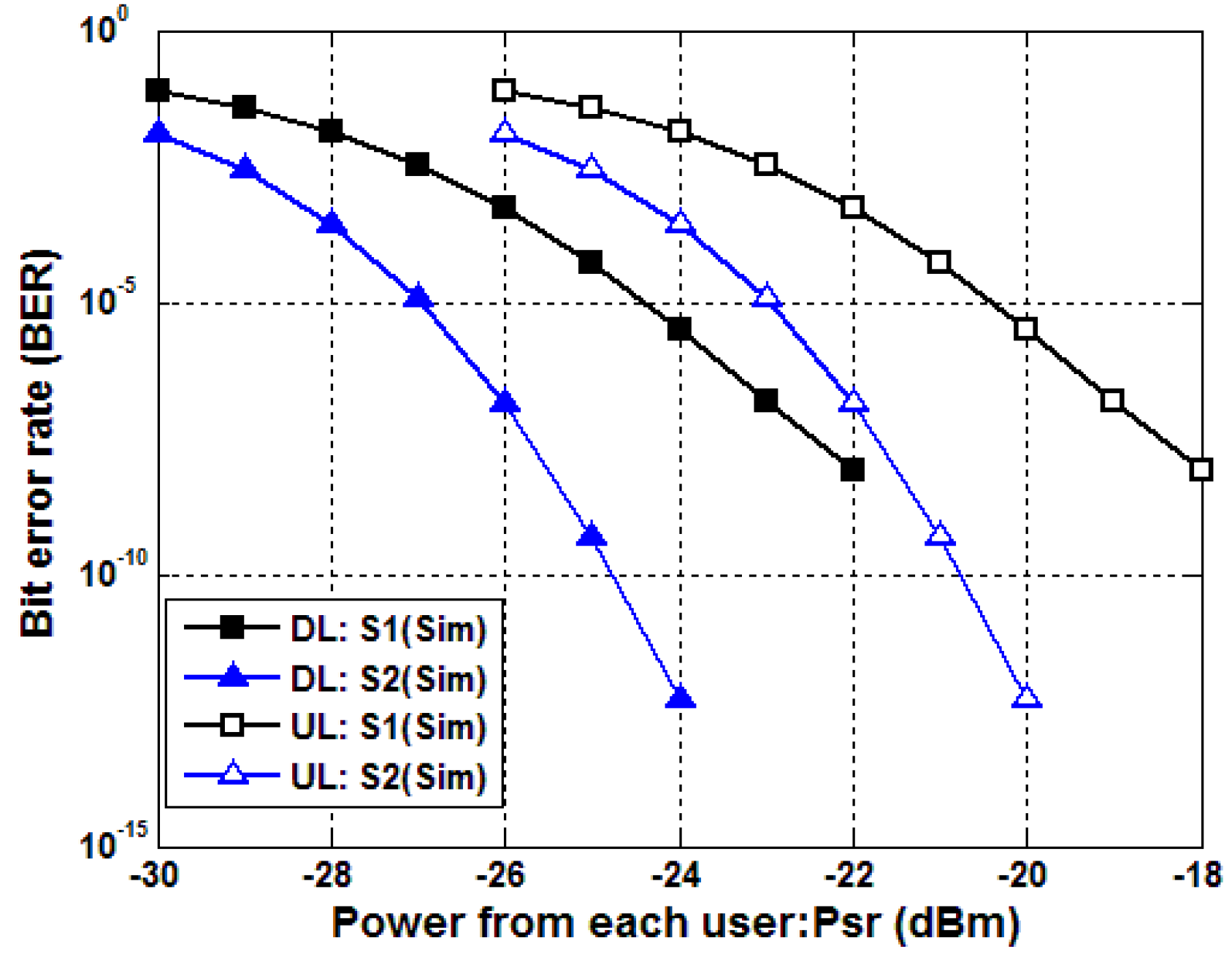
4. Simulation Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, Z.Z.; Wang, H.X.; Ji, Y.F. Multichannel resource allocation mechanism for 60 GHz radio-over-fiber local access networks. J. Lightw. Technol. 2013, 5, 254–260. [Google Scholar] [CrossRef]
- Chang, C.Y.; Yang, G.C.; Chang, C.Y.; Kwong, W.C. Study of a diversity O-CDMA scheme for optical wireless. J. Lightw. Technol. 2012, 30, 1549–1558. [Google Scholar] [CrossRef]
- Yang, C.C.; Huang, J.F.; Chang, H.H.; Chen, K.S. Radio transmissions over residue-stuffed-QC-coded optical CDMA network. IEEE Commun. Lett. 2014, 18, 329–331. [Google Scholar] [CrossRef]
- Yang, C.C. Optical CDMA-based fiber-radio networks with improved power efficiency. IEEE Trans. Commun. 2012, 60, 810–816. [Google Scholar] [CrossRef]
- Ahmed, M.; Ahmad, I.; Habibi, D. Service class resource management for green wireless-optical broadband access networks (WOBAN). J. Lightw. Technol. 2015, 33, 7–18. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Pavel, L. Enabling differentiated services using generalized power control model in optical networks. IEEE Trans. Commun. 2009, 57, 2570–2575. [Google Scholar]
- Matsuura, M.; Oki, E. Optical carrier regeneration for carrier wavelength reuse in a multicarrier distributed WDM network. IEEE Photon. Technol. Lett. 2010, 22, 808–810. [Google Scholar] [CrossRef]
- Cui, W.T.; Shao, T.; Yao, J.P. Wavelength reuse in a UWB over fiber system based on phase-modulation to intensity-modulation conversion and destructive interferencing. J. Lightw. Technol. 2013, 31, 2904–2912. [Google Scholar] [CrossRef]
- Kaszubowska, L.H.; Barry, L. Remote down conversion with wavelength reuse for the radio/fiber uplink connection. IEEE Photon. Technol. Lett. 2006, 18, 562–564. [Google Scholar] [CrossRef]
- Attygalle, M.; Lim, C.; Pendock, P.J.; Nirmalathas, A.; Edvell, G. Transmission improvement in fiber wireless links using fiber bragg gratings. IEEE Photon. Technol. Lett. 2005, 17, 190–192. [Google Scholar] [CrossRef]
- Chen, K.S.; Yang, C.C.; Huang, J.F. Using stuffed quadratic congruence codes for SAC labels in optical packet switching network. IEEE Commun. Lett. 2015, 19, 1093–1096. [Google Scholar] [CrossRef]
- Yang, C.C. Optical CDMA passive optical network using prime code with interference elimination. IEEE Photon. Technol. Lett. 2007, 19, 516–518. [Google Scholar] [CrossRef]
- Noshad, M.; Jamshidi, K. Bounds for the BER of codes with fixed cross correlation in SAC-OCDMA Systems. J. Lightw. Technol. 2011, 29, 1944–1950. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.-C.; Chen, K.-S.; Huang, J.-F.; Kuo, J.-C. Differential Service in a Bidirectional Radio-over-Fiber System over a Spectral-Amplitude-Coding OCDMA Network. Photonics 2016, 3, 53. https://doi.org/10.3390/photonics3040053
Yang C-C, Chen K-S, Huang J-F, Kuo J-C. Differential Service in a Bidirectional Radio-over-Fiber System over a Spectral-Amplitude-Coding OCDMA Network. Photonics. 2016; 3(4):53. https://doi.org/10.3390/photonics3040053
Chicago/Turabian StyleYang, Chao-Chin, Kai-Sheng Chen, Jen-Fa Huang, and Jia-Cyuan Kuo. 2016. "Differential Service in a Bidirectional Radio-over-Fiber System over a Spectral-Amplitude-Coding OCDMA Network" Photonics 3, no. 4: 53. https://doi.org/10.3390/photonics3040053
APA StyleYang, C.-C., Chen, K.-S., Huang, J.-F., & Kuo, J.-C. (2016). Differential Service in a Bidirectional Radio-over-Fiber System over a Spectral-Amplitude-Coding OCDMA Network. Photonics, 3(4), 53. https://doi.org/10.3390/photonics3040053




