Analytical Investigations on Carrier Phase Recovery in Dispersion-Unmanaged n-PSK Coherent Optical Communication Systems
Abstract
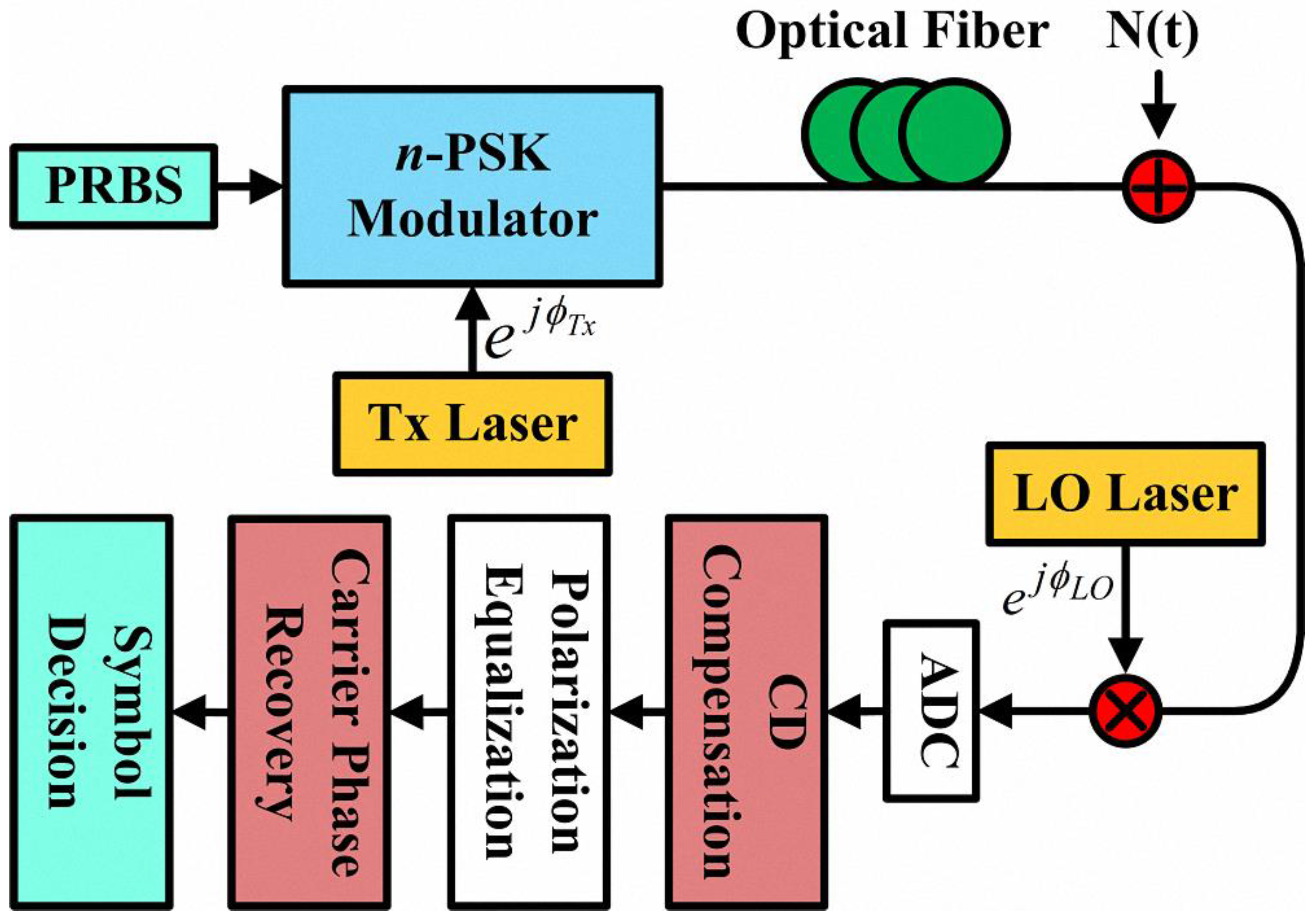
:1. Introduction
2. Laser Phase Noise and Equalization Enhanced Phase Noise
3. Analysis of Carrier Phase Recovery Approaches
3.1. One-Tap Normalized Least-Mean-Square (LMS) Carrier Phase Recovery
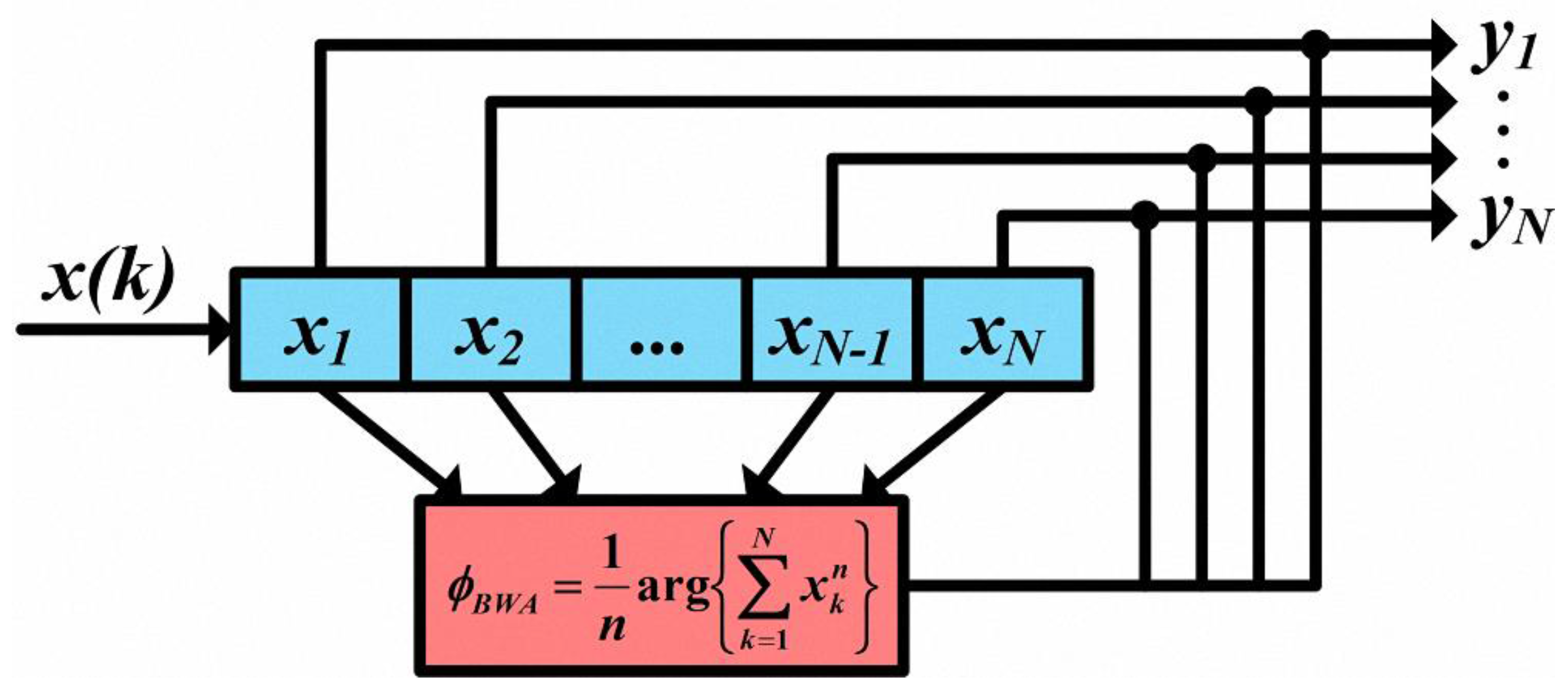
3.2. Block-Wise Average Carrier Phase Recovery
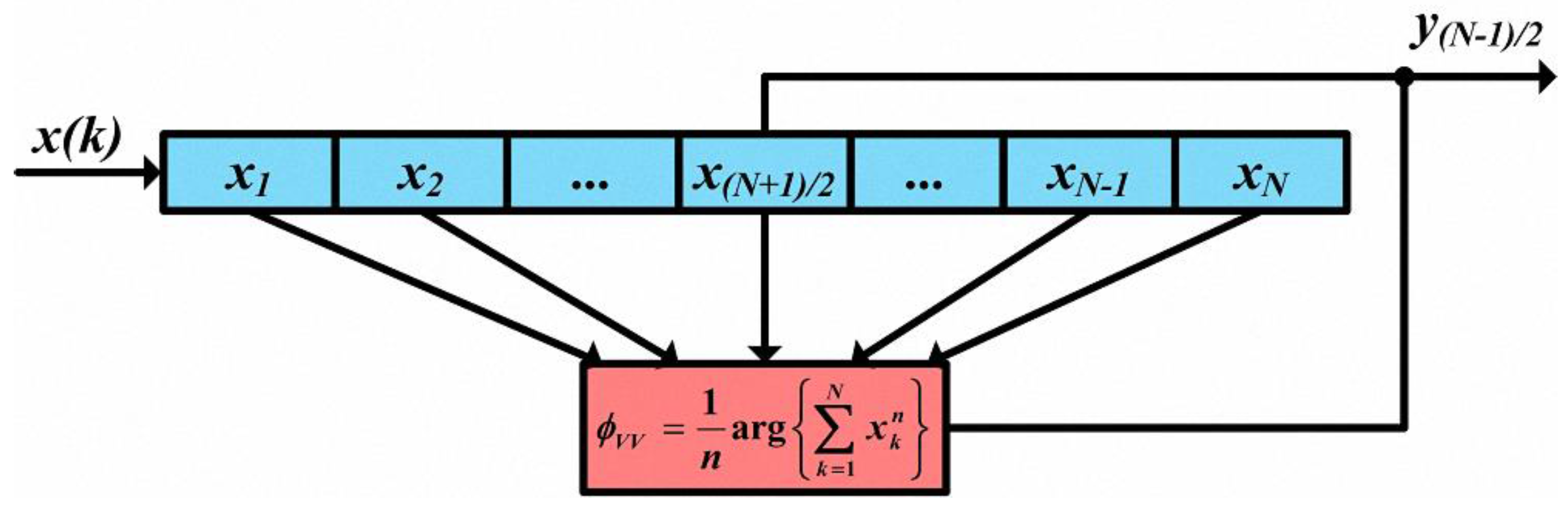
3.3. Viterbi-Viterbi Carrier Phase Recovery
4. Results and Discussion
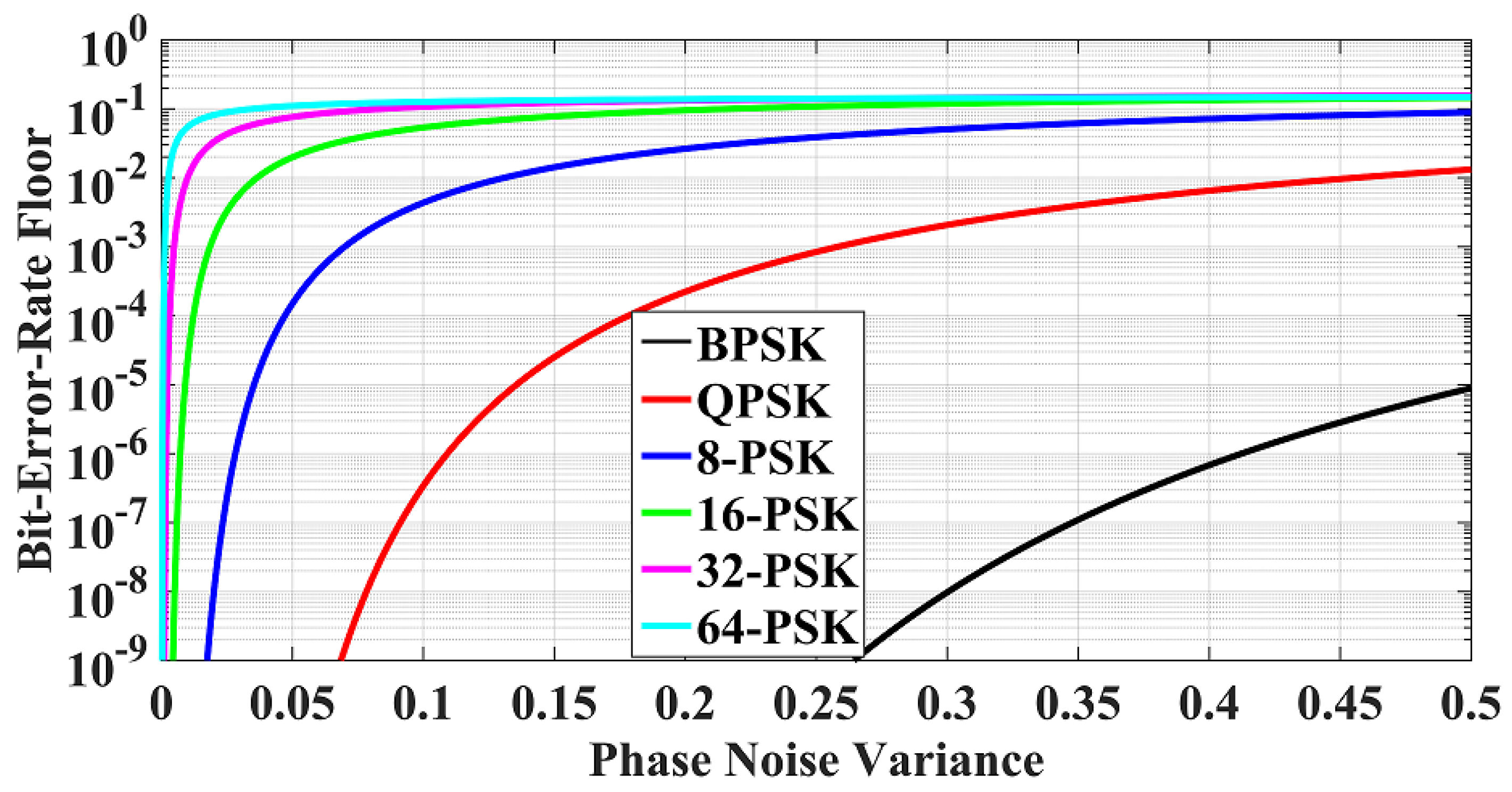
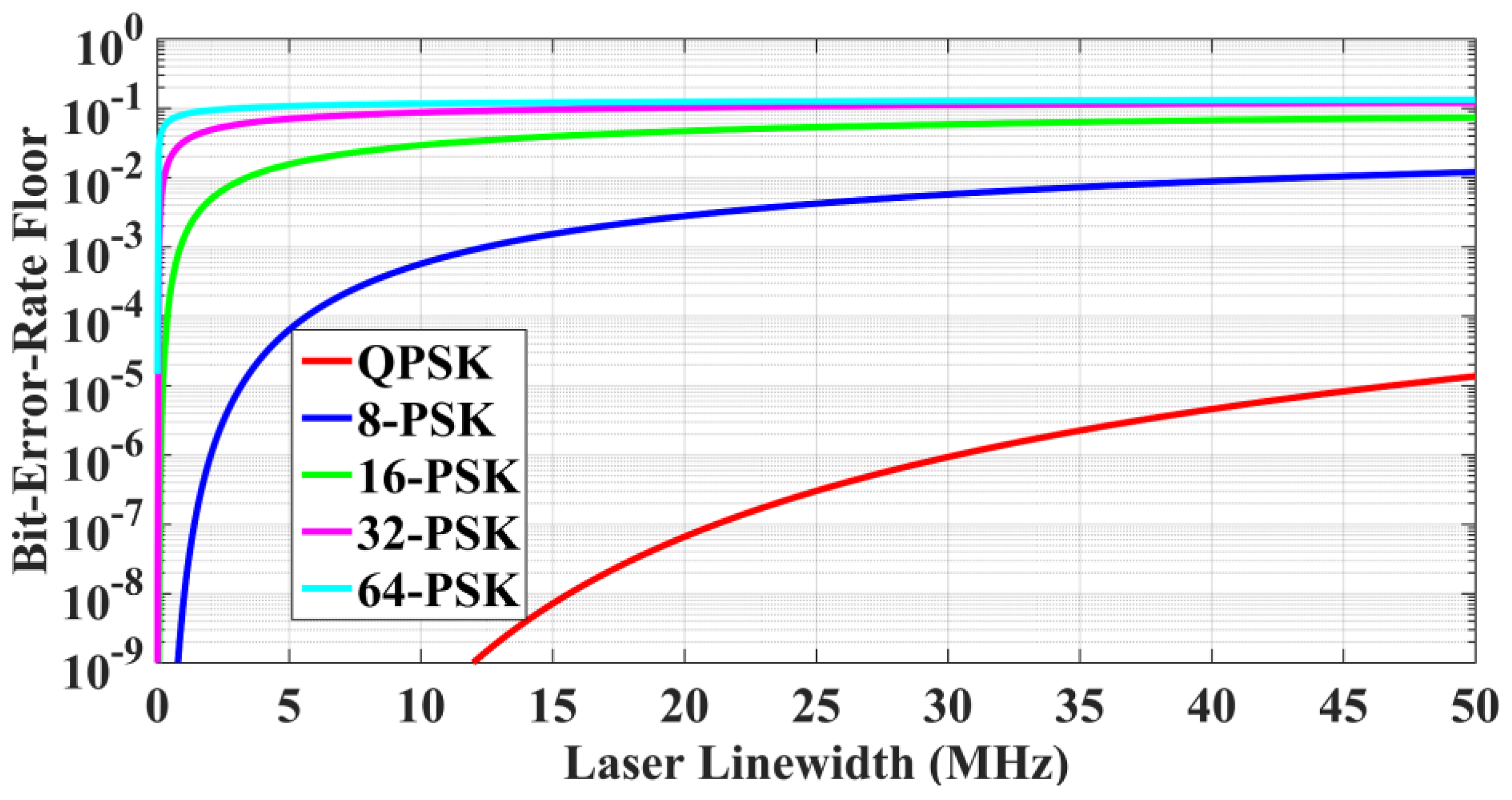
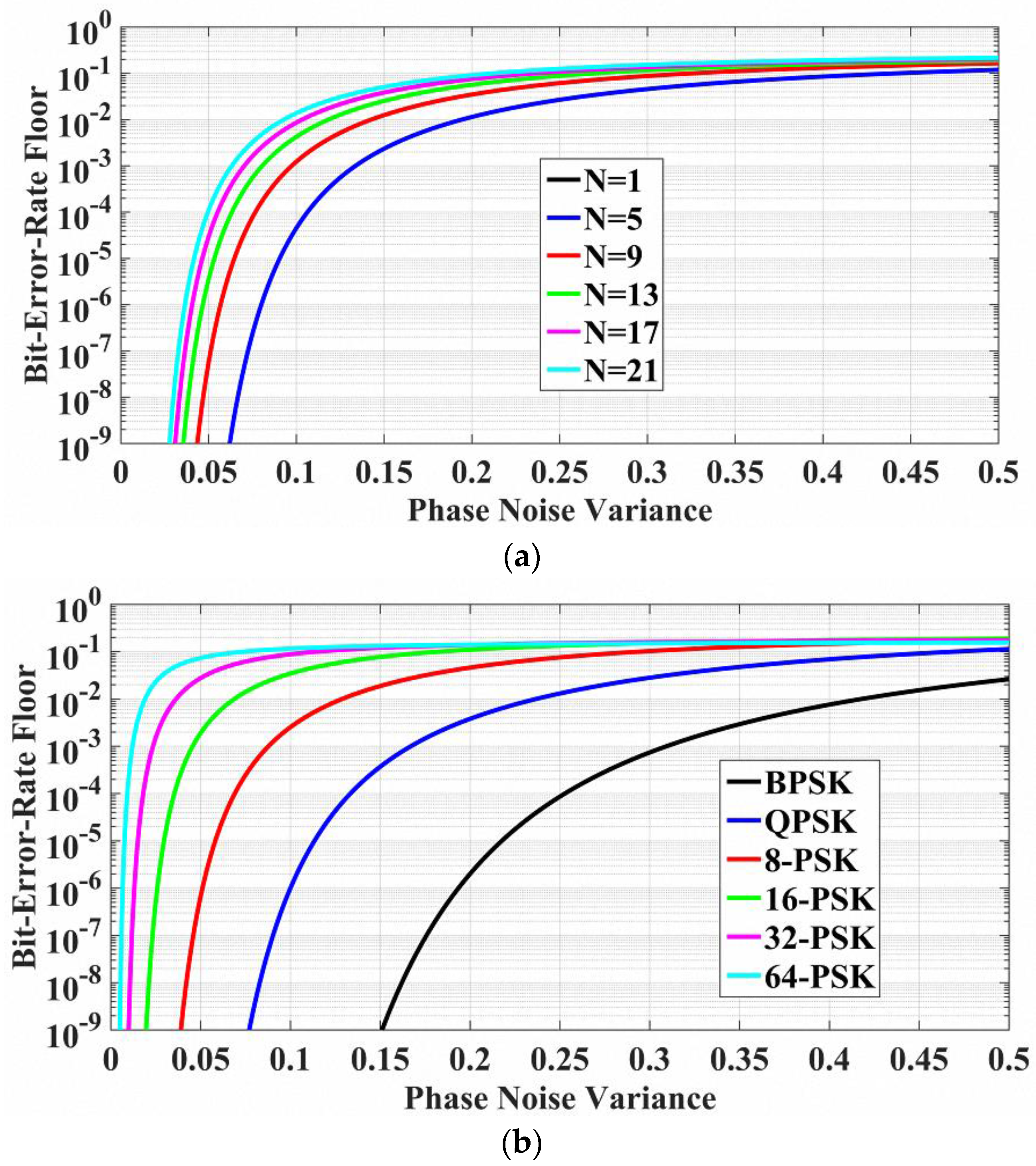
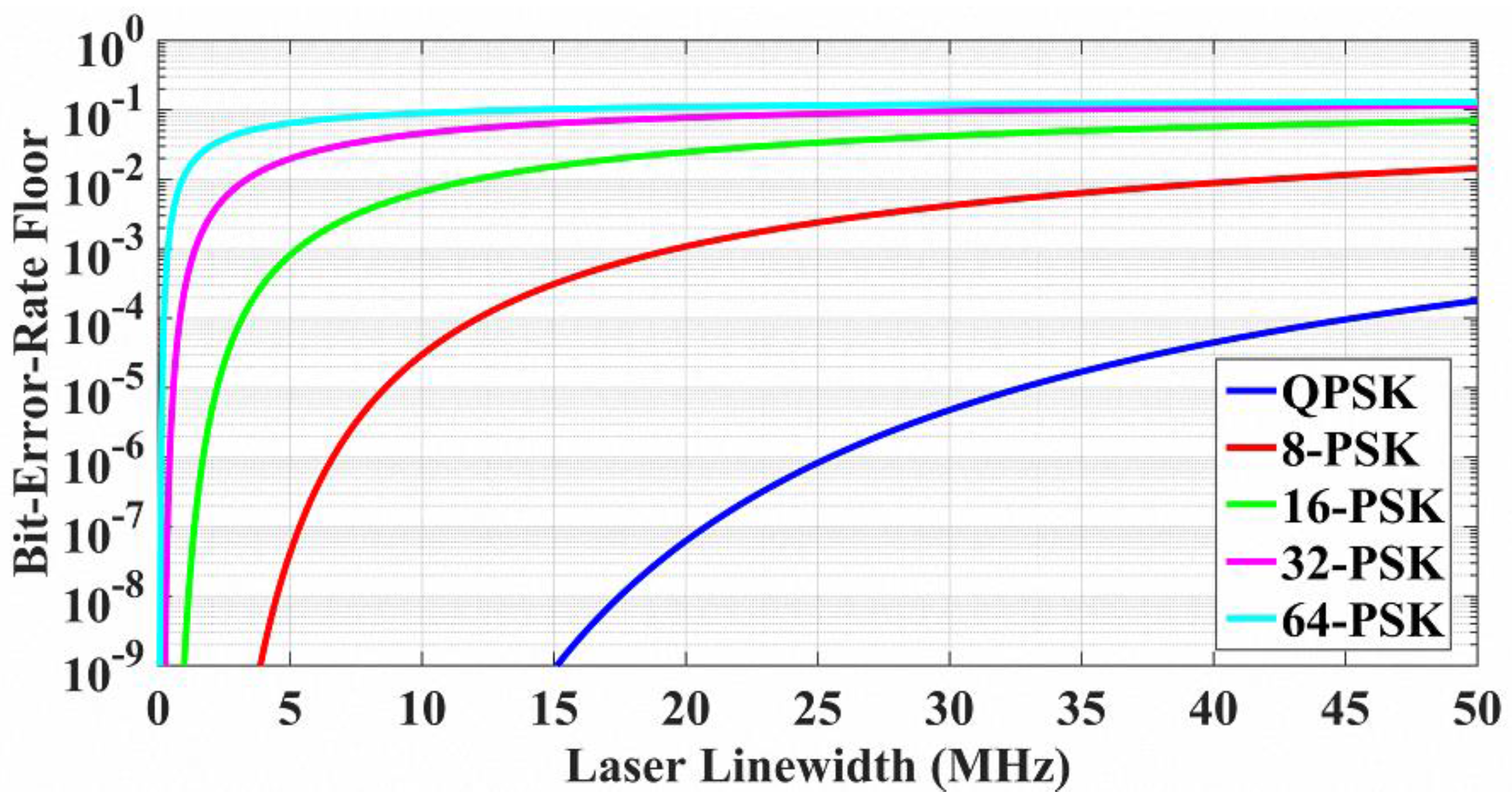
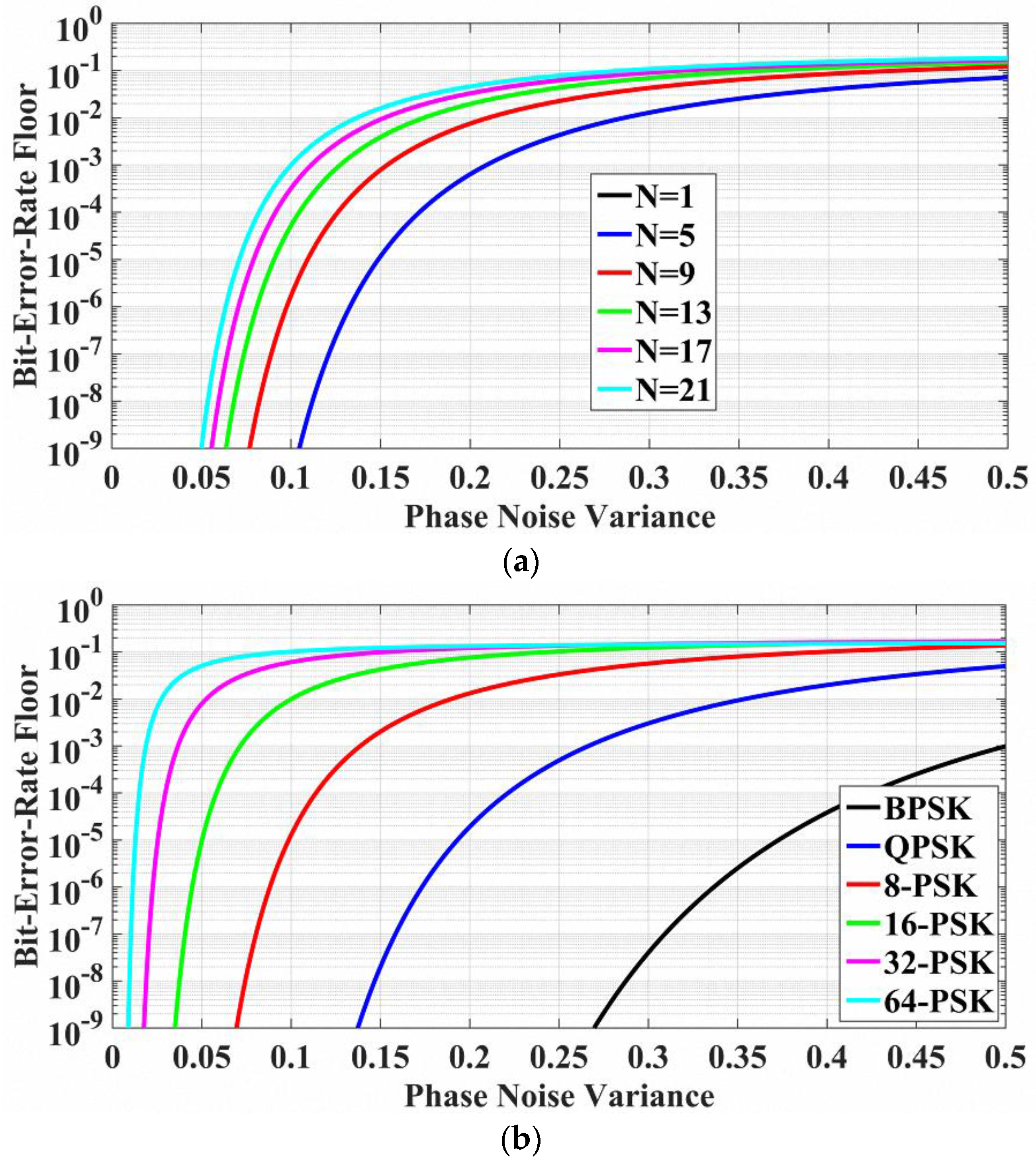
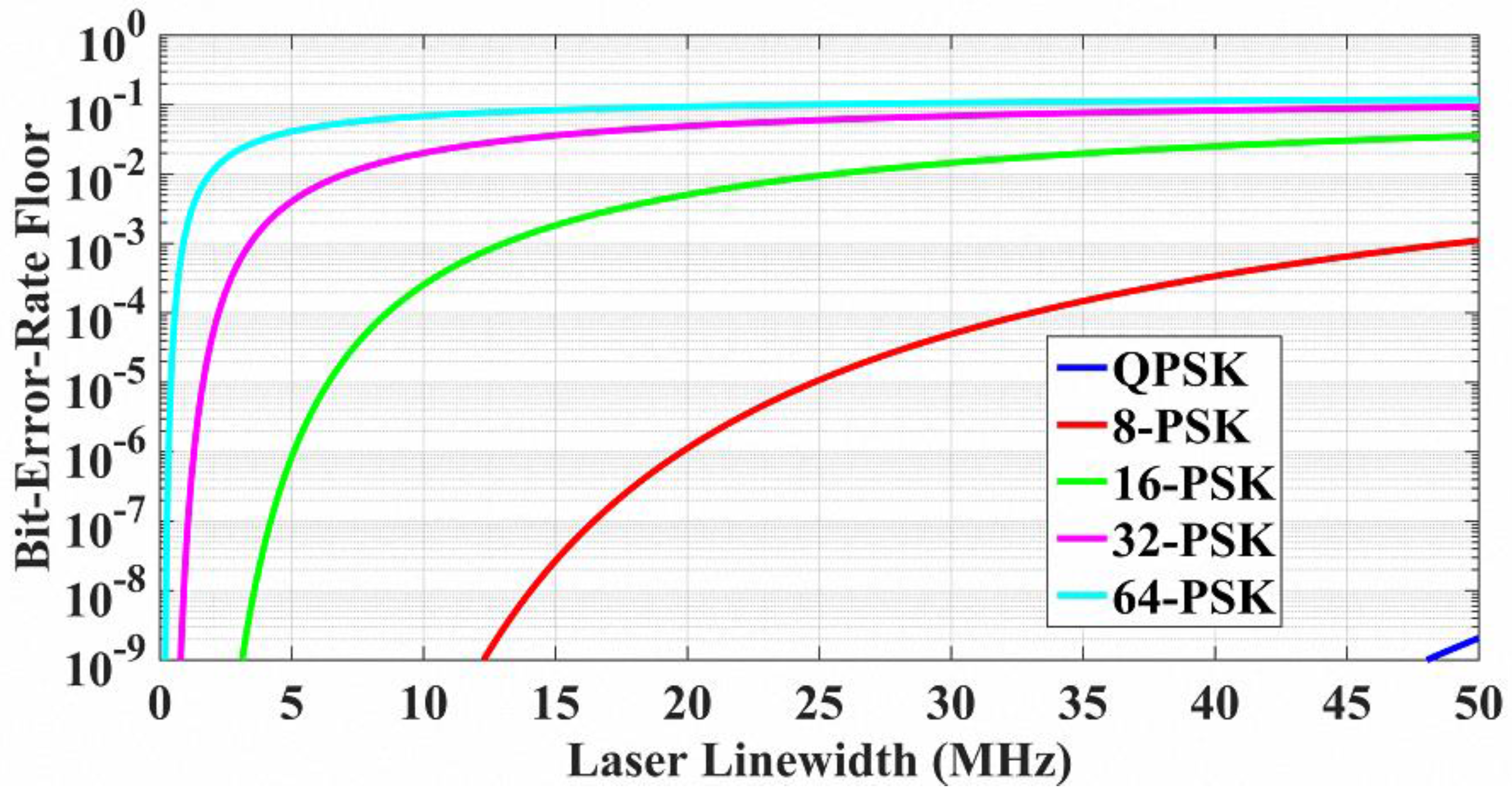
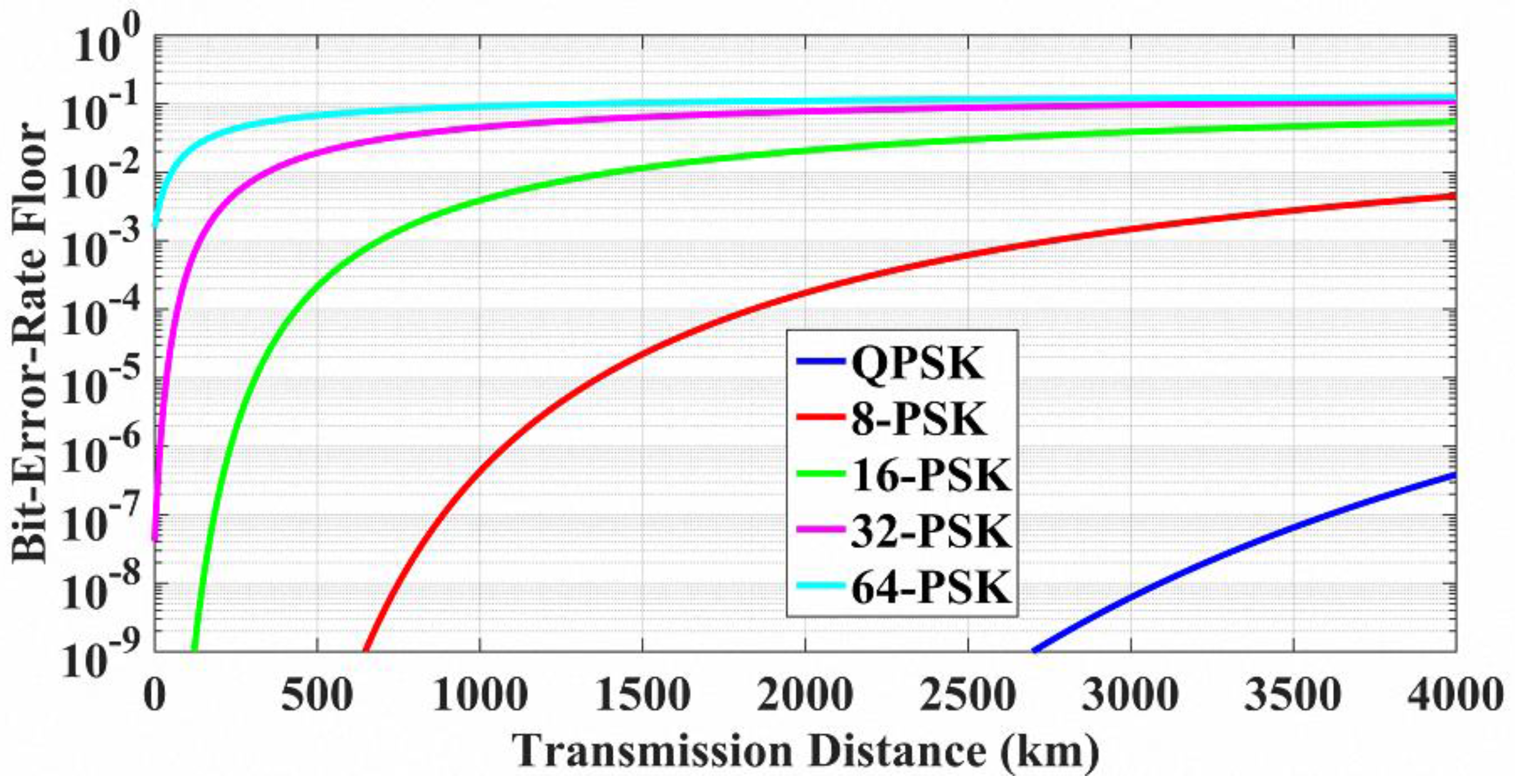
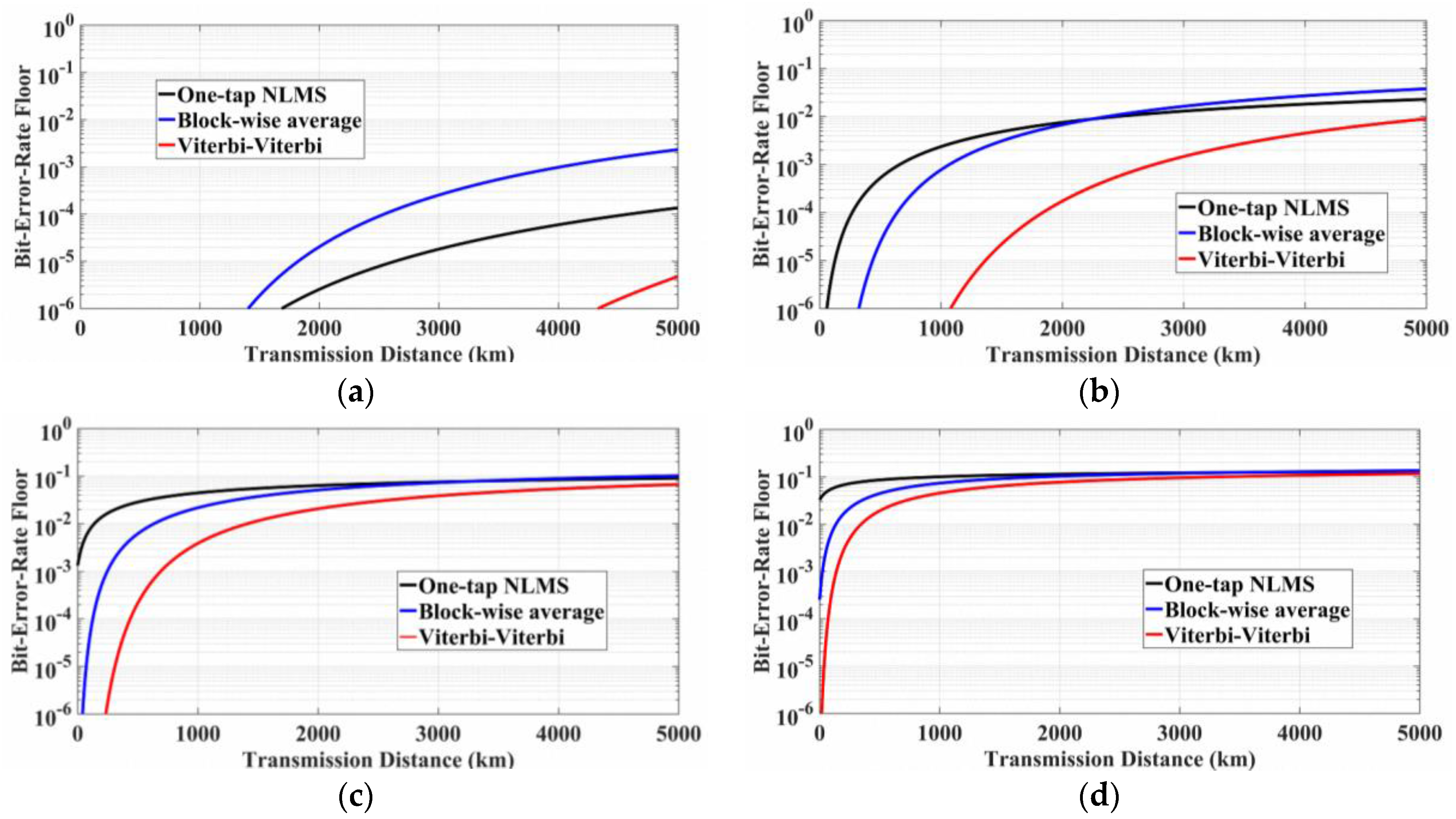
4.1. Results
4.2. Ideal Spectral Efficiency in Carrier Phase Recovery
4.3. Complexity of Carrier Phase Recovery Approaches
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Essiambre, R.J.; Foschini, G.J.; Kramer, G.; Winzer, P.J. Capacity limits of information transport in fiber-optic networks. Phys. Rev. Lett. 2008, 101, 163901. [Google Scholar] [CrossRef] [PubMed]
- Bayvel, P.; Maher, R.; Xu, T.; Liga, G.; Shevchenko, N.A.; Lavery, D.; Alvarado, A.; Killey, R.I. Maximising the optical network capacity. Philos. Trans. R. Soc. A 2016, 374, 20140440. [Google Scholar] [CrossRef] [PubMed]
- Essiambre, R.J.; Tkach, R.W. Capacity trends and limits of optical communication networks. Proc. IEEE 2012, 100, 1035–1055. [Google Scholar] [CrossRef]
- Kaminow, I.; Li, T.; Willner, A.E. Optical Fiber Telecommunications VB: System and Networks; Academic Press: Oxford, UK, 2010. [Google Scholar]
- Agrawal, G.P. Fiber-Optic Communication Systems, 4th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Li, Y.; Xu, T.; Jia, D.; Jing, W.; Hu, H.; Yu, J.; Zhang, Y. Dynamic dispersion compensation in a 40 Gb/s single-channeled optical fiber communication system. Acta Opt. Sin. 2007, 27, 1161–1165. [Google Scholar]
- Xu, T.; Li, J.; Jacobsen, G.; Popov, S.; Djupsjöbacka, A.; Schatz, R.; Zhang, Y.; Bayvel, P. Field trial over 820 km installed SSMF and its potential Terabit/s superchannel application with up to 57.5-Gbaud DP-QPSK transmission. Opt. Commun. 2015, 353, 133–138. [Google Scholar] [CrossRef]
- Galili, M.; Hu, H.; Mulvad, H.C.H.; Medhin, A.K.; Clausen, A.; Oxenløwe, L.K. Optical systems for ultra-high-speed TDM networking. Photonics 2014, 1, 83–94. [Google Scholar] [CrossRef]
- Ip, E.; Lau, A.P.T.; Barros, D.J.F.; Kahn, J.M. Coherent detection in optical fiber systems. Opt. Express 2008, 16, 753–791. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Vanin, E.; Wang, K.; Friberg, A.T.; Zhang, Y. Chromatic dispersion compensation in coherent transmission system using digital filters. Opt. Express 2010, 18, 16243–16257. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.G. Coherent detection method using DSP for demodulation of signal and subsequent equalization of propagation impairments. IEEE Photonics Technol. Lett. 2004, 16, 674–676. [Google Scholar] [CrossRef]
- Savory, S.J. Digital filters for coherent optical receivers. Opt. Express 2008, 16, 804–817. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Wang, K.; Friberg, A.T. Normalized LMS digital filter for chromatic dispersion equalization in 112-Gbit/s PDM-QPSK coherent optical transmission system. Opt. Commun. 2010, 283, 963–967. [Google Scholar] [CrossRef]
- Kudo, R.; Kobayashi, T.; Ishihara, K.; Takatori, Y.; Sano, A.; Miyamoto, Y. Coherent optical single carrier transmission using overlap frequency domain equalization for long-haul optical systems. J. Lightwave Technol. 2009, 27, 3721–3728. [Google Scholar] [CrossRef]
- Ip, E.; Kahn, J.M. Digital equalization of chromatic dispersion and polarization mode dispersion. J. Lightwave Technol. 2007, 25, 2033–2043. [Google Scholar] [CrossRef]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. Carrier phase estimation methods in coherent transmission systems influenced by equalization enhanced phase noise. Opt. Commun. 2013, 293, 54–60. [Google Scholar] [CrossRef]
- Liga, G.; Xu, T.; Alvarado, A.; Killey, R.; Bayvel, P. On the performance of multichannel digital backpropagation in high-capacity long-haul optical transmission. Opt. Express 2014, 22, 30053–30062. [Google Scholar] [CrossRef] [PubMed]
- Maher, R.; Xu, T.; Galdino, L.; Sato, M.; Alvarado, A.; Shi, K.; Savory, S.J.; Thomsen, B.C.; Killey, R.I.; Bayvel, P. Spectrally shaped DP-16QAM super-channel transmission with multi-channel digital back propagation. Sci. Rep. 2015, 5, 08214. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Essiambre, R.J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity limits of optical fiber networks. J. Lightwave Technol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Kazovsky, L.G. Impact of laser phase noise on optical heterodyne communication systems. J. Opt. Commun. 1986, 7, 66–78. [Google Scholar] [CrossRef]
- Zhang, S.; Kam, P.Y.; Yu, C.; Chen, J. Laser linewidth tolerance of decision-aided maximum likelihood phase estimation in coherent optical M-ary PSK and QAM systems. IEEE Photonics Technol. Lett. 2009, 21, 1075–1077. [Google Scholar] [CrossRef]
- Taylor, M.G. Phase estimation methods for optical coherent detection using digital signal processing. J. Lightwave Technol. 2009, 17, 901–914. [Google Scholar] [CrossRef]
- Fatadin, I.; Ives, D.; Savory, S.J. Differential carrier phase recovery for QPSK optical coherent systems with integrated tunable lasers. Opt. Express 2013, 21, 10166–10171. [Google Scholar] [CrossRef] [PubMed]
- Ip, E.; Kahn, J.M. Feedforward carrier recovery for coherent optical communications. J. Lightwave Technol. 2007, 25, 2675–2692. [Google Scholar] [CrossRef]
- Goldfarb, G.; Li, G. BER estimation of QPSK homodyne detection with carrier phase estimation using digital signal processing. Opt. Express 2006, 14, 8043–8053. [Google Scholar] [CrossRef] [PubMed]
- Mori, Y.; Zhang, C.; Igarashi, K.; Katoh, K.; Kikuchi, K. Unrepeated 200-km transmission of 40-Gbit/s 16-QAM signals using digital coherent receiver. Opt. Express 2009, 17, 1435–1441. [Google Scholar] [CrossRef] [PubMed]
- Fatadin, I.; Ives, D.; Savory, S.J. Blind equalization and carrier phase recovery in a 16-QAM optical coherent system. J. Lightwave Technol. 2009, 27, 3042–3049. [Google Scholar] [CrossRef]
- Kikuchi, K. Phase-diversity homodyne detection of multilevel optical modulation with digital carrier phase estimation. IEEE J. Sel. Top. Quant. Electron. 2006, 12, 563–570. [Google Scholar] [CrossRef]
- Ly-Gagnon, D.S.; Tsukamoto, S.; Katoh, K.; Kikuchi, K. Coherent detection of optical quadrature phase-shift keying signals with carrier phase estimation. J. Lightwave Technol. 2006, 24, 12–21. [Google Scholar] [CrossRef]
- Viterbi, A.J.; Viterbi, A.M. Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmission. IEEE Trans. Inf. Theory 1983, 29, 543–551. [Google Scholar] [CrossRef]
- Jacobsen, G.; Xu, T.; Popov, S.; Sergeyev, S. Study of EEPN mitigation using modified RF pilot and Viterbi-Viterbi based phase noise compensation. Opt. Express 2013, 21, 12351–12362. [Google Scholar] [CrossRef] [PubMed]
- Shieh, W.; Ho, K.P. Equalization-enhanced phase noise for coherent detection systems using electronic digital signal processing. Opt. Express 2008, 16, 15718–15727. [Google Scholar] [CrossRef] [PubMed]
- Xie, C. Local oscillator phase noise induced penalties in optical coherent detection systems using electronic chromatic dispersion compensation. In Proceedings of the Conference on Optical Fiber Communication (OFC), San Diego, CA, USA, 22–26 March 2009.
- Lau, A.P.T.; Shen, T.S.R.; Shieh, W.; Ho, K.P. Equalization-enhanced phase noise for 100 Gb/s transmission and beyond with coherent detection. Opt. Express 2010, 18, 17239–17251. [Google Scholar] [CrossRef] [PubMed]
- Fatadin, I.; Savory, S.J. Impact of phase to amplitude noise conversion in coherent optical systems with digital dispersion compensation. Opt. Express 2010, 18, 16273–16278. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. Analytical estimation of phase noise influence in coherent transmission system with digital dispersion equalization. Opt. Express 2011, 19, 7756–7768. [Google Scholar] [CrossRef] [PubMed]
- Ho, K.P.; Lau, A.P.T.; Shieh, W. Equalization-enhanced phase noise induced time jitter. Opt. Lett. 2011, 36, 585–587. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, G.; Xu, T.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. EEPN and CD study for coherent optical nPSK and nQAM systems with RF pilot based phase noise compensation. Opt. Express 2012, 20, 8862–8870. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Sergeyev, S.; Friberg, A.T.; Zhang, Y. Analytical BER performance in differential n-PSK coherent transmission system influenced by equalization enhanced phase noise. Opt. Commun. 2015, 334, 222–227. [Google Scholar] [CrossRef]
- Xu, T.; Liga, G.; Lavery, D.; Thomson, B.C.; Savory, S.J.; Killey, R.I.; Bayvel, P. Equalization enhanced phase noise in Nyquist-spaced superchannel transmission systems using multi-channel digital back-propagation. Sci. Rep. 2015, 5, 13990. [Google Scholar] [CrossRef] [PubMed]
- Zhuge, Q.; Morsy-Osman, M.H.; Plant, D.V. Low overhead intra-symbol carrier phase recovery for reduced-guard-interval CO-OFDM. J. Lightwave Technol. 2013, 31, 1158–1169. [Google Scholar] [CrossRef]
- Jacobsen, G.; Lidón, M.; Xu, T.; Popov, S.; Friberg, A.T.; Zhang, Y. Influence of pre- and post-compensation of chromatic dispersion on equalization enhanced phase noise in coherent multilevel systems. J. Opt. Commun. 2011, 32, 257–261. [Google Scholar] [CrossRef]
- Kakkar, A.; Navarro, J.R.; Schatz, R.; Pang, X.; Ozolins, O.; Louchet, H.; Jacobsen, G.; Popov, S. Equalization enhanced phase noise in coherent optical systems with digital pre- and post-processing. Photonics 2016, 3, 12. [Google Scholar] [CrossRef]
- Ho, K.P.; Shieh, W. Equalization-enhanced phase noise in mode-division multiplexed systems. J. Lightwave Technol. 2013, 31, 2237–2243. [Google Scholar]
- Shieh, W. Interaction of laser phase noise with differential-mode-delay in few-mode fiber based MIMO systems. In Proceedings of the Conference on Optical Fiber Communication (OFC), Los Angeles, CA, USA, 4–8 March 2012.
- Colavolpe, G.; Foggi, T.; Forestieri, E.; Secondini, M. Impact of phase noise and compensation techniques in coherent optical systems. J. Lightwave Technol. 2011, 29, 2790–2800. [Google Scholar] [CrossRef]
- Farhoudi, R.; Ghazisaeidi, A.; Rusch, L.A. Performance of carrier phase recovery for electronically dispersion compensated coherent system. Opt. Express 2012, 20, 26568–26582. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, G.; Xu, T.; Popov, S.; Li, J.; Friberg, A.T.; Zhang, Y. Receiver implemented RF pilot tone phase noise mitigation in coherent optical nPSK and nQAM systems. Opt. Express 2011, 19, 14487–14494. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, T.; Sugihara, T.; Uto, K. DSP-based optical modulation technique for long-haul transmission. In Proceedings of the Next-Generation Optical Communication: Components, Sub-Systems, and Systems IV, San Francisco, CA, USA, 7 February 2015.
- Vanin, E.; Jacobsen, G. Analytical estimation of laser phase noise induced BER floor in coherent receiver with digital signal processing. Opt. Express 2010, 18, 4246–4259. [Google Scholar] [CrossRef] [PubMed]
- Kakkar, A.; Navarro, J.R.; Schatz, R.; Louchet, H.; Pang, X.; Ozolins, O.; Jacobsen, G.; Popov, S. Comprehensive study of equalization-enhanced phase noise in coherent optical systems. J. Lightwave Technol. 2015, 33, 4834–4841. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kojima, K.; Koike-Akino, T.; Millar, D.S.; Parsons, K. BICM capacity analysis of 8QAM-alternative modulation formats in nonlinear fiber transmission. In Proceedings of the IEEE Tyrrhenian International Workshop on Digital Communications, Florence, Italy, 22 September 2015; pp. 57–59.
- Kojima, K.; Koike-Akino, T.; Millar, D.S.; Pajovic, M.; Parsons, K.; Yoshida, T. Investigation of low code rate DP-8PSK as an alternative to DP-QPSK. In Proceedings of the Conference on Optical Fiber Communication (OFC), Anaheim, CA, USA, 20–22 March 2016.





| One-Tap Normalized LMS | Block-Wise Average | Viterbi-Viterbi |
|---|---|---|
| 5 | n | n |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Jacobsen, G.; Popov, S.; Li, J.; Liu, T.; Zhang, Y.; Bayvel, P. Analytical Investigations on Carrier Phase Recovery in Dispersion-Unmanaged n-PSK Coherent Optical Communication Systems. Photonics 2016, 3, 51. https://doi.org/10.3390/photonics3040051
Xu T, Jacobsen G, Popov S, Li J, Liu T, Zhang Y, Bayvel P. Analytical Investigations on Carrier Phase Recovery in Dispersion-Unmanaged n-PSK Coherent Optical Communication Systems. Photonics. 2016; 3(4):51. https://doi.org/10.3390/photonics3040051
Chicago/Turabian StyleXu, Tianhua, Gunnar Jacobsen, Sergei Popov, Jie Li, Tiegen Liu, Yimo Zhang, and Polina Bayvel. 2016. "Analytical Investigations on Carrier Phase Recovery in Dispersion-Unmanaged n-PSK Coherent Optical Communication Systems" Photonics 3, no. 4: 51. https://doi.org/10.3390/photonics3040051
APA StyleXu, T., Jacobsen, G., Popov, S., Li, J., Liu, T., Zhang, Y., & Bayvel, P. (2016). Analytical Investigations on Carrier Phase Recovery in Dispersion-Unmanaged n-PSK Coherent Optical Communication Systems. Photonics, 3(4), 51. https://doi.org/10.3390/photonics3040051





