1. Introduction
Quantum cascade lasers (QCLs) [
1] are widely used in high resolution molecular spectroscopy and trace gas sensing applications in the mid-infrared spectral region owing to their unique spectral and wavelength tuning properties. QCLs can be designed to emit in a broad wavelength region ranging from below 4 μm to more than 10 μm based on the mature InP semiconductor material. Singlemode continuous wave operation with output powers reaching more than 100 mW is routinely achieved nowadays at room temperature using a distributed feedback (DFB) grating [
2], or by placing the QCL chip in an external cavity configuration [
3]. QCLs can be continuously tuned in wavelength through their temperature or injection current. Temperature tuning is rather slow as the QCL temperature is generally controlled with a thermo-electrical cooler (TEC) through a fairly massive sub-mount. However, with a typical temperature-tuning coefficient of (Δν/ν)/
T ≈ 10
−4 K
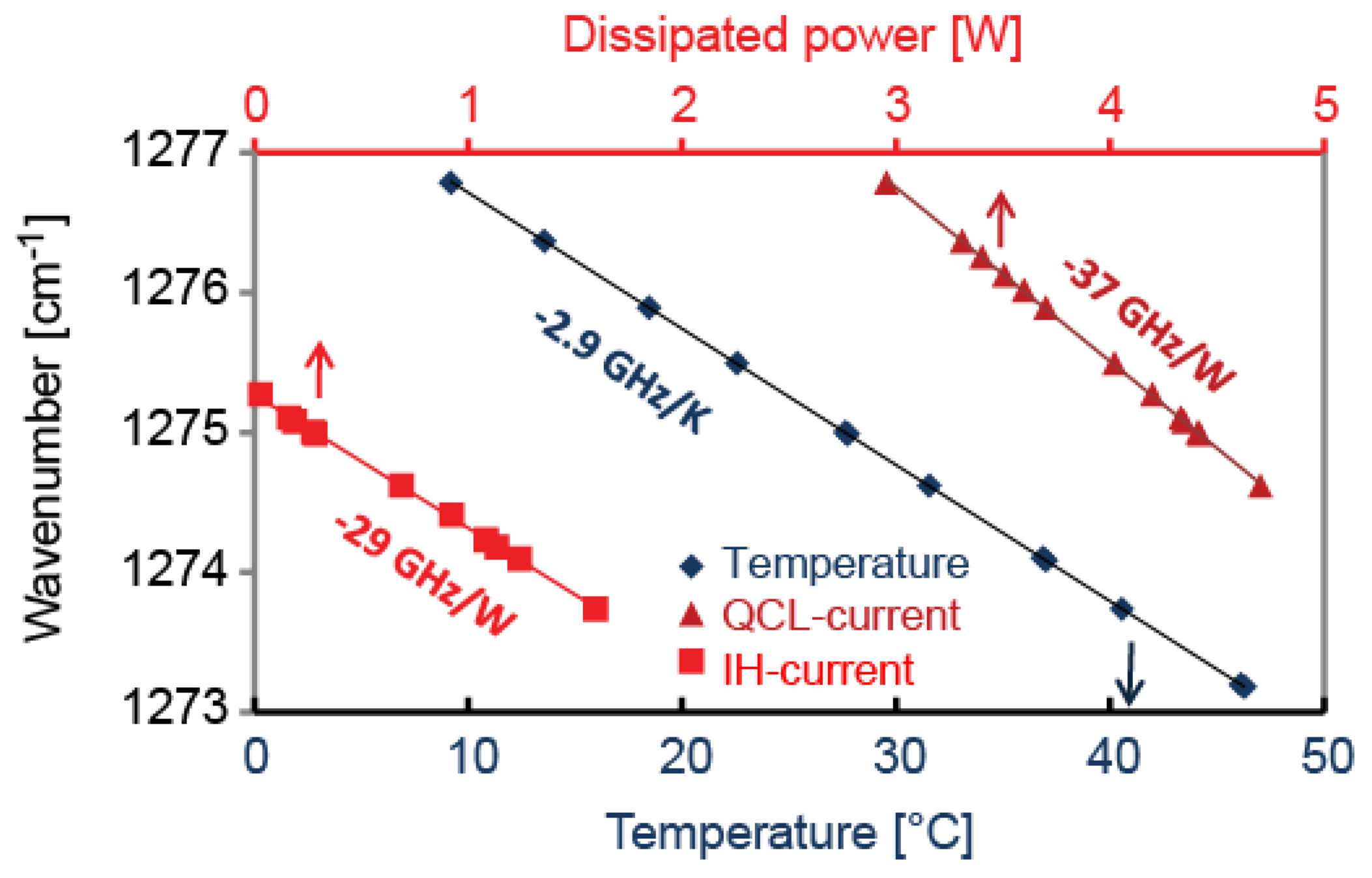
−1 corresponding to ~3 GHz/K in the wavelength range of 8 μm, a large tuning range can be achieved by varying the QCL temperature with a moderate change of the optical output power. Temperature tuning is, thus, mainly used for large but slow frequency sweeping. On the other hand, the QCL wavelength can be rapidly changed with the injection current, at frequencies exceeding 100 kHz [
4]. However, the tuning range is limited and current modulation induces a significant change of the emitted optical power. QCL current modulation is widely used in sensitive spectroscopic techniques for trace gas sensing like wavelength/frequency modulation spectroscopy (WMS/FMS) [
5,
6] or photoacoustic spectroscopy (PAS) [
7]. Each of these techniques involves a modulation of the laser wavelength and a harmonic demodulation of the output signal detected after light-gas interaction (optical signal in WMS or acoustic signal in PAS). A derivative-like signal of the gas absorption feature is thus obtained, which is used to quantify the gas concentration. However, the strong variation in the optical power induced by the QCL current modulation leads to residual amplitude modulation (RAM). This RAM can distort the harmonic signals of a gas absorption line, in particular by inducing an offset in the first harmonic signal (1
f detection) that can be detrimental in some applications, for instance when using this signal as an error signal in a feedback loop to stabilize a laser at the center of a molecular or atomic transition. RAM also results in an asymmetry of the second harmonic signal (2
f detection) of a gas absorption line.
A novel tuning actuator in QCLs was recently developed by Alpes Lasers. It consists of a small heating element incorporated next to the active region of DFB QCLs [
8]. This integrated heater (IH) is a resistive element driven by an electrical current, which heats the laser via Joule’s dissipation. This novel design allows the temperature of the active region to be varied much faster than by direct temperature control with a TEC, with a reduced associated change in optical power compared to QCL current modulation. These properties make this new tuning actuator attractive for gas phase spectroscopy applications.
The IH current also constitutes a novel channel to apply fast corrections for frequency stabilization and noise reduction in a QCL. Electrical feedback applied to the QCL current is the standard approach to stabilize a QCL to an optical reference, such as a molecular transition or the resonance of an optical cavity, where an error signal proportional to the QCL frequency fluctuations is generated. However, other methods have been demonstrated for frequency noise reduction in QCLs that circumvent the use of an optical reference by exploiting the correlation observed between fluctuations of the optical frequency and of the voltage between the QCL terminals [
9]. Using the QCL voltage noise as an error signal to reduce the frequency noise requires another actuator that enables fast internal temperature corrections to be applied to the QCL. The reason is that temperature variations were identified to be the major contribution in the conversion of the terminal voltage noise into frequency noise in QCLs [
9]. Such a correction signal cannot be applied directly to the QCL current, as it would simply transpose the QCL voltage noise into current noise without significantly changing the fluctuations of the electrical power dissipated in the laser that are responsible for the frequency noise. Therefore, a fast control of the internal temperature of a QCL for noise reduction was implemented by Tombez et al. by illuminating the top surface of the QCL with a near-infrared laser radiation that could be quickly modulated [
10]. A feedback bandwidth in the range of 300 kHz was, thus, obtained. Another approach reported by Sergachev et al., consisted of driving the QCL at constant electrical power instead of constant current, which was realized using fast signal processing of the measured voltage noise [
11]. The novel actuator based on an IH is attractive for the realization of such noise reduction loops in a significantly simpler and more compact implementation. However, prior to this, a first step consists in properly characterizing the properties of this new IH actuator.
In this article, we present a detailed characterization of the modulation properties of such new IH in a QCL emitting at 7.8 μm. The reported characterization includes the tuning coefficients, frequency modulation transfer function, as well as the step response. As an example of applications that can benefit from this new actuator, we present a proof-of-principle experiment of WMS of N2O using a modulation of the IH current, and compare it to the standard approach of injection current modulation.
2. Materials and Methods
The QCL manufactured by Alpes Lasers incorporates an integrated resistive heater, as described by Bismuto et al. [
8]. The laser is a buried-heterostructure DFB-QCL with a width of the active region of 10.3 μm and a length of 2.25 mm. The integrated heater has a thickness of 2 μm and a width of 8 μm, and is located at a distance of ~1 μm from the active region. The QCL emits in the spectral range between 1273 and 1278 cm
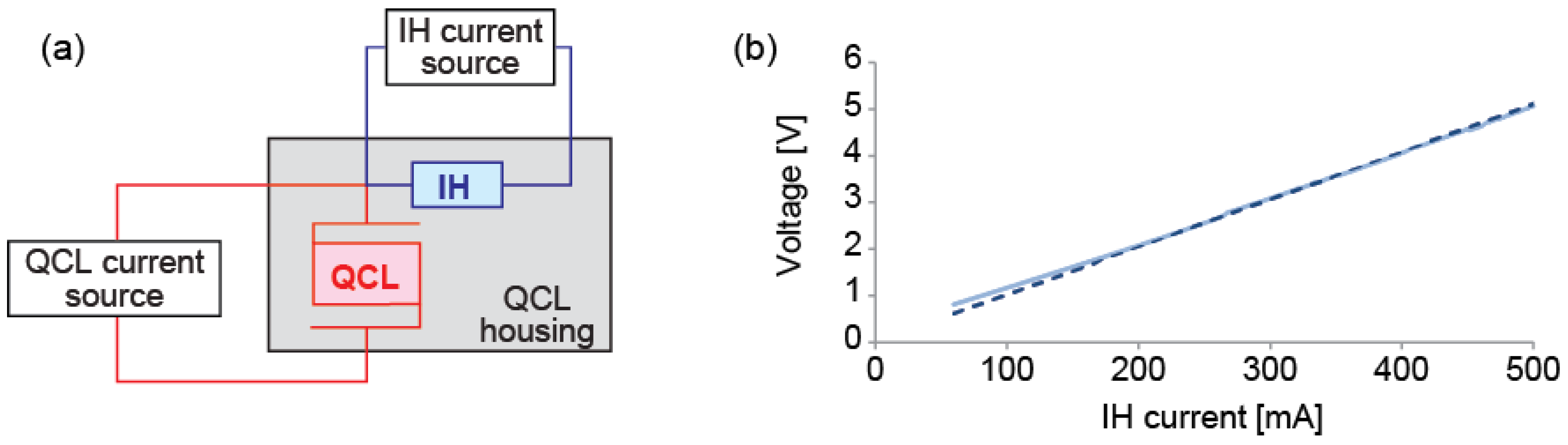
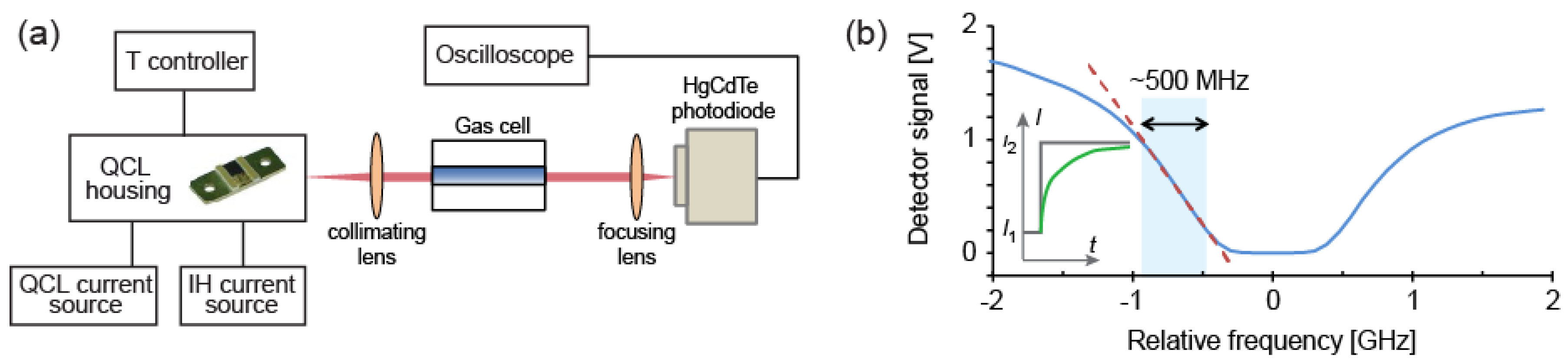
−1 within a temperature range of 0 °C to 45 °C and delivers up to 80 mW of output power. It was mounted on a copper sub-mount housed in a modified version of the laser laboratory housing (LLH) of Alpes Lasers, which accommodated the additional electrical connections to drive the IH. The laser and the IH share a common electrical potential at the laser cathode, as shown in
Figure 1a, and were driven by two separate home-made low-noise current sources [
9]. These drivers can deliver a current up to 1 A and have a noise spectral density lower than 1 nA/Hz
1/2 at Fourier frequencies higher than 1 kHz. This feature generally enables accessing the frequency noise inherent to a QCL itself, without technical limitation resulting from the QCL current source [
12]. The IH has a nearly ohmic response, as shown in
Figure 1b, with an assessed resistance of ~9 Ω that is almost independent of temperature. The QCL temperature was regulated at the mK level with a double-stage TEC and a negative thermal coefficient (NTC) resistor as temperature sensor, controlled by a home-made temperature regulator.
The frequency tuning, impulse response and modulation transfer function of the laser were measured using a spectroscopic set-up that involved a 10-cm long low-pressure gas cell filled with a nominal pressure of 10 mbar of pure N
2O. However, the imperfect tightness of the cell induced a contamination by air at a total pressure of ~70 mbar (see
Section 3.1), which broadened the absorption lines. The tuning coefficients as a function of temperature, injection current and IH current were obtained by performing a large frequency scan with each actuator and comparing the position of several N
2O absorption lines to their reference frequency extracted from the HITRAN database [
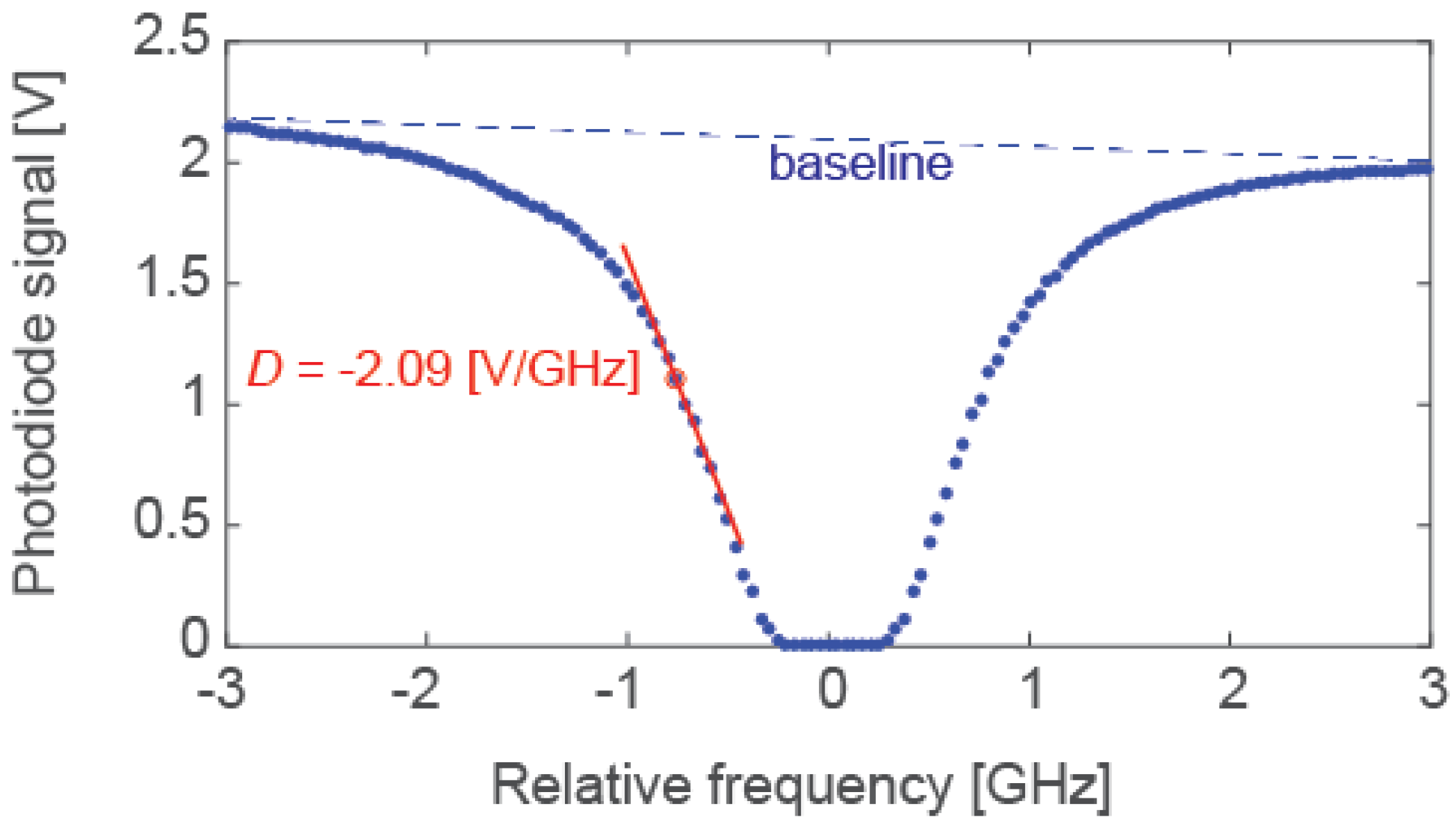
13]. The frequency modulation (FM) response of the QCL was measured by tuning the laser to the side of an absorption line used as a frequency discriminator that linearly converted the frequency modulation of the laser (induced by a small modulation of the injection current or of the IH current) into intensity modulation that was detected with a photodiode (PVI-4TE-5 from Vigo, Ozarow Mazowiecki, Poland, with a bandwidth of 100 MHz). The resulting intensity modulation was measured in amplitude and phase using a lock-in amplifier and converted into frequency modulation using the measured slope of the absorption line (see
Figure 2).
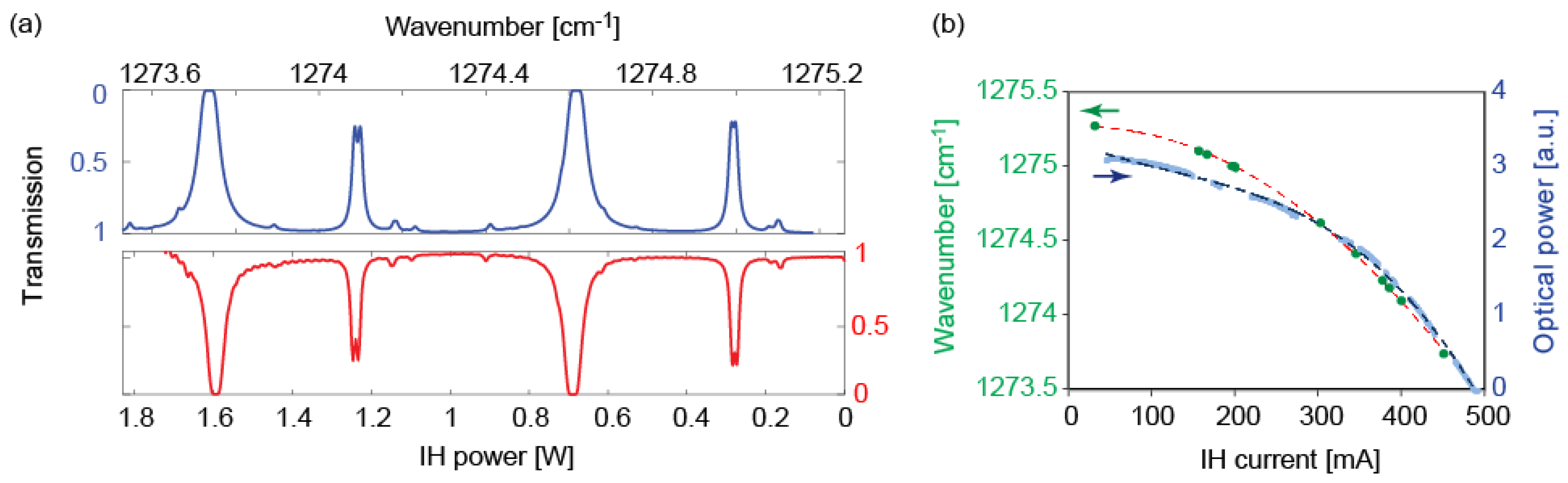
Finally, the applicability of the IH for spectroscopy applications was evaluated by the measurement of the first harmonic WMS signal of a N2O transition obtained by modulating either the IH current or the QCL current at the same frequency of 25 kHz and at different IH or QCL currents.
4. Conclusions and Outlook
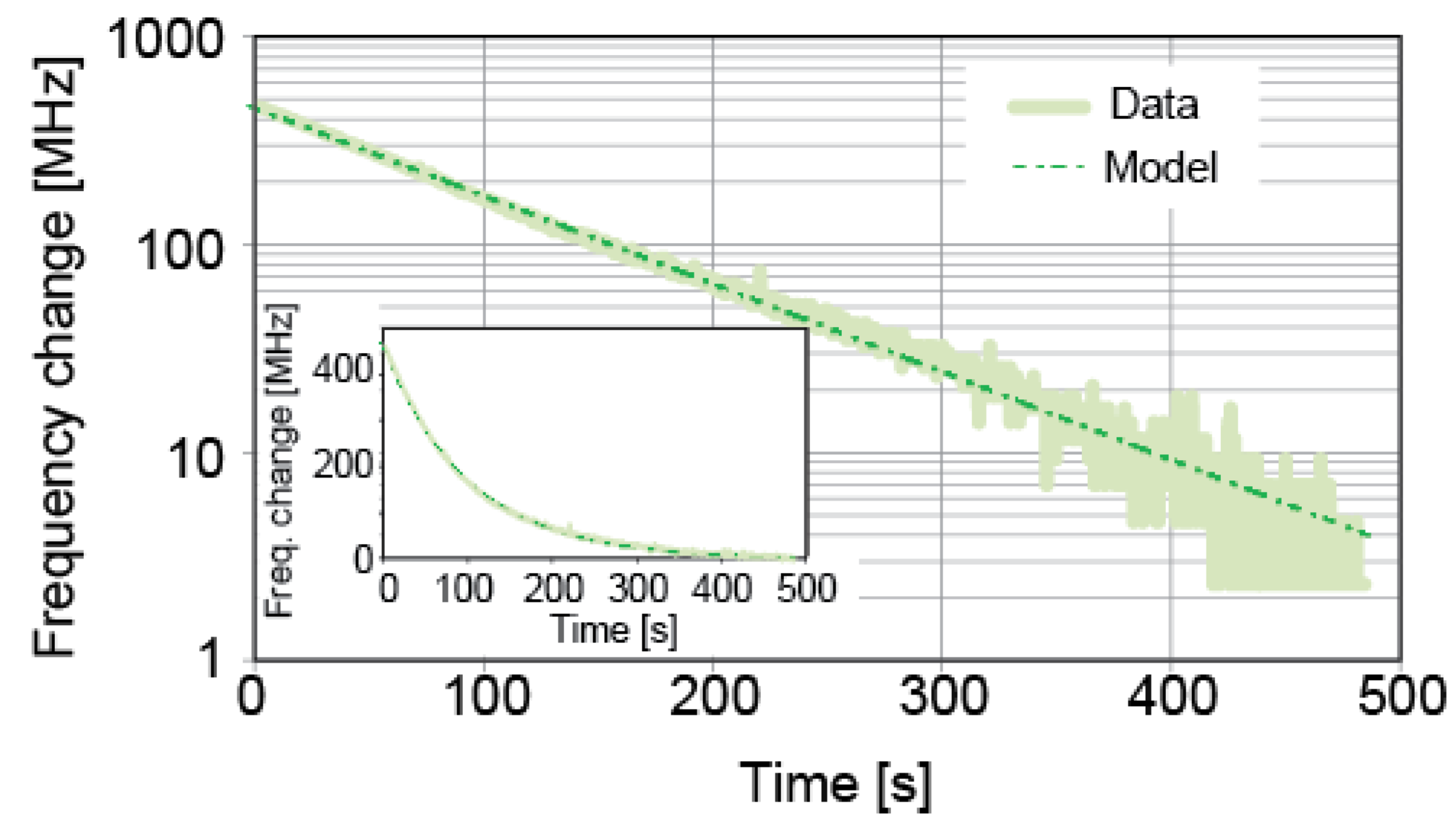
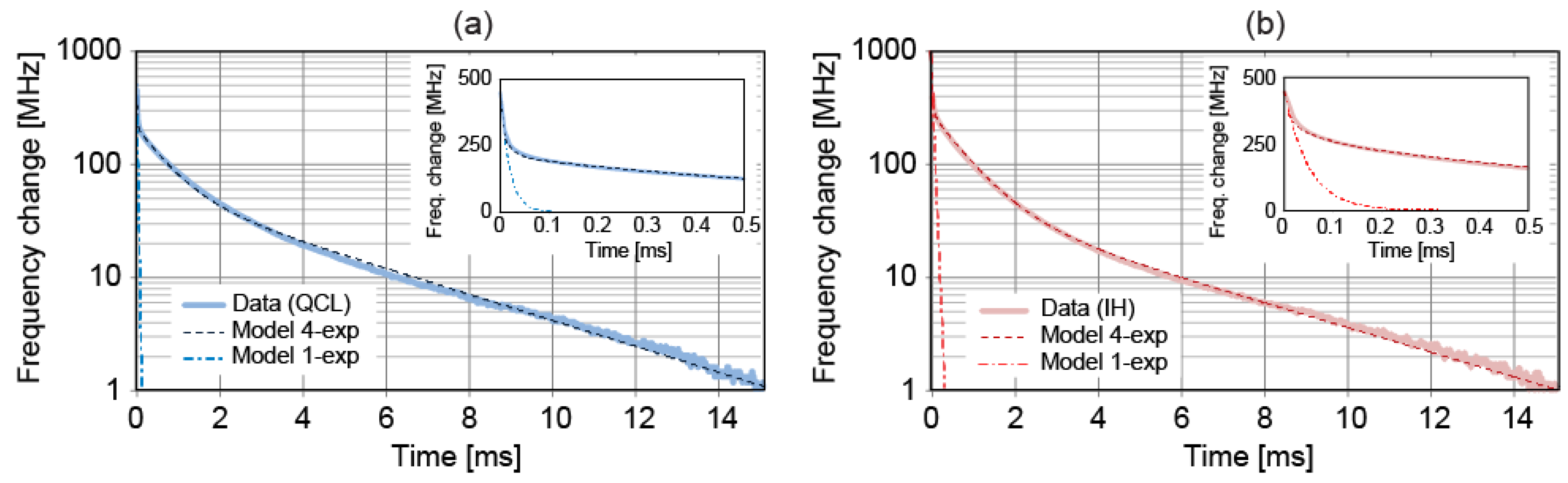
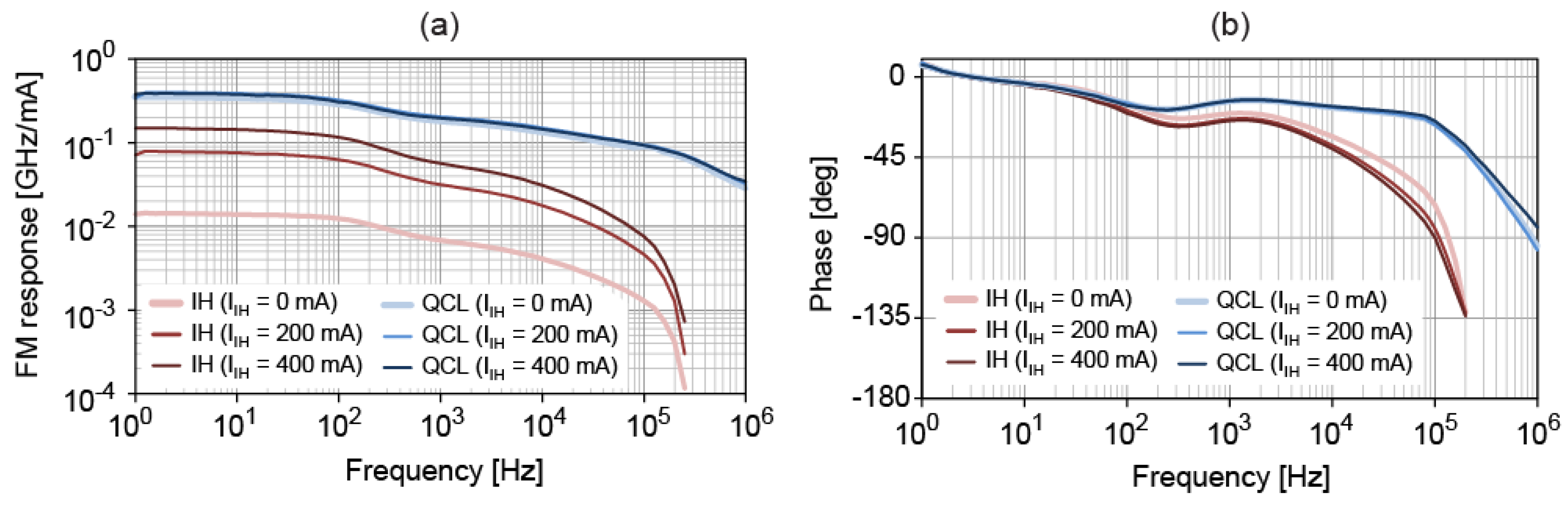
In conclusion, we have characterized in detail a new frequency tuning actuator in a QCL emitting at 7.8 μm. A resistive IH placed in the vicinity of the active region can be electrically controlled, enabling fast changes of the internal temperature of the laser to be applied, which results in a fast control of the emission frequency. The laser output frequency has a linear dependence on the electrical power dissipated in the resistive heater and this frequency tuning occurs with a minor change of the emitted optical power. The impulse response of the laser frequency to a current step applied to the IH is as fast as for a step change of the QCL current and a frequency change of 500 MHz was achieved in a few milliseconds, limited by the head dissipation out of the active region towards the laser sub-mount. For a sine modulation, the QCL current remains approximatively one order of magnitude faster and enables frequency-modulating the QCL radiation with a bandwidth in the MHz range (corresponding to a drop in amplitude of ~10 dB and an associated phase shift of −90°), whereas the bandwidth is limited to ~100 kHz when modulating the IH current. A thermal model was presented to describe the transfer functions experimentally measured for a modulation of the QCL current and IH current. Four different time constants were determined and identified to the heat dissipation in different parts of the device. The shortest time constant is one order of magnitude shorter in the case of QCL current modulation, corresponding to a cut-off frequency higher than 200 kHz, compared to ~20 kHz for IH current modulation.
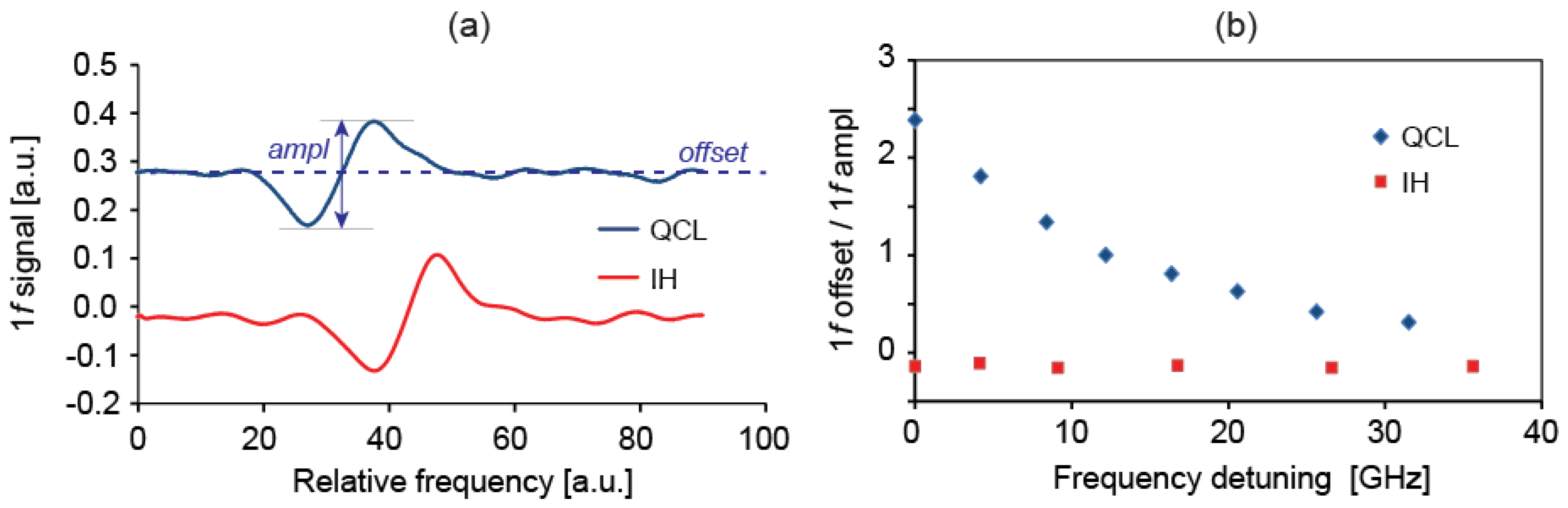
Nevertheless, the modulation bandwidth achieved with the IH is sufficient for most spectroscopic applications of QCLs, such as WMS for trace gas sensing or laser stabilization. Modulating the IH current also has the further advantage of a reduced RAM compared to a direct modulation of the QCL current in some conditions. We showed a proof-of-principle demonstration of the benefit of this decoupled frequency/amplitude modulation in the case of the 1f signal of a N2O absorption line, where the spectroscopic signal was almost free of background offset for a modulation of the IH current, whereas a higher offset was observed when modulating the QCL current. In this latter case, the relative magnitude of the background offset could be reduced by adjusting the phase of the demodulation, or by operating the QCL at a higher current. However, the first solution might also lead to a decrease of the amplitude of the absorption signal depending on the phase shift between AM and FM induced by the current modulation. For the modulation of the IH current, the relative background offset is fairly independent of the DC current, as both the optical frequency and output power of the QCL have a similar dependence on the IH current.
Finally, the new IH provides an additional channel to apply fast frequency corrections to a QCL for frequency stabilization and noise reduction. This is attractive to reduce the short-term linewidth of a QCL without using an optical reference such as a molecular transition, by directly exploiting the noise on the voltage between the QCL terminals, as previously demonstrated [
10,
11]. Whereas a former implementation used an external near-infrared laser diode shining on the top surface of a QCL for fast control of the QCL internal temperature, the new IH provides a much more compact all-electrical solution that we will investigate in the future.