Rapid and Sensitive Quantification of Isotopic Mixtures Using a Rapidly-Swept External Cavity Quantum Cascade Laser †
Abstract
:1. Introduction
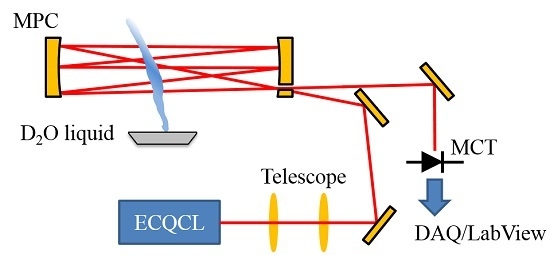
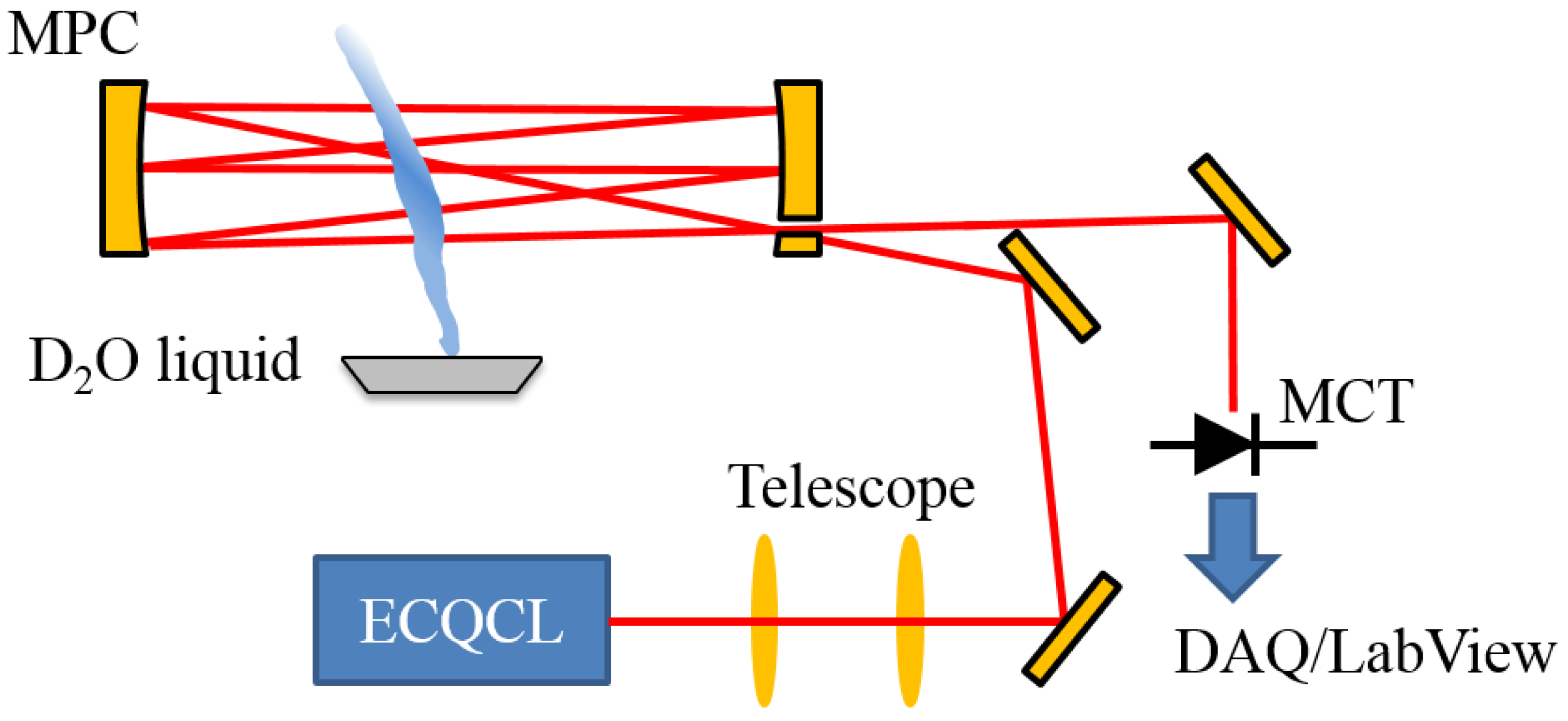
2. Experimental Section
2.1. Optical Layout and Data Collection
2.2. Spectral Processing and Analysis
3. Results and Discussion
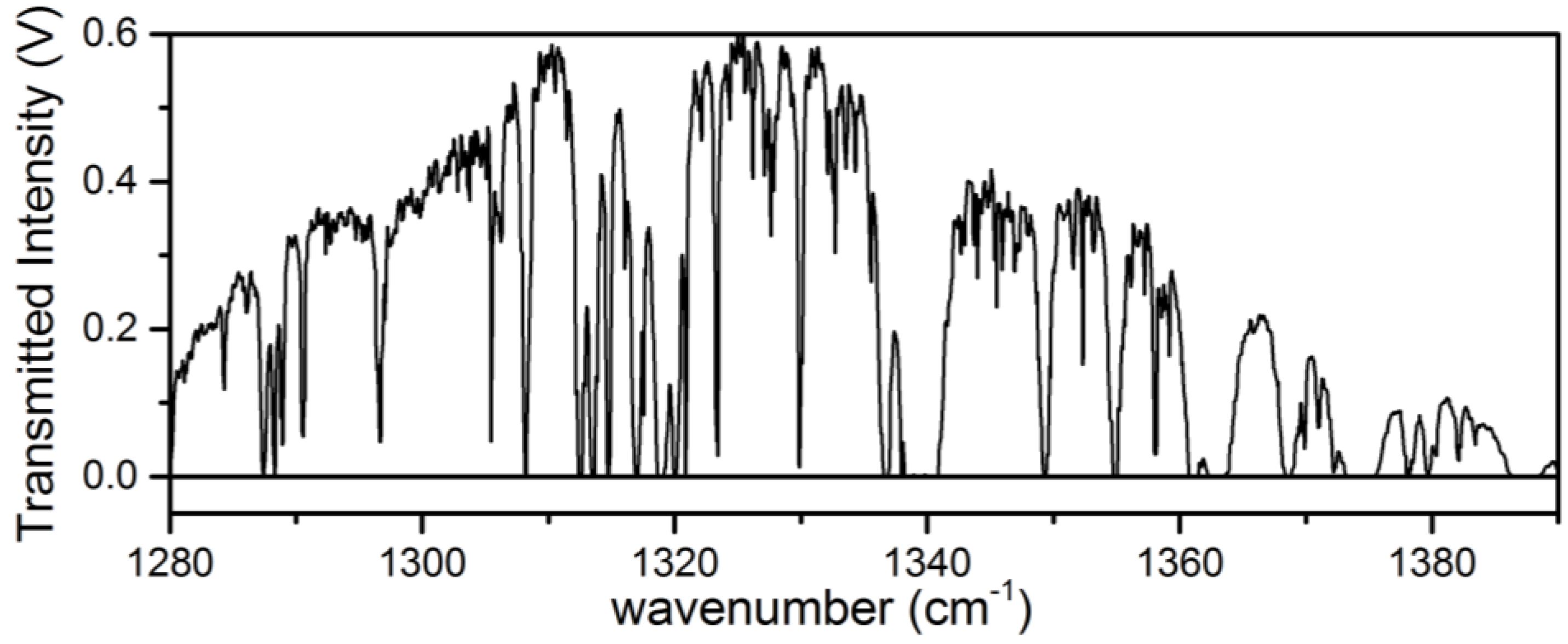
3.1. Analysis of an Isotopic Mixture Containing HDO and D2O
3.2. Calculation of NECs for D2O, HDO and Other Chemicals
3.3. Evaluation of the Isotopic Precision for Measurement of [D2O]/[HDO]
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| 1,1,1,2-tetrafluoroethane | F134A |
| DFB | Distributed feedback |
| MIR | Mid-infrared |
| ECQCL | External-cavity quantum cascade laser |
| MEMS | Microelectromechanical |
| NEC | Noise equivalent concentration |
| DAQ | Digital acquisition system |
| MCT | Mercury cadmium telluride |
| WLS | Weighted least squares |
| NECD | Noise-equivalent column density |
References
- Gong, L.; Lewicki, R.; Griffin, R.J.; Flynn, J.H.; Lefer, B.L.; Tittel, F.K. Atmospheric ammonia measurements in Houston, TX using an external-cavity quantum cascade laser-based sensor. Atmos. Chem. Phys. 2011, 11, 9721–9733. [Google Scholar] [CrossRef]
- Stockwell, C.E.; Yokelson, R.J.; Kreidenweis, S.M.; Robinson, A.L.; DeMott, P.J.; Sullivan, R.C.; Reardon, J.; Ryan, K.C.; Griffith, D.W.T.; Stevens, L. Trace gas emissions from combustion of peat, crop residue, domestic biofuels, grasses, and other fuels: Configuration and Fourier transform infrared (FTIR) component of the fourth Fire Lab at Missoula Experiment (FLAME-4). Atmos. Chem. Phys. 2014, 14, 9727–9754. [Google Scholar] [CrossRef]
- Spearrin, R.M.; Ren, W.; Jeffries, J.B.; Hanson, R.K. Multi-band infrared CO2 absorption sensor for sensitive temperature and species measurements in high-temperature gases. Appl. Phys. B 2014, 116, 855–865. [Google Scholar] [CrossRef]
- Brandstetter, M.; Genner, A.; Anic, K.; Lendl, B. Tunable external cavity quantum cascade laser for the simultaneous determination of glucose and lactate in aqueous phase. Analyst 2010, 135, 3260–3265. [Google Scholar] [CrossRef] [PubMed]
- Brandstetter, M.; Sumalowitsch, T.; Genner, A.; Posch, A.E.; Herwig, C.; Drolz, A.; Fuhrmann, V.; Perkmann, T.; Lendl, B. Reagent-free monitoring of multiple clinically relevant parameters in human blood plasma using a mid-infrared quantum cascade laser based sensor system. Analyst 2013, 138, 4022–4028. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J.; Ostendorf, R.; Grahmann, J.; Merten, A.; Hugger, S.; Jarvis, J.P.; Fuchs, F.; Boskovic, D.; Schenk, H. Widely tuneable quantum cascade lasers for spectroscopic sensing. Proc. SPIE 2015, 9370. [Google Scholar] [CrossRef]
- Kotidis, P.; Deutsch, E.R.; Goyal, A. Standoff detection of chemical and biological threats using miniature widely tunable QCLs. Proc. SPIE 2015, 9467. [Google Scholar] [CrossRef]
- Lyakh, A.; Barron-Jimenez, R.; Dunayevskiy, I.; Go, R.; Patel, C.K.N. External cavity quantum cascade lasers with ultra rapid acousto-optic tuning. Appl. Phys. Lett. 2015, 106, 141101. [Google Scholar] [CrossRef]
- Hugger, S.; Fuchs, F.; Jarvis, J.; Kinzer, M.; Yang, Q.K.; Driad, R.; Aidam, R.; Wagner, J. Broadband-tunable external-cavity quantum cascade lasers for the spectroscopic detection of hazardous substances. Proc. SPIE 2013, 8631. [Google Scholar] [CrossRef]
- Joly, L.; Zéninari, V.; Parvitte, B.; Courtois, D.; Durry, G. Water-vapor isotope ratio measurements in air with a quantum-cascade laser spectrometer. Opt. Lett. 2006, 31, 143–145. [Google Scholar] [CrossRef] [PubMed]
- Worle, K.; Seichter, F.; Wilk, A.; Armacost, C.; Day, T.; Godejohann, M.; Wachter, U.; Vogt, J.; Radermacher, P.; Mizaikoff, B. Breath Analysis with Broadly Tunable Quantum Cascade Lasers. Anal. Chem. 2013, 85, 2697–2702. [Google Scholar] [CrossRef] [PubMed]
- Mohn, J.; Tuzson, B.; Manninen, A.; Yoshida, N.; Toyoda, S.; Brand, W.A.; Emmenegger, L. Site selective real-time measurements of atmospheric N2O isotopomers by laser spectroscopy. Atmos. Meas. Tech. 2012, 5, 1601–1609. [Google Scholar] [CrossRef]
- Kasyutich, V.L.; Martin, P.A. 13CO2/12CO2 isotopic ratio measurements with a continuous-wave quantum cascade laser in exhaled breath. Infrared Phys. Technol. 2012, 55, 60–66. [Google Scholar] [CrossRef]
- Wang, W.E.; Michel, A.P.M.; Wang, L.; Tsai, T.; Baeck, M.L.; Smith, J.A.; Wysocki, G. A quantum cascade laser-based water vapor isotope analyzer for environmental monitoring. Rev. Sci. Instrum. 2014, 85, 10. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.D.; McManus, J.B.; Herndon, S.C.; Zahniser, M.S.; Tuzson, B.; Emmenegger, L. New method for isotopic ratio measurements of atmospheric carbon dioxide using a 4.3 μm pulsed quantum cascade laser. Appl. Phys. B 2008, 90, 301–309. [Google Scholar] [CrossRef]
- Barthel, M.; Sturm, P.; Hammerle, A.; Buchmann, N.; Gentsch, L.; Siegwolf, R.; Knohl, A. Soil H218O labelling reveals the effect of drought on C18OO fluxes to the atmosphere. J. Exp. Bot. 2014, 65, 5783–5793. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Nikodem, M.; Zhang, E.; Cikach, F.; Barnes, J.; Comhair, S.; Dweik, R.A.; Kao, C.; Wysocki, G. Shot-noise Limited Faraday Rotation Spectroscopy for Detection of Nitric Oxide Isotopes in Breath, Urine, and Blood. Sci. Rep. 2015. [Google Scholar] [CrossRef] [PubMed]
- Zhang, E.; Huang, S.; Ji, Q.X.; Silvernagel, M.; Wang, Y.; Ward, B.; Sigman, D.; Wysocki, G. Nitric Oxide Isotopic Analyzer Based on a Compact Dual-Modulation Faraday Rotation Spectrometer. Sensors 2015, 15, 25992–26008. [Google Scholar] [CrossRef] [PubMed]
- Brumfield, B.E.; Taubman, M.S.; Suter, J.D.; Phillips, M.C. Characterization of a swept external cavity quantum cascade laser for rapid broadband spectroscopy and sensing. Opt. Express 2015, 23, 25553–25569. [Google Scholar] [CrossRef] [PubMed]
- Li, J.S.; Zhang, L.Z.; Yu, B.L. Site-selective nitrogen isotopic ratio measurement of nitrous oxide using a TE-cooled CW-RT-QCL based spectrometer. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2014, 133, 489–494. [Google Scholar] [CrossRef] [PubMed]
- Phillips, M.C.; Taubman, M.S.; Bernacki, B.E.; Cannon, B.D.; Stahl, R.D.; Schiffern, J.T.; Myers, T.L. Real-time trace gas sensing of fluorocarbons using a swept-wavelength external cavity quantum cascade laser. Analyst 2014, 139, 2047–2056. [Google Scholar] [CrossRef] [PubMed]
- Phillips, M.C.; Taubman, M.S.; Bernacki, B.E.; Cannon, B.D.; Schiffern, J.T.; Myers, T.L. Design and performance of a sensor system for detection of multiple chemicals using an external cavity quantum cascade laser. Proc. SPIE 2010, 7608. [Google Scholar] [CrossRef]
- Phillips, M.C.; Taubman, M.S.; Kriesel, J. Use of external cavity quantum cascade laser compliance voltage in real-time trace gas sensing of multiple chemicals. Proc. SPIE 2015, 9370. [Google Scholar] [CrossRef]
- Phillips, M.C.; Taubman, M.S. Trace-gas sensing using the compliance voltage of an external cavity quantum cascade laser. Proc. SPIE 2013, 8726. [Google Scholar] [CrossRef]
- Suter, J.D.; Bernacki, B.; Phillips, M.C. Spectral and angular dependence of mid-infrared diffuse scattering from explosives residues for standoff detection using external cavity quantum cascade lasers. Appl. Phys. B 2012, 108, 965–974. [Google Scholar] [CrossRef]
- Phillips, M.C.; Suter, J.D.; Bernacki, B.E. Hyperspectral microscopy using an external cavity quantum cascade laser and its applications for explosives detection. Proc. SPIE 2012, 8268. [Google Scholar] [CrossRef]
- Craig, I.M.; Taubman, M.S.; Lea, A.S.; Phillips, M.C.; Josberger, E.E.; Raschke, M.B. Infrared near-field spectroscopy of trace explosives using an external cavity quantum cascade laser. Opt. Express 2013, 21, 30401–30414. [Google Scholar] [CrossRef] [PubMed]
- Phillips, M.C.; Bernacki, B.E. Hyperspectral microscopy of explosives particles using an external cavity quantum cascade laser. Opt. Eng. 2013, 52, 061302. [Google Scholar] [CrossRef]
- Taubman, M.S. Low-noise high-performance current controllers for quantum cascade lasers. Rev. Sci. Instrum. 2011, 82, 064704. [Google Scholar] [CrossRef] [PubMed]
- Sharpe, S.W.; Johnson, T.J.; Sams, R.L.; Chu, P.M.; Rhoderick, G.C.; Johnson, P.A. Gas-phase databases for quantitative infrared spectroscopy. Appl. Spectrosc. 2004, 58, 1452–1461. [Google Scholar] [CrossRef] [PubMed]
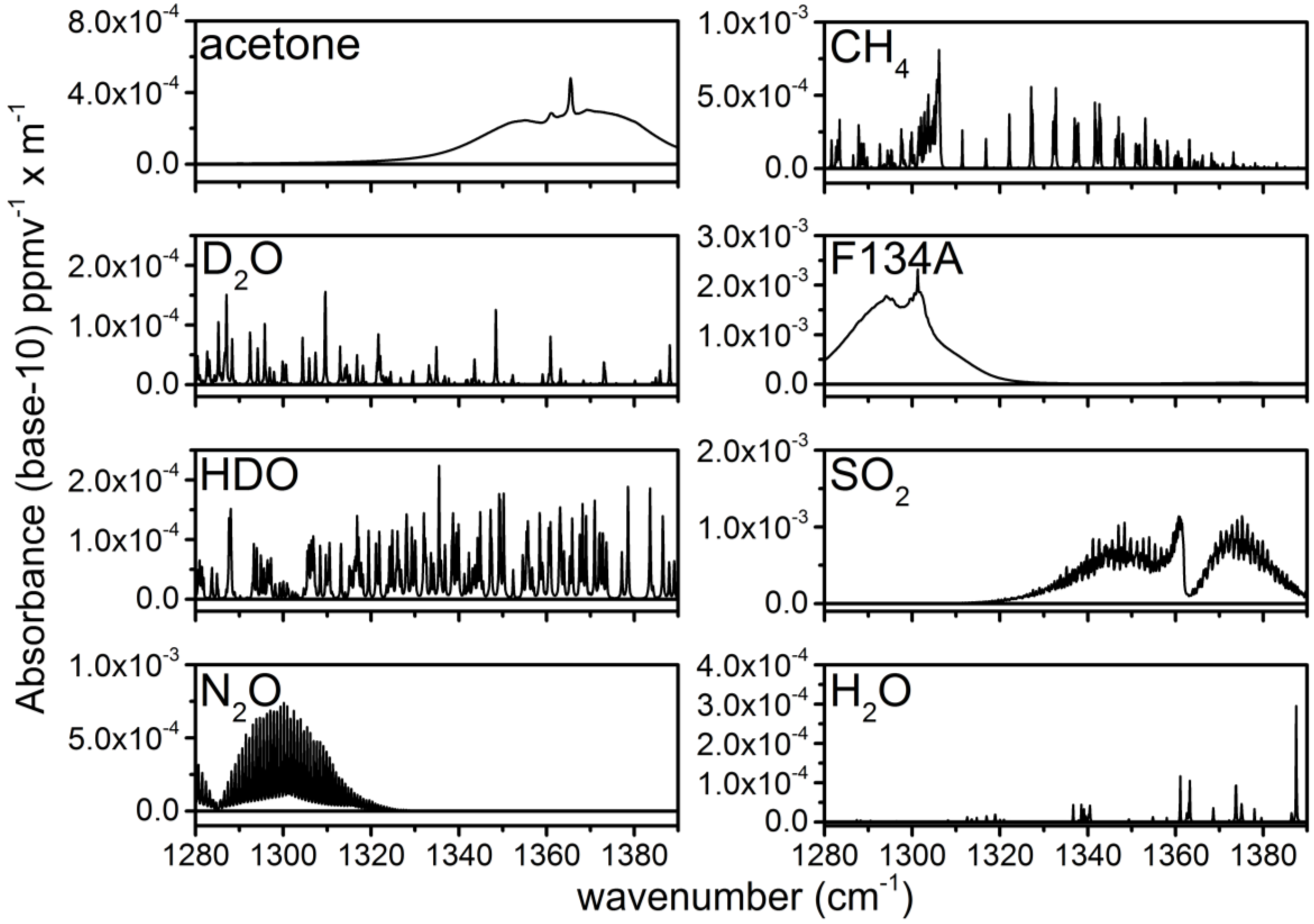
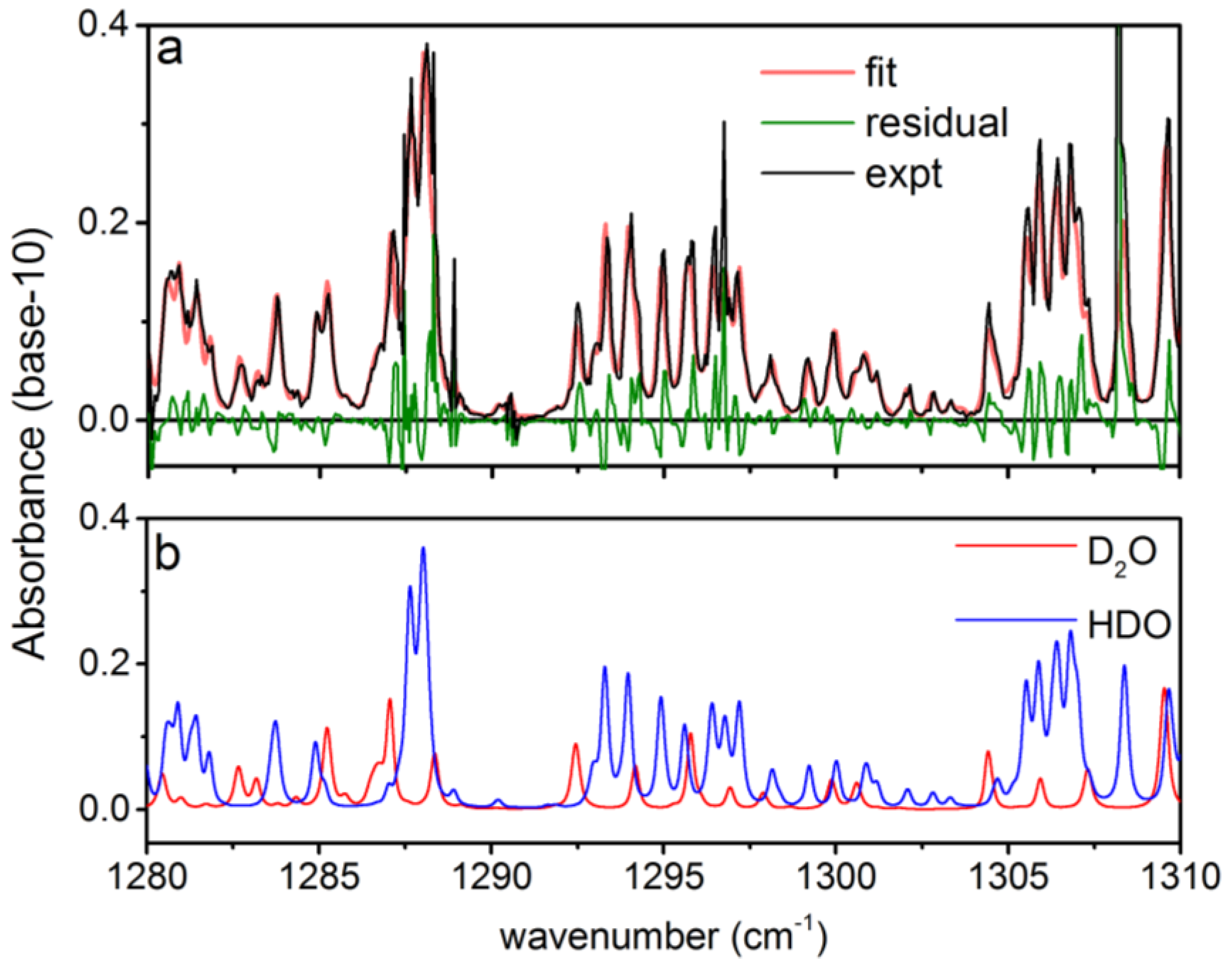
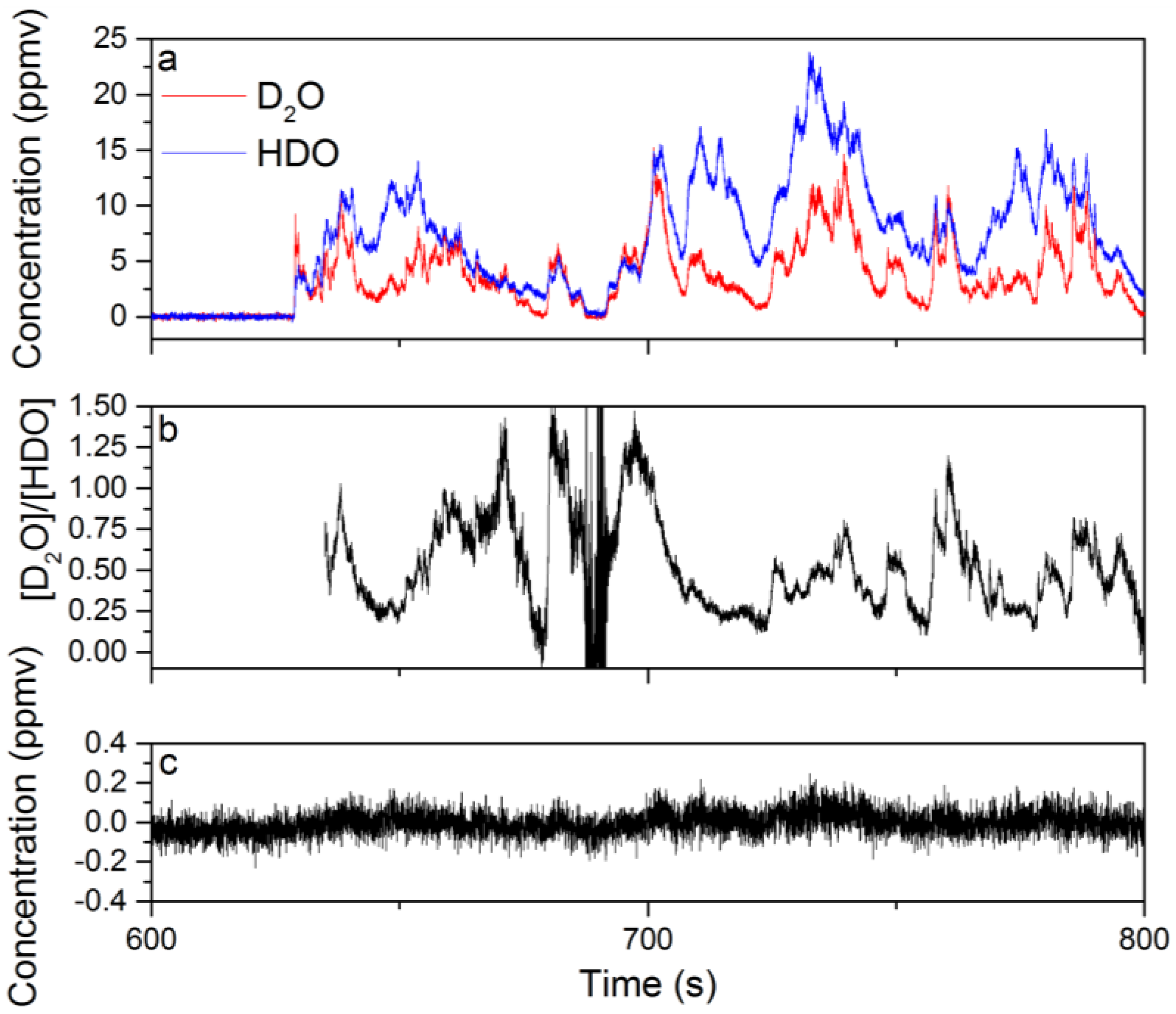
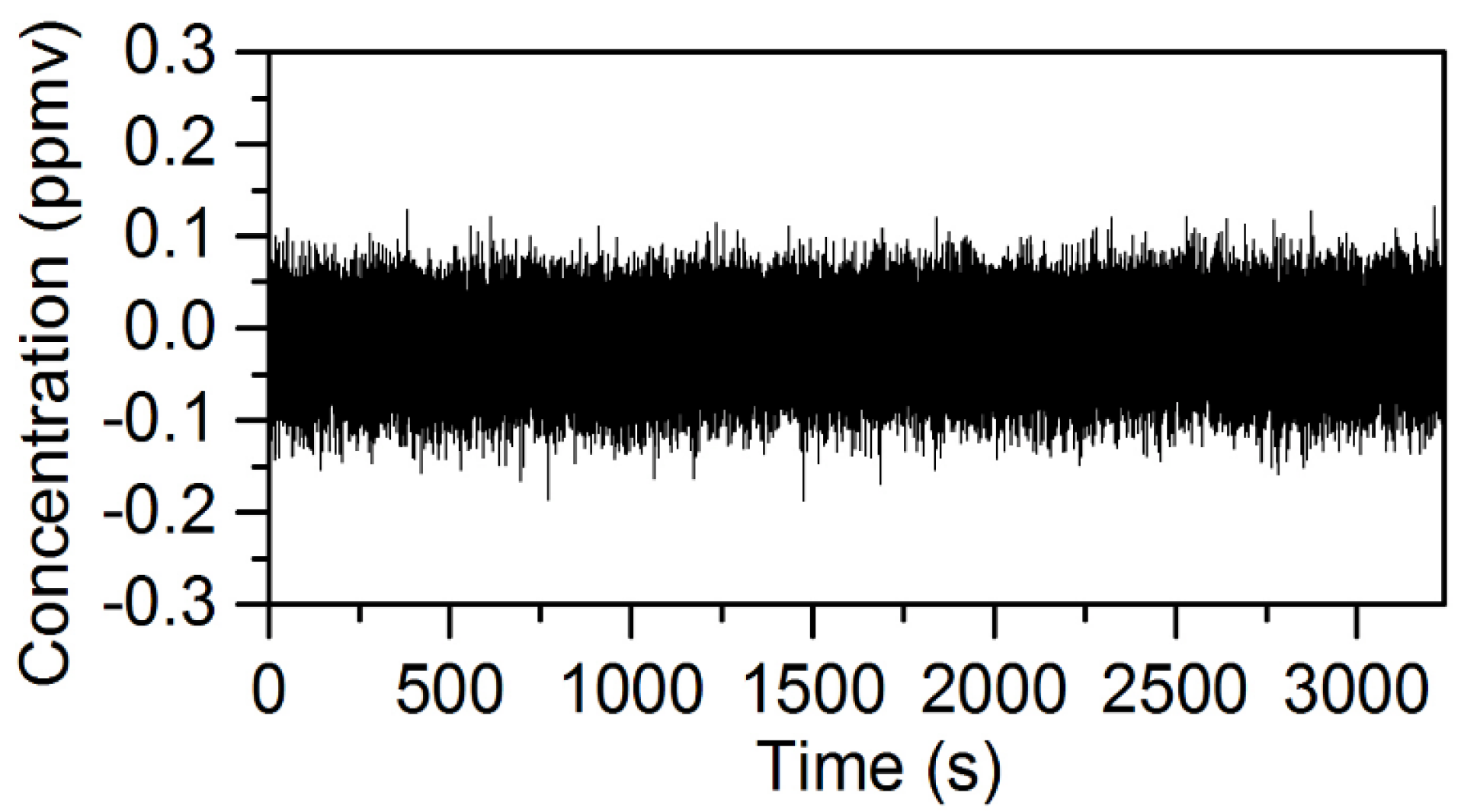
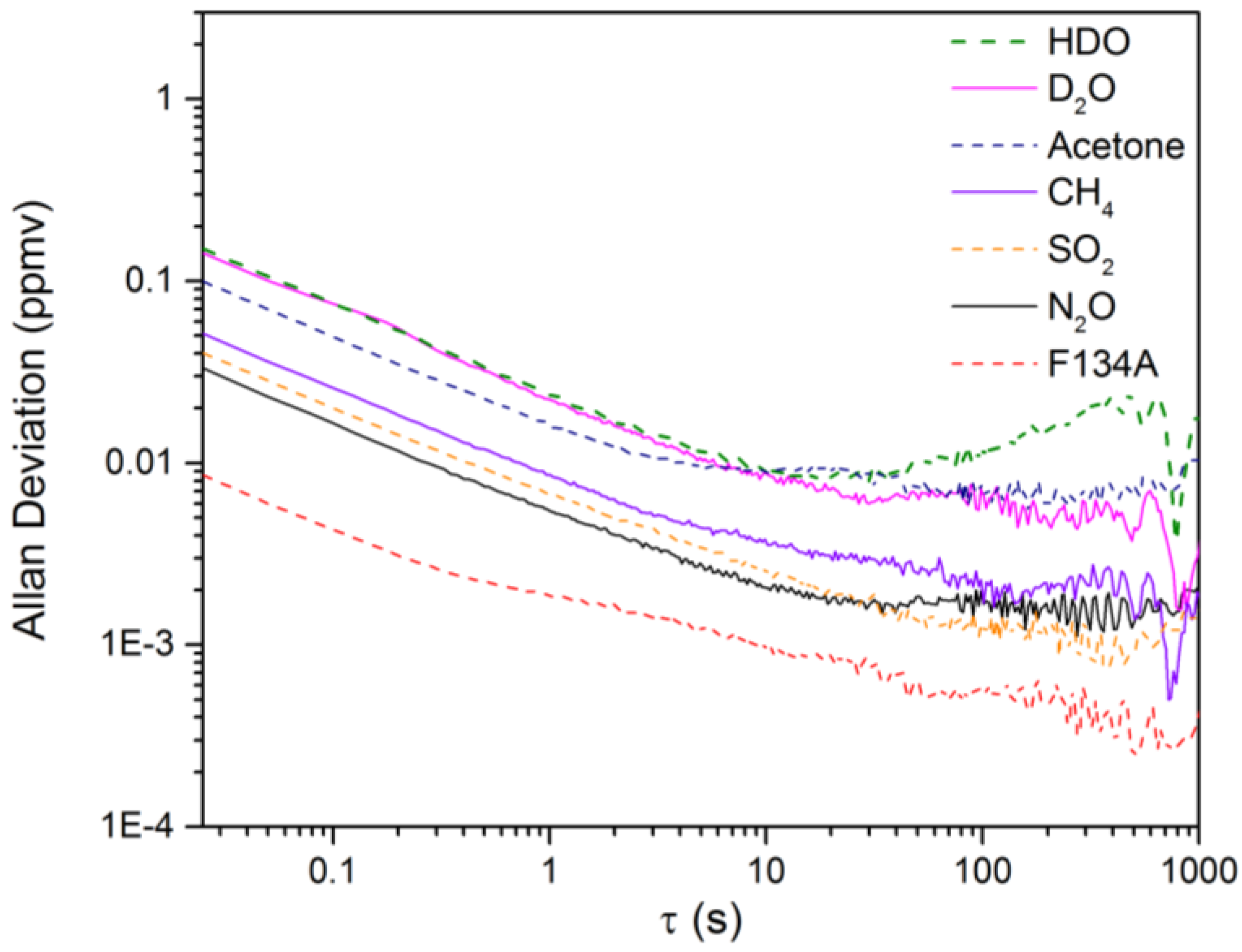
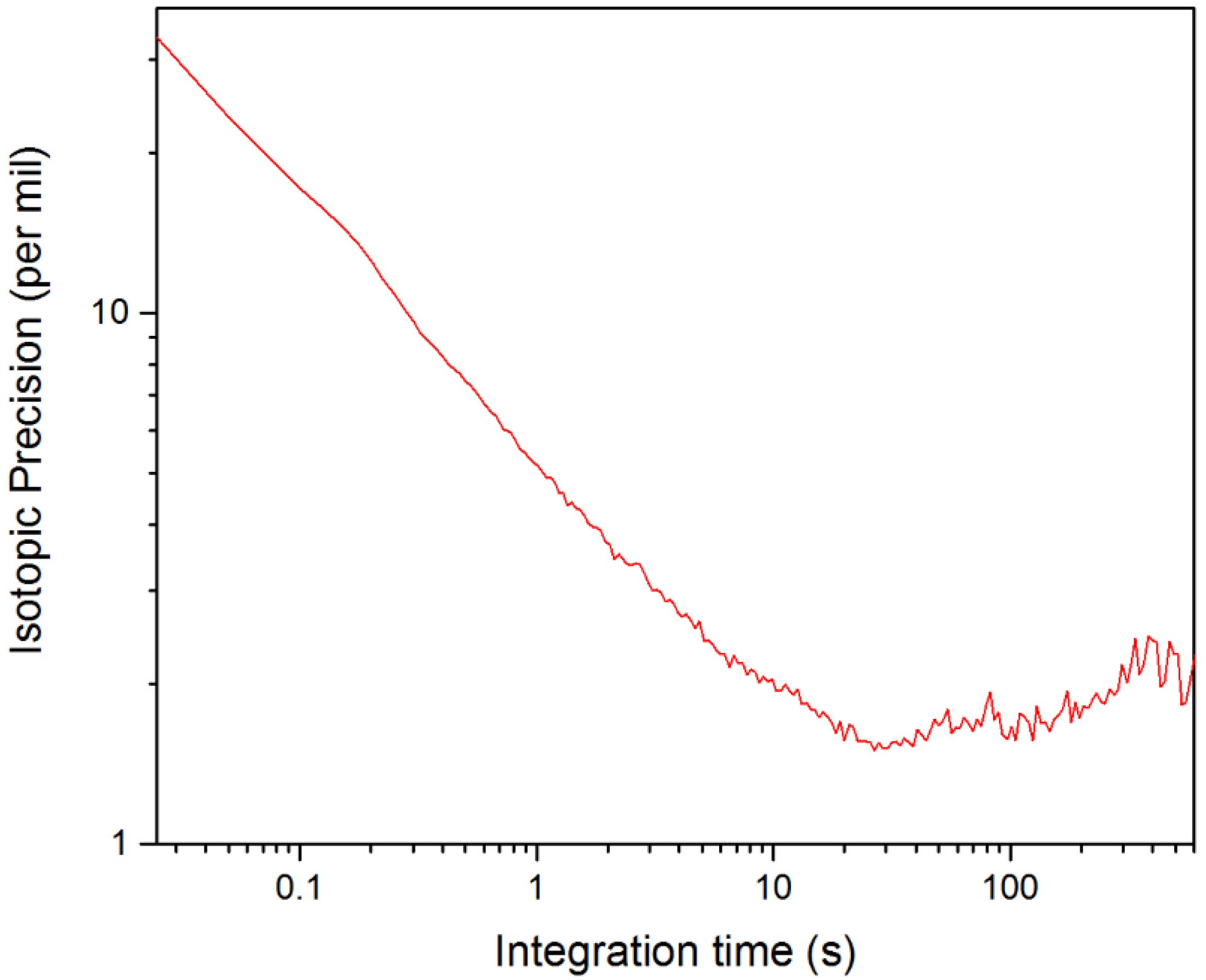
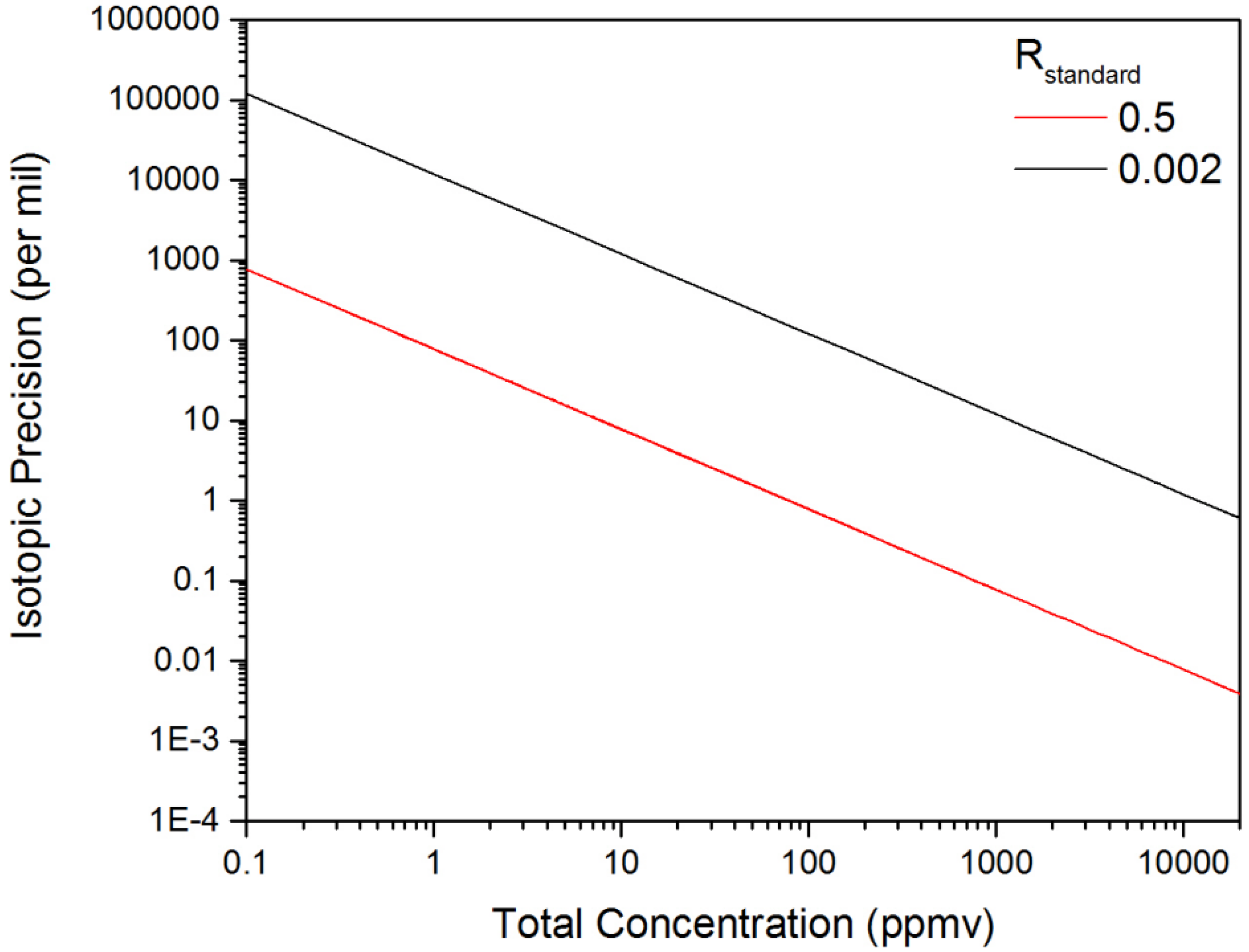
| Chemical | Peak Absorbance (× 10−3) | 25 ms NEC (ppbv) | 25 ms NECD (ppmv × m) | 1 s NEC (ppbv) | 1 s NECD (ppmv × m) |
|---|---|---|---|---|---|
| F134A | 2.3 | 9.1 | 1.16 | 2.1 | 0.27 |
| SO2 | 1.1 | 40.6 | 5.16 | 6.8 | 0.86 |
| CH4 | 0.81 | 51.3 | 6.55 | 8.7 | 1.10 |
| N2O | 0.74 | 34.3 | 4.36 | 5.6 | 0.71 |
| Acetone | 0.48 | 92.1 | 11.70 | 15.6 | 1.98 |
| HDO | 0.22 | 151.6 | 19.25 | 24.0 | 3.05 |
| D2O | 0.18 | 147.0 | 18.67 | 23.0 | 2.92 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brumfield, B.E.; Taubman, M.S.; Phillips, M.C. Rapid and Sensitive Quantification of Isotopic Mixtures Using a Rapidly-Swept External Cavity Quantum Cascade Laser. Photonics 2016, 3, 33. https://doi.org/10.3390/photonics3020033
Brumfield BE, Taubman MS, Phillips MC. Rapid and Sensitive Quantification of Isotopic Mixtures Using a Rapidly-Swept External Cavity Quantum Cascade Laser. Photonics. 2016; 3(2):33. https://doi.org/10.3390/photonics3020033
Chicago/Turabian StyleBrumfield, Brian E., Matthew S. Taubman, and Mark C. Phillips. 2016. "Rapid and Sensitive Quantification of Isotopic Mixtures Using a Rapidly-Swept External Cavity Quantum Cascade Laser" Photonics 3, no. 2: 33. https://doi.org/10.3390/photonics3020033
APA StyleBrumfield, B. E., Taubman, M. S., & Phillips, M. C. (2016). Rapid and Sensitive Quantification of Isotopic Mixtures Using a Rapidly-Swept External Cavity Quantum Cascade Laser. Photonics, 3(2), 33. https://doi.org/10.3390/photonics3020033