Estimation of BER from Error Vector Magnitude for Optical Coherent Systems

Abstract

This paper presents the estimation of bit error ratio (BER) from error vector magnitude (EVM) for M-ary quadrature amplitude modulation (QAM) formats in optical coherent systems employing carrier phase recovery with differential decoding to compensate for laser phase noise. Simulation results show that the relationship to estimate BER from EVM analysis for data-aided reception can also be applied to nondata-aided reception with a correction factor for different combined linewidth symbol duration product at the target BER of 10${}^{-3}$. It is demonstrated that the calibrated BER, which would otherwise be underestimated without the correction factor, can reliably monitor the performance of optical coherent systems near the target BER for quadrature phase shift keying (QPSK), 16-QAM, and 64-QAM.

1. Introduction

Spectrally-efficient modulation formats are currently receiving significant attention for next-generation high-capacity optical communication systems [1,2,3]. With information encoded on both the amplitude and phase of the optical carrier for M-ary quadrature amplitude modulation (QAM), accurate measurement analysis needs to be developed to quantify the novel modulation schemes and to reliably predict the performance of optical coherent systems. A number of performance metrics, such as bit error ratio (BER), eye diagram, Q-factor, and, more recently, error vector magnitude (EVM), can be used in optical communications to assess the quality of the transmitted signals [4,5,6].

While BER is the most conclusive figure of merit compared to the other performance metrics for advanced modulation formats, it requires a known pattern, e.g., a training sequence, to be transmitted for continuous performance monitoring in optical networks. On the other hand, EVM is a well known performance metric in wireless digital communication systems to evaluate the quality of vector-modulated signals [7] and is a more appropriate figure of merit at high signal-to-noise ratio (SNR) where a large number of symbols will otherwise be required for accurate error counting [8]. EVM has also been applied to assess the performance of optical channels corrupted by amplified spontaneous emission (ASE) noise and to characterize optical I-Q transmitters [5,6]. Since EVM is better suited than BER counting for unknown symbol sequences, the relationship between EVM and BER is of significant interest for optical coherent systems. In [5], the authors noted that the established relationship between EVM and BER for data-aided reception [9] can also be applied to nondata-aided reception provided that the BER $<{10}^{-2}$. However, for the estimated BER from EVM analysis to reflect the expected performance achievable with digital coherent receivers, the relationship between EVM and BER needs to be validated following the compensation of optical impairments using algorithms suitable for real-time implementation.

In this paper, the estimation of BER from EVM analysis for quadrature phase shift keying (QPSK), 16-QAM, and 64-QAM with carrier phase recovery and differential decoding to compensate for laser phase noise is presented. Differential decoding is commonly employed with carrier phase recovery algorithms to solve the four-fold ambiguity associated with the recovered phase for square-QAM constellations and also to avoid performance degradation due to cycle slips [10,11]. As such, the BER estimated from EVM in this work is compared to the actual BER expected with differential decoding. The BER derived from EVM analysis for nondata-aided reception is demonstrated to be underestimated following the compensation of laser phase noise for the different modulation formats. A correction factor is thus necessary to reliably estimate the actual BER from EVM and to accurately monitor the performance of optical coherent systems.

2. Error Vector Magnitude

EVM is extensively applied as a performance metric for digital wireless communication systems and is defined as the root-mean-square (rms) value of the difference between a collection of ideal transmitted symbols and the received symbols in the I-Q plane. The rms EVM can be expressed as [5,12]

$$EV{M}_{rms}=\sqrt{\frac{\frac{1}{N}{\sum }_{i=1}^N{|E_{r,i}-E_{t,i}|}^2}{P_a}}$$

(1)

where N is the number of symbols over which the EVM is estimated, $E_r$ is the received signal vector, $E_t$ is the ideal transmitted vector, and $P_a$ is the average transmitted power for the chosen modulation. $E_t$ can either be a known reference pattern for data-aided reception or computed relative to the closest symbol in the constellation for nondata-aided reception. For M-ary square QAM constellations and data-aided reception, where the EVM is caused by ASE noise, the BER can be estimated using [5,9]

$$BER=\frac{(1-M^{-1/2})}{\frac{1}{2}{log}_{2}M}erfc\left[\sqrt{\frac{3/2}{(M-1)EV{M}_{rms}^2}}\right]$$

(2)

3. BER Estimation from EVM with Carrier Phase Recovery and Differential Decoding

The estimation of BER from EVM analysis is discussed in this section for QPSK, 16-QAM, and 64-QAM in the presence of laser phase noise and additive white Gaussian noise (AWGN). The carrier phase recovery was implemented using the feedforward blind phase search algorithm [10] which is applicable to arbitrary M-QAM constellations and suitable for real-time implementation with high linewidth tolerance. The number of test phases was set to 32 for QPSK/16-QAM and 64 for 64-QAM. The filter half width was set to 9 for the different modulation formats and the phase noise was modeled as the Wiener process [10]

$${\theta }_k=\sum _{i=-\infty }^k{\nu }_i$$

(3)

where ${\nu }_i$’s are independent and identically distributed (i.i.d) random Gaussian variables with zero mean and variance

$${\sigma }_p^2=2\pi (\Delta \nu ·T_s)$$

(4)

where $\Delta \nu$ is the combined linewidth of the transmitter and LO lasers and $T_s$ is the symbol period. The simulation was performed over 200,000 symbols.

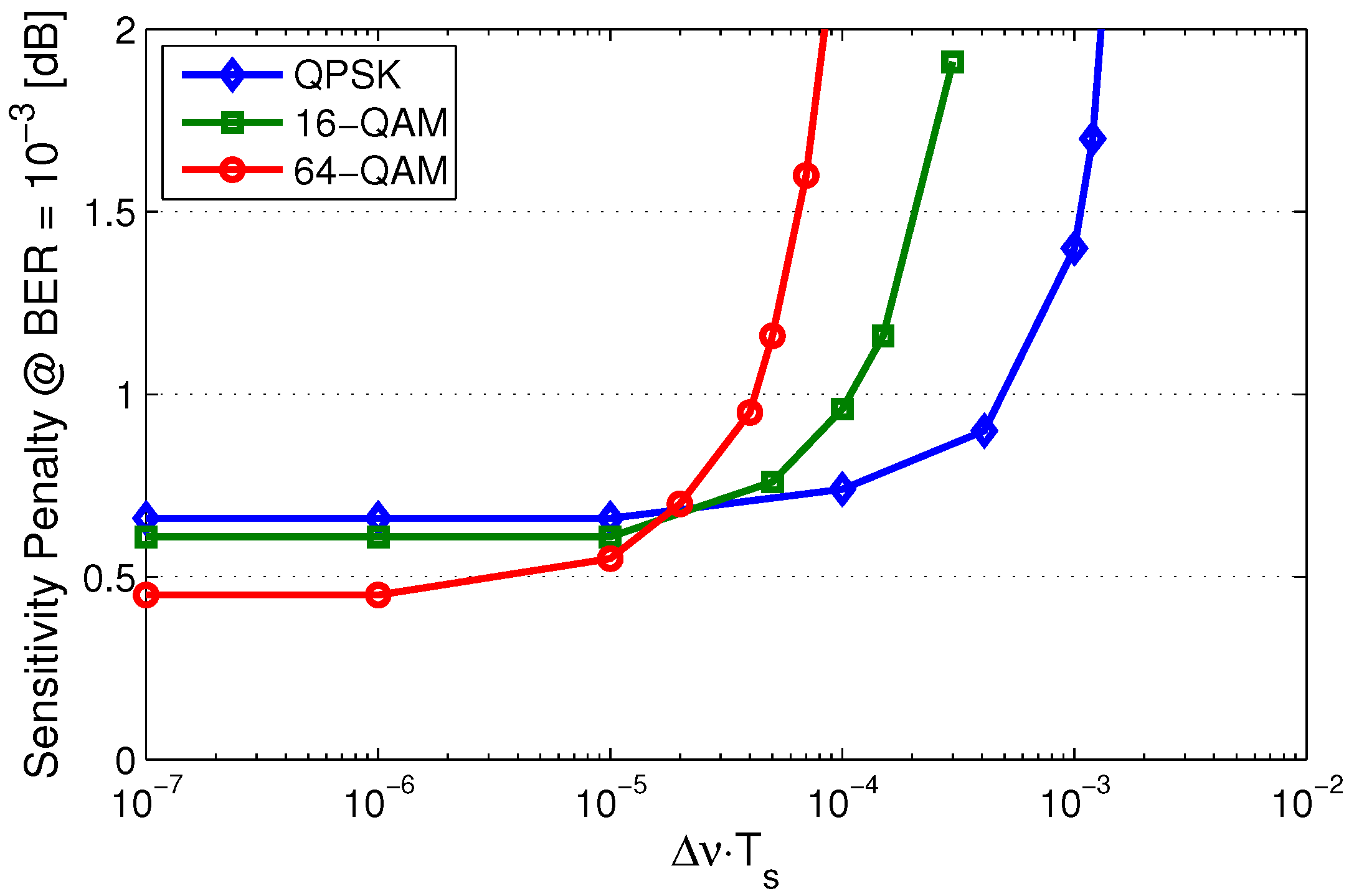
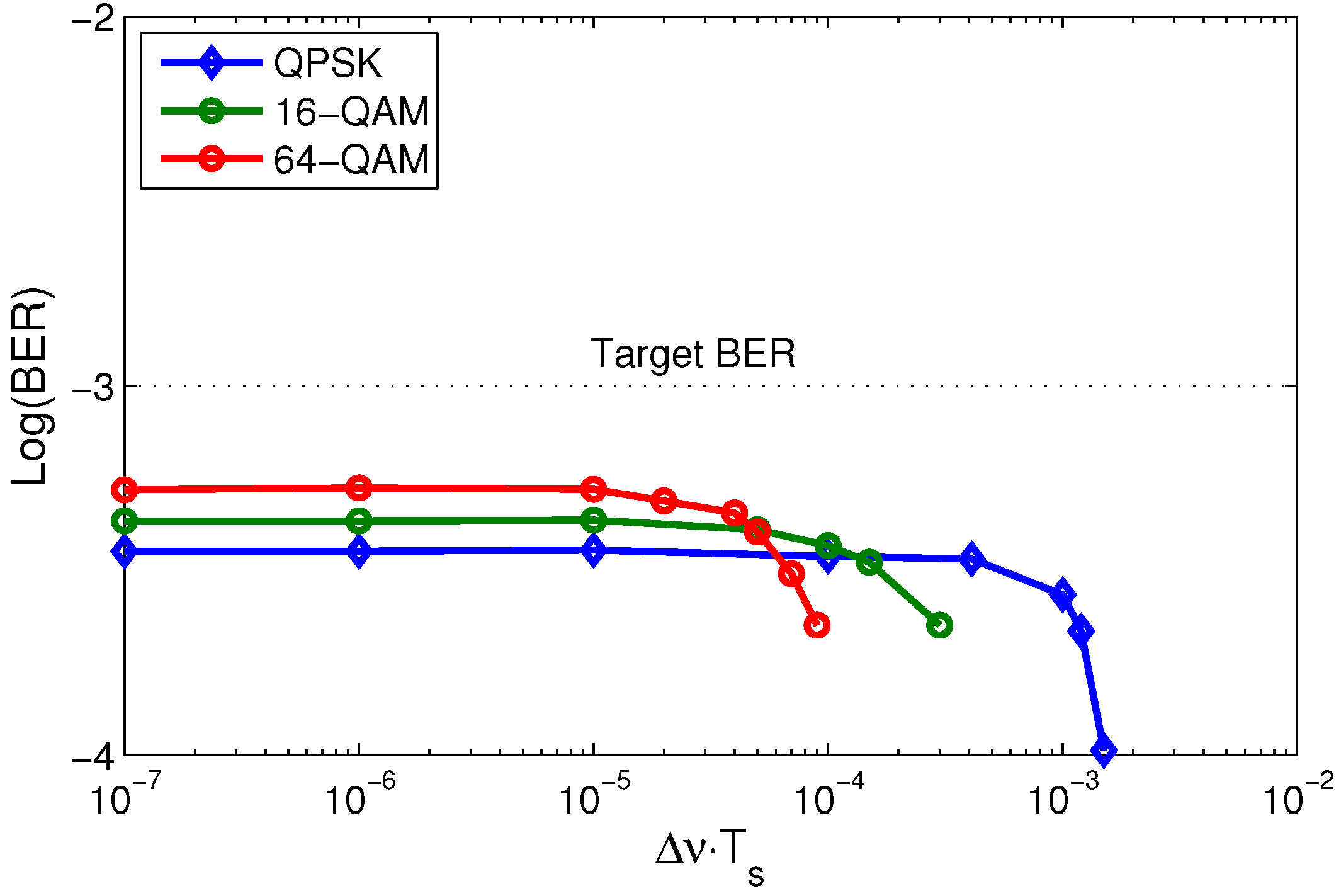
Figure 1 shows the sensitivity penalty at the target BER of 10${}^{-3}$ for the different modulation formats and also includes the coding penalty due to the differential encoding/decoding process. Figure 2 shows the estimated BER from EVM using Equation (2) for nondata-aided reception following the compensation of the laser phase noise. As it can be seen, the target BER of 10${}^{-3}$ is constantly underestimated for the different values of $\Delta \nu ·T_s$. A calibration of the estimated BER is thus necessary to reliably predict the performance of optical coherent systems with EVM analysis.

4. BER Estimation with Correction Factor

The simulation results shown in Figure 2 reveal that the relationship Equation (2) underestimates the actual BER at the target BER of 10${}^{-3}$. The BER estimated from EVM analysis, $BE{R}_{EVM}$, can be calibrated using

$$BE{R}_{cal}=k·BE{R}_{EVM}$$

(5)

where k is a correction factor given as

$$k=\frac{BE{R}_{ideal}}{BE{R}_{EVM}}$$

(6)

at the calibration point and $BE{R}_{ideal}$ is the target BER. The residual sensitivity penalty shown in Figure 1 is due to the differential coding penalty and the implementation penalty of the carrier recovery process. For the square-QAM constellations, the differential coding penalty is given as [13]

$$F=1+\frac{{log}_2\left(M\right)}{2(\sqrt{M}-1)}$$

(7)

Thus, the values of F are 2, 1.67, and 1.43 for QPSK, 16-QAM, and 64-QAM, respectively. For data-aided reception with an ideal carrier phase recovery process, F can be used as the correction factor to take into account the above differential coding penalty. In this work, the correction factor, k, to calibrate the BER estimated from EVM analysis using Equation (5) includes the contributions from the differential coding penalty and also the additional implementation penalty of the carrier phase recovery process.

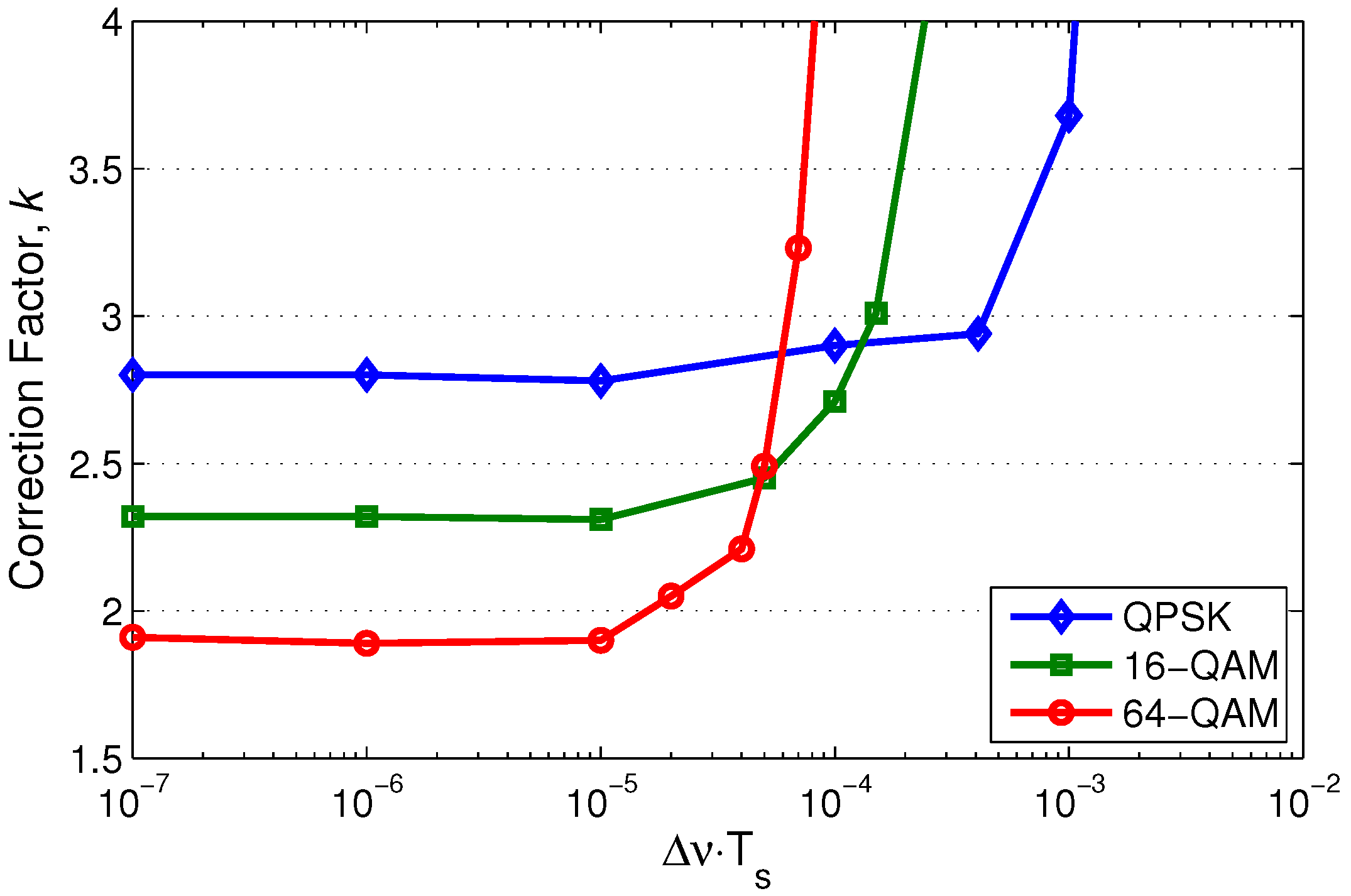
Figure 3 shows the values of k for the different modulation formats at the target BER of 10${}^{-3}$ following the compensation of laser phase noise with differential decoding as discussed in Section 3. The values of k were found to be steady for the respective modulation formats with $\Delta \nu ·T_s<{10}^{-5}$ and higher than the differential coding penalty given by Equation (7) with the carrier phase recovery.

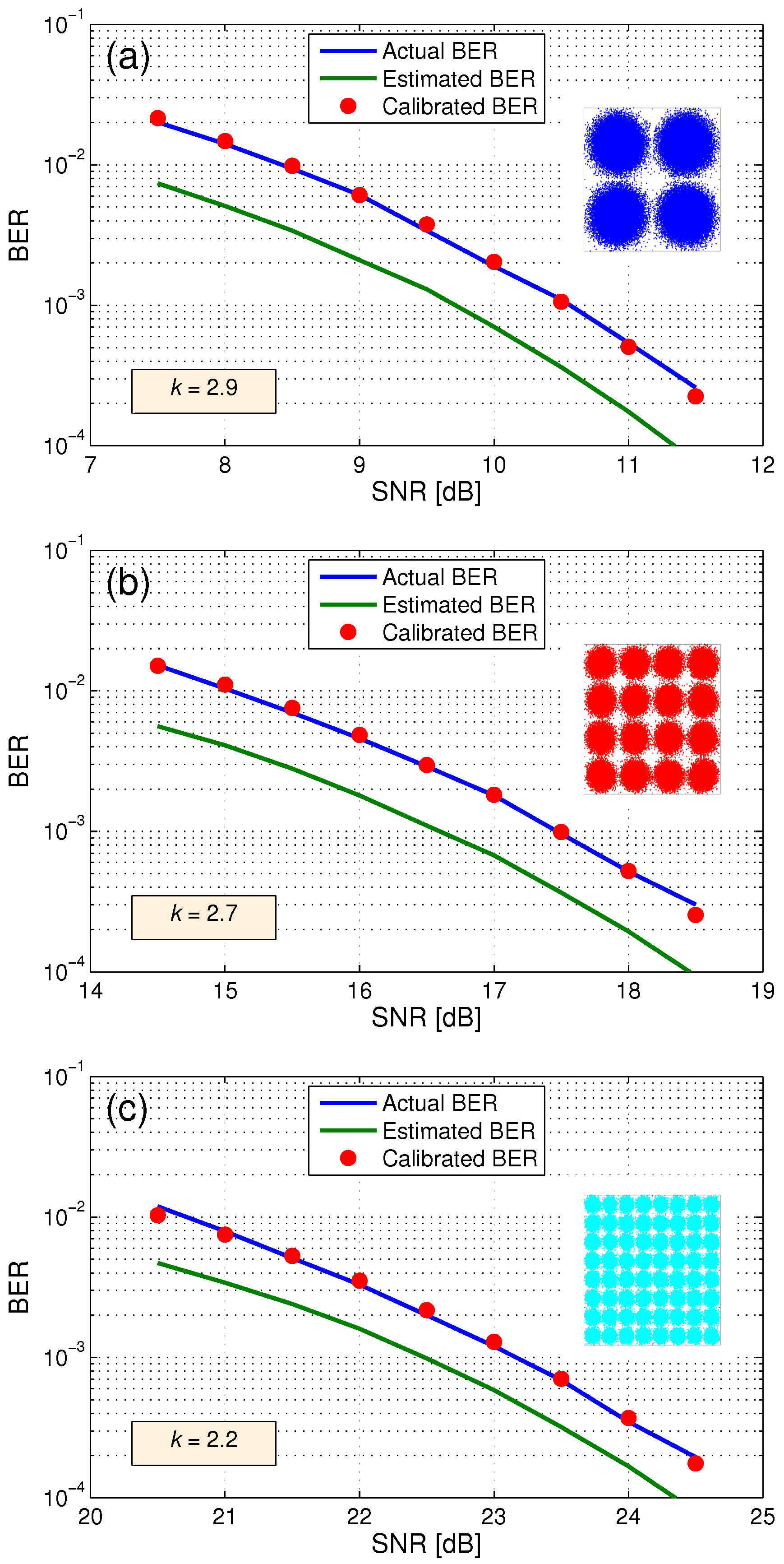
Finally, the accuracy of $BE{R}_{cal}$ to track BER fluctuations up to a BER of ~ 10${}^{-2}$ was investigated for reliable performance monitoring. The values of $\Delta \nu ·T_s$ were set to ${10}^{-4}$ for QPSK/16-QAM and ${10}^{-5}$ for 64-QAM. Figure 4a–c show the BER estimated from EVM analysis for QPSK, 16-QAM, and 64-QAM, respectively, with and without the correction factor. The insets show the recovered constellations at the BER of ${10}^{-3}$. For QPSK as well as 16-QAM, the values of k derived at the target BER of 10${}^{-2}$ and 10${}^{-3}$ were found to be similar with $\Delta \nu ·T_s={10}^{-4}$ for the respective modulation formats. For 64-QAM with $\Delta \nu ·T_s={10}^{-5}$, the mean value of k derived at the target BER of 10${}^{-2}$ and 10${}^{-3}$ was chosen to calibrate the estimated BER for the results shown in Figure 4c. Without the correction factor, the relationship (2) underestimates the BER at the different SNR. However, the calibrated BER using Equation (5) can be seen to be in close agreement with the actual BER obtained by error counting. The calibrated BER from EVM analysis can thus be used to reliably monitor the performance near the target BER for the different modulation formats. Moreover, although the estimated BER from Equation (2) assumes data-aided reception, the simulation results in Figure 4 demonstrate that the relationship can also be applied to nondata-aided reception with the correction factor even when the symbol sequences are unknown and SNR is relatively low near the target BER of 10${}^{-3}$.

5. Conclusions

The estimation of BER from EVM analysis has been investigated for QPSK, 16-QAM, and 64-QAM with carrier phase recovery and differential decoding. The laser phase noise was compensated using the feedforward blind phase search algorithm which is suitable for real-time implementation. It has been demonstrated that the relationship between EVM and BER for data-aided reception can also be applied to nondata-aided reception with a correction factor for different values of $\Delta \nu ·T_s$. The calibrated BER has also been shown to reliably monitor the performance near the target BER for the different modulation formats.